2. 航空工业成都飞机工业(集团)有限责任公司,成都 510100
2. AVIC Chengdu Aircraft Industry (Group) Co., Ltd., Chengdu 510100, China
超重力技术作为一种具有代表性的过程强化技术,在材料、化工、冶金等行业领域得到广泛应用[1-3]。旋转填充床是实现超重力技术的典型设备之一,其通过转子高速旋转产生的离心力来模拟超重力场,具有强化微观混合和传质的功能[4-5],能够提高产品质量,降低能耗,且设备体积较小[6-8]。然而,物料中一些未反应的和反应生成的固体颗粒会不规律地黏附在旋转填充床正在高速旋转的转子填料上,造成转子质量不平衡,并且不平衡质量会随时间不断变化,从而引发转子剧烈振动。而转子作为旋转填充床的核心内构件之一,当其不平衡振动严重时,会频繁挤压摩擦轴承和密封,导致设备损坏和物料泄漏[9-10]。
转子不平衡质量的产生会影响旋转填充床的运行状态参数变化,进而严重影响设备长周期运行和传质效率。控制化学反应工艺参数变化可以延缓黏附和减小振动。因此,对旋转填充床运行过程参数进行预警和调控是保障旋转填充床长周期稳定运行的重要途径[11]。旋转填充床转子结构复杂,流体流动状况及影响转子质量不平衡的很多参数无法直接测量、预警和调控。计算流体动力学(CFD)模拟方法因具有信息处理量大、成本低、易并行化、响应快等优势,逐渐成为分析流体流动特征及传质过程的有效工具[12-13]。Yang等[14]研究了旋转床内速度场与压力场的分布,发现旋转床内压降随转速的增大而增大,揭示了压力场与速度场的分布规律。欧阳毅[15]通过液相的分布、演化等瞬态信息,分析了黏度、转速和流量对于填料区持液量的影响。孙润林等[16]模拟旋转床内的气相流场,分析了气相压力在径向的分布情况。然而目前很少有文献结合化学反应和转子动力学,通过调控转子不平衡质量分布来减缓吸附和减小转子机械振动。
本文基于化学反应和转子动力学的研究成果,利用流体动力学模拟方法,通过正交试验研究多参数变化对目标参数的影响趋势规律,确定构建影响预测模型的关键参数,拟合构建旋转填充床运行过程重要参数的预警调控模型,揭示多参数变化对持液量和气相压降的影响规律。由此提出旋转填充床运行过程重要参数预警调控模型构建方法,将有助于监测预警重要工艺参数,在发现异常时及时采取有效措施调控,降低振动效应和物料泄漏概率。本文工作由北京化工大学高性能计算平台提供计算服务。
1 模型构建方法在旋转填充床运行过程中,填料内液膜厚度、填料持液量、气相压降以及物料停留时间等参数都是衡量旋转填充床性能的重要指标,旋转填充床传质效率的优劣、负荷的大小以及操作的稳定性等在很大程度上都取决于这些参数。然而,受转速、流量及填料孔隙率等多个因素的耦合影响,监测预警单一工艺参数变化并不能实现对这些重要目标参数的调控。因此,本文通过正交试验确定影响旋转填充床运行过程中重要目标参数的相关工艺参数,研究多参数耦合对目标参数的影响效应,建立旋转填充床运行过程中工艺参数与目标参数间的经验数据模型,以实现多种工况下旋转填充床运行重要参数的监测预警和调控。具体方法流程如图 1所示。
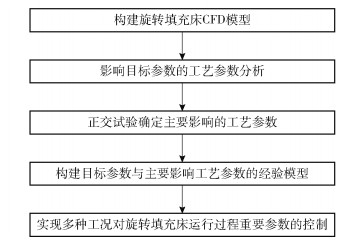
|
图 1 旋转填充床运行过程重要参数预警调控模型构建方法流程 Fig.1 Construction method flow of the early warning control model for the important parameters of the rotating packed bed operation process |
旋转填充床结构如图 2所示。旋转填充床的转子由转鼓及内部填料层构成,其壳体内容纳了转子、液体分布器、迷宫密封、传动轴等,壳体外传动轴与电机相连接,壳体上分布有气液相进出口,转子及转子内部丝网填料在电机驱动下高速旋转。
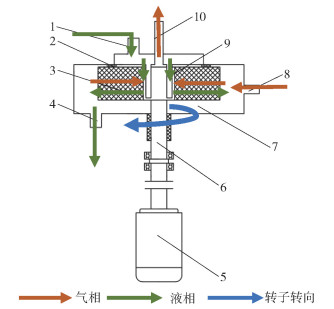
|
1—液相进口;2—气体迷宫密封;3—丝网填料;4—液相出口;5—电机;6—传动轴;7—外壳;8—气相进口;9—液体分布器;10—气相出口。 图 2 旋转填充床结构示意图 Fig.2 Schematic diagram of the rotating packed bed structure |
旋转填充床工作时,填料区和外空腔区所在位置为原料的主要流动区域,这两个区域构成流体域。建立旋转填充床流场空间的物理模型,如图 3所示。模型采用非结构网格划分方式,总网格数量为47万,节点数量为12万。通过网格无关性验证发现,当网格数量从447 935增加到466 731时,旋转填充床填料持液量出现小幅变化,数值变化率为1.7%,即网格数量的变化并不影响仿真计算结果。
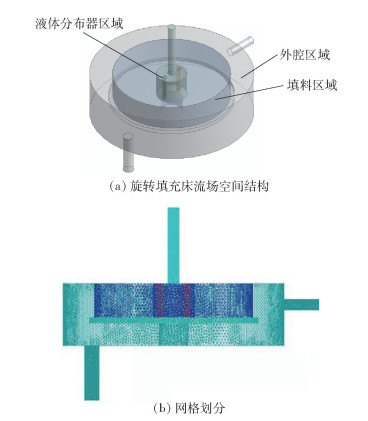
|
图 3 旋转填充床流场空间模型 Fig.3 Spatial model of the flow field in the rotating packed bed |
超重力场条件下合成纳米碳酸钙的过程及工艺研究已较为成熟,为更好地对旋转填充床运行过程中重要参数的预警调控模型进行研究,本文基于不平衡质量的产生原理,选择该过程中流体的流动行为进行分析。浆料在此过程中同时含有液相与固相物质,因此采用Eulerian多相流模型来模拟旋转填充床内气、液、固三相的流动;浆料中的液相与固相物质均是含有多种物质的混合物,因此采用组分运输模型;模拟采用瞬态模拟,监测旋转填充床内从浆料喷入到最后稳定的过程。
相间作用力模型对流动特性结果的影响很大。由于曳力对流型的影响远高于其他相间作用力[17],本文考虑将曳力作为唯一的相间作用力,采用默认的Schiler-Naumann模型计算气液两相间的曳力,并对气液两相间的曳力系数进行适当的修正。气液两相间曳力模型为[16]
| $ f = \frac{{{C_{\rm{D}}}Re}}{{24}} $ | (1) |
式中,Re为雷诺数,CD为两相间曳力系数,其在不同雷诺数下有不同的取值。
| $ {C_{\rm{D}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{24\left( {1 + 0.15R{e^{0.678}}} \right)}}{{Re}}, }&{Re \le 1000}\\ {0.44, }&{Re > 1000} \end{array}} \right. $ | (2) |
连续性方程为[18]
| $ \frac{\partial }{{\partial t}}\left( {{\mathit{\boldsymbol{\alpha }}_q}{\mathit{\boldsymbol{\rho }}_q}} \right) + \nabla {\mathbf{\cdot}} \left( {{\mathit{\boldsymbol{\alpha }}_q}{\mathit{\boldsymbol{\rho }}_q}{\mathit{\boldsymbol{v}}_q}} \right) = {S_{\rm{p}}} $ | (3) |
式中,下标q表示流动中的气相、液相与固相,αq为q相的体积分数矢量,ρq为q相的密度矢量,▽表示对各矢量做偏导,vq为q相的速度矢量,Sp为源项,在本节模拟中此项为0。
动量方程为[16]
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\; \frac{\partial }{{\partial t}}\left( {{\mathit{\boldsymbol{\alpha }}_q}{\mathit{\boldsymbol{\rho }}_q}{\mathit{\boldsymbol{v}}_q}} \right) + \nabla {\mathbf{\cdot}} \left( {{\mathit{\boldsymbol{\alpha }}_q}{\mathit{\boldsymbol{\rho }}_q}{\mathit{\boldsymbol{v}}_q}{\mathit{\boldsymbol{v}}_q}} \right) = - {\mathit{\boldsymbol{\alpha }}_q}\nabla \mathit{\boldsymbol{p}} + \\ \nabla {\mathbf{\cdot}} {{\mathit{\boldsymbol{\bar {\bar \tau} }}}_q} + {\mathit{\boldsymbol{\alpha }}_q}{\mathit{\boldsymbol{\rho }}_q}\mathit{\boldsymbol{g}} + {\mathit{\boldsymbol{F}}_q} \end{array} $ | (4) |
式中,p为所有相共享的压力,τq为第q相的压力应变张量,g为重力矢量,Fq为外部体积力,表示各相之间的相互作用力。
组分质量守恒方程为[19]
| $ \frac{{\partial \left( {\rho {C_S}} \right)}}{{\partial t}} + {\mathop{\rm div}\nolimits} \left( {\rho u{C_S}} \right) = {\mathop{\rm div}\nolimits} \left( {{D_S}{\mathop{\rm grad}\nolimits} \left( {\rho {C_S}} \right)} \right) $ | (5) |
式中,CS为混合相中组分S的体积分数,ρ为混合相中组分S的质量浓度,u为混合相中组分S的速度,DS为混合相中组分S的有效扩散系数。
本文采用Standard k-ε模型模拟流体的流动。湍动能方程为[19]
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial t}}\left( {{\rho _{\rm{m}}}k} \right) + \nabla {\mathbf{\cdot}} \left( {{\rho _{\rm{m}}}{v_{\rm{m}}}k} \right) = \nabla {\mathbf{\cdot}} \left( {\frac{{{\mu _{t, {\rm{m}}}}}}{{{\sigma _k}}}\nabla k} \right) + \\ {G_{k, {\rm{m}}}} - {\rho _{\rm{m}}}\varepsilon \end{array} $ | (6) |
湍流耗散方程为[19]
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\frac{\partial }{{\partial t}}\left( {{\rho _{\rm{m}}}\varepsilon } \right) + \nabla {\mathbf{\cdot}} \left( {{\rho _{\rm{m}}}{v_{\rm{m}}}} \right) = \nabla {\mathbf{\cdot}} \left( {\frac{{{\mu _{t, {\rm{m}}}}}}{{{\sigma _\varepsilon }}}\nabla \varepsilon } \right) + \\ \frac{\varepsilon }{k}\left( {{C_{1\varepsilon }}{G_{k, {\rm{m}}}} - {C_{2\varepsilon }}{\rho _{\rm{m}}}\varepsilon } \right) \end{array} $ | (7) |
式中,ρm为流体密度,k为湍动能,vm为流速,μt, m为湍流黏度,Gk, m为速度梯度产生的湍动能,ε为湍流耗散率,σk、σε、C1ε、C2ε代表模型常数,默认取值为σk=1.0,σε=1.3,C1ε=1.44,C2ε=1.92。
多孔介质是由气体、液体或不均匀混合物填充的、渗透至多个空隙的固体材料。旋转填充床使用不锈钢丝网波纹填料,可近似为多孔结构。本文采用多孔介质模型模拟旋转填充床的填料结构,多孔介质模型为[19]
| $ {S_i} = \left( {\sum\limits_{j = 1} {{D_{ij}}} \mu {v_j} + \sum\limits_{j = 1}^3 {{C_{ij}}} \frac{1}{2}\rho {v_{\rm{m}}}{v_j}} \right) $ | (8) |
式中,Si为动量方程中的源项,Dij为黏性阻力系数,Dij=1.71×105,μ为流体黏度,vj为j向速度分量,Cij为惯性阻力系数,Cij=21.66。
2.3 边界条件与求解过程气相与液相进口均定义为速度进口,需要根据工艺中设定的气液流量来设置进口处速度值。通过式(9)计算气液进口管处的湍流强度I,并根据进口处圆管直径设置水力直径[20]。
| $ I = 0.16R{e^{ - \frac{1}{8}}} $ | (9) |
气相和液相出口设置为压力出口,出口压力为大气压;壳体设置为无滑移的固体壁面;填料边界设置为旋转运动边界,转轴和旋转方向与多孔介质区域的一致。
将压力、密度、动量、湍流动能和湍流耗散率松弛因子分别设置为0.3、1、0.7、0.8和0.8,之后进行流场初始化,设置时间步长为0.001 s,最多模拟20 000步。
3 基于关键参数耦合的调控模型构建 3.1 旋转填充床运行过程中重要参数分析 3.1.1 填料持液量旋转填充床流场稳定状态下的液相分布云图如图 4(a)所示。从图中可以看出,由于重力的作用,液相流体靠近反应器底部。液相流体从喷射源进入外腔的流线图如图 4(b)所示。从图中可以看出,液相从喷射源喷出后由于填料的旋转,流向是弯曲的,同时由于离心力作用,液相流体绕转子周向运动,并在填料内流动,最终从液相出口流出。液相在填料区的流动对旋转填充床转子的运行状态有着重要的影响,由于液相在转子上分布不均匀产生瞬时偏心质量,使得转子高速运转时出现偏心扰动,最终导致转子转动失衡。本文通过填料持液量来表征旋转填充床转子运行状态参数,持液量过大,转子的负载会增大,将会导致旋转填充床的传动装置负荷增大,严重时会影响设备的正常运行;持液量过小,又无法满足实际生产的需求,会影响传质效率和产品质量。
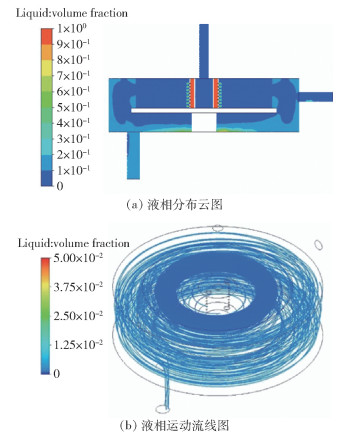
|
图 4 旋转填充床液相流场分布 Fig.4 Liquid flow field distribution in the rotating packed bed |
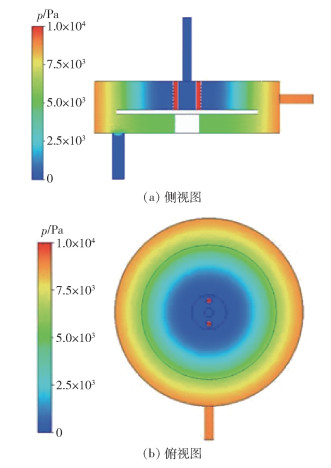
气体压降是衡量旋转填充床性能指标的重要因素,本文对旋转填充床的气相压降性能进行分析。旋转填充床气相压力分布云图如图 5所示。从图中可以看出,气相流体从切向进入反应器内部后,沿着设备径向从气相进口到气相出口的压力值逐渐减小,压力分布均呈中心对称分布,且反应器外腔区域和填料区域内产生了明显的气相压降。
|
图 5 旋转填充床气相压力分布云图 Fig.5 Contours of gas phase pressure distribution in the rotating packed bed |
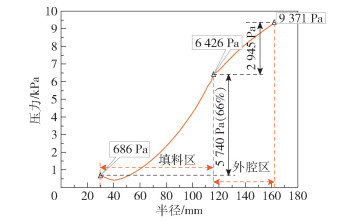
进一步对不同区域位置处的压降进行研究,并对气相压力值沿旋转填充床径向的分布曲线进行分析,结果如图 6所示。由图中曲线可以看出,从反应器填料区到外空腔区,填料区内侧压力最小,外空腔区外侧压力最大,压力值随反应器径向厚度的增大而升高。填料区域内,旋转填充床压力值从686 Pa增大到6 426 Pa,压降为5 740 Pa;外空腔区域内,旋转填充床压力值从6 426 Pa增大到9 371 Pa,压降为2 945 Pa。由此得出,旋转填充床的整床压降为8 685 Pa,填料区压降占整床压降的66%。旋转填充床的压降主要是由离心压降和摩擦压降引起的,离心压降由转子填料旋转产生,摩擦压降由气体在填料中流动时受到的阻力而产生。在离心压降和摩擦压降的共同作用下,填料区压降对整床压降的影响明显。本文通过气相压降来表征旋转填充床转子的运行状态参数。
|
图 6 气相压力值沿旋转填充床径向分布 Fig.6 The gas pressure value distributed radially along the rotating packed bed |
影响旋转填充床填料持液量和气相压降的因素较多,为了进一步分析各因素影响的重要性,需要确定各变量的参数取值范围。在旋转填充床实际工况的基础上,选择转速、液体流量、气体流量、孔隙率以及固含率这5个因素进行分析,分别根据实际的工况条件选择4个变量波动值,通过正交试验的方法对模拟数据进行分析。
以转速、液体流量、气体流量、孔隙率和固含率作为正交试验的5个因素,每个因素取4个水平,因素水平表见表 1。由于该试验为五因素四水平试验,选择L16(45)作为试验方案,并根据该方案利用CFD模拟计算,判断因素的主次顺序。
| 下载CSV 表 1 因素水平表 Table 1 Factor level table |
按照五因素四水平正交试验建立因素水平表,共计16组试验,如表 2所示。提取填料持液量计算结果如表 3所示。
| 下载CSV 表 2 五因素四水平正交试验方案 Table 2 Five-factor four-level orthogonal test scheme |
| 下载CSV 表 3 旋转填充床填料持液量正交试验计算结果 Table 3 Calculation results of orthogonal tests of the liquid holding capacity of the rotating packed bed |
使用极差分析法对填料持液量正交试验计算结果进行分析。首先得出所有因素下每一水平对应的试验指标值,记各因素m水平的试验指标之和为Km,将Km除以各因素下m水平的试验组数得到km,若找出各因素下数值最大的k值,则该因素在此水平下对所监测的状态参数影响最显著。将每个因素下数值最大的km减去数值最小的km即可得到极差R,极差R值的具体计算公式如式(10)所示。
| $ R = \max \left( {{k_1}, {k_2}, \cdots , {k_m}} \right) - \min \left( {{k_1}, {k_2}, \cdots , {k_m}} \right) $ | (10) |
依据极差R值可对各因素的影响作用进行判断,R值越大,意味着该因素对试验指标的影响作用越明显。填料持液量正交试验分析结果如表 4所示。
| 下载CSV 表 4 填料持液量正交试验分析结果 Table 4 Orthogonal test analysis results of packing liquid holdup |
将R值进行排序,能够得到各因素影响转子填料持液量的主次顺序,从而确定出主要影响因素。在众多影响转子填料持液量的因素中,根据正交试验分析结果,得出因素影响的主次顺序为:液量(液体流量)>固含率>转速>孔隙率>气量(气体流量)。由极差计算结果发现,液量的极差值最大,固含率的极差值次之,其次是转速的极差值,以上三者的极差值较孔隙率和气量的差距较大,意味着在当前分析的试验条件下,液量、固含率以及转速对于填料持液量的影响比其他因素显著。
3.2.2 影响气相压降的主要因素关于压降的正交试验方案与3.2.1节对于填料持液量的分析一致,本节不再赘述。建立压降正交试验方案并提取计算结果,如表 5所示。
| 下载CSV 表 5 旋转填充床气相压降正交试验计算结果 Table 5 Calculation results of orthogonal tests of the gas phase pressure drop in the rotating packed bed |
使用极差分析法对压降正交试验计算结果进行分析,结果如表 6所示。依据极差R值,可对各因素的影响作用进行判断。
| 下载CSV 表 6 气相压降正交试验分析结果 Table 6 Orthogonal test analysis results of the gas-phase pressure drop |
根据上述转子旋转填充床气相压降的正交试验分析结果,可得出因素影响的主次顺序为:转速>液量>固含率>气量>孔隙率。根据极差计算结果发现,转速的极差值最大,液量的极差值次之,其次是固含率的极差值,以上三者的极差值较孔隙率和气量的差距较大,意味着在当前分析的试验条件下,转速、液量以及固含率对于气相压降的影响比其他因素显著。
3.3 旋转填充床运行过程重要参数与各工况耦合的经验模型 3.3.1 填料持液量与各工况间的经验模型为了提高各状态参数的准确性,选取影响作用最大的3个因素作为主要影响因素。基于前文对旋转填充床填料持液量影响因素的分析,可以确定转速、液体流量及固含率这3个工艺参数对填料持液量的影响最为显著。因此利用试验数据进行回归拟合得到经验公式,根据该公式并通过各工艺参数推算得到填料持液量,可以较准确地掌握持液量与各工艺参数间的耦合关系。以转速、液体流量和固含率为多因素变量进行模拟,得到旋转填充床填料持液量实验数据,借助Matlab软件对所得实验数据进行拟合,得到转速、液体流量及固含率与持液量之间的经验公式。
设填料持液量为y,转速为x1,液体流量为x2,固含率为x3,经过回归拟合推导出工艺参数与持液量的关系如下。
| $ y = {a_1}/{x_3} + {a_2}x_1^{{a_3}} + {a_4}\lg {x_1}\lg {x_2} + {a_5} + {a_6}{x_1} $ | (11) |
式中,a1=-0.017 3;a2=4.608 5×1019;a3=-317.482 5;a4=-0.008 5;a5=0.401 8;a6=2.326 8×10-5。
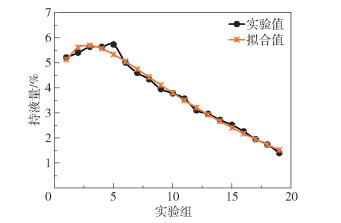
计算拟合得到的经验公式的拟合系数R2为0.991 3,意味着拟合程度良好,误差较小。将实验值与拟合值进行对比,如图 7所示,可看出拟合值与实验值吻合较好,因此认为该拟合公式在一定范围内计算结果是可信的。
|
图 7 旋转填充床填料持液量实验值与拟合值对比 Fig.7 Comparison of experimental values and fitting values of the packing liquid holding capacity of the rotating packed bed |
根据模拟仿真建立的工艺参数与持液量之间的耦合关系式,结合实际的生产需求,可通过修正相应的工艺参数对反应器的持液量进行调整,在维持反应器稳定运行的同时,提高设备的传质效率或产品质量。
3.3.2 气相压降与各工况间的经验模型基于前文对旋转填充床气相压降影响因素的分析,可确定转速、液体流量及固含率这3个工艺参数对压降的影响最为显著。因此利用试验数据进行回归拟合得到经验公式,根据该公式并通过各工艺参数推算得到气相压降,可以较准确掌握气相压降与各工艺参数间的耦合关系。
设压降为z,转速为x1,液体流量为x2,固含率为x3,经过回归拟合推导出工艺参数与压降的关系如下。
| $ z = {a_1} + {a_2}{x_1}{x_2} + {a_3}\sin {a_4}{x_3} - {a_5}{x_2} $ | (12) |
式中,a1=-4.939 2×103;a2=0.021 5;a3=1.951 6×103;a4=4.923 5×105;a5=-22.786 9。
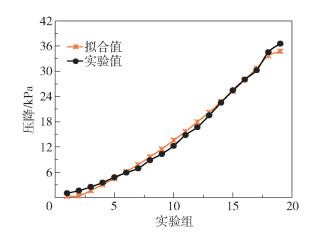
计算拟合得到的经验公式的拟合系数R2为0.992 8。旋转填充床压降实验值与拟合值对比如图 8所示,可以看出实验值与拟合值拟合程度良好,误差较小。
|
图 8 旋转填充床气相压降实验值与拟合值对比 Fig.8 Comparison of experimental values and fitting values of the gas phase pressure drop in the rotating packed bed |
根据模拟仿真建立的工艺参数与压降之间的耦合关系式,可通过对转速、流量以及固含率的控制来调整反应器内压力,从而保证反应器的连续操作以及长周期稳定运行。
以上通过多因素变量模拟得到旋转填充床相关试验数据,经数据拟合后得到经验模型,虽然旋转填充床数据的实验值与该经验模型的拟合值吻合较好,但可能存在拟合过度的风险。若需要预测得更加精确,可以综合3个以上的参数来构建耦合模型,但也可能会带来过拟合的问题。
4 结论(1) 本文构建了旋转填充床运行过程填料持液量和气相压降两个重要参数的预警调控模型,通过正交试验计算多参数对持液量和气相压降的影响效应程度,确定了影响持液量和气相压降的关键参数为转速、液体流量以及固含率。
(2) 选取转速、液体流量和固含率3个工艺参数拟合建立了基于关键参数耦合的持液量和气相压降预警调控模型,实验值与拟合值的吻合度较好,可认为所建立模型正确可信。基于该预警调控模型,结合实际生产需求,通过调整工艺参数可以提高设备的传质效率和产品质量,保证反应器的连续操作和长周期稳定运行。
后续将搭建旋转填充床实验台进行实验,结合CFD模拟结果和实验数据验证基于关键参数耦合的持液量和气相压降预警调控模型,并在保证模型可靠性的基础上进行工艺参数的调整和分析。预警数值需要结合实际工程设计要求、反应条件工况和预警调控模型去设定,当工艺参数、反应过程和反应条件不同时,持液量和压降的具体预警数值也不同,后续将通过实验等方式确定与优化数值,此外也将参照超重力场条件下合成纳米碳酸钙的过程,更换新的物质开展研究。
| [1] |
李沃源, 毋伟, 邹海魁, 等. 超重力旋转填充床用于高黏聚合物脱挥的研究进展[J]. 化工进展, 2010, 29(2): 211-216, 232. LI W Y, WU W, ZOU H K, et al. Devolatilization of high viscous polymer via high gravity rotating packed bed[J]. Chemical Industry and Engineering Progress, 2010, 29(2): 211-216, 232. (in Chinese) |
| [2] |
郭正东, 苏梦军, 刘含笑, 等. 旋转填充床基础研究及工业应用进展[J]. 化工进展, 2018, 37(4): 1335-1346. GUO Z D, SU M J, LIU H X, et al. States-of-the-arts progress on fundamental research and industrial applications of rotating packed bed[J]. Chemical Industry and Engineering Progress, 2018, 37(4): 1335-1346. (in Chinese) |
| [3] |
刘晨民, 刘曦曦, 陈小鹏, 等. 超重力反应结晶碳化法制备球形碳酸钙[J]. 化工进展, 2021, 40(11): 6323-6331. LIU C M, LIU X X, CHEN X P, et al. Preparation of spherical calcium carbonate by high-gravity reaction crystallization carbonization[J]. Chemical Industry and Engineering Progress, 2021, 40(11): 6323-6331. (in Chinese) |
| [4] |
曾东, 李振虎. 超重力技术的应用研究[J]. 石油化工, 2018, 47(7): 763-768. ZENG D, LI Z H. Application progress of high gravity technology[J]. Petrochemical Technology, 2018, 47(7): 763-768. (in Chinese) DOI:10.3969/j.issn.1000-8144.2018.07.019 |
| [5] |
ZHANG L L, WU S Y, LIANG Z Z, et al. Hydrogen sulfide removal by catalytic oxidative absorption method using rotating packed bed reactor[J]. Chinese Journal of Chemical Engineering, 2017, 25(2): 175-179. DOI:10.1016/j.cjche.2016.08.032 |
| [6] |
邹海魁, 初广文, 向阳, 等. 超重力反应强化技术最新进展[J]. 化工学报, 2015, 66(8): 2805-2809. ZOU H K, CHU G W, XIANG Y, et al. New progress of HIGEE reaction technology[J]. CIESC Journal, 2015, 66(8): 2805-2809. (in Chinese) |
| [7] |
邹海魁, 邵磊, 陈建峰. 超重力技术进展-从实验室到工业化[J]. 化工学报, 2006, 57(8): 1810-1816. ZOU H K, SHAO L, CHEN J F. Progress of HIGEE technology-from laboratory to commercialization[J]. Journal of Chemical Industry and Engineering(China), 2006, 57(8): 1810-1816. (in Chinese) DOI:10.3321/j.issn:0438-1157.2006.08.013 |
| [8] |
王峰, 孙思, 郭锴. 旋转填充床一次碳化法制备轻质碳酸镁[J]. 无机盐工业, 2006, 38(2): 31-33. WANG F, SUN S, GUO K. The production of light magnesium carbonate by one-time carbonation with rotating packed bed[J]. Inorganic Chemicals Industry, 2006, 38(2): 31-33. (in Chinese) DOI:10.3969/j.issn.1006-4990.2006.02.011 |
| [9] |
关妍. 基于超声清洗的双电磁离合式旋转填充床设计与预警研究[D]. 北京: 北京化工大学, 2019. GUAN Y. Design and early warning methods of RPB based on double electromagnetic clutch and ultrasonic cleaning[D]. Beijing: Beijing University of Chemical Technology, 2019. (in Chinese) |
| [10] |
张正辉. 旋转填充床结构设计及不平衡控制策略[D]. 北京: 北京化工大学, 2021. ZHANG Z H. Structural design of rotating packed bed and unbalance control strategy[D]. Beijing: Beijing University of Chemical Technology, 2021. (in Chinese) |
| [11] |
ZHANG Z H, GUAN Y, ZHAO Q, et al. Early warning on mass imbalance and clean-in-place strategy for rotor of rotating packed bed[J]. IEEE Access, 2020, 8: 44503-44510. DOI:10.1109/ACCESS.2020.2976518 |
| [12] |
谭丽媛, 袁希钢, KALBASSI M A. 规整填料结构对液相分布影响的计算流体力学[J]. 化工进展, 2015, 34(11): 3869-3878. TAN L Y, YUAN X G, KALBASSI M A. Effect of structured packing's structure on liquid distribution by computational fluid dynamics[J]. Chemical Industry and Engineering Progress, 2015, 34(11): 3869-3878. (in Chinese) |
| [13] |
叶非华, 廖虎, 易国斌. 基于多孔介质模型的膜式氧合器内部流场分析[J]. 化工进展, 2020, 39(3): 898-905. YE F H, LIAO H, YI G B. Internal flow field analysis of membrane oxygenator based on porous media model[J]. Chemical Industry and Engineering Progress, 2020, 39(3): 898-905. (in Chinese) |
| [14] |
YANG Y C, XIANG Y, LI Y G, et al. 3D CFD modelling and optimization of single-phase flow in rotating packed beds[J]. The Canadian Journal of Chemical Engineering, 2015, 93: 1138-1148. |
| [15] |
欧阳毅. 旋转填充床内黏性流体混合反应过程的CFD模拟与实验研究[D]. 北京: 北京化工大学, 2019. OUYANG Y. Study on micromixing process of vicous liquids in rotating packed bed by CFD simulation and experiment[D]. Beijing: Beijing University of Chemical Technology, 2019. (in Chinese) |
| [16] |
孙润林, 向阳, 初广文, 等. 旋转填充床气相流场模拟与验证[J]. 北京化工大学学报(自然科学版), 2012, 39(4): 6-11. SUN R L, XIANG Y, CHU G W, et al. Computational fluid dynamics (CFD) simulation and validation of the gas flow field in a rotating packed bed[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2012, 39(4): 6-11. (in Chinese) |
| [17] |
李蔚玲, 钟文琪, 金保昇, 等. 气液固三相浆态床流型转变特性的试验研究[J]. 工程热物理学报, 2014, 35(1): 100-103. LI W L, ZHONG W Q, JIN B S, et al. Experimental analysis of flow characteristics in a gas-liquid-solid three-phase bubble column[J]. Journal of Engineering Thermophysics, 2014, 35(1): 100-103. (in Chinese) |
| [18] |
李昭, 王文瑞, 张佳明. 新型钾盐结晶器内部流场模拟及性能预测[J]. 北京化工大学学报(自然科学版), 2018, 45(3): 27-34. LI Z, WANG W R, ZHANG J M. Simulation of the flow field and performance prediction for a new crystallizer[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2018, 45(3): 27-34. (in Chinese) |
| [19] |
刘玉杰. 旋转填充床内流体流动与传质的三维CFD模拟[D]. 北京: 北京化工大学, 2017. LIU Y J. Three dimensional CFD modeling of gas-liquid flow and mass transfer in rotating packed beds[D]. Beijing: Beijing University of Chemical Technology, 2017. (in Chinese) |
| [20] |
王辰宇, 刘玉杰, 高雪颖, 等. 应用CFD方法分析球填料旋转床内气相流动特征[J]. 高校化学工程学报, 2018, 32(5): 1004-1011. WANG C Y, LIU Y J, GAO X Y, et al. CFD analysis of gas flow in a rotating ball-packed bed[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(5): 1004-1011. (in Chinese) |








