引言

神经系统主导着生物体生理活动的调节，其功能主要通过神经元产生、处理和传递电信号来实现^[1-2]。1952年，基于乌贼巨型轴突上电位变化的实验数据，Hodgkin等^[3]建立了一个四维非线性连续数学模型—Hodgkin-Huxley模型(HH模型)，开启了对神经元电活动的数学研究。随后，FitzHugh^[4]在保留系统主要动态的基础上，将HH模型简化为二维系统；之后Nagumo等^[5]通过电路实验成功实现了该模型的动态，因此该模型也被称为FitzHugh-Nagumo模型(FHN模型)。由于系统的复杂性，针对FHN模型的动态研究一直备受关注。Hayashi^[6]给出了FHN模型非平凡闭轨唯一性的充分条件。Rocşoreanu等^[7]证明了FHN模型中saddle-node分支、Hopf分支以及Bogdanov-Takens分支的存在性。Jing等^[8]对FHN模型应用Euler方法得到离散FHN系统，证明了该系统存在周期10轨、倍周期级联以及混沌等复杂动态。之后，Zhan等^[9]推广了一类离散FHN模型，通过数值模拟分析了系统产生混沌的内外机制，以及延滞反馈项、高斯白色噪声项和磁场对激发神经元放电模式的影响。随着对该模型研究的深入，大量结果表明模型的动态对揭示现实中神经元放电活动的机制具有重要的参考价值。

本文以文献[9]中的离散FHN模型为研究对象，从理论上分析了系统中Marotto混沌的存在性，得到了这类混沌存在的参数充分条件，并通过数值模拟展示了混沌吸引子、高周期解等复杂的非线性动态，这些结果丰富了对该模型的研究。

1 离散FHN模型 1.1 模型描述

考虑如下离散FHN模型^[9]

$ f:\left(\begin{array}{l} x \\ y \end{array}\right) \rightarrow\left(\begin{array}{c} x+\delta\left(x-\frac{x^3}{3}-y+I\right) \\ y+\frac{\delta}{\tau}(a x+b-y) \end{array}\right) $

(1)

式中，x表示神经元膜电位；y表示与膜电位恢复到静息电位过程有关的恢复变量；参数I(∈R)表示神经元接受的外界刺激强度或输入电流，其他系统参数a(＞0)、b(∈R)、τ(>0)、δ(0＜δ＜1)的说明参见文献[9]。

1.2 Marotto意义下混沌的存在性

在高维离散系统中存在的最典型的混沌吸引子是Marotto混沌，这类混沌系统的动态十分复杂，如：该系统存在任意正整数周期的周期轨；同时拥有“scrambled”集，这是一个不包括周期点、不可数的、具有初值敏感性、没有渐近周期点的不变集。此类混沌的存在性完全由系统是否拥有某类特殊不动点即snap-back repeller所决定^[10-11]。本文将从理论上研究Marotto意义下的混沌在系统(1)中的参数存在条件。

应用离散动力系统的定性理论可得，当b=I，0＜a＜1时，系统(1)存在一个不动点Z₀(x₀, y₀)=$ (\sqrt{3(1-a)}, a \sqrt{3(1-a)}+b)$。此不动点Z₀是snap-back repeller需要满足以下条件：

① 存在Z₀的一个邻域U_Z0，在此邻域中Z₀是expanding不动点，即∀Z(x, y)∈U_Z0，Z所有特征值的模长均大于1；

② U_Z0中存在一点Z^*(x^*, y^*)≠Z₀，满足f^M(Z^*)=Z₀，|Df^M(Z^*)|≠0，M∈N⁺。

下面讨论Z₀(x₀, y₀)是snap-back repeller，即满足条件①、②的参数充分条件。

引理1  若

$ \frac{2}{3}<a<1 $

(2)

$ \frac{2 a-1}{3 a-2}<\tau<\frac{1}{2-a-2 \sqrt{2 a(1-a)}} $

(3)

$ \frac{\tau(2-3 a)+1}{2(1-a)}<\delta<1 $

(4)

则

(ⅰ)存在点集U={(x, y)|x∈$ \left.\left(\sqrt{1+\frac{1-2 \sqrt{a \tau}}{\tau}}, \sqrt{1+\frac{1-\delta a}{\delta-\tau}}\right), y \in R\right\}$，该集合中任意点的特征值都是一对共轭复数，且模长大于1；

(ⅱ)存在不动点Z₀(x₀, y₀)=$ (\sqrt {3(1 - a)} , a\sqrt {3(1 - a)} + b)$的邻域$ {U_{{Z_0}}} = \left\{ {(x, y)\mid \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{r_{{x_0}}^2}} + } \right.\left. {\frac{{{{\left( {y - {y_0}} \right)}^2}}}{{r_{{y_0}}^2}} \le 1, {r_{{x_0}}}, {r_{{y_0}}} \in {R^ + }} \right\}$，满足U_Z0⊂U。

证明：(ⅰ)首先证明$ \frac{{2a - 1}}{{3a - 2}} < \frac{1}{{2 - a - 2\sqrt {2a(1 - a)} }}$。

因为$ \frac{2}{3} < a < 1$，所以$ \frac{{2a - 1}}{{3a - 2}} = \frac{{3a - 2 + 1 - a}}{{3a - 2}} = 1 + \frac{{1 - a}}{{3a - 2}} > 1$。由$ {\rm{ }}(a(1 - a) - (2a - 1)\sqrt {2a(1 - a)} ) \cdot $$ (a(1 - a) + (2a - 1)\sqrt {2a(1 - a)} ) = {(a(1 - a))^2} - $$ {((2a - 1)\sqrt {2a(1 - a)} )^2} = - 9a(1 - a)\left( {a - \frac{2}{3}} \right)\left( {a - \frac{1}{3}} \right) < 0$，可得$ a(1 - a) - (2a - 1)\sqrt {2a(1 - a)} < 0$。

又因为$ (2 - a - 2\sqrt {2a(1 - a)} )(2 - a + 2\sqrt {2a(1 - a)} ) = {(2 - a)^2} - {(2\sqrt {2a(1 - a)} )^2} = 9{\left( {a - \frac{2}{3}} \right)^2} > 0$，故$ 2 - a - 2\sqrt {2a(1 - a)} > 0$，从而有$ \frac{{2a - 1}}{{3a - 2}} - \frac{1}{{2 - a - 2\sqrt {2a(1 - a)} }} = \frac{{2(a(1 - a) - (2a - 1)\sqrt {2a(1 - a)} )}}{{(3a - 2)(2 - a - 2\sqrt {2a(1 - a)} )}} < 0$。

其次证明$ 1 + \frac{{1 - \delta a}}{{\delta - \tau }} > 1 + \frac{{1 - 2\sqrt {a\tau } }}{\tau } > 0$。

显然$ \tau + 1 > 2\sqrt \tau > 2\sqrt {a\tau } $，故$ 1 + \frac{{1 - 2\sqrt {a\tau } }}{\tau } > 0$。

由式(2)以及$ \tau > \frac{{2a - 1}}{{3a - 2}}$，可得$ \frac{{\tau - 1}}{{1 - a}} > \frac{{\frac{{2a - 1}}{{3a - 2}} - 1}}{{1 - a}} = \frac{1}{{3a - 2}} > 1$。又由$ \frac{{2a - 1}}{{3a - 2}} > 1 > \delta $，可知$ \frac{{\tau - 1}}{{1 - a}} > \delta $，τ＞δ，从而有

$ \begin{aligned} & \;\;\;\;1+\frac{1-\delta a}{\delta-\tau}=\frac{\delta(1-a)+1-\tau}{\delta-\tau}= \\ & \frac{(1-a)\left(\frac{\tau-1}{1-a}-\delta\right)}{\tau-\delta}>0 \text { 。} \end{aligned} $

因为$ \frac{{2a - 1}}{{3a - 2}} - \frac{1}{a} = \frac{{2{{(a - 1)}^2}}}{{a(3a - 2)}} > 0$，所以$ \frac{{2a - 1}}{{3a - 2}} > \frac{1}{a}$。由$ \tau > \frac{{2a - 1}}{{3a - 2}} > \frac{1}{a}$，可得aτ＞1，从而$ \frac{{2\tau }}{{1 - \sqrt {a\tau } }} < 0$。

注意到$ \left( {1 + \frac{{1 - 2\sqrt {a\tau } }}{\tau }} \right) - \left( {1 + \frac{{1 - \delta a}}{{\delta - \tau }}} \right) = \frac{{{{(1 - \sqrt {a\tau } )}^2}\left( {\delta - \frac{{2\tau }}{{1 - \sqrt {a\tau } }}} \right)}}{{\tau (\delta - \tau )}} < 0$，故$ 1 + \frac{{1 - 2\sqrt {a\tau } }}{\tau } < 1 + \frac{{1 - \delta a}}{{\delta - \tau }}$。

又因为$ \frac{{1 - \delta a}}{{\delta - \tau }} < 0 < \frac{{1 + 2\sqrt {a\tau } }}{\tau }$，所以$ 1 + \frac{{1 - \delta a}}{{\delta - \tau }} < 1 + \frac{{1 + 2\sqrt {a\tau } }}{\tau }$。

综上可得，点集U={(x, y)|x∈ $ \left.\left(\sqrt{1+\frac{1-2 \sqrt{a \tau}}{\tau}}, \sqrt{1+\frac{1-\delta a}{\delta-\tau}}\right), y \in R\right\}$是存在的。

任取Z(x, y)∈U，下面证明Z(x, y)具有一对共轭复特征值，且模长大于1。

易知系统(1)在点Z(x, y)处的Jacobian矩阵为

$ \boldsymbol{J}=\left(\begin{array}{cc} 1+\delta\left(1-x^2\right) & -\delta \\ \frac{\delta a}{\tau} & 1-\frac{\delta}{\tau} \end{array}\right) $

其特征方程为λ²+p(x)λ+q(x)=0，其中$ p(x) = - 2 + \frac{\delta }{\tau } - \delta \left( {1 - {x^2}} \right), q(x) = 1 - \frac{\delta }{\tau } + \delta (1 - \left. {{x^2}} \right) - \frac{{{\delta ^2}}}{\tau }\left( {1 - {x^2}} \right) + \frac{{{\delta ^2}a}}{\tau }$，特征值为λ_{1, 2}=$ \frac{{ - p(x) \pm \sqrt {{p^2}(x) - 4q(x)} }}{2}$。

因为$ x \in \left( {\sqrt {1 + \frac{{1 - 2\sqrt {a\tau } }}{\tau }} , \sqrt {1 + \frac{{1 - \delta a}}{{\delta - \tau }}} } \right)$，0＜δ＜τ，所以p²(x)－4q(x)=$ {\delta ^2}\left( {{x^2} - (} \right.1 + \frac{{1 - \sqrt {a\tau } }}{\tau }))\left( {{x^2} - \left( {1 + \frac{{1 + 2\sqrt {a\tau } }}{\tau }} \right)} \right) < 0$, $ q(x) - 1 = \frac{{\delta (\delta - \tau )}}{\tau }\left( {{x^2} - \left( {1 + \frac{{1 - \delta a}}{{\delta - \tau }}} \right)} \right) > 0$，从而有点Z(x, y)的特征值为一对共轭复数$ {\lambda _{1, 2}} = \frac{{ - p(x)}}{2} \pm {\rm{i}}\frac{{\sqrt {4q(x) - {p^2}(x)} }}{2}$，且$ \left\| {{\lambda _{1, 2}}} \right\| = \sqrt {q(x)} > 1$。

(ⅱ)为选取适当的r_x0和r_y0，先证明$ \sqrt{1+\frac{1-2 \sqrt{a \tau}}{\tau}}<\sqrt{3(1-a)}<\sqrt{1+\frac{1-\delta a}{\delta-\tau}}$。

因为a＜1，$ \frac{\tau(2-3 a)+1}{2(1-a)}<\delta$，所以$ \tau (2 - 3a) + 1 < 2\delta (1 - a)$，从而δ－τ+1－δa＜3(1－a)(δ－τ)。又δ＜τ，故

$ 3(1-a)<1+\frac{1-\delta a}{\delta-\tau} $

(5)

由$ a > \frac{2}{3}$，$ 0 < \tau < \frac{1}{{2 - a - 2\sqrt {2a(1 - a)} }}$，可得$ (3a - 2)\tau - 2\sqrt {a\tau } + 1 < \frac{{3a - 2}}{{2 - a - 2\sqrt {2a(1 - a)} }} - $$ 2\sqrt {a\tau } + 1 < \frac{{3a - 2}}{{2 - a - 2\sqrt {\frac{4}{3} \times \frac{1}{3}} }} - 2\sqrt {a\tau } + 1 = - 2 - $$ 2\sqrt {a\tau } < 0$，从而有$ 1+\frac{1-2 \sqrt{a \tau}}{\tau}-3(1-a)=$$ \frac{(3 a-2) \tau-2 \sqrt{a \tau}+1}{\tau}<0$，即

$ 1+\frac{1-2 \sqrt{a \tau}}{\tau}<3(1-a) $

(6)

由式(5)、(6)可知

$ \sqrt{1+\frac{1-2 \sqrt{a \tau}}{\tau}}<\sqrt{3(1-a)}<\sqrt{1+\frac{1-\delta a}{\delta-\tau}} $

取$ 0 < {r_{{x_0}}} < \min \left\{ {\sqrt {1 + \frac{{1 - \delta a}}{{\delta - \tau }}} - \sqrt {3(1 - a)} } \right., \left. {\sqrt {3(1 - a)} - \sqrt {1 + \frac{{1 - 2\sqrt {a\tau } }}{\tau }} } \right\}$，r_y0∈R⁺，考虑不动点Z₀(x₀, y₀)=$ (\sqrt {3(1 - a)} , a\sqrt {3(1 - a)} + b)$的邻域$ {U_{{z_0}}} = \left\{ {(x, y)\mid \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{r_{{x_0}}^2}} + \frac{{{{\left( {y - {y_0}} \right)}^2}}}{{r_{{y_0}}^2}} \le 1} \right\}$，任取点Z(x, y)∈U_Z0，则其横坐标x∈[x₀－r_x0, x₀+r_x0]，显然[x₀－r_x0, x₀+r_x0]⊂$ \left( {\sqrt {1 + \frac{{1 - 2\sqrt {a\tau } }}{\tau }} } \right., \left. {\sqrt {1 + \frac{{1 - \delta a}}{{\delta - \tau }}} } \right)$，故U_Z0⊂U。命题得证。

引理2  考虑不动点Z₀(x₀, y₀)=$ (\sqrt {3(1 - a)} , a\sqrt {3(1 - a)} + b)$，及其邻域U_Z0=$ \left\{ {(x, y)\mid \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{r_{{x_0}}^2}} + \frac{{{{\left( {y - {y_0}} \right)}^2}}}{{r_{{y_0}}^2}} \le 1, {r_{{x_0}}} = 0.1, {r_{{y_0}}} \in } \right.\left. {{R^ + }} \right\}$，若式(2)~(4)，以及

$ \delta \ne \frac{\tau }{{1 + \sqrt {a\tau } }} $

(7)

$ \begin{array}{l} \;\;\;\;\;\;\;30\mid {x_0} + \frac{{100}}{\delta }\left( {2{x_0} - \sqrt {3\left( {3a + 1 + \frac{4}{\delta } + \frac{{4\delta a}}{{\tau - \delta }}} \right)} } \right) \cdot \\ \left( {\frac{{{\delta ^2}a\tau }}{{{{(\tau - \delta )}^2}}} - 1} \right)\mid + 1 < 300\left( {3a - 2 + \frac{1}{\delta } + \frac{{\delta a}}{{\tau - \delta }}} \right) \end{array} $

(8)

成立，则在邻域U_Z0中存在一点Z^*(x^*, y^*)，满足Z^*≠Z₀，f²(Z^*)=Z₀，且|Df²(Z^*)|≠0。

证明：设有点Z^*(x^*, y^*)，令Z₁(x₁, y₁)=f(Z^*)，f²(Z^*)=f(Z₁)=Z₀，即

$ \left\{\begin{array}{l} x_1=x^*+\delta\left(x^*-\frac{\left(x^*\right)^3}{3}-y^*+I\right) \\ y_1=y^*+\frac{\delta}{\tau}\left(a x^*-y^*+b\right) \end{array}\right. $

(9)

且

$ \left\{\begin{array}{l} x_1+\delta\left(x_1-\frac{x_1^3}{3}-y_1+I\right)=x_0 \\ y_1+\frac{\delta}{\tau}\left(a x_1-y_1+b\right)=y_0 \end{array}\right. $

(10)

易知方程组(10)的一组解为

$ \left\{\begin{array}{l} x_{1+}=\frac{-x_0+\sqrt{3\left(3 a+1+\frac{4}{\delta}+\frac{4 \delta a}{\tau-\delta}\right)}}{2} \\ y_{1+}=y_0-\frac{\delta a\left(x_{1+}-x_0\right)}{\tau-\delta} \end{array}\right. $

(11)

先证(x₁₊, y₁₊)≠(x₀, y₀)。由$ a > \frac{2}{3}$，τ＞δ可得$ \left( {2{x_0} - \sqrt {3\left( {3a + 1 + \frac{4}{\delta } + \frac{{4\delta a}}{{\tau - \delta }}} \right)} } \right)\left( { - 2{x_0} - } \right.\left. {\sqrt {3\left( {3a + 1 + \frac{4}{\delta } + \frac{{4\delta a}}{{\tau - \delta }}} \right)} } \right)$$ = 3\left( {7a - 3 + \frac{4}{\delta } + \frac{{4\delta a}}{{\tau - \delta }}} \right) > 3\left( {7 \times \frac{2}{3} - 3 + \frac{4}{\delta } + \frac{{4\delta a}}{{\tau - \delta }}} \right)$$ = 5 + 12\left( {\frac{1}{\delta } + \frac{{\delta a}}{{\tau - \delta }}} \right) > 0$，从而

$ x_0-x_{1+}=2 x_0-\sqrt{3\left(3 a+1+\frac{4}{\delta}+\frac{4 \delta a}{\tau-\delta}\right)} \neq 0 $

(12)

将式(11)代入到方程组(10)可得

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;{\left( {{x^*}} \right)^3} - \frac{3}{\delta }\left( {1 + \delta + \frac{{{\delta ^2}a}}{{\tau - \delta }}} \right){x^*} + \frac{3}{\delta }(1 - \\ \left. {\frac{{{\delta ^2}a\tau }}{{{{(\tau - \delta )}^2}}}} \right){x_{1 + }} + \frac{{3a{\tau ^2}}}{{{{(\tau - \delta )}^2}}}{x_0} = 0 \end{array} $

(13)

$ {y^*} = \frac{{\tau (\tau - \delta ){y_0} - \delta a\tau \left( {{x_{1 + }} - {x_0}} \right) - \delta \left( {a{x^*} + b} \right)(\tau - \delta )}}{{{{(\tau - \delta )}^2}}} $

(14)

为求方程(13)在[x₀－0.1, x₀+0.1]内的解x^*，令x^*=s+x₀，代入方程(13)可得

$ \begin{aligned} & \quad \quad g(s) \equiv s^3+3 s^2 x_0+3 s\left(x_0^2-1-\frac{1}{\delta}-\frac{\delta a}{\tau-\delta}\right)+\frac{3}{\delta} \times \\ & \left(\frac{\delta^2 a \tau}{(\tau-\delta)^2}-1\right)\left(x_0-x_{1+}\right)=0 \end{aligned} $

(15)

下面证明方程(15)在[－0.1, 0.1]内有非零解，即g(s)有非零的零点。

令$ {g^\prime }(s) = 3\left( {{s^2} + 2{x_0}s + x_0^2 - 1 - \frac{1}{\delta } - \frac{{\delta a}}{{\delta - \tau }}} \right) = 0$，可得g(s)的两个驻点$ {s_{1, 2}} = - {x_0} \pm \sqrt {1 + \frac{1}{\delta } + \frac{{\delta a}}{{\tau - \delta }}} $，其中s₁＜s₂，显然当s∈(s₁, s₂)时，g′(s)＜0。因为τ＞δ＞0，所以$ 1 + \frac{{1 - \delta a}}{{\delta - \tau }} = 1 + \frac{{\delta a}}{{\tau - \delta }} - $$ \frac{1}{{\tau - \delta }} < 1 + \frac{{\delta a}}{{\tau - \delta }} + \frac{1}{\delta }$，从而有$ {\rm{ }}{s_2} = \sqrt {1 + \frac{1}{\delta } + \frac{{\delta a}}{{\tau - \delta }}} - \sqrt {3(1 - a)} > \sqrt {1 + \frac{{1 - \delta a}}{{\delta - \tau }}} - \sqrt {3(1 - a)} > 0.1$，且$ {s_1} = - {s_2} - 2\sqrt {3(1 - a)} < - 0.1{\rm{ }}$，故[－0.1, 0.1]⊂(s₁, s₂)。因此当s∈[－0.1, 0.1]时，g′(s)＜0，即g(s)在区间[-0.1, 0.1]是单调递减函数。

由式(7)及aτ＞1，有

$ \begin{aligned} & \;\; \;\; \;\;\delta^2 a \tau-(\tau-\delta)^2=(\delta(1+\sqrt{a \tau})-\tau)(\delta(\sqrt{a \tau}- \\ & 1)+\tau) \neq 0 \end{aligned} $

(16)

由式(12)、(16)及τ＞δ＞0可得

$ g(0)=\frac{3\left(x_0-x_{1+}\right)\left(\delta^2 a \tau-(\tau-\delta)^2\right)}{\delta(\tau-\delta)^2} \neq 0。$

且由式(8)、(12)可知，g(－0.1)g(0.1)=$ {\left( {\frac{{30}}{{1000}}\left( {{x_0} + \frac{{100\left( {{x_0} - {x_{1 + }}} \right)}}{\delta }\left( {\frac{{{\delta ^2}a\tau }}{{{{(\tau - \delta )}^2}}} - 1} \right)} \right)} \right)^2} - {\left( {\frac{1}{{1000}}\left( {300\left( {3a - 2 + \frac{1}{\delta } + \frac{{\delta a}}{{\tau - \delta }}} \right) - 1} \right)} \right)^2} < 0$，根据零点定理得，$ \exists$s^*∈(－0.1, 0.1)，g(s^*)=0，又因g(0)≠0，故s^*≠0。综上方程(13)有实根x^*=x₀+ s^*∈(x₀－0.1, x₀+0.1)，且x^*≠x₀。取r_y0＞|y^*－y₀|，从而Z^*(x^*, y^*)∈U_Z0, Z^*≠Z₀，f²(Z^*)=Z₀。下证|Df²(Z^*)|≠0。

$ \begin{array}{l} \;\; \;\; \;\; \left|\boldsymbol{D} f\left(Z^*\right)\right|>0 \\ \;\; \;\; \;\;\left|\boldsymbol{D} f\left(Z_1\right)\right|=\frac{\delta^2 a}{\tau}+\left(1-\frac{\delta}{\tau}\right)\left(1+\delta\left(1-x_{1+}^2\right)\right)= \\ -\left(1-\frac{\delta}{\tau}\right)\left(\frac{3 \delta \sqrt{(1-a)\left(3 a+1+\frac{4}{\delta}+\frac{4 \delta a}{\tau-\delta}\right)}}{4}+\right. \\ \left.\frac{3 \delta a}{2}+2+\delta\right)-\frac{2 \delta^2 a}{\tau}<0 \end{array} $

故|Df²(Z^*)|=|Df(Z₁)‖Df(Z^*)|≠0。命题得证。

说明：引理2中的r_x0取值为0.1，事实上只要r_x0取充分小的正数，补充形如式(8)的条件，即可得相同的结论。

综上所述，可得如下定理。

定理  若系统参数a、τ、δ满足引理1与引理2中的条件，则系统(1)的不动点Z₀(x₀, y₀)=$ (\sqrt{3(1-a)}, a \sqrt{3(1-a)}+b)$是snap-back repeller，此时系统(1)是Marotto混沌的，即存在：

1) 一个正整数N，使得对于任一整数p≥N，f有周期p点。

2) 一个“scrambled set”，即一个不含周期点的不可数集S满足

(a) f[S]⊂S；

(b) 对于S中任意不相同的两点X和Y，有

$ \mathop {\lim }\limits_{k \to \infty } \sup \left\| {{f^k}(X) - {f^k}(Y)} \right\| > 0{\rm{; }} $

(c) 对于S中任意点X，以及f的任意周期点Y，有

$ \mathop {\lim \sup }\limits_{k \to \infty } \left\| {{f^k}(X) - {f^k}(Y)} \right\| > 0。$

3) S有一个不可数子集S₀，对于S₀中任意点X和Y，有

$ \mathop {\lim \inf }\limits_{k \to \infty } \left\| {{f^k}(X) - {f^k}(Y)} \right\| = 0。$

2 数值模拟

本节取两组参数，通过数值计算，对Marotto混沌吸引子及周期轨等复杂动态进行模拟。

1) 参数组1：b=I=1，a=0.9，τ=2.47，δ=0.992。

系统(1)存在一个不动点。

$ Z_0\left(x_0, y_0\right)=(0.547\;722\;557\;505\;17 {, } $

1.492 950 301 754 653)，其特征值为λ_{1, 2}=1.146 39± 0.241 35i，‖λ_{1, 2}‖＞1。此时参数满足引理1与引理2的条件：

$ \begin{aligned} & \;\;\;\;a=0.9>\frac{2}{3} \\ & \;\;\;\;\frac{\tau(2-3 a)+1}{2(1-a)}=-3.645<\delta<1 \\ & \;\;\;\;1.143=\frac{2 a-1}{3 a-2}<\tau<\frac{1}{2-a-2 \sqrt{2 a(1-a)}}=3.977 \\ & \;\;\;\;\delta \neq \frac{\tau}{1+\sqrt{a \tau}}=0.991\;58 \\ & \;\;\;\;30 \mid x_0+\frac{100}{\delta}\left(2 x_0-\sqrt{3\left(3 a+1+\frac{4}{\delta}+\frac{4 \delta a}{\tau-\delta}\right)}\right) \times \\ & \left(\frac{\delta^2 a \tau}{(\tau-\delta)^2}-1\right) \mid+1=3.488<300\left(3 a-2+\frac{1}{\delta}+\right. \\ & \left.\frac{\delta a}{\tau-\delta}\right)=693.637 \end{aligned} $

引理1中的点集U与Z₀的邻域U_Z0分别为

$ \begin{array}{l} \;\;\;\; U=\left\{(x, y) \mid x \in\left(\sqrt{1+\frac{1-2 \sqrt{a \tau}}{\tau}}, \right.\right. \\ \left.\left.\sqrt{1+\frac{1-\delta a}{\delta-\tau}}\right)=(0.444\;5, 0.963\;1), y \in R\right\} \\ \;\;\;\;U_{Z_0}=\left\{(x, y) \mid \frac{\left(x-x_0\right)^2}{0.01}+\frac{\left(y-y_0\right)^2}{4} \leqslant 1\right\} \end{array} $

显然U_Z0⊂U。∀Z(x, y)∈U_Z0，Z(x, y)的特征方程为λ²+p(x)λ+q(x)=0，特征值为

$ \lambda_{1, 2}=\frac{-p(x) \pm \sqrt{p^2(x)-4 q(x)}}{2}, \left\|\lambda_{1, 2}\right\|=\sqrt{q(x)} $

其中p²(x)－4q(x)＜p²(x₀－0.1)－4q(x₀－ 0.1)=－0.006 79＜0，q(x)－1＞q(x₀+0.1)－1=0.446 06>0，即Z的特征值为一对模长大于1的共轭复数。U_Z0中存在一点Z^*(x^*, y^*)=(0.546 528 029 406 18, -0.462 001 800 839 748)，Z₁(x₁, y₁)=f(Z^*)=(2.485 010 260 145 796, 0.322 713 183 407 19)，f²(Z^*)=Z₀，且|Df²(Z^*)|= -2.904 5。由定理可得Z₀是一个snap-back repeller，即系统(1)存在Marotto混沌吸引子。

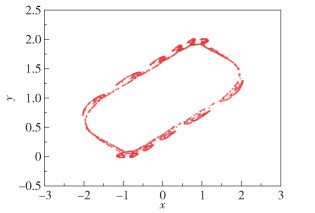
选取不动点Z₀(x₀, y₀)=(0.547 722 557 505 17, 1.492 950 301 754 653)的邻域U_Z0中的点(0.547 7, 1.493)为初始点，其相图见图 1，这条轨道的Lyapunov指数为{-0.241 97，0.078 66}，即为Marotto混沌吸引子。

不同于前一组Z₀的邻域U_Z0中r_x0(=0.1)的取值，将r_x0设置为0.08，仍能证明在一定参数条件下系统是Marotto意义下混沌的。

2) 参数组2：b=I=1，a=0.91，τ=2.4，δ=0.99。

系统(1)存在不动点。

$ Z_0\left(x_0, y_0\right)=(0.519\;615\;242\;270\;663, $

1.472 849 870 466 304)，其特征值为λ_{1, 2}=1.155 1± 0.233 4i，‖λ_{1, 2}‖＞1。存在Z₀的邻域

$ \begin{array}{l} \;\;\;\;\;\;U_{Z_0} =\left\{(x, y) \mid \frac{\left(x-x_0\right)^2}{r_{x_0}^2}+\frac{\left(y-y_0\right)^2}{r_{y_0}^2} \leqslant 1, r_{x_0}=\right. \\ 0.08, r_{y_0} =2.2\} \end{array} $

任取Z(x, y)∈U_Z0，因为p²(x)－4q(x)＜p²(x₀－0.08)－4q(x₀－0.08)=－0.019 55＜0，q(x)－1>q(x₀+0.08)=0.331 63>0，所以Z(x, y)有一对模长大于1的共轭复特征值$ \frac{{ - p(x) \pm {\rm{i}}\sqrt {4q(x) - {p^2}(x)} }}{2}$，且其模长$ \sqrt {q(x)} > 1$。U_Z0中存在点Z^*(x^*, y^*)=(0.455 258 552 583 97, 0.664 929 193 926 399)，Z₁(x₁, y₁)=f(Z^*)=(2.523 106 596 180 992, 0.192 746 777 744 48)，f²(Z^*)=Z₀，|Df²(Z^*)|=－3.070 4≠0，由条件①、②得，Z₀(x₀, y₀)是snap-back repeller，系统(1)存在Marotto混沌吸引子，这条轨道的Lyapunov指数为{-0.182 54，0.065 1}。

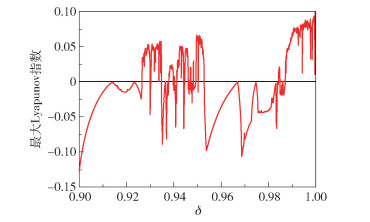
针对第一组参数值，在δ=0.992时系统(1)出现了Marotto混沌吸引子。本文计算了参数δ∈(0.9, 1)时，以不动点Z₀邻域中的点(0.547 7, 1.493)为初始点的轨道的最大Lyapunov指数，如图 2所示。很明显，系统在δ参数区间(0.988, 1)内始终保持混沌状态。

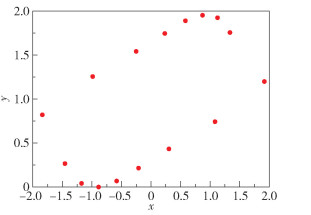
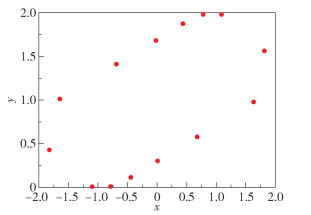
通过数值模拟计算，我们还发现系统存在高周期轨道，如周期16轨、周期14轨，如图 3、4所示。

3 结束语

本文研究了一类离散FHN神经系统的混沌现象，主要从理论上严格证明了该系统Marotto意义下混沌的存在性。此外通过数值计算模拟出Marotto混沌吸引子，同时还发现系统中存在周期14轨和周期16轨，这些复杂动态的发现丰富了对此系统的理解。