2. 中国空间技术研究院 钱学森空间技术实验室, 北京 100094
2. Qian Xuesen Laboratory of Space Technology, China Academy of Space Technology, Beijing 100094, China
球形机器人是一类利用质心偏移和动量守恒等原理实现滚动运动的新型移动机器人,一般具有全封闭的球壳,在球壳内部包含执行系统、动力系统、控制系统和传感器等[1]。与传统的移动机器人相比,球形机器人在运动性能上具有较强的灵活性与平衡性,具有一定的陆地运动能力,且具有倒立摆性质,故不存在侧翻问题[2]。此外,由于球形机器人具有球形或类球形的外壳,其不仅具有良好的密封性,还能利用外壳对冲击进行有效缓冲从而保护内部机械结构与电子器件[3]。因此球形机器人是目前智能机器人研究领域的热点之一[4]。
球形机器人的主要驱动方式有5类,即直接驱动式[5]、双半球驱动式[6]、重力驱动式[7]、角动量驱动式[8]与变形驱动式[9-10]。其中重力驱动式球形机器人通常内部会有一个重摆,因此也被称为重摆驱动式球形机器人。重力驱动式球形机器人利用球体的不平衡力矩和重力矩实现滚动,这种力矩是通过旋转重摆改变球形机器人系统的质心来主动产生和控制的[11]。重力驱动式球形机器人与其他驱动方式的球形机器人相比具有结构简单、易于控制、有一定的通行能力、球体内部空间较大等优点[12-13]。本文以重力驱动式球形机器人的运行原理作为设计依据,集成跳跃模块,合理调节球体内部构件质量分布,设计了一种滚-跳多运动模式球形机器人,并根据设计方案建立了球形机器人动力学方程,构建虚拟样机对其进行动力学仿真,最后对制作样机进行测试,实验结果验证了动力学仿真的正确性。
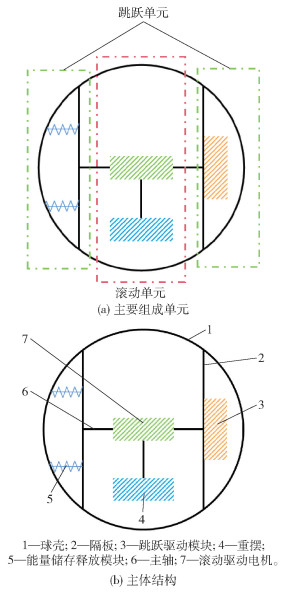
1 机器人机构设计如图 1(a)所示,滚-跳多运动模式球形机器人主要由跳跃单元和滚动单元组成。在滚动单元中,由处于主轴(6)上的滚动驱动电机(7)作为滚动运动的驱动,即为滚动驱动模块,如图 1(b)所示。由转向调整电机与电池作为单摆结构中的重摆(4),为转向调整模块。该转向调整电机通过齿轮齿条实现自身即重摆的左右移动,从而实现球形机器人的转向功能。跳跃驱动单元由跳跃驱动模块(3)和能量储存释放模块(5)两部分组成。在球形机器人的跳跃过程中,由跳跃驱动模块(3)中的跳跃驱动电机通过贯穿主轴(6)的绳索的拉伸对能量储存释放模块(5)中的储能弹簧进行能量的储存与释放,从而实现跳跃功能。隔板(2)能起到滚动单元、跳跃单元和球壳(1)3部分之间的连接,并隔离保护滚动单元与跳跃单元各个部件之间不发生干涉等作用。
|
图 1 球形机器人设计方案 Fig.1 The design scheme of the spherical robot |
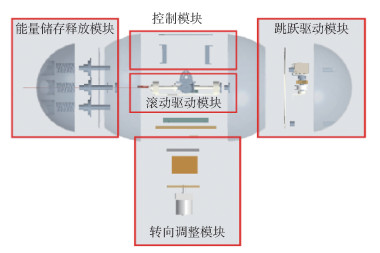
上述滚动驱动模块、转向调整模块、跳跃驱动模块以及能量储存释放模块,连同球形机器人的控制模块组成了该球形机器人的5个功能模块。控制模块通过对滚动驱动电机、转向驱动电机的控制来实现球形机器人的滚动和转向功能,并通过蓝牙通信来控制跳跃驱动电机,实现对球形机器人跳跃功能的控制。根据上述设计方案,利用三维建模软件CREO设计并建立球形机器人三维模型,如图 2所示。
|
图 2 球形机器人模型示意图 Fig.2 Model diagram of the spherical robot |
动力学模型是球形机器人研究领域的核心问题之一[12],针对动力学模型的研究可以从理论上对设计方案进行验证。在本文的设计方案中,由于所设计的球形机器人的转向、滚动、跳跃3种运动的驱动源分别为转向调整电机、滚动驱动电机与跳跃驱动电机,且传动机构相互独立,故认为这3种运动驱动间的耦合程度低。将球形机器人的运动系统抽象为一个多体系统,并做出如下假设:
1) 球形机器人滚动时与地面无相对滑动(刚体无滑滚动约束条件);
2) 球形机器人各零部件均质量分布均匀;
3) 球形壳体为均质薄壁球壳;
4) 忽略球形机器人运动过程中的内部摩擦;
5) 仅在建立转向运动动力学模型时考虑球壳与地面的摩擦。
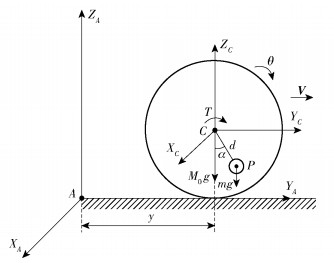
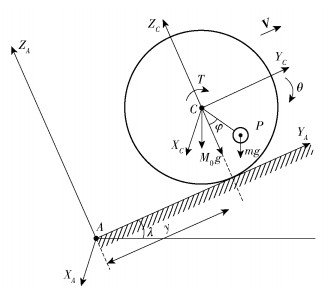
2.1 滚动、爬坡运动球形机器人的平面滚动、爬坡运动均是拥有绕XA轴转动和沿YA轴平动的双自由度系统,扭矩作用于P点,系统的输入是扭矩为T的一个典型的欠驱动系统,见图 3、4,其中静坐标系记为∑A(XAYAZA),ZA轴正向垂直地面向上,YA轴正向为机器人运动方向,坐标原点为A点。将球形机器人初始状态和初始位置定义为其动坐标系,记作∑C(XCYCZC),ZC轴正向垂直地面向上,YC正向为机器人运动方向,坐标原点为C点。
|
图 3 球形机器人滚动运动动力学模型 Fig.3 Rolling dynamics model of the spherical robot |
|
图 4 球形机器人爬坡运动动力学模型 Fig.4 Climbing dynamics model of the spherical robot |
图 3、4中,P为重摆质心,M为球形机器人总质量,m为重摆质量,M0为除去重摆的球形机器人质量,故M0=M-m;θ为球形机器人滚动角速度,V的方向表示球形机器人的滚动或爬坡的滚动方向,y为球形机器人滚动运动时的位移,α为球形机器人滚动运动时的摆锤偏转角,φ为球形机器人爬坡运动时的摆锤偏转角,d为摆臂长度,λ为爬坡角度。
对于欠驱动系统,需要广义坐标下的第二类Lagrange方程进行求解,如式(1)所示。
| $ \frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{\partial L}{\partial \dot{q}_i}\right)-\frac{\partial L}{\partial q_i}=F_i $ | (1) |
式中,动势L=E-P,Fi是广义力,E是系统运动时的动能,P是系统运动时的势能,qi为广义坐标。
分别分析滚动运动与爬坡运动时的动能与势能,可得滚动运动的动能和势能如方程(2)、(3)所示,爬坡运动的动能和势能如方程(4)、(5)所示。
在滚动运动中,球形机器人的动能由球壳(球壳半径为R)和重摆的平动动能以及自身旋转的动能组成。
| $ \begin{aligned} & \quad E=\frac{1}{2} M_0 \dot{y}^2+\frac{1}{2} M_0 R^2\left(\frac{y}{R}\right)^2+\frac{1}{2} m(\dot{y}+ \\ & \dot{\alpha} d \cos \alpha)^2+\frac{1}{2} m(\dot{\alpha} d \sin \alpha)^2 \end{aligned} $ | (2) |
| $ P=-m g d \cos \alpha $ | (3) |
在爬坡运动中,球形机器人的动能由球壳的动能E1和重摆的动能E2组成,球壳和重摆的动能均包括平动动能和自身旋转的动能。
| $ E=E_1+E_2 $ | (4) |
其中,
| $ \begin{aligned} & E_1=\left(\frac{1}{2} M_0 R^2+I_M\right) \dot{\theta}^2 \\ & E_2=\frac{1}{2} J_1 \dot{\theta}^2+\frac{1}{2} J_2 \dot{\varphi}^2+m d R \dot{\theta} \cdot \dot{\varphi} \cos \varphi \\ & J_1=M_0 R^2+m R^2+I_M \\ & J_2=m d^2+I_m \\ & P\left(m+M_0\right)(\theta \sin \lambda+\cos \lambda) g R-m g d \cos (\lambda+ \varphi) \end{aligned} $ | (5) |
其中,IM与Im分别为球壳的转动惯量与重摆的转动惯量。
将方程(2)、(3)代入方程(1)中可得球形机器人滚动运动动力学方程如下。
| $ \left\{\begin{array}{l} 2 M_0 \ddot{y}+m \ddot{y}+m R \cos \dot{\alpha} \cdot \ddot{\alpha}=0 \\ m L \ddot{y} \cos \alpha+m R^2 \ddot{\alpha}+m g R \sin \alpha=T(y, \alpha) \end{array}\right. $ | (6) |
将方程(4)、(5)代入方程(1)中可得球形机器人爬坡运动动力学方程如下。
| $ \left\{\begin{array}{l} J_1 \frac{\ddot{y}}{R}+m d R \ddot{\varphi} \cos \varphi-m d R \dot{\varphi}^2+ \\ \left(M_0+m\right) g R \sin \alpha=T(x, \phi) \\ J_2 \ddot{\varphi}+m d \frac{\ddot{y}}{R} \cos \frac{y}{R}+m g d \sin (\lambda+\varphi)=T(y, \varphi) \end{array}\right. $ | (7) |
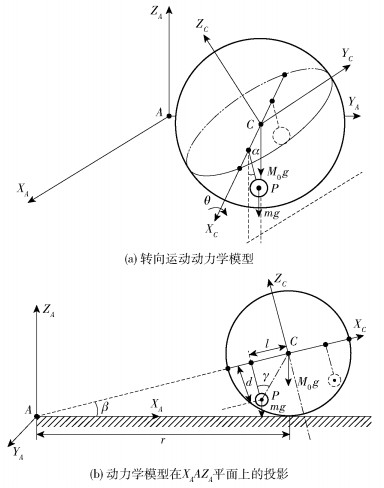
球形机器人转向运动的动力学模型如图 5(a)所示。为了更好地分析转向运动中的受力情况,将球形机器人的运动学模型投影到XAAZA平面,如图 5(b)所示。根据几何关系,球形机器人的转弯半径可以近似表示为
| $ r=\frac{R}{\tan \beta} $ | (8) |
|
图 5 球形机器人转向运动动力学模型 Fig.5 Steering dynamic model of the spherical robot |
式中,β为球形机器人主轴与水平面的夹角。
当球形机器人系统处于倾斜角度β恒定的平衡状态时,重摆和滚动单元沿XC方向产生的重力矩分量分别为MP和MC。由力矩平衡条件可得
| $ M_P-M_C+f R=0 $ | (9) |
式中,f为球壳与地面间的摩擦力。
其中C点在滚动单元的重力方向上,故有MC=0,可得
| $ M_P+f R=0 $ | (10) |
沿XC轴方向取矩,得
| $ M_P=m g \sqrt{d^2+l^2} \sin (\gamma+\beta) $ | (11) |
式中,γ为重摆质心P和球壳中心C的连线与摆臂的夹角,l为球形机器人重摆的左右偏移行程长度。
根据方程(8)~(11)可得,在转向运动中r和l满足以下关系。
| $ r=-\frac{m g \sqrt{d^2+l^2} \sin (\gamma+\beta)}{f \tan \beta} $ | (12) |
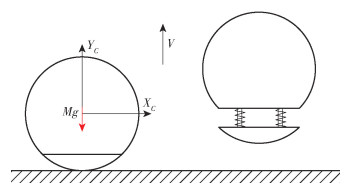
对球形机器人的跳跃过程进行分析发现,一方面球形机器人侧向跳跃时球壳会与地面发生相对滑动,产生的能量损失无法量化且不可忽略,故竖直向上跳跃能更好地排除外界的影响;另一方面,竖直向上跳跃时,球形机器人弹簧储存的能量完全转换为跳跃到最高点时的重力势能,能较好地描述球形机器人的最大跳跃高度。根据上述设计方案,建立如图 6所示的球形机器人跳跃运动动力学模型。
|
图 6 球形机器人跳跃运动动力学模型 Fig.6 Jumping dynamic model of the spherical robot |
在跳跃过程中,不考虑弹簧释放能量过程中的损耗,即弹簧储存的能量全部转换为球形机器人跳跃至最高点的重力势能,即有
| $ \frac{1}{2} k D^2=M g h $ | (13) |
式中,k为弹簧的劲度系数,D为弹簧的压缩长度,h为球形机器人的跳跃高度。
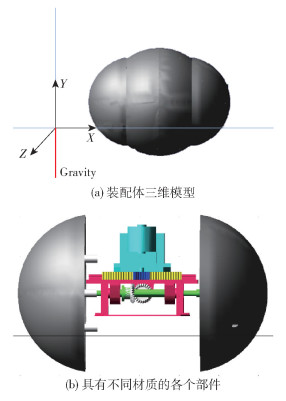
3 动力学仿真 3.1 虚拟样机的构建为模拟所设计球形机器人的运动情况,在动力学仿真软件ADAMS中构建虚拟样机。首先在三维建模软件CREO中将球形机器人零件组成为装配体,如图 7(a)所示。将该三维模型导入ADAMS,并对不同材质的零件(如图 7(b)所示)密度赋值,经计算该球形机器人质量为2.42kg。
|
图 7 球形机器人虚拟样机模型 Fig.7 Virtual prototype model of the spherical robot |
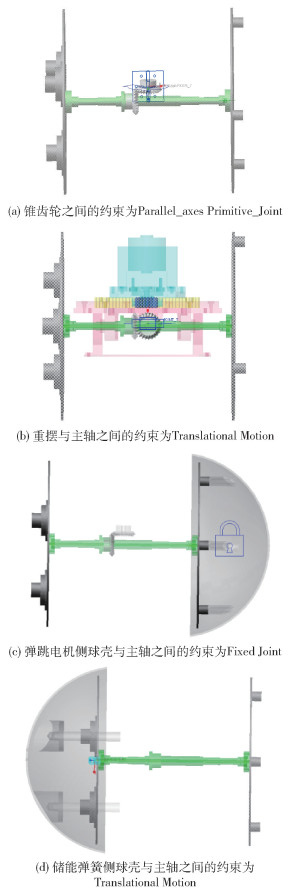
设置全局坐标系下的重力场为9806.65mm/s2,动摩擦系数与静摩擦系数分别为0.05与0.10[12]。按照设计方案与实际运动过程中零件间的相互位置关系为模型设置合理的约束关系,如图 8所示。
|
图 8 模型中重要零件之间的约束关系 Fig.8 Constraint relationships between the important parts |
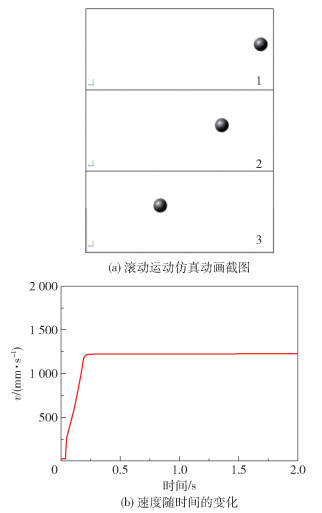
由于在滚动运动中,球形机器人的动力来源于滚动驱动电机,故在与滚动驱动电机连接的锥齿轮上添加了转动驱动。经ADAMS仿真计算,滚动运动的仿真动画截图如图 9(a)所示,球形机器人在平面上沿直线滚动前行,滚动速度如图 9(b)所示。由图 9(b)可知,球形机器人运行约0.25s后速度达到一个较为稳定的最大速度,其中加速过程的加速度约为8266.7mm/s2。球形机器人在最大速度阶段速度存在小幅度波动,波动数值范围为1237~1243mm/s,取其平均值1240mm/s为球形机器人滚动运动的滚动速度。
|
图 9 球形机器人滚动运动ADAMS仿真结果 Fig.9 ADAMS simulation results of the rolling motion |
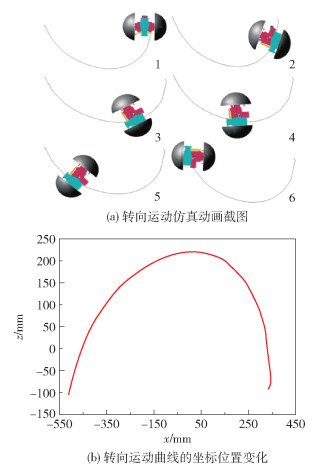
与滚动运动相比,转向运动为滚动运动加上重摆在轴向的运动,因此在摆锤与主轴连接的移动副上添加移动驱动。经ADAMS仿真计算,滚动运动的仿真动画截图如图 10(a)所示,球形机器人在平面作转向运动,转向运动中的位置坐标如图 10(b)所示,其中横坐标为球形机器人质心的x轴坐标,纵坐标为球形机器人质心的z轴坐标。可以看出,z轴的数值差代表了球形机器人整体转动时最小的转弯半径,z的最大值为220,最小值为-100,由此得知球形机器人转弯时的半径约为320mm。
|
图 10 球形机器人转向运动ADAMS仿真结果 Fig.10 ADAMS simulation results of the steering motion |
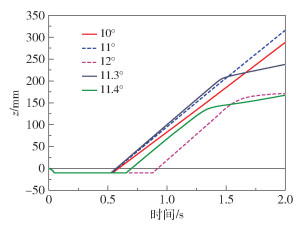
根据设计方案,球形机器人爬坡运动的驱动源与滚动运动相同,故不需要添加新的驱动。在ADAMS中构建与水平面呈一定角度的平板作为坡面,如图 11所示。爬坡运动中不同斜坡角度下球形机器人上升高度与时间之间的关系如图 12所示。可以看出,当斜面倾角为10°、11°时球形机器人都能顺利爬上斜坡,当斜坡倾角增加到12°时,球形机器人在爬升1.5s后高度达到稳定值,无法继续向上滚动。造成此现象的原因为,球形机器人在爬坡前具备一定的初速度和惯性,能依靠惯性在斜坡上进行一定路程的向上滚动,当球形机器人的驱动力以及与地面间的摩擦力不足以克服其所受重力沿斜坡面方向的分力时,球形机器人的速度逐渐减至0,此时就会处于原地打滑状态。因此,球形机器人的最大爬坡角度在11°~12°之间。选取0.1°为间隔进行仿真,结果见图 12,可以看出当斜坡角度为11.3°时,球形机器人能顺利爬上斜坡,当角度增大为11.4°时会出现原地打滑现象,因此可得出球形机器人的最大爬坡角度约为11.3°。
|
图 11 球形机器人爬坡ADAMS仿真示意图 Fig.11 ADAMS simulation diagram of the climbing motion |
|
图 12 球形机器人爬坡运动ADAMS仿真结果 Fig.12 ADAMS simulation results of the climbing motion |
在跳跃运动中,球形机器人的动力来源于跳跃驱动电机,故在与跳跃驱动电机连接的直齿轮上添加转动驱动。改变重力方向为系统坐标系的-x轴方向,并在3根弹簧导柱的位置增加弹簧。
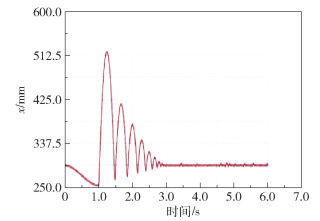
如图 13所示,起始位置装置的球形机器人质心位置在x轴的坐标为293mm,球形机器人自压缩弹簧后开始释放弹起,在1.25s左右达到弹起的最高点,此时的x轴坐标为519mm,弹起最大高度为519-293=226mm。之后球形机器人来回不断跳跃,且高度不断衰减,大约经历9次往复跳跃后,其跳跃高度衰减至0。故球形机器人最大跳跃高度约为226mm。
|
图 13 球形机器人跳跃运动ADAMS仿真结果 Fig.13 ADAMS simulation results of the jumping motion |
利用ADAMS软件对球形机器人的4种基本运动(滚动、转向、爬坡和跳跃)进行了动力学仿真,经过合理的模型简化,添加驱动与约束并设定驱动函数,得到球形机器人虚拟样机的运动性能仿真结果。制作实验室用滚-跳多运动模式球形机器人样机,并对该球形机器人样机进行测试[13]。球形机器人实验室样机如图 14所示,虚拟样机和实验室样机运动性能数据及相对误差如表 1所示。可以看出,球形机器人最大跳跃高度的实验测试数据和动力学仿真数据的相对误差为7.08%,大于滚动、转向和爬坡的相对误差。该较大误差产生的主要原因为在进行动力学仿真时为了简化模型,均忽略了跳跃时弹簧释放过程中振动所损失的能量,且均未考虑机械传动的内摩擦所产生的热量。球形机器人最小转弯半径的实验测试数据和动力学仿真数据的相对误差较大,为6.25%,分析该误差产生的主要原因在于,在转向运动过程中,随着速度的增加会产生一定的离心力,导致重摆的移动引起的整体质心偏移的效果减弱,转弯半径随着速度的增加而增加。在实际测试过程中,一直控制球形机器人的滚动速度在低速状态;而在动力学仿真过程中未控制滚动速度,滚动轨迹呈现为半径逐渐增大的圆弧,因此在理论最小转弯半径的分析中选取转向运动的前半圈来计算最小转弯半径,故测试数值小于仿真数值。尽管最大跳跃高度和最小转弯半径这两项的相对误差数值较大,但仍可以在一定程度上验证理论建模与动力学仿真的正确性。球形机器人最大滚动速度的实验测试数据和动力学仿真数据的相对误差较小,为1.24%,分析该误差产生的主要原因在于,在理论建模过程中未考虑滚动运动时球壳与地面间的滑动摩擦与机械传动中的内摩擦,在动力学仿真过程中未考虑机械传动中的内摩擦,而相对摩擦较小,所以理论建模与动力学仿真符合程度较高。球形机器人最大爬坡角度的实验测试数据和动力学仿真数据的相对误差最小,为0.08%,表明仿真模型简化合理,仿真参数与实测过程一致。

|
图 14 球形机器人实验室样机实物照片 Fig.14 Laboratory prototype of the spherical robot |
| 下载CSV 表 1 球形机器人虚拟样机和实验室样机运动性能数据 Table 1 Kinematic performance data for the virtual prototype and the laboratory prototype of the spherical robot |
本文设计了一种新颖的滚-跳多运动模式球形机器人结构方案,可实现滚动、转向、爬坡、跳跃功能的集成,获得球形机器人的多运动模式。根据设计方案建立了球形机器人4种基本运动的动力学模型,随后构建球形机器人虚拟样机并对其滚动、转向、爬坡和跳跃分别进行动力学仿真,最后通过物理样机实测数据验证了动力学仿真的正确性。围绕该滚-跳多运动模式球形机器人的动力学仿真分析对于后续探究其运动规律、实现轨迹规划与控制、快速调整落地后姿态等工作具有理论指导意义。
| [1] |
战强, 李伟. 球形移动机器人的研究进展与发展趋势[J]. 机械工程学报, 2019, 55(9): 1-17. ZHAN Q, LI W. Research progress and development trend of spherical mobile robots[J]. Journal of Mechanical Engineering, 2019, 55(9): 1-17. (in Chinese) |
| [2] |
HALME A, SCHÖNBERG T, WANG Y. Motion control of a spherical mobile robot[C]//Proceedings of 4th IEEE International Workshop on Advanced Motion Control. Mie, 1996: 259-264.
|
| [3] |
KAO W F, HSU C F. Motion control design for dynamic spherical mobile robot via fuzzy control approach[C]//2019 International Conference on Machine Learning and Cybernetics. Kobe, 2019: 8949225.
|
| [4] |
白杰, 党建军, 张谋, 等. 一种新型球形机器人机构设计及运动仿真[J]. 机械与电子, 2010(11): 73-75. BAI J, DANG J J, ZHANG M, et al. Design and motion simulation of a new kind of a spherical robot[J]. Machinery & Electronics, 2010(11): 73-75. (in Chinese) |
| [5] |
ALVES J, DIAS J. Design and control of a spherical mobile robot[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ: Journal of Systems and Control Engineering, 2003, 217(6): 457-467. |
| [6] |
KENYON S H, CREARY D, THI D, et al. A small, cheap, and portable reconnaissance robot[C]//Proceedings of SPIE 5778, Sensors, and Command, Control, Communications, and Intelligence (C3I) Technologies for Homeland Security and Homeland Defense Ⅳ. Orlando, 2005: 434-443.
|
| [7] |
MICHAUD F, DE LAFONTAINE J, CARON S. A spherical robot for planetary surface exploration[C]//6th International Symposium on Artificial Intelligence and Robotics & Automation in Space. Munich, 2001.
|
| [8] |
赵伟, 孙汉旭, 贾庆轩, 等. 具有两种运动模式的球形机器人动力学建模与设计[J]. 吉林大学学报(工学版), 2013, 43(5): 1386-1394. ZHAO W, SUN H X, JIA Q X, et al. Mechanical analysis and optimal design of a new spherical mobile robot with two moving modes[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(5): 1386-1394. (in Chinese) |
| [9] |
ZHAO B, LI M T, YU H T, et al. Dynamics and motion control of a two pendulums driven spherical robot[C]//The 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, 2010: 147-153.
|
| [10] |
AHN S S, LEE Y J. Novel spherical robot with hybrid pendulum driving mechanism[J]. Advances in Mechanical Engineering, 2014, 2014: 456727. |
| [11] |
孙汉旭, 赵伟, 张延恒. 新型变结构球形机器人运动分析[J]. 机械工程学报, 2013, 49(19): 40-47. SUN H X, ZHAO W, ZHANG Y H. Mechanical analysis about a new kind of variable structure spherical mobile robot[J]. Journal of Mechanical Engineering, 2013, 49(19): 40-47. (in Chinese) |
| [12] |
杨伟. 一种全向运动的球形机器人研究[D]. 天津: 天津大学, 2017. YANG W. Research on an omnidirectional spherical robot[D]. Tianjin: Tianjin University, 2017. (in Chinese) |
| [13] |
WU H S, LI B Y, WANG F T, et al. Design and analysis of the rolling and jumping compound motion robot[J]. Applied Sciences, 2021, 11: 10667. |








