2. 国网浙江省电力有限公司 电力科学研究院, 杭州 310014
2. Power Science Research Institute of Zhejiang Electric Power Co., Ltd., Hangzhou 310014, China
配电系统是电网系统重要的一环,当配电网出现故障,需及时辨别故障种类,以进行抢修工作,避免损失进一步扩大。随着电力系统不断扩大发展,现代配电网分支多且复杂,传统的配电网故障分类方法无论是在速度还是精度上都不能够满足现代配电网故障的分类需求[1-3]。
为满足现代配电网系统的分类需求,当前许多算法已被应用于配电网故障分类。文献[4]利用离散小波包变换对故障电量信号进行分解并构建时频域矩阵,再将其输入卷积深度置信网络中,该网络能自主提取特征量并进行分类,所提方法不仅获取的特征量辨识度高,而且能适应多种不同的运行环境;文献[5]针对现代智能配电网故障信号不易采集等问题,提出基于微型同步相量测量单元量测数据的状态估计数据处理方法,提高了测试数据集的准确性;文献[6]针对配电网分支多等问题,将配电网的实际监测数据导入深度置信模型,采用对比歧化算法优化初始参数选择和加速模型训练,再测试模型对样本的识别精度,提高了配电网故障分类的辨识度;文献[7]提出通过多任务隐学习结构对标记数据进行信息补充,以有限的故障数据得到更高精度的分类。
随着人工智能技术的迅速发展,神经网络算法逐渐成为配电网故障诊断和定位领域的热点,但是该算法需要大量的样本且模型极易出现过拟合[8]。在长期处于平稳运行状态的电力系统中,故障发生的概率很小,属于小样本事件,且要求对故障进行迅速的处理。支持向量机(support vector machine,SVM)具备完善的数学理论,不需要过多的样本,与神经网络相比是一类泛化能力优秀且收敛迅捷的算法[9],非常适合于配电网故障分类任务[10]。事实上,支持向量机已经在电力系统故障分类中得到广泛应用,文献[11]用小波分解方法对故障分量进行分解,获取重构信号的均方根和欧式距离作为特征量输入SVM,充分体现了所有故障类型的特征,便于SVM识别,提高了SVM的分类精度;文献[12]对故障处三相电压进行小波变换,以三相电压的小波变换奇异熵值和零序电压第一层低频能量为特征量输入SVM,避免了复杂的整定计算,大幅提升了SVM的运算速度,在实际应用中可起到极为关键的作用;文献[13]分析了相电压差与故障类型的相关性,通过距离可分性判断提取特征量,然后输入SVM模型进行故障分类,该方法仅需少量测点电压数据即可完成故障分类,节省了资源成本;文献[14]考虑了反射信号的幅值以及反射波与入射波之间的互相关峰值,为支持向量机生成故障电流数据集,并提出一种多层增强SVM分类器结合经典的多维尺度(multidimensional scaling,MDS)特征提取算法,该算法优化了核参数,提高了训练速度,可达到高速高效分类的效果;文献[15]利用希尔伯特-黄变换带通滤波算法对三相电压三相电流以及零序电压进行等宽频分解,构建时频矩阵,以时频矩阵得到的有效奇异值作为特征量输入SVM进行分类训练,该方法在存在噪声干扰、采样不同步等环境下均有较好的适应性;文献[16]利用卷积神经网络(convolutional neural networks,CNN)调整SVM参数,以达到提高SVM故障分类精度的目的;文献[17]通过自适应进化学习优化神经网络,并将其应用于SVM调参,以提高SVM在配网故障分类中的泛化性与时效性。
文献[11-17]以SVM为中心,通过放大故障特征区分度或利用其他算法对SVM进行调参等手段提高SVM的分类精度与速度,虽然取得了一定的效果,但仍存在改进空间:①文献[11-15]注重故障信号的特征量提取,但忽视了对SVM的优化改进;②文献[16-17]则是注重对SVM的调参,但故障数据的处理工作较为简单。
为全面提升SVM的故障分类精度,针对上述问题①,本文提出采用综合S变换对故障数据处理以提取特征量,S变换作为经典的数据处理法,具备良好的线性与局部性[18]。此外,考虑到均方根可以体现数据自身的幅值特性[19],具有增加数据间区分度的作用,将处理结果的均方根作为一种特征量。同时,因均值在数字信号处理中具有平滑噪声、保护信号边缘的作用[20],故将处理结果的均值作为特征量之一。针对问题②,目前有许多针对SVM的参数优化方法,文献[21]基于差分进化(differential evolution,DE)算法的全局寻优能力,对SVM的核参数和惩罚参数进行优化,以提高SVM的分类精度与泛化能力;文献[22]引入量子遗传算法(quantum genetic algorithm,QGA)对核参数进行寻优,与传统的遗传算法(genetic algorithm,GA)相比,QGA具有更优的多样性特征以及更佳的收敛性, 但是传统的量子遗传算法中基于固定步长旋转角调整策略的量子旋转门更新操作可能会让寻优过程存在陷入局部极值的风险。因此本文在QGA的基础上引入一种自适应动态旋转角,它能有效避免算法在迭代初期陷入局部收敛。随后在Simulink上建立IEEE33模型并进行仿真实验,实验结果表明,本文针对两种问题提出的改进方案取得了预期效果。
1 数据处理 1.1 数据采集构建性能稳定的故障分类模型的前提是提取有足够区分度的特征量[23],特征量来源于配电网故障点数据,因此需采集配电网故障点数据。根据叠加定理,配电网故障电流为故障分电流与正常运转时负荷电流之和,零序故障电压同理[10]。本文通过Simulink软件仿真各故障类型,选取故障后一个周波的三相电压和三相电流信号作为分析数据。
1.2 特征量提取由Simulink仿真获取的数据需经过提取以得到有一定辨识度的特征量。S变换是在小波变换的基础上进行拓展,采用高斯窗函数且窗宽与频率的倒数成正比,免去了窗函数的选择问题且改善了窗宽固定的缺陷[24],使得从原始数据中提取的特征量的区分性更为明显。因此本文采用S变换对数据进行提取。
以故障点三相电压信号u(t)为例,其S变换的表达式如下。
| $ S(\tau, f)=\int_{-\infty}^{\infty} u(t) w(t-\tau, f) \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} f t} \mathrm{~d} t $ | (1) |
| $ w(t-\tau, f)=\frac{|f|}{\sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{\frac{-(t-\tau) 2 f^2}{2}} $ | (2) |
式中,
将数据经S变换后可得到一个二维矩阵,可以从这个矩阵的元素中获取幅值和相位信息。考虑到我国电网频率为50 Hz,为契合实际,本文以f=50 Hz时所得的S变换处理结果为特征量之一。
为直观表现出故障发生时故障分量的波形特征,需要进一步对底层低频分量进行提取,而不是直接使用S变换处理结果作为最终特征量。洪涛等[19]在数据处理过程中发现,均方根可以体现数据自身的幅值特性,不同类型故障下的数据幅值特性能被均方根放大,区分度也随之增加。然而只采用均方根作为特征量,在遇到噪声干扰时,会引起数据失真,影响分类精度。为解决上述问题,考虑到均值特征在数字信号处理中具备平滑噪声、保护信号边缘的作用,本文提出一种结合均方根与均值的特征提取方法,具体如下。
首先,根据式(1)、(2)得到故障信号的S变换结果,并求出该结果的均方根和均值,分别如下。
故障分量二重重构信号均方根
| $ R_j=\sqrt{\frac{1}{N} \sum\limits_{n=1}^N S^2(\tau, f)} \quad j=a, b, c $ | (3) |
故障分量二重重构信号均值
| $ M_j=\frac{1}{N} \sum\limits_{n=1}^N S(\tau, f) \quad j=a, b, c $ | (4) |
式中,N为一个工频周期;j为电压/电流相位;a, b, c分别代表a相、b相、c相。
通过上述方法提取特征量,解决了噪声干扰引起的数据偏差问题,增强了数据可靠性,为配电网故障分类奠定了良好基础。
2 量子遗传进化算法及优化 2.1 量子遗传进化算法量子遗传算法在2000年由Han等[25]提出,是基于量子计算理论的一个分支。量子遗传算法与遗传算法的区别在于它们的种群编码方式和进化策略均不相同。QGA种群编码方式是利用量子位和量子叠加态对染色体进行编码,即通过量子比特编码的方式编码,使一个染色体同时表示多个状态的信息,丰富种群多样性;同时使用量子旋转门对种群进行更新,以当前最优个体的信息为引导进化。在迭代过程中,每个量子位的叠加态将会塌缩到一个确定的状态,从而趋于稳定,达到收敛,最后实现寻优的目的。由于采用了独特的编码方式和更新方式,量子遗传算法比传统遗传算法更具种群多样性、高速度与高精度。QGA流程如下。
1) 量子比特编码
量子差分进化算法基于量子位和量子叠加态原理。量子位一般有3种状态,即分别处于1、0态(分别代表|1〉态和|0〉态)或者两种状态之间,通常量子位|φ〉的表达式为
| $ |\varphi\rangle=a|0\rangle+b|1\rangle $ | (5) |
式中,a、b分别代表量子态处于0态和1态的概率,且满足|a|2+|b|2=1。
在量子遗传算法中,量子比特编码被用来储存和表达一个基因,该基因即|φ〉,处且仅处于上述3种状态,这意味着单个基因是一个不确定的信息。当多个基因组合成为单个染色体Pi=
2) 种群更新策略
量子门是量子遗传算法更新种群的工具,它的结构直接影响QGA的质量[26]。QGA通常采用量子旋转门作为更新策略,其定义如下。
| $ \boldsymbol{h}(\theta)=\left[\begin{array}{c} \cos \theta_i-\sin \theta_i \\ \sin \theta_i \cos \theta_i \end{array}\right] $ | (6) |
式中,θ代表旋转角度, i代表迭代次数。当QGA量子旋转门进一步更新时,表达式为
| $ \boldsymbol{h}(\theta)\left[\begin{array}{l} a_i \\ b_i \end{array}\right]=\left[\begin{array}{c} \cos \theta_i-\sin \theta_i \\ \sin \theta_i \cos \theta_i \end{array}\right]\left[\begin{array}{l} a_i \\ b_i \end{array}\right] $ | (7) |
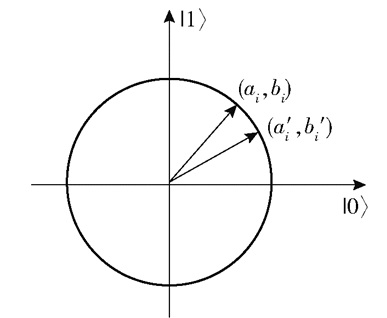
量子旋转门为更新策略中的旋转角度,旋转角度由种群策略进行调整,决定量子坍塌至某一状态的概率,图 1为其示意图。
|
图 1 量子旋转门示意图 Fig.1 Schematic diagram of the quantum revolving door |
从图 1中可以看到,基因的状态概率[ai, bi]T经过更新策略变换至[ai′, bi′]T,进而影响多样性与寻优范围。若能让状态概率的旋转角度θ根据当前迭代状况自行合理调整,就能将算法的多样性与寻优区域控制在合理区间,使算法不会在前期就陷入局部收敛状态。
组合差分进化算法(combined differential evolution algorithm,CoDE)在传统差分进化算法的基础上,增加了自适应向量产生策略和控制参数,缓解了局部收敛的问题[27]。受此启发,本文提出一种自适应动态旋转角,当处于算法迭代初期时,将其控制在π/4(设定角度范围[0, π/2])左右,即aj, bj的数值保持在
| $ \Delta \theta=\frac{\left|H_{\text {best }}-H_{\text {current }}\right|}{H_{\text {best }}} $ | (8) |
式中,Hbest代表该次迭代种群中最佳个体适应值,Hcurrent代表该次迭代种群中当前正在被更新的个体适应值。最终Δθ∈[0.001π,0.005π]。
设定好量子旋转门的自适应旋转角后,还需对量子状态概率设定阈值X,当种群更新过程出现过早陷入收敛或错误等情况,可将阈值作为判别标准检测出错误并强制修复概率,具体如式(9)所示。
| $ \left[a_i, b_i\right]^{\mathrm{T}}= \begin{cases}{[\sqrt{X}, \sqrt{1-X}]^{\mathrm{T}}, } & a_i^2>X \\ {[\sqrt{1-X}, \sqrt{X}]^{\mathrm{T}}, } & a_i^2<1-X\end{cases} $ | (9) |
在式(8)和式(9)的作用下,量子旋转门的旋转角能根据当前情况作出自适应调整,量子遗传算法在算法初中期多样性显著提高,全局寻优能力更强且不会过早陷入局部收敛,进而导致分类精度不佳;同时,量子旋转门的旋转角在算法后期会控制基因的状态概率偏向最优区域,增强算法的局部寻优能力,不至于错过最优参数,为提高配电网故障分类精度起到了决定性作用。
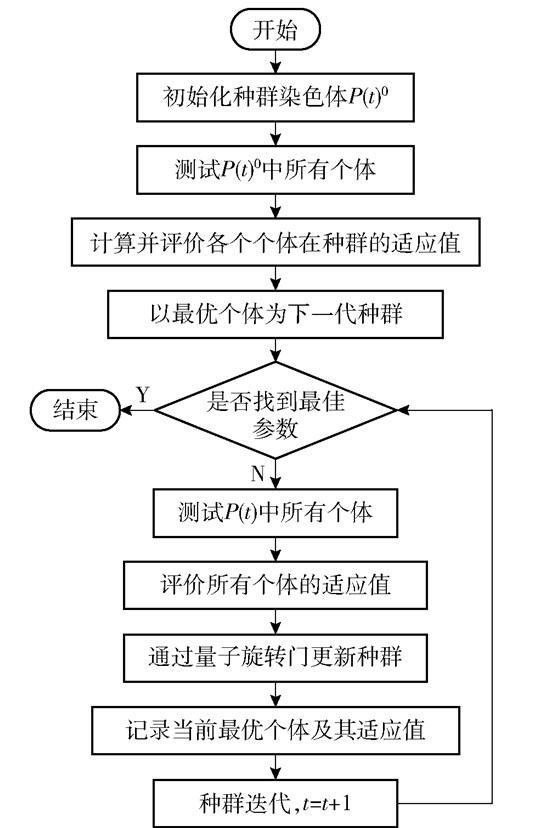
3 基于改进量子遗传算法的SVM本文提出的故障分类方法核心是通过改进后的QGA帮助SVM找到最优正则化参数和核函数参数,其具体步骤如下,流程图如图 2所示。
|
图 2 SVM结合改进量子遗传算法应用流程 Fig.2 Application flow of SVM combined with the improved quantum genetic algorithm |
步骤1 初始化量子遗传算法种群的染色体数量P(t)={P1t, P2t, P3t, …, Pnt},n代表种群规模,Pnt代表第t代种群中的单个染色体。
步骤2 测量当前代数种群中的所有独立染色体。
步骤3 计算所有个体在当前种群中的适应值。
步骤4 记录当代种群中的最佳个体和适应值。
步骤5 检测当前代数种群最佳个体是否满足目标要求,若寻找到SVM最优参数或迭代次数达到最大值,则结束QGA并将结果输入至SVM,否则以最佳个体和适应值作为下一代种群继续执行。
步骤6 利用式(8)根据种群代数自适应调整量子旋转门算子的角度,通过旋转门算子更新个体。
步骤7 利用基因突变算子突变并更新染色体,得到下一代种群,返回至步骤2继续执行。
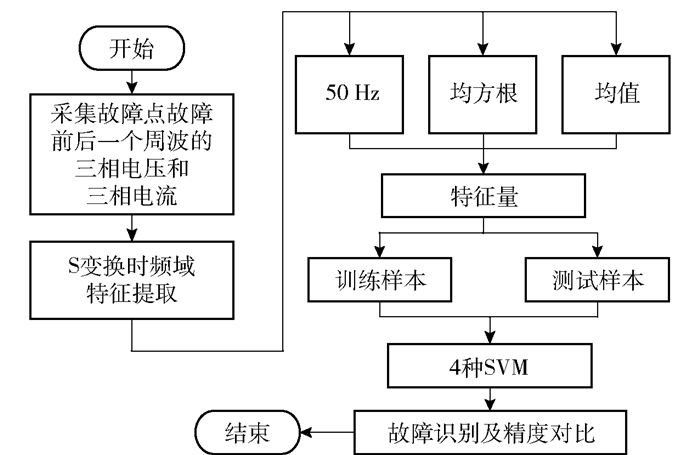
4 仿真算例分析 4.1 仿真流程为了验证第3节所提组合算法的优越性,采用标准量子遗传、改进量子遗传、差分进化、组合差分进化共4种不同算法对SVM进行调参,并对比结果。整个仿真流程如图 3所示,具体步骤如下。
|
图 3 4种不同调参方式下的SVM应用流程 Fig.3 SVM application flow of four different optimization algorithms |
1) 将故障发生后一个周波内的三相电压信号和三相电流信号输入至故障分类系统。
2) 利用S变换处理输入信号,以50 Hz下的结果以及全频率处理结果的均方根和均值作为特征量。
3) 将特征量数据按比例通过随机森林分类划分为训练样本和测试样本,输入至4种SVM中。
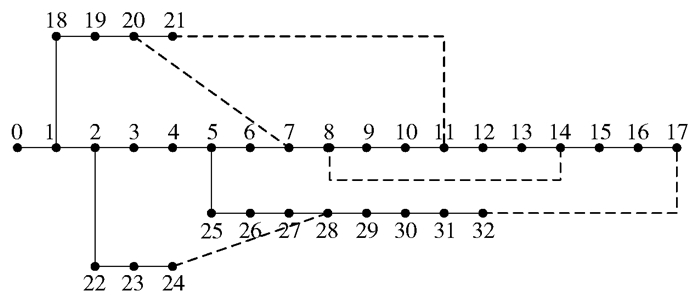
4.2 仿真模型与样本数据为验证基于改进量子遗传算法的SVM在配电网故障分类中相较于未优化SVM的优越性,利用Simulink建立IEEE33节点配电网模型作为研究对象,配电网结构拓扑图如图 4所示。
|
图 4 配电网仿真模型拓扑图 Fig.4 Topology diagram of the distribution network simulation model |
配电网电压基值为12.66 kV,功率基值为100 MW,仿真样本频率为50 Hz,仿真步长为33.333 μs,仿真时长为0.1 s,故障发生时段为1/50~3/50 s。模型节点数为33个,支路数为37个,在10个节点处分别设置10种不同类型的故障;同时,针对不同的故障类型设置不同的过渡电阻和初始相角,通过仿真收集数据,数据经S变换处理得到故障特征量样本数据共7 500组,接着按照随机森林分类划分为5 250个训练样本,2 250个测试样本,数据分布如表 1所示。
| 下载CSV 表 1 各类型故障分布数据 Table 1 Distribution data of various types of faults |
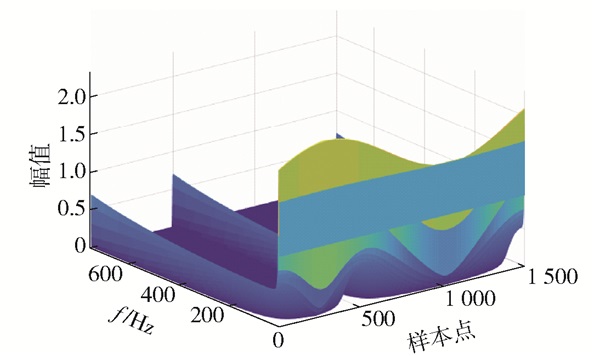
当故障发生时,通过BUS原件中的示波器收集故障时间段内的三相电压、三相电流的波形和数据,经S变换处理,得到50 Hz下的S变换处理数据,同时求出S变换处理所有频率下的平均值和均方根,以上述三者作为特征量。现以AG故障A相电压作为故障相代表,展示S变换处理得到的特征量结果,如图 5所示。
|
图 5 AG故障A相电压S变换结果 Fig.5 A-phase voltage S conversion result for an AG fault |
从图 5可以看出,S变换的处理结果随着频率和样本点的变化,幅值都有较为明显的变换区分度,足够支撑SVM对故障分类的需求。
4.3 故障识别结果分析 4.3.1 不同参数寻优算法获取特征量后,按照随机森林分布得到训练样本与测试样本,将所得样本同时输入至量子遗传算法SVM中,并将分别用未改进的量子遗传算法、差分进化算法、组合差分进化算法进行调参的SVM作为对比,依次完成计算后,所得分类准确度与耗时对比如表 2、3所示。
| 下载CSV 表 2 不同寻优算法的故障分类精度对比 Table 2 Comparison of fault classification accuracy with different optimization algorithms |
| 下载CSV 表 3 各算法的分类耗时对比 Table 3 Comparison of classification time for each algorithm |
从表 2、3的数据可知,经过改进QGA算法优化后的SVM在进行故障分类时,相较传统差分进化算法优化后的SVM的分类精度更佳,计算耗时是DE的1/5。而标准QGA算法在经过改进后,SVM故障分类精度从98.18%进一步提高至99.69%,验证了优化方向的正确性。
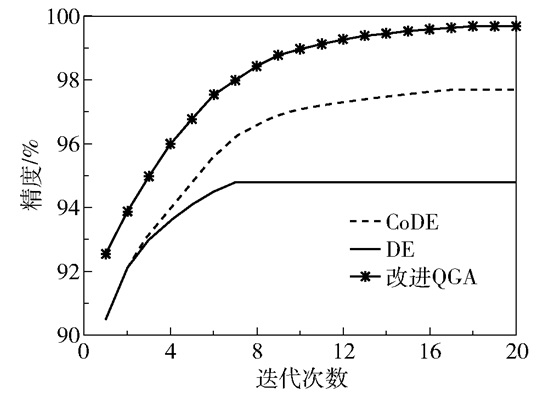
为更直观展示改进后QGA相对于传统差分进化算法的优越性,将改进QGA、DE、CoDE的精度迭代曲线进行对比,如图 6所示。
|
图 6 精度进化曲线对比 Fig.6 Comparison of accuracy evolution curves |
从图 6可以看出,DE算法的精度进化曲线在第8次迭代时就陷入局部收敛,导致精度止步于94.86%。相比之下,CoDE算法的有效迭代次数达到17次,最终的分类精度也更高,为97.57%。然而改进QGA算法的种群更新策略明显更佳,最终分类精度达到99.69%。
4.3.2 不同特征量提取方法为体现综合S变换结果的均方根和均值作为特征量的效果,设置对照实验,将处理结果原数值作为特征量1,处理结果均方根作为特征量2,处理结果均值作为特征量3,4.2节处理方式所得样本数据作为特征量4,均采用改进后的量子遗传算法对SVM进行优化,最终SVM分类结果如表 4所示。
| 下载CSV 表 4 不同特征量下故障分类精度对比 Table 4 Comparison of fault classification accuracy with different characteristic quantities |
从表 4中的数据可以判断,以综合S变换处理结果的均方根和均值作为特征量,可有效提高故障分类精度。可见该特征量的提取方式有效综合了均方根与均值的优点,放大了不同故障特征量的区分度,使得最终故障分类结果的精度提高。
5 结论(1) 在S变换数据处理过程中,综合工频状态下的S变换结果以及S变换结果的均值和方差为特征量,可有效提高数据的抗噪声干扰能力和特征量辨识度,分类精度较原始数据提高了2.09%。
(2) 针对其他算法耗时较长、故障分类实用性欠佳的问题,提出的量子遗传算法的运算速度比传统的差分进化算法快4倍,在配电网故障分类工作中更具备实用性。
(3) 针对量子遗传算法可能陷入局部收敛的情况,提出将自适应动态旋转角应用至QGA中,改进后的QGA分类准确率达99.69%,较标准QGA提高了1.51%。
| [1] |
MORA-FLÓREZ J, CORMANE-ANGARITA J, ORDÓÑEZ-PLATA G. k-means algorithm and mixture distributions for locating faults in power systems[J]. Electric Power Systems Research, 2009, 79(5): 714-721. DOI:10.1016/j.epsr.2008.10.011 |
| [2] |
MIRZAEI M, A AB KADIR M Z, MOAZAMI E, et al. Review of fault location methods for distribution power system[J]. Australian Journal of Basic and Applied Sciences, 2009, 3(3): 2670-2676. |
| [3] |
徐先峰, 徐晨杰, 张艳波, 等. 基于行波特征分类的有源配电网故障定位[J]. 重庆大学学报, 2022(11): 59-68. XU X F, XU C J, ZHANG Y B, et al. Fault location of active distribution network based on traveling wave feature classification[J]. Journal of Chongqing University, 2022(11): 59-68. (in Chinese) |
| [4] |
洪翠, 付宇泽, 郭谋发, 等. 基于卷积深度置信网络的配电网故障分类方法[J]. 电力自动化设备, 2019, 39(11): 64-70. HONG C, FU Y Z, GUO M F, et al. Fault classification method based on CDBN for distribution network[J]. Electric Power Automation Equipment, 2019, 39(11): 64-70. (in Chinese) |
| [5] |
张麒. 基于深度学习的智能配电网故障识别与分类方法研究[D]. 北京: 北京理工大学, 2018. ZHANG Q. Research on fault identification and classifi-cation method of smart distribution network with deep learning[D]. Beijing: Beijing Institute of Technology, 2018. (in Chinese) |
| [6] |
杨启洪, 秦川, 刘杰荣, 等. 基于对比歧化和深度置信网络的配电网故障类型识别[J]. 电网与清洁能源, 2019, 35(2): 52-57. YANG Q H, QIN C, LIU J R, et al. Fault identification of distribution network based on contrast disproportionate algorithm and deep belief network[J]. Power System and Clean Energy, 2019, 35(2): 52-57. (in Chinese) DOI:10.3969/j.issn.1674-3814.2019.02.008 |
| [7] |
GILANIFAR M, WANG H, CORDOVA J, et al. Fault classification in power distribution systems based on limited labeled data using multi-task latent structure learning[J]. Sustainable Cities and Society, 2021, 73: 103094. DOI:10.1016/j.scs.2021.103094 |
| [8] |
詹惠瑜, 刘科研, 盛万兴, 等. 有源配电网故障诊断与定位方法综述及展望[J/OL]. 高电压技术. (2022-02-25). DOI: 10.13336/j.1003-6520.hve.20211604. ZHAN H Y, LIU K Y, SHENG W X, et al. Literature review and prospects of fault diagnosis in active distribution network[J/OL]. High Voltage Engineering. (2022-02-25). DOI: 10.13336/j.1003-6520.hve.20211604.(inChinese) |
| [9] |
WU Y H. Statistical learning theory[J]. Technometrics, 1999, 41(4): 377-378. DOI:10.1080/00401706.1999.10485951 |
| [10] |
何旭, 姜宪国, 张沛超, 等. 基于SVM的小样本条件下继电保护可靠性参数估计[J]. 电网技术, 2015, 39(5): 1432-1437. HE X, JIANG X G, ZHANG P C, et al. SVM based pa-rameter estimation of relay protection reliability with small samples[J]. Power System Technology, 2015, 39(5): 1432-1437. (in Chinese) |
| [11] |
洪翠, 付宇泽, 郭谋发, 等. 改进多分类支持向量机的配电网故障识别方法[J]. 电子测量与仪器学报, 2019, 33(1): 7-15. HONG C, FU Y Z, GUO M F, et al. Identification method of distribution network faults based on improved multi-classification support vector machine[J]. Journal of Electronic Measurement and Instrumentation, 2019, 33(1): 7-15. (in Chinese) |
| [12] |
胡伟, 李勇, 曹一家, 等. 基于LOF和SVM的智能配电网故障辨识方法[J]. 电力自动化设备, 2016, 36(6): 7-12. HU W, LI Y, CAO Y J, et al. Fault identification based on LOF and SVM for smart distribution network[J]. Electric Power Automation Equipment, 2016, 36(6): 7-12. (in Chinese) |
| [13] |
刘科研, 董伟杰, 肖仕武, 等. 基于电压数据SVM分类的有源配电网故障判别及定位[J]. 电网技术, 2021, 45(6): 2369-2379. LIU K Y, DONG W J, XIAO S W, et al. Fault identification and location of active distribution network based on SVM classification of voltage data[J]. Power System Technology, 2021, 45(6): 2369-2379. (in Chinese) |
| [14] |
CHO M Y, THOM H T. Fault diagnosis for distribution networks using enhanced support vector machine classi-fier with classical multidimensional scaling[J]. Journal of Electrical Systems, 2017, 13(3): 415-428. |
| [15] |
高伟, 陈伟凡, 杨耿杰, 等. 基于奇异值分解和多级支持向量机的配电网故障类型识别[J]. 电子测量与仪器学报, 2018, 32(2): 62-71. GAO W, CHEN W F, YANG G J, et al. Fault type identification for distribution network based on singular value decomposition and multi-level support vector machine[J]. Journal of Electronic Measurement and Instrumentation, 2018, 32(2): 62-71. (in Chinese) |
| [16] |
吉兴全, 陈金硕, 张玉敏, 等. 基于CNN-SVM的配电网故障分类研究[J]. 智慧电力, 2022, 50(1): 94-100. JI X Q, CHEN J S, ZHANG Y M, et al. Fault classification in distribution network based on CNN-SVM[J]. Smart Power, 2022, 50(1): 94-100. (in Chinese) |
| [17] |
SRINIVASA RAO T C, TULASI RAM S S, SUBRAH-MANYAM J B V. Neural network with adaptive evolutionary learning and cascaded support vector machine for fault localization and diagnosis in power distribution system[J]. Evolutionary Intelligence, 2022, 15(2): 1171-1182. |
| [18] |
魏学强, 秦晶晶, 万森林, 等. 广义S变换在地震数据处理中的应用与展望[J]. 大地测量与地球动力学, 2017, 37(3): 327-330. WEI X Q, QIN J J, WAN S L, et al. The applications and prospects of generalized S transformation in seismic data processing[J]. Journal of Geodesy and Geodynamics, 2017, 37(3): 327-330. (in Chinese) |
| [19] |
洪涛, 黄志奇, 杨畅. 涡轮泵实时故障检测的快速支持向量机算法[J]. 仪器仪表学报, 2012, 33(8): 1786-1792. HONG T, HUANG Z Q, YANG C. Fast support vector machine algorithm for turbopump real-time fault detection[J]. Chinese Journal of Scientific Instrument, 2012, 33(8): 1786-1792. (in Chinese) |
| [20] |
王欣, 王德隽. 离散信号的近均值滤波[J]. 电子学报, 1989, 17(4): 7-12. WANG X, WANG D J. A nearest-mean filter of discrete signals[J]. Acta Electronica Sinica, 1989, 17(4): 7-12. (in Chinese) |
| [21] |
陈涛, 雍龙泉, 邓方安, 等. 基于差分进化算法的支持向量机参数选择[J]. 计算机工程与应用, 2011, 47(5): 24-26. CHEN T, YONG L Q, DENG F A, et al. Parameters se-lection of support vector machine based on differential evolution[J]. Computer Engineering and Applications, 2011, 47(5): 24-26. (in Chinese) |
| [22] |
王波, 刘树林, 蒋超, 等. 基于量子遗传算法优化RVM的滚动轴承智能故障诊断[J]. 振动与冲击, 2015, 34(17): 207-212. WANG B, LIU S L, JIANG C, et al. Rolling bearings' intelligent fault diagnosis based on RVM optimized with quantum genetic algorithm[J]. Journal of Vibration and Shock, 2015, 34(17): 207-212. (in Chinese) |
| [23] |
杨凤生, 熊波, 蔡广林, 等. 基于数据分析的配电网故障数据特征变量提取[J]. 电力大数据, 2018, 21(3): 22-26. YANG F S, XIONG B, CAI G L, et al. Characteristic variable extraction of fault data in distribution feeder based on data analysis[J]. Power Systems and Big Data, 2018, 21(3): 22-26. (in Chinese) |
| [24] |
易吉良, 彭建春, 谭会生. S变换在电能质量扰动分析中的应用综述[J]. 电力系统保护与控制, 2011, 39(3): 141-147. YI J L, PENG J C, TAN H S. A summary of S transform applied to power quality disturbances analysis[J]. Power System Protection and Control, 2011, 39(3): 141-147. (in Chinese) |
| [25] |
HAN K H, KIM J H. Genetic quantum algorithm and its application to combinatorial optimization problem[C]// Proceedings of the 2000 Congress on Evolutionary Computation. La Jolla, 2000: 1354-1360.
|
| [26] |
周晟. 基于改进量子遗传算法的机械臂轨迹优化[J]. 组合机床与自动化加工技术, 2021(6): 33-37. ZHOU S. Manipulator based on improved quantum ge-netic algorithm trajectory optimization[J]. Modular Machine Tool and Automatic Manufacturing Technique, 2021(6): 33-37. (in Chinese) |
| [27] |
董明刚, 王宁, 艾兵, 等. 基于差分进化的优化方法及应用[M]. 北京: 人民邮电出版社, 2019. DONG M G, WANG N, AI B, et al. Differential evolu-tion-based optimization methods and applications[M]. Beijing: Posts and Telecom Press, 2019. (in Chinese) |








