2. 辽宁沃尔德沃克科技有限公司, 沈阳 110121
2. Liaoning World Walker Technology Co., Ltd., Shenyang 110121, China
燃气轮机作为能源动力设备被广泛应用于我国天然气长输管道上,主要是用作驱动离心式压缩机。燃气轮机长期在高温、高压、高转速、高机械应力等恶劣环境下工作,随着时间的推移,其主要部件(如压气机、燃烧室、涡轮等)的性能会逐渐偏离设计点,出现积垢、泄漏、磨损、机械损伤、热畸变等状况,进而导致发生重大安全生产事故[1-5]。而以上这些故障均与燃气轮机的气路健康状态有关。
目前,关于燃气轮机的气路分析主要有基于模型机理和基于数据驱动两种方法[6-7]。其中,基于模型机理的故障诊断方法无需大量的数据样本集,可以通过热力学建模对故障类型进行量化,但其本身属于逆求解过程,在与实际系统同步时容易出现算法发散;气路故障数据具有非线性、小样本、高维度等特点,因此采用数据驱动的方式将故障类型进行分类是一种有效的方法。涂雷等[8]、张云等[9]采用支持向量机(support vector machine,SVM)对三轴燃气轮机气路故障进行诊断,并分别利用人工蜂群算法、灰狼算法对SVM的超参数进行寻优,但评价过程中未给出样本的故障特征向量,且SVM模型在多分类问题上表现一般;Kou等[10]对比了卡尔曼滤波器、反向传播(back propagation,BP)神经网络及宽神经网络模型的诊断结果,但所诊断的故障种类较少,不具有代表性;Stamatis等[11]提出一种非线性优化模型,但结果难以跳出局部最优解,导致诊断结果出现大量偏差;Zedda等[12]采用遗传算法优化目标函数并计算了燃气轮机性能退化的程度,然而算法控制变量较多,收敛慢;Meskin等[13]采用逻辑回归方法对故障模式进行混合建模,数据对噪声的敏感适应性较差。以上智能算法的应用对于燃气轮机气路故障的诊断具有重要意义,但研究对象多为三轴燃气轮机且数据多取自电厂,对于长输管道中常见的双轴燃气轮机涉及较少,另外数据样本大多不均衡,所选智能算法受浅层神经网络本身结构限制[14-17],泛化能力较弱。基于此,本文通过建模获得不同气路故障类型的数据集,运用相关向量机(relevance vector machine,RVM)模型对燃气轮机气路故障进行分类诊断,并采用改进鸡群算法(enhanced chicken swarm optimization,ECSO)对RVM模型的超参数进行寻优,确定最佳的RVM模型,以提高燃气轮机气路故障诊断的准确性。
1 ECSO模型与RVM模型 1.1 ECSO模型鸡群算法(chicken swarm optimization,CSO)模型属于群体智能仿生算法[18-19]。设鸡群搜索空间维数为D,鸡群总体数量为N,公鸡、母鸡、小鸡和小鸡与母鸡有母子关系的母鸡数量分别为NR、NH、NC和NM,不同鸡种均有不同的运行规律,公鸡位置更新公式为
| $ x_{i, j}(t+1)=x_{i, j}(t) \times\left[1+\operatorname{randn}\left(0, \sigma^2\right)\right] $ | (1) |
| $ \sigma^2= \begin{cases}1, & f_i \leqslant f_r \\ \exp \left(\frac{f_r-f_i}{\left|f_i\right|+\varepsilon}\right), & f_i>f_r\end{cases} $ | (2) |
式中,xi,j(t+1)为第t+1次迭代中第i只公鸡在j维空间上的位置;randn(0, σ2)表示均值为0、标准差为σ2的高斯随机数;ε为极小常数,用于避免分母为0;fi和fr分别表示第i只公鸡和第r只公鸡的适应度,其中个体r为随机抽取,i≠r。母鸡位置更新公式为
| $ \begin{aligned} & \quad x_{i, j}(t+1)=x_{i, j}(t)+\exp \left(\frac{f_i-f_{r 1}}{\left|f_i\right|+\varepsilon}\right) \times {rand} \times \\ & {\left[x_{r 1, j}(t)-x_{r 2, j}(t)\right]+\exp \left(f_{r 2}-f_i\right) \times {rand} \times\left[x_{r 2, j}(t)-\right.} \\ & \left.x_{r 1, j}(t)\right] \end{aligned} $ | (3) |
式中,rand表示(0, 1)之间的随机数;r1为第i个母鸡对应的公鸡;r2为除小鸡外任意个体;fr1和fr2分别表示r1和r2的适应度。小鸡位置更新公式为
| $ x_{i, j}(t+1)=x_{i, j}(t)+F L\left[x_{m, j}(t)-x_{i, j}(t)\right] $ | (4) |
式中,m为第i只小鸡跟随的母鸡,xm,j(t)为母鸡所在的位置;FL为跟随系数,在(0, 2)之间取值。
鸡群算法中公鸡位置更新属于高斯变异过程,只是标准差选择有所不同,母鸡位置更新与粒子群寻优方法类似。然而在公鸡位置更新过程中没有考虑算法迭代后期种群多样性的下降过程,母鸡位置更新则缺乏对个体自身位置的信息记忆。针对这些不足,分别采用柯西变异和莱维飞行对公鸡、母鸡的位置更新进行优化。
采用自适应策略将公鸡位置更新分为两部分:前期采用高斯变异,后期采用柯西变异以增强种群多样性。通过线性递减方式增加后期收敛速度,将式(1)优化为
| $ x_{i, j}(t+1)= \\ \left\{\begin{array}{cl} \frac{\max t-t}{\max t} \times x_{i, j}(t) \times\left[1+\operatorname{randn}\left(0, \sigma^2\right)\right], & 0<t \leqslant \frac{\max t}{2} \\ \frac{\max t-t}{\max t} \times x_{i, j}(t) \times\left[1+\operatorname{cauchy}\left(0, \sigma^2\right)\right], & \frac{\max t}{2}<t<\max t \end{array}\right. $ | (5) |
式中,cauchy(0, σ2)为柯西随机数,maxt为最大迭代次数。
母鸡位置更新借鉴布谷鸟算法中的莱维飞行理论,增加权重因子进行偏好随机游动,将式(3)优化为
| $ \begin{aligned} & \quad x_{i, j}(t+1)=\omega(t) \times x_{i, j}(t)+\exp \left(\frac{f_i-f_{r 1}}{\left|f_i\right|+\varepsilon}\right) \times \\ & {rand} \times\left[x_{r 1, j}(t)-x_{r 2, j}(t)\right]+\exp \left(f_{r 2}-f_i\right) \times {rand} \times \\ & {\left[x_{r 2, j}(t)-x_{r 1, j}(t)\right]} \end{aligned} $ | (6) |
| $ \omega (t)={{\omega }_{\min }}+\left( {{\omega }_{\max }}-{{\omega }_{\min }} \right)\times \exp -\left( k\times {{\left( \frac{t}{\max t} \right)}^{2}} \right) $ | (7) |
式中,ω为惯性权重;ωmax和ωmin分别为惯性权重的最大值和最小值;k为游走因子。
综上所述,形成改进鸡群算法。该算法有效平衡了局部搜索和整体搜索之间的算力,增强了算法的稳定性及提高了收敛速度,减少了搜索的盲目性。
1.2 RVM模型RVM模型通过对先验数据进行一系列筛选,删除不相干的点,从而保留体现数据特征的相关向量,得到更稀疏的解,与SVM模型相比在处理小样本、非线性、多分类的数据上表现更好[20]。假设输入样本为xi,输出样本为ti,N为样本数量,则此时输入样本和输出样本的非线性关系式为
| $ t_i=\sum\limits_{i=1}^N \boldsymbol{\tau}_i K\left(x, x_i\right)+\tau_0 $ | (8) |
式中,τ0为偏置;τi为权重向量;K(x, xi)为核函数。针对二分类问题,权重向量满足高斯先验概率基本分布
| $ p(\boldsymbol{\tau} \mid \boldsymbol{\alpha})=\prod\limits_{i=1}^N N\left(\boldsymbol{\tau}_i \mid 0, \alpha_i-1\right) $ | (9) |
式中,α为确定权重向量的先验分布的超参数。根据贝叶斯理论,采用Laplace逼近法对α进行迭代更新,使α无穷大,从而τi趋于0,则RVM模型的解稀疏性更强。燃气轮机气路故障诊断属于一对多分类问题,因此采用一对一方式将二分类扩展为多分类,即将g个分类两两组合,构建g(g-1)/2个RVM分类器,每个分类器只对两个不同的类别进行训练,再利用投票法策略确定未知样本的类别。RVM模型训练中核函数K(x, xi)的选取对其预测精度的影响较大,在此采用非线性处理能力较好的高斯径向基核函数,具体为
| $ K\left(x, x_i\right)=\exp \left[-\left\|x-x_i\right\|^2 /\left(2 \gamma^2\right)\right] $ | (10) |
式中,γ为核函数宽度。核函数宽度γ的取值会直接影响RVM模型的预测效果,目前尚没有统一的方法对γ值进行寻优,通常采用网格搜索法和梯度下降法,但这两种方法受搜索步长的影响,得到的解不一定是全局最优解。ECSO算法在使用过程中需要人为设定的参数较少,且在面对典型单峰、多峰函数时收敛速度和寻优精度均较优,故对于核函数宽度γ的确定采用ECSO算法。
2 基于ECSO-RVM模型的气路故障诊断方法基于ECSO-RVM模型的燃气轮机气路故障诊断方法实现步骤如下。
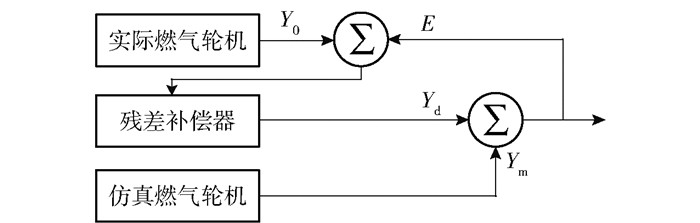
1) 基于气路可测参数、压气机特性曲线和涡轮特性曲线,采用模块化和容积化的方法将燃气轮机系统分为两类:一类为具有一定容积的模块,如燃烧室和管路;一类为压气机、涡轮、转子、负载等物理截面明确的模块。在Matlab Simulink平台中按模块建立仿真模型,并采用真实燃气轮机运行数据进行残差实时修正。设实际输出为Y0,仿真输出Ym,残差补偿为Yd,此时只需通过函数逼近使误差E=Y0-(Ym+Yd)最小,即可得到无故障模式下的燃气轮机模型,见图 1。仿真模型的输入为环境温度、压力、燃气涡轮和动力涡轮转速、燃料流量等;仿真模型的输出为各部件截面参数,如出口温度、出口压力、流量、输出功率等。将仿真输出结果与实际监测结果对比,通过残差修正使仿真燃气轮机的输出结果更加可靠,最终所得模型可作为模拟各类气路故障的基准模型。
|
图 1 基于残差修正的燃气轮机模型 Fig.1 Gas turbine model based on residual correction |
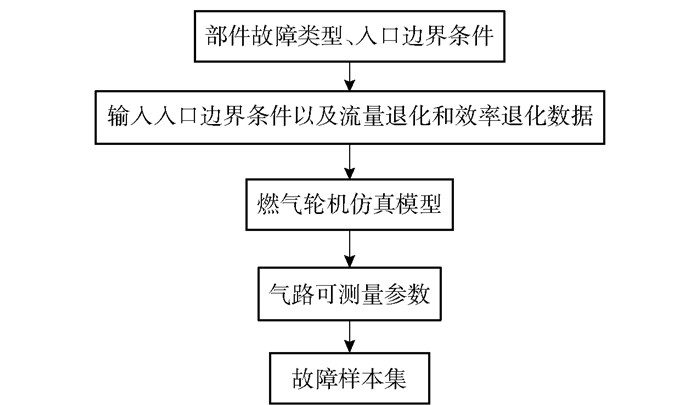
2) 根据典型气路故障类型及燃气轮机实际运行下的入口边界条件(大气压力、大气温度等参数),设置不同的入口边界条件以及流量退化和效率退化数据,在仿真模型中得到气路可测量参数,形成边界条件、可测量参数和故障类型的样本集,如图 2所示。
|
图 2 样本集形成过程 Fig.2 Sample set formation process |
3) 将边界条件和可测量参数作为输入,故障类型作为输出,采用ECSO-RVM模型进行分类诊断。将故障样本集进行归一化处理,分为训练集和测试集;初始化种群并对ECSO算法的相关参数进行设定,计算鸡群内每个个体的适应度值;判断是否需要更新子群,如需要则更新鸡群内个体位置,如不需要则保持原有位置,再按照各自的位置更新策略计算个体适应度值;判断个体位置适应度值是否优于原位置适应度值,如是则更新全局最优适应度值,在达到设定精度或最大迭代次数时,输出RVM模型的最优核函数宽度。
4) 将测试集输入至最优RVM模型中后输出分类预测结果,并对其评价。
5) 将训练好的ECSO-RVM模型布置到燃气轮机诊断系统中,根据燃气轮机实际运行下的入口边界条件和可测量参数,对各部件的健康状态进行实时评估。
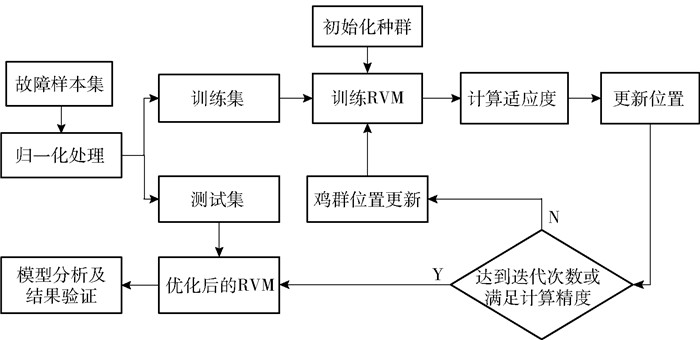
算法的步骤流程见图 3。
|
图 3 ECSO-RVM模型算法流程图 Fig.3 Algorithm flow chart of the ECSO-RVM model |
以某输气管道LM2500+双轴燃气轮机为研究对象,该燃气轮机主要部件包括压气室、燃烧室、燃气涡轮和动力涡轮,其中燃气涡轮与压气室相连,动力涡轮与负载相连。设计参数为输出轴功率29 MW,进气折合流量85 kg/s,燃气发生器转速9 587 r/min,压气机压比23.3,热效率38%,额定运行参数见表 1。
| 下载CSV 表 1 LM2500+额定运行参数 Table 1 Rated operating parameters of LM2500+ |
由于Matlab Simulink平台中建立的通用模型是基于各部件的性能曲线,而性能曲线来源于厂家数据。在运行过程中,往往同一型号的燃气轮机其性能也会存在一定差异,故通用模型的误差较大。采用图 1中的模型不断修正相关部件的截面参数,提高仿真精度。
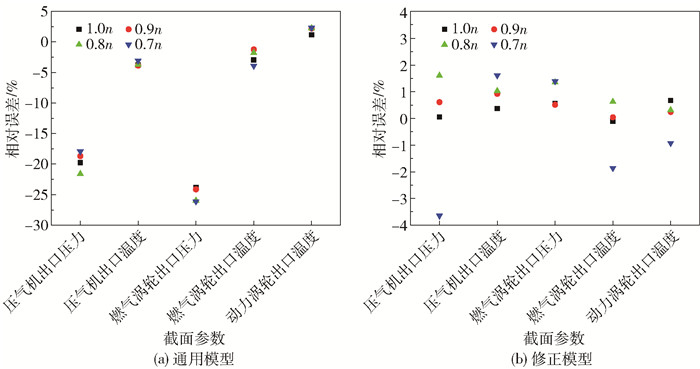
按转速n区分不同工况(1.0n、0.9n、0.8n、0.7n),分别采用通用模型和修正模型燃气轮机的截面参数进行仿真,结果见表 2,相对误差如图 4所示。
| 下载CSV 表 2 燃气轮机截面参数仿真结果 Table 2 Simulation results of gas turbine cross section parameters |
|
图 4 不同工况下仿真模型相对误差 Fig.4 Relative errors of simulation models under different working conditions |
从图 4可以看出,不同工况下通用模型的相对误差趋势大致相同,最大相对误差为26.12%,未出现偏离工况的离群点,温度参数的仿真精度普遍高于压力参数,且动力涡轮的预测精度高于压气机和燃气涡轮。各截面参数误差较大的原因是各部件特性曲线与实际燃气轮机特性曲线存在一定偏差,且气体热力学性质的处理方式不同。修正模型可以显著提高仿真精度,最大相对误差为3.64%,与通用模型相比误差大幅降低,其中对压力参数仿真精度的改善尤为明显。修正模型为后续气路故障的精确诊断建立了基础。
利用仿真可输出大量与燃气轮机运行相关的可测量参数,通过与现场设置的可测量仪表进行对照,选择大气压力(E1)、大气温度(E2)、大气相对湿度(E3)、压气机压比变化量(E4)、压气机出口温度变化量(E5)、燃气涡轮出口温度变化量(E6)、动力涡轮出口温度变化量(E7)、燃料流量变化量(E8)等8个故障特征向量作为ECSO-RVM模型的输入。其中,传感器主要传输的是静态数据,但气路故障主要体现数据的动态变化,故采用变化量作为输入,输入变量可根据实际情况变化,及时更新样本集维度。选择压气机叶片结垢、压气机叶片磨损、压气机叶片机械损伤、压气机顶端间隙增大、涡轮叶片结垢、涡轮叶片磨损、涡轮叶片机械损伤、涡轮叶片热腐蚀和燃烧室故障等9种故障为模型输出,并依次编号为故障类型1~9,对其进行分类运算。最终获得每种故障样本为20组,共计180组样本,在各类型中选取15组样本为训练集,其余5组样本为测试集,部分样本见表 3。训练完成后的模型可被应用于相应的燃气轮机上,只需输入入口边界条件和可测量参数,即可输出对应的故障类型。
| 下载CSV 表 3 燃气轮机气路故障部分样本 Table 3 Sample of gas turbine circuit faults |
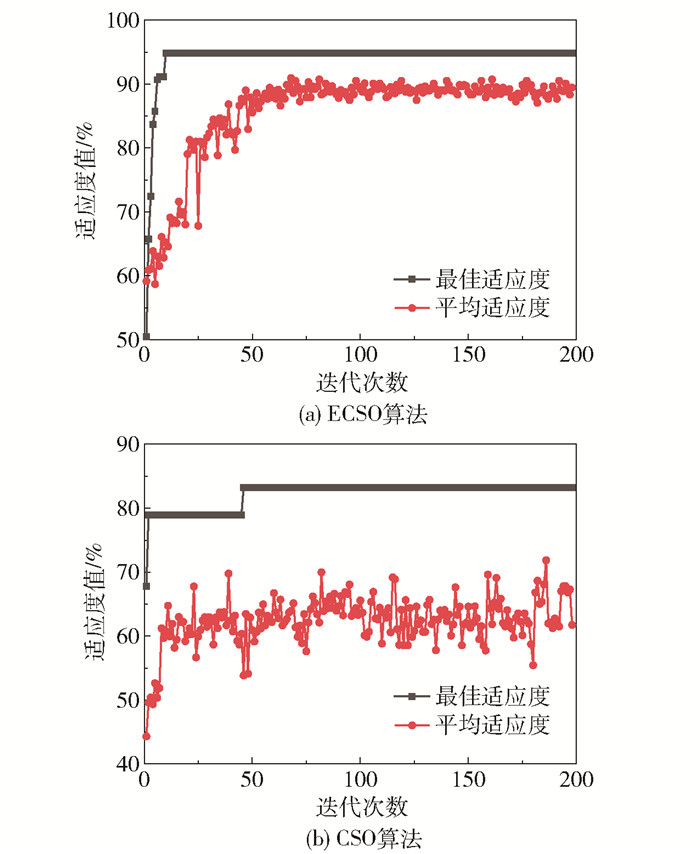
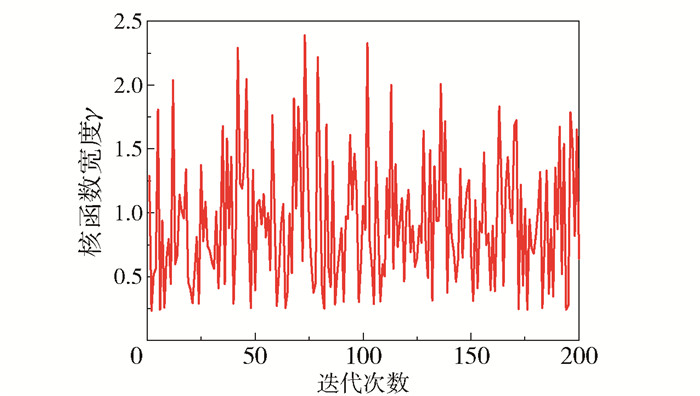
对训练样本进行归一化并作为RVM模型的输入,采用ECSO算法对γ值进行寻优,设置CSO算法中的搜索空间为10维,种群更新频率为10,种群规模为100,NR、NH、NC、NM值分别为20、60、20、6,FL为[0.4, 1];设置ECSO算法中的k=1 000,ωmin=0.4,ωmax=0.9,其余设置与CSO算法一致,迭代次数均为200次。模型在训练中的迭代进化过程见图 5,可以看出ECSO算法在前10次迭代中不断跳出局部最优,其适应度值在第10次后达到最大,为94.81%;CSO算法的适应度值在第2~45次保持不变,在第46次达到最大值后保持不变,其最佳适应度值为83.70%。此外,ECSO算法的平均适应度曲线在迭代过程中更易收敛,可见ECSO算法搜索能力的稳定性和准确性均高于标准CSO算法。在迭代次数达到200时,最优参数γ=0.617 8。参数迭代过程见图 6。
|
图 5 不同超参数寻优算法对比 Fig.5 Comparison of different hyperparameter optimization algorithms |
|
图 6 参数γ迭代历史 Fig.6 Iteration history of the parameter γ |
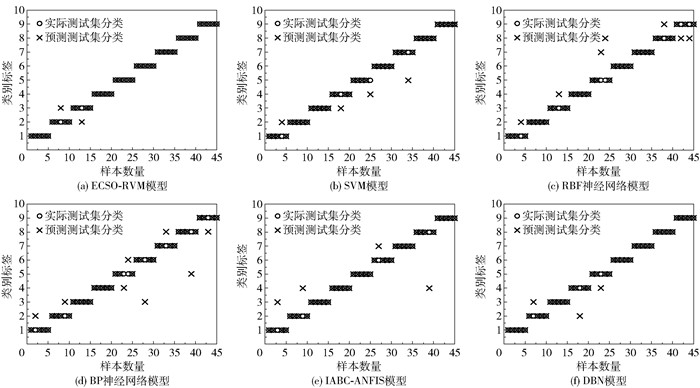
将测试集代入训练好的ECSO-RVM模型中进行测试,为了验证所提模型的有效性及优势,将测试结果分别与SVM[8]、径向基核函数(radial basis function,RBF)神经网络[21]、反向传播(back propagation,BP)神经网络[14]、改进蜂群算法(improved artificial bee colony algorithm,IABC)-自适应模糊推理系统(adaptive network-base fuzzy inference system,ANFIS)[22]、深度置信网络(deep belief network,DBN)[23]等模型进行对比,如图 7所示。其中,SVM分类器采用高斯径向基核函数,惩罚因子和核函数宽度通过网格搜索及交叉验证确定,分别为15.146 1和5.789 6;RBF神经网络结构为8-61-9,散布常数为0.215,期望误差为10-8;BP神经网络结构为8-15-9,学习率为0.458,中间层采用tan-sig-moid函数,连接权值和阈值的调节采用梯度下降法;ANFIS算法网络结构为8-12-9,最小误差为10-8,采用减法聚类的方法生成ANFIS网络,利用IABC算法对聚类超参数寻优,确定影响范围、排除概率、上限排除概率和下限排除概率分别为0.214 5、1.75、0.336 8、0.217 5;DBN网络结构为8-9-7-9,最优学习速率为0.085,动量因子为0.35,预训练和微调阶段的最大迭代次数均为500。
|
图 7 不同模型故障分类结果 Fig.7 Fault classification results of different models |
从图 7可以看出,RBF、BP神经网络模型各有7个和8个测试样本分类错误,分类效果最差;两者均为神经网络类算法,其中RBF神经网络模型的非线性逼近能力较好,具有较强的聚类分析能力,但径向基核函数本身仍易陷入局部最优。SVM模型、IABC-ANFIS模型的分类效果居中,均有4个测试样本分类错误,准确率为91.11%;SVM模型对于二分类问题的表现较好,但针对多分类问题由于不提供后验概率因此表现较差,存在二分类的累积误差;ANFIS模型将模糊控制与神经网络相结合,并通过IABC算法进行聚类参数寻优,但当初始参数存在缺失值、异常点、噪声点时,会对分类效果产生较大影响。DBN模型的分类精度仅次于ECSO-RVM模型,有3个测试样本分类错误,准确率为93.33%;DBN模型通过自下而上的无监督训练保留了更多的样本特征信息,但其初始权值参数通过随机初始化方式产生,降低了网络的分类精度。
ECSO-RVM模型只有2个测试样本分类错误,即在识别压气机叶片磨损和叶片机械损伤故障上发生了混淆,这可能是由于两者均会造成叶片叶型损失,气流流动受到干扰,摩擦阻力系数上升,压气机的压比和效率也会发生改变,从判断依据上反映,两者只是效率退化上有所差别。ECSO-RVM模型的分类精度最高,为95.55%,且泛化能力较好,说明不存在过拟合现象,模型鲁棒性较好。
3.3 噪声敏感性分析从传感器收集到的样本数据经常受到人为、环境和机械设备的影响,致使数据中含有不同程度的噪声。以现场使用的3051型压力传感器(罗斯蒙特公司)为例,其在使用过程中曾出现小于3%的数据偏差,经重新标定、改善封装后,数据偏差有所减小,但随着使用年限的增加,偏差在不断变化。在测试集中添加1%~3%的白噪声后进行分类,结果见表 4。可以看出,随着噪声的增加,各模型的分类精度均有所下降,其中RBF神经网络模型和BP神经网络模型的下降速度较快,其余模型的下降速度较缓,ECSO-RVM模型的分类精度始终保持在80%以上。在训练时间上,ECSO-RVM模型介于SVM模型和IABC-ANFIS模型之间,这可能是由于RVM模型需要对矩阵进行逆运算,从而增加了训练时间,但对于燃气轮机气路故障而言,在实现抗噪效果的同时可获得较高的分类精度,训练时间稍长也在可控范围内。
| 下载CSV 表 4 ESCO-RVM模型与其余模型的抗噪性能对比 Table 4 Comparison of anti-noise performance between the ESCO-RVM model and other models |
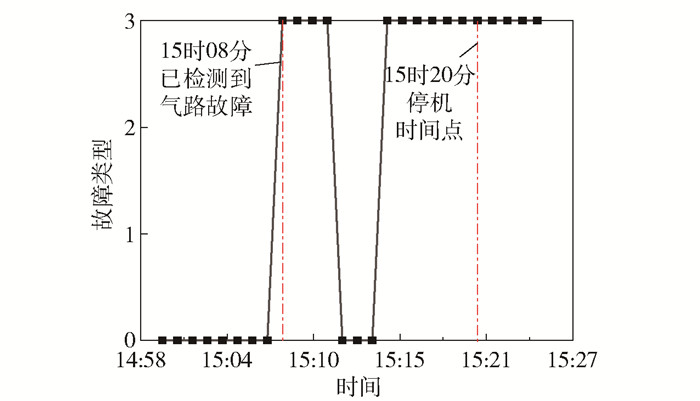
2020年5月20日15时20分,西气东输二线某站开展负荷分配控制,其中一台压气机振动监测数据出现高高报警,并引发停机,多次启动后仍存在报警现象。利用ECSO-RVM模型对报警之前的数据进行故障诊断,结果如图 8、表 5所示。以连续两个时间点的判定结果为最终结果,确定故障类型为压气机叶片机械损伤,且在振动测点报警前已预知了故障的发生。经孔探检查发现第9级和第10级动叶叶片从环槽中断裂,静叶叶片表面也存在不同程度的颗粒磨损,对叶片进行拆卸检查和现场更换后,报警故障消除。模型诊断结果与孔探结果基本一致,说明采用本文算法可实现燃气轮机气路故障的实时预警,避免传统方法的拖尾现象。此外,在第一次启动失败后已检测到严重的气路故障,这时应立刻停止再次启动并进行孔探实验,避免压气机叶片二次损伤。
|
图 8 故障类型实时计算结果(故障类型0表示无故障) Fig.8 Real-time calculation results of fault type (fault type 0 means no fault) |
| 下载CSV 表 5 燃气轮机实际气路故障参数(部分) Table 5 Actual gas circuit fault parameters of gas turbine (in part only) |
(1) 针对双轴燃气轮机气路故障诊断方法进行研究,提出一种基于改进鸡群算法自适应调整相关向量机超参数的优化模型,经验证,该模型的分类精度为95.55%,泛化能力和分类精度较好,明显优于其余对比模型。
(2) 通过添加不同强度的噪声来测试模型的抗噪能力,其中ECSO-RVM模型的分类精度始终保持在80%以上,因算法结构、迭代次数的影响其训练时间只比SVM模型稍长,但仍在可控范围内。
| [1] |
张霄. 基于热力参数的燃气轮机故障建模及诊断研究[D]. 上海: 上海电力大学, 2019. ZHANG X. Research on fault modeling and diagnosis of gas turbine based on thermodynamic parameters[D]. Shanghai: Shanghai University of Electric Power, 2019. (in Chinese) |
| [2] |
赵雄飞, 刘永葆, 贺星, 等. 基于小偏差方法的燃气轮机气路故障判据的建立[J]. 机械工程与自动化, 2011(4): 115-117. ZHAO X F, LIU Y B, HE X, et al. Creation of gas path fault criterion based on small deviation method for gas turbine[J]. Mechanical Engineering & Automation, 2011(4): 115-117. (in Chinese) |
| [3] |
林新智, 冯坤, 胡明辉, 等. 基于性能仿真的燃气轮机气路故障预警方法[J]. 热能动力工程, 2020, 35(9): 36-43. LIN X Z, FENG K, HU M H, et al. Early warning method of gas path fault of gas turbine based on performance simulation[J]. Journal of Engineering for Thermal Energy and Power, 2020, 35(9): 36-43. (in Chinese) |
| [4] |
李世尧, 李振林, 谷思宇. 一种输气管道燃气轮机性能计算方法及其验证[J]. 油气储运, 2019, 38(6): 678-684. LI S Y, LI Z L, GU S Y. A performance calculation method for gas turbines used in gas pipelines and its validation[J]. Oil & Gas Storage and Transportation, 2019, 38(6): 678-684. (in Chinese) |
| [5] |
李刚, 谷思宇, 贾东卓, 等. 一种输气管道燃气轮机的综合故障诊断方法[J]. 油气储运, 2019, 38(5): 568-573. LI G, GU S Y, JIA D Z, et al. A comprehensive fault diagnosis method used for the gas turbines in gas pipelines[J]. Oil & Gas Storage and Transportation, 2019, 38(5): 568-573. (in Chinese) |
| [6] |
蒋东翔, 刘超, 杨文广, 等. 关于重型燃气轮机预测诊断与健康管理的研究综述[J]. 热能动力工程, 2015, 30(2): 173-179. JIANG D X, LIU C, YANG W G, et al. Overview concerning the study of the prediction, diagnosis and health management(PHM) of heavy-duty gas turbines[J]. Journal of Engineering for Thermal Energy and Power, 2015, 30(2): 173-179. (in Chinese) |
| [7] |
URBAN L A. Gas path analysis applied to turbine engine condition monitoring[J]. Journal of Aircraft, 1973, 10(7): 400-406. |
| [8] |
涂雷, 茅大钧, 李伯勋, 等. 基于CGABC-SVM的燃气轮机气路故障诊断[J]. 汽轮机技术, 2020, 62(5): 377-380. TU L, MAO D J, LI B X, et al. Gas turbine fault diagnosis based on CGABC-SVM[J]. Turbine Technology, 2020, 62(5): 377-380. (in Chinese) |
| [9] |
张云, 钱玉良, 邱正, 等. 采用GWO优化SVM的燃气轮机气路故障诊断[J]. 上海电力学院学报, 2019, 35(2): 187-192, 196. ZHANG Y, QIAN Y L, QIU Z, et al. Gas turbine fault diagnosis using GWO optimized SVM[J]. Journal of Shanghai University of Electric Power, 2019, 35(2): 187-192, 196. (in Chinese) |
| [10] |
KOU L Z, TANG C, GUO W L, et al. Tunable magnetism in strained graphene with topological line defect[J]. ACS Nano, 2011, 5(2): 1012-1017. |
| [11] |
STAMATIS A, MATHIOUDAKIS K, SMITH M, et al. Gas turbine component fault identification by means of adaptive performance modeling[C]// Gas Turbine and Aeroengine Congress and Exposition. Brussels, 1990.
|
| [12] |
ZEDDA M, SINGH R. Gas turbine engine and sensor fault diagnosis using optimization techniques[J]. Journal of Propulsion and Power, 2002, 18(5): 1019-1025. |
| [13] |
NADERI E, MESKIN N, KHORASANI K. Nonlinear fault diagnosis of jet engines by using a multiple model- based approach[C]// Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition. Volume 1: Aircraft Engine; Ceramics; Coal, Biomass and Alternative Fuels; Wind Turbine Technology. Vancouver, 2011: 63-75.
|
| [14] |
张霄, 钱玉良, 邱正, 等. 基于蜻蜓算法优化BP神经网络的燃气轮机故障诊断[J]. 热能动力工程, 2019, 34(3): 26-32. ZHANG X, QIAN Y L, QIU Z, et al. Gas turbine fault diagnosis based on BP neural network optimized by dragonfly algorithm[J]. Journal of Engineering for Thermal Energy and Power, 2019, 34(3): 26-32. (in Chinese) |
| [15] |
ARETAKIS N, MATHIOUDAKIS K, STAMATIS A. Non-linear engine component fault diagnosis from a limited number of measurements using a combinatorial approach[J]. Journal of Engineering for Gas Turbines and Power, 2003(3): 642-650. |
| [16] |
肖旺, 陈成, 杨坤, 等. 燃驱压缩机组气路故障预测诊断与健康管理技术[J]. 油气储运, 2021, 40(6): 699-707. XIAO W, CHEN C, YANG K, et al. Prognostics health management technology of gas path in turbine-driven compressor set[J]. Oil & Gas Storage and Transportation, 2021, 40(6): 699-707. (in Chinese) |
| [17] |
应雨龙, 李靖超, 庞景隆, 等. 基于热力模型的燃气轮机气路故障预测诊断研究综述[J]. 中国电机工程学报, 2019, 39(3): 731-743, 952. YING Y L, LI J C, PANG J L, et al. Review of gas turbine gas-path fault diagnosis and prognosis based on thermodynamic model[J]. Proceedings of the CSEE, 2019, 39(3): 731-743, 952. (in Chinese) |
| [18] |
任婷, 刘石, 姜越, 等. 基于CSO算法优化的LSSVM熔盐温度预测[J]. 可再生能源, 2017, 35(2): 224-231. REN T, LIU S, JIANG Y, et al. Temperature prediction of the molten salt using the CSO algorithm optimized LSSVM[J]. Renewable Energy Resources, 2017, 35(2): 224-231. (in Chinese) |
| [19] |
程乐, 冯钢, 徐义晗, 等. 改进的CSO算法应用于连续优化问题[J]. 计算机工程与设计, 2011, 32(2): 689-692. CHENG L, FENG G, XU Y H, et al. Improved CSO algorithm application in continuous optimization problem[J]. Computer Engineering and Design, 2011, 32(2): 689-692. (in Chinese) |
| [20] |
蔡潇, 李大超, 翁永祥, 等. 基于多域特征提取和RVM的有源压制干扰识别方法[J]. 舰船电子对抗, 2021, 44(2): 23-27, 47. CAI X, LI D C, WENG Y X, et al. Identification method of active blanket jamming based on multi-domain feature extraction and RVM[J]. Shipboard Electronic Countermeasure, 2021, 44(2): 23-27, 47. (in Chinese) |
| [21] |
闫斌斌. 基于气路性能混合模型的燃气轮机叶片故障预警及诊断方法研究[D]. 北京: 北京化工大学, 2021. YAN B B. Research on early warning and diagnosis method of gas turbine blade fault based on gas path performance hybrid model[D]. Beijing: Beijing University of Chemical Technology, 2021. (in Chinese) |
| [22] |
黄伟, 景晓宁, 高斌. 基于IABC-ANFIS的燃气轮机气路故障诊断[J]. 热能动力工程, 2019, 34(7): 30-36. HUANG W, JING X N, GAO B. Gas turbine fault diagnosis based on IABC-ANFIS[J]. Journal of Engineering for Thermal Energy and Power, 2019, 34(7): 30-36. (in Chinese) |
| [23] |
闫丽萍, 董学智, 张永军, 等. 基于深度置信网络的燃气轮机气路故障诊断方法[J]. 工程热物理学报, 2020, 41(4): 840-844. YAN L P, DONG X Z, ZHANG Y J, et al. A gas path fault diagnostic method of gas turbine based on deep belief network[J]. Journal of Engineering Thermophysics, 2020, 41(4): 840-844. (in Chinese) |








