2. 中国核动力研究设计院 核反应堆系统设计技术重点实验室,成都 610041
2. Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu 610041, China
人类社会对能源需求量的不断增大使得能源浪费问题备受关注,而蓄热技术的合理应用可以有效提高热效率和调节热不平衡性[1],达到节约能源的目的。相变蓄热技术以相变材料(phase-change material,PCM)作为基础,具有相变材料温度保持不变和相变潜热大的优点。在蓄热水箱中加入相变材料可有效提升其蓄热性能,因此针对相变蓄热水箱的研究在能源及相关领域受到广泛关注,成为国内外学者的研究热点。
张洪宇等[2]搭建了相变蓄热水箱实验台,发现相对于单熔点相变材料,采用多熔点相变材料可进一步提高水箱的蓄热能力。Bayomy等[3]将相变材料应用于太阳能加热系统中,有效地提高了蓄热罐的蓄热效率。Koželj等[4]对比了传统的显热蓄热罐和混合潜热蓄热罐,证明了相变材料可以提高常规水蓄热罐的能量密度。Wang等[5]研究了相变材料对蓄热水箱热分层的影响,发现热分层的程度与相变材料的布置位置有关,越靠近入水口热分层越明显。周利强等[6]采用三水合醋酸钠作为相变材料,研究了不同流速下相变蓄热球对蓄热水箱温升的影响特性。Li等[7]借助实验对相变蓄热球融化过程的数值模拟结果进行了验证,讨论了球的半径、水浴温度、相变材料种类和球壳材料对球内相变材料熔化速率的影响。Abdulateef等[8]对相变蓄热水池中石蜡的熔化和凝固过程进行了实验研究,发现在石蜡中加入泡沫金属会大大缩短相变材料的熔化时间。
已有研究证明添加相变材料能够有效提高蓄热水箱的热容量,但是这些研究大多采用强制对流换热方式在相变材料与传热流体间进行传热,少有以自然对流传热方式来熔化相变材料的研究。自然对流广泛存在于封闭的非能动安全系统中,例如可以在以自然对流为主的压水堆非能动内置换料水箱中加入相变材料来改善其蓄热性能[9]。本文将相变材料应用于封闭静止蓄热水箱中,通过数值模拟方法探讨封闭水箱加热过程中相变材料的熔化规律和相变材料对水箱温升的影响规律,得到封闭相变蓄热水箱的蓄热特性,为相变蓄热水箱在工程领域的应用提供参考。
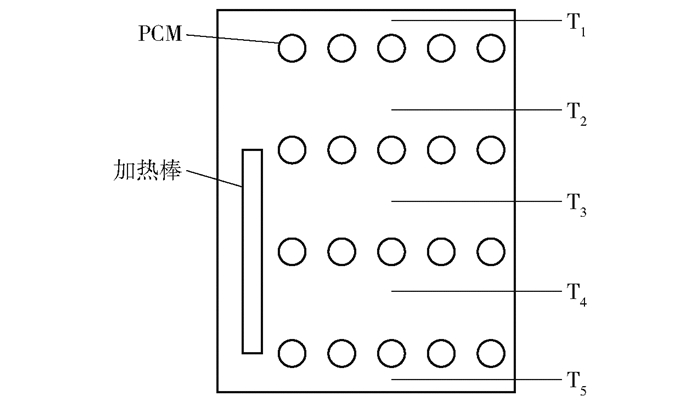
1 模型的建立 1.1 物理模型本文研究的蓄热水箱为规则长方体,相变单元为圆柱体且横向固定在水池中,多根加热棒置于水箱左下方。封闭静止的相变蓄热水箱二维物理模型如图 1所示,水箱长130 mm,高150 mm,加热棒高80 mm,长8 mm。相变单元材料选用Na2SO4 ·10H2O,其具体的热物性参数见表 1[10-11]。半径为5 mm的相变单元以4行5列均匀分布在水箱中,总计20个,占水箱有效体积的8.05%。加热棒占水箱容积的3.55%,恒定功率为500 W。水箱内其余空间填充介质为水,重力作用向下,考虑由密度差引起的自然对流。水箱为封闭的方腔,在纵向上设置5个监测点等距分布在水箱中线上,分别对应图 1中的T1~T5。
|
图 1 相变蓄热水箱二维物理模型 Fig.1 Two-dimensional physical model of the phase change heat storage tank |
| 下载CSV 表 1 相变材料和换热流体的热物性参数 Table 1 Thermophysical parameters of the phase change materials and heat transfer fluids |
为便于数值计算,对相变蓄热水箱物理模型作以下假设[12-14]:水箱壁面均为绝热壁面,不计热损失;相变材料均匀且各向同性;采用Boussinesq假设[12],考虑自然对流的影响;相变单元封装外壳相变材料的接触热阻忽略不计。
1.2 数学模型考虑到Boussinesq假设,水的密度会随温度变化,必然会引起密度差,在重力作用下产生浮升力,形成自然对流现象。对于水箱内的液相流体,其流动方程包括质量守恒方程、动量守恒方程和能量守恒方程[15]。质量守恒方程可表示为
| $ \frac{\partial \rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho \nu)}{\partial y}=0 $ | (1) |
动量守恒方程表示为
| $ \frac{\partial(\rho u)}{\partial t}+\frac{\partial\left(\rho u^2\right)}{\partial x}+\frac{\partial(\rho u \nu)}{\partial y}=\frac{\partial \tau_{x x}}{\partial x}+\frac{\partial \tau_{y x}}{\partial y}-\frac{\partial p}{\partial x} $ | (2) |
| $ \frac{\partial(\rho \nu)}{\partial t}+\frac{\partial(\rho u \nu)}{\partial x}+\frac{\partial\left(\rho \nu^2\right)}{\partial y}=\frac{\partial \tau_{x y}}{\partial x}+\frac{\partial \tau_{y y}}{\partial y}-\frac{\partial p}{\partial y}-\rho g $ | (3) |
能量守恒方程表示为
| $ \;\;\;\;\;\frac{\partial(\rho T)}{\partial t}+\frac{\partial(\rho u T)}{\partial x}+\frac{\partial(\rho \nu T)}{\partial y}=\frac{\partial}{\partial x}\left(k \frac{\partial T}{\partial x}\right)+\frac{\partial}{\partial y}(k·\\ \frac{\partial T}{\partial y}) $ | (4) |
式中,T为介质温度,K;ρ为流体密度,kg/m3;k为导热系数,W/(m ·K);t为时间,s;u,ν分别为x,y方向上的流速分量,m/s;p为压力,Pa;g为重力加速度,m/s2;τ为流体之间的剪切应力,Pa。
相变材料的熔化过程采用焓法模型进行求解,过程如下[15-16]。
| $ \rho_{\mathrm{c}} \frac{\partial H}{\partial t}=k \nabla^2 T $ | (5) |
| $ H=h_{\mathrm{S}}+h_{\mathrm{L}} $ | (6) |
| $ h_{\mathrm{S}}=h_{\mathrm{a}}+\int_{T_{\mathrm{a}}}^T c_p \mathrm{~d} T $ | (7) |
| $ h_{\mathrm{L}}=\beta \mathit{\Gamma} $ | (8) |
| $ \beta=\left\{\begin{array}{ll} 0, & T \leqslant T_{\mathrm{S}} \\ \frac{T-T_{\mathrm{S}}}{T_{\mathrm{L}}-T_{\mathrm{S}}}, & T_{\mathrm{S}} <T <T_{\mathrm{L}} \\ 1, & T \geqslant T_{\mathrm{L}} \end{array}\right. $ | (9) |
式中,ρc为相变材料密度,kg/m3;H为相变材料的焓,kJ/kg;hS为显焓;hL为潜热焓;ha为参考焓;Ta为参考温度;cp为比热容,kJ/(kg ·K);Γ为Na2SO4·10H2O的相变潜热,kJ/kg;TS、TL分别为相变材料的熔点和冷凝点;β为液相率,β=0时相变单元内均为固相,β=1时相变单元内均为液相,0 < β < 1时相变单元内为固液混合物,表示处在熔化过程中。
初始时刻整体水箱温度一致,相变材料此时为固态
| $ T_{(x, y, t=0)}=298.15 \mathrm{~K} ; \beta=0 $ | (10) |
利用Fluent软件对封闭相变蓄热水箱的加热过程进行数值仿真计算。加热棒功率设置为500 W,相变蓄热水箱内水和相变材料的初始温度为298.15 K,水箱外壁面设置为绝热壁面,压力和速度求解方式使用SIMPLE算法。
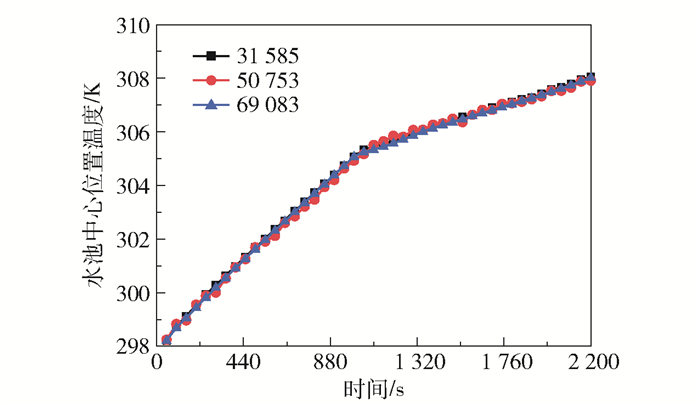
为了保证模拟结果的准确性,首先进行网格独立性验证。将二维模型作网格划分,网格数分别为31 585、50 753、69 083,在相同设置下进行仿真运算,监测T3点的温度变化,结果如图 2所示。对比3种不同网格数量的模拟结果,可以发现同一点的瞬时温度基本一致,考虑到精度要求和计算效率,选择31 585的网格量进行后续计算。
|
图 2 不同网格数量下T3点温度变化曲线 Fig.2 Temperature change of the T3 point with different number of grids |
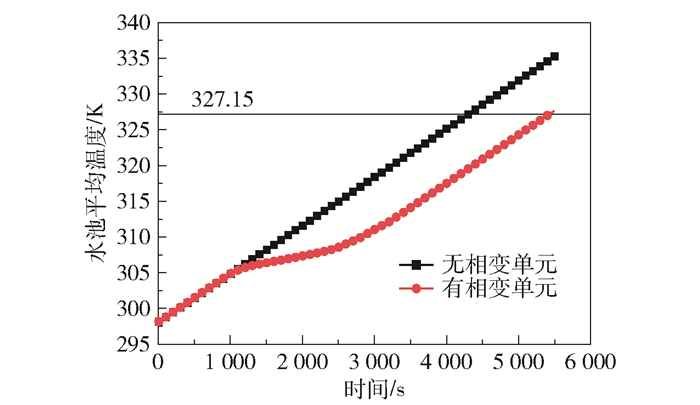
为了对比有、无相变单元条件下蓄热水箱的热容量变化特征,对有、无相变单元的蓄热水箱蓄热过程进行数值模拟,并监测水箱的平均温度。图 3对比了有、无相变单元蓄热水箱的平均温度随时间的变化规律,可以明显看出在相变单元未熔化前(0~1 000 s),有、无相变单元蓄热水箱监测点的温度变化基本相同。水和固相相变材料的单位体积热容量之比α可由式(11)表示。
| $ \alpha=\frac{c_{p 1} \rho_1}{c_{p 2} \rho_2} $ | (11) |
|
图 3 有、无相变单元的蓄热水箱平均温度对比 Fig.3 Comparison of the average temperature of heat storage tanks with and without a phase change element |
式中,cp1、ρ1分别为水的比热和密度;cp2、ρ2分别为固相相变材料的比热和密度。经计算α=1.041,说明水和固相Na2SO4·10H2O的单位体积热容量差别不大。因此,在相变单元未熔化前,有、无相变单元蓄热水箱的平均温度变化基本相同。
加热1 000 s后,同一时刻下含相变单元蓄热水箱的平均温度要低于纯水蓄热水箱,由此可初步得出结论:相变单元的加入提高了蓄热水箱的热容量。当温度达到327.15 K时,纯水蓄热水箱所需的加热时长为4 300 s,含相变单元的蓄热水箱则需要5 400 s,则通过加热时间可得出当蓄热水箱水温由298.15 K升高至327.15 K时,相对于纯水蓄热水箱,加入相变单元后蓄热水箱的热容量提升了25.58%。
另外,通过理论计算对有、无相变单元蓄热水箱的热容量进行对比分析,相关计算式可表示为
| $ Q_1=c_{p 1} \rho_1 V_1 \Delta T $ | (12) |
| $ Q_2=c_{p 1} \rho_1\left(V_1-V_2\right) \Delta T+c_{p 2} \rho_2 V_2 \Delta T+Q_{\mathrm{L}} $ | (13) |
| $ Q_{\mathrm{L}}=m r $ | (14) |
式中,V1、V2分别为蓄热水箱的容积和相变单元所占的容积,m3;Q1、Q2分别为纯水蓄热水箱和加入相变单元蓄热水箱的热容量,kJ;QL为相变单元熔化过程的吸热量,kJ;m为相变单元总质量,kg;r为相变潜热,kJ/kg。
基于式(12)~(14)进行计算,发现当蓄热水箱温度由298.15 K升高至327.15 K时,含相变单元蓄热水箱的热容量比纯水蓄热水箱提高了28.93%,该结果与数值模拟结果接近,进一步证明了在蓄热水箱中加入相变单元可以大幅提升蓄热水箱的热容量,起到延时升温的效果。
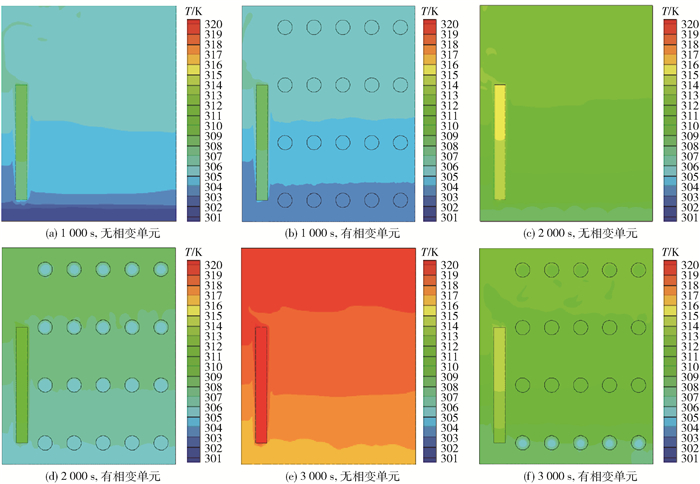
2.2 蓄热水箱温度特性分析图 4为有、无相变单元蓄热水箱在加热时间为1 000、2 000、3 000 s时的温度分布云图。从图中可以发现蓄热水箱水平方向上的温度变化极小,可以忽略不计,垂直方向上则出现热分层现象。对比1 000 s时有、无相变单元蓄热水箱的温度云图可以发现,当水箱内水温没有加热到相变材料的熔点时,含相变单元蓄热水箱与纯水蓄热水箱的温度相似,且水箱的温度分布情况大体保持一致,说明相变材料在1 000 s内未发生相变,此时的Na2SO4 ·10H2O以固态显热形式吸热,故其温度与周围水温一致。
|
图 4 不同时刻有、无相变单元蓄热水箱的温度云图对比 Fig.4 Comparison of temperature nephogram of heat storage tanks with and without a phase change unit at different times |
当蓄热水箱加热至2 000 s时,从图 4(d)中可以明显观察到含相变单元蓄热水箱的平均温度要低于纯水蓄热水箱。此时水箱温度高于相变材料的熔点,相变材料已经熔化,且温度保持不变。相变材料熔化过程中需要向周围流体吸热,所以降低了整个蓄热水箱的温度。
当蓄热水箱加热至3 000 s时,从图 4(f)可以看到含相变单元蓄热水箱与纯水蓄热水箱的整体温差进一步增大。相变单元基本熔化成液相,温度几乎与周围水温保持一致,此时相变单元以液相显热形式吸收热量。
图 5为不同位置处相变单元液相率变化曲线。可以看出,第一排相变单元最先达到相变温度,熔化速率最高。由于前排相变单元较早达到相变温度,因此可在一定程度上降低较高位置处水的温升速率,进而影响蓄热水箱内热分层的剧烈程度。

|
图 5 相变单元液相率变化曲线 Fig.5 Variation in liquid content of the phase transformation unit |
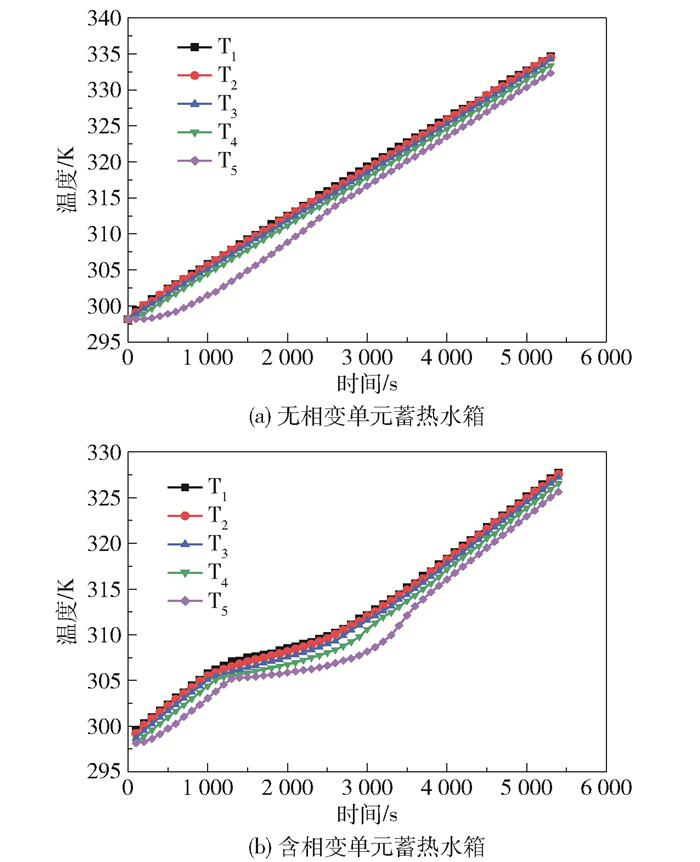
图 6给出了有、无相变单元蓄热水箱内监测点的温度随时间的变化曲线。可以看出,纯水蓄热水箱在加热过程中,每一个监测点的温度都以一定速率持续升高,而含相变单元蓄热水箱监测点的温度在1 000~2 700 s期间变化则相对较为平缓。这说明相变材料在熔化过程中,不断吸收周围水的热量并保持温度恒定,从而影响了蓄热水箱内水的升温速率。
|
图 6 有、无相变单元的蓄热水箱监测点温度随时间的变化曲线 Fig.6 Temperature change curves of the thermal storage tank monitoring point with and without a phase change element with time |
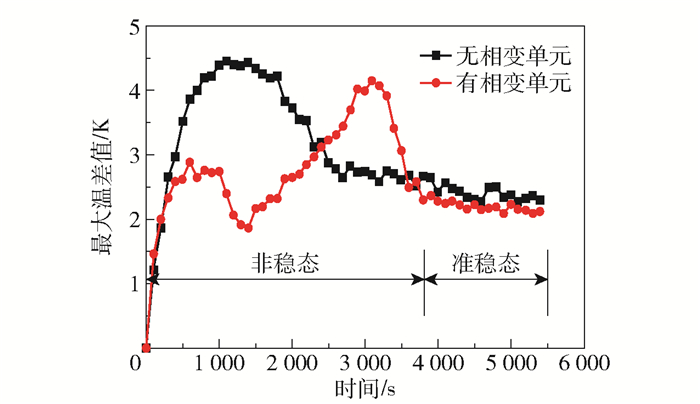
为研究有、无相变单元蓄热水箱的热分层特性,将顶层温度与底层温度的差值作为判断蓄热水箱热分层剧烈程度的依据[17]。在本文中监测点T1与T5的温度差值为整个水箱中的最大温差值。最大温差值越大,热分层越剧烈。有、无相变单元蓄热水箱最大温差值随时间的变化曲线如图 7所示。在加热过程中,根据最大温差值的变化规律,将加热过程分为非稳态阶段和准稳态阶段:非稳态阶段是由于加热棒加热打破了原有的静态平衡,产生自然对流使得顶层水温高于底层水温,水箱内逐渐形成热分层现象;随着水箱内最大温差不断增大,意味着水箱顶层与底层流体之间的热传导驱动力也越大,此时水箱底层温度的升高速率逐渐增大,最终最大温差值达到一个相对稳定的动态平衡,即准稳态阶段。由图 7可以看到,在非稳态阶段,相对于纯水蓄热水箱,含有相变单元蓄热水箱在500~1 500 s时间范围内出现最大温差值降低的现象,热分层剧烈程度有所缓解,原因在于含有相变单元蓄热水箱的顶层相变单元较早达到相变温度,顶层的升温速率有所降低。相变蓄热水箱在1 500~3 750 s时间范围内最大温差值出现升高又降低的现象,这是由于上层相变单元已熔化完毕,导致上层水升温较快,待下层相变单元也熔化完毕后,温升加快并且逐渐接近上层温升速率,向准稳态阶段过渡;在准稳态阶段,由于所有相变单元均已熔化,此时有、无相变材料蓄热水箱的最大温差大体一致。
|
图 7 有、无相变单元蓄热水箱最大温差值随时间的变化曲线 Fig.7 Variation in the maximum temperature difference of thermal storage tanks with and without a phase change element as a function of time |
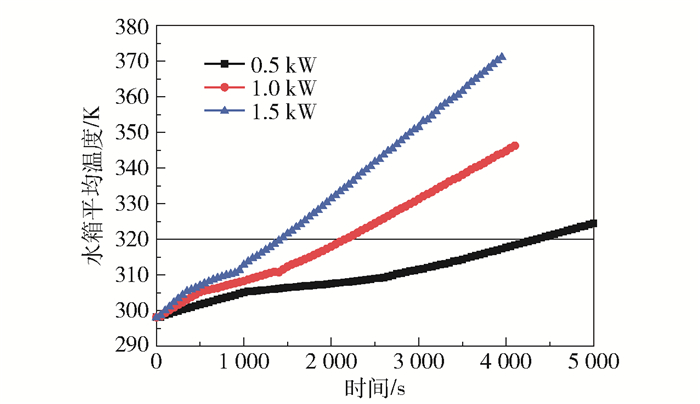
采用不同功率(0.5、1.0、1.5 kW)的加热棒对含相变单元蓄热水箱进行加热,通过观察水箱的平均温度来分析整个水箱的温度特性变化。从图 8可以看出,加热功率越大,温度升高得越快。当不同加热功率(0.5、1.0、1.5 kW)蓄热水箱平均温度由298.15 K升高至320 K时,所需加热时长分别为4 300、2 150、1 400 s,与加热功率呈反比关系,表明不同的加热功率不会对含有相同相变单元量的蓄热水箱的热容量产生影响。
|
图 8 不同加热功率下相变蓄热水箱的平均温度变化曲线 Fig.8 Average temperature curves of phase change heat storage tanks with different heating powers |
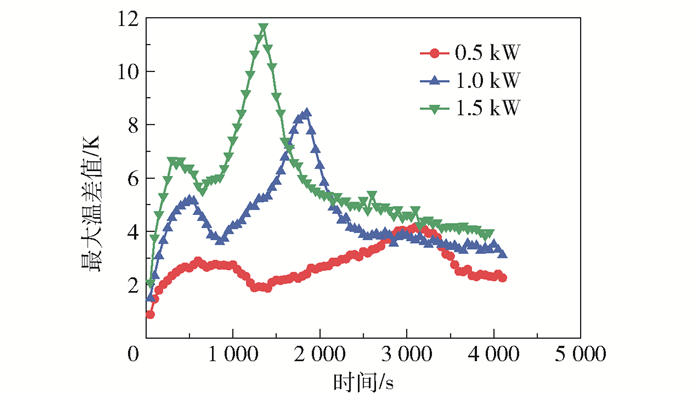
图 9给出了不同加热功率下含相变单元蓄热水箱的最大温差值(T1与T5的温度差值)变化曲线。可以看出,在不同加热功率下,相变蓄热水箱的热分层特征变化规律大致相同—热分层剧烈程度变化趋势均是先增大后减小,再增大,最后减小至某一稳定值。在非稳态阶段,当加热功率由0.5 kW增加至1.5 kW时,最大温差值的波动幅值增大,由4 K增加至12 K,同时进入准稳态阶段的时间缩短,由3 500 s缩短至2 000 s。在准稳态阶段,加热功率越大,最大温差稳定值越大,热分层越剧烈。
|
图 9 不同加热功率下相变蓄热水箱最大温差值的变化曲线 Fig.9 Maximum temperature difference curves of phase change heat storage tanks with different heating powers |
(1) 在其他条件相同的情况下,蓄热水箱内加入相变材料可有效提高蓄热水箱的热容量。当蓄热水箱中加入有效容积占比为9.05%的Na2SO4 ·10H2O、水箱温度由298.15 K加热至327.15 K时,相对于纯水蓄热水箱,含相变单元蓄热水箱的加热时间延长了1 100 s,蓄热热容量提高了25.58%。
(2) 蓄热水箱加热过程中在垂直方向上存在热分层现象,水平方向温度基本保持一致,这导致含相变单元蓄热水箱在较高位置处的相变单元先熔化,降低了较高位置处水的升温速率,使得含相变单元蓄热水箱相对于纯水蓄热水箱,在非稳态阶段热分层的剧烈程度有所缓解。
(3) 不同加热功率下,相变蓄热水箱的热分层特征变化规律大致相同,热分层剧烈程度均是先增大后减小,再增大,最后减小至某一稳定值。在非稳态阶段和准稳态阶段,热分层剧烈程度均随着加热功率的增加而增大。
| [1] |
王迎斌, 张海峰, 贺行洋, 等. 相变材料的研究进展及应用[J]. 建材世界, 2020, 41(2): 6-8. WANG Y B, ZHANG H F, HE X Y, et al. Research progress and application of phase change materials[J]. The World of Building Materials, 2020, 41(2): 6-8. (in Chinese) |
| [2] |
张洪宇, 卢军, 庄春龙, 等. 地下防护工程空调相变储热水池储热性能实验研究[J]. 天津大学学报(自然科学与工程技术版), 2019, 52(11): 1187-1193. ZHANG H Y, LU J, ZHUANG C L, et al. Performance of the phase change heat storage air-conditioning reservoir for underground protective engineering[J]. Journal of Tianjin University (Science and Technology), 2019, 52(11): 1187-1193. (in Chinese) |
| [3] |
BAYOMY A, DAVIES S, SAGHIR Z. Domestic hot water storage tank utilizing phase change materials (PCMs): numerical approach[J]. Energies, 2019, 12: 2170. DOI:10.3390/en12112170 |
| [4] |
KOŽELJ R, MLAKAR U, ZAVRL E, et al. An experimental and numerical analysis of an improved thermal storage tank with encapsulated PCM for use in retrofitted buildings for heating[J]. Energy and Buildings, 2021, 248: 111196. DOI:10.1016/j.enbuild.2021.111196 |
| [5] |
WANG Z L, ZHANG H, DOU B L, et al. The thermal stratification evaluation of phase-change materials in a heat storage tank: computational fluid dynamics and experimental study[J]. Journal of Solar Energy Engineering, 2020, 142: 021012. DOI:10.1115/1.4045342 |
| [6] |
周利强, 王子龙, 张华, 等. 相变蓄热水箱温度特性的试验研究[J]. 流体机械, 2019, 47(11): 79-84. ZHOU L Q, WANG Z L, ZHANG H, et al. Experimental study on temperature characteristics of phase change hot water tank[J]. Fluid Machinery, 2019, 47(11): 79-84. (in Chinese) DOI:10.3969/j.issn.1005-0329.2019.11.015 |
| [7] |
LI W, LI S G, GUAN S K, et al. Numerical study on melt fraction during melting of phase change material inside a sphere[J]. International Journal of Hydrogen Energy, 2017, 42(29): 18232-18239. DOI:10.1016/j.ijhydene.2017.04.136 |
| [8] |
ABDULATEEF J, HASAN A F, MAHDI M S. Role of composite phase change material on the thermal performance of a latent heat storage system: experimental investigation[J]. Journal of Harbin Institute of Technology (New Series), 2020, 27(1): 44-51. |
| [9] |
田文喜, 王明军, 秋穗正, 等. 基于CFD方法的核动力系统热工安全特性研究进展[J]. 原子能科学技术, 2019, 53(10): 1968-1982. TIAN W X, WANG M J, QIU S Z, et al. Review on safety characteristics research progress of nuclear power plant thermal-hydraulics using CFD method[J]. Atomic Energy Science and Technology, 2019, 53(10): 1968-1982. (in Chinese) |
| [10] |
赵顺. 有机无机复合相变储能材料的制备及性能研究[D]. 北京: 北京化工大学, 2020. ZHAO S. Preparation and properties of organic-inorganic composite phase change energy storage materials[D]. Beijing: Beijing University of Chemical Technology, 2020. (in Chinese) |
| [11] |
黄金, 柯秀芳. 无机水合盐相变材料Na2SO4 ·10H2O的研究进展[J]. 材料导报, 2008, 22(3): 63-67. HUANG J, KE X F. Research and development of Na2SO4 ·10H2O as phase change materials[J]. Materials Reports, 2008, 22(3): 63-67. (in Chinese) DOI:10.3321/j.issn:1005-023X.2008.03.016 |
| [12] |
VOLLER V R, SHADABI L. Enthalpy methods for tracking a phase change boundary in two dimensions[J]. International Communications in Heat and Mass Transfer, 1984, 11(3): 239-249. DOI:10.1016/0735-1933(84)90040-X |
| [13] |
LIN W Z, LING Z Y, FANG X M, et al. Experimental and numerical research on thermal performance of a novel thermal energy storage unit with phase change material[J]. Applied Thermal Engineering, 2021, 186: 116493. DOI:10.1016/j.applthermaleng.2020.116493 |
| [14] |
贾兴龙, 陈宝明, 张艳勇, 等. 梯度骨架对固液相变蓄热特性影响研究[J]. 山东建筑大学学报, 2020, 35(2): 56-63. JIA X L, CHEN B M, ZHANG Y Y, et al. Study on the effect of gradient skeleton on the heat storage characteristics of solid-liquid phase change[J]. Journal of Shandong Jianzhu University, 2020, 35(2): 56-63. (in Chinese) |
| [15] |
杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006. YANG S M, TAO W Q. Heat transfer[M]. 4th ed. Beijing: Higher Education Press, 2006. (in Chinese) |
| [16] |
郭梦雪. 套管式相变蓄热器内管排列方式和壁温的影响[J]. 煤气与热力, 2019, 39(5): 1-7, 41. GUO M X. Heat source and cold source influence of inner tube arrangement and wall temperature of casing-type phase-change heat accumulator[J]. Gas & Heat, 2019, 39(5): 1-7, 41. (in Chinese) |
| [17] |
YANG Z, CHEN H S, WANG L, et al. Comparative study of the influences of different water tank shapes on thermal energy storage capacity and thermal stratification[J]. Renewable Energy, 2016, 85: 31-44. DOI:10.1016/j.renene.2015.06.016 |








