非线性薛定谔方程广泛应用于非线性量子场论、等离子体物理学、光子学、流体力学、半导体电子学、生物物理学、经济物理学等诸多领域,其表达式为
| $ {\rm{i}}{u_t} - \frac{{{\beta _2}}}{2}{u_{xx}} + {\alpha _1}{\left| u \right|^2}u = 0 $ | (1) |
它是数学物理学中最重要的模型之一,在Bose-Einstein凝聚中也被称为Gross-Pitaevskii(GP)方程。该方程存在孤立子解。由于孤立子在运动过程中有保持形状不变的性质,可应用于光纤通信领域,故寻找该系统的孤立子解具有重要意义。
在非线性光学中,系统(1)描述了皮秒光脉冲在单模光纤中的传播[1],这里u(x, t)表示复包络振幅,x和t分别表示空间和时间变量,β2表示群速度色散系数,α1表示自相位调制参数。但是,当超短脉冲接近50fs,甚至低于10fs,或光场频率接近光纤材料的谐振频率时,单模光纤中高能超短脉冲传输的理论和实验结果表明,系统(1)失效, 这时必须考虑对系统(1)增加由拉曼散射引发的附加项[2-3]。
文献[4]对系统(1)增加了五次非线性项、自陡峭项和自频移项
| $ \begin{array}{l} \;\;\;\;\;\;\;{\rm{i}}{u_t} - \frac{{{\beta _2}}}{2}{u_{xx}} + ({\alpha _1}{\left| u \right|^2} + {\alpha _2}{\left| u \right|^4})u = {\rm{i}}[{\gamma _1}\\ {({\left| u \right|^2}u)_x} + {\gamma _2}{({\left| u \right|^2})_x}u] \end{array} $ | (2) |
并且运用试探函数法得到孤子解。文献[5-8]对系统(1)增加了三阶色散项、自陡峭项和自频移项
| $ \begin{array}{l} \;\;\;\;\;\;\;{\rm{i}}{u_t} - \frac{{{\beta _2}}}{2}{u_{xx}} + {\alpha _1}{\left| u \right|^2}u = {\rm{i}}\left[ {\frac{{{\beta _3}}}{6}{u_{xxx}} + {\gamma _1}{{({{\left| u \right|}^2}u)}_x} + } \right.\\ \left. {{\rm{ }}{\gamma _2}{{({{\left| u \right|}^2})}_x}u} \right] \end{array} $ | (3) |
同时运用了Sine-Gordon方程法、F- 展开法、Exp- 展开法等方法求解。
本文综合所有影响因素,寻找系统
| $ \begin{array}{l} \;\;\;\;\;\;\;{\rm{i}}{u_t} - \frac{{{\beta _2}}}{2}{u_{xx}} + ({\alpha _1}{\left| u \right|^2} + {\alpha _2}{\left| u \right|^4})u = {\rm{i}}\left[ {\frac{{{\beta _3}}}{6}{u_{xxx}} + } \right.\\ \left. {{\gamma _1}{{({{\left| u \right|}^2}u)}_x} + {\gamma _2}{{({{\left| u \right|}^2})}_x}u} \right] \end{array} $ | (4) |
的精确解。由于系统(4)中出现了五次非线性项α2|u|4u和三阶色散项uxxx的并存现象,导致一些常用的求解方法不适用,为此我们选择合适的变量代换,并选用3种辅助函数展开法—Riccati方程- 展开法、Riccati方程- 倒数展开法和Exp- 展开法来寻求方程(4)的解析解。
1 行波变换对方程(4)作行波变换:u(x, t)=ϕ(ξ)eiζ, 其中ξ=v0t-vx, ζ=ω0t-ωx,可得
| $ \left\{ {\begin{array}{*{20}{l}} {{l_1}\phi ''' + {l_2}\phi \prime + {l_3}{\phi ^2}\phi \prime = 0}\\ {{l_4}\phi '' + {l_5}\phi + {l_6}{\phi ^3} + {\alpha _2}{\phi ^5} = 0} \end{array}} \right. $ | (5) |
式中,
对方程(5)第一个式子积分,并选取首次积分常数为0,通过代入消去ϕ的三次项,可得
| $ A\phi '' + B\phi + C{\phi ^5} = 0 $ | (6) |
式中,A=l1l6-l3l4/3,B=l2l6-l3l5/3,C=-α2l3/3。
下面对方程(6)使用辅助函数展开法,求解出函数ϕ的表达式,从而给出方程(4)的解析解。
2 辅助函数展开法设方程(6)的解具有如下展开结构
| $ \phi = \sum\limits_{k = 0}^N {{A_k}{{\left( {f\left( V \right)} \right)}^k}, {\rm{ }}V\prime \left( \xi \right) = g\left( {V\left( \xi \right)} \right)} $ | (7) |
式中,Ak为待定常数,N为平衡整数。先将式(7)代入到方程(6)中,再利用齐次平衡原理确定N,最后通过求解方程(7)给出系统(4)的解。为此选择代换ϕ=Q1/4,则方程(6)化简成
| $ - 3A{\left( {Q\prime } \right)^2} + 4AQQ'' + 16B{Q^2} + 16C{Q^3} = 0 $ | (8) |
选取f(V)=V和g(V)=S2V2+S1V+S0,则式(7)变为
| $ \begin{array}{l} \;\;\;\;\;\;\;Q\left( \xi \right) = \sum\limits_{k = 0}^N {{A_k}{V^k}\left( \xi \right), V\prime \left( \xi \right) = {S_2}{V^2}\left( \xi \right) + {S_1}\cdot} \\ V\left( \xi \right) + {S_0} \end{array} $ | (9) |
式中,S0、S1和S2为常数且S2≠0。易知Riccati方程的解如下。
当s>0时,
| $ V\left( \xi \right) = - \frac{{{S_1}}}{{2{S_2}}} - \frac{{\sqrt s }}{{2{S_2}}}{\rm{tanh}}\left( {\frac{{\sqrt s }}{2}(\xi + {\xi _0})} \right) $ | (10) |
| $ V\left( \xi \right) = - \frac{{{S_1}}}{{2{S_2}}} - \frac{{\sqrt s }}{{2{S_2}}}{\rm{coth}}\left( {\frac{{\sqrt s }}{2}(\xi + {\xi _0})} \right) $ | (11) |
当s < 0时,
| $ V\left( \xi \right) = - \frac{{{S_1}}}{{2{S_2}}} + \frac{{\sqrt { - s} }}{{2{S_2}}}{\rm{tan}}\left( {\frac{{\sqrt { - s} }}{2}(\xi + {\xi _0})} \right) $ | (12) |
| $ V\left( \xi \right) = - \frac{{{S_1}}}{{2{S_2}}} - \frac{{\sqrt { - s} }}{{2{S_2}}}{\rm{cot}}\left( {\frac{{\sqrt { - s} }}{2}(\xi + {\xi _0})} \right) $ | (13) |
当s=0时,
| $ V\left( \xi \right) = - \frac{{{S_1}}}{{2{S_2}}} - \frac{1}{{{S_2}(\xi + {\xi _0})}} $ | (14) |
式中,s=S12-4S0S2,且ξ0为初始常数[5]。
将方程(9)代入方程(8)后,通过比较Q3、(Q′)2和QQ″关于V的最高次幂,可得N=2以及关于V的一元高次方程。由于V≠0,于是选取Vk(k=0, 1,…, 6)的系数为0,可得如下方程组
| $ \left\{ {\begin{array}{*{20}{l}} {{V^6}:4(3AS_2^2 + 4{A_2}C)A_2^2 = 0}\\ {{V^5}:4(5A{A_1}S_2^2 + 4A{A_2}{S_1}{S_2} + 12C{A_1}{A_2}){A_2} = 0}\\ \begin{array}{l} {V^4}:(24{A_0}{A_2} + 5A_1^2)AS_2^2 + 28{A_1}A{A_2}{S_1}{S_2} + \\ \;\;\;\;\;\;\;\;8AA_2^2{S_0}{S_2} + 4AA_2^2S_1^2 + 16(3{A_0}{A_2}C + \\ \;\;\;\;\;\;\;\;{\rm{ }}3A_1^2C + B{A_2}){A_2} = 0 \end{array}\\ \begin{array}{l} {V^3}:8A{A_0}{A_1}S_2^2 + (40{A_0}{A_2} + 6A_1^2)A{S_1}{S_2} + \\ \;\;\;\;\;\;\;\;{\rm{ }}16A{A_1}{A_2}{S_0}{S_2} + 8A{A_1}{A_2}S_1^2 + 16(6{A_0}{A_2}C + \\ {\rm{ }}\;\;\;\;\;\;\;\;A_1^2C + 2B{A_2}){A_1} = 0 \end{array}\\ \begin{array}{l} {V^2}:12A{A_0}{A_1}{S_1}{S_2} + 2(16{A_0}{A_2} + A_1^2)A{S_0}{S_2} + \\ \;\;\;\;\;\;\;\;(16{A_0}{A_2} + A_1^2)AS_1^2 + 4A{A_1}{A_2}{S_0}{S_1}4AA_2^2S_0^2 + \\ \;\;\;\;\;\;\;\;16(3A_0^2{A_2}C + 3{A_0}A_1^2C + 2B{A_0}{A_2} + BA_1^2) = 0 \end{array}\\ \begin{array}{l} V:8A{A_0}{A_1}{S_0}{S_2} + 4A{A_0}{A_1}S_1^2 + 2(12{A_0}{A_2} - A_1^2){\rm{ }}\cdot\\ {\rm{ }}\;\;\;\;\;\;A{S_0}{S_1} - 4A{A_1}{A_2}S_0^2 + 16(3{A_0}C + 2B){A_0}{A_1} = 0 \end{array}\\ \begin{array}{l} {V^0}:4{A_1}A{A_0}{S_0}{S_1} + (8{A_0}{A_2}3A_1^2)AS_0^2 + \\ \;\;\;\;\;\;\;\;16({A_0}C + B)A_0^2 = 0 \end{array} \end{array}} \right. $ |
借助Maple可求解出在A0满足A(A0C+3B) < 0条件时,A2、S0、S1、S2分别为
当AB < 0时,
| $ \begin{array}{l} \;\;\;\;\;\;\;{u_1}\left( {x, t} \right) = \left\{ { - \frac{{3B}}{C}{\rm{sec}}{{\rm{h}}^2}\left( {2\sqrt { - \frac{B}{A}} ({v_0}t - } \right.} \right.\\ {\left. {vx)} \right\}^{\frac{1}{4}}}{e^{{\rm{i}}({\omega _0}t - \omega x)}} \end{array} $ | (15) |
| $ \begin{array}{l} \;\;\;\;\;\;\;{u_2}\left( {x, t} \right) = {\left\{ {\frac{{3B}}{C}{\rm{csc}}{{\rm{h}}^2}\left( {2\sqrt { - \frac{B}{A}} ({v_0}t - vx)} \right)} \right\}^{\frac{1}{4}}}\cdot\\ {e^{{\rm{i}}({\omega _0}t - \omega x)}} \end{array} $ | (16) |
当AB>0时,
| $ \begin{array}{l} \;\;\;\;\;\;\;{u_3}\left( {x, t} \right) = {\left\{ { - \frac{{3B}}{C}{\rm{se}}{{\rm{c}}^2}\left( {2\sqrt {\frac{B}{A}} ({v_0}t - vx)} \right)} \right\}^{\frac{1}{4}}}\cdot\\ {e^{{\rm{i}}({\omega _0}t - \omega x)}} \end{array} $ | (17) |
| $ \begin{array}{l} \;\;\;\;\;\;\;{u_4}\left( {x, t} \right) = {\left\{ { - \frac{{3B}}{C}{\rm{cs}}{{\rm{c}}^2}\left( {2\sqrt {\frac{B}{A}} ({v_0}t - vx)} \right)} \right\}^{\frac{1}{4}}}\cdot\\ {e^{{\rm{i}}({\omega _0}t - \omega x)}} \end{array} $ | (18) |
选取参数β2=1, β3=1, α1=2, γ1=1, γ2=1, v0= 1, v=1, ω0=1进行图示。在α2=-1, ω=2时,有
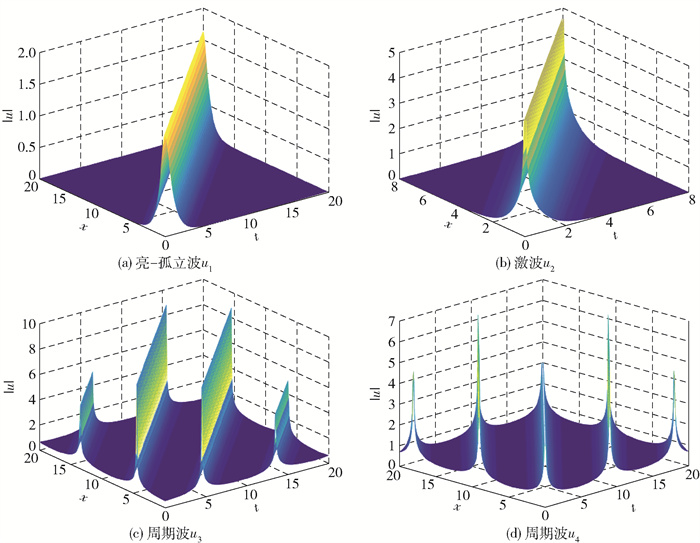
|
图 1 亮- 孤立波u1,激波u2和周期波u3、u4的三维波形图 Fig.1 Three-dimensional waveforms of the bright-soliton wave u1, shock wave u2 and periodic waves u3, u4 |
选取f(V)=1/V和g(V)=S2V2+S1V+S0, 则式(7)变为
| $ Q\left( \xi \right) = \sum\limits_{k = 0}^N {{A_k}{{\left\{ {\frac{1}{{V\left( \xi \right)}}} \right\}}^k}} , {\rm{ }}V\prime \left( \xi \right) = {S_2}{V^2} + {S_1}V + {\rm{ }}{S_0} $ | (19) |
将方程(19)代入方程(8)后,通过比较Q3、(Q′)2和QQ″关于1/V(ξ)的最高次幂,可得N=2以及关于1/V(ξ)的高次方程。由于V≠0,故选取(1/V(ξ))k(k=0, 1,…, 6)的系数为0,可得类似的系数方程组。借助Maple求解,可知在A0满足条件A(A0C+3B) < 0时,S0、S1、S2、A2分别为
| $ \begin{array}{l} {S_0} = \frac{{ \pm |{A_1}C|}}{{\sqrt { - 3A({A_0}C + 3B)} }}{\rm{sgn}}\left( A \right)\\ {S_1} = \mp 4\sqrt { - \frac{{{\rm{ }}{A_0}C + 3B}}{{3A}}} {\rm{sgn}}({A_1}C)\\ {S_2} = \mp \frac{{4{A_0}}}{{|{A_1}|}}\sqrt { - \frac{{{\rm{ }}{A_0}C + 3B}}{{3A}}} {\rm{sgn}}\left( C \right)\\ {\rm{ }}{A_2} = \frac{{A_1^2C}}{{4(C{A_0} + 3B)}} \end{array} $ |
其中A1为任意非0常数,s=-16B/A。利用式(10)~(13)可得方程(4)的解如下。
当AB < 0时,
| $ {u_5}\left( {x, t} \right) = {\left\{ {\frac{{ - 3{A_0}B{\rm{sec}}{{\rm{h}}^2}\left( {2\sqrt { - \frac{B}{A}({v_0}t - vx)} } \right)}}{{({A_0}C + 3B){{\left( {\sqrt {\frac{{3B}}{{{A_0}C + 3B}}} {\rm{tanh}}\left( {2\sqrt { - \frac{B}{A}({v_0}t - vx)} } \right) - {\rm{sgn}}({A_1}C)} \right)}^2}}}} \right\}^{\frac{1}{4}}}{e^{{\rm{i}}({\omega _0}t - \omega x)}} $ | (20) |
| $ {u_6}\left( {x, t} \right) = {\left\{ {\frac{{3{A_0}B{\rm{csc}}{{\rm{h}}^2}\left( {2\sqrt { - \frac{B}{A}({v_0}t - vx)} } \right)}}{{({A_0}C + 3B){{\left( {\sqrt {\frac{{3B}}{{{A_0}C + 3B}}} {\rm{coth}}\left( {2\sqrt { - \frac{B}{A}({v_0}t - vx)} } \right) - {\rm{sgn}}({A_1}C)} \right)}^2}}}} \right\}^{\frac{1}{4}}}{e^{{\rm{i}}({\omega _0}t - \omega x)}} $ | (21) |
当AB>0时,
| $ {u_7}\left( {x, t} \right) = {\left\{ {\frac{{ - 3{A_0}B{\rm{se}}{{\rm{c}}^2}\left( {2\sqrt {\frac{B}{A}({v_0}t - vx)} } \right)}}{{({A_0}C + 3B){{\left( {\sqrt { - \frac{{3B}}{{{A_0}C + 3B}}} {\rm{tan}}\left( {2\sqrt {\frac{B}{A}({v_0}t - vx)} } \right) + {\rm{sgn}}({A_1}C)} \right)}^2}}}} \right\}^{\frac{1}{4}}}{e^{{\rm{i}}({\omega _0}t - \omega x)}} $ | (22) |
| $ {u_8}\left( {x, t} \right) = {\left\{ {\frac{{ - 3{A_0}B{\rm{cs}}{{\rm{c}}^2}\left( {2\sqrt {\frac{B}{A}({v_0}t - vx)} } \right)}}{{({A_0}C + 3B){{\left( {\sqrt { - \frac{{3B}}{{{A_0}C + 3B}}} {\rm{cot}}\left( {2\sqrt {\frac{B}{A}({v_0}t - vx)} } \right) - {\rm{sgn}}({A_1}C)} \right)}^2}}}} \right\}^{\frac{1}{4}}}{e^{{\rm{i}}({\omega _0}t - \omega x)}} $ | (23) |
选取参数A1=1, β2=1, β3=1, α1=2, γ1=1, γ2= 1, v0=1, v=1, ω0=1进行图示(图 2)。当A0=-1, α2=-1, ω=2时,有
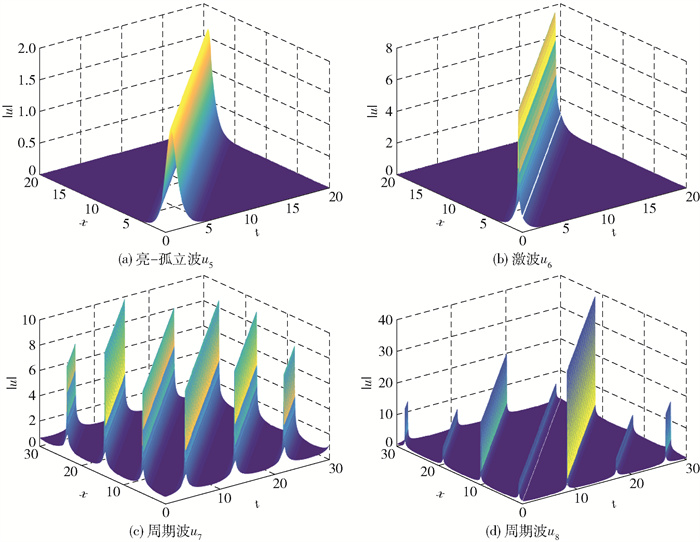
|
图 2 亮- 孤立波u5,激波u6和周期波u7、u8的三维波形图 Fig.2 Three-dimensional waveforms of the bright-soliton u5, shock wave u6 and periodic waves u7, u8 |
选取f(V)=exp (-V)和g(V)=exp (-V)+R1exp (V)+R0, 则式(7)变为
| $ \begin{array}{l} Q\left( \xi \right) = \sum\limits_{k = 0}^N {{A_k}{{\{ {\rm{exp}}\left( { - V\left( \xi \right)} \right)\} }^k}} \\ V\prime \left( \xi \right) = {\rm{exp}}\left( { - V\left( \xi \right)} \right) + {R_1}{\rm{exp}}\left( {V\left( \xi \right)} \right) + {R_0} \end{array} $ | (24) |
式中R0和R1均为常数。易知上述关于V(ξ)的微分方程的解如下。
当μ>0, R1≠0时,
| $ V\left( \xi \right) = {\rm{ln}}\left( { - \frac{{{R_0}}}{{2{R_1}}} - \frac{{\sqrt \mu }}{{2{R_1}}}{\rm{tanh }}\left( {\frac{{\sqrt \mu }}{2}(\xi + {\xi _0})} \right)} \right) $ | (25) |
| $ V\left( \xi \right) = {\rm{ln}}\left( { - \frac{{{R_0}}}{{2{R_1}}} - \frac{{\sqrt \mu }}{{2{R_1}}}{\rm{coth }}\left( {\frac{{\sqrt \mu }}{2}(\xi + {\xi _0})} \right)} \right) $ | (26) |
当μ < 0, R1≠0时,
| $ \begin{array}{l} \;\;\;\;\;\;\;V\left( \xi \right) = {\rm{ln }}\left( { - \frac{{{R_0}}}{{2{R_1}}} - \frac{{\sqrt { - \mu } }}{{2{R_1}}}{\rm{tan}}} \right.{\rm{ }}\left( {\frac{{\sqrt { - \mu } }}{2}(\xi + } \right.\\ \left. {\left. {{\xi _0})} \right)} \right) \end{array} $ | (27) |
| $ \begin{array}{l} \;\;\;\;\;\;\;V\left( \xi \right) = {\rm{ln }}\left( { - \frac{{{R_0}}}{{2{R_1}}} - \frac{{\sqrt { - \mu } }}{{2{R_1}}}{\rm{cot}}} \right.{\rm{ }}\left( {\frac{{\sqrt { - \mu } }}{2}(\xi + } \right.\\ \left. {\left. {{\xi _0})} \right)} \right) \end{array} $ | (28) |
当μ = 0, R1≠0, R0≠0时,
| $ V\left( \xi \right) = {\rm{ln}}\left( { - \frac{{2{R_0}(\xi + {\xi _0}) + 2}}{{R_0^2(\xi + {\xi _0})}}} \right) $ | (29) |
其中μ=R02-4R1,且ξ0为初始常数[5]。
将方程(24)代入方程(8)后,通过比较Q3、(Q′)2和QQ″关于exp (-V(ξ))的最高次幂,可得N=2以及关于exp (-V(ξ))的高次方程。由于exp (-V(ξ))≠0,故选取exp (-kV(ξ))(k=0, 1,…, 6)的系数为0,可得如下方程组。
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{exp}}\left( { - 6V} \right):4(4C{A_2} + 3A)A_2^2 = 0}\\ {{\rm{exp}}\left( { - 5V} \right):4(4A{A_2}{R_0} + 12C{A_1}{A_2} + 5A{A_1}){A_2} = 0}\\ \begin{array}{l} {\rm{exp}}\left( { - 4V} \right):(48{A_2}C + 5A)A_1^2 + (4AR_0^2 + 8A{R_1} + \\ \;\;\;\;\;\;\;\;16B)A_2^2 + 4(7A{A_1}{R_0} + 6A{A_0}){A_2} = 0 \end{array}\\ \begin{array}{l} {\rm{exp}}\left( { - 3V} \right):8(AR_0^2 + 2A{R_1} + 12{A_0}C + 4B){A_1}{A_2} + \\ \;\;\;\;\;\;{\rm{ }}40A{A_0}{A_2}{R_0} + 2(3A{A_1}{R_0} + 8CA_1^2 + 4A{A_0}){A_1} = 0 \end{array}\\ \begin{array}{l} {\rm{exp}}\left( { - 2V} \right):(A{R_0} - 4AR_1^2 + 2A{R_1} + 48{A_0}C + \\ \;\;\;\;\;\;{\rm{ }}16B)A_1^2 + (16AR_0^2 + 32A{R_1} + 48{A_0}C + {\rm{ }}32B){A_0}{A_2} + 4({A_2}{R_1} + 3{A_0})A{A_1}{R_0} = 0 \end{array}\\ \begin{array}{l} {\rm{exp}}\left( { - V} \right):{\rm{ }}(4AR_0^2 + 8A{R_1} + 48{A_0}C + 32B){A_0}{A_1} + \\ \;\;\;\;\;\;{\rm{ }}(24{A_0}{A_2}2A_1^2)A{R_0}{R_1}4A{A_1}{A_2}R_1^2 = 0 \end{array}\\ \begin{array}{l} {\rm{Constant}}:4A{A_0}{A_1}{R_0}{R_1} + (8{A_0}{A_2} - 3A_1^2)AR_1^2 + \\ \;\;\;\;\;\;{\rm{ }}16A_0^2({A_0}C + B) = 0 \end{array} \end{array}} \right. $ |
借助Maple求解出A0、A2、R0、R1分别为
| $ \begin{array}{l} {A_0} = - \frac{{A_1^2{C^2} + 9AB}}{{3AC}}, {A_2} = - \frac{{3A}}{{4C}}\\ {R_0} = - \frac{{4{A_1}C}}{{3A}}, {R_1} = \frac{{4(A_1^2{C^2} + 9AB)}}{{9{A^2}}} \end{array} $ |
其中A1为任意常数,且μ=R02-4R1=-16B/A。利用式(25)~(28), 可得到方程(6)的解析解如下。
当AB < 0时,
| $ \begin{array}{l} \;\;\;\;\;\;\;{u_9}\left( {x, t} \right) = \\ {\left\{ {\frac{{ - 3(A_1^2{C^2} + 9AB)B\;{\rm{sec}}{{\rm{h}}^2}\left( {2\sqrt { - \frac{B}{A}} ({v_0}t - vx)} \right)}}{{C{{\left( {3A\sqrt { - \frac{B}{A}} {\rm{tanh}}\left( {2\sqrt { - \frac{B}{A}} ({v_0}t - vx)} \right) - {A_1}C} \right)}^2}}}} \right\}^{\frac{1}{4}}}\\ {{{\rm{e}}^{{\rm{i}}({\omega _0}t - \omega x)}}} \end{array} $ | (30) |
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;{u_{10}}\left( {x,t} \right) = }\\ {{{\left\{ {\frac{{3(A_1^2{C^2} + 9AB)B\;{\rm{csc}}{{\rm{h}}^2}\left( {2\sqrt { - \frac{B}{A}} ({v_0}t - vx)} \right)}}{{C{{\left( {3A\sqrt { - \frac{B}{A}} {\rm{coth}}\left( {2\sqrt { - \frac{B}{A}} ({v_0}t - vx)} \right) - {A_1}C} \right)}^2}}}} \right\}}^{\frac{1}{4}}}}\\ {{{\rm{e}}^{{\rm{i}}({\omega _0}t - \omega x)}}} \end{array} $ | (31) |
当AB>0时,
| $ \begin{array}{l} \;\;\;\;\;\;\;{u_{11}}\left( {x, t} \right) = \\ {\left\{ { - \frac{{3(A_1^2{C^2} + 9AB)B\;{\rm{se}}{{\rm{c}}^2}\left( {2\sqrt {\frac{B}{A}} ({v_0}t - vx)} \right)}}{{C{{\left( {3A\sqrt {\frac{B}{A}} {\rm{tan}}\left( {2\sqrt {\frac{B}{A}} ({v_0}t - vx)} \right) + {A_1}C} \right)}^2}}}} \right\}^{\frac{1}{4}}}\\ {{{\rm{e}}^{{\rm{i}}({\omega _0}t - \omega x)}}} \end{array} $ | (32) |
| $ \begin{array}{l} \;\;\;\;\;\;\;{u_{12}}\left( {x, t} \right) = \\ {\left\{ { - \frac{{3(A_1^2{C^2} + 9AB)B\;{\rm{cs}}{{\rm{c}}^2}\left( {2\sqrt {\frac{B}{A}} ({v_0}t - vx)} \right)}}{{C{{\left( {3A\sqrt {\frac{B}{A}} {\rm{cot}}\left( {2\sqrt {\frac{B}{A}} ({v_0}t - vx)} \right) - {A_1}C} \right)}^2}}}} \right\}^{\frac{1}{4}}}\\ {{{\rm{e}}^{{\rm{i}}({\omega _0}t - \omega x)}}} \end{array} $ | (33) |
选取参数β2=1, β3=1, α1=2, γ1=1, γ2=1, v0=1, v=1, ω0=1进行图示。当A1=1, α2=1, ω=2时,有
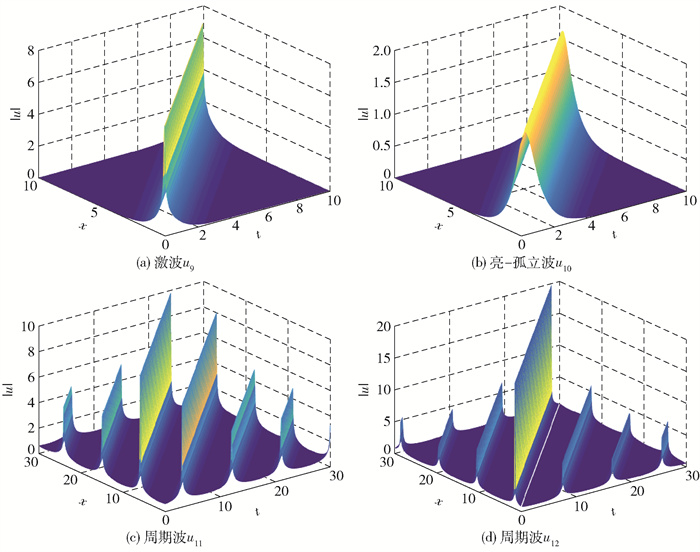
|
图 3 激波u9,亮- 孤立波u10和周期波u11、u12的三维波形图 Fig.3 Three-dimensional waveforms of the shock wave u9, bright-soliton wave u10 and periodic waves u11, u12 |
通过比较可以发现以上3种方法存在内在关联性:
1) Riccati方程- 展开法的解表达最简,不含自由参数,倒数展开法的解有2个待定参数A0、A1转化为非0自由参数,Exp- 展开法中有1个待定参数A1转化为自由参数;
2) 倒数展开法中限定参数S0=1,所得解即为Exp- 展开法求得的解;
3) Exp- 展开法限定参数A1=0,所得解即为Riccati方程- 展开法求得的解。
3 结束语本文结合文献[4-8]对系统(1)进行改进得到新方程(4)。该方程通过行波变换化简为二阶常微分方程(6)。由于高次项ϕ5和二阶导项ϕ″在辅助函数法代入过程中关于V的次数变化幅度不同,导致无法选出合适的N来达到次数平衡。为此,引入变量代换ϕ=Q1/4,将方程(6)转化为方程(8),运用多种辅助函数展开法—Riccati方程- 展开法、Riccati方程- 倒数展开法、Exp- 展开法,求解出几种类型的解析解,如亮- 孤立波、激波和周期波,并且发现这3种方法求得的解存在一定的交集。
| [1] |
HASEGAWA A, TAPPERT F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. anomalous dispersion[J]. Applied Physics Letters, 1973, 23(3): 142-144. DOI:10.1063/1.1654836 |
| [2] |
PALACIOS S L, FERNÁNDEZ-DÍAZ J M. Bright solitary waves in high dispersive media with parabolic nonlinearity law: the influence of third order dispersion[J]. Journal of Modern Optics, 2001, 48(11): 1691-1699. DOI:10.1080/09500340120145 |
| [3] |
BAI C L, ZHAO H, WANG W T. Exact solutions to extended nonlinear Schrödinger equation in monomode optical fiber[J]. Communications in Theoretical Physics, 2006, 45(1): 131-134. DOI:10.1088/0253-6102/45/1/025 |
| [4] |
TRIKI H, WAZWAZ A M. Soliton solutions of the cubic-quintic nonlinear Schrödinger equation with variable coefficients[J]. Romanian Journal of Physics, 2016, 61(3/4): 360-366. |
| [5] |
YILDIRIM Y, BISWAS A, ASMA M, et al. Optical solitons with Sasa-Satsuma equation[J]. Optik-International Journal for Light and Electron Optics, 2020, 219: 165183. DOI:10.1016/j.ijleo.2020.165183 |
| [6] |
JHANGEER A, SEADAWYA R, ALI F, et al. New complex waves of perturbed Schrödinger equation with Kerr law nonlinearity and Kundu-Mukherjee-Naskar equation[J]. Results in Physics, 2020, 16: 102816. DOI:10.1016/j.rinp.2019.102816 |
| [7] |
ZHANG Z Y, LIU Z H, MIAO X J, et al. New exact solutions to the perturbed nonlinear Schrödinger's equation with Kerr law nonlinearity[J]. Applied Mathematics and Computation, 2010, 216: 3064-3072. DOI:10.1016/j.amc.2010.04.026 |
| [8] |
YILDIRIM Y. Optical solitons to Sasa-Satsuma model with trial equation approach[J]. Optik-International Journal for Light and Electron Optics, 2019, 184: 70-74. DOI:10.1016/j.ijleo.2019.03.024 |








