2. 北京化工大学 机电工程学院,北京 100029;
3. 首都航天机械有限公司,北京 100076
2. College of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing 100029;
3. Capital Aerospace Machinery Co. Ltd., Beijing 100076, China
数控机床是工业生产中的重要工具[1],在航空航天、军工、汽车等各个领域均有广泛应用,可显著提高机械生产加工的生产效率。角度头可对与主轴之间有一定角度的工件进行操作处理[2],是数控机床上的典型部件。角度头若发生故障将直接影响机床的加工精度和质量,因此研究其故障机理及诊断方法具有重要意义。
角度头常见的故障包括壳体损坏,锥齿轮磨损、齿轮裂纹和齿面断齿,轴承磨损、胶合和点蚀等。因工作时会受到多种因素的干扰,针对角度头提取到的信号经常伴有噪声干扰,因此需要对采集信号进行降噪和分类处理。赵德尊等[3]提出基于经验模态分解(empirical mode decomposition,EMD)和峰值啮合倍频(instantaneous dominant meshing multiply,IDMM)的诊断方法,通过对混合信号重新采样筛选,达到有效去除噪声的目的。Zhang等[4]比较了经验模态分解和变分模态分解(variational mode decomposition,VMD)对轴承特征提取的性能,结果表明VMD的性能更优。Liu等[5]提出总体平均经验模态分解(ensemble empirical mode decomposition,EEMD)和贝叶斯网络相结合的诊断方法,通过多特征信息源融合来提高诊断的准确性,对于特征信息不完善的情况诊断效果良好。Shi等[6]将自适应随机共振方法和EEMD相结合,有效提高了信噪比,并优化了分解后的结果。Zhu等[7]将粒子群算法和SVM算法进行融合,有效提高了收敛速度,对样本数据的分类效果更加精确。吕锋等[8]采用支持向量数据描述(support vector data description,SVDD)和支持向量机(support vector machine,SVM)对故障样本的不完备数据进行分类,对于已知和未知故障均有较好的判断识别效果。然而目前已提出的研究方法大都是关于信号特征提取方面,对于角度头故障识别涉及较少,针对其中样本数据的筛选方法也相应较少。
本文应用变分模态分解来分解获取的信号,通过遗传算法(genetic algorithm,GA)对该方法中的关键性参数进行优化,求得分解之后对应的本征模态分量(intrinsic mode function,IMF)的信号熵,再通过SVM算法对有效故障信号进行筛选,采用峭度和相关系数相结合的方法从分解后所有IMF分量中选取合适的分量进行信号重构,获取并分析其故障特征,最终实现对故障的识别。最后对所提方法进行了仿真和实验验证,证明了该方法在角度头故障识别领域的适用性。
1 基于GA优化的VM D- SVM算法 1.1 VMD算法VMD算法是Dragomiretskiy等[9]基于时频分析提出的信号处理和降噪方法。该方法的主要思想是将所有本征模态函数均看作是中心频率不同且有限带宽的函数,通过转换或者优化等方式获得所有IMF分量,并可以同时获得相应的中心频率。
将变分模态分解算法中分解出的分量uk, 即IMF定义为调幅- 调制(A M- FM)信号
| $ u_{k}(t)=A_{k}(t) \cos \left[\phi_{k}(t)\right] $ | (1) |
式中,Ak(t)为uk(t)的瞬时幅值, ϕk(t)为uk(t)的相位。
将初始信号设为f,其由K个带宽有限的IMF分量uk构成,中心频率为ωk,且频谱具有稀疏性。通过构造出约束问题,最终得到约束变分模型为
| $ \left\{\begin{array}{l} {\mathop {\min }\limits_{\left\{u_{k}\right\}, \left\{\omega_{k}\right\}} }\left\{\sum\limits_{k}\left\|\partial_{t}\left[\left(\sigma(t)+\frac{j}{\pi t}\right) * u_{k}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k} t}\right\|_{2}^{2}\right\} \\ \text { s.t. } \sum\limits_{k} u_{k}(t)=f(t) \end{array}\right. $ | (2) |
式中,{uk}={u1, u2, …, uk}为K个IMF分量集;{ωk}={ω1, ω2, …, ωk}为K个频率中心集。
为得到式(2)的最优解,将此约束变分问题改为非约束变分问题,因此需借助于式(3)所示的增广Lagrange函数[10]
| $ \begin{array}{l} \;\;\;\;\;\;L\left(\left\{u_{k}\right\}, \left\{\omega_{k}\right\}, \lambda\right)=\alpha \sum\limits_{k} \| \partial_{t}\left[\left(\sigma(t)+\frac{\mathrm{j}}{\pi t}\right) *\right. \\ \left.u_{t}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k} \|_{2}}\left\|_{2}^{2}+\right\| f(t)-\sum\limits_{k} u_{k}(t) \|+{\left\langle \lambda(t), \right.}\\ {\left. f(t)-\sum\limits_{k} u_{k}(t) \right\rangle} \end{array} $ | (3) |
式中,α为二次项惩罚因子;λ为Lagrange乘子。采用交替乘子方向算法(alternate direction method of multipliers,ADMM)不断更新各IMF的中心频率和带宽,同时找到式(3)的鞍点,作为式(2)的解[11]。
1.2 SVM算法SVM算法是针对训练数据线性可分而做出最优化的超平面,即间隔最大的支持向量[12]。在此基础上,又引申出针对训练数据线性不可分的非线性支持向量,从而出现了多分类SVM。
对于训练数据线性可分的情况,SVM是通过一个最优分类线来划分数据,同时具备有且仅有的最高正确率和确信度[13],其方程表示为
| $ \omega * x+b=0 $ | (4) |
相应的分类决策函数为
| $ f(x)=\operatorname{sign}(\omega * x+b) $ | (5) |
对其进行归一化处理后,训练样本集(xi, yi), i=1, 2, …, n, x∈Rn, y∈{-1, 1},满足约束
| $ y_{i}(\omega * x+b)-1 \geqslant 0, i=1, 2, \cdots, n $ | (6) |
此时满足式(6)且分类间隔
对于训练数据线性不可分的情况,通过将数据映射到高维空间的方法,引入松弛变量和核函数,在新创建的空间中寻找最优分类面[14]。此时的分类决策函数经过对偶后为
| $ f(x)=\operatorname{sign}\left(\sum\limits_{i=1}^{N} \alpha_{i} y_{i} K\left(x, x_{i}\right)+b\right) $ | (7) |
式中,K(x, xi)为正定核函数。
1.3 IMF筛选准则如果仅选择用峭度[15]或相关系数[16]其中的一种方法筛选IMF分量,则可能会出现信号信息丢失或者筛选不充分等情况,因此采用将两者相结合的方法筛选出合适的IMF分量,这两者之间的乘积表示为相关峭度系数[17]。对经SVM筛选后的有效故障数据进行系数计算,最终选择出最优的IMF分量对信号作重构处理。通过此方法,可以获得更全面的故障信号信息,更有效地进行降噪处理,获得更精确的高信噪比。
1.4 GA优化VMD参数VMD算法的主要参数包括惩罚因子α、分量个数K和判别精度ξ等[18]。遗传算法是根据进化论和遗传学机理研究得出的搜索方法,具有全局搜索的优势[19]。由于关键参数K和α的取值对于VMD分解得到的IMF分量的结果影响较大[20],因此本文采用遗传算法对这两个参数作优化处理,以获得最优参数。
在利用遗传算法对关键参数进行优化处理之前,首先需要选择良好的适应度函数。信息熵可以比较有效地反映信号的稀疏性特征,其数值的差异即对应于信号的不确定程度,信息熵值越大,则其对应的不确定性越大,反之亦然[21]。解调分解处理运算操作后的包络信号数据序列ej,其对应的熵值称为包络熵,可以反映信号的稀疏性特征。将零均值信号x(j)(j=1, 2,…,N)的包络熵用Ee表示
| $ \left\{\begin{array}{l} E_{e}=-\sum\limits_{j=1}^{N} e_{j} \lg e_{j} \\ e_{j}=a(j) / \sum\limits_{j=1}^{N} a(j) \end{array}\right. $ | (8) |
式中,ej为a(j)的归一化形式,a(j)为信号x(j)经希尔伯特变换后的包络信号。
角度头若发生故障,故障特征信息一般呈现出较为复杂的情况,但其对应信号中的冲击脉冲会呈现一定的周期性,即表示其具有的稀疏性较强,对应的包络熵值较小。当测试信号中含有较多干扰时,对应的冲击特征则表现较弱,即表示其稀疏性较弱,对应的包络熵值较大。因此,选择IMF对应的包络熵值为优化处理的适应度函数。先从区域中筛选出最小的熵值,求得对应的IMF分量,再利用遗传算法对全局搜索,寻找到最小的包络熵值,即为最优输入参数(K, α)。
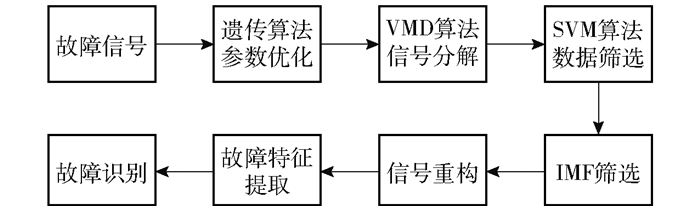
1.5 流程图本文采用基于GA优化的VM D- SVM算法故障特征识别方法。首先获得角度头的振动信号,之后通过GA优化关键参数后的VMD算法进行分解,再通过SVM算法筛选出有效的故障信号,选择合适的IMF分量以实现对信号的重构;最后提取故障特征,实现对角度头的故障识别。该方法的具体流程如图 1所示。
|
图 1 角度头振动故障信号特征识别流程图 Fig.1 Flow chart of angle head vibration fault signal feature recognition |
由于加工过程和环境的影响,角度头中轴承和齿轮是极其容易受损的部件,而此时对应的故障信号会呈现出明显的周期性和调制特征。因此根据实际情况下受到的噪声和环境影响,可将仿真信号设置为
| $ x_{1}(t)=0.5 \sin \left(2 \pi \times 30 t+\frac{\pi}{5}\right) $ | (9) |
| $ x_{2}(t)=\cos (2 \pi \times 100 t+\sin (2 \pi \times 5 t)) $ | (10) |
| $ x_{3}(t)=(2+0.3 \cos (2 \pi \times 5 t)) \sin (2 \pi \times 200 t) $ | (11) |
| $ f(t)=x_{1}(t)+x_{2}(t)+x_{3}(t)+\sigma(t) $ | (12) |
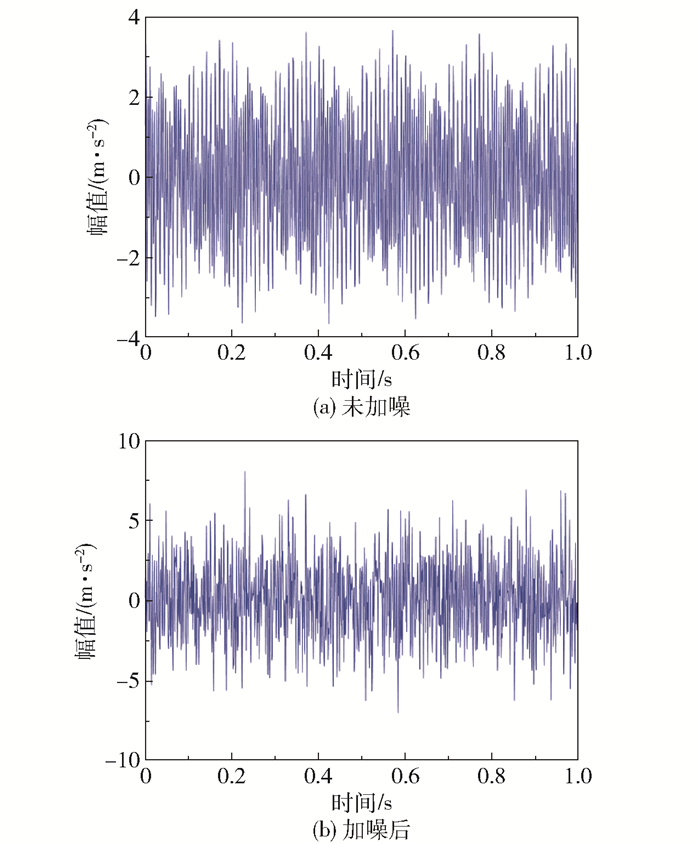
含噪仿真的信号表达式如式(12)所示,该信号由正弦模拟信号x1(t)、调频模拟信号x2(t)、调幅模拟信号x3(t)和信噪比为-5 dB的高斯白噪声σ(t)组成。设定采样频率为1 024 Hz,未加噪和加噪后的时域图如图 2(a)、(b)所示。
|
图 2 未加噪和加噪后的时域波形图 Fig.2 Time domain waveform without added noise and with added noise |
计算得出此时的信噪比为-0.64 dB。从图 2(a)、(b)的对比可以看出,加噪前后的波形呈现较大的差别,加入噪声的信号中有许多信息无法直接识别,导致对其特征提取的效果非常差,因而对于故障识别的准确率也非常低。
2.2 VMD仿真采用本文所提方法对加噪后的信号进行优化分解处理,最终获得6个IMF分量。通过峭度和相关系数相结合的原则进行选择,计算得出前3个分量符合上述原则,选择这3个分量对信号进行重构,得到其对应的重构信号时域图和频谱图如图 3(a)、(b)所示。

|
图 3 重构信号的时域图和频谱图 Fig.3 Time domain plot and spectrum of the reconstructed signal |
从图 3可以看出,随机噪声受到明显的抑制,信噪比达到7.997 6 dB,此时重构的时域图也能够相对准确地代表测试信号的时域。同时,30、100 Hz和200 Hz处的频率成分相对比较明显,说明噪声成分受到有效抑制。以上仿真结果表明本文所提方法对随机噪声有较好的抑制作用,从而突出了特征频率。
3 实测信号分析对实测角度头振动信号进行分析。通过加速度传感器采集角度头的振动信息,采集工况如下:工作转速1 500 r/min(25 Hz,记为X),切削频率50 Hz(即2X)。设定采样频率20 kHz,关于加速度传感器的布点一共有4个,分别位于加工近端面和远端面的X、Y方向[22]。
3.1 角度头故障分析通过对比所采集的故障角度头各个测点的信号,发现近端面X方向测点的信号较为明显,因此将此测点的信号作为分析数据。对采集到的原始数据进行预处理,通过VMD算法对其分解后得到各IMF,再求得各IMF对应的能量熵。对角度头数据多次信号分解后发现,前6项数据即可代表原始信号,因此选取前6项的熵值作为特征向量,并均作归一化处理。能量熵可以反映所获得信号的复杂程度,角度头在复杂工作情况下,易出现较多的无效数据,因此根据能量熵对所获得的数据进行信号筛选,将有效数据用于后续的诊断。随机选取多次实测时间、不同工况中的10组数据作为训练数据,其中5组为有效故障数据,5组为无效故障数据,并随机选取10组作为测试数据,各组训练样本部分IMF熵值和测试样本部分IMF熵值分别如表 1、2所示。
| 下载CSV 表 1 训练样本IMF熵值 Table 1 IMF entropy of the training sample |
| 下载CSV 表 2 测试样本IMF熵值 Table 2 IMF entropy of the test sample |
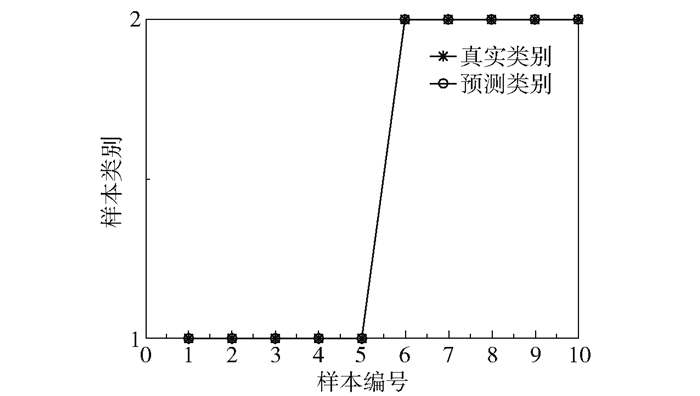
选取径向基函数(radial basis function,RBF),并通过交叉验证方法得到最佳的参数值。对所选取的随机数据进行分类,结果如图 4所示,其中样本类别的1类表示有效故障数据,2类表示无效故障数据。从图 4可以看出,该方法可以将有效故障数据和无效故障数据准确分开,正确率达到100%,因此可将有效故障数据应用于后续的识别中。
|
图 4 SVM算法数据分类 Fig.4 Data classification with SVM algorithm |
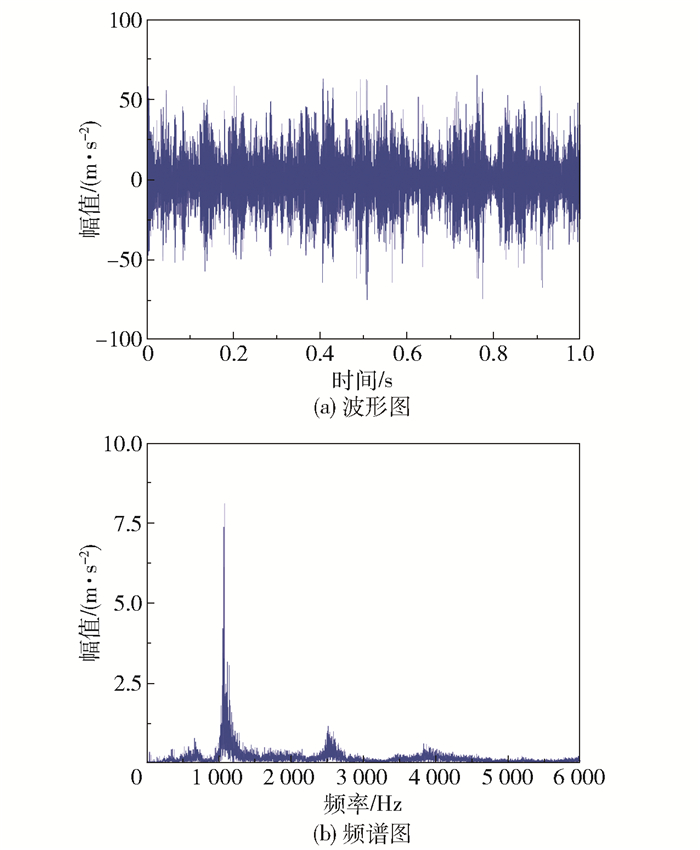
计算该角度头的轴承故障特征频率,结果如表 3所示。故障角度头的原始波形图和频谱图如图 5(a)、(b)所示。
| 下载CSV 表 3 角度头轴承故障特征频率 Table 3 Fault characteristic frequencies of bearings in the angle head |
|
图 5 故障角度头原始波形图和频谱图 Fig.5 Original waveform and spectrum of the failure angle milling head |
从时域波形图(图 5(a))来看,信号呈现明显的周期性,但同时其幅值较大,且存在分布不均匀的情况。从频谱图(图 5(b))来看,故障角度头振动能量主要集中在1 kHz左右,其边频带的数值也较大,但整体呈现下降的趋势。
采用所提方法对故障信号进行处理,最终得到最优参数(K, α)为(8,20 600)。通过VMD算法处理后获得8个IMF分量,计算其对应的相关峭度系数,结果如表 4所示。根据峭度和相关系数筛选原则,对得到的8个数据进行筛选,最终选择IMF2、IMF3和IMF4这3个分量来重构信号。采用本文方法得到的包络解调谱与未优化参数方法得到的包络解调谱如图 6(a)、(b)所示。
| 下载CSV 表 4 各IMF分量的相关峭度系数 Table 4 Correlation kurtosis coefficient of IMFs |
|
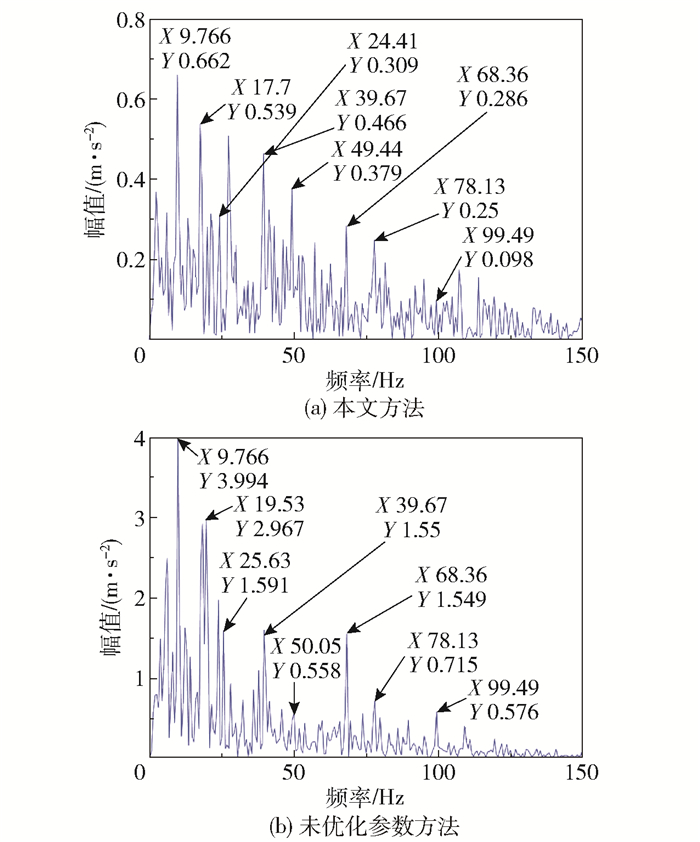
图 6 分别采用本文方法和未优化参数方法得到的包络解调谱 Fig.6 Envelope demodulation spectrum obtained by the method described in this work and an unoptimized envelope demodulation spectrum |
从图 6(a)、(b)的重构信号包络解调谱对比来看,本文方法的降噪效果比较明显,整体数值趋于正常化。图 6(a)中,转频X、切削频率2X均比较明显,但幅值较初始数值均有所下降,其中9.766 Hz及其倍频较为突出,但它们的幅值相对于图 6(b)明显下降,其特征与轴承保持架故障特征相似,故推测该角度头的轴承保持架出现了损坏。
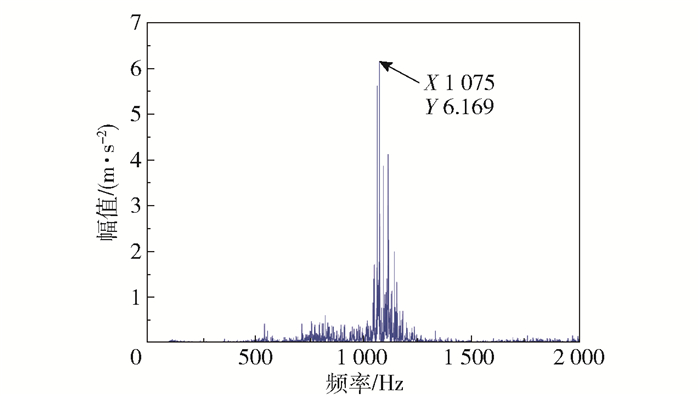
从图 5可以看到,角度头信号能量在1 kHz附近分布较为明显,故对其高频部分再次单独进行分析,得到对应的高频频谱如图 7所示。从图 7可知,以1 075 Hz成分(即43X频率)为中心频率的边频带信号非常突出,幅值较大,即振动能量偏大,且整体呈现下降的趋势。此特征即表明该部件齿轮存在局部异常,且为包含齿轮断齿、裂纹和严重磨损等多种情况的组合故障。
|
图 7 故障角度头高频频谱图 Fig.7 High frequency spectrum of the failure angle milling head |
综上,推测故障角度头的轴承保持架出现损伤问题,使得部分轴承传达出故障信息,同时由其幅值较大的情况推断出轴承内外圈也出现磨损;齿轮存在较为严重的局部异常,包括齿轮磨损和齿轮裂纹等问题。
3.2 故障角度头检修结果对故障角度头拆解后发现,轴承保持架出现较严重的变形,内外圈出现较严重的磨损,齿轮部分也有较为严重的磨损情况,如图 8所示,验证了3.1节分析结果。

|
图 8 故障角度头齿轮拆卸图 Fig.8 Disassembly drawing of the returned gear |
本文通过改进的VM D- SVM算法对角度头进行故障特征识别,该方法能够准确地选择出有效故障数据,降低噪声对信号的影响,自适应性良好。针对分解过程中易出现的信号模态混叠、数据复杂、重构信号选择不准确等问题,选择用遗传算法对VMD中的关键参数进行优化后再分解信号,并通过SVM对所得数据进行筛选,得到有效故障数据;采用相关峭度系数筛选原则,在保留原始信号相关信息的基础上,降低噪声信号的干扰,大幅度提高信噪比。根据频谱图数据对比,可明显看到信号幅值趋于正常,特征更加明显。信号实测分析验证了本文方法的可行性和稳定性,表明其在角度头的故障诊断中可以取得较好的应用效果。
| [1] |
GARG J, GARG S B. A simplified methodology for finding the natural frequencies and mode shapes of the machine tool structures[J]. Materials Today: Proceedings, 2021, 38(1): 99-104. |
| [2] |
周进, 王鹏程. 角度头在飞机结构件五轴数控加工中的应用[J]. 制造技术与机床, 2016(12): 138-142. ZHOU J, WANG P C. Application of angle head in five axis NC machining of aircraft structure[J]. Manufacturing Technology & Machine Tool, 2016(12): 138-142. (in Chinese) |
| [3] |
赵德尊, 李建勇, 程卫东. 变转速及齿轮噪源干扰下基于IDMM与EMD的滚动轴承故障诊断方法[J]. 振动与冲击, 2016, 35(10): 101-107, 119. ZHAO D Z, LI J Y, CHENG W D. Method for rolling element bearing fault diagnosis based on IDMM and EMD under time-varying rotational speed and gear noise[J]. Journal of Vibration and Shock, 2016, 35(10): 101-107, 119. (in Chinese) |
| [4] |
ZHANG M, JIANG Z N, FENG K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump[J]. Mechanical Systems and Signal Processing, 2017, 93: 460-493. DOI:10.1016/j.ymssp.2017.02.013 |
| [5] |
LIU Z K, LIU Y H, SHAN H K, et al. A fault diagnosis methodology for gear pump based on EEMD and Bayesian network[J]. PLoS One, 2015, 10(5): 0125703. |
| [6] |
SHI P M, SU C J, HAN D Y. Fault diagnosis of rotating machinery based on adaptive stochastic resonance and AM D- EEMD[J]. Shock and Vibration, 2016, 2016: 9278581. |
| [7] |
ZHU W, WEI Y S, XIAO H. Fault diagnosis of neural network classified signal fractal feature based on SVM[J]. Cluster Computing, 2019, 22: 4249-4254. DOI:10.1007/s10586-018-1795-x |
| [8] |
吕锋, 李华, 孙昊, 等. 基于SVD D- SVM分类器的风力发电机故障诊断方法[J]. 计算机辅助工程, 2015, 24(3): 67-71, 77. LYU F, LI H, SUN H, et al. Method of fault diagnosis on wind power generator based on SVD D- SVM classifier[J]. Computer Aided Engineering, 2015, 24(3): 67-71, 77. (in Chinese) |
| [9] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [10] |
BERTSEKAS D P. Constrained optimization and Lagrange multiplier methods[M]. New York: Academic Press, 1982: 383-392.
|
| [11] |
ARORA J S, CHAHANDE A I, PAENG J K. Multiplier methods for engineering optimization[J]. International Journal for Numerical Methods in Engineering, 1991, 32(7): 1485-1525. DOI:10.1002/nme.1620320706 |
| [12] |
吴贝. 基于EEMD和SVM分类器的电机系统故障诊断研究[D]. 长沙: 湖南大学, 2018. WU B. Research on fault diagnosis of motor system based on EEMD and support vector machine classifier[D]. Changsha: Hunan University, 2018. (in Chinese) |
| [13] |
CHENG J S, YU D J, TANG J S, et al. Application of SVM and SVD technique based on EMD to the fault diagnosis of the rotating machinery[J]. Shock and Vibration, 2019, 16: 89-98. |
| [14] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2018: 133-142. LI H. Statistical learning methods[M]. Beijing: Tsinghua University Press, 2018: 133-142. (in Chinese) |
| [15] |
MIAO Y H, ZHAO M, LIN J, et al. Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2017, 92: 173-195. DOI:10.1016/j.ymssp.2017.01.033 |
| [16] |
TANG G J, WANG X L, HE Y L. Diagnosis of compound faults of rolling bearings through adaptive maximum correlated kurtosis deconvolution[J]. Journal of Mechanical Science and Technology, 2016, 30(1): 43-54. DOI:10.1007/s12206-015-1206-7 |
| [17] |
WANG Y, GU L C, QING L J, et al. An improved k-value symmetrical difference analytic energy operator with HTFIF and L- KCA for bearing fault diagnosis[J]. IEEE Access, 2021, 9: 34307-34324. DOI:10.1109/ACCESS.2020.3046249 |
| [18] |
DING J K, XIAO D M, LI X J. Gear fault diagnosis based on genetic mutation particle swarm optimization VMD and probabilistic neural network algorithm[J]. IEEE Access, 2020, 8: 18456-18474. DOI:10.1109/ACCESS.2020.2968382 |
| [19] |
CERRADA M, SÁNCHEZ R V, CABRERA D, et al. Multi-stage feature selection by using genetic algorithms for fault diagnosis in gearboxes based on vibration signal[J]. Sensors, 2015, 15(9): 23903-23926. DOI:10.3390/s150923903 |
| [20] |
张树, 刘德平. BFA优化VMD参数的轴承故障诊断[J]. 组合机床与自动化加工技术, 2020(5): 45-47, 51. ZHANG S, LIU D P. Bearing fault diagnosis based on BFA optimized VMD parameters[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020(5): 45-47, 51. (in Chinese) |
| [21] |
WANG Y K, LI H R, WANG B, et al. Spatial information entropy and its application in the degradation state identification of hydraulic pump[J]. Mathematical Problems in Engineering, 2015, 2015: 532684. |
| [22] |
高树成, 姚剑飞, 陈建, 等. 一种用于机床角度头故障诊断的双重降噪方法[J]. 北京化工大学学报(自然科学版), 2020, 47(5): 97-103. GAO S C, YAO J F, CHEN J, et al. A dual noise reduction method for angle head fault diagnosis[J]. Journal of Beijing University of Chemical Technology(Natural Science), 2020, 47(5): 97-103. (in Chinese) |








