2. 河北工业大学 机械工程学院,天津 300401
2. School of Mechanical Engineering, Hebei University of Technology, Tianjin 300401, China
3D打印技术又称为增材制造技术,是20世纪80年代后期发展起来的一种新型制造技术[1],它是一种集成了机械、控制和计算机技术于一体的复杂的、一体化的成型系统[2]。随着增材制造技术的快速发展,其在航空航天、交通运输、生物医疗、建筑等方面逐渐得到广泛应用[3]。近年来,3D打印技术逐渐向打印多材料零件的方向发展,能用于多材料的3D打印成型工艺主要有材料挤出、材料喷射和粉末床熔融,而对于材料挤出式的3D打印成型工艺,具有良好混合性能的螺杆挤出方式为其提供了一种新的研究路径[4]。
目前,国内外学者对螺杆式3D打印机进行了大量研究。Valkenaers等[5]的研究表明采用螺杆挤出进料方式可以显著改善材料因长时间受热而发生降解、进料不均匀而挤出不稳定等问题。Li等[6]研制了螺杆动态混合器,通过实验对各组分的氧化铝和氧化锆梯度元件进行了样品打印、烧结和测试,结果表明挤出成形技术能够打印出功能分级的陶瓷零件。任礼等[7]分析了传统桌面级熔融沉积制造(fused deposition modeling,FDM)型3D打印机与螺杆挤出式3D打印机的挤出原理,设计了一种新型螺杆挤出式3D打印机,可实现小流率高精度打印。丁承君等[8]改进了陶瓷3D打印机螺杆挤出装置的喷头结构,可实现连续供料。陈磊[9]结合螺杆挤压技术与FDM型Delta并联式打印机研制了一套小型螺杆挤出装置,利用STAR-CCM+仿真软件对物料在挤压系统中的粒料输送与熔体挤压传动过程进行了数值模拟研究,最终得到了合理的螺杆挤压工艺参数范围。Silveira等[10]设计了一种基于双螺杆挤出的创新型三维打印头,该打印头专用于允许在过程中混合多种材料并直接沉积产品的3D打印机。
针对多材料混合打印,现阶段国内外学者对单螺杆挤出的研究较多,可以在一定程度上解决材料应用范围有限、喷头易堵塞的问题,但在打印精度方面仍存在混合效果不佳、挤出连续性差等问题。针对当前所存在问题,本文设计了一种基于双螺杆多材料的3D打印挤出机构,不仅可以弥补单螺杆挤压输送能力弱等不足,而且其优良的混合性能、剪切作用等可为解决单螺杆应用受限问题提供有效的解决方案,对在打印过程中需要保持挤出速度稳定,高效率打印出表面平整、纹理清晰、成型精度较高的零件具有较为实际的意义。本文分析了双螺杆挤出机构的运动原理,对螺杆进行了结构设计,最后通过软件仿真对其流场进行了分析以及混合性能的评估。
1 3D打印机挤出机构设计 1.1 整体结构挤出机构是整个3D打印机的关键部件。本文设计的双螺杆多材料3D打印机挤出机构如图 1所示。
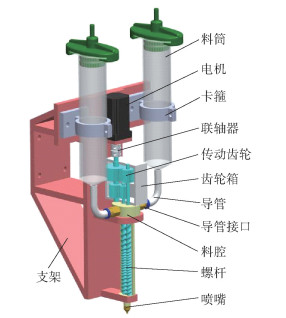
|
图 1 挤出机构结构 Fig.1 Structure of the extrusion mechanism |
为使双螺杆能实现同步转动,以步进电机驱动齿轮转动,从而带动双螺杆实现同步旋转。双料筒的设计用于存储两种材料以实现多材料打印,料筒上方的接口与气泵相连,气泵产生的气压能将陶瓷浆料通过输料导管顺利流入料腔中。导管接口与导管连接处易于拆卸,紧固性和密封性都能达到挤出要求。料腔与螺杆之间使用的密封轴承能保证螺杆旋转的稳定性,同时也能防止在料腔浆料压力过大时从料腔上方溢出。浆料进入料腔后,由于螺杆的挤压输送,浆料会在料腔中不断地进行挤压、剪切、拉伸和混合,最后将混合好的浆料通过挤出喷嘴稳定挤出。该3D打印挤出机构具有正常的挤出功能,且结构紧凑、易拆卸,对于多材料的陶瓷浆料挤出打印具有兼容性并降低了其打印成本。
1.2 双螺杆结构双螺杆螺纹元件的型线从本质上决定了挤出机构的剪切、混合、输送等性能,螺杆端面型线的设计对提高双螺杆挤出机构的整体性能具有重要意义。本文基于相对运动法设计啮合型同向双螺杆螺纹元件端面型线,其原理图如图 2所示,其中O1、O2为圆心,B1~B4为圆上的点,A为两圆盘中心距。
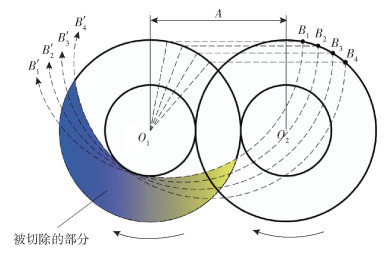
|
图 2 相对运动法原理图 Fig.2 Schematic diagram of the relative motion method |
根据微流挤出3D打印机的特性,螺杆不宜太大,在满足挤出流量的条件下,应合理选用螺杆结构参数。本文初步确定螺纹头数Z=2,中心距A=5 mm,螺杆外径Do=6 mm,则螺杆顶径Ro=Do/2=3 mm,螺杆根径Ri=A-Ro=2 mm,则螺杆内径Di=4 mm,根据经验公式在螺纹头数为2时,其中心距比Cr需满足式(1),计算得Cr=A/2Ro=0.9≥
| $ {C_{\rm{r}}} = A/2{R_{\rm{o}}} \ge \cos \left( {{{90}^\circ }/Z} \right) $ | (1) |
| $ \alpha = \pi /Z - 2\phi $ | (2) |
| $ \beta = \alpha $ | (3) |
| $ \varphi = {\cos ^{ - 1}}\left( {A/2{R_{\rm{o}}}} \right) $ | (4) |
| $ \phi = \varphi $ | (5) |
根据同向啮合型双螺杆相对运动的形成过程,可以得出螺纹元件的端面型线方程(式(6))。
| $ \rho (\theta ) = \left\{ {\begin{array}{*{20}{l}} {{R_{\rm{i}}}, }&{ - \frac{\alpha }{2} \le \theta \le \frac{\alpha }{2}{\rm{或}}\pi - \frac{\alpha }{2} \le \theta \le \pi + \frac{\alpha }{2}}\\ { - {R_{\rm{o}}} \cdot \cos \left( {\theta - \frac{\alpha }{2}} \right) + \sqrt {{A^2} - R_{\rm{o}}^2 \cdot {{\sin }^2}\left( {\theta - \frac{\alpha }{2}} \right), } }&{\frac{\alpha }{2} \le \theta \le \frac{\pi }{2} - \frac{\beta }{2}}\\ {{R_{\rm{o}}}, }&{\frac{\pi }{2} - \frac{\beta }{2} \le \theta \le \frac{\pi }{2} + \frac{\beta }{2}{\rm{或 }}\frac{{3\pi }}{2} - \frac{\beta }{2} \le \theta \le \frac{{3\pi }}{2} + \frac{\beta }{2}}\\ { - {R_{\rm{o}}} \cdot \cos \left( {\pi - \theta - \frac{\alpha }{2}} \right) + \sqrt {{A^2} - R_{\rm{o}}^2 \cdot {{\sin }^2}\left( {\pi \theta - \frac{\alpha }{2}} \right), } }&{\frac{\pi }{2} + \frac{\beta }{2} \le \theta \le \pi - \frac{\alpha }{2}}\\ { - {R_{\rm{o}}} \cdot \cos \left( {\theta - \pi - \frac{\alpha }{2}} \right) + \sqrt {{A^2} - R_{\rm{o}}^2 \cdot {{\sin }^2}\left( {\theta - \pi - \frac{\alpha }{2}} \right)} , }&{\pi + \frac{\alpha }{2} \le \theta \le \frac{{3\pi }}{2} - \frac{\beta }{2}}\\ { - {R_{\rm{o}}} \cdot \cos \left( {2\pi - \theta - \frac{\alpha }{2}} \right) + \sqrt {{A^2} - R_{\rm{o}}^2 \cdot {{\sin }^2}\left( {2\pi - \theta - \frac{\alpha }{2}} \right)} , }&{\frac{{3\pi }}{2} + \frac{\beta }{2} \le \theta \le 2\pi - \frac{\alpha }{2}} \end{array}} \right. $ | (6) |
将式(2)~(5)计算得出的数值代入式(6)中,可以得到双螺杆的端面型线图如图 3所示,之后再通过SolidWorks三维建模软件建立三维模型。螺杆设计为三段式,包括输送段(L1)、混合段(L2)和计量段(L3):输送段螺距较大,输送能力强,将刚进入料腔的陶瓷浆料沿着挤出方向输送;混合段螺距最小,提升剪切拉伸作用,使得陶瓷浆料得到充分混合;计量段螺距适中,能有效稳定浆料从打印喷嘴挤出。为了防止螺杆与料腔内壁的磨损和碰撞,保持螺杆与螺杆之间、螺杆与料腔内壁之间的间隙(分别为δ1、δ2)非常重要。双螺杆和料腔总体结构如图 4所示,螺杆各参数及数值如表 1所示。
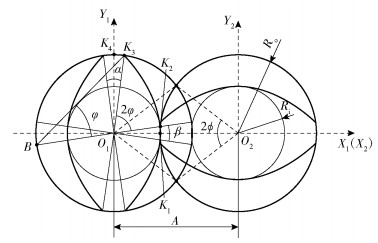
|
图 3 双螺杆端面型线 Fig.3 Profile diagram of the twin-screw |
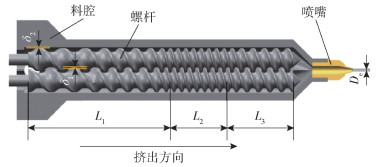
|
图 4 双螺杆与料腔结构 Fig.4 Structure of the twin-screw and material cavity |
| 下载CSV 表 1 螺杆各参数及数值 Table 1 Screw parameters and dimensions |
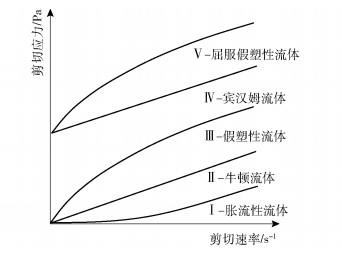
本文选用可打印的高固含量陶瓷浆料作为研究对象。高固含量陶瓷浆料是一种高黏度的非牛顿流体,浆料黏度由式(7) 计算得出。
| $ \mu = \frac{\tau }{{\dot \gamma }} $ | (7) |
式中,μ为黏度,Pa ·s,τ为剪切应力,Pa,
| $ \mu = \frac{{{\tau _0}}}{{\dot \gamma }} + K{\left( {\frac{{\dot \gamma }}{{{{\dot \gamma }_{\rm{c}}}}}} \right)^{n - 1}} $ | (8) |
|
图 5 流体剪切应力随剪切速率的变化 Fig.5 Fluid shear stress as a function of shear rate |
式中,τ0为屈服应力,Pa,K为黏度系数,Pa ·sn,n为流动系数,
| 下载CSV 表 2 陶瓷浆料物性参数 Table 2 Physical parameters of the ceramic slurry |
考虑流体的性质以及双螺杆运动网格划分难度较大,选用ANSYS中的POLYFLOW模块进行流体仿真分析。POLYFLOW是一个主要用于黏性流体的动力学仿真CFD模块,拥有较多的流体计算模型,其独特的网格重叠技术(mesh superposition technology,MST)有效避免了重新划分网格的过程,并具备较高的精度[14]。流场分析过程中,根据具体情况给出如下假设:
1) 浆料充满整个流道且不可压缩;
2) 不计重力、惯性力等远小于黏性力的体积力;
3) 料腔内壁和螺杆表面无滑移;
4) 流场中浆料温度不变。
同时设定流体域的边界条件:每个入口压力为5 000 Pa;左右两个内孔为无滑移边界,无流体能够穿透该边界流动;外壁面为无滑移边界;出口为outflow;设定两个螺杆为运动部件,螺杆转速为1~15 r/min。
2.2 流体区域网格模型的划分双螺杆挤出过程中料腔与螺杆之间的间隙对浆料的剪切有很大影响。为了描述间隙内的物料流动,需要对间隙局部进行合理的网格划分。在流体外壁设定4层膨胀层,每层宽度为0.05 mm,总宽度与料腔和螺杆之间的间隙一致。同时在浆料入口、混合段区域和喷嘴流体位置施加局部网格细化命令。其余流体域与螺杆的网格单元尺寸均设定为0.3 mm,且均用四面体网格划分,最终得到网格数2 498 338、节点数608 915的网格模型。单元网格质量评估平均值为0.775 81,评估值大于0.6,满足仿真计算的要求。划分好的网格模型如图 6所示。
|
图 6 流体域与螺杆网格划分 Fig.6 Fluid domain and screw meshing |
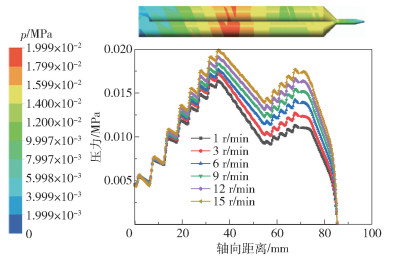
5 r/min螺杆转速下的压力云图和各转速下压力沿挤出方向的变化趋势如图 7所示。由图 7可以看出沿着浆料挤出方向,输送段整体压力呈现增大的趋势,这是由于输送段到混合段螺杆的螺距是逐渐减小的,螺距的减小使得输送能力减弱,浆料在挤出过程中不断向结构密集的流道汇集,造成压力增大;混合段压力又呈现出降低的趋势,这是由于混合段螺距增大,其流道空间逐渐变大,起到一定的释压效果;计量段压力呈现小幅度上升,这是由于在螺杆尾部区域流道逐渐变小,浆料在此处不断被挤压,使得压力上升;最后当浆料脱离有螺杆存在的流道后一直到从喷嘴挤出,其压力逐渐减小到0,这是由于随着挤出头的不断挤出,流道压力得到了释放。整个流道压力的大体趋势是升- 降- 升- 降。同时从图中也可以看出,在有螺杆存在的区域,每隔一段距离都会有一个较小的先上升后下降的现象,这是浆料在每一个螺距内所呈现的压力变化,越靠近螺棱处压力越大,螺槽处压力最小。另外从图 7也可以看出随着螺杆转速的提升,流道整体的压力也是逐渐上升的,说明螺杆转速上升对螺杆建压能力有着正向作用。在螺杆各转速下,最大压力比入口压力提高3~4倍,表明本文所设计的三段式双螺杆挤出结构建压能力强,能够将浆料稳定地挤出进行打印。
|
图 7 螺杆转速5 r/min下的压力云图与各转速下的压力变化对比 Fig.7 The pressure cloud diagram and the comparison of pressure change at each speed when the screw speed was 5 r/min |
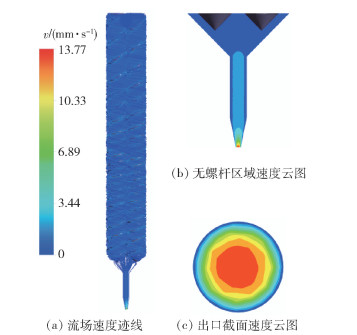
图 8为螺杆转速5 r/min下的流体在料腔中形成的迹线、无螺杆区域速度云图及出口截面速度云图。从迹线图中可以看出浆料在随着螺杆转动的同时也被螺杆挤压沿着挤出方向运动,且越靠近出口速度越大。从出口截面速度云图可以看出,越靠近出口浆料挤出的中心速度越大,在出口边缘处速度很小,这是由浆料黏度高、与流道内壁面间的阻力系数大造成的。对出口截面速度进行数据提取,计算出口挤出速度的平均值,得出当螺杆转速为5 r/min时,双螺杆挤出机构的浆料挤出速度为8.53 mm/s。
|
图 8 螺杆转速为5 r/min时的流场速度 Fig.8 Flow field speed for a screw rotation speed of 5 r/min |
图 9为不同螺杆转速下的出口挤出速度与出口流率曲线,其中出口流率由流体仿真结果得出,出口理论速度通过出口流率除以出口截面面积(0.28 mm2)计算得出,出口平均速度通过提取出口截面速度数据再求平均值得出。从图中可以看出出口理论速度、出口平均速度两条曲线基本吻合。对不同螺杆转速进行速度仿真分析,结果表明出口流率、出口速度与螺杆转速均成正比,出口挤出速度范围为2~23 mm/s,对比市面上陶瓷3D打印机的挤出速度(1~50 mm/s),其能够满足陶瓷浆料挤出3D打印机的要求。
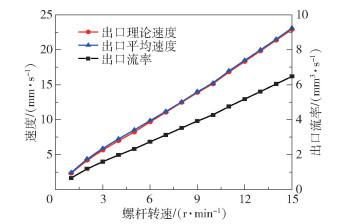
|
图 9 螺杆转速为1~15 r/min下的出口挤出速度与流率 Fig.9 The exit extrusion speed and flow rate when the screw rotation speed was 1-15 r/min |
图 10给出了不同螺杆转速下料腔内剪切速率的分布状态。从图中可以看出螺纹尖端的剪切速率大,螺槽处的剪切速率小,说明螺纹尖端的剪切作用比螺槽处强;在螺纹尖端陶瓷浆料受到更大的拉伸作用,特别是在啮合区域,浆料会受到向里与向外两个剪切力,所以此处的剪切速率最大,更有利于浆料的混合。以螺杆转速5 r/min下的仿真结果为例,其螺纹尖端的剪切速率由式(9)计算得出,其中N为螺杆转速,计算结果为7.85 s-1,螺纹尖端处最大剪切速率仿真结果为7.88 s-1,计算结果与仿真结果相近。通过仿真实验发现,不同转速的螺纹尖端剪切速率最大值均出现在Z=13 mm处,这是由于此时浆料从入口随着螺杆输送到此处的填充率是最高的。螺杆转速提高,螺纹尖端处的剪切速率也随之增加,且沿挤出方向剪切速率呈以升- 降- 升为周期的变化趋势,两峰值之间的距离与螺距相对应,表明螺棱处剪切速率最大,螺槽底部剪切速率最小,本文所设计的双螺杆挤出机构剪切速率大小适宜。
| $ \dot \gamma = \frac{{2\pi {D_0}N}}{{2{\delta _2}}} $ | (9) |
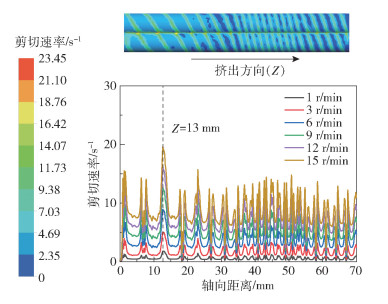
|
图 10 螺杆转速为5 r/min时的剪切速率云图与各转速下的剪切速率变化对比 Fig.10 Shear rate cloud diagram at 5 r/min and comparison of shear rate variation for different screw rotation speeds |
由于双螺杆挤出机构啮合区域存在高剪切速率,所以在双螺杆挤出过程中,输送和混合是同步进行的。当料腔流道趋于稳定时,不同螺杆转速下两种陶瓷浆料在流道中的组分分布情况如图 11所示,两种陶瓷浆料同时从两个入口进入,进入速率比为1 ∶1。随着螺杆的转动,左右螺杆通道的浆料会通过啮合区域进行材料交换,组分云图中显示Al2O3陶瓷浆料的分布情况,红色代表含量为100%,蓝色代表含量为0,绿色部分代表浆料组分占比50%,认为此时浆料混合完成。从图中可以看出,随着螺杆转速的提高,浆料混合完成所需要的时间缩短。在螺杆转速为1 r/min时,螺杆输送能力与混合能力均较差,在螺杆的计量段浆料未完成完全混合,但是从图中也可以看出当浆料输送到混合段时,浆料在高剪切速率的作用下,其分散频率明显增加。在螺杆转速为5 r/min时,浆料通过混合段的高频分散之后,浆料混合基本完成。对比Z=70 mm处3种转速的组分分布情况,发现在螺杆转速10 r/min时浆料混合效果最好,5 r/min时基本混合完成,1 r/min时混合未完成,说明转速太低不适用于混合打印。组分云图在一定程度上反映出浆料在流道中的分布情况,为进行实物实验提供了一定的数据支撑。螺杆混合段的设计在低转速下起着非常大的分散剪切作用,在高转速下也对浆料的混合效率发挥着积极作用。
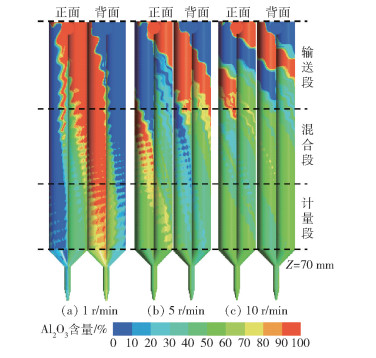
|
图 11 不同转速下流道浆料组分分布 Fig.11 Distribution of slurry components in the flow passage at different rotation speeds |
流体在流道内混合情况的优劣,不仅受物料承受的剪切拉伸应力影响,还与物料在流道内停留的时间有关。因此在评价混合能力时,必须考虑流体在流道中停留的时间。采用示踪粒子分析法(partical tracking analysis, PTA)计算浆料在螺杆流道中的停留时间。在入口处设置进入2 000个粒子,运动时长为1 200 s,得出粒子的停留时间分布函数(RTD)和累积停留时间分布函数(CRTD),分别由概率密度函数和概率函数表示[15]。
停留时间分布反映了轴向混合的能力[16],其不仅可以反映混合性能及输送行为,还可以结合局部微观分析为研究挤出材料性能提供依据[17]。停留时间分布的函数表达式为
| $ E(t) = c(t)/\int_0^\infty c (t){\rm{d}}t \cong c(t)/\sum\limits_0^\infty c (t)\Delta t $ | (10) |
式中,c(t)为示踪粒子的浓度。累积停留时间分布为0到t时间内对停留时间分布的积分,其表达式为
| $ F(t) = \int_0^t E (t){\rm{d}}t \cong \sum\limits_0^t c (t)\Delta t/\sum\limits_0^\infty c (t)\Delta t $ | (11) |
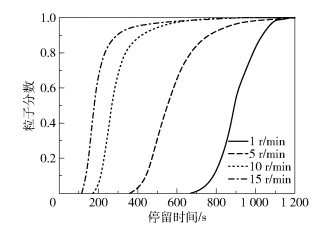
根据仿真结果统计,不同螺杆转速下的停留时间分布函数和累积停留时间分布函数如图 12、13所示。示踪粒子最快流出流道的时间为图像与水平轴的第一个交点,用t0表示,t01则表示转速为1 r/min时的流出时间,得出t01=670.6 s、t05=357.9 s、t010=173.7 s、t015=114.4 s,可以发现随着转速的增大,t0是逐渐减小的。通过仿真结果计算得出各转速下的平均停留时间,分别为t11=956.3 s、t15=580.2 s、t110=292.5 s、t115=206.4 s,t1越大代表轴向的混合性能越强,以上结果表明随着转速升高,轴向混合能力呈下降的趋势。
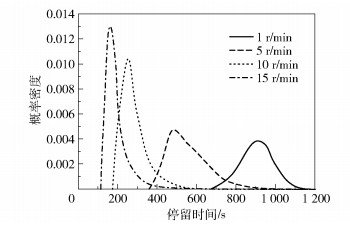
|
图 12 不同螺杆转速下的停留时间分布函数 Fig.12 Residence time distribution functions at different screw speeds |
|
图 13 不同螺杆转速下的累积停留时间分布函数 Fig.13 Cumulative residence time distribution functions at different screw speeds |
累积停留时间分布函数可以代表在某一时刻有多少粒子已经流出流道。用t2表示有90%的粒子已经流出通道的时间,不同转速下有t21=1 035.8 s、t25=760.8 s、t210=402.5 s、t215=299.6 s,t2越小代表自洁作用越强,以上数据表明转速越高,双螺杆挤出机构的自洁效果越好。螺杆转速越高,粒子流出流道的时间越短,轴向混合能力越弱,自洁效果越好。仿真数据为实际的打印实验提供一定的数据支撑,然而在实际打印零件过程中要达到最佳的打印效果,还需在后续的打印实验中进一步探究。
4 结论(1) 对双螺杆挤出式多材料3D打印挤出机构进行了结构设计,并分析其运动原理;重点对双螺杆的端面型线进行了设计和计算,确定了三段式变螺距螺杆的功能段划分及螺杆与螺杆的间隙(δ1=0.4 mm)、螺杆与料腔内壁的间隙(δ2=0.2 mm)等关键参数。
(2) 针对高固含量陶瓷浆料,对所设计的挤出机构进行流体仿真分析。通过对压力场、速度场和剪切速率场进行分析,得出螺杆转速1~15 r/min下的流道压力、速度和剪切速率沿轴向的分布趋势,结果表明出口流率范围0.66~6.48 mm3/s,打印速度范围2~23 mm/s为适宜的挤出成型参数。
(3) 对混合性能进行评估,得出不同螺杆转速下的组分分布,并采用示踪粒子法得到粒子的停留时间分布函数和累积停留时间分布函数,结果表明转速越高,粒子流出流道的时间越短,螺杆的轴向混合能力越弱,自洁效果越好,可为多材料实时混合打印实验提供有效的数据参考。
| [1] |
卢秉恒. 增材制造技术-现状与未来[J]. 中国机械工程, 2020, 31(1): 19-23. LU B H. Additive manufacturing-current situation and future[J]. China Mechanical Engineering, 2020, 31(1): 19-23. (in Chinese) |
| [2] |
KRAKHMATOVA V Y, ZAKHAROV A I, ANDREEV D V, et al. Methods of additive technologies for the manufacture of ceramic products[J]. Glass and Ceramics, 2019, 75(11-12): 479-484. DOI:10.1007/s10717-019-00116-3 |
| [3] |
NGO T D, KASHANI A, IMBALZANO G, et al. Additive manufacturing (3D printing): a review of materials, methods, applications and challenges[J]. Composites Part B: Engineering, 2018, 143: 172-196. DOI:10.1016/j.compositesb.2018.02.012 |
| [4] |
田静, 薛平, 孙华, 等. 微型螺杆挤出式3D打印机的研究进展[J]. 塑料, 2018, 47(1): 46-51. TIAN J, XUE P, SUN H, et al. Research development of micro-screw extrusion 3D printer[J]. Plastics, 2018, 47(1): 46-51. (in Chinese) |
| [5] |
VALKENAERS H, VOGELER F, FERRARIS E, et al. A novel approach to additive manufacturing: screw extrusion 3D-printing[C]//Proceedings of the 10th International Conference on Multi-material Micro Manufacture. San Sebastián, 2013: 235-238.
|
| [6] |
LI W B, ARMANI A, MARTIN A, et al. Extrusion-based additive manufacturing of functionally graded ceramics[J]. Journal of the European Ceramic Society, 2021, 41(3): 2049-2057. DOI:10.1016/j.jeurceramsoc.2020.10.029 |
| [7] |
任礼, 白海清, 鲍骏, 等. 螺杆挤出式3D打印机结构设计与仿真分析[J]. 中国塑料, 2021, 35(4): 98-105. REN L, BAI H Q, BAO J, et al. Structural design and simulation analysis of screw extrusion 3D printer[J]. China Plastics, 2021, 35(4): 98-105. (in Chinese) |
| [8] |
丁承君, 吴畏, 朱智辉. 陶瓷3D打印机喷头结构设计与仿真分析[J]. 天津工业大学学报, 2017, 36(4): 84-88. DING C J, WU W, ZHU Z H. Structure design and simulation analysis of ceramic 3D printer nozzle[J]. Journal of Tianjin Polytechnic University, 2017, 36(4): 84-88. (in Chinese) |
| [9] |
陈磊. 基于数值模拟的塑料颗粒3D打印机关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. CHEN L. The research of key technologies of plastic particles 3D printer based on simulation[D]. Harbin: Harbin Institute of Technology, 2016. (in Chinese) |
| [10] |
JUSTINO NETTO J M, SILVEIRA Z D C. Design of an innovative three-dimensional print head based on twin-screw extrusion[J]. Journal of Mechanical Design, 2018, 140(12): 125002. DOI:10.1115/1.4041175 |
| [11] |
魏静, 张光辉. 双螺杆捏合机螺纹元件型线设计[M]. 北京: 科学出版社, 2018. WEI J, ZHANG G H. Design theory and method of profile of screw element for twin-screw kneader[M]. Beijing: Science Press, 2018. (in Chinese) |
| [12] |
李耀刚, 叶晓濛, 纪宏超, 等. 先驱体陶瓷材料3D打印机螺杆挤出装置的设计与优化[J]. 北京工业大学学报, 2019, 45(12): 1173-1180. LI Y G, YE X M, JI H C, et al. Design and optimization of the screw extrusion device for a precursor ceramic material 3D printer[J]. Journal of Beijing University of Technology, 2019, 45(12): 1173-1180. (in Chinese) |
| [13] |
夏晓光, 段国林. 基于溶剂挥发的陶瓷直写成型工艺[J]. 硅酸盐学报, 2020, 48(12): 1880-1885. XIA X G, DUAN G L. Ceramic direct ink writing process based on solvent evaporation[J]. Journal of the Chinese Ceramic Society, 2020, 48(12): 1880-1885. (in Chinese) |
| [14] |
陈晋南, 胡冬冬, 彭炯. Polyflow软件包在聚合物挤出成型中的应用[J]. 世界科技研究与发展, 2002, 24(1): 28-34. CHEN J N, HU D D, PENG J. Applications of Polyflow in extrusion process[J]. World Sci-Tech R&D, 2002, 24(1): 28-34. (in Chinese) |
| [15] |
秦望. 螺杆挤出式3D打印机结构设计及其数值模拟研究[D]. 汉中: 陕西理工大学, 2021. QIN W. Structure design and numerical simulation of screw extrusion 3D printer[D]. Hanzhong: Shaanxi University of Technology, 2021. (in Chinese) |
| [16] |
张先明. 挤出过程停留时间分布的实验研究和数值模拟[D]. 杭州: 浙江大学, 2008. ZHANG X M. Studies on residence time distribution in twin-screw extruders using experimental method and numerical simulation[D]. Hangzhou: Zhejiang University, 2008. (in Chinese) |
| [17] |
ZIEGLER G R, AGUILAR C A. Residence time distribution in a co-rotating, twin-screw continuous mixer by the step change method[J]. Journal of Food Engineering, 2003, 59(2-3): 161-167. |







