2. 北京化工大学 有机无机复合材料国家重点实验室,北京 100029;
3. 北京化工大学 北京市能源环境催化重点实验室,北京 100029;
4. 中国科学院大学,北京 100049;
5. 电磁散射重点实验室,北京 100854
2. State Key Laboratory of Organic-Inorganic Composites, Beijing University of Chemical Technology, Beijing 100029;
3. Beijing Key Laboratory of Energy Environmental Catalysis, Beijing University of Chemical Technology, Beijing 100029;
4. University of Chinese Academy of Sciences, Beijing 100049;
5. Key Laboratory of Electromagnetic Scattering, Beijing 100854, China
随着微波技术的不断发展,电介质材料的介电常数作为描述材料电磁特性的重要参数,反映了材料对外界电磁场的响应,目前已广泛应用于飞机隐身材料[1-2]、雷达探测[3-4]以及5G通讯[5-6]等重要领域。介电弛豫光谱法[7-9]由于具有非侵入性、检测迅速等优点,常用于测定电介质材料的介电常数,但该方法往往受限于实际应用中的复杂环境以及缺乏较为精确的参数模型。
近年来,随着计算机技术的不断发展,分子动力学模拟方法为学者在原子或分子尺度上理解材料的介电特性提供了重要帮助。除了可以有效预测实际工作情况下电介质的介电特性,目前分子模拟方法已经将频率拓展到太赫兹(THz)光谱。Kirkwood[10]提出了介电常数的经典统计理论,这是利用计算机模拟介电常数的基石;Neumann等[11-13]基于线性响应理论,利用分子动力学模拟将晶体的偶极矩涨落与周期性边界条件下的频率相关介电常数联系起来,得到频率相关介电常数的计算表达式;Caillol等[14-16]以离子- 溶剂混合物体系为研究对象,根据电流和微观极化的相关函数,计算与频率相关的介电常数和电导率,得到相对复杂的复介电常数表达式,该表达式包含偶极子- 偶极子、电流- 偶极子、电流- 电流相关函数的贡献;Thomas等[17]提出了利用从头计算分子动力学的方法计算二丁醇的磁偶极矩;Chen等[18]利用机器学习结合分子动力学的方法提高了介电常数的计算精度;Yang等[19]研究了高分子溶液中浓度变化导致的聚合物结构转变对体系介电常数的影响。目前,对电介质材料介电常数的研究主要集中于固体材料和聚合物体系方面,但是针对体系中存在含净电荷的离子、分子或熔融盐晶体的计算机模拟介电常数的相关研究却很少。这是由于传统的偶极矩涨落方法无法适用于体系中存在含自由电荷的粒子的情况,其原因是:体系内存在导电介质,无法维持静电场平衡;周期性边界对离子偶极矩计算会产生数值跳跃,这是因为偶极矩定义为粒子所带电荷与位移矢量的乘积,当体系中施加周期性边界条件时,对于类似水的这种极性分子,其具有完整的分子信息,周期性边界条件并不会影响分子的偶极矩,然而对于含有自由电荷的体系,自由电荷可跨越周期性边界条件,导致体系的偶极矩值不能收敛[20]。针对上述问题,Sega等[21-22]提出了利用电导率计算NaCl溶液介电频谱的方法;Schröder等[23-25]致力于计算离子液体介电常数的研究,建立了计算离子液体介电常数和电导率的理论基础,研究分析了极化的微观机制对离子液体广义介电常数或磁化率的贡献。
本文基于Neumann介电理论公式[11-13],进一步推导了适用于离子溶液或熔融盐晶体体系的介电常数解析表达式;以熔融氯化钠(NaCl)晶体为研究算例,利用分子动力学方法测定了不同温度下NaCl晶体的介电常数和频率相关的介电谱,研究了NaCl晶体熔化过程中介电特性的变化;最后利用经典外加电场法计算了熔融NaCl晶体的静态介电常数,从而对本文的方法进行了验证。
1 介电常数计算及分子模拟方法 1.1 介电常数计算基于线性响应理论,Neumann等[11-13]将分子动力学模拟得到的晶体偶极矩涨落与周期性边界条件下的频率相关介电常数联系起来,得到与频率ω相关的经典介电常数ε的计算表达式(式(1))。
| $ \varepsilon (\omega ) = 1 + \frac{{4\pi }}{{3V{k_{\rm{B}}}T}}\mathscr{F}\left[ { - \frac{{{\rm{d}}\varphi (t)}}{{{\rm{d}}t}}} \right] $ | (1) |
式中:V为模拟体系的体积,kB为玻尔兹曼常数,T为模拟体系温度。
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathscr{F}\left[ { - \frac{{{\rm{d}}\varphi (t)}}{{{\rm{d}}t}}} \right] = \int_0^{ + \infty } {{{\rm{e}}^{ - \Im 2\pi \omega t}}} \left[ {\frac{{ - {\rm{d}}\varphi (t)}}{{{\rm{d}}t}}} \right]{\rm{d}}t = \\ \varphi (0) - \Im 2\pi \omega \int_0^{ + \infty } {{{\rm{e}}^{ - {\rm{2}}2\pi \omega t}}} \varphi (t){\rm{d}}t, {\Im ^2} = - 1 \end{array} $ | (2) |
式中,φ(t)是总偶极矩Mtot的自相关函数。
| $ \varphi (t) = \left\langle {{\mathit{\boldsymbol{M}}_{{\rm{tot}}}}(0){\mathit{\boldsymbol{M}}_{{\rm{tot}}}}(t)} \right\rangle $ | (3) |
考虑一个由N个带电粒子组成、体积为V、温度为T、粒子位移矢量为ri以及所带电荷量为Qi(i=1,2,…,N)的体系,根据Schröder等[26]的研究,可以将体系的总偶极矩Mtot划分为平动偶极矩MJ和质心修正偶极矩MD,如公式(4)所示。
| $ {\mathit{\boldsymbol{M}}_{{\rm{tot}}}}(t) = {\mathit{\boldsymbol{M}}_{\rm{D}}} + {\mathit{\boldsymbol{M}}_{\rm{J}}} $ | (4) |
考虑到模拟系统中存在Nmol个分子,分子i包含ni个电荷,每个自由离子也被视为ni=1的分子,因此
| $ \begin{array}{l} \;\;\;\;\;\;\;{\mathit{\boldsymbol{M}}_{{\rm{tot}}}} = \sum\limits_{i = 1}^N {{Q^i}} \mathit{\boldsymbol{r}}_j^i = \sum\limits_{i = 1}^{{N_{{\rm{mol}}}}} {\sum\limits_{j = 1}^{{n_i}} {Q_j^i} } \mathit{\boldsymbol{r}}_j^i = \sum\limits_{i = 1}^{{N_{{\rm{mol}}}}} {\sum\limits_{j = 1}^{{n_i}} {\left[ {Q_j^i\left( {\mathit{\boldsymbol{r}}_j^i - } \right.} \right.} } \\ \left. {\left. {\mathit{\boldsymbol{r}}_{{\rm{cm}}}^i} \right) + Q_j^i\mathit{\boldsymbol{r}}_{{\rm{cm}}}^i} \right] = \sum\limits_{i = 1}^{{N_{{\rm{mol}}}}} {{\mathit{\boldsymbol{\mu }}_i}} + \sum\limits_{i = 1}^{{N_{{\rm{mol}}}}} {{Q^i}} \mathit{\boldsymbol{r}}_{{\rm{cm}}}^i \end{array} $ | (5) |
公式(5)中,等号右边第一项表示质心矫正的分子偶极矩μi,可以表示为
| $ {\mathit{\boldsymbol{\mu }}_i} = \sum\limits_{j = 1}^{{n_i}} {Q_j^i} \left( {\mathit{\boldsymbol{r}}_j^i - \mathit{\boldsymbol{r}}_{{\rm{cm}}}^i} \right) $ | (6) |
式中,rcmi表示分子i的质心位置。故考虑分子上每个电荷的坐标都表示为相对于质心的相对位置。由于分子偶极矩MD不受限于周期性边界条件,因此可以对其进行有效定义和计算。对于带电荷的自由离子,由于离子位置与质心位置重合,即rji= rcmi,因此对分子偶极矩不提供贡献。
公式(5)中,等号右边第二项是平动偶极矩MJ,
| $ {\mathit{\boldsymbol{M}}_{\rm{J}}} = \sum\limits_{i = 1}^{{N_{{\rm{mol}}}}} {{Q^i}} \mathit{\boldsymbol{r}}_{{\rm{cm}}}^i $ | (7) |
式中,
| $ \mathit{\boldsymbol{J}} = \sum\limits_{i = 1}^{{N_{{\rm{mol}}}}} {{Q^i}} \mathit{\boldsymbol{v}}_{{\rm{cm}}}^i = \sum\limits_{i = 1}^{{N_{{\rm{mol}}}}} {{Q^i}} \frac{{{\rm{d}}\mathit{\boldsymbol{r}}_{{\rm{cm}}}^i}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{\mathit{\boldsymbol{M}}_{\rm{J}}}}}{{{\rm{d}}t}} $ | (8) |
将公式(4)和(8)带入公式(1)的傅里叶- 拉普拉斯变换中,可以得到频率相关介电常数的表达式(式(9))。
| $ \begin{array}{l} \;\;\;\;\;\;\;\varepsilon (\omega ) = 1 + \frac{{4\pi }}{{3V{k_{\rm{B}}}T}}\left\{ {\left\langle {\mathit{\boldsymbol{M}}_{\rm{D}}^2} \right\rangle + \mathfrak{J}\omega \mathscr{F} \left[ {\left. {{\mathit{\boldsymbol{M}}_{\rm{D}}}(0) \cdot } \right\rangle } \right.} \right.\\ \left. {\left. {\left\langle {{\mathit{\boldsymbol{M}}_{\rm{D}}}(t)} \right.} \right] - \left\langle {{\mathit{\boldsymbol{M}}_{\rm{D}}}(0)\mathit{\boldsymbol{J}}(t)} \right\rangle } \right\} + \frac{{\mathfrak{J}}}{\omega }\frac{{4\pi }}{{3V{k_{\rm{B}}}T}}\{ \mathfrak{J}[\langle \mathit{\boldsymbol{J}}(0) \cdot \\ \left. {\mathit{\boldsymbol{J}}(t)\rangle ] + \mathfrak{J} \omega \mathscr{F} \left[ {\left\langle {\mathit{\boldsymbol{J}}(0) \cdot {\mathit{\boldsymbol{M}}_{\rm{D}}}(t)} \right\rangle } \right]} \right\} \end{array} $ | (9) |
由于公式(9)考虑了体系中分子偶极贡献与离子电流贡献,故可广泛作为体系的介电常数解析表达式。对于本文考虑的熔融NaCl晶体体系,随着温度升高,NaCl晶体结构被破坏,体系中含有自由移动的离子电流,离子i的坐标位置rji等于其质心坐标位置rcmi,那么体系中分子偶极矩μi=0,即体系中不存在分子偶极矩贡献,故仅考虑体系中离子电流贡献,其频率相关介电常数的解析表达式为
| $ \varepsilon (\omega ) = 1 + \frac{\Im }{\omega }\frac{{4\pi }}{{3V{k_{\rm{B}}}T}}\{ \Im [\langle \mathit{\boldsymbol{J}}(0) \cdot \mathit{\boldsymbol{J}}(t)\rangle ]\} $ | (10) |
当频率小于103 Hz时,体系的介电常数称为静态介电常数,利用电流法计算静态介电常数εstatic,其表达式为
| $ {\varepsilon _{{\rm{static }}}} = 1 - \frac{{4\pi }}{{3V{k_{\rm{B}}}T}}\int_0^{ + \infty } t \langle \mathit{\boldsymbol{J}}(0) \cdot \mathit{\boldsymbol{J}}(t)\rangle {\rm{d}}t $ | (11) |
利用分子建模脚本Moltemplate[27]搭建了包含有1 000个原子的NaCl晶体的初始构型,立方体模拟盒在3个方向上的大小均为2.8 nm。对模拟盒的3个方向都应用周期性边界条件,选用经典原子间相互作用势函数Born-Mayer-Huggins(BMH)势[28-30]描述熔融NaCl晶体离子之间的相互作用势。
| $ {u_{ij}} = {A_{ij}}{{\rm{e}}^{\frac{{ - {r_{ij}}}}{{{\rho _{ij}}}}}} - \frac{{{C_{ij}}}}{{r_{ij}^6}} - \frac{{{D_{ij}}}}{{r_{ij}^8}} + \frac{{{q_i}{q_j}}}{{4\pi {\varepsilon _0}{r_{ij}}}} $ | (12) |
式中:uij为NaCl晶体离子之间的相互作用势,Aij为BMH势排斥参数,Cij和Dij为范德华参数,rij为粒子i和j之间的距离,ρij为离子对ij的长度参数,qi和qj分别为i和j的电荷量,ε0为真空介电常数。
选用经典分子模拟软件Lammps进行分子动力学模拟[31],选取随机数种子为825 577,使体系中粒子的速度在给定的温度下满足玻尔兹曼分布;之后运行100 ps的能量最小化过程,防止不合理的初始结构导致模拟过程崩溃。采用NPT系综,分别使用Nosé-Hoover热浴法和Berendsen耦合方法使体系维持给定的温度和1个标准大气压。使用Ewlad求和法计算长程库仑相互作用,截断半径为12 Å,采用Velocity-Verlet算法求解运动方程的积分,时间步长设置为1 fs;每次进行MD模拟过程时首先运行2 ns以达到平衡状态,之后进行1 ns的数据采样过程,每隔0.005 ps进行一次体系平均,从而计算静态介电常数、频率相关介电谱以及进行后处理。使用可视化软件VMD[32]对轨迹文件进行观察。本研究的模拟温度区间为300~1 500 K,调节不同温度大小是为了揭示NaCl晶体的相变演化过程,研究相变过程中晶体材料介电特性的变化。NaCl晶体的初始构型由VMD绘制[32],如图 1所示。

|
绿色代表氯离子,黄色代表钠离子。 图 1 NaCl晶体的初始结构模型 Fig.1 Initial structure model of NaCl crystals |
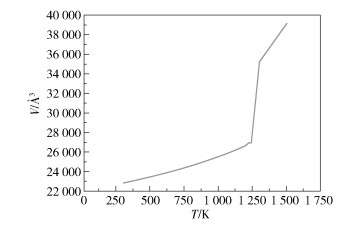
在1个标准大气压下,分别在300、500、700、900、1 100、1 180、1 200、1 220、1 240、1 300、1 500 K的温度下计算体系的体积V,结果如图 2所示。可以看出,体系体积随着温度的升高而增加。当温度升高至1 240K时,体积开始快速膨胀,这表明固态NaCl开始熔化为液态,这与实验测得的NaCl的熔点(1 074 K)[33]基本吻合。当温度达到1 300 K时,体系已经完全成为液态。
|
图 2 NaCl的体积- 温度相图 Fig.2 Volume- temperature phase diagram of NaCl |
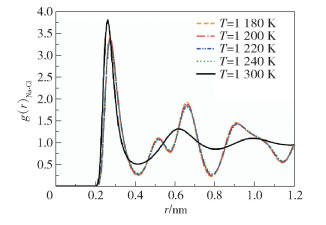
此外,径向分布函数(radial distribution function,RDF)[34]也可以作为分析体系结构变化的重要参数用来研究物质的有序性,其定义为一个系统在距离一个标记粒子的r处找到其他粒子的概率。图 3为不同温度下体系中Na- Cl的RDF图,其中g(r)Na- Cl表示钠离子周围距离半径r到r+dr处发现氯离子的概率。当温度由1 180 K升高至1 240 K时,RDF在不同位置呈现出4个离散峰,并且随着温度升高,g(r)Na-Cl几乎没有增加,最大峰值大约在3.4左右,表示此时熔融态NaCl晶体中仍有较强的约束作用,结构只存在轻微扰动。随着温度升高到1 300 K时,原来有序的熔融NaCl晶体结构被破坏,相互作用力减弱,分子结构变得杂乱无序,RDF峰值发生了显著变化,并且仅保留两个较为明显的离散峰,表明体系已经转变为液态。
|
图 3 不同温度下Na-Cl的径向分布函数 Fig.3 Radial distribution function of Na-Cl at different temperatures |
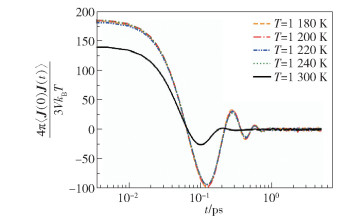
根据上文推导的介电常数的计算方法,为了获得不同温度下熔融NaCl晶体体系的频率相关性,首先需要获得体系中离子电流- 电流随时间的变化规律。由于时间相关函数本身就是信号与自身之间相关性程度的度量,因此深入分析相关函数的行为有助于理解频率相关介电谱的特性[21]。图 4给出了1 180~1 300 K的温度下熔融NaCl晶体的电流相关函数。可以看出,NaCl电流自相关函数在约10-1 ps处呈现极大的振荡行为,随后电流自相关函数逐渐衰减为零,表明该模拟体系在给定的时间尺度内达到收敛。值得注意的是,当温度升高至1 300 K时,不仅电流相关函数迅速降低,而且峰值出现的频率位置也发生了显著变化,这可能表明随着体系相态结构的改变,共振频率发生了变化。由于时间相关函数十分依赖于较长的模拟时间尺度,并且在分子模拟过程中,由于原子轨迹上的每个点只提供一个值,难以对每个粒子残留物进行平均,这导致即使在长时间模拟下,无穷远处的自相关函数仍然在零附近不停振荡。此外,使用傅里叶- 拉普拉斯变换的方法计算解析介电频谱时,离散傅里叶变换算法将从分子动力学模拟中获得的有限数据点进行周期性扩展,这并不是公式中简单的连续函数积分。为了减少数学算法差异,往往需要更多的数据点,这增加了模拟的负担,而离散傅里叶变换算法中使用的矩形积分方法将会引入显著的误差。因此,本文利用非线性最小二乘法将模拟数据拟合成特定的连续函数[35],并直接解析计算这些函数的傅里叶- 拉普拉斯变换,这大大平滑了介电谱中的统计粗糙度。
|
图 4 不同温度下NaCl的电流相关函数 Fig.4 Current correlation function of NaCl at different temperatures |
由于电流自相关函数的行为类似于阻尼振荡,通常在几皮秒内迅速振荡,随后逐渐衰减到零,因此可以使用多指数余弦相关函数来拟合相应的模拟结果。
| $ \langle \mathit{\boldsymbol{J}}(0) \cdot \mathit{\boldsymbol{J}}(t)\rangle \approx \sum\limits_{k = 1}^2 {{A_k}} {{\rm{e}}^{\frac{{ - t}}{{{\tau _k}}}}}\cos \left( {{\omega _k}t + {\delta _k}} \right) $ | (13) |
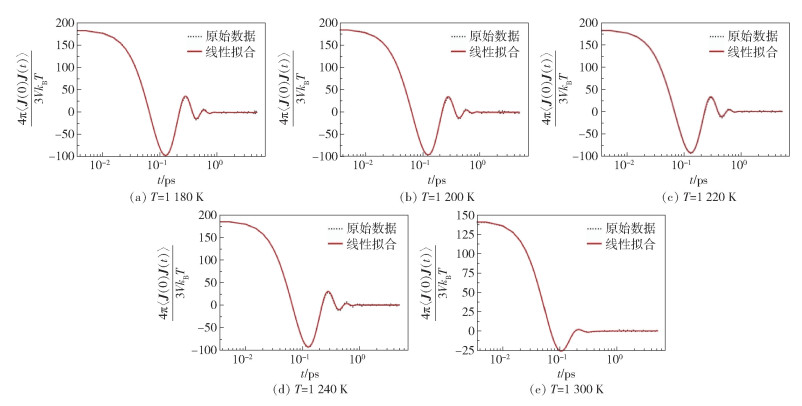
式中,Ak、τk、ωk和δk均为拟合参数(k=1,2),分别代表振幅、弛豫时间、频率和相位。图 5为不同温度下NaCl电流相关函数的拟合结果,可以看出,电流自相关函数拟合曲线与原模拟曲线的吻合程度较高。表 1为电流相关函数的拟合参数,可以发现,当温度升高至1 300 K时,振幅Ak及频率ωk均发生了相当大的变化。随着温度升高,氯化钠晶体熔化为液态,振幅A1减小,对应的电流相关函数峰值减小,ω1减小,表明相变过程导致体系的共振频率减小,体系中各组分的介电贡献减少。
|
图 5 不同温度下NaCl电流相关函数的拟合结果 Fig.5 Fitting results of the current correlation function of NaCl at different temperatures |
| 下载CSV 表 1 电流相关函数的拟合参数 Table 1 Fitting parameters of the current correlation function |
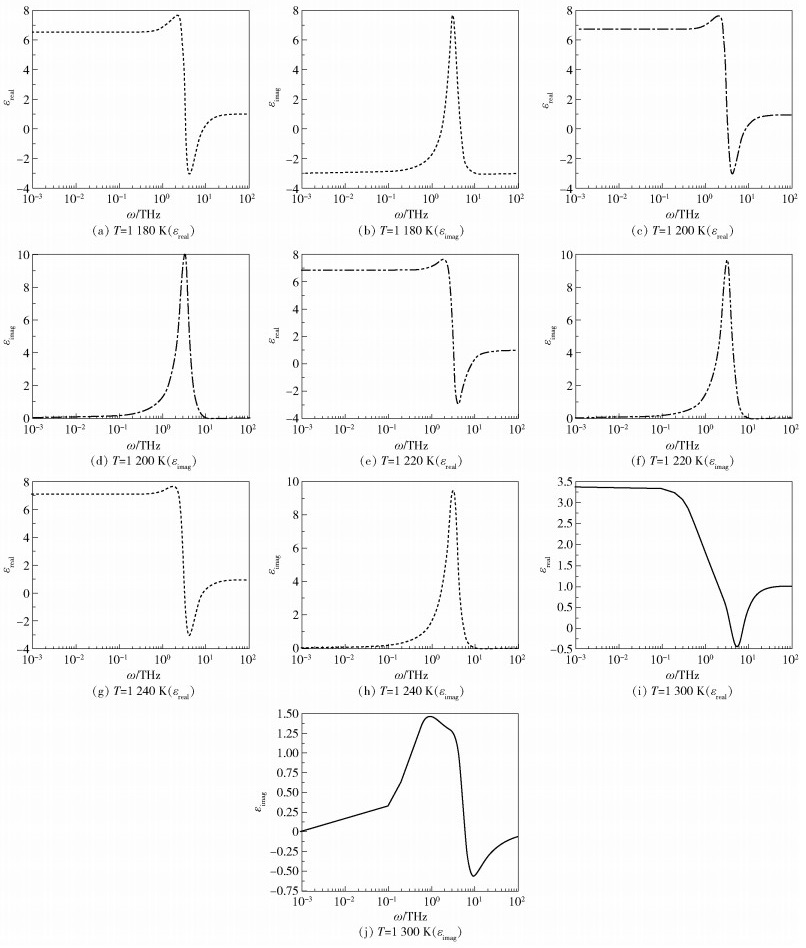
将电流拟合函数代入公式(10),利用Python脚本可以得到熔融NaCl晶体的频率相关介电谱。图 6为对数坐标系中熔融NaCl晶体在不同温度下的频率相关介电谱。在1 180~1 240 K的温度范围内,随着频率的增加,大约在3 THz处外场与NaCl晶体的偶极子振荡频率发生共振,介电常数的实部εreal开始加速增大,达到峰值后快速减小,演化为接近于无外场作用下的极化状态。同样地,在达到共振频率时,虚部介电损耗εimag从0逐渐增大到峰值,随后又减小到0。当温度进一步升高到1 300 K时,NaCl开始熔化发生相变,与NaCl为晶体状态时相比,熔融NaCl晶体的介电谱发生了显著变化。在NaCl熔化以后,由于体系中存在不同组分,各组分的介电响应相互重叠,介电谱的共振吸收峰的带宽变宽,波形发生了明显变化,导致体系的介电频谱十分复杂。可以发现,此时介电损耗峰值降低到约1.5,而实部处的共振峰值几乎消失。这是因为NaCl晶体结构随体系温度改变而发生了变化,体系中离子组分随频率增加发生离子极化,分子的固有偶极矩的转向极化不再响应。
|
图 6 不同温度下NaCl的频率相关介电谱 Fig.6 Frequency dependent dielectric spectra of NaCl at different temperatures |
为了进一步验证上述推导的介电常数计算的准确性,本文使用外加电场法计算静态介电常数。所谓静态介电常数是指当频率很低或接近零时,介电常数是与电场频率无关的量。利用外加电场法计算体系的静态介电常数εstatic,其表达式为
| $ {\varepsilon _{{\rm{static }}}} = 1 + \frac{{4\pi {M_{\rm{E}}}}}{{EV}} $ | (14) |
式中:E为外电场强度,ME为施加电场后介质的偶极矩,V为模拟体系的体积。因此,可以利用分子动力学模拟的方法在平衡态的NaCl分子构型的Z方向上施加静电场EZ,电场强度以0.01 V/Å为间隔,从0.01 V/Å逐渐增大至0.1 V/Å。然而当T=1 100 K时,如果继续向体系中施加0.1 V/Å的电场强度,此时NaCl晶体的偶极矩大小受电场强度的影响会发生剧烈波动,这会无法保证电场强度与诱导偶极矩之间高度一致的线性关系,从而影响静态介电常数的估算。因此本文选择从0.001 V/Å逐渐增大至0.01 V/Å。根据电场诱导偶极矩和电场强度之间的线性关系,利用最小二乘法拟合可得到不同温度下NaCl晶体的静态介电常数。
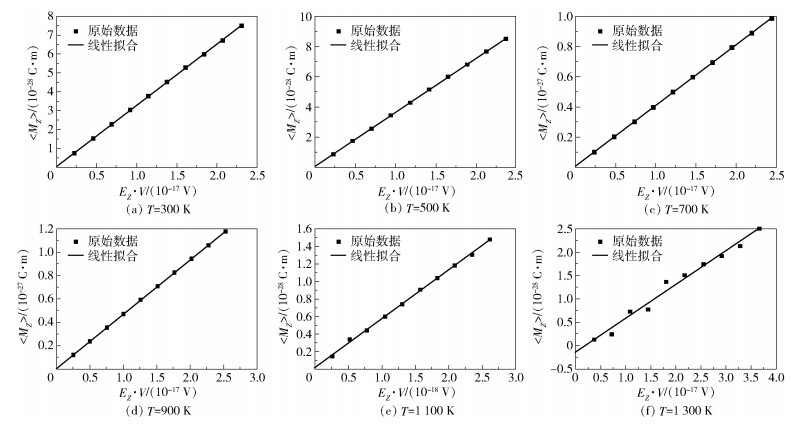
图 7为诱导偶极矩和电场强度之间的线性拟合结果。可以发现,随着体系施加的电场强度的增加,诱导偶极矩增大。在300~1 100 K的温度范围内,电场强度和诱发偶极矩之间保持着良好的线性关系。随着温度进一步升高至1 300 K,NaCl晶体开始熔化,采样点的波动明显增大,这可能与NaCl晶体结构被破坏有关。
|
图 7 不同温度下电场诱导偶极矩MZ和电场强度EZ之间的线性关系 Fig.7 Linear relationship between the electric field induced dipole moment and the electric field intensity at different temperatures |
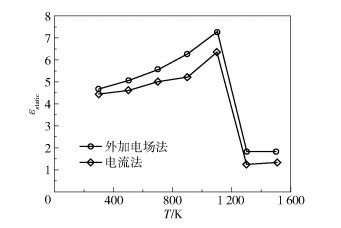
分别采用电流法和外加电场法计算NaCl的静态介电常数与温度的相关性,结果如图 8所示。可以看出:当NaCl为固态晶体时,静态介电常数随着温度的升高而逐渐增加;当温度升高到固液临界点(T=1 100 K)时,静态介电常数达到最大;随着温度进一步升高,NaCl发生固- 液相变过程,体系的静态介电常数迅速下降。电流法和外加电场法的计算结果有着良好的一致性,电流法能够有效反映NaCl体系相变过程中静态介电常数的变化规律,广泛适用于熔融盐晶体以及溶液中含有自由电荷的体系。根据文献[36]的实验测定结果,室温下NaCl晶体的静态介电常数在5.45~5.9之间。本文用电流法计算得到的静态介电常数为4.5(T=300 K),小于实验观测值,这可能与描述NaCl晶体的力场参数有关。在今后的研究中,本文将采用机器学习结合量子力学第一性原理的计算方式来提高力场的精度。此外,由公式(11)可知,对于电流法,如果要准确计算静态介电常数,需要从0积分到无穷大,而实际上本文首先用最小二乘法将电流关联函数拟合成一个解析函数,然后对解析函数进行积分,这样会引入误差,导致计算结果偏低。
|
图 8 采用电流法和外加电场法计算得到的NaCl静态介电常数与温度的相关性 Fig.8 Correlation between the static dielectric constant of NaCl and the temperature calculated by the current method and the external electric field method |
(1) 基于经典介电理论公式,进一步推导了适用于熔融盐晶体以及溶液中含有自由电荷的体系的介电常数表达式,该公式可以用于计算熔融NaCl晶体的介电性质。
(2) 利用电流拟合相关函数分析了不同温度下NaCl的频率相关介电谱,结果表明:随着温度升高(300~1 100 K),在共振吸收峰处,介电常数的实部先增大,达到峰值后快速减小;当温度升高至1 300 K时,NaCl晶体发生相变,介电损耗显著下降,在共振频率处介电常数的实部峰值几乎消失。
(3) 分别利用电流法和外加电场法计算了不同温度下NaCl的静态介电常数,结果显示:随着体系温度升高(300~1 100 K),NaCl晶体的介电常数呈上升趋势;当温度高于相变点时,NaCl的静态介电常数快速下降。电流法和外加电场法的计算结果有着良好的一致性,表明电流法可以有效描述NaCl的相变过程。
| [1] |
YIN X W, CHENG L F, ZHANG L T, et al. Fibre-reinforced multifunctional SiC matrix composite materials[J]. International Materials Reviews, 2016, 62: 1-56. |
| [2] |
ZHENG L G, ZHANG K, LI W Z, et al. Ultra-lightweight 3D woven spacer integrated composites with stabilization of dielectric and robust mechanical properties at room and elevated temperatures[J]. Polymer Composites, 2022, 43: 6125-6134. DOI:10.1002/pc.26917 |
| [3] |
GAO Z Q, XU C L, TIAN X X, et al. Multifunctional ultra-thin metasurface with low infrared emissivity, microwave absorption and high optical transmission[J]. Optics Communications, 2021, 500: 127327. DOI:10.1016/j.optcom.2021.127327 |
| [4] |
ZHANG L, XU Y, CHEN R, et al. Calculation of dielectric constant, loss property and scattering characteristics from the future martian GPR data[J]. Icarus, 2022, 386: 115181. DOI:10.1016/j.icarus.2022.115181 |
| [5] |
HE G Q, MA X Y, LIU Y J, et al. Sintering characteristics and microwave dielectric properties of ultralow-loss SrY2O4 ceramics[J]. Ceramics International, 2022, 48: 21299-21304. DOI:10.1016/j.ceramint.2022.04.081 |
| [6] |
LI F Y, LI Y X, ZHANG J P, et al. 5G array antenna substrate for electromagnetic beam splitting via cobalt-substituted zinc molybdate low temperature co-fired ceramics[J]. Journal of the European Ceramic Society, 2022, 42: 5771-5777. DOI:10.1016/j.jeurceramsoc.2022.06.082 |
| [7] |
BUCHNER R, BAAR C, FERNANDEZ P, et al. Dielectric spectroscopy of micelle hydration and dynamics in aqueous ionic surfactant solutions[J]. Journal of Molecular Liquids, 2005, 118: 179-187. DOI:10.1016/j.molliq.2004.07.035 |
| [8] |
FELDMAN Y, KOZLOVICH N, NIR I, et al. Dielectric spectroscopy of microemulsions[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 1997, 128: 47-61. |
| [9] |
FERNANDEZ P, SCHRÖDLE S, BUCHNER R, et al. Micelle and solvent relaxation in aqueous sodium dodecylsulfate solutions[J]. ChemPhysChem, 2003, 4: 1065-1072. DOI:10.1002/cphc.200300725 |
| [10] |
KIRKWOOD J G. Statistical mechanics of fluid mixtures[J]. Journal of Chemical Physics, 1935, 3: 300-313. DOI:10.1063/1.1749657 |
| [11] |
NEUMANN M, STEINHAUSER O. On the calculation of the frequency-dependent dielectric constant in computer simulations[J]. Chemical Physics Letters, 1983, 102(6): 508-513. DOI:10.1016/0009-2614(83)87455-7 |
| [12] |
NEUMANN M, STEINHAUSER O. Computer simulation and the dielectric constant of polarizable polar systems[J]. Chemical Physics Letters, 1984, 106(6): 563-569. DOI:10.1016/0009-2614(84)85384-1 |
| [13] |
NEUMANN M, STEINHAUSER O, PAWLEY G S. Consistent calculation of the static and frequency-dependent dielectric constant in computer simulations[J]. Molecular Physics, 1984, 52(1): 97-113. DOI:10.1080/00268978400101081 |
| [14] |
CAILLOL J M, LEVESQUE D, WEIS J J. Theoretical calculation of ionic solution properties[J]. The Journal of Chemical Physics, 1986, 85(11): 6645-6657. DOI:10.1063/1.451446 |
| [15] |
CAILLOL J M, LEVESQUE D, WEIS J J. Electrical properties of polarizable ionic solutions. Ⅱ. Computer simulation results[J]. The Journal of Chemical Physics, 1989, 91(9): 5555-5566. DOI:10.1063/1.457558 |
| [16] |
CAILLOL J M, LEVESQUE D, WEIS J J. Electrical properties of polarizable ionic solutions. Ⅰ. Theoretical aspects[J]. The Journal of Chemical Physics, 1989, 91(9): 5544-5554. DOI:10.1063/1.457557 |
| [17] |
THOMAS M, KIRCHNER B. Classical magnetic dipole moments for the simulation of vibrational circular dichroism by ab initio molecular dynamics[J]. The Journal of Physical Chemistry Letters, 2016, 7(3): 509-513. DOI:10.1021/acs.jpclett.5b02752 |
| [18] |
CHEN W, LI L S. The study of the optical phonon frequency of 3C-SiC by molecular dynamics simulations with deep neural network potential[J]. Journal of Applied Physics, 2021, 129: 244104. DOI:10.1063/5.0049464 |
| [19] |
YANG X D, CHEN W, REN Y, et al. Exploring dielectric spectra of polymer through molecular dynamics simulations[J]. Molecular Simulation, 2022, 48(10): 935-943. DOI:10.1080/08927022.2022.2083122 |
| [20] |
RESTA R, VANDERBILT D. Theory of polarization: a modern approach[M]//RABE K M, AHN C H, TRISCONE J M. Physics of ferroelectrics. Heidelberg: Springer, 2007: 31-68.
|
| [21] |
SEGA M, KANTOROVICH S S, ARNOLD A, et al. On the calculation of the dielectric properties of liquid ionic systems[M]//KALMYKOV Y P. Recent advances in broadband dielectric spectroscopy. Dordrecht: Springer, 2013: 103-122.
|
| [22] |
SEGA M, KANTOROVICH S S, HOLM C, et al. Communication: kinetic and pairing contributions in the dielectric spectra of electrolyte solutions[J]. The Journal of Chemical Physics, 2014, 140: 211101. DOI:10.1063/1.4880237 |
| [23] |
SCHRÖDER C, HABERLER M, STEINHAUSER O. On the computation and contribution of conductivity in molecular ionic liquids[J]. The Journal of Chemical Physics, 2008, 128: 134501. DOI:10.1063/1.2868752 |
| [24] |
SCHRÖDER C, RUDAS T, STEINHAUSER O. Simulation studies of ionic liquids: orientational correlations and static dielectric properties[J]. The Journal of Chemical Physics, 2006, 125: 244506. DOI:10.1063/1.2404674 |
| [25] |
SCHRÖDER C, STEINHAUSER O. On the dielectric conductivity of molecular ionic liquids[J]. The Journal of Chemical Physics, 2009, 131: 114504. DOI:10.1063/1.3220069 |
| [26] |
SCHRÖDER C, WAKAI C, WEINGÄRTNER H, et al. Collective rotational dynamics in ionic liquids: a computational and experimental study of 1-butyl-3-methyl-imidazolium tetrafluoroborate[J]. The Journal of Chemical Physics, 2007, 126: 084511. DOI:10.1063/1.2464057 |
| [27] |
JEWETT A I, STELTER D, LAMBERT J, et al. Moltemplate: a tool for coarse-grained modeling of complex biological matter and soft condensed matter physics[J]. Journal of Molecular Biology, 2021, 433: 166841. DOI:10.1016/j.jmb.2021.166841 |
| [28] |
DING J, PAN G, DU L, et al. Theoretical prediction of the local structures and transport properties of binary alkali chloride salts for concentrating solar power[J]. Nano Energy, 2017, 39: 380-389. DOI:10.1016/j.nanoen.2017.07.020 |
| [29] |
SANZ E, VEGA C. Solubility of KF and NaCl in water by molecular simulation[J]. The Journal of Chemical Physics, 2007, 126: 014507. DOI:10.1063/1.2397683 |
| [30] |
GALAMBA N, NIETO DE CASTRO C A, ELY J F. Thermal conductivity of molten alkali halides from equilibrium molecular dynamics simulations[J]. The Journal of Chemical Physics, 2004, 120(18): 8676-8682. DOI:10.1063/1.1691735 |
| [31] |
PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117: 1-19. DOI:10.1006/jcph.1995.1039 |
| [32] |
HUMPHREY W, DALKE A, SCHULTEN K. VMD: visual molecular dynamics[J]. Journal of Molecular Graphics, 1996, 14: 33-38. DOI:10.1016/0263-7855(96)00018-5 |
| [33] |
RANKIN D W H. CRC handbook of chemistry and physics[M]. 89th ed. Abingdon: Taylor & Francis Group, 2009.
|
| [34] |
AI Z, LI S J, ZHAO Y L, et al. Effect of magnesium ion on sylvite flotation: an experiment and molecular dynamic simulation study[J]. Chemical Physics Letters, 2020, 752: 137586. DOI:10.1016/j.cplett.2020.137586 |
| [35] |
SCHRÖDER C, STEINHAUSER O. Using fit functions in computational dielectric spectroscopy[J]. The Journal of Chemical Physics, 2010, 132: 244109. DOI:10.1063/1.3432620 |
| [36] |
ROESSLER D M, WALKER W C. Electronic spectra of crystalline NaCl and KCl[J]. Physical Review, 1968, 166(3): 599-606. DOI:10.1103/PhysRev.166.599 |








