近年来，随着计算流体力学的发展，通过计算机模拟的方式以及利用数值优化进一步提高挤出机机头流场稳定性的方法越来越受到重视。关于运用计算流体力学软件进行流体仿真已有大量研究^[1-3]，但模拟过程普遍缺乏对非等温模型的涉及，且在优化过程中采用的主要方法仍然是借助设计经验进行优化，得到结果往往耗时长、精准度差。林丽红等^[4]采用经验设计与数值分析相结合的方法对挤出机流道进行设计，改进了阻尼的3个重要结构参数，分析各参数对流道内胶料流动状态的影响，并根据影响规律选定了最终的结构参数。梁晨等^[5]利用流体计算软件Polyflow分析了两种熔体在口型内的流动规律，提出增加窄缝区域高度和扩充口模入口的方法，并分析了不同口型流道结构对共挤出产品尺寸、速度和压力分布的影响规律。Smith等^[6-7]基于衣架式口模熔体的流动机理，结合灵敏度分析和数值模拟的方法，对衣架式口模流道进行了优化设计，使得口模出口处的速度分布和胶料滞留时间更加均匀。然而大部分针对机头流场模拟的研究主要以挤出质量为目标，且只能得到各参数间的定性关系，优化目标单一且未建立起关于各参数与优化目标之间的定量数学模型。在保证产品质量的前提下实现高效率的生产，需要确定合理的机头结构参数及工艺参数，所以非常有必要在数值模拟的基础上寻求合理的实验方法及手段。响应面法是一种用于探究多个变量之间、变量与目标函数之间定量关系的常见方法，可由获得的理论方程来对生产进行更有针对性的指导。王春林等^[8]和彭光杰等^[9]利用响应面法探究泵体的叶片及管道参数与泵最高效率之间的定量方程关系，进而得到各参数的最优设计。

本文利用流体计算软件Fluent，以L型宽幅挤出机头的三维非等温挤出流体为研究对象，基于单因素试验设计筛选出重要参数，再利用响应面法分析重要参数对反映挤出稳定性的关键目标函数—挤出速度均值及标准差的影响，通过显著性分析确定目标函数的回归方程，建立多目标优化分析过程，确定了挤出速度均值与标准差的最佳匹配点，并得到对应的最优工艺及结构参数，以期为生产提供理论指导。

出口截面挤出速度和速度分布是评价生产效率和挤出质量的关键参数。出口截面速度分布不均匀会导致挤出制品壁厚不均、制品使用性能下降，因此在生产中如何选取合理的结构及工艺参数，在保证制品质量的前提下提高生产效率是工厂亟待解决的问题之一。本文建立了以机头出口截面挤出速度均值V和标准差σ为目标函数的多目标优化过程，其中V与机头的挤出效率相关，σ与产品质量相关，计算式见式(1)、(2)，其中m为统计点个数，本文中m为机头出口截面中间层处均匀选取的48个点。

出口截面挤出速度均值计算公式为

出口截面挤出速度标准差计算公式为

式中，V_i为每个统计点的速度。

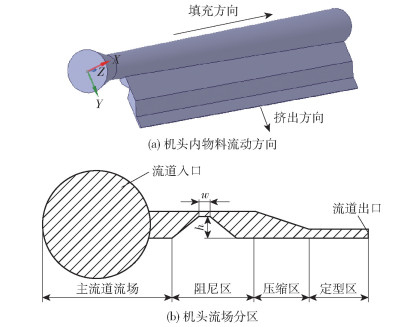
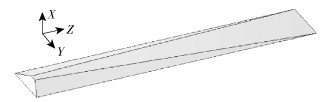
L型机头挤出生产时，胶料从主流道一侧进入机头，通过小流道转向，在与主流道垂直方向上挤出宽幅胶片。如图 1所示，机头内流场由主流道流场和小流道流场两部分组成，其中小流道流场包括阻尼区、压缩区和定型区，流体流场在阻尼区逐渐分布均匀，而压缩区和定型区是出口成型区，最终挤出符合要求的片材。流场几何模型的坐标原点建立在入口挤出中心位置，物料的挤出方向为Y方向，物料的填充方向为Z方向。本文挤出片材毛坯宽度为1 400 mm，厚度为3 mm。由于一端进料且挤出产品幅宽大，故流场中的速度、压力不均匀易造成挤出制品均匀性和稳定性差。为改善挤出质量，采用如图 2所示的阻尼块来调整流场中的压力与速度。阻尼块是一个梯形的柱形条，梯形的上底面宽度沿Z方向由靠近入口的w=4 mm逐渐增加至与下底面同宽，阻尼块高度沿Z方向由靠近入口的h=9 mm逐渐降低至与小流道底部平齐。

图 1(Fig. 1)

图 1 L型机头流场几何模型 Fig.1 Geometric model of the flow field in the L-shaped head

图 2(Fig. 2)

图 2 阻尼块形状 Fig.2 Shape of the damping block

合理的网格数量是保证计算精度和效率的关键。图 3为网格数量对目标函数V和σ的影响，可以看出在网格数量为90万左右时，V稳定在7.4×10^-3 m/s左右，σ稳定在2.5×10^-4，说明此时网格数对计算结果的影响较小，计算结果稳定，故取网格数量为880 562进行后续的模拟分析。如图 4所示，为了提高阻尼区和机头出口处模拟计算结果的精度，在相应结构处进行网格加密，并采用钻石型网格。

图 3(Fig. 3)

图 3 网格独立性检验结果 Fig.3 Grid independence test results

图 4(Fig. 4)

图 4 L型机头流场网格 Fig.4 Flow field grid of the L-shaped head

本文采用非等温Carreau流变模型，其本构方程为

式中，η为剪切黏度，Pa·s；η_∞为无穷剪切黏度，Pa·s；η₀为零剪切黏度，Pa·s；λ为松弛时间，s；$ \dot{\gamma}$为剪切速率，s^-1；n为非牛顿指数；E₀为活化能，J/(kg·mol)；R₀为理想气体常量，J/(mol·K)；T为温度，K；T₀为参考温度，K。

本文所用物料三元乙丙橡胶(EPDM)的非牛顿指数n为0.6，密度为1 200 kg/m³，比热容C_p=2 200 J/(kg·K)，导热系数为0.26 W/(m·K)。模型的边界条件如表 1所示。

表 1(Table 1

表 1 模型的边界条件 Table 1 Boundary conditions of the model 模型区域 边界条件 入口 压力入口，温度为120 ℃ 出口 相对压力为0 壁面 壁面速度为零，温度保持恒温

下载CSV 表 1 模型的边界条件 Table 1 Boundary conditions of the model

设h为阻尼高度，w为阻尼宽度，p为入口压力，T为壁面温度。通过单因素试验分析各参数对目标函数影响的显著性，并确定是否存在对目标函数影响不显著的参数，为参数选择提供依据。

对上述参数进行Plackett-Burman设计，因素水平设计如表 2所示。对4个优化设计变量进行筛选，另加7个虚拟变量，每个变量分别定义(+)和(-)2个水平，共进行12次试验以确定每个因素的影响因子。

表 2(Table 2

表 2 Plackett-Burman设计因子水平 Table 2 Levels for factors of Plackett-Burman design 因素 低水平 高水平 h/mm 9 13.5 w/mm 2 8 p/MPa 10 25 T/℃ 70 85

下载CSV 表 2 Plackett-Burman设计因子水平 Table 2 Levels for factors of Plackett-Burman design

根据表 3中影响因子的显著性分析，w对目标函数V和σ的影响程度为不显著，因此在下文的响应面法分析中只考虑h、p、T这3个关键影响因素。其中，阻尼高度h的增大导致胶料在靠近入口侧的挤出量变小，从而影响挤出速度在出口截面的分布；入口压力p的增大导致胶料在流道内的流动加快，从而对V和σ产生影响；壁面温度T对胶料黏度有显著影响，而胶料黏度的变化会导致胶料与流道之间的摩擦力发生变化。

表 3(Table 3

表 3 影响因子的显著性分析 Table 3 Significance analyses of effect factors 因素 V σ P值 显著性 P值 显著性 h 0.153 2 * 0.032 1 ** w 0.865 2 N 0.952 3 N p 0.012 5 ** ＜0.000 1 *** T ＜0.000 1 *** ＜0.000 1 *** N—P＞0.5，不显著；*—P＜0.5，一般显著；**—P＜0.05，显著；***—P＜0.01，极显著。

下载CSV 表 3 影响因子的显著性分析 Table 3 Significance analyses of effect factors

响应面法利用合理的试验设计方法并通过试验得到数据, 采用多元回归方程拟合因子和响应值之间的函数关系, 来指导多变量优化问题。通过响应面法建立目标函数V、σ与已筛选重要影响参数(阻尼高度h、入口压力p、壁面温度T)关系的回归方程，并通过优化分析确定各参数的最优设计点。

采用Box-Behnken法，对阻尼高度h、入口压力p、壁面温度T进行试验设计，以-1、0、1作为各因素的低、中和高水平，变量因素编码及水平见表 4。试验分析时其他参数保持初始值，非牛顿指数n为0.6，阻尼宽度w为2 mm。

表 4(Table 4

表 4 试验因素和水平 Table 4 Experimental factors and levels 水平 因素 阻尼高度h/mm 入口压力p/MPa 壁面温度T/℃ -1 9 10 70 0 11.25 17.5 77.5 1 13.5 25 85

下载CSV 表 4 试验因素和水平 Table 4 Experimental factors and levels

根据试验设计，共需进行17组模拟试验，其中12个试验点是析因点，5个试验点为区域中心点，重复计算用以估算试验误差。对模拟试验结果进行回归分析，各因素对V和σ的显著性结果如表 5所示。

表 5(Table 5

表 5 V和σ影响因子的显著性分析 Table 5 Significance analysis of influence factors for V and σ 来源 V σ F值 P值 显著性 F值 P值 显著性 回归模型 3.60 0.042 8 ** 12.60 0.001 5 *** A 1.15 0.452 1 * 1.48 0.462 1 * B 13.11 0.008 5 *** 69.19 0.030 7 ** C 6.69 0.036 1 ** 4.53 ＜0.000 1 *** AB 5.20 0.036 7 ** 0.606 4 0.046 7 ** AC 0.007 1 0.935 1 N 0.917 5 0.037 0 ** BC 0.761 0 0.411 9 * 0.128 4 0.730 7 N A2 2.13 0.188 2 * 36.46 0.000 5 *** B2 0.992 1 0.352 4 * 0.014 4 0.907 7 N C2 2.57 0.153 1 * 0.140 4 0.719 0 N N—P＞0.5，不显著；*—P＜0.5，一般显著；**—P＜0.05，显著；***—P＜0.01，极显著。

下载CSV 表 5 V和σ影响因子的显著性分析 Table 5 Significance analysis of influence factors for V and σ

由表 5可知关于V的回归模型显著，说明此回归方程在回归区域内拟合较好，入口压力(B)对V的影响极显著，壁面温度(C)对V的影响显著，阻尼高度(A)对V的影响一般显著；二次项A²、B²、C²对试验的影响为一般显著水平；各因素的交互作用中AB影响显著。综合以上因素进行分析，由F检验可知影响V的因素主次关系为B＞C＞A，即入口压力>壁面温度>阻尼高度。同理，由F检验可知影响σ的因素主次关系为C＞B＞A，即壁面温度>入口压力>阻尼高度。

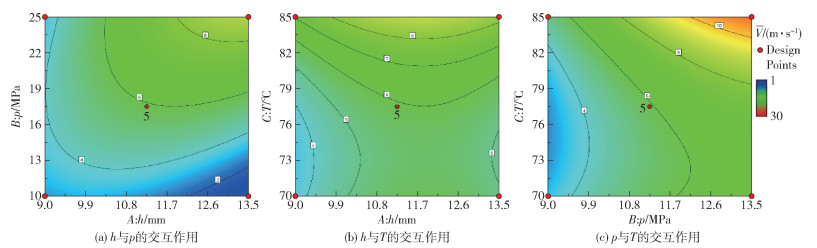
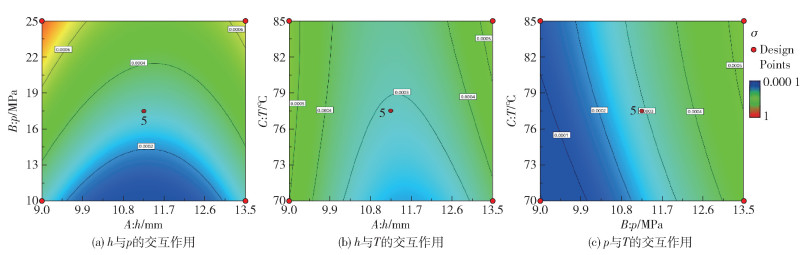
影响V的参数间的交互作用如图 5所示。从图中可以看出，p的影响较大，在h和T处于一定水平时，目标函数V随着p的增大而增大；h对目标函数V的影响最小，且当h处于中间水平时，T对V的影响程度最显著。影响σ的参数间的交互作用如图 6所示。由图 6(a)、(b)可知，h在11.2 mm附近时目标函数σ取得较小值；由图 6(c)，p对目标函数σ的影响较大，在h和T处于一定水平时，目标函数σ随着p的增大而增大。

图 5(Fig. 5)

图 5 影响出口截面挤出速度均值V的因素间交互作用 Fig.5 The interaction between factors affecting the mean extrusion velocity V at the exit section

图 6(Fig. 6)

图 6 影响出口截面挤出速度标准差σ的因素间交互作用 Fig.6 The interaction between factors affecting the standard deviation σ of the extrusion velocity at the exit section

通过模拟数据，利用最小二乘法得到各因素关于目标函数V和σ的回归方程，再由表 5中数据对V回归方程进行方差分析，可得F=3.60，P＜0.05，表明模型具有良好的预测显著性，其中AC对V的影响程度不显著，故在回归方程中不考虑该项的影响。同理对σ回归方程进行方差分析可知，F=12.60，P＜0.05，表明模型具有良好的预测显著性，其中BC、B²、C²对σ的影响程度不显著，故在回归方程中不考虑这3项的影响，最终得到的方程如式(4)、(5)所示。

为验证建立的二次回归方程的有效性，另取10组试验参数代入方程(4)、(5)中，得到目标函数V和σ的预测值，将预测值与Fluent模拟值进行比较，结果如表 6所示。

表 6(Table 6

表 6 V和σ的预测值和模拟值比较 Table 6 Comparison between the predicted and simulated values of V and σ h/mm p/MPa T/℃ V/(m·s-1) V偏差/% σ σ偏差/% 预测值 模拟值 预测值 模拟值 11.25 10 77.5 8.88×10-3 8.71×10-3 1.95 7.46×10-6 7.56×10-6 -1.32 9 17.5 70 9.63×10-3 9.72×10-3 -0.93 4.53×10-4 4.39×10-4 3.19 11.25 17.5 70 1.01×10-2 9.90×10-3 2.02 1.56×10-4 1.49×10-4 4.7 11.25 17.5 77.5 1.22×10-2 1.18×10-2 3.39 2.25×10-4 2.21×10-4 1.8 11.25 25 85 1.965×10-2 1.973×10-2 -0.68 4.62×10-4 4.74×10-4 -2.53 9 17.5 77.5 1.176×10-2 1.12×10-2 -2.14 4.87×10-4 4.78×10-4 1.88 9 17.5 85 1.45×10-2 1.39×10-2 2.88 4.93×10-4 4.99×10-4 -1.2 13.5 15 85 1.38×10-2 1.32×10-2 4.55 4.08×10-4 4.21×10-4 -3.09 13.5 15 77.5 1.15×10-2 1.2×10-2 -4.17 3.26×10-4 3.16×10-4 3.16 9 17.5 75 1.1×10-2 1.13×10-2 -2.65 4.79×10-4 4.70×10-4 1.91

下载CSV 表 6 V和σ的预测值和模拟值比较 Table 6 Comparison between the predicted and simulated values of V and σ

由表 6中数据可知，目标函数V和σ的预测值与模拟值的偏差均在允许范围(5%)以内，说明该回归方程对实际生产具有指导意义。

为找到平衡挤出效率和质量的最佳点的工况参数，以工厂实际生产该制品的质量标准为依据，寻求与之匹配的最优生产效率并确定最优结构和工艺参数。其中工厂实际生产中产品质量满足要求的标准如下：挤出制品在厚度方向的尺寸偏差在±4%以内。因制品厚度偏差受挤出均匀性影响，经计算可得评价挤出均匀性的指标为目标函数σ不超过2.6×10^-4。

多目标优化的过程如下：以目标函数σ不超过2.6×10^-4、V最大为优化目标，获得100组的迭代优化数据，得到最优设计参数为阻尼高度11.15 mm，入口压力14.95 MPa，壁面温度85 ℃，此时V为8.58× 10^-3 m/s，较工厂原有参数模拟得到的V提高13.2%。

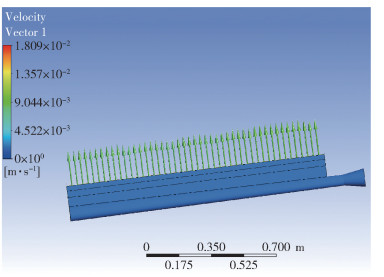
用最优设计参数模拟得到的出口截面挤出速度云图如图 7所示，经计算得σ=2.51×10^-4，V =8.37×10^-3 m/s，与优化结果的偏差分别为3.6%和2.4%，均在偏差允许范围内，表明响应面法优化设计是合理有效的。

图 7(Fig. 7)

图 7 优化结果试验出口速度分布 Fig.7 Exit velocity distribution for optimized result test

(1) 利用响应面法对高分子流体的挤出工艺条件进行优化，结果表明影响V的因素主次关系为入口压力p＞壁面温度T＞阻尼高度h，影响σ的因素主次关系为壁面温度T＞入口压力p＞阻尼高度h。

(2) 基于Box-Behnken法和响应面法建立了L型宽幅机头出口截面挤出速度均值V和标准差σ与阻尼高度h、入口压力p、壁面温度T的回归方程，预测值与模拟值的偏差均在5%以内，可以对生产中各参数的选择提供理论依据。

(3) 以出口截面挤出速度标准差σ符合生产要求、出口截面挤出速度均值V最大为目标，经过优化设计最终确定最优设计点，在满足出口截面挤出速度标准差的情况下，较工厂原有参数模拟得到的挤出速度均值提高13.2%，对实际生产具有指导意义。