不平衡数据是指样本集中某类样本的数目远远小于其他类样本数目的数据集(通常将少数类样本称为正类样本,多数类样本称为负类样本)[1]。不平衡数据问题存在于诸多生产生活领域中,如通讯欺诈检测[2]、医学诊断[3]、工业故障检测[4]等等。传统分类算法通常以类分布大致相等为前提,因此当数据集类别分布不均衡时,易使分类器的决策边界偏移,导致漏判,即将正类样本错分为负类样本[5]。而在实际应用中,对正类样本的错误分类往往会产生更严重的后果,如将工业故障误判为正常或在医疗诊断中将患病判断为正常。因此,面对数据不平衡问题,改善不平衡数据的分类性能,特别是提高正类样本的识别精度十分必要。
学者们对于不平衡数据分类问题进行了诸多研究,主要分为从数据层面和从分类器层面两类[5]。其中从数据层面又主要分为对正类样本进行过采样和对负类样本进行欠采样两种方式。由于欠采样方式可能会损失数据特征[1],因此采取对正类样本进行过采样获得平衡样本集再进行分类的研究思路更为常见。Chawla等[6]提出的人工合成过采样技术(synthetic minority oversampling technique,SMOTE)是最为广泛引用和应用的过采样方法之一。SMOTE算法通过增加正类样本实现数据平衡,方法简单易行且可有效提高分类器的性能,因而成为研究热点。后续学者在SMOTE基础上又作了诸多改进,如提出了SMOM(SMOTE for multiclass classification)算法,其通过为负类样本分配不同权重来改善SMOTE的过泛化问题[7];G- SMOTE(geometric SMOTE)算法则通过在每个选定的少数类样本周围的几何区域内人工生成样本,以达到增强数据生成机制的目的[8]。从分类器层面,支持向量机(support vector machine,SVM)分类器是经典的非线性分类器,在诸多应用中都能够取得较好的分类结果[9-10]。为解决不平衡数据分类问题,人们将SMOTE与SVM相结合,取得了多种研究成果。Deepa等[11]提出不平衡高维数据支持向量机分类方法,对正、负样本集分别单独作过采样处理,再将其映射到特征空间进行SVM训练并得到决策函数。Zhang等[12]在实验中将基于SVM的重采样特征消除(resampling feature elimination based on SVM, SVM-RFE)、基于SVM的边界重采样特征消除(border-resampling feature elimination based on SVM, SVM-BRFE)算法分别与SMOTE相结合,较好地解决了高维问题对分类结果的负面影响。Zhou等[13]提出用SMOTE结合TomekLinks算法获得平衡集,再使用决策树进行特征提取,最后用SVM进行分类的方法。以上这些方法在处理不平衡数据问题上都取得了相对较好的效果。然而,SMOTE在生成样本时采用的是线性插值方法,当用于解决非线性分类问题时生成样本的可靠性无法衡量。如当SMOTE与SVM联合使用时,SMOTE算法工作在输入空间,SVM工作在核空间。前者通过线性插值获得的新样本投影到核空间中用于分类时,算法的分类性能可能会因为两者工作空间不一致而受到影响。此外,在样本集中边界样本对分类面的构建起到决定性影响,因此在样本生成时可只考虑边界样本以减少计算量。
鉴于上述问题,本文提出一种自适应核SMOTE-SVM不平衡数据分类算法。该算法利用SVM找到训练集的边界样本—支持向量(SV),在核空间下对其进行自适应内外插值,将新插入的样本与原有样本的表示式一同计算形成增广Gram矩阵,再利用SVM算法生成分类决策函数,从而实现分类。该算法使样本的生成与分类统一在同一核空间中,增强了新样本集的可信性;同时内外插值的方式提高了新样本的多样性。通过在多个数据集上进行实验,结果表明了所提算法可以有效改善不平衡数据的分类效果。
1 SMOTE算法与SVM算法 1.1 SMOTE算法SMOTE算法通过将正类样本与其邻近的正类样本之间随机线性插值合成新样本,整个计算过程在输入空间中完成[6]。假设有训练样本集S,其中正类样本集Smin ∈S,负类样本集Smax ∈S。对于正类中的每一个样本xi∈Smin,其k个近邻的同类样本为
| $ \boldsymbol{x}_{\mathrm{new}}=\boldsymbol{x}_i+\delta \times\left(\tilde{\boldsymbol{x}}_j-\boldsymbol{x}_i\right) $ | (1) |
式中,δ是(0, 1)之间的一个随机数,新样本标签与正类样本标签一致。
1.2 SVM算法SVM算法自诞生以来已在诸多应用领域中取得了良好的分类结果,它是一种经典的分类算法,本质是求解一个满足分类要求的最优超平面,该超平面既要保证分类精度又要保证到其最近样本的距离间隔最大。给定样本集S={(x1, y1), (x2, y2), …, (xN, yN)},其中x1, x2, …, xN∈Rm,y1,y2,…,yN∈{-1, +1}。则超平面记为w·xi+b=0, 其中参数w代表权值向量,参数b代表阈值。非线性SVM通过解决以下凸优化问题来求解最优超平面
| $ \begin{aligned} & \min _{\boldsymbol{w}, b, \xi} \frac{1}{2} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w}+C \sum\limits_{i=1}^N \xi_i \\ & \text { s. t. }\; y_i\left(\boldsymbol{w}^{\mathrm{T}} {\varphi}\left(\boldsymbol{x}_i\right)+b\right) \geqslant 1-\xi_i, \xi_i \geqslant 0 \end{aligned} $ | (2) |
式中,φ(·)为将输入样本点映射到高维特征空间的函数,ξi为松弛因子,C为惩罚系数。
通过将目标函数公式(2)转化为其Lagrange对偶形式求解
| $ \begin{array}{ll} \max \limits_\alpha & \sum\limits_{i=1}^N \alpha_i-\frac{1}{2} \sum\limits_{i=1}^N \sum\limits_{j=1}^N \alpha_i \alpha_j y_i y_j \boldsymbol{K}\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right) \\ \text { s.t. } & \sum\limits_{i=1}^N \alpha_i y_i=0, 0 \leqslant \alpha_i \leqslant C \end{array} $ | (3) |
式中,αi为Lagrange乘子,核函数K(xi, xj)=φ(xi)Tφ(xj)为xi、xj特征空间下的内积。运用此核计算公式,整个过程只需计算特征空间中样本的内积,无需对生成点作繁琐的显式映射。
通过式(3)计算出最优Lagrange乘子αi*,进而求得超平面参数w、b。
最终决策函数为
| $ f(\boldsymbol{x})=\operatorname{sgn}\left\{\sum\limits_{i=1}^N \alpha_i^* \boldsymbol{K}\left(\boldsymbol{x}, \boldsymbol{x}_i\right)+b\right\} $ | (4) |
其中sgn {·}为阶跃函数。待测样本x通过式(4)的决策函数实现分类。其中,支持向量即为αi*中非零解所对应的样本。由此可知,支持向量集组成了分类边界样本集。
为处理不平衡数据分类问题,许多SMOTE-SVM方法先通过SMOTE对不平衡数据集进行预处理,得到平衡的数据集,再结合SVM实现样本分类。这种先得到平衡集再利用SVM分类的处理方式可以在一定程度上改善分类面偏移的问题,但也存在生成空间与分类空间不一致的情况。为解决此问题,提高不平衡样本集的分类准确率,本文提出一种自适应核SMOTE-SVM算法。
2 自适应核SMOTE-SVM分类算法 2.1 算法流程SMOTE-SVM算法主要分为两个部分:第一部分基于自适应核SMOTE算法,用于新样本生成;第二部分基于增广Gram矩阵获得决策函数。算法流程如图 1所示。算法前半部分根据少数类样本集的支持向量(SV+)在核距离下的近邻样本的分布情况,设计内插或外推方法进行新样本生成。算法后半部分考虑到无法在核空间内获得新样本的显式表达,因此构造增广Gram矩阵,基于SVM分类算法获得分类决策函数,最终实现分类。
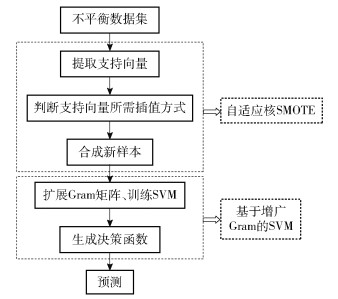
|
图 1 算法流程图 Fig.1 Algorithm flow chart |
自适应核SMOTE算法以正类样本的支持向量作为依据合成新样本, 这是因为支持向量可以看作核空间中的边界样本,而边界样本对分类面的构建至关重要。
算法具体步骤如下。
1) 利用SVM分类器得到Smin的支持向量SV+。
2) 基于核距离找出SV+在S中的k个近邻,核距离计算方法为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;d^{\varphi}\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)^2=\left\|\varphi\left(\boldsymbol{x}_i\right)-\varphi\left(\boldsymbol{x}_j\right)\right\|^2=\boldsymbol{K}\left(\boldsymbol{x}_i, \boldsymbol{x}_i\right)- \\ 2 \boldsymbol{K}\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)+\boldsymbol{K}\left(\boldsymbol{x}_j, \boldsymbol{x}_j\right) \end{array} $ | (5) |
式中,xi, xj是SV+中任意一点。需要指出的是在本算法所有核映射的运算中应采用统一核函数,保证样本生成和分类统一在同一核空间中。
3) 根据SV+中xi的k近邻类别属性选择新样本的生成方式,即内插或外推。
设xi所在的k个近邻样本中,多数类样本的个数为m。若m=k,认为xi为噪声样本,重新标记;若m>k/2,对xi进行内插值,如图 2(b)中1处所示;若m<k/2,对xi进行外插值,如图 2(b)中2处所示。该方法实质是基于支持向量作过采样,以支持向量为分类边界,根据决策机制生成少数类样本,剔除了噪声点,帮助正类群体扩大到负类样本密度不高的区域,从而提高分类的准确性。
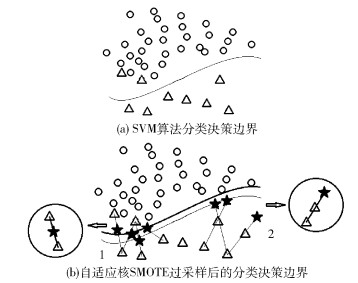
|
图 2 决策边界的调整 Fig.2 Adjustment of the decision boundary |
4) 找出xi在Smin中的N个近邻(N即SV+数量的倍数,下文简称为过采样倍数),进行内插外推操作,生成新样本。假设xj是近邻之一,则特征空间下的新生成点xij表示为
| $ \boldsymbol{x}^{i j}=\varphi\left(\boldsymbol{x}_i\right)+\delta^{i j}\left(\varphi\left(\boldsymbol{x}_j\right)-\varphi\left(\boldsymbol{x}_i\right)\right) $ | (6) |
式中,δij为随机数。当新生成样本为内插所产生时,新生成点在xi、xj两点之间的连线上,δij取值为(0, 1);反之,新生成点在两点的延长线上,δij取值为(-1, 0)。
SVM原本的分类决策边界位置如图 2(a)中的细实线所示。自适应核SMOTE过采样算法通过对不同样本分布情况采取不同方式生成新样本,实现改善决策边界的目的。在正类样本与负类样本重叠区域(图 2(b)区域1处),此区域的样本分布情况会导致决策边界向正类倾斜,本文算法在此区域选择内插值增多正类样本,进而使决策边界向负类移动(粗实线位置);在正类样本和负类样本相距较远的区域,如图 2(b)区域2处所示,算法则作外推操作,使正类边界向外扩展,为正类样本获取更多的分布空间,决策边界为粗实线位置。整个过程在核空间下进行,当近邻样本中负类样本占多数时,可知该边界样本处于核空间中正类和负类交叠区域,因此对该边界样本做内插值;若近邻样本中正类样本占多数,可知该边界样本处于两类数据相距较远区域,因此对该样本做外插值。利用这种基于核的自适应样本生成方式可使样本生成与后续分类统一在同一空间下,既能使分类面更理想,也能保证样本生成的可靠性。
2.3 基于Gram矩阵的样本分类在核映射中φ(·)的显式表达难以获得,利用2.1节所述方法得到的新样本实际为原始样本的代数表达,而非显式表达。由于SVM实际上是建立在对Gram矩阵训练的基础上,因此为实现分类面建模,对原始的Gram矩阵进行增广,使其包含新合成样本的核映射,无需额外求取新样本的显式表达。利用增广Gram矩阵训练支持向量机,进而建立决策函数。
1) 增广核矩阵(Gram矩阵)
根据SVM的对偶公式(式(3))可知,要得到决策函数,需求出新生成样本点到其他样本点在特征空间下的内积。令此内积由Gram矩阵G1∈RN×N表示,具体表达式为Gkl1=K(xk, xl)=φ(xk)Tφ(xl),其中xk、xl是训练集样本。为了把通过内外插值得到的新生成点加至Gram矩阵G1中,将G1扩展,定义新的增广矩阵为Gaug。扩展如式(7)所示。
| $ \boldsymbol{G}_{\text {aug }}=\left[\begin{array}{cc} \boldsymbol{G}^1 & \boldsymbol{G}^2 \\ \boldsymbol{G}^{2^{\mathrm{T}}} & \boldsymbol{G}^3 \end{array}\right] $ | (7) |
式中,矩阵G1为原数据集中所有样本点之间的内积矩阵
| $ \boldsymbol{G}^1 \in \boldsymbol{R}^{N \times N} \quad \boldsymbol{G}_{k l}^1=\boldsymbol{K}\left(\boldsymbol{x}_k, \boldsymbol{x}_l\right), \boldsymbol{x}_k, \boldsymbol{x}_l \in S $ |
矩阵G2为原始数据集中所有样本点与新生成样本点(假设新生成P个样本点)的内积矩阵
| $ \boldsymbol{G}^2 \in \boldsymbol{R}^{N \times P} \quad \boldsymbol{G}_{k l}^2=\boldsymbol{K}\left(\boldsymbol{x}_k, \boldsymbol{x}_l^{i j}\right), \boldsymbol{x}_k \in S, \boldsymbol{x}_l^{i j} \in S_{\min }^* $ |
矩阵G3为两两新生成样本点的内积矩阵
| $ \boldsymbol{G}^3 \in \boldsymbol{R}^{P \times P} \quad \boldsymbol{G}_{k l}^3=\boldsymbol{K}\left(\boldsymbol{x}_k^{p q}, \boldsymbol{x}_l^{i j}\right), \boldsymbol{x}_k^{p q}, \boldsymbol{x}_l^{i j} \in S_{\min }^* $ |
其中,G2可通过式(6)进一步得到。
| $ \begin{aligned} & \quad \quad\boldsymbol{K}\left(\boldsymbol{x}_k, \boldsymbol{x}_l^{i j}\right)=\varphi\left(\boldsymbol{x}_k\right) \cdot \varphi\left(\boldsymbol{x}_l^{i j}\right)=\varphi\left(\boldsymbol{x}_k\right) \cdot\left[\varphi\left(\boldsymbol{x}_i\right)+\right. \\ & \left.\delta^{i j}\left(\varphi\left(\boldsymbol{x}_j\right)-\varphi\left(\boldsymbol{x}_i\right)\right)\right]=\left(1-\delta^{i j}\right) \boldsymbol{K}\left(\boldsymbol{x}_k, \boldsymbol{x}_i\right)+\delta^{i j} \cdot \\ & \boldsymbol{K}\left(\boldsymbol{x}_k, \boldsymbol{x}_j\right) \end{aligned} $ | (8) |
式中,xk表示S中任意一点,xlij表示新生成的点。xlij又可用式(6)及核函数进一步表示,最后G2可由式(8)计算得出,避免了新样本的显式表达。
G3的计算与G2同理。G3可由式(9)计算。
| $ \begin{aligned} & \;\;\;\;\boldsymbol{K}\left(\boldsymbol{x}_k^{p q}, \boldsymbol{x}_l^{i j}\right)=\boldsymbol{x}_k^{p q} \cdot \boldsymbol{x}_l^{i j}=\left[\varphi\left(\boldsymbol{x}_p\right)+\delta^{p q}\left(\varphi\left(\boldsymbol{x}_q\right)-\right.\right. \\ & \left.\left.\varphi\left(\boldsymbol{x}_p\right)\right)\right] \cdot\left[\varphi\left(\boldsymbol{x}_i\right)+\delta^{i j}\left(\varphi\left(\boldsymbol{x}_j\right)-\varphi\left(\boldsymbol{x}_i\right)\right)\right]=(1- \\ & \left.\delta^{i j}\right)\left(1-\delta^{p q}\right) \boldsymbol{K}\left(\boldsymbol{x}_i, \boldsymbol{x}_p\right)+\left(1-\delta^{i j}\right) \delta^{p q} \boldsymbol{K}\left(\boldsymbol{x}_i, \boldsymbol{x}_q\right)+ \\ & \delta^{i j}\left(1-\delta^{p q}\right) \boldsymbol{K}\left(\boldsymbol{x}_j, \boldsymbol{x}_p\right)+\delta^{i j} \delta^{p q} \boldsymbol{K}\left(\boldsymbol{x}_j, \boldsymbol{x}_q\right) \end{aligned} $ | (9) |
从上述公式可以看出,增广核矩阵Gaug只使用了数据集中的训练样本和核函数K(·, ·),无需映射φ(·)的显式表达。需要注意的是,对于新生成样本求核矩阵时,内插、外推所产生的样本需按同一次序排列,且不同插值方式对应的随机数不同。
2) 基于SVM生成决策函数
对式(3)引入增广核矩阵。设P为新增行列数,增广Gram矩阵用N+P个Lagrange乘子求解。待测数据点x对应的类别f(x),即决策函数的表示为
| $ \begin{array}{l} \;\;\;\;\;\;f(\boldsymbol{x})=\operatorname{sgn}\left\{\sum\limits_{i=1}^N \alpha_i \boldsymbol{K}\left(\boldsymbol{x}, \boldsymbol{x}_i\right)+\sum\limits_{j=N+1}^{N+P} \alpha_j \boldsymbol{K}(\boldsymbol{x}, \right. \\ \left.\left.\boldsymbol{x}_j^{p q}\right)+b\right\} \end{array} $ | (10) |
式中,xjpq∈Smin*为新生成样本。
2.4 算法伪代码对2.2节的自适应核SMOTE过采样过程和2.3节的基于Gram矩阵的样本分类过程进行整合,得到算法主要步骤的伪代码如下。
输入:S训练集;
k最近邻的个数;
N过采样倍数;
输出:Smin*合成样本集;
变量:Smin正类样本;
SV+正类样本的支持向量集;
步骤:
1) 从S中提取Smin;
2) 在S中训练SVM,提取SV+;
3) 在核空间下,找出SV+在S中的k个近邻;
4) 在k个近邻中统计属于负类的点,记m个;
5) 若k个近邻中属于负类的支持向量的个数小于k值的一半,即m<k/2,则该样本归为需要外推值的样本;反之,归为需要内插的样本。根据式(6)生成新样本(内插值时随机数取(0, 1),外推时随机数取(-1, 0));
6) 将新生成样本与原始样本一同带入式(7)~(9),得到增广核矩阵Gaug。内插、外推按顺序放置,生成样本数(即需要插值操作的支持向量整数倍)由N决定;
7) 由式(10)得到决策函数。
3 实验及结果分析 3.1 实验数据集本文用Python语言实现所提出的算法,并将其与SVM、SMOTE-SVM等方法进行比较,以验证算法的优越性。实验使用了9个不平衡数据集,其中8个来自University of California Irvine(UCI)数据库,分别是Iris、Spect、Glass、Yeast、Balancescale、Ecoli、Car、Abalone数据集,另一个为真实工业生产过程中聚乙烯流化床声波故障数据集,相关反应装置以及数据信息在文献[14]中有详细介绍,本文不再赘述。数据集详细描述如表 1所示,其中不平衡比指正类样本与负类样本数量的比值。
| 下载CSV 表 1 实验数据集描述 Table 1 Description of the experimental data set |
本文实验分别选择每个数据集的70%的样本作为训练集,剩余的样本作为测试集。所有实验皆采用高斯核函数,惩罚因子C和参数g的选取采用网格搜索和10次交叉验证测试所得的最优值。除此以外,过采样倍数N的选择对最终分类结果也有重要影响,3.3节对此进行了说明。
3.2 评估指标对于不平衡数据分类水平的评估,常用G-mean、F-value两种评价标准,这两种评价标准均建立在混淆矩阵(表 2)的基础上。其中,TP为预测对的正类样本数,TN为预测对的负类样本数,FP和FN分别为预测错的负类样本数和预测错的正类样本数。
| 下载CSV 表 2 混淆矩阵 Table 2 Confusion matrix |
G-mean表示正类分类精度和负类分类精度的几何平均值,需要正负类样本正确率均较高,G-mean才会高。G-mean越高,说明模型越稳健,其定义如下。
| $ G {-mean }=\sqrt{\frac{T P}{T P+F N} \times \frac{T N}{T N+F P}} $ | (11) |
F-value为精确率和召回率的调和平均,令P(precision)和R(recall)分别表示样本的查准率和查全率,P=TP/(TP+FP),R=TP/(TP+FN)。F-value定义如下。
| $ F {-value }=\frac{\left(1+\beta^2\right) \times P \times R}{\beta^2 \times P+R} $ | (12) |
实验中β取1,表示P和R的重要性相同。F-value越高,说明正类样本被错分的越少,错分的代价越小。
3.3 过采样倍数的选择过采样倍数即需要作插值操作的正类支持向量数量的倍数,是影响最终分类结果的重要参数。本文采用不同的过采样倍数对所提方法及SMOTE-SVM方法进行实验,N=1即为生成与当前正类样本中支持向量数量相等的新样本。在实验过程中,令N从1开始增加,直至样本集基本平衡。结果发现,数据并非是达到平衡时的分类效果才最好。以Balancescale数据集为例,过采样倍数依次取1、5、10、15、20、25、30、35(N=26时,数据集平衡),所得分类结果如图 3所示,其中内外插值SMOTE-SVM算法为样本仅在输入空间进行内外插值上采样后送入SVM获得分类器的方法。
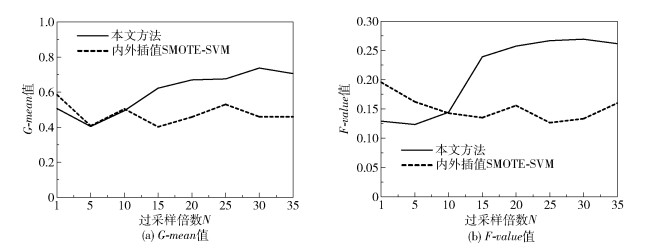
|
图 3 不同过采样倍数分类结果 Fig.3 Results with different oversampling multiples |
由图 3可见,当过采样倍数N=30时,分类效果最好。过采样倍数直接关系到新生成样本的数量,新生成样本数量过多会造成数据冗余,过少则达不到提高分类准确率的目的,这两种情况都无宜于分类,故对具体的数据集需要根据实际情况进一步通过实验确定。本文其他数据集的过采样倍数取值方法同上。
3.4 结果分析本文所提算法及其对比算法的实验结果如表 3、4所示,分别为不同算法在不同数据集上的G-mean和F-value结果。
| 下载CSV 表 3 不同算法的G-mean值 Table 3 G-mean values of different algorithms |
| 下载CSV 表 4 不同算法的F-value值 Table 4 F-values of different algorithms |
分析表 3和表 4的实验结果可以发现:采用SMOTE算法进行采样时,由于对各个正类样本不作具体区分,所以不能很好地增强决策边界,导致边界处样本被错分的概率较大,表现在虽然其提高了正类样本的F-value,但是在总体分类准确率上有待改善。内插外推的过采样方法摒弃了噪声点,在一定程度上增强了边界,对分类效果起到积极作用。考虑到样本投射到特征空间中可能出现坏点的情况,本文算法既增强了决策边界,又改善了这一问题,因此G-mean和F-value两个指标结果均有所提升。
4 结束语本文针对不平衡数据集的分类问题,提出了一种基于核的非线性插值分类算法。该算法全部工作于核空间下,有效解决了样本生成与分类空间不一致的问题,并通过两种插值方式调整了分类边界,使得样本生成更具多样性,且保证了样本生成的可靠性。在多个UCI数据集上与常用算法的实验对比结果表明,所提算法在多数情况下可以获得最优性能。为进一步验证算法的可推广性,本文还采用一个真实工业故障数据集进行实验,也得到了与UCI数据集类似的实验结果,表明该方法可有效解决数据不平衡问题,提高分类效果。需要指出的是,本文方法在小数据集分类中较占优势,当数据集较大时,算法可能存在耗时较长现象。因此,如何增强算法的实用性以及提高算法速度是需要进一步解决的问题。
| [1] |
石洪波, 陈雨文, 陈鑫. SMOTE过采样及其改进算法研究综述[J]. 智能系统学报, 2019, 14(6): 1073-1083. SHI H B, CHEN Y W, CHEN X. Summary of research on SMOTE oversampling and its improved algorithms[J]. CAAI Transactions on Intelligent Systems, 2019, 14(6): 1073-1083. (in Chinese) |
| [2] |
JURGOVSKY J, GRANITZER M, ZIEGLER K, et al. Sequence classification for credit-card fraud detection[J]. Expert Systems with Applications, 2018, 100: 234-245. DOI:10.1016/j.eswa.2018.01.037 |
| [3] |
RAWASHDEH H, AWAWDEH S, SHANNAG F, et al. Intelligent system based on data mining techniques for prediction of preterm birth for women with cervical cerclage[J]. Computational Biology and Chemistry, 2020, 85: 107233. DOI:10.1016/j.compbiolchem.2020.107233 |
| [4] |
YI H K, JIANG Q C, YAN X F, et al. Imbalanced classification based on minority clustering synthetic minority oversampling technique with wind turbine fault detection application[J]. IEEE Transactions on Industrial Informatics, 2021, 17(9): 5867-5875. DOI:10.1109/TII.2020.3046566 |
| [5] |
李艳霞, 柴毅, 胡友强, 等. 不平衡数据分类方法综述[J]. 控制与决策, 2019, 34(4): 673-688. LI Y X, CHAI Y, HU Y Q, et al. Review of unbalanced data classification methods[J]. Control and Decision, 2019, 34(4): 673-688. (in Chinese) |
| [6] |
CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357. |
| [7] |
ZHU T F, LIN Y P, LIU Y H. Synthetic minority oversampling technique for multiclass imbalance problems[J]. Pattern Recognition, 2017, 72: 327-340. DOI:10.1016/j.patcog.2017.07.024 |
| [8] |
GEORGIOS D, FERNANDO B. Geometric SMOTE a geometrically enhanced drop-in replacement for SMOTE[J]. Information Sciences, 2019, 501: 118-135. DOI:10.1016/j.ins.2019.06.007 |
| [9] |
GAO J F, SHI W G, TAN J X, et al. Support vector machines based approach for fault diagnosis of valves in reciprocating pumps[C]//Canadian: Electrical and Computer Engineering. Winnipeg, 2002: 1622-1627.
|
| [10] |
ZHANG C Q, ZHANG H, HU X T. A contrastive study of machine learning on funding evaluation prediction[J]. IEEE Access, 2019, 7: 106307-106315. |
| [11] |
DEEPA T, PUNITHAVALLI M. A new sampling technique and SVM classification for feature selection in high-dimensional imbalanced dataset[C]//3rd International Conference on Electronics Computer Technology(ICECT). Kanyakumari, 2011.
|
| [12] |
ZHANG C K, GUO J W, LU J R. Research on classification method of high-dimensional class-imbalanced data sets based on SVM[C]//IEEE Second International Conference on Data Science in Cyberspace. Shenzhen, 2017: 60-67.
|
| [13] |
ZHOU H, YU K M, CHEN Y C, et al. A hybrid feature selection method RFSTL for manufacturing quality prediction based on a high dimensional imbalanced dataset[J]. IEEE Access, 2021, 9: 29719-29735. DOI:10.1109/ACCESS.2021.3059298 |
| [14] |
CHEN Y, WU H Y, WANG J, et al. Agglomeration-monitoring method for a fluidized bed with multiacoustic sensors[J]. Industrial & Engineering Chemistry Research, 2019, 58(42): 19531-19544. |







