2. 清华大学 摩擦学国家重点实验室, 北京 100084
2. State Key Laboratory of Tribology, Tsinghua University, Beijing 100084, China
磁性液体是一种新型功能材料,是将使用表面活性剂包覆的纳米级磁性固体颗粒均匀弥散在基载液中所形成的稳定的胶体溶液。磁性液体具有超顺磁性[1]和流动性,在磁场作用下纳米级磁性固体颗粒对外界磁场会有即时响应并向磁场较强的区域运动,使得磁性液体密封成为可能。磁性液体密封是磁性液体最重要的应用之一,作为一种新型非固体接触式密封,其对于不同的应用环境适应能力很强,与传统密封相比具有零泄漏、密封寿命长、密封可靠性高、无污染、黏性摩擦低等优点。近年来磁性液体密封在中低速、中小直径的真空密封以及正压气体密封领域的应用渐趋成熟,在航空航天[2-4]、石化工业[5-9]、环境保护[10-12]、军事装备[13-14]等不同领域都得到了广泛的应用。
随着磁性液体密封应用领域的扩展,很多密封场合除了保证耐压能力之外对磁性液体密封提出了新的要求。磁性液体密封增强耐压能力的主要途径包括开发性能优异的磁性液体、设计磁源和极靴等的几何结构、选择磁化强度更高更合适的磁源、增加密封级数等。然而对于密封空间受限的场合,如光电吊舱的轴系密封,是不能够仅通过增加密封级数来增强耐压能力的,需要在保证耐压能力的同时兼顾密封结构的尺寸要求,且要求密封结构的尺寸越小越好。此时就需要对单磁源磁性液体密封的不同结构形式展开探索。目前的重点研究方向之一为不同结构形式的磁性液体密封。研究不同结构形式的磁性液体密封,目的在于适应不同的工况要求,拓展磁性液体密封的应用范围。此外,磁性液体密封结构磁路设计的一个基本原则是在密封间隙内建立所需形态的磁场(即所需数值、方向及分布结构)[15],而使密封间隙之外的漏磁场强度最小。设计磁源时不是其磁化强度越大越好,而要使其工作点在最大磁能积处。通常的对称型磁性液体密封结构并不能使密封间隙内处处工作在最大磁能积点上,因此为了尽可能地利用磁源提供的外磁场,也有必要探索不同结构形式的密封性能。
目前针对磁性液体密封的不同结构形式已有了一些研究,所研究的密封结构通常是空间轴对称的,这样的结构在磁场模拟时可以利用两条对称轴简化为平面问题,计算分析更为简单。在磁性液体密封极靴的设计中,出于加工装配考虑通常保持磁源两侧极靴相同,对于不同结构形式的研究主要着眼于密封级数、极齿齿形参数等的区别上,而对非对称结构考虑较少,对于同一密封结构内部不同极靴、不同极齿分布间的相互影响乃至不同极齿齿形间的相互影响等没有形成系统认识,仍需要进一步的研究。李保锋等[16]证实了磁极与转轴件沿轴向磁场分布的不均匀性,据此提出变齿宽结构以提高耐压能力、减小结构尺寸。何新智等[17]比较了对称极齿型密封结构与非对称极齿型密封结构的密封耐压能力大小,发现非对称极齿型结构的密封耐压理论上要稍小于对称极齿型结构,然而在工程实践中却存在非对称极齿型结构密封耐压能力更高的现象。可见非对称极齿型结构具有更充分利用密封装置轴向空间的潜力。杨文明等[18]研究了对称极齿型结构中密封间隙、极齿齿形结构参数、密封级数等对磁性液体密封装置漏磁场的影响规律,但没有考虑这些因素对非对称极齿型结构漏磁场的影响规律。陈帆[19]提出一种极齿递增型磁性液体密封结构,该结构密封级数在极靴上非均匀、非对称分布,可最大限度地合理利用磁场能,减小了密封结构外围的漏磁场。
本文通过仿真模拟手段对非对称极齿型结构磁性液体密封进行研究,分析计算了不同轴径、不同密封间隙结构的密封耐压,并针对不同应用场景下磁性液体密封装置两轴端漏磁场的需求差异,探讨了非对称极齿型结构轴端漏磁场分布的影响因素及影响规律,为拓宽磁性液体密封应用场景和设计新型结构形式提供参考。
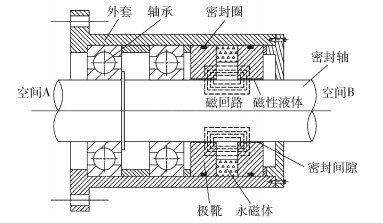
1 磁性液体密封 1.1 磁性液体密封原理磁性液体密封原理示意图如图 1所示。磁性液体密封装置一般由外套、轴承、密封圈、永磁体(磁源)、极靴、密封轴及磁性液体等组成。利用磁性液体对外磁场的响应,将磁性液体加注在极靴内周面与轴所构成的密封间隙内部,形成“O”形密封液环。当受到外加压差作用时,磁性液体液环在磁场中发生位移、变形,磁场力与外加压差对抗并达到新的动态平衡,起到密封作用。当外加压差过大时,磁场力不能够与外加压差相平衡,磁性液体密封失效[20]。
|
图 1 磁性液体密封原理示意图 Fig.1 Schematic diagram of the magnetic fluid sealing principle |
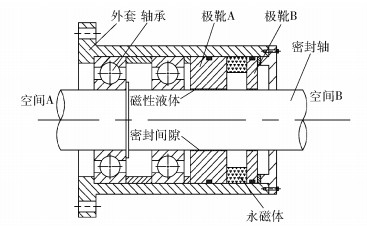
非对称极齿型结构磁性液体密封示意图如图 2所示。令永磁体两边极靴内周面上加工的矩形极齿齿形结构参数(齿高、齿宽、齿槽宽)均保持一致,永磁体两侧极齿的数量不等,即为非对称极齿型结构。
|
图 2 非对称极齿型结构磁性液体密封示意图 Fig.2 Schematic diagram of a magnetic fluid seal with an asymmetric polar teeth structure |
根据磁性液体的伯努利方程,在不考虑重力、离心力等影响时可以推得磁性液体密封第i个极齿所能提供的耐压为[21]
| $\begin{array}{l} \;\;\;\;\;\;\;\;\Delta {p_i} = {\mu _0}\int_{{H_{i, \min }}}^{{H_{i, \max }}} M {\rm{d}}H = {\mu _0}M\left( {{H_{i, \max }} - {H_{i, \min }}} \right) = \\ {\mu _0}M\Delta {H_i} \end{array}$ | (1) |
式中,Δpi为磁性液体密封第i个极齿所能提供的耐压值,MPa;μ0为真空磁导率(μ0=4π×10-7 T ·m/A);H为密封间隙处的磁场强度,kA/m;M为磁性液体的饱和磁化强度,T;ΔHi为第i个极齿处磁场强度最大值与最小值的差值,kA/m。磁性液体密封装置的总耐压值可以近似认为是密封间隙内所有极齿所能够提供的耐压值之和,由此得到总耐压值公式为
| $\Delta p=\sum\limits_{i=1}^n \Delta p_i=\sum\limits_{i=1}^n \mu_0 M \Delta H_i$ | (2) |
使用COMSOL对非对称极齿型结构进行磁场仿真模拟,利用磁场分布分析其密封耐压能力和相应的影响因素以及漏磁场分布规律。
由式(2)可知,要根据密封结构的磁场分布计算其密封耐压,首先需要确定所使用的磁性液体的磁化曲线。酯基磁性液体饱和磁化强度较高,一般不易与密封介质发生反应,适用性强,因此选用酯基磁性液体。根据酯基磁性液体的磁化曲线[22],当磁场强度大于200 kA/m时,磁性液体磁化强度随磁场强度增大而增大的幅度比较平缓,可以认为此时该酯基磁性液体的磁化强度已接近其饱和磁化强度值。此外,酯基磁性液体的相对磁导率约为1.05,与空气的相对磁导率非常接近[23]。
磁源在磁性液体密封中提供外磁场,电磁铁和永磁体常被选择作为磁源。因永磁体结构简单、加工方便,其作为磁源的磁性液体密封问题属于相对简单的静磁场问题,因此本文选择永磁体作为磁源。永磁体种类繁多,其中以稀土永磁钕铁硼材料最为典型,其在剩磁、矫顽力、最大磁能积等参数上均表现优异,所以本文选择牌号为N40的钕铁硼永磁体。N40钕铁硼永磁体的回复磁导率为1.05,剩磁为1.28 T,最大磁能积为342 kJ/m3,矫顽力为915 kA/m。密封轴和极靴的材料选择导磁性能好的电工硅钢材料,取其相对磁导率为4 000。
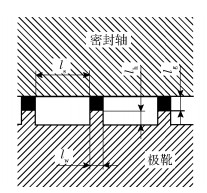
在极靴内周面上加工极齿,并控制变量展开研究。磁性液体密封设计极齿齿形结构参数主要包括密封间隙lg、极齿宽度lw、齿槽宽度ls、极齿高度lh以及极齿形状等。极齿形状以矩形极齿加工最为简单,也具有较好的耐压性能,因此选择矩形极齿。矩形极齿齿形结构参数示意图如图 3所示。
|
图 3 矩形极齿齿形结构参数示意图 Fig.3 Schematic diagram of the structural parameters of rectangular polar teeth |
根据数值计算和实验验证得到的矩形极齿齿形结构参数关系如下[24]。
| $\frac{l_{\mathrm{w}}}{l_{\mathrm{g}}}=2, \frac{l_{\mathrm{s}}}{l_{\mathrm{g}}}=8, \frac{l_{\mathrm{h}}}{l_{\mathrm{s}}}=0.875$ | (3) |
当密封间隙lg确定后,即可利用式(3)确定其他矩形极齿齿形的结构参数。lg通常在0.075~0.15 mm范围内,取密封间隙lg=0.1 mm,则可以确定矩形极齿其他各结构参数分别为lw=0.2 mm,ls=0.8 mm,lh=0.7 mm。
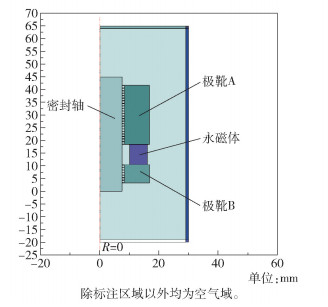
确定了极齿齿形结构参数后,设置总的密封级数为32级。建立非对称极齿型结构磁性液体密封几何模型如图 4所示,其由空气域、极靴、密封轴和永磁体等组成。为明确区分几何模型中极齿数量分布不同的两个极靴,在下文中将极靴上极齿数量多的称为极靴A,极齿数量少的称为极靴B。
|
图 4 非对称极齿型结构磁性液体密封几何模型 Fig.4 Geometric model of a magnetic fluid seal with an asymmetric polar teeth structure |
在规定了总的密封级数不变的前提下,通过逐个增加极靴A上的极齿数量,一共能够获得15个不同的非对称极齿型结构和1个对称极齿型结构,其详细信息如表 1所示。针对这16种极齿数量分布不同的结构分别进行物理建模,赋予各密封结构组成部分相应的材料属性,添加磁力线平行边界、磁通量守恒等边界条件,划分网格并进行数值求解。
| 下载CSV 表 1 不同密封结构上的极齿数量分布信息 Table 1 Number distribution information for polar teeth on different sealing structures |
为了探究密封间隙、密封轴径等因素对非对称极齿型结构密封耐压、磁场分布等的影响,判断非对称极齿型结构在不同密封间隙、轴径等工况要求下是否具有应用可行性,设计了如下模拟方案。
方案1 控制密封轴径为15 mm、密封间隙为0.1 mm,对表 1中各极靴A、B上极齿数量差不同的密封结构进行模拟分析。
方案2 控制密封轴径为15 mm不变,改变各密封结构的密封间隙大小(0.1、0.2、0.3、0.4 mm)进行模拟分析。
方案3 控制密封间隙为0.1 mm不变,改变各密封结构的密封轴径大小(15、30、100、150、300 mm) 进行模拟分析。
3 模拟结果讨论与分析 3.1 方案1保持密封间隙0.1 mm、密封轴径15 mm不变,对表 1中16种不同密封结构分别进行模拟计算。选取对称极齿型结构和其中一个非对称极齿型结构(该结构的极靴A上有24个极齿,极靴B上有8个极齿,本文仅以该结构为例进行分析说明,下文不再赘述)对比分析二者的磁场模拟结果。
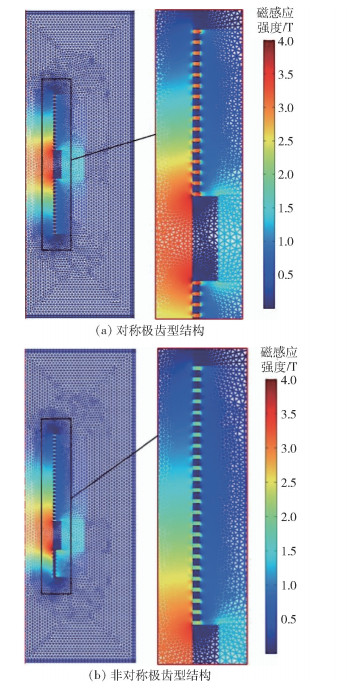
图 5为对称极齿型结构与非对称极齿型结构磁性液体密封的磁感应强度分布。为清晰展示密封间隙内部的磁感应强度分布,将两种结构黑框内部的区域放大两倍左右放于右侧。
|
图 5 对称极齿型结构与非对称极齿型结构的磁感应强度分布 Fig.5 Magnetic induction intensity distributions of the symmetric polar teeth and asymmetric polar teeth structures |
由图 5可以看出,对称极齿型结构和非对称极齿型结构密封间隙内各极齿附近的颜色要比周边的颜色更深,这说明密封间隙内主要的磁感应强度集中在极齿上。其中对称极齿型结构上所有极齿对应的颜色都是红色略带橙色,该颜色范围在颜色条带上约为1格大小,对应的磁感应强度大小范围约为2.5T~3.5 T,可以发现不同极齿间磁感应强度大小存在一定差距但是差距不大。反观图 5(b)非对称极齿型结构的磁感应强度分布情况,在极靴A上的极齿对应的颜色为蓝绿色,该颜色范围在颜色条带上对应的磁感应强度大小范围为2 T以下。而在极靴B上的极齿对应的颜色为深红色,该颜色在颜色条带上对应的磁感应强度大于3.5 T,显然要远远大于极靴A上极齿对应的磁感应强度值。因此对于非对称极齿型结构,最大磁感应强度与最小磁感应强度之差相比于对称极齿型结构的更大。
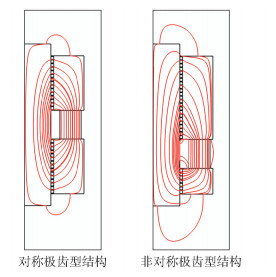
图 6为对称极齿型结构与非对称极齿型结构磁性液体密封的磁力线分布。对称极齿型结构的磁力线在磁源两侧对称分布,磁源附近区域比较密集,远离磁源区域较为稀疏;非对称极齿型结构的磁力线除了根据距离磁源的远近表现出稀疏和密集的区别以外,还表现出了在极靴B侧分布相对密集、而在极靴A侧分布相对稀疏的特点。
|
图 6 对称极齿型结构与非对称极齿型结构的磁力线分布 Fig.6 Distribution of the magnetic field lines of symmetric and asymmetric polar teeth structures |
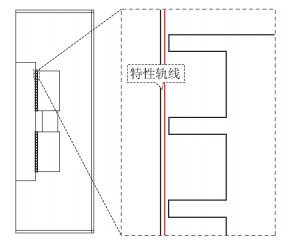
在密封间隙内定义一条特性轨线l1,该特性轨线与密封轴轴线平行,如图 7所示。以特性轨线l1在模型空间内的几何纵坐标为横轴、以对应的磁感应强度值大小为纵轴,绘制密封间隙磁场分布图如图 8所示。由图 8可知,对称极齿型结构和非对称极齿型结构在密封间隙内的磁场强度分布区别较大,但同一极靴下各极齿处磁场强度最大值接近,各齿槽内磁场强度最小值接近。对称极齿型结构的极齿处磁场强度最大值约为1 100 kA/m,齿槽内磁场强度最小值约为280 kA/m;非对称极齿型结构极齿处磁场强度最大值由于分布在永磁体两侧的极齿数量差而有所不同,极靴A侧极齿处磁场强度最大值在700~800 kA/m左右,极靴B侧极齿处磁场强度最大值约为2 000 kA/m,非对称极齿型结构极靴B侧极齿的磁场强度最大值要远远大于对称极齿型结构的磁场强度最大值,极靴A侧极齿磁场强度最大值则要略小于对称极齿型结构的磁场强度最大值;不同极靴下齿槽内的磁场强度最小值也有所不同,极靴A侧齿槽内的平均磁场强度最小值约为200 kA/m,而极靴B侧齿槽内的平均磁场强度最小值约为500 kA/m,可见对称极齿型结构齿槽内的磁场强度最小值大小介于非对称极齿型结构两极靴下齿槽内的平均磁场强度最小值之间。
|
图 7 密封间隙内定义特性轨线l1 Fig.7 Definition of the characteristic track l1 in seal clearance |
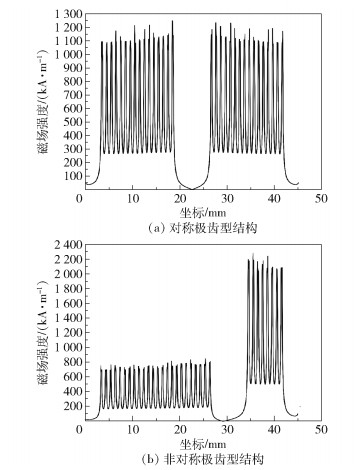
|
图 8 不同极齿型结构在轴向特性轨线l1上的磁场强度分布 Fig.8 Magnetic field intensity distributions of different polar teeth shapes on the axial characteristic track l1 |
在特性轨线l1上密封间隙部分每间隔0.1 mm设置数据点,提取各个极齿处对应的最大磁场强度值以及各个齿槽处对应的最小磁场强度值用于计算密封耐压。通过初筛发现在永磁体区域以外的密封间隙内,一般各数据点处磁场强度均大于200 kA/m,说明密封间隙内的磁场强度能使得该酯基磁性液体饱和磁化。为简化计算可以直接使用酯基磁性液体的饱和磁化强度Ms结合式(2)求解磁性液体密封总耐压大小。计算各模型总密封耐压大小,并绘制密封耐压能力随磁源两侧极齿数量差的变化曲线,如图 9所示。
|
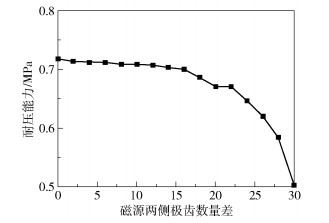
图 9 耐压能力随磁源两侧极齿数量差的变化曲线 Fig.9 Variation curve of pressure resistance with the difference in the number of polar teeth on both sides of the magnetic source |
由图 9可知,随着磁源两侧极齿数量差增大,非对称极齿型结构的密封耐压能力总体呈降低趋势。起初密封耐压能力随永磁体两侧极齿数量差的增大降幅较小,当磁源两侧极齿数量差超过总密封级数的约1/2以后,密封耐压能力降低的幅度逐渐增大。当磁源两侧极齿数量差达到最大值时,密封耐压取得最小值,经计算其大小为对称极齿型结构密封耐压的70.1%,即仍能保持一定的密封耐压能力。作者认为,磁性液体密封的磁回路由极靴极齿、密封轴、磁源以及磁性液体等构成,极齿数量分布及位置改变势必会影响到磁回路的磁阻和磁导。磁源两侧的极齿数量差过于悬殊,会严重影响到密封间隙内外的磁场分布以及磁回路的形状,由磁力线分布图(图 6)也能看出大量的磁力线集中在极靴B上的几个极齿处,因此造成了大量磁场分散在密封间隙以外。根据图 9,可以认为当磁源两侧的极齿数量差超过一定水平后会造成密封耐压能力急剧降低,但是该水平是否就是“总密封级数或者总极齿数的1/2”,还有待进一步更广泛的数值模拟以及实验研究来确定。
3.2 方案2保持密封轴径不变、仅改变密封间隙大小(0.1、0.2、0.3、0.4 mm),研究密封间隙变化对非对称极齿型结构密封耐压的影响。计算不同密封间隙下的密封耐压并与对称极齿型结构进行比较,结果如图 10所示。
|
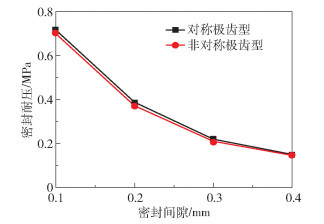
图 10 对称极齿型结构和非对称极齿型结构的耐压与密封间隙的关系曲线 Fig.10 Relationship between the pressure resistance and seal clearance for symmetrical and asymmetric polar teeth structures |
如图 10所示,在轴径均为15 mm的前提下,密封间隙的变化对于对称极齿型结构和非对称极齿型结构密封耐压的影响很大。随着密封间隙的增大,两种不同结构的密封耐压都急剧降低,且总体降幅一致。这说明密封间隙是非对称极齿型结构密封耐压能力的重要影响因素,在大间隙磁性液体密封应用场合中需要采取其他方法来增强其耐压能力。由图 8和图 10可知,两种结构在密封间隙相同时密封耐压能力相差较小但磁场分析结果差异显著,密封耐压能力接近即两种结构各自所有极齿处最大磁场强度之和与所有齿槽处最小磁场强度之和的差值接近,说明两种结构在其磁源、总极齿数、总齿槽个数等参数量相同的情况下,能够提供的密封耐压能力的总体有效磁场是接近的,而两种结构的磁场分析结果差异显著是由两种结构在各自极靴上不同的极齿分布导致的。改变磁源两侧的极齿数量分布,虽然不改变磁源提供的总磁场大小(在不考虑极靴等磁路组成部分对永磁体造成的退磁效应的前提下),却能够通过极齿的聚磁作用改变密封结构内局部的磁场分布,从而导致两种结构的磁场分析结果差异显著。
3.3 方案3保持密封间隙为0.1 mm不变、改变密封轴径大小,探究密封轴径变化对于非对称极齿型结构密封耐压的影响。计算不同轴径下的密封耐压并与对称极齿型结构比较,结果如图 11所示。需要明确的前提是随着密封轴径的变化,磁源的体积也在不断变化,但是其磁化强度保持不变。
|
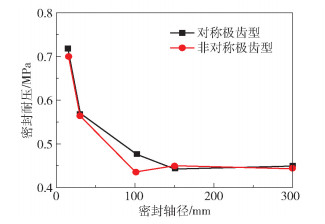
图 11 对称极齿型结构和非对称极齿型结构密封的轴径与耐压的关系曲线 Fig.11 Relationship between the axial diameter and sealing pressure resistance for symmetric and asymmetric polar teeth structures |
如图 11所示,对称极齿型结构和非对称极齿型结构在密封间隙保持不变、密封轴径改变的情况下密封耐压能力非常接近,甚至在轴径为30 mm时二者的密封耐压几乎相等。图 11表明在磁源的磁化强度始终不变(忽略极靴等磁路组成部分对永磁体造成的退磁效应)的前提下,存在一密封轴径临界值,当密封轴径小于该临界值时,磁性液体在极齿处形成的密封液环轴径随密封轴径增大而增大,密封耐压则随之减小;当密封轴径增大至超过该临界值时,密封间隙内的磁感应强度分布不再随密封轴径的增大而减小,密封耐压基本保持不变。通过计算可知,轴径分别为30、100、150、300 mm的密封结构的密封泄漏通道截面积分别为轴径15 mm的密封结构的2倍、3.33倍、5倍、10倍,而磁源和极靴连接处等漏磁区域随轴径增大而引起的面积变化倍数更大,若密封耐压降低完全是由密封泄漏通道截面积以及其他漏磁区域面积增大引起,显然与图 11中的分析结果乃至工程实践不符。作者认为导致出现该现象的原因可能是:当密封轴径增大时,密封结构发生磁场泄漏的面积(即漏磁接触面积)随之增大,因此导致在磁源和极靴相连接处、密封轴端处的漏磁场增大,密封间隙内的磁场强度减小;但由于极齿的聚磁作用,密封间隙内磁场强度的减小程度与漏磁接触面积的变化并不成比例;而当密封轴径增大到一临界值之上后,密封间隙内各极齿与齿槽下的磁场强度已经减小到一个相对较小的数值,此时即使密封轴径继续增大,极齿结构仍然发挥聚磁作用将该部分磁场留在密封间隙内而不是泄漏至密封间隙以外。
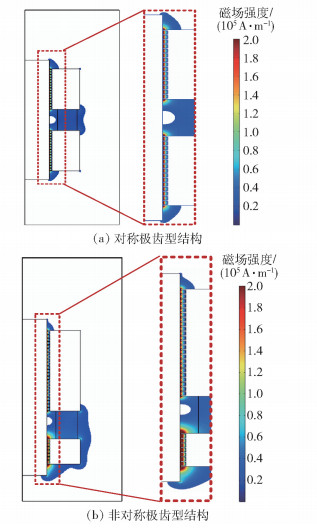
3.4 漏磁场分析除密封间隙内的磁场外,其他区域如轴端、永磁体和极靴连接处的磁场一般称为漏磁场。在仪器仪表、光电导航等密封场合需要尽量降低漏磁场的影响[14]。由前文可知,非对称极齿型结构密封间隙内的磁场分布迥异于对称极齿型结构,它们的轴端漏磁场同样存在较大区别。图 12为对称极齿型结构和非对称极齿型结构的漏磁场强度分布云图。酯基磁性液体的饱和磁化强度为20 kA/m,约为密封间隙内部磁场强度最大值的几十分之一,因分析需要在图 12中不显示小于20 kA/m的漏磁场分布区域。图 12红色虚线框内部分系放大前后的密封间隙内磁场强度分布。
|
图 12 对称极齿型结构和非对称极齿型结构的漏磁场强度分布 Fig.12 Magnetic leakage intensity distribution for symmetric and asymmetric polar teeth structures |
对非对称极齿型结构轴端漏磁场作进一步量化分析。以特性轨线l1在轴端位置对应的磁场强度数据导出得到对称极齿型结构和非对称极齿型结构不同极靴侧轴端的漏磁场对比,如图 13、14所示,其中横坐标的轴端距离是按照特性轨线l1上的点与极靴外侧面所在平面间的最小距离来计算的。
|
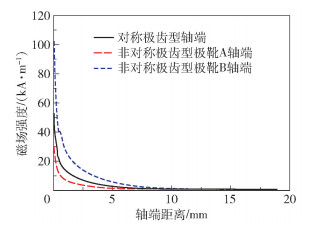
图 13 不同结构的轴端漏磁场对比 Fig.13 Comparison of axial end magnetic fields leakage for different structures |
|
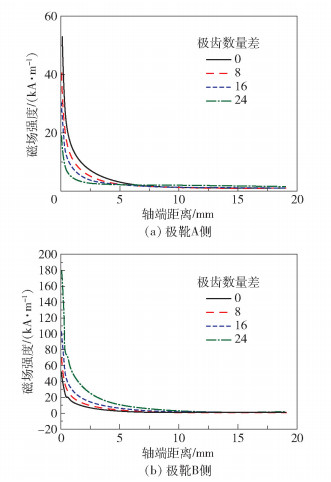
图 14 非对称极齿型结构磁源两侧极齿数量差对漏磁场分布的影响 Fig.14 Influence of the difference in the number of polar teeth on the two sides of the magnetic source on the distribution of magnetic field leakage |
如图 12所示,对称极齿型结构的轴端漏磁场是对称分布的,而非对称极齿型结构的轴端漏磁场则根据其更接近极靴A或极靴B而有所不同,极靴A侧轴端漏磁场区域面积要小于对称极齿型结构的轴端漏磁场区域面积,极靴B侧轴端漏磁场区域面积则要大于对称极齿型结构的轴端漏磁场区域面积。另外非对称极齿型结构的磁源与两侧极靴连接处的漏磁场分布区域面积也要大于对称极齿型结构的。
由图 13可见,不管是对称极齿型还是非对称极齿型结构,其轴端漏磁场都随轴端距离的增大而降低,且前期降低速度较大。当轴端距离足够大时(在图中约为10 mm左右),预期漏磁场将最终都会降低到0。非对称极齿型结构的轴端漏磁场具有一端较强、一端较弱的特征,轴端漏磁场较弱的一端是极靴A的轴端,其初始漏磁场强度约为30 kA/m,而轴端漏磁场较强的一端是极靴B的轴端,其初始漏磁场强度几乎相当于极靴A轴端的3倍以上,约为102 kA/m。而在轴端距离为0时,对称极齿型结构的轴端漏磁场强度约为52 kA/m,且在轴端距离达到一定数值(在图中约为10 mm)前始终处于极靴A和极靴B的初始轴端漏磁场强度值之间。此外,对称极齿型结构的初始轴端漏磁场强度之和为104 kA/m,显然小于非对称极齿型结构的132 kA/m,可见对称极齿型结构总体上具有较好的聚磁作用,能够将磁场充分聚集在密封间隙内起到密封作用。
如图 14所示,选取磁源两侧极齿数量差分别为0、8、16、24的4种密封结构,对比观察图中的曲线变化趋势,可以发现无论是极靴A还是极靴B以及无论磁源两侧的极齿数量差的大小,漏磁场随轴端距离增大而降低的总体趋势是一致的,但不同的极齿数量差可能会导致轴端漏磁场在一定范围内出现数值上甚至数量级上的差距。随着轴端距离不断增大,不同结构、不同极靴的轴端漏磁场最终都衰退到0。在漏磁场由于轴端距离过大而衰退至0之前,极靴B侧轴端的漏磁场大小要远远超过极靴A侧轴端漏磁场。
由图 14,极靴A侧的起始轴端漏磁场强度随磁源两侧极齿数量差的增大而减小,极靴B侧的起始轴端漏磁场强度随磁源两侧极齿数量差增大而增大,这说明磁源两侧极齿数量差的增大将会导致极靴A侧起始轴端漏磁场减小、极靴B侧起始轴端漏磁场增大。图 14中,极靴A侧最小起始轴端漏磁场约为20 kA/m,极靴B侧最大起始轴端漏磁场约为180 kA/m,此时磁源两侧极齿数量差取到最大值,密封结构不同轴端的漏磁场强度差也最大。
总之,增大磁源两侧极齿的数量差能够增强较强端漏磁场、减小较弱端漏磁场,起到“强者愈强,弱者愈弱”的效果,由此可以利用磁源两侧的极齿数量差对密封结构不同轴端的漏磁场进行调控。因此,利用上述非对称极齿型结构的漏磁特征规律,一方面可以使漏磁场较弱端适应某些需要磁屏蔽排除静磁场干扰的光电仪器仪表密封场合,另一方面可以利用漏磁场较强端来回收多余磁性液体或者为设计组合式密封提供便利。如何合理利用非对称极齿型以及其他不同结构形式的磁性液体密封结构漏磁规律以拓宽磁性液体密封的应用场景仍需要进一步的研究。
4 结论(1) 非对称极齿型结构密封耐压能力随磁源两侧极齿数量差的增大而逐渐降低。与对称极齿型结构相比,非对称极齿型结构密封耐压能力稍小,当磁源两侧极齿数量差取最大值时,其密封耐压约为对称极齿型结构的70.1%。
(2) 密封间隙和密封轴径是非对称极齿型结构密封耐压能力的重要影响因素。密封间隙或密封轴径的变化对非对称极齿型结构和对称极齿型结构二者的密封耐压造成的影响非常接近,因此在对称极齿型结构能够生效的应用场合,非对称极齿型结构也可以胜任。此外,发现当密封间隙不变时,在密封轴径上存在一临界值,当密封轴径小于该临界值时密封耐压随轴径增大而减小,当超过该临界值时,密封耐压保持不变。
(3) 磁性液体密封轴端漏磁场具有随轴端距离增大而降低的整体趋势,且降低速度随轴端距离增大而减小。非对称极齿型结构的漏磁场主要集中在极靴B(极齿数量少)侧轴端处,极靴A(极齿数量多)侧轴端漏磁场相比对称极齿型结构的轴端漏磁场要更小。非对称极齿型结构的轴端漏磁场具有一端较强、一端较弱的特征,可以利用磁源两侧的极齿数量差对密封结构不同轴端的漏磁场进行调控。非对称极齿型结构的漏磁特征为设计适用于不同应用场景尤其是要求低漏磁影响的应用场景的磁性液体密封结构提供了经验参考。
| [1] |
杨春成. 磁性液体的磁性及磁粘性质研究[D]. 济南: 山东大学, 2016. YANG C C. Research on the magnetic and magneto-viscous properties of ferrofluids[D]. Jinan: Shandong University, 2016. (in Chinese) |
| [2] |
张柱, 吴智政, 江新祥, 等. 磁液变形镜的镜面动力学建模和实验验证[J]. 物理学报, 2018, 67(3): 034702. ZHANG Z, WU Z Z, JIANG X X, et al. Modeling and experimental verification of surface dynamics of magnetic fluid deformable mirror[J]. Acta Physica Sinica, 2018, 67(3): 034702. (in Chinese) |
| [3] |
王宇鑫, 赵慎强, 杜春风, 等. 纳米磁性液体的制备方法[J]. 金属功能材料, 2010, 17(1): 62-65. WANG Y X, ZHAO S Q, DU C F, et al. Preparation methods of nanosized magnetic fluids[J]. Metallic Functional Materials, 2010, 17(1): 62-65. (in Chinese) |
| [4] |
RAJ K, BOULTON R J. Ferrofluids-properties and applications[J]. Materials and Design, 1987, 8(4): 233-236. DOI:10.1016/0261-3069(87)90139-7 |
| [5] |
蔡玉强. 蒸汽压缩蒸馏装置关键技术研究[D]. 北京: 北京交通大学, 2016. CAI Y Q. The research of key technology on vapor compression distillation assembly [D]. Beijing: Beijing Jiaotong University, 2016. (in Chinese) |
| [6] |
CHEN F, ZHANG C F, YANG X L. Numerical analysis and experimental verification of magnetic fluid sealing for air cylinder in aerospace engineering[J]. International Journal of Applied Electromagnetics and Mechanics, 2021, 66(4): 581-597. DOI:10.3233/JAE-201572 |
| [7] |
赵少迪, 鲍久圣, 徐浩, 等. 矿用带式输送机承载托辊的磁性液体润滑与密封性能[J]. 机械工程学报, 2021, 57(21): 211-219. ZHAO S D, BAO J S, XU H, et al. Magnetic fluid lubrication and sealing performance of mining belt conveyor roller[J]. Journal of Mechanical Engineering, 2021, 57(21): 211-219. (in Chinese) |
| [8] |
ZHANG Z L, DI N N, CHENG H H, et al. The research on magnetic fluid shaft sealing for chemical reactor[M]// TAN J, GAO F, XIANG C. Advances in mechanical design. ICMD 2017. Mechanisms and Machine Science, vol 55. Singapore: Springer, 2017.
|
| [9] |
金亚男, 王琨, 王晓茸. 浅谈预灰桶搅拌器轴封的选择[J]. 纯碱工业, 2021(6): 9-12. JIN Y N, WANG K, WANG X R. Selection of shaft seal for agitator of prelimer[J]. Soda Industry, 2021(6): 9-12. (in Chinese) DOI:10.3969/j.issn.1005-8370.2021.06.002 |
| [10] |
邢斐斐, 季君, 郝瑞参, 等. 高速离心泵磁性液体新型旋转密封结构的设计及实验研究[J]. 润滑与密封, 2021, 46(10): 100-104. XING F F, JI J, HAO R C, et al. Theoretical and experimental research on new type ferrofluid rotary sealing for high speed centrifugal pump[J]. Lubrication Engineering, 2021, 46(10): 100-104. (in Chinese) DOI:10.3969/j.issn.0254-0150.2021.10.015 |
| [11] |
柴波, 张文军, 李德忠. 纳米磁流体及其在水资源保护中的应用前景[J]. 环境科学与技术, 2004(S1): 159-161. CHAI B, ZHANG W J, LI D Z. Nano-magnetic fluid and its application in water resource conservation[J]. Environmental Science and Technology, 2004(S1): 159-161. (in Chinese) |
| [12] |
伍绍文. 磁性液体密封在机械和化工行业的应用[J]. 化工装备技术, 2002, 23(6): 48-51. WU S W. Application of magnetic fluid sealing in machine and chemical field[J]. Chemical Equipment Technology, 2002, 23(6): 48-51. (in Chinese) |
| [13] |
陈燕, 李德才. 坦克周视镜磁性液体密封的设计与实验研究[J]. 兵工学报, 2011, 32(11): 1428-1432. CHEN Y, LI D C. Design and experiments for magnetic fluid seal of tank panoramic mirror[J]. Acta Armamentarii, 2011, 32(11): 1428-1432. (in Chinese) |
| [14] |
张恒. 磁性液体旋转密封耐压与启动力矩研究[D]. 北京: 北京交通大学, 2019. ZHANG H. Study on pressure resistance and starting torque of magnetic fluid rotary seal[D]. Beijing: Beijing Jiaotong University, 2019. (in Chinese) |
| [15] |
易敬曾. 磁场计算与磁路设计[M]. 成都: 成都电讯工程学院出版社, 1987.
|
| [16] |
李保锋, 刘颖, 余智勇. 磁性流体密封的新思路——变磁极齿宽结构[J]. 润滑与密封, 2004(6): 104, 112. LI B F, LIU Y, YU Z Y. A new thinking for magnetic fluid seals-the structure with unfixed pole width[J]. Lubrication Engineering, 2004(6): 104, 112. (in Chinese) |
| [17] |
何新智, 李德才, 兰惠清, 等. 两种磁性液体密封结构耐压能力的比较[J]. 真空科学与技术学报, 2005, 25(3): 238-240. HE X Z, LI D C, LAN H Q, et al. Comparison of anti-pressure capacity for two different structures of magnetic fluid seals[J]. Journal of Vacuum Science and Technology (China), 2005, 25(3): 238-240. (in Chinese) |
| [18] |
杨文明, 李德才, 何新智, 等. 磁性液体密封结构中漏磁的研究[J]. 北京交通大学学报, 2011, 35(1): 123-127. YANG W M, LI D C, HE X Z, et al. Research on magnetic leakage in the structure of magnetic fluid sealing[J]. Journal of Beijing Jiaotong University, 2011, 35(1): 123-127. (in Chinese) |
| [19] |
陈帆. 工程机械液压缸磁流体密封的数值分析与试验验证[D]. 柳州: 广西科技大学, 2019. CHEN F. Numerical analysis and experimental verification of magnetic fluid seal of engineering machinery hydraulic cylinder[D]. Liuzhou: Guangxi University of Science and Technology, 2019. (in Chinese) |
| [20] |
朱景建. 爪型干式真空泵磁流体密封的研究[J]. 真空科学与技术学报, 2017, 37(7): 660-664. ZHU J J. Sealing of claw-type dry vacuum pump with magnetic fluid[J]. Chinese Journal of Vacuum Science and Technology, 2017, 37(7): 660-664. (in Chinese) |
| [21] |
于文娟, 李德才, 李艳文, 等. 真空镀膜机用小型磁性液体密封设计[J]. 北京交通大学学报, 2021, 45(5): 124-129. YU W J, LI D C, LI Y W, et al. Design of magnetic fluid seal of small vacuum coating machine[J]. Journal of Beijing Jiaotong University, 2021, 45(5): 124-129. (in Chinese) |
| [22] |
刘嘉伟, 李德才. 基于无齿极靴结构的磁性液体密封耐压仿真分析[J]. 磁性材料及器件, 2022, 53(5): 45-51. LIU J W, LI D C. Simulation analysis of pressure resistance of magnetic liquid seal based on toothless pole shoe structure[J]. Journal of Magnetic Materials and Devices, 2022, 53(5): 45-51. (in Chinese) |
| [23] |
杨永明, 陈世强, 李强. 一种磁性液体加速度传感器模型的参数辨识方法[J]. 传感技术学报, 2019, 32(2): 251-257. YANG Y M, CHEN S Q, LI Q. Parameter identification method for ferrofluid acceleration sensor model[J]. Chinese Journal of Sensors and Actuators, 2019, 32(2): 251-257. (in Chinese) |
| [24] |
YANG X L, ZHANG Z L, LI D C. Numerical and experimental study of magnetic fluid seal with large sealing gap and multiple magnetic sources[J]. Science China Technological Sciences, 2013, 56(11): 2865-2869. |








