我国是粮油生产大国,据统计,2020年我国豆油产量约1 960万吨[1]。大豆皂脚是在大豆油碱炼脱酸工序中形成的副产物,其占油脂总产量的6%(质量分数)左右,总量非常可观。皂脚中含有脂肪酸钠盐、三甘油脂和少量的二甘油酯,同时还含有大量的水分,如果处理不当,则会造成严重的环境污染和资源浪费。
传统的大豆皂脚处理方式包括填埋、焚烧以及饲料化处理[2]等,处理过程中会产生渗透液污染土壤和地下水、油脂中的有害物质对家禽的内脏造成伤害等问题。近年来,热解技术以减容率高、产品多元、能源利用率高、二次污染物少等特点受到广泛关注,并开始应用于皂脚的处理中。现阶段,大部分学者的研究重点是通过皂脚的热解产物产率和性质,实现热解过程的定向调控和产物应用[3-4]。
热解动力学是一种全面分析热解过程的研究方法,对预测、优化和控制热解过程具有重要意义。通过热解动力学的研究,可以确定热解反应机制及热解难易程度、推测热解过程和产物,同时为工业转化的可行性、生产的规模化以及反应器的设计等提供理论参考和数据支撑。在单物质热解、催化热解和共热解等方面,都有学者进行过热解动力学的研究。Leung等[5]对废轮胎的热解特性进行探究,提出的Three-Component-Simulation模型和Three-Elastomer-Simulation模型可以较好地模拟轮胎粉的热解过程,为轮胎热解过程的机理研究提供了依据。林小羽[6]对油脂催化热解的动力学进行研究,结果表明,使用同类型催化剂的反应过程大致相似,使用γ型氧化铝催化剂后,比表面积的增大能够使热解反应的活化能降低。Wang等[7]对污泥和稻壳共热解反应动力学进行分析,发现与单独热解相比,共热解活化能较低,反应在较易条件下就能够进行。
然而目前针对大豆皂脚热解动力学的相关研究较少,因此本文采用Flynn-Wall-Ozawa法和Kissinger-Akahira-Sunose法两种等转化率法对大豆皂脚热解动力学进行分析,得到表观活化能、指前因子和机理函数,探索了大豆皂脚的热解反应特征,在热解设备工艺参数及内部反应条件设计等方面为大豆皂脚的资源化利用提供参考。
1 实验部分 1.1 实验原料实验所用大豆皂脚来自山东某大豆油精炼企业,将其在80 ℃烘箱中烘干12 h,烘干后的原料经过研磨和筛分,选取粒径在105~150 μm的颗粒进行热重实验。原料(烘干基)的基本特性见表 1。
| 下载CSV 表 1 大豆皂脚的基本特性 Table 1 Key properties of soybean soapstock |
采用日本日立公司STA 3700型热重分析仪进行热重实验。称取50 mg待测样品放入坩埚中,以N2作为保护气,设置通气量为200 mL/min,终温为850 ℃,在3个不同升温速率(10、20、40 ℃/min)下进行测试。
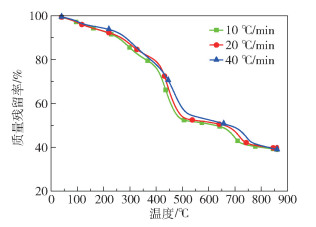
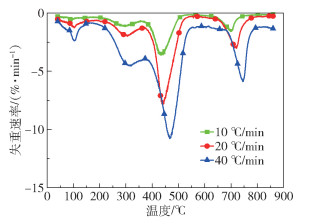
2 结果与分析 2.1 大豆皂脚的热解过程图 1和图 2分别为大豆皂脚在不同升温速率(10、20 ℃/min和40 ℃/min)下热解的热重分析(TG)和微商热重分析(DTG)曲线。可以看出,不同升温速率下得到的TG和DTG曲线形状相似。热解可分为4个阶段:第一个阶段从常温到155 ℃,此阶段主要去除的是结合水和部分轻组分[8-9],因为在热重测试前已将大豆皂脚原料在80 ℃烘箱中烘干了12 h,所以此阶段失重率较低,且数值比较接近,在4.7%~5.1%之间;第二阶段为155~380 ℃,主要是大豆皂脚的深度干燥和有机物的初始热解,此阶段的失重率较第一阶段有所增大,失重率数值在16%左右;第三阶段为380~565 ℃,此阶段是失重率最大的阶段,在这个阶段有机物裂解,分解成各种低分子量的气体和液体产物,失重率可达27.9%以上,是热解的主要阶段;最后一个阶段为565~850 ℃(测试结束温度),可以看出,在650~780 ℃大豆皂脚存在一个明显的失重峰,这主要是因为挥发相中的自由基在热解时会攻击炭的表面,使其发生部分氧化造成炭失重;此外,有些固相无机物的分解(如铵盐和霰石)也会加速失重;800 ℃之后,失重率基本保持不变,表明有机物降解与无机物分解趋于完成。10、20 ℃/min和40 ℃/min这3个加热速率下得到的最终固体残余量(质量分数)分别为38.74%、38.98%和39.39%,三者相差较小,这是因为较低的加热速率延长了反应时间,促进了气固反应,从而降低了热解炭产率。此外,从TG图中还可以看出,当达到同一失重率时,较高的升温速率条件下所需要的温度更高,这是由热解过程中存在的热滞后现象引起的[10]。
|
图 1 不同升温速率下大豆皂脚的TG曲线 Fig.1 TG curves of soybean soapstock at different heating rates |
|
图 2 不同升温速率下大豆皂脚的DTG曲线 Fig.2 DTG curves of soybean soapstock at different heating rates |
鉴于等转化率法可以避免反应机理函数带来的误差,本文采用Flynn-Wall-Ozawa法(以下简称FWO法)和Kissinger-Akahira-Sunose法(以下简称KAS法)两种等转化率法来计算表观活化能[11-12]。
FWO法计算式为
| $ \ln \beta=\ln \frac{A E_\alpha}{R G(\alpha)}-5.331-1.052 \frac{E_\alpha}{R T} $ | (1) |
KAS法计算式为
| $ \ln \frac{\beta}{T_\alpha^2}=\ln \frac{A E_\alpha}{R G(\alpha)}-\frac{E_\alpha}{R T_\alpha} $ | (2) |
其中,α通过式(3)计算。
| $ \alpha=\left(m_0-m_T\right) /\left(m_0-m_{\infty}\right) $ | (3) |
式中,α为热解转化率;Eα代表转化率为α时对应的表观活化能,kJ/mol;m0为样品的起始质量,g; mT代表温度为T时的样品质量,g; m∞为反应结束后样品的剩余质量,g;R为理想气体常数,通常取值为8.314 J/(mol·K);A为反应指前因子;β为升温速率,℃/min;Tα代表转化率为α时对应的温度,K;G(α)为机理函数f(α)的积分形式。
采用FWO法计算活化能时,截取不同升温速率下、相同转化率时T的值,以lnβ对1/T作图,根据斜率得出活化能E。采用KAS方法计算活化能时,同样截取不同升温速率下等转化率时T的值,以ln(β/T2)对1/T作图,最终根据斜率得出活化能E。
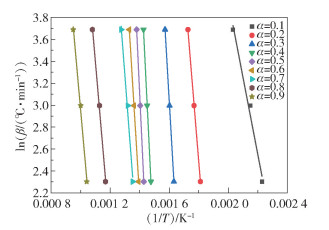
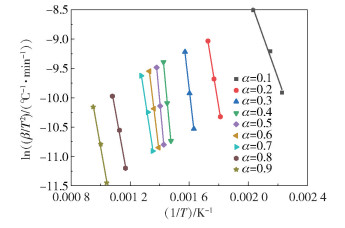
图 3和图 4分别显示的是大豆皂脚转化率为0.1~0.9下,FWO法和KAS法的线性拟合曲线,表 2为线性拟合结果和活化能数值。从表 2可以看出,采用FWO法拟合的大豆皂脚的表观活化能在55.38~226.97 kJ/mol,采用KAS法拟合的大豆皂脚的表观活化能在58.93~226.92 kJ/mol。从拟合结果来看,两种方法整体的拟合性较好,拟合度R2均在0.97以上。
|
图 3 大豆皂脚FWO法拟合曲线图 Fig.3 FWO curves of soybean soapstock |
|
图 4 大豆皂脚KAS法拟合曲线图 Fig.4 KAS curves of soybean soapstock |
| 下载CSV 表 2 大豆皂脚的FWO法和KAS法线性拟合结果 Table 2 Curve fitting for soybean soapstock using FWO and KAS methods |
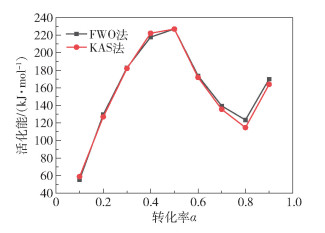
将两种方法下得到的表观活化能进行比较,如图 5所示,可以看出,两种方法下的活化能随转化率的变化趋势一致。在转化率小于0.5时,活化能呈现不断升高的趋势,当转化率高于0.5后,活化能随转化率的升高呈先降低后升高的趋势。当转化率较低时,热解过程中主要是一些轻组分的挥发,需要的活化能较低;随着大组分有机物裂解反应的进行,活化能逐渐增大;当转化率大于0.5后,活化能逐渐降低,这是因为此时有大量有机物挥发出来,逐渐形成多孔结构的固相反应物,使反应更加容易进行,从而使得活化能降低[13];在热解反应后期,发生有机物二次裂解和无机物分解反应,所需的活化能再次增加。
|
图 5 FWO法和KAS法下的活化能比较 Fig.5 Comparison of activation energies for FWO and KAS methods |
动力学机理函数表示的是物质反应速率与转化率之间的某种函数关系,这种关系通过热分析曲线体现。通常情况下,在反应物为复杂有机物时,认为它的热解过程是复杂、多步的,需要用分峰方法确定机理模型;当反应物组分相对简单,且转化率在一定范围内变化量不是特别大时,可假设某个已知的热解机理模型是影响整个热解过程的主要因素,该模型就是整个热解过程的主导机理模型。在本文实验中,大豆皂脚的成分以脂肪酸为主,在转化率为0.2~0.9期间,活化能的变化程度相对较小,因此用已知模型作为大豆皂脚热解主导反应模型的方法具有一定的可行性。
用于机理函数选择的方法有很多[14],其中Malek法是将实验数据曲线与标准理论曲线进行拟合度对比,从而确定热解反应机理的一种方法。这种方法减少了对机理模型逐一验证的时间,效率较高。在本文中,通过Malek法确定机理函数的计算和推导过程如下。
根据质量转化定律,样品的动力学方程可用式(4)表示。
| $ \frac{\mathrm{d} \alpha}{\mathrm{d} t}=k(T) f(\alpha) $ | (4) |
由阿伦尼乌斯定律,可将式(4)转化成方程式(5)。
| $ \frac{\mathrm{d} \alpha}{\mathrm{d} T}=A \mathrm{e}^{-\frac{E}{R T}} f(\alpha) $ | (5) |
f(α)的积分形式用G(α)表示,两者之间的关系如式(6)所示。
| $ G(\alpha)=\int_0^\alpha \frac{\mathrm{d} \alpha}{f(\alpha)} $ | (6) |
将式(4)~(6)进行合并,得到方程式(7)。
| $ \int_0^\alpha \frac{\mathrm{d} \alpha}{f(\alpha)}=G(\alpha)=\frac{A R T^2}{E \beta} \exp \left(-\frac{E}{R T}\right) $ | (7) |
由式(7)可推导得到
| $ G(\alpha)=\frac{\mathrm{d} \alpha}{\mathrm{d} t} \frac{R T^2}{E \beta} \frac{1}{f(\alpha)} $ | (8) |
在式(8)基础上,定义一个新的函数y(α),并将α=0.5代入y(α)中,如式(9)所示。
| $ y(\alpha)=\left(\frac{T}{T_{0.5}}\right)^2 \frac{\frac{\mathrm{d} \alpha}{\mathrm{d} t}}{\left(\frac{\mathrm{d} \alpha}{\mathrm{d} t}\right)_{0.5}}=\frac{f(\alpha) G(\alpha)}{f(0.5) G(0.5)} $ | (9) |
Coats-Redfern方程(C-R方程)经整理后可得方程式(10)。
| $ \ln \left[\frac{G(\alpha)}{T^2}\right]=-\frac{E}{R T}+\ln \left[\frac{A R}{\beta E\left(1-\frac{2 R T}{E}\right)}\right] $ | (10) |
对于一般温度范围的反应区间和大部分E值而言,
| $ \ln \left[\frac{G(\alpha)}{T^2}\right]=\ln \left(\frac{A R}{\beta E}\right)-\frac{E}{R T} $ | (11) |
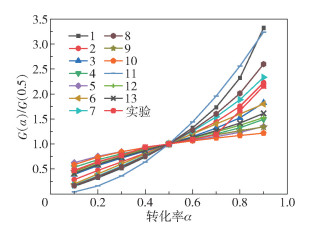
将实验数据代入式(11)中,计算出转化率0.2~0.9间的G(α)/G(0.5)数值,得到G(α)/G(0.5)与α的曲线。经过初步筛选,从25个机理模型中选取了匹配度较高的13个机理模型[15],相应的函数名称及表达式见表 3。通过函数表达式计算出不同机理模型在转化率为0.2~0.9下G(α)/G(0.5)的值,得到G(α)/G(0.5)与α的曲线。利用origin软件将实验曲线和机理模型曲线通过最小二乘法进行拟合,实验曲线和机理模型曲线模拟的相关系数见表 3,对比图如图 6所示。
| 下载CSV 表 3 机理模型函数与线性相关系数 Table 3 Functions and linear correlation coefficients for different mechanism models |
|
图 6 实验曲线与机理模型曲线的对比 Fig.6 Comparison of experimental and Malek model curves |
通过表 3可以看出,大豆皂脚热解机理模型与Jander方程三维扩散模型(n=1/2)的相关系数最大,达到0.996 7。Jander 3D(n=1/2)方程三维扩散模型的积分形式和微分形式的表达式如式(12)、(13)所示。
| $ f(\alpha)=6(1-\alpha)^{\frac{2}{3}}\left[\left(1-(1-\alpha)^{\frac{1}{3}}\right]^{\frac{1}{2}}\right. $ | (12) |
| $ G(\alpha)=\left[1-(1-\alpha)^{\frac{1}{3}}\right]^{\frac{1}{2}} $ | (13) |
在确定机理模型之后,对不同升温速率下的ln[G(α)/T2]和1/T作拟合曲线,通过截距计算出不同升温速率下的指前因子A,具体数据见表 4。可以看出随着升温速率的增大,指前因子不断变大,从升温速率10 ℃/min时的1 953.44升高到40 ℃/min时的7 438.61,说明升温速率越高,大豆皂脚热解越困难。这是因为高升温速率下,热解时间变短,原料内外受热不均匀,生成的油和炭易堵塞扩散通道,传质传热受阻,内外压差较大。
| 下载CSV 表 4 不同升温速率下大豆皂脚热解反应的指前因子 Table 4 The kinetic parameters of soybean soapstock pyrolysis at different heating rates |
动力学补偿效应主要体现活化能E和lnA对转化率的依赖性。以线性方程的模式(式(14))对两者之间的关系进行探讨,此方程可用于在已知其中一个值时,近似推导出另一个参数值的情况,减少了求解特定目标参数的工作量。此外,通过计算a、b两个补偿参数,还可以更好地分析热解影响规律和探索适宜的实验条件,从侧面验证热解动力学计算方法和过程的合理性。动力学补偿效应的方程式如式(14)所示。
| $ \ln A=a E+b $ | (14) |
式中,a和b为补偿参数。
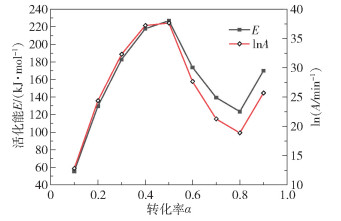
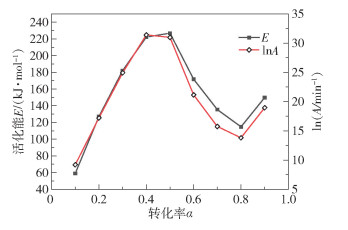
图 7、8分别为FWO法和KAS法两种等转化率法下的E-lnA曲线图,表 5为两种方法下的动力学补偿效应方程和相关系数。从图中可以看出,两种方法下得到的E和lnA随转化率增大都呈现出先升高后降低,之后再升高的趋势。在转化率低于0.5时,E和lnA曲线的重合度比较高,在转化率高于0.5后,两者的数值稍有差别。在FWO方法下,补偿方程的参数a和b分别为0.152和2.38,在KAS方法下,a和b分别为0.139和-1.106。从表 5也可以看出,拟合后E和lnA的相关系数均达到0.94以上,拟合性较好, 说明FWO、KAS两种等转化率法在计算大豆皂脚活化能等动力学参数方面均具有一定的合理性和有效性。此外,相比于FWO方法,KAS方法的线性相关程度更高,计算效果更好。
|
图 7 FWO法下大豆皂脚的E-lnA曲线 Fig.7 E-lnA curve for soybean soapstock using the FWO method |
|
图 8 KAS法下大豆皂脚的E-lnA曲线 Fig.8 E-lnA curve for soybean soapstock using the KAS method |
| 下载CSV 表 5 大豆皂脚的动力学补偿效应方程 Table 5 Kinetic compensation effect equations for soybean soapstock |
(1) 大豆皂脚热解共分为4个阶段,其中第三阶段是热解的最主要阶段,此阶段温度区间为380~565 ℃,失重率达到27.9%以上。
(2) 采用FWO法计算的表观活化能在55.38~226.97 kJ/mol之间,采用KAS法计算的表观活化能在58.93~226.92 kJ/mol之间。转化率为0.5时的活化能最大。
(3) 用Malek法确定大豆皂脚的热解机理模型为Jander 3D (n=1/2)方程三维扩散模型。
(4) FWO方法下,E和lnA补偿方程的a和b分别是0.152和2.38;KAS方法下E和lnA补偿方程的a和b分别是0.139和-1.106,两种方法拟合的相关系数均达到0.94以上,说明FWO方法和KAS方法在计算大豆皂脚活化能等动力学参数方面具有一定的合理性和有效性。
| [1] |
王瑞元. 2020年我国粮油产销情况[J]. 中国油脂, 2021, 46(8): 1-5. WANG R Y. Introduction of grain and oil production and marketing in 2020 in China[J]. China Oils and Fats, 2021, 46(8): 1-5. (in Chinese) |
| [2] |
黄玲巍, 单荣, 潘福强, 等. 废弃油脂的处理技术及现状[J]. 农产品加工, 2019(10): 75-76. HUANG L W, SHAN R, PAN F Q, et al. Disposal technology and status quo of waste oil[J]. Farm Products Processing, 2019(10): 75-76. (in Chinese) |
| [3] |
WANG Y P, KE L Y, PENG Y J, et al. Characteristics of the catalytic fast pyrolysis of vegetable oil soapstock for hydrocarbon-rich fuel[J]. Energy Conversion and Management, 2020, 213: 112860. DOI:10.1016/j.enconman.2020.112860 |
| [4] |
DAI L L, FAN L L, DUAN D L, et al. Microwave-assisted catalytic fast co-pyrolysis of soapstock and waste tire for bio-oil production[J]. Journal of Analytical and Applied Pyrolysis, 2017, 125: 304-309. DOI:10.1016/j.jaap.2017.03.012 |
| [5] |
LEUNG D Y C, WANG C L. Kinetic modeling of scrap tire pyrolysis[J]. Energy & Fuels, 1999, 13: 421-427. |
| [6] |
林小羽. 油脂催化裂解与非均相催化酯化制备生物燃油基础研究[D]. 北京: 中国林业科学研究院, 2012. LIN X Y. Catalytic pyrolysis and heterogeneous catalytic esterification of triglyceride for bio-fuel[D]. Beijing: Chinese Academy of Forestry, 2012. (in Chinese) |
| [7] |
WANG C X, BI H B, LIN Q Z, et al. Co-pyrolysis of sewage sludge and rice husk by TG-FTIR-MS: pyrolysis behavior, kinetics, and condensable/non-condensable gases characteristics[J]. Renewable Energy, 2020, 160: 1048-1066. DOI:10.1016/j.renene.2020.07.046 |
| [8] |
AL-LAYLA N M T, SALEH L A, FADHIL A B. Liquid bio-fuels and carbon adsorbents production via pyrolysis of non-edible feedstock[J]. Journal of Analytical and Applied Pyrolysis, 2021, 156: 105088. DOI:10.1016/j.jaap.2021.105088 |
| [9] |
MANA M, OUALI M S, DE MENORVAL L C. Removal of basic dyes from aqueous solutions with a treated spent bleaching earth[J]. Journal of Colloid and Interface Science, 2007, 307(1): 9-16. DOI:10.1016/j.jcis.2006.11.019 |
| [10] |
CHEN J B, MU L, JIANG B, et al. TG/DSC-FTIR and Py-GC investigation on pyrolysis characteristics of petrochemical wastewater sludge[J]. Bioresource Technology, 2015, 192: 1-10. DOI:10.1016/j.biortech.2015.05.031 |
| [11] |
KHAWAM A, FLANAGAN D R. Role of isoconversional methods in varying activation energies of solid-state kinetics Ⅱ. Nonisothermal kinetic studies[J]. Thermochimica Acta, 2005, 436(1-2): 101-112. DOI:10.1016/j.tca.2005.05.015 |
| [12] |
付一轩. 毛竹碳化产物热解动力学及其在超级电容器方面的研究[D]. 合肥: 合肥工业大学, 2019. FU Y X. Pyrolysis kinetics of carbonation products of bamboo and its research on supercapacitors[D]. Hefei: Hefei University of Technology, 2019. (in Chinese) |
| [13] |
LIU Y, SONG Y M, FU J, et al. Co-pyrolysis of sewage sludge and lignocellulosic biomass: synergistic effects on products characteristics and kinetics[J]. Energy Conversion and Management, 2022, 268: 116061. DOI:10.1016/j.enconman.2022.116061 |
| [14] |
PINZI S, BURATTI C, BARTOCCI P, et al. A simplified method for kinetic modeling of coffee silver skin pyrolysis by coupling pseudo-components peaks deconvolution analysis and model free-isoconversional methods[J]. Fuel, 2020, 278: 118260. DOI:10.1016/j.fuel.2020.118260 |
| [15] |
MISHRA R K, MOHANTY K. Kinetic analysis and pyrolysis behaviour of waste biomass towards its bioenergy potential[J]. Bioresource Technology, 2020, 311: 123480. DOI:10.1016/j.biortech.2020.123480 |








