2. 成都德美机电设备有限公司, 成都 610200
2. Chengdu Demi Electromechanical Equipment Co., Ltd., Chengdu 610200, China
天然气在输送过程中,气体中常夹带粉尘、颗粒、腐蚀产物、轻烃、游离水等物质,这些杂质会对燃气轮机、压缩机组、管道仪表等设备的运行产生影响,因此有必要采用过滤和分离设备对天然气中的固液杂质进行处理[1-2]。目前,输气站场上多采用切向入口式多管旋风分离器,其压降和分离效率是评价旋风分离器性能的主要参数,也是确定后续压缩机组设计的重要依据[3]。旋风分离器的压降模型主要分为半经验模型、统计模型和计算流体力学(CFD)模型3类[4-5]。半经验模型以Shepherd-Lapple模型[6]、Alexander模型[7]、Barth模型[8]等为主,这些模型均在旋风分离器内部流场和能量耗散的基础上建立平衡方程,为了计算方便,使用了不同程度的假设和简化处理,部分数据在计算精度上与实验值差距较大;统计模型是通过大量的实验数据对压降进行多元回归,以Casal模型[9]、Dirgo模型[10]等为主,但该方法很难找到合适的拟合函数来回归实验数据,在预测过程中易出现过拟合或欠拟合;CFD模型使用Fluent建模对旋风分离器内部的压降进行预测[11-13],计算结果可靠度较高,但步骤复杂、不易掌握。
随着人工智能的发展,部分学者开始利用机器学习的方式预测压降。Zhao[14]通过训练不同的神经网络模型来预测旋风分离器压降与几何参数之间的非线性关系,但未针对模型参数进行选取;Elsayed等[15]采用最小二乘支持向量机对旋风分离器压降进行预测,但该模型在测试集上的泛化性能较差;王兆熙等[16]采用粒子群算法(particle swarm optimization,PSO)优化极限学习机(extreme learning machine,ELM)对压降进行了预测,但ELM本质上属于浅层神经网络,在解决弱条件约束的问题上性能难以进一步增强。深度学习算法中的深度置信网络(deep belief network,DBN)是机器学习的前沿技术,具有强大的特征自提取能力,在处理高维、非线性数据上具有较强的优势,且预测精度和泛化能力也优于传统浅层机器学习,在管道风险评价[17]、滴流床持液量预测[18]、原油闪点预测[19]等方面均有应用。但在预训练阶段,DBN模型各节点连接权重和偏置通过随机初始化产生,会使模型在训练过程中陷入局部最优解,并增加训练时间,因此需预先优化各节点的初始化参数。狼群算法(grey wolf optimizer,GWO)由Mirjalili等[20]在2014年提出,属于一种较新的仿生学算法,具有收敛性能强、可调参数少、容易实现等优点[21]。文献[20]在29个已知的测试函数上对算法进行了基准测试,并与PSO算法、万有引力算法(gravitation search algorithm,GSA)、差分进化算法(differential evolution,DE)、进化规划算法(evolutionary programming,EP)等进行对比,验证了GWO算法在搜索最优解上的优势。但GWO算法仍存在种群多样性差、后期收敛慢的缺陷,这与其初始化种群方式和搜索机制有关。基于此,本文采用DBN模型对旋风分离器压降数据进行预测,利用改进的狼群算法(improved grey wolf optimizer,IGWO)选取DBN模型的最优初始化权重和偏置参数,形成IGWO-DBN组合模型,并与其余常见模型的预测结果进行对比,为旋风分离器结构设计和优化提供实际参考。
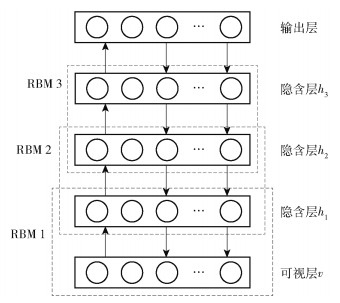
1 IGWO-DBN模型 1.1 DBN模型DBN模型包括生成模型和判别模型[22]:前者由多个受限的玻尔兹曼单元(restricted Boltzmann machine,RBM)组成,一个RBM由1个可视层和隐含层组成,层与层之间采用全连接,每个神经元节点满足随机二值分布,即只有0和1两种状态,由多个RBM通过无监督学习完成逐层预训练过程;后者由有监督学习功能的反向传播神经网络(back propagation neural network,BPNN)完成误差反向微调,实现数据的回归或分类。3个RBM结构的DBN模型如图 1所示。
|
图 1 DBN模型网络结构 Fig.1 Network structure of the DBN model |
RBM是基于能量生成的随机概率模型,可通过图模型描述变量间的相互作用关系[23]。设可视层各神经元节点状态为v={v1,v2,…, vn},隐含层各神经元节点状态为h={h1,h2,…, hm},则RBM的能量函数为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;E(v, h \mid \theta)=-\sum\limits_{i=1}^n a_i v_i-\sum\limits_{j=1}^m b_j h_j- \\ \sum\limits_{i=1}^n \sum\limits_{j=1}^m h_j w_{i j} v_i \end{array} $ | (1) |
式中,θ={wij, ai, bj},wij为可视层与隐含层之间的连接权重,ai、bj分别为可视层和隐含层的节点偏置。对能量函数进行正则化处理,则可视层和隐含层的联合概率分布为
| $ P(v, h \mid \theta)=\frac{1}{Z(\theta)} \mathrm{e}^{-E(v, h \mid \theta)} $ | (2) |
| $ Z(\theta)=\sum\limits_{v, h} \mathrm{e}^{-E(v, h \mid \theta)} $ | (3) |
由于RBM模型层内无连接,当可视层状态确定时,隐含层各节点的激活概率条件独立;反之亦然。
训练RBM是利用对比散度(CD)的方式迭代求解参数θ={wij, ai, bj},从底层RBM开始,自下而上逐层训练,前一个RBM的输出作为后一个RBM的输入。预训练完成后,各层RBM得到最优的初始化参数,随后采用有标签的样本进行训练,利用反向传播自上而下对各层参数微调,从而确定最终模型。
1.2 改进的狼群算法狼作为群居动物,狼群内部执行严格的等级制度,设自上而下分为α、β、γ和δ狼,其中α狼的位置为最优解,余下依次为β、γ和δ狼的位置。该算法分为搜索和围捕猎物两个阶段[24],数学模型为
| $ \left\{\begin{array}{l} \boldsymbol{X}(t+1)=\boldsymbol{X}_p(t)-\boldsymbol{A} \circ \boldsymbol{D} \\ \boldsymbol{D}=\boldsymbol{C} \circ \boldsymbol{X}_p(t)-\boldsymbol{X}(t) \\ \boldsymbol{A}=2 e \circ r _1-e \\ \boldsymbol{C}=2 r_2 \\ e=2-t \frac{2}{t_{\max }} \end{array}\right. $ | (4) |
式中,t为当前迭代次数;tmax为最大迭代次数;X(t)为当前狼的位置向量;Xp为猎物的位置向量;A、C均为协同系数向量;e为收敛因子,遵循线性过程从2变化到0;r1、r2为[0, 1]的随机数。根据不同等级狼的位置来更新个体位置,当|A|>1时,狼群分散在各个区域进行搜索;当|A|≤1时,狼群集中在某个区域进行搜索。
标准GWO算法采用随机初始化方式确定种群初始位置,这种方式可能会使狼群搜索的范围过大,搜索时间过长,因此引入对立搜索计策[25],即当对立个体适应度值优于原个体适应度值时,则选用对立个体,反之采用原个体,具体公式为
| $ \boldsymbol{X}^{\prime}=L_{\mathrm{b}}+U_{\mathrm{b}}-\boldsymbol{X} $ | (5) |
式中,X′为对立个体的位置向量;Lb、Ub分别为原个体X的上下限阈值。此外,根据式(4)可知,收敛因子e决定了搜索的空间和范围。在迭代过程中,若前期搜索范围大,应降低e的递减速度,而后期为改进局部寻优过程,应加大e的递减速度,故引入余弦函数对e进行更新,最终形成改进的GWO算法。
| $ e= \begin{cases}e_{\max } \cdot \frac{1+\left[\cos \left(t \pi / t_{\max }\right)\right]^z}{2}, & t \leqslant \frac{1}{2} t_{\max } \\ e_{\max } \cdot \frac{1-\left[\cos \left(t \pi / t_{\max }\right)\right]^z}{2}, & \frac{1}{2} t_{\max }<t<t_{\max }\end{cases} $ | (6) |
式中,emax为收敛因子的极大值;z为递减系数。
为验证IGWO算法的性能,采用Benchmark标准测试函数(表 1)进行测试,其中f1为单峰函数,用于测试算法的收敛速度;f2为非连续性阶梯函数,用于测试算法的有效性;f3、f4均为多峰函数,用于测试算法是否有跳出局部最优值的能力。分别选择人工蜂群算法(artificial bee colony,ABC)、PSO算法和标准GWO算法作为对比算法,结果见表 2。
| 下载CSV 表 1 基本测试函数 Table 1 Basic test functions |
| 下载CSV 表 2 不同算法结果对比 Table 2 Comparison of results for different algorithms |
从表 2可以看出,无论是从收敛速度、计算精度还是算法稳定性上衡量,IGWO算法的迭代过程、均值和标准差均明显优于其余3种算法,说明IGWO算法具有更好的收敛性能和寻优精度。
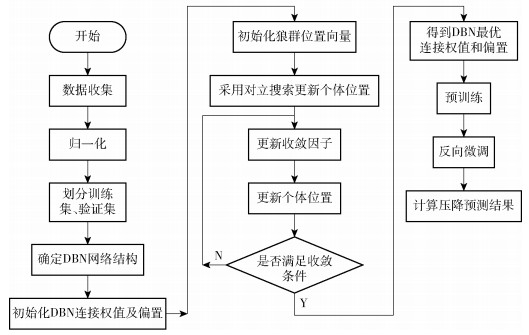
1.3 IGWO-DBN模型预测流程本文模型采用Matlab软件编程实现,IGWO-DBN模型的旋风分离器压降预测流程见图 2,具体说明如下。
|
图 2 IGWO-DBN模型预测流程 Fig.2 Prediction flow of the IGWO-DBN model |
1) 确定影响旋风分离器压降的主要因素,收集相关数据,建立样本集,对数据进行归一化处理,并划分训练集和验证集。
2) 确定DBN网络结构,确定隐含层层数及各层节点数,由此确定狼群算法维度。
3) 初始化GWO算法参数,以均方根误差(RMSE)为适应度函数,计算对立个体适应度值与原个体适应度值,更新个体位置。
4) 采用式(6)更新收敛因子,计算新个体位置,当迭代次数达到最大限值时,IGWO算法终止,获得DBN的最优连接权值和偏置,对DBN进行预训练和反向微调。
5) 代入训练集和验证集对模型进行评估,得到预测结果。
为综合评估IGWO-DBN模型的预测效果,采用2个统计学指标—平均绝对误差EMAE(MAE)、决定系数R2来评价模型的优劣性。
| $ E_{\mathrm{MAE}}=\frac{1}{n} \sum\limits_{i=1}^n\left|y_i-\hat{y_i}\right| $ | (7) |
| $ \begin{array}{l} R^2= \\ \frac{\left(n \sum\limits_{i=1}^n \hat{y}_i y_i-\sum\limits_{i=1}^n \hat{y}_i \sum\limits_{i=1}^n y_i\right)^2}{\left[n \sum\limits_{i=1}^n \hat{y}_i^2-\left(\sum\limits_{i=1}^n \hat{y}_i\right)^2\right]\left[n \sum\limits_{i=1}^n y_i^2-\left(\sum\limits_{i=1}^n y_i\right)^2\right]} \end{array} $ | (8) |
式中,n为样本数量;yi为第i个样本的实际值;
旋风分离器的压降特性与其几何参数和运行条件有关。一般用无量纲的欧拉数Eu来表示压降。研究表明,在高雷诺数的流动条件下,Eu与几何参数的关联性较大,而与运行条件的关联性较小[4, 26]。这是由于入口流量越大,压降越大,但入口速度也会随之增大,故Eu基本保持不变。因此,对于不同工况条件下运行的旋风分离器,只需考虑几何参数对压降的影响即可。旋风分离器的几何结构如图 3所示。

|
图 3 旋风分离器几何结构示意图 Fig.3 Geometric structure diagram of the cyclone separator |
从入口截面尺寸、排气管尺寸、旋风分离器高度、排尘口直径等4个方面考虑几何参数对压降的影响。随着入口高度h和宽度b的增大,分离器内部的最大切向速度减小,压降减小;随着排气管直径Dx的增大,最大切向速度减小,压降减小;随着排气管插入深度S的增大,壁面摩擦引起压降增大,但增大幅度较小;随着旋风分离器总高度H和圆柱段高度hc的增大,分离器内漩涡强度减小,压降减小;随着排尘口直径Bc的增大,排气管中的耗散动能降低,因摩擦损失引起的压降降低。综上所述,选取h、b、Dx、S、H、hc、Bc等7个参数作为IGWO-DBN压降预测模型的输入变量,为统一变量参数,将各输入变量分别除以旋风分离器圆柱段直径D,选取Eu为输出变量。提取公开文献[3, 6, 26]中的98组实验数据进行验算,数据集分布情况见表 3。采用五折交叉验证,随机抽取其中的78组为训练集,20组为验证集。
| 下载CSV 表 3 数据集分布情况 Table 3 Data set distribution |
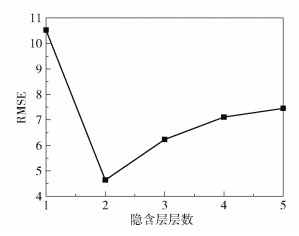
当样本集数量较大时,较多的隐含层层数可发挥DBN模型的优势,但本文训练集数量有限,隐含层层数过多会使误差无法有效地反向传播,网络参数不能及时更新,模型效率下降。根据经验,确定DBN模型中可视层节点数为输入变量的维数,输出层节点数为输出变量的维数,以隐含层节点数10为固定参数,确定所需的隐含层层数。不同隐含层层数对应的预测误差见图 4,由图可知,当隐含层层数为2时,压降预测结果的RMSE最小。
|
图 4 不同隐含层层数下的预测误差 Fig.4 Prediction errors for different numbers of hidden layers |
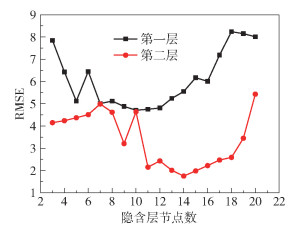
隐含层节点数是构建DBN模型的基础,目前通常采用经验公式
|
图 5 不同隐含层节点数下的预测误差 Fig.5 Prediction errors for different numbers of hidden layer nodes |
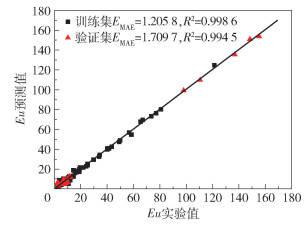
采用IGWO算法确定DBN模型的最优连接权值和偏置,最终生成7×10+10×14+14×1=224个连接权值,10+14+1=25个偏置。设置DBN网络学习率为0.001,动量因子为0.35,IGWO中设置狼群数量为20,最大迭代次数为1000。将预测结果与实验结果进行对比,结果如图 6所示。训练集的MAE为1.2058,R2为0.9986,验证集的MAE为1.7097,R2为0.9945,验证集的预测精度有所下降,其MAE虽然较训练集增加了0.5039,但模型仍保持了较佳的拟合效果和泛化能力,说明IGWO-DBN模型能够反映旋风分离器几何参数与压降的非线性关系,可用于旋风分离器压降预测。
|
图 6 IGWO-DBN模型预测结果 Fig.6 Prediction results of the IGWO-DBN model |
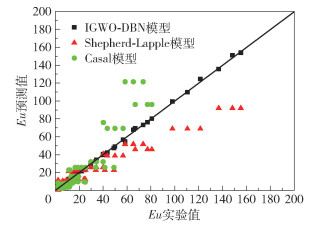
为了验证IGWO-DBN模型的优越性,将其与Shepherd-Lapple模型、Casal模型这两种传统模型的计算结果进行对比,结果如图 7、表 4所示。从图 7可以看出,传统模型的预测值大多偏离斜率为1的回归线,其中Shepherd-Lapple模型的计算结果大部分在回归线下方,即预测值低于实验值,而Casal模型的计算结果大部分高于实验值,且Eu值越大,偏离程度越大。此外,还存在不同几何参数下部分压降的计算结果相同的现象,这是由于传统模型只考虑了h、b、Dx等3个参数对压降的影响,而忽略了其余几何参数的影响,导致其离群点远多于IGWO-DBN模型。从表 4可以看出,IGWO-DBN模型的MAE为1.2313,R2为0.9975,其MAE较Shepherd-Lapple模型、Casal模型分别降低了6.2185、15.3316,R2则分别提高了0.06和0.08,预测精度大幅提高。
|
图 7 IGWO-DBN与传统模型的预测结果对比 Fig.7 Comparison of the prediction results between IGWO-DBN and traditional models |
| 下载CSV 表 4 IGWO-DBN与传统模型的误差统计对比 Table 4 Error statistics of IGWO-DBN and traditional models |
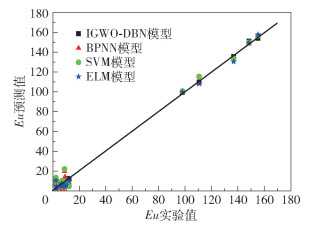
在Matlab中固定验证集,将IGWO-DBN模型与反向传播神经网络(BPNN)、支持向量机(SVM)和ELM等机器学习模型进行对比,其中BPNN模型的网络结构为7-10-1,学习率0.05,通过IGWO优化参数;SVM模型采用径向基核函数,通过IGWO寻优设置惩罚函数为15.42,核函数宽度为1.439;ELM的网络结构设置为7-10-1,通过IGWO优化参数,对比结果见图 8、表 5。可以看出,IGWO-DBN模型在训练集和验证集上的MAE和R2均优于其余模型,而BPNN、SVM模型在验证集上的MAE较训练集分别增加了7.7895、6.9210,说明这两种模型的泛化能力较差。ELM模型与IGWO-DBN模型的R2接近,但ELM模型的MAE较大,说明DBN在网络结构上优于ELM模型。在同样的工作站配置下,IGWO-DBN模型的训练时间最短,说明采用IGWO对DBN模型进行参数优化是合理的,且IGWO算法与DBN模型的匹配程度较好,最终计算效率大幅提高。综上可得,IGWO-DBN模型在预测旋风分离器压降上具有很好的泛化性能和预测精度。
|
图 8 IGWO-DBN与机器学习模型在验证集上的预测结果对比 Fig.8 Comparison of prediction results between IGWO-DBN and the machine learning model for the validation set |
| 下载CSV 表 5 IGWO-DBN与机器学习模型的误差统计和训练时间对比 Table 5 Comparison of error statistics and training time of IGWO-DBN and machine learning models |
针对现有旋风分离器压降计算模型在准确性和实用性上的不足,采用DBN模型对旋风分离器压降数据进行预测,通过IGWO算法对DBN模型的最优初始化权重和偏置参数进行选取,构建了IGWO-DBN组合模型。与传统计算模型相比,IGWO-DBN模型的MAE较Shepherd-Lapple模型、Casal模型分别降低了6.2185、15.3316,R2分别提高了0.06和0.08,预测精度大幅提高;与BPNN、SVM、ELM等机器学习模型相比,IGWO-DBN模型的MAE和R2均优于上述模型,表明其泛化能力和鲁棒性更好。本文工作为旋风分离器的压降预测提供了一个新的有效方法。
| [1] |
蒲红宇, 刘仕鳌, 蒋洪. 天然气管道清管作业风险分析及应对措施[J]. 油气储运, 2012, 31(6): 461-462. PU H Y, LIU S A, JIANG H. Risk analysis and countermeasures for pigging operation of gas pipelines[J]. Oil & Gas Storage and Transportation, 2012, 31(6): 461-462. (in Chinese) |
| [2] |
梁政, 杨志, 邓雄, 等. 在役天然气分离除尘设备性能评价[J]. 天然气工业, 2006, 26(11): 144-147. LIANG Z, YANG Z, DENG X, et al. Performance evaluation of natural gas separation and dedusting facility in service[J]. Natural Gas Industry, 2006, 26(11): 144-147. (in Chinese) DOI:10.3321/j.issn:1000-0976.2006.11.044 |
| [3] |
ZHAO B T. Modeling pressure drop coefficient for cyclone separators: a support vector machine approach[J]. Chemical Engineering Science, 2009, 64(19): 4131-4136. DOI:10.1016/j.ces.2009.06.017 |
| [4] |
张林林. 旋风分离器的性能建模及多目标粒子群优化[D]. 太原: 太原理工大学, 2019. ZHANG L L. Performance modeling and multi-objective particle swarm optimization of cyclone separator[D]. Taiyuan: Taiyuan University of Technology, 2019. (in Chinese) |
| [5] |
于洲, 马春元. 旋风分离器压降及分离效率计算模型[J]. 化工生产与技术, 2014, 21(3): 51-55, 10. YU Z, MA C Y. Calculation models of pressure drop and separating efficiency inside cyclone separator[J]. Chemical Production and Technology, 2014, 21(3): 51-55, 10. (in Chinese) DOI:10.3969/j.issn.1006-6829.2014.03.013 |
| [6] |
SHEPHERD C B, LAPPLE C E. Flow pattern and pressure drop in cyclone dust collectors[J]. Industrial and Engineering Chemistry, 1939, 31(8): 972-984. DOI:10.1021/ie50356a012 |
| [7] |
ALEXANDER R M. Fundamentals of cylone design and operation[J]. Proceedings of the Australian Institute of Mining and Metallurgy, 1949, 152: 203-228. |
| [8] |
BARTH W. Design and layout of the cyclone separator on the basis of new investigations[J]. Brennst Warme Kraft, 1956, 8: 1-9. |
| [9] |
CASAL J, MARTINEZ-BENET J M. A better way to calculate cyclone pressure drop[J]. Chemical Engineering, 1983, 90(2): 99-100. |
| [10] |
DIRGO J, LEITH D. Cyclone collection efficiency: comparison of experimental results with theoretical predictions[J]. Aerosol Science and Technology, 1985, 4(4): 401-415. DOI:10.1080/02786828508959066 |
| [11] |
耿光伟, 李天静, 唐建峰, 等. 气-液稳流式旋风分离器性能优化分析[J]. 应用力学学报, 2021, 38(4): 1629-1635. GENG G W, LI T J, TANG J F, et al. Separation efficiency optimization of SFS-GLCC separator[J]. Chinese Journal of Applied Mechanics, 2021, 38(4): 1629-1635. (in Chinese) DOI:10.11776/cjam.38.04.A053 |
| [12] |
魏培, 杨淼, 尤燕妮. 入口结构对旋风分离器性能的影响[J]. 安全与环境学报, 2021, 21(3): 1257-1262. WEI P, YANG M, YOU Y N. Impact of the inlet structure on the performance of the cyclone separator[J]. Journal of Safety and Environment, 2021, 21(3): 1257-1262. (in Chinese) |
| [13] |
赵洋, 陈建义, 曹鸣谦, 等. 入口面积可变式旋风分离器的性能[J]. 石油学报(石油加工), 2021, 37(5): 1031-1039. ZHAO Y, CHEN J Y, CAO M Q, et al. Performance of the cyclone separator with variable inlet area[J]. Acta Petrolei Sinica(Petroleum Processing Section), 2021, 37(5): 1031-1039. (in Chinese) |
| [14] |
ZHAO B T. Development of a new method for evaluating cyclone efficiency[J]. Chemical Engineering and Processing, 2005, 44(4): 447-451. DOI:10.1016/j.cep.2004.06.007 |
| [15] |
ELSAYED K, LACOR C. Modeling and Pareto optimization of gas cyclone separator performance using RBF type artificial neural networks and genetic algorithms[J]. Powder Technology, 2012, 217: 84-99. DOI:10.1016/j.powtec.2011.10.015 |
| [16] |
王兆熙, 延会波, 张玮. 粒子群算法优化极限学习机的旋风分离器压降建模[J]. 天然气化工—C1化学与化工, 2021, 46(4): 119-125. WANG Z X, YAN H B, ZHANG W. Pressure drop modeling of cyclone separator based on extreme learning machine optimized by particle swarm optimization[J]. Natural Gas Chemical Industry, 2021, 46(4): 119-125. (in Chinese) |
| [17] |
王新颖, 张惠然, 张瑞程, 等. 基于深度学习的大数据管网风险评价方法[J]. 消防科学与技术, 2019, 38(6): 902-905. WANG X Y, ZHANG H R, ZHANG R C, et al. Big data pipeline network risk assessment method based on deep learning[J]. Fire Science and Technology, 2019, 38(6): 902-905. (in Chinese) |
| [18] |
翟剑, 张玮, 李立毅, 等. 基于深度置信网络的滴流床反应器持液量预测[J]. 天然气化工—C1化学与化工, 2020, 45(6): 93-98. ZHAI J, ZHANG W, LI L Y, et al. Prediction of liquid holdup in trickle bed reactor based on deep belief network[J]. Natural Gas Chemical Industry, 2020, 45(6): 93-98. (in Chinese) |
| [19] |
王焕维, 俞英, 景冬莲, 等. 原油闪点预测模型的研究[J]. 天然气化工—C1化学与化工, 2020, 45(2): 113-120. WANG H W, YU Y, JING D L, et al. Research on flash point prediction model of crude oil[J]. Natural Gas Chemical Industry, 2020, 45(2): 113-120. (in Chinese) |
| [20] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. |
| [21] |
梁昌晶, 谢波, 刘延庆, 等. 基于KPCA-GWO-SVM的埋地管道土壤腐蚀速率预测[J]. 油气储运, 2021, 40(8): 938-944. LIANG C J, XIE B, LIU Y Q, et al. Prediction of soil corrosion rate of buried pipeline based on KPCA-GWO-SVM[J]. Oil & Gas Storage and Transportation, 2021, 40(8): 938-944. (in Chinese) |
| [22] |
王新颖, 张惠然, 黄旭安, 等. 深度信念网络在管道故障诊断中的应用[J]. 常州大学学报(自然科学版), 2020, 32(3): 71-78. WANG X Y, ZHANG H R, HUANG X A, et al. Application research of deep belief network in pipeline fault identification[J]. Journal of Changzhou University(Natural Science Edition), 2020, 32(3): 71-78. (in Chinese) |
| [23] |
姚志强. 基于深度置信网络的管网泄漏故障诊断方法研究[J]. 中国安全生产科学技术, 2018, 14(4): 101-106. YAO Z Q. Study on fault diagnosis method of pipelines leakage based on deep belief network[J]. Journal of Safety Science and Technology, 2018, 14(4): 101-106. (in Chinese) |
| [24] |
洪洋, 汪家兴, 宁宇航. 基于GWO-RBF神经网络的天线建模参数预测[J]. 电子测试, 2021(19): 60-62. HONG Y, WANG J X, NING Y H. Antenna modeling parameter prediction based on GWO-RBF neural network[J]. Electronic Test, 2021(19): 60-62. (in Chinese) |
| [25] |
万周立, 刘辉. 改进GWO优化DBN网络的变压器故障诊断研究[J]. 现代电子技术, 2021, 44(19): 163-168. WAN Z L, LIU H. Research on transformer fault diagnosis based on IGWO-optimized DBN[J]. Modern Electronics Technique, 2021, 44(19): 163-168. (in Chinese) |
| [26] |
徐洋洋. 旋风分离器数值模拟分析与优化设计研究[D]. 成都: 西南石油大学, 2017. XU Y Y. Numerical simulation analysis and optimization design of cyclone separator[D]. Chengdu: Southwest Petroleum University, 2017. (in Chinese) |







