近年来,人工智能技术已经大量应用到人类生活中,如自动分拣机器人[1]、VR虚拟现实、自动驾驶[2]等。深度信息帮助这些应用理解并分析场景的3D结构,提高执行具体任务的准确率。传统的深度信息获取方式主要有两种:一种是通过硬件设备直接测量,如Kinect[3]和LiDAR传感器,然而该方式存在设备昂贵、受限多、捕获的深度图像分辨率低等缺点; 另一种是基于图像处理估计像素点深度[4],根据视觉传感器数量的多少又可分为单目、双目、多目等深度估计方法。其中双目深度估计主要利用双目立体匹配原理[5]生成深度图,多目深度估计则是利用同一场景的多视点二维图像来计算深度值[6],这两种方法存在的共同缺点是对硬件设备参数要求高、计算量大,而且对于远距离物体会产生严重的深度精度误差。相比之下,单目深度估计从单幅图像估计像素深度信息,对摄像机参数方面的要求更少、成本低、应用灵活方便。因此,单目图像深度估计受到越来越多研究者的重视[7-16]。
随着深度学习的快速发展,深度卷积神经网络[8]凭借其高效的图像特征提取性能和优越的表达能力不断刷新计算机视觉各领域的记录。在基于深度学习单目图像预测深度图的研究方面,Eigen等[9]在2014年最先采用粗糙-精细两个尺度的卷积神经网络实现了单目图像深度估计:首先通过粗尺度网络预测全局分布的低分辨率深度图,接着将低分辨率深度图输入到精细尺度网络模块中,学习更加精确的深度值。次年,该团队基于深度信息、语义分割和法向量之间具有相关性的特点提出了多任务学习模型[10],该模型将深度估计、语义法向量、语义标签结合在一起进行训练,最终提高了深度图的分辨率和质量。随后,大量的团队开始利用深度神经网络进行单目深度估计的研究。Laina等[11]为了提高输出深度图的分辨率,提出了全卷积残差网络(fully convolutional residual networks, FCRN),FCRN采用更加高效的上采样模块作为解码器,同时在网络训练阶段加入了berHu损失函数[12],通过阈值实现了L1和L2两种函数的自适应结合,进一步提高了网络的性能。Fu等[13]引入了一个离散化策略来离散深度,将深度网络学习重新定义为一个有序回归问题,最终该方法使得网络收敛更快,同时提升了深度图的整体精度。Cao等[14]将深度估计回归任务看作一个像素级分类问题,有效避免了预测的深度值出现较大偏差的现象,获得了更准确的深度值。Lee等[15]提出了从绝对深度转变为相对深度的预测像素点的算法。Hu等[16]设计了一个新的网络架构,该架构包含编码模块、解码模块、特征融合模块、精细化模块4个模块,针对边缘设计了梯度损失函数,进一步提升了神经网络的训练效果。
虽然深度学习在单目图像深度估计任务中取得了较大的进展,但是依然存在以下问题:在单目图像深度估计任务中,现实场景具有复杂性,比如物体尺寸大小不一、较小的物体需要背景才能被更好地识别等,这增加了网络特征提取的难度。现有的单目图像深度估计方法通常通过增加网络层数来提高网络提取特征能力[17-24],在这个过程中,层级之间采用固定尺度的卷积核或卷积模块对特征图提取特征,导致层级之间提取的特征尺度单一,多尺度特征提取不够充分,最终获得的深度图整体精度不高。
针对以上问题,本文提出了一种基于多尺度特征提取的单目图像深度估计方法,该方法引入Res2Net网络作为特征提取器,以提高网络的多尺度特征提取和表达能力;其次设计了边缘增强模块,解决了网络训练过程中物体边缘像素丢失问题,提高深度图的质量;最后在损失函数中引入了结构相似性损失函数,提高网络提取局部特征的能力。
1 基于多尺度特征提取的单目图像深度估计方法 1.1 基础网络目前,大部分单目图像深度估计方法通常采用编解码结构作为网络架构,本文基于编解码结构对网络中多尺度特征提取、表达不够充分的问题展开研究。
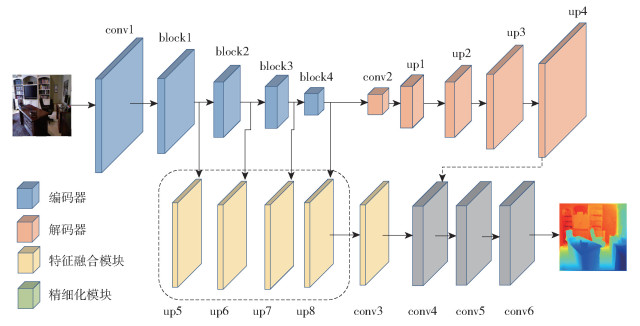
由于文献[16]通过特征融合和边缘损失函数提高了网络的性能,可获得较高的整体深度图精度,因此本文选择该文献中的网络模型作为基础网络。基础网络以编解码结构作为网络架构,如图 1所示。网络结构一共分为4个模块,即编码器模块(Encoder)、解码器模块(Decoder)、特征融合模块(MFF)和精细化模块(Refine)。
|
图 1 基础网络 Fig.1 The basic network |
编码器作为特征提取器,主要由1个卷积层和4个下采样模块组成,分别是conv1、block1、block2、block3、block4,其对输入图像的下采样提取不同分辨率的细节特征和多尺度特征,然后将最后一个下采样模块(block4)输出的特征图传递到解码器中。解码器主要由1个卷积层和4个上采样层组成,分别是conv2、up1、up2、up3、up4,编码器提取的特征图经过上采样模块一方面可以恢复空间分辨率,另一方面可实现对特征不同方式的表达。特征融合模块主要由up5、up6、up7、up8这4个上采样模块组成, 它对编码器中4个下采样模块输出的特征图进行空间恢复,然后将空间恢复的特征图与解码器输出的特征图串联,传递到精细化模块中。精细化模块主要由conv4、conv5、conv6这3个5×5的卷积组成,特征图经过精细化模块输出最终的深度图。
基础网络通过多阶段的运行,有效地将浅层的细节特征与深层的全局特征进行融合,解决了深度图丢失细节信息的问题,最终提升了深度图的整体精度。但是该网络存在以下几个问题: (1)ResNet50、DenseNet161、SENet154作为网络特征提取器,它们都有一个共性,即层级之间只使用一个固定大小的卷积核提取特征,导致层级之间的特征提取能力受限,网络提取多尺度特征不充分,最终深度估计的精度不高[25-26]; (2)网络在下采样过程中丢失边缘像素信息,降低了输出的深度图质量; (3)损失函数只考虑了单个像素点之间的深度值差值,没有考虑相邻像素点间深度值具有相关性的特点,使得网络在学习的过程中无法充分提取局部特征,影响最终深度图的精度。
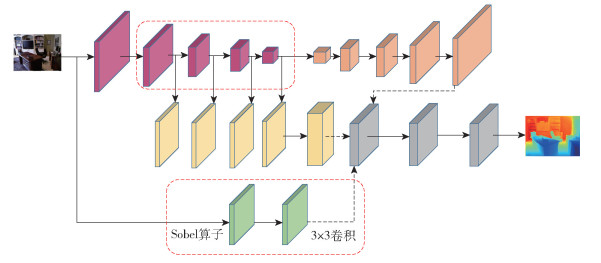
1.2 方法构建 1.2.1 网络模型针对基础网络存在的问题,本文提出基于多尺度特征提取的单目图像深度估计方法,以提高深度图的整体精度。本文方法的网络结构如图 2所示,红色框表示在基础网络上所作的改进。输入图像经过两个分支:第一个分支是对输入图像采用Res2Net编码器[27]提取丰富的多尺度特征,接着将编码器提取的特征传递到解码器、特征融合模块中恢复空间分辨率,最后将解码器和特征融合模块输出的特征进行融合,得到第一个分支输出的特征图;第二个分支是将二维图像经过一个高通滤波器提取边缘信息,然后再经过3×3的卷积得到指定尺寸的特征图。最后将以上两个分支的特征图融合,通过精细化模块输出深度图。
|
图 2 本文方法的网络模型 Fig.2 The network model of the method used in this work |
现实场景具有环境复杂和物体多样性的特点,大大增加了网络提取多尺度特征的难度。为了提高网络的多尺度特征提取能力,本文引入Res2Net卷积神经网络作为特征提取器。Res2Net网络是对ResNet网络的改进,它在单个残差块之间对特征图通道进行平均划分,然后对划分出来的不同小组通道采用阶梯形卷积方式连接,使得在层级之间不再提取单一尺度的特征,实现了不同大小尺度的特征提取,提高了网络的多尺度特征提取能力。
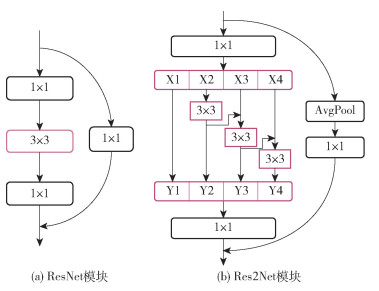
关于ResNet与Res2Net模块之间差异的详细概述如下。如图 3所示,其中图 3(a)是ResNet残差块,图 3(b)是Res2Net残差块。ResNet残差块经过一个1×1的卷积,减少输入的特征图通道数,接着对1×1卷积后的特征图通过3×3卷积提取特征,最后使用1×1的卷积对提取的特征恢复通道数。Res2Net与ResNet残差块不同的是,Res2Net网络对1×1卷积后的特征图进行通道小组划分,除了第一组以外,每组特征图都要经过一个3×3的卷积,并且将3×3卷积后的特征图与下一组特征图融合再次经过一个3×3的卷积。通过这种方式,使得每组3×3的卷积不仅是对当前通道小组提取特征,同时也对之前所有小组3×3卷积后的特征图再次计算3×3的卷积。由此采用阶梯形3×3的卷积方式相比于ResNet残差块中3×3的卷积可以提取更丰富的多尺度特征。最后将3×3卷积后的特征小组串联起来传递到1×1的卷积恢复通道数。Res2Net采用这种阶梯形卷积方式可以在不增加参数量的情况下表达出更丰富的多尺度特征。
|
图 3 ResNet模块和Res2Net模块 Fig.3 ResNet module and Res2Net module |
Res2Net模块详细计算过程可以通过式(1)说明。
| $ y_i= \begin{cases}x_i, & i=1 \\ K_i\left(x_i\right), & i=2 \\ K_i\left(x_i+y_{i-1}\right), & 2<i \leqslant s\end{cases}$ | (1) |
首先输入的特征图经过1×1的卷积输出特征图,然后对输出的特征图划分为s个小组,分别用xi(i∈(1, 2, …, s))表示,并且每一小组的特征数为原来的通道数的1/s,图 3(b)为s取4的情况。除了第一个小组x1的特征图外,其他小组xi(i∈(2, 3, …, s))的特征图都有3×3卷积层。用Ki表示卷积层,并将xi(i∈(2, 3, …, s))卷积后的输出用yi表示,当前小组的特征xi与上一小组输出的特征yi-1相加作为Ki的输入,因此每一个Ki()的输入都包含了之前{xj, j≤i}的小组特征,并且由于采用的是阶梯形连接,所以每个yi都在yi-1基础上提取更多的尺度特征。由于这种组合的激发效果,Res2Net中的残差模块可以提取更细粒度的不同尺度大小的特征,提高了网络的多尺度特征提取能力。最后将各个小组输出的特征串联起来,输入到1×1的卷积层中,恢复特征通道数。由此可以看出,Res2Net残差模块使用阶梯形卷积提取了更丰富的多尺度特征,解决了原网络中特征提取单一的问题,提高了整体的网络特征提取能力。
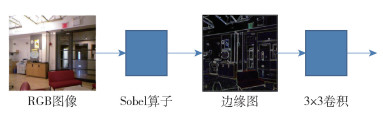
1.2.3 边缘增强网络二维图像(RGB图像)经过编码器下采样提取抽象特征,然后经过上采样恢复到原来的尺寸。在这个过程中由于图像的分辨率不断的缩放,导致物体的结构像素不断丢失,为了更直观地加以说明,本文对文献[16]里SENet154网络中特征融合模块4个阶段的特征图进行可视化,如图 4所示。由图 4可以发现,第一阶段可以学习到更多的边缘信息,但是边缘不够清晰,包含较多的噪声,随着第二阶段、第三阶段、第四阶段网络的加深,网络可学习更多的全局特征,边缘细节信息更加模糊。为了解决该问题,本文设计了边缘增强网络,保留边缘像素信息,具体的网络结构如图 5所示。

|
图 4 特征融合模块4个阶段输出的特征图 Fig.4 Feature map output by four stages of the feature fusion module |
|
图 5 边缘增强网络示意图 Fig.5 Schematic diagram of the edge enhancement network |
首先输入的RGB图像通过Sobel算子提取边缘信息,然后边缘特征依次通过3×3的卷积、像素值归一化、ReLU激活函数运算以加强边缘特征,最后将边缘特征与解码器、特征融合模块输出的特征图通道连接,输出最终的深度图,整体结构如图 2所示。边缘增强模块通过提取和加强图像中物体的边缘信息,有效地保留了物体边缘像素特征。
1.2.4 结构相似性损失函数文献[16]中采用了3个损失函数来估计深度,如式(2)~(4)所示。
真实深度图像素值深度gi和预测深度图像素值深度di的绝对误差为
| $ l_{\text {depth }}=\frac{1}{n} \sum\limits_{i=1}^n F\left(e_i\right), F(x)=\ln (x+\alpha) $ | (2) |
式中,ei=‖di-gi‖1, n是像素点总数,α是自定义参数。
物体边缘像素点的误差为
| $ l_{\text {grad }}=\frac{1}{n} \sum\limits_{i=1}^n\left(F\left(\mathrm{~d} x\left(e_i\right)\right)+F\left(\mathrm{~d} y\left(e_i\right)\right)\right) $ | (3) |
式中,dx(ei)、dy(ei)为像素点在x方向和y方向的导数。
物体表面法向量误差为
| $ l_{\text {normal }}=\frac{1}{n} \sum\limits_{i=1}^n\left(1-\frac{\left(\boldsymbol{n}_i^d, \boldsymbol{n}_i^g\right)}{\left(\sqrt{\left.n_i^d, n_i^d\right)} \sqrt{\left(n_i^g, n_i^g\right)}\right.}\right) $ | (4) |
式中,预测深度图法向量nid=[-dx(di), -dy(di), 1]T,真实深度图法向量nig=[-dx(gi), -dy(gi), 1]T。
损失函数公式(2)~(4)都是基于真实深度图和预测深度图单个像素点之间的差值,忽略了空间域中相邻像素点之间的相关性,而这种相关性承载着视觉场景中物体结构的信息。因此,本文引入了结构性相似损失函数(SSIM)[28],增强网络对物体结构信息的关注度,从而提高整体深度图的精度。
SSIM主要从局部区域的亮度、对比度、结构这3个方面来综合度量两个图像的相似性。SSIM的具体公式可以表示如下。
| $ F_{\mathrm{SSIM}}(X, Y)=L(X, Y) * C(X, Y) * S(X, Y) $ | (5) |
式中,L(X, Y)为亮度的相似度估计,计算公式为
| $ L(X, Y)=\frac{2 \mu_x \mu_y+c_1}{\mu_x^2+\mu_y^2+c_1} $ | (6) |
C(X, Y)为对比度的相似度估计,计算公式为
| $ C(X, Y)=\frac{2 \sigma_x \sigma_y+c_2}{\sigma_x^2+\sigma_y^2+c_2} $ | (7) |
S(X, Y)为结构的相似度估计,计算公式为
| $ S(X, Y)=\frac{\sigma_{x, y}+c_3}{\sigma_x \sigma_y+c_3} $ | (8) |
上述公式中,X为原始图像,Y为预测图像,μx、μy分别为图像X、Y的均值,σx2、σy2分别为图像X、Y的方差,σx, y为图像X、Y的协方差,c1、c2、c3为常数,以防止出现分母为零的情况。最后的损失函数可表示为
| $L=l_{\text {depth }}+l_{\text {grad }}+l_{\text {normal }}+F_{\text {SSIM }} $ | (9) |
本文在ubuntu 16.04系统下,显存大小为11GB的NVIDIAGeForce RTX 2080Ti显卡上进行实验。网络结构通过主流深度学习框架pytorch1.0.0实现。根据网络模型结构以及显卡的性能,设置批尺寸(batch size)为8,初始学习率为0.0001,每5个epoch衰减10%。采用Adam优化器作为网络优化器,权重衰减设置为1×10-4。
2.2 实验数据集NYU Depth V2是常用的室内深度估计数据集[29],该深度数据通过微软公司的Kinect深度摄像头采集得到,本文采用NYU Depth V2作为实验数据集。原始彩色图片及对应的深度图大小为640×480,为加速训练将原始数据下采样到320×240。该数据集包含464个不同室内场景的原始数据,其中249个场景用于训练,215个场景用于测试。由于用于训练集的数据量太少,本文对采样的原始训练数据通过水平翻转、随机旋转、尺度缩放、色彩干扰等数据增强方式来进行数据增广。
2.3 评价指标在单目图像深度估计方法中,通常采用以下几个评价指标来度量方法的性能。
1) 均方根误差(RMSE)
| $ E_{\mathrm{RMSE}}=\sqrt{\frac{1}{N} \sum\limits_i^N\left(d_i-d_i^*\right)^2} $ | (10) |
2) 平均相对误差(REL)
| $ E_{\mathrm{REL}}=\frac{1}{N} \sum\limits_i^N \frac{\left|d_i-d_i^*\right|}{d_i^*} $ | (11) |
3) 对数平均误差(LG10)
| $ E_{\mathrm{LG} 10}=\sqrt{\frac{1}{N} \sum\limits_i^N\left\|\log _{10} d_i-\log _{10} d_i^*\right\|^2} $ | (12) |
4) 不同阈值下的准确度
| $ \operatorname{Max}\left(\frac{d_i}{d_i^*}, \frac{d_i^*}{d_i}\right)=\delta<t h r, t h r=\left\{1.25, 1.25^2, \right. 1. \left.25^3\right\} $ | (13) |
式中,di为像素i的预测深度值,di*为像素i的真实深度值,N为图像中像素的总和。
以上3个误差越小表示预测深度值越接近真实深度值,代表网络性能越好;准确度越大表示在不同阈值下,预测深度值达到指定误差范围的像素点个数越多,获得的深度图精度越高。
2.4 实验结果及分析 2.4.1 实验结果1) Res2Net的有效性验证
为了验证Res2Net的有效性,本文将基础网络中的编码器ResNet50替换成Res2Net50。为了验证网络层数不变的情况下,对Res2Net50中的通道数进行细分可以提高网络的特征提取能力,将残差块中的通道分别划分为4、6、8个不同的小组数,每个小组的通道数为26,分别表示为Res2Net50-4s、Res2Net50-6s、Res2Net50-8s。将基础网络中的ResNet50依次替换成Res2Net50-4s、Res2Net50-6s、Res2Net50-8s。为了验证增加Res2Net50的层数可以提高网络的特征提取能力,将编码器中的Res2Net50-4s替换成Res2Net101-4s(Res2Net101-4s为在ResNet101基础上将单个残差块中通道数划分为4个小组)。实验结果如表 1所示。
| 下载CSV 表 1 数据集NYU Depth V2上ResNet与Res2Net的实验结果对比 Table 1 Comparison between ResNet and Res2Net of experimental results on the NYU Depth V2 dataset |
从表 1结果可以看出,Res2Net50-4s相比ResNet50在所有指标上均有提升,其中均方根误差RMSE减小了0.9%,在阈值δ < 1.25的准确度上提升了0.7%。同样,Res2Net50-6s、Res2Net50-8s与ResNet50相比在误差上均有减小,在准确度上均有所提升。以上实验结果说明在网络层数不变的情况下,对ResNet50中残差块的通道数进行细分可以提高网络多尺度特征的提取能力,最终提高深度图的整体精度。另外,由Res2Net50-4s、Res2Net50-6s、Res2Net50-8s结果可以看出,随着划分通道小组数增加,误差越来越小,这是因为在网络层数不变的情况下,增加通道小组数可以提高网络提取多尺度特征的能力,从而提高深度图的整体精度。
Res2Net101-4s相比于Res2Net50-4s在均方根误差上减少了2%,在阈值δ < 1.25的准确度上提升了1.6%,说明在保持通道小组数不变的情况下,进一步增加网络层数可以提高Res2Net网络的特征提取能力,提高深度值精度。Res2Net50-4s相比ResNet50[16]参数量仅增加了0.14×106,但是所得深度图的整体精度明显提升,说明在网络参数一致的条件下,Res2Net相比ResNet可以学习更丰富的特征。Res2Net50-6s相比Res2Net50-4s参数量增加了11.35×106,Res2Net50-8s相比Res2Net50-6s参数量增加了11.36×106,说明在通道数层数保持不变的情况下,逐步增加小组数会增加整体网络的参数量,但模型获得了更高的深度图整体精度。
以上实验结果表明,与ResNet50相比,Res2Net50通过通道数的划分可以提高网络的多尺度特征提取能力,并且划分的小组数越多,提取的特征越丰富,网络整体性能越好。而Res2Net101相比Res2Net50在保持通道小组划分一致的条件下增加网络层数,进一步提高了网络的特征提取能力,从而提高了深度图整体精度。
在层数不变的前提下,增加通道小组数会提高网络模型的参数量。为了不过多地增加模型参数量,本文选择通道小组数为4的ResNet101网络作为编码器,即Res2Net101-4s,继续验证结构损失函数和边缘增强模块的有效性。
2) 结构相似性损失函数和边缘增强模块的有效性验证
为了验证结构相似性损失函数的有效性,本文在Res2Net101-4s网络模型基础上增加了结构相似性损失函数,用R2S表示该网络模型;为了验证边缘增强网络的有效性,在R2S网络模型基础上又增加了边缘增强模块,用R2SE表示该网络。为了验证本文设计模型的有效性,将R2S、R2SE与基础网络中以SENet154作为编码器的模型的实验结果进行对比,如表 2所示,其中SENet154表示基础网络中以SENet154作为编码器结构的模型[16]。
| 下载CSV 表 2 不同模型在NYU Depth V2数据集上的实验结果对比 Table 2 Comparison of experimental results for different models on the NYU Depth V2 dataset |
从表 2可以看出,R2S相比Res2Net101-4s在均方根误差上减小了1.9%,在阈值δ < 1.25的准确度上提升了0.7%,说明本文加入的结构性损失函数可以有效提高深度图的整体精度。R2SE相比R2S误差更小,准确度更高,说明本文加入的边缘增强模块可以提升深度图的精度。
此外还可以看出,Res2Net101-4s、R2SE相比SENet154误差均有所减小,准确度更高,并且需要的参数量更少。这一方面说明了本文引入的Res2Net相比于SENet154可以更少的参数量学习更多的特征,另一方面说明了本文方法通过引入Res2Net、边缘增强模块和SSIM提高了网络的整体特征提取能力,获得更高质量的深度图。
3) 与其他方法的性能对比
将本文算法得到的评价指标与其他单目图像深度估计方法进行对比,结果如表 3所示。可以发现本文方法在图像深度估计上的预测误差更小,准确度更高,表明本文方法获得的深度图的精度更高。
| 下载CSV 表 3 R2SE在NYU Depth V2数据集上与其他方法的实验结果比较 Table 3 Comparison between R2SE and other methods of experimental results on the NYU Depth V2 dataset |
为了验证本文方法的有效性,选择4组图像进行实验,对不同方法得到的深度图以图像形式呈现,比较主观效果,如图 6所示。
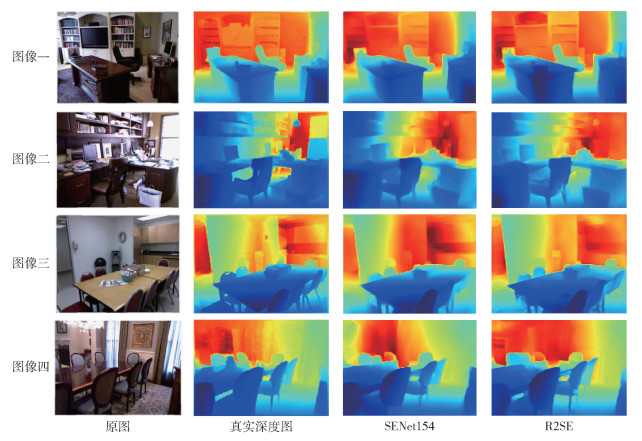
|
图 6 在NYU Depth V2数据集上的可视化结果 Fig.6 Visualization of results on the NYU Depth V2 dataset |
从图像一实验结果可以看出,本文方法相比基础网络在两侧书柜上具有更清晰的分层,可以识别出书柜每层的上下轮廓和左右轮廓,而且颜色更加接近真实深度值。在电视结构上,本文方法识别的结构相比基础网络具有更清晰的上下轮廓,而且电视的整体颜色更浅,更加接近真实深度值。
从图像二实验结果可以看出,本文方法相比基础网络可以提取更清晰的电脑轮廓,更加接近真实深度图。对于上方书柜,本文方法得到的深度图相比基础网络具有更清晰的分层结构,以及更多的细节信息。
从图像三、图像四的实验结果可以看出,本文方法预测的远处墙壁的误差更小,更加接近真实的深度图。
综上可知,本文方法相比基础网络可提取更多的细节特征与多尺度特征,得到更加精确的深度图。
3 结论本文提出了一种基于多尺度特征提取的单目图像深度估计方法,该方法以Res2Net作为特征提取器,可以提取图像中更丰富的多尺度特征;引入的边缘增强模块有效解决了网络训练过程中边缘像素丢失问题;在损失函数中引入结构相似性损失函数提高了网络学习局部特征的能力。在NYU Depth V2室内数据集上的实验结果显示,本文提出的R2SE比基础网络中的SENet154在均方根误差上减小了2.2%,同时在阈值δ < 1.25的准确度上提升了0.9%。表明本文所提方法通过引入Res2Net、边缘增强模块和结构相似性损失函数提高了网络的特征提取能力,可得到具有更多物体结构信息的深度图,提升了深度图的整体精度。
| [1] |
王欣, 伍世虔, 邹谜. 基于Kinect的机器人采摘果蔬系统设计[J]. 农机化研究, 2018, 40(10): 199-202, 207. WANG X, WU S Q, ZOU M. Design of robot picking fruit and vegetable system based on with Kinect sensor[J]. Journal of Agricultural Mechanization Research, 2018, 40(10): 199-202, 207. (in Chinese) DOI:10.3969/j.issn.1003-188X.2018.10.037 |
| [2] |
曾仕峰, 吴锦均, 叶智文, 等. 基于ROS的无人驾驶智能车[J]. 物联网技术, 2020, 10(6): 62-63, 66. ZENG S F, WU J J, YE Z W, et al. Driverless intelligent vehicle based on ROS[J]. Internet of Things Technologies, 2020, 10(6): 62-63, 66. (in Chinese) |
| [3] |
OLIVA A, TORRALBA A. Modeling the shape of the scene: a holistic representation of the spatial envelope[J]. International Journal of Computer Vision, 2001, 42(3): 145-175. DOI:10.1023/A:1011139631724 |
| [4] |
冯桂, 林其伟. 用离散分形随机场估计图像表面的粗糙度[C]//第八届全国多媒体技术学术会议. 成都, 1999: 378-381. FENG G, LIN Q W. Using DFBR field to estimate the roughness of image surface[C]//The 8th National Conference on Multimedia Technology. Chengdu, 1999: 378-381. (in Chinese) |
| [5] |
SAXENA A, SUN M, NG A Y. Make3D: learning 3D scene structure from a single still image[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2009, 31(5): 824-840. |
| [6] |
FURUKAWA Y, HERNÁNDEZ C. Multi-view stereo: a tutorial[J]. Foundations and Trends® in Computer Graphics and Vision, 2013, 9(1-2): 1-148. |
| [7] |
BAIG M H, TORRESANI L. Coupled depth learning[C]//2016 IEEE Winter Conference on Applications of Computer Vision(WACV). Lake Placid, 2016.
|
| [8] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [9] |
EIGEN D, PUHRSCH C, FERGUS R. Depth map prediction from a single image using a multi-scale deep network[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems(ICONIPS2014). Montreal, 2014.
|
| [10] |
EIGEN D, FERGUS R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture[C]//2015 IEEE International Conference on Computer Vision(ICCV). Santiago, 2015.
|
| [11] |
LAINA I, RUPPRECHT C, BELAGIANNIS V, et al. Deeper depth prediction with fully convolutional residual networks[C]// 2016 4th International Conference on 3D Vision(3DV). Stanford, 2016.
|
| [12] |
OWEN A B. A robust hybrid of lasso and ridge regression[M]// VERDUCCI J S, SHEN X T, LAFFERTY J. Contemporary mathematics. Providence: American Mathematical Society, 2007: 59-72.
|
| [13] |
FU H, GONG M M, WANG C H, et al. Deep ordinal regression network for monocular depth estimation[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, 2018.
|
| [14] |
CAO Y Z H, WU Z F, SHEN C H. Estimating depth from monocular images as classification using deep fully convolutional residual networks[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2018, 28(11): 3174-3182. DOI:10.1109/TCSVT.2017.2740321 |
| [15] |
LEE J H, KIM C S. Monocular depth estimation using relative depth maps[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition(CVPR). Long Beach, 2019.
|
| [16] |
HU J J, OZAY M, ZHANG Y, et al. Revisiting single image depth estimation: toward higher resolution maps with accurate object boundaries[C]//2019 IEEE Winter Conference on Applications of Computer Vision (WACV). Waikoloa, 2019.
|
| [17] |
WANG J R, ZHANG G, YU M, et al. Attention-based dense decoding network for monocular depth estimation[J]. IEEE Access, 2020, 8: 85802-85812. DOI:10.1109/ACCESS.2020.2990643 |
| [18] |
LIN L X, HUANG G H, CHEN Y J, et al. Efficient and high-quality monocular depth estimation via gated multi-scale network[J]. IEEE Access, 2020, 8: 7709-7718. DOI:10.1109/ACCESS.2020.2964733 |
| [19] |
LIU P, ZHANG Z H, MENG Z Z, et al. Joint attention mechanisms for monocular depth estimation with multi-scale convolutions and adaptive weight adjustment[J]. IEEE Access, 2020, 8: 184437-184450. DOI:10.1109/ACCESS.2020.3030097 |
| [20] |
SWAMI K, BONDADA P V, BAJPAI P K. Aced: accurate and edge-consistent monocular depth estimation[C]//2020 IEEE International Conference on Image Processing (ICIP). Abu Dhabi, 2020.
|
| [21] |
CHEN Y R, ZHAO H T, HU Z W, et al. Attention-based context aggregation network for monocular depth estimation[J]. International Journal of Machine Learning and Cybernetics, 2021, 12(6): 1583-1596. DOI:10.1007/s13042-020-01251-y |
| [22] |
SU W, ZHANG H F, ZHOU Q, et al. Monocular depth estimation using information exchange network[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(6): 3491-3503. DOI:10.1109/TITS.2020.3008991 |
| [23] |
YE X C, CHEN S D, XU R. DPNet: detail-preserving network for high quality monocular depth estimation[J]. Pattern Recognition, 2021, 109: 107578. DOI:10.1016/j.patcog.2020.107578 |
| [24] |
LIU P, ZHANGZ H, MENG Z Z, et al. Monocular depth estimation with joint attention feature distillation and wavelet-based loss function[J]. Sensors, 2021, 21(1): 54. |
| [25] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Las Vegas, 2016.
|
| [26] |
HU J, SHEN L, SUN G. Squeeze-and-excitation networks[C]// 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, 2018.
|
| [27] |
GAO S H, CHENG M M, ZHAO K, et al. Res2Net: a new multi-scale backbone architecture[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(2): 652-662. DOI:10.1109/TPAMI.2019.2938758 |
| [28] |
WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
| [29] |
SILBERMAN N, HOIEM D, KOHLI P, et al. Indoor segmentation and support inference from RGBD images[C]// 12th European Conference on Computer Vision(ECCV). Florence, 2012.
|
| [30] |
HAO Z X, LI Y, YOU S D, et al. Detail preserving depth estimation from a single image using attention guided networks[C]//6th International Conference on 3D Vision (3DV). Verona, 2018.
|







