2. 沈阳工业大学 环境与化学工程学院, 沈阳 110870
2. School of Environmental and Chemical Engineering, Shenyang University of Technology, Shenyang 110870, China
人类生活、生产过程中不可避免地排放大量的CO2,作为主要的温室气体,过量的CO2排放将加剧温室效应,造成气候变化和海洋酸化等负面影响。2020年9月我国在联合国大会上庄严承诺2030年前实现“碳达峰”、2060年前实现“碳中和”,为了尽快实现“双碳”目标,大力发展捕集CO2技术和可再生能源技术变得刻不容缓[1]。相比于碳捕集与封存(carbon capture and sequestration, CCS)技术仅能将CO2作为“废弃物”进行处理,碳捕集与利用(carbon capture and utilization, CCU)技术能将由风能、太阳能、地热能等分布式可再生能源获得的氢气与CO2进行化学反应,生成燃料和高附加值化学单品——低碳烯烃[2]。
低碳烯烃(C2=~C4=,乙烯、丙烯和丁烯)是有机材料合成的重要化工原料,此外,以低碳烯烃作为单体进行齐聚化学反应可以高选择性地生成清洁燃料,这是一条清洁高效、经济价值高的热化学储能技术路线[1-3]。许多研究者致力于开发高活性、高稳定性的CO2氢化合成低碳烯烃的催化剂,研究了化学反应机理以及载体、助剂、活性组分等对催化剂性能的影响[4-5]。为了提升储能过程的整体效率,亟需对该储能技术路径中的CO2氢化反应开展热力学优化研究。
化学反应必须受到热力学的约束,而化学反应热力学研究的对象是基于平衡态的反应系统,热力学平衡态是化学反应在理论上的极限状态。一些学者对CO2氢化反应进行了热力学分析,研究了反应条件对反应系统平衡状态的影响[6-10]。刘业奎等[6]在反应体系中CO浓度为零的假设条件下对CO2加氢合成低碳烯烃的理想反应体系进行了热力学研究,得到了反应体系中CO2的理论最高转化率。张磊等[7]基于Gibbs自由能最小化和熵最大化的方法对CO2加氢合成低碳烯烃反应进行了平衡态热力学研究,系统分析了反应条件、工业操作等因素对平衡转化率(等温等压条件)和平衡温度(等压等焓条件)的影响。Torrente-Murciano等[8]使用Gibbs自由能最小化方法计算了CO2还原反应和费托合成反应的热力学平衡态,并考虑了催化剂选择性、工业条件(膜反应器除水)等因素对反应性能的影响。基于反应性能的实验研究和基于单目标的数值模拟仿真与优化研究均只考虑了化学反应单一性能指标随反应条件的变化规律,而化学反应的强耦合性和强非线性导致实际上可能存在互相影响、甚至矛盾的优化结论。在实际工业应用中也仅是通过先验信息和设计经验来选取合适的操作参数以使反应系统尽可能在多目标、多性能上达到协同最佳,这是一种反复进行实验或模拟尝试的方法,缺少明确和系统的理论依据。多目标最优化方法考虑到实际工业过程的多方面因素,有助于打破依靠先验信息的限制,明确反应性能协同最佳的参数最优值。
对于复杂反应体系平衡态热力学的模拟,结合统计学理论的回归模型建模方法能有效解决使用Gibbs自由能最小化方法进行建模带来的模型高度非线性化和难收敛的难题[11-14]。Tabrizi等[11]建立了甲烷水蒸汽重整反应中甲烷平衡转化率和氢气选择性等性能指标与反应条件之间的统计学模型,并详细分析了参数对反应性能的影响。Atashi等[12]结合Gibbs自由能最小化和响应面方法对甲烷二氧化碳重整反应进行了热力学分析,并使用满意度函数法得到了约束条件下H2产率最大的最优反应条件。快速非支配排序遗传算法(NSG A-Ⅱ)是一种基于Pareto最优概念的多目标优化算法,可根据个体的非劣解水平对种群分层,快速收敛到多目标优化问题的Pareto最优解集,在化工过程优化方面应用广泛。Shahhosseini等[15]使用NSG A-Ⅱ方法对工业甲烷水蒸汽重整膜反应器进行了多目标优化,得到了CH4转化率、H2选择性和CO选择性这3个性能指标最大的Pareto最优前沿。Dehghani等[16]使用NSG A-Ⅱ方法对甲醇合成过程中的径向流气冷反应器和径向流气冷膜反应器进行了多目标优化,得到了甲醇产率和选择性最大的Pareto最优前沿。鉴于统计学建模方法和NSG A-Ⅱ多目标优化方法在化学反应过程参数优化方面的优越性,本文在文献[7]的热力学平衡模型的基础上,结合统计学理论和多目标优化方法,对CO2氢化合成低碳烯烃反应进行热力学分析与优化研究,得到平衡反应体系在多个目标下的最优反应性能。
1 数学模型 1.1 反应模型CO2氢化合成低碳烯烃反应可通过以下反应方程式进行描述[2, 7]。
| $ \mathrm{CO}_2+\mathrm{H}_2 \rightleftharpoons \mathrm{CO}+\mathrm{H}_2 \mathrm{O} \quad \Delta_{\mathrm{r}} H>0 $ | (1) |
| $ n \mathrm{CO}+2 n \mathrm{H}_2 \rightarrow \mathrm{C}_n \mathrm{H}_{2 n}+n \mathrm{H}_2 \mathrm{O} \quad \Delta_{\mathrm{r}} H <0 $ | (2) |
| $ n \mathrm{CO}_2+3 n \mathrm{H}_2 \rightarrow \mathrm{C}_n \mathrm{H}_{2 n}+2 n \mathrm{H}_2 \mathrm{O} \quad \Delta_{\mathrm{r}} H <0 $ | (3) |
其中ΔrH为反应焓,kJ/mol。式(1)为逆水气变换(reverse water gas shift, RWGS)反应,式(2)为费托合成(Fischer-Tropsch synthesis, FTS)反应,式(3)为CO2直接氢化(direct hydrogenation, DH)反应。其中,RWGS反应为吸热可逆反应,FTS和DH反应为放热不可逆反应。依据现有催化剂的实际性能,反应体系中往往存在一定量的C1甲烷化反应:
| $ \mathrm{CO}_2+4 \mathrm{H}_2 \rightarrow \mathrm{CH}_4+2 \mathrm{H}_2 \mathrm{O} $ | (4) |
在完全不考虑催化剂动力学效应的情况下对CO2氢化反应体系进行平衡态热力学研究时,烷烃(尤其是C1甲烷CH4)收率将远远大于期望的低碳烯烃产物,与实际的工业催化反应数据不符[6, 8]。不考虑副产物生成的热力学平衡态反应系统在一定程度上考虑了催化剂的动力学效应(产物选择性),其产物分布更贴近于实际的催化反应数据。因此,本文对CO2氢化合成低碳烯烃反应系统做出如下假设[7]:所使用的催化剂只对C2=~C4=的低碳烯烃具有选择性,且对其他副反应具有完全抑制作用。因此,可认为该理想反应系统的平衡态仅包括以下7种组分:CO2、H2、CO、C2H4、C3H6、C4H8和H2O。
1.2 热力学平衡模型本文采用Gibbs自由能最小化方法[16]对该多组分化学反应体系进行热力学平衡计算。在等温等压条件下,反应系统的Gibbs自由能极小值点即为反应体系的平衡态稳定点。
多相、多组分化学反应系统总的Gibbs自由能(G)可表示为[7, 17]
| $ G=\sum\limits_{i=1}^N\left(n_i^{\mathrm{g}} \mu_i^{\mathrm{g}}+n_i^1 \mu_i^1+n_i^{\mathrm{s}} \mu_i^{\mathrm{s}}\right) $ | (5) |
式中:N为反应体系的组分数量;ni为组分i的物质的量,mol;μi为组分i的化学势,kJ/mol;上标g、l、s分别代表气相、液相、固相。对于CO2氢化合成低碳烯烃反应,在工业反应条件下组分均为气相,反应达到热力学平衡态时,反应系统总的Gibbs自由能(kJ)最小(式(6))。
| $ \min G=\min \left(\sum\limits_{i=1}^N n_i \mu_i\right) $ | (6) |
式(6)所示的优化问题还需满足组分物质的量非负(式(7))和质量守恒(式(8))。
| $ n_i \geqslant 0 \quad i=1, 2, \cdots, N $ | (7) |
| $ \sum\limits_{i=1}^N a_{m i} n_i=\sum\limits_{i=1}^N a_{m i} n_i^0 \quad m=1, 2, \cdots, N_{\mathrm{E}} $ | (8) |
式中:ami为组分i的化学式中元素m的系数;NE为反应系统中总的元素数目;ni0为进料气中组分i的物质的量,mol。
热力学平衡计算问题可转化为最优化计算问题,本文使用Matlab R2010a全局优化工具箱中的全局优化函数“GlobalSearch”进行优化计算,式(6)为优化目标函数,式(7)和式(8)为优化过程中的约束条件。在最优化计算过程中,反应混合物中各组分的物质的量ni为优化变量,反应系统的温度T(K)、压力p(MPa)和进料气组分的物质的量ni0(mol)为给定输入参数。
反应混合物中组分i的摩尔Gibbs自由能(Gi)可通过下式计算。
| $ G_i=\mu_i=\mu_i^0+R T \ln \left(\hat{f}_i / f_i^0\right) $ | (9) |
式中:μi0为组分i在标准态下的化学势;R为通用气体常数,kJ/(mol·K);fi0为纯组分i在理想气体状态下的逸度(MPa),对于理想气体,fi0=0.101 325 MPa;
| $ \hat{f}_i=\hat{\phi}_i y_i p $ | (10) |
式中:
使用Soave-Redlich-Kwong(SRK)状态方程[18]对反应混合物的逸度系数进行计算,并对反应体系中具有量子气体效应的组分H2的状态方程系数进行修正[7]。标准态下的化学势μi0可通过热力学关系式进行计算,计算过程中涉及到的组分摩尔热容采用与温度相关的真实比热容多项式,所需的热力学数据均根据文献[19]进行取值。
反应系统热力学平衡态下的CO2转化率(XCO2)、低碳烯烃选择性(SHC)分别表示为
| $ X_{\mathrm{CO}_2}=\left[\left(n_{\mathrm{CO}_2}^0-n_{\mathrm{CO}_2}\right) / n_{\mathrm{CO}_2}^0\right] \times 100 \% $ | (11) |
| $ S_{\mathrm{HC}}=\frac{2 \times n_{\mathrm{C}_2}=+3 \times n_{\mathrm{C}_3}=+4 \times n_{\mathrm{C}_{4}^{=}}}{n_{\mathrm{CO}_2}^0-n_{\mathrm{CO}_2}} \times 100 \% $ | (12) |
由于Gibbs自由能最小化问题的计算成本较高,利用严格的数理模型对不同条件下的热力学平衡态进行计算或者利用优化算法对平衡态反应条件进行优化的计算量大且收敛困难,时效性极差[13]。因此,可根据模拟计算中获得的有限样本量数据,建立基于统计学理论的回归函数模型来表征关键指标与反应条件之间的函数关系。通过得到的有一定可信度的函数方程,可快速对不同反应条件下反应系统的反应状态进行判断,并能极大提高优化计算的时效性。
使用二阶多元通用回归模型构建函数方程,回归函数模型变量为反应温度T、反应压力p和进料气H2与CO2的物质的量比M。
| $ \begin{array}{l} \;\;\;\;\;\;\;f(T, p, M)=\beta_1 T^2+\beta_2 p^2+\beta_3 M^2+\beta_4 T p+ \\ \beta_5 T M+\beta_6 p M+\beta_7 T+\beta_8 p+\beta_9 M+\beta_{10} \end{array} $ | (13) |
式中β1~β10为待拟合参数。
本文基于非线性最小二乘法,利用模拟计算得到的样本量数据对式(13)的回归函数模型进行拟合,使用Matlab R2010a优化工具箱中的非线性最小二乘函数“lsqnonlin”对数据进行拟合。
1.4 多目标优化模型在实际工业操作中,设计人员往往期望反应系统在多个目标上均能提升性能,但多个目标可能相互制约,一个指标的提升可能引起另一个指标的下降,同时使所有目标都达到最优一般是不可能的,只能在多个目标之间进行折中和权衡,使多个目标尽可能接近最优。
CO2氢化合成低碳烯烃的反应过程中会有大量的H2O生成,催化反应过程中过量的H2O会对催化剂的结构、性能和寿命产生影响,甚至会导致催化剂水解失效[7-8]。因此,在实际工业反应中除需采取化学工艺手段(分离工程工艺、膜反应器等)尽可能地移除反应过程中的H2O以外,还需要选择合适的反应条件以减少H2O的生成。根据上文建立的回归函数模型,为了提高CO2转化率或低碳烯烃选择性,并同时考虑减少反应中H2O的摩尔分数(yH2O),分别以CO2平衡转化率最大和H2O平衡摩尔分数最小、低碳烯烃选择性最大和H2O平衡摩尔分数最小为优化目标对反应系统进行多目标优化。最优化问题可分别表示为式(14)和(15)。
| $ \begin{cases}\max & X_{\mathrm{CO}_2} \\ \min & y_{\mathrm{H}_2 \mathrm{O}}\end{cases} $ | (14) |
| $ \begin{cases}\max & S_{\mathrm{HC}} \\ \min & y_{\mathrm{H}_2 \mathrm{O}}\end{cases} $ | (15) |
选择反应温度T、反应压力p和进料气H2与CO2的物质的量比M为优化变量,根据工程经验确定优化变量的取值范围如下[2, 6-8]。
| $ \begin{aligned} & 400 \mathrm{~K} \leqslant T \leqslant 850 \mathrm{~K} \\ & 1 \mathrm{~MPa} \leqslant p \leqslant 5 \mathrm{~MPa} \\ & 2 \leqslant M \leqslant 5 \end{aligned} $ | (16) |
本文使用Matlab R2010a全局优化工具箱中的“gamultiobj”函数对多目标优化问题进行数值求解。
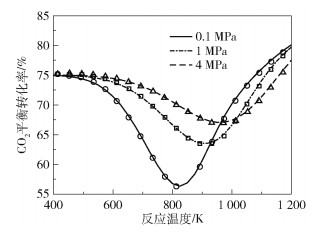
2 结果与讨论 2.1 热力学平衡计算结果为了验证本文建立的热力学平衡模型的正确性和数值算法的准确性,利用该热力学平衡模型对文献[2]中的平衡体系(该平衡体系包含CO2、H2、H2O、CO、CH3OH、C2H5OH、C1~C10直链烷烃以及C2~C10端位烯烃共25种组分)进行计算。图 1为反应温度和反应压力对文献[2]的平衡体系中CO2平衡转化率的影响。由图 1可见,利用本文热力学平衡模型计算得到的数值结果与文献[2]得到的热力学平衡态结果的吻合度较高。
|
曲线为本文数值模型的计算结果,数据点为文献[2]中的数值。 图 1 反应温度和反应压力对文献[2]的反应体系中CO2平衡转化率的影响 Fig.1 Influences of reaction temperature and reaction pressure on CO2 equilibrium conversion in the reaction system of reference [2] |
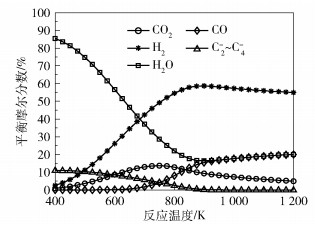
选取CO2氢化合成低碳烯烃反应的典型反应条件[2, 5-8]对热力学平衡态计算结果进行分析,图 2为p=2 MPa、M=3的条件下反应系统中各组分平衡摩尔分数随温度的变化情况。由图 2可见,CO2转化率随着反应温度的升高先减小后增大(即CO2平衡摩尔分数随反应温度的升高先增大后减小);H2O的平衡摩尔分数随着反应温度的升高先快速减小后缓慢增加;当反应温度较低时,反应系统中CO的含量约为0,CO全部转化为低碳烯烃,随着反应温度的升高,CO的平衡摩尔分数逐渐增大,相应地反应系统中低碳烯烃含量逐渐减少,这是由于FTS反应是放热反应,高温条件不利于反应的进行。
|
图 2 p=2 MPa、M=3的条件下各组分平衡摩尔分数随反应温度的变化 Fig.2 Equilibrium mole fraction of each component as a function of reaction temperature at p=2 MPa and M=3 |
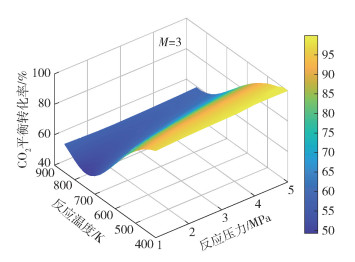
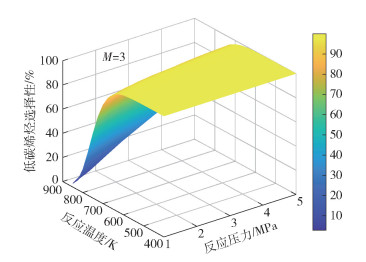
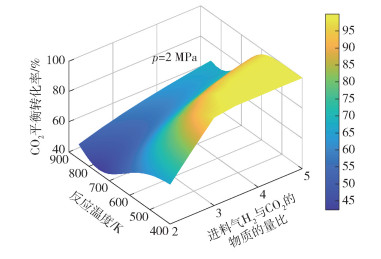
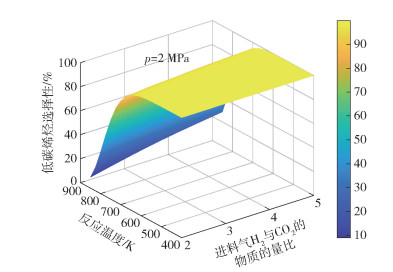
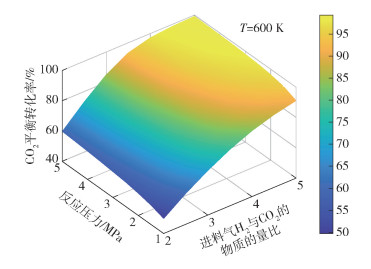
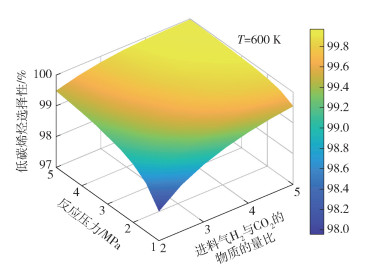
图 3~8分别为CO2平衡转化率XCO2和低碳烯烃选择性SHC随反应温度T、反应压力p和进料气H2与CO2的物质的量比M的变化情况。由图 3可见,不同反应压力条件下,CO2平衡转化率均随反应温度的升高先减小后增大,并且反应压力越大,CO2平衡转化率减小的幅度越小。随着温度的升高,吸热的RWGS反应开始占据主导,CO2平衡转化率随着温度的升高逐渐增大,反应系统内的CO摩尔分数逐渐增大(见图 2)。由图 3还可以看出,在较低温度条件下(如600 K时),CO2平衡转化率随着压力的增大而增大,这是由于在低温条件下,物质的量减小的DH反应在反应体系中占主导,压力的升高有利于平衡向消耗CO2的方向移动。由图 4可见,不同反应压力条件下,低碳烯烃选择性随温度的升高先缓慢变化后快速减小,这是因为FTS反应和DH反应均为放热反应,高温条件不利于平衡产物的生成。在高温条件下,低碳烯烃选择性随压力的增大而单调递增,这是由于生成低碳烯烃的FTS反应是物质的量减小的反应,高压条件有利于反应平衡态向正方向移动。由图 5~8可见,CO2平衡转化率和低碳烯烃选择性均随反应压力和进料气H2与CO2的物质的量比的增大而单调增大,原因是反应物H2物质的量的增加能促使反应平衡态向正方向移动。
|
图 3 M=3条件下CO2平衡转化率随反应温度和反应压力的变化 Fig.3 CO2 equilibrium conversion as a function of reaction temperature and reaction pressure at M=3 |
|
图 4 M=3条件下低碳烯烃选择性随反应温度和反应压力的变化 Fig.4 Lower olefin selectivity as a function of reaction temperature and reaction pressure at M=3 |
|
图 5 p=2 MPa条件下CO2平衡转化率随反应温度和进料气H2与CO2的物质的量比的变化 Fig.5 CO2 equilibrium conversion as a function of reaction temperature and the molar ratio of H2 to CO2 in the feed gas at p=2 MPa |
|
图 6 p=2 MPa条件下低碳烯烃选择性随反应温度和进料气H2与CO2的物质的量比的变化 Fig.6 Lower olefin selectivity as a function of reaction temperature and the molar ratio of H2 to CO2 in the feed gas at p=2 MPa |
|
图 7 T=600 K条件下CO2平衡转化率随反应压力和进料气H2与CO2的物质的量比的变化 Fig.7 CO2 equilibrium conversion as a function of reaction pressure and the molar ratio of H2 to CO2 in the feed gas at T=600 K |
|
图 8 T=600 K条件下低碳烯烃选择性随反应压力和进料气H2与CO2的物质的量比的变化 Fig.8 Lower olefin selectivity as a function of reaction pressure and the molar ratio of H2 to CO2 in the feed gas at T=600 K |
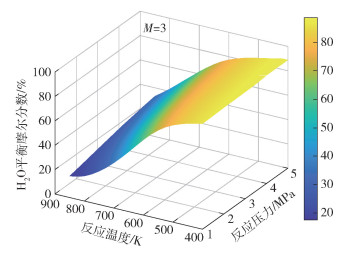
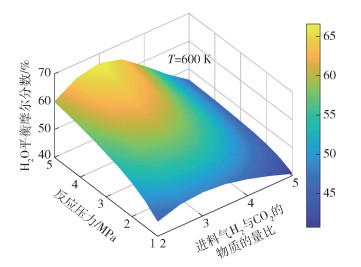
图 9~11分别为H2O的平衡摩尔分数yH2O随反应温度T、反应压力p和进料气H2与CO2的物质的量比M的变化情况。由图 9可见,在给定进料气H2与CO2的物质的量比(M=3)的条件下,H2O的平衡摩尔分数随反应温度的增大而减小,减小的幅度先增大后减小。由图 11可见,在给定的反应温度(T=600 K)条件下,H2O的平衡摩尔分数随反应压力的增大而增大,随进料气H2与CO2的物质的量比的增加先增大后减小,这是由于高压条件和过量的H2有利于FTS反应和DH反应平衡态向正方向移动,随着进料气H2与CO2的物质的量比进一步增大,H2O的含量由于反应系统中反应物CO2含量的限制而降低。压力的升高有利于低碳烯烃产物的生成,使得体系中H2O的含量增加,从而引起RWGS反应平衡态向左移动,而在高温条件下H2O的平衡摩尔分数随反应压力的变化幅度更大,导致在高温条件下CO2平衡转化率随着压力的升高而降低(图 3)。
|
图 9 M=3条件下H2O的平衡摩尔分数随反应温度和反应压力的变化 Fig.9 Equilibrium mole fraction of H2O as a function of reaction temperature and reaction pressure at M=3 |
|
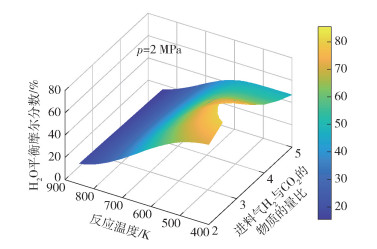
图 10 p=2 MPa条件下H2O的平衡摩尔分数随反应温度和进料气H2与CO2的物质的量比的变化 Fig.10 Equilibrium mole fraction of H2O as a function of reaction temperature and the molar ratio of H2 to CO2 in the feed gas at p=2 MPa |
|
图 11 T=600 K条件下H2O的平衡摩尔分数随反应压力和进料气H2与CO2的物质的量比的变化 Fig.11 Equilibrium mole fraction of H2O as a function of reaction pressure and the molar ratio of H2 to CO2 in the feed gas at T=600 K |
基于式(13)的回归函数模型,使用由热力学平衡模型计算的结果对模型参数进行拟合,回归方程的决定系数R2的大小可以表示回归方程对数据拟合的准确度与可信性,R2越接近1表示参数拟合效果越好[13]。表 1为使用非线性最小二乘法拟合得到的模型参数及回归方程的决定系数R2,由表 1可见,参数拟合精度均在0.92以上,说明该回归函数模型可以较好地反映CO2平衡转化率、低碳烯烃选择性、H2O的平衡摩尔分数与反应温度、反应压力和进料气H2与CO2的物质的量比之间的关系。
| 下载CSV 表 1 回归函数模型参数及决定系数 Table 1 Regression function model parameters and determination coefficients |
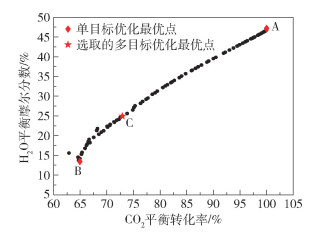
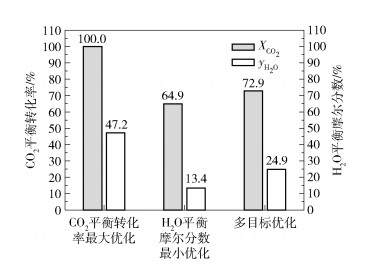
图 12为反应系统基于CO2平衡转化率最大和H2O平衡摩尔分数最小多目标优化的Pareto最优前沿,图 13为单目标优化与多目标优化结果比较。图 12中,A点表示CO2平衡转化率最大的单目标优化最优点,此时CO2平衡转化率最大在多目标优化中的优化权重为1,H2O的平衡摩尔分数最小在多目标优化中的优化权重为0;B点表示H2O平衡摩尔分数最小的单目标优化最优点,此时H2O的平衡摩尔分数最小在多目标优化中的优化权重为1,CO2平衡转化率最大在多目标优化中的优化权重为0;C点为选取的多目标优化最优点。由图 13可见,选取的多目标优化最优点相比CO2平衡转化率最大的单目标优化结果,虽然CO2转化率从100%减少到72.9%,但同时H2O平衡摩尔分数从47.2%减少到24.9%;相比H2O平衡摩尔分数最小的单目标优化结果,虽然H2O的平衡摩尔分数从13.4%增加到24.9%,但同时CO2平衡转化率从64.9%增大到72.9%。以上结果说明C点的多目标优化性能点能够折中考虑两个优化目标,使反应系统在互相矛盾的两个优化目标中协同达到最优。
|
图 12 CO2平衡转化率最大和H2O平衡摩尔分数最小多目标优化的Pareto最优前沿 Fig.12 Pareto optimal frontier for multi-objective optimization of maximum CO2 equilibrium conversion and minimum H2O equilibrium mole fraction |
|
图 13 CO2平衡转化率最大和H2O平衡摩尔分数最小的单目标优化和多目标优化结果比较 Fig.13 Comparison of single-objective optimization and multi-objective optimization results of maximum CO2 equilibrium conversion and minimum H2O equilibrium mole fraction |
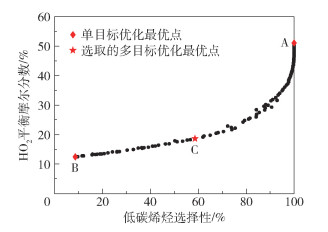
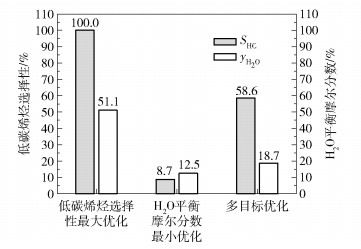
图 14为反应系统基于低碳烯烃选择性最大和H2O平衡摩尔分数最小多目标优化的Pareto最优前沿,图 15为单目标优化与多目标优化结果比较。图 14中,A点表示低碳烯烃选择性最大的单目标优化最优点,此时低碳烯烃选择性最大在多目标优化中的优化权重为1,H2O的平衡摩尔分数最小在多目标优化中的优化权重为0;B点表示H2O平衡摩尔分数最小的单目标优化最优点,此时H2O平衡摩尔分数最小在多目标优化中的优化权重为1,低碳烯烃选择性最大在多目标优化中的优化权重为0;C点为选取的多目标优化最优点。由图 15可见,选取的多目标优化最优点相比低碳烯烃选择性最大的单目标优化结果,虽然低碳烯烃选择性从100%减少到58.6%,但同时H2O的平衡摩尔分数从51.1%减少到18.7%;相比H2O平衡摩尔分数最小的单目标优化结果,虽然H2O平衡摩尔分数从12.5%增加到18.7%,但同时低碳烯烃选择性从8.7%增大到58.6%。以上结果说明C点的多目标优化性能点能够折中考虑两个优化目标,使反应系统在互相矛盾的两个优化目标中协同达到最优。
|
图 14 低碳烯烃选择性最大和H2O平衡摩尔分数最小多目标优化的Pareto最优前沿 Fig.14 Pareto optimal frontier for multi-objective optimization of maximum lower olefin selectivity and minimum H2O equilibrium mole fraction |
|
图 15 低碳烯烃选择性最大和H2O平衡摩尔分数最小的单目标优化和多目标优化结果比较 Fig.15 Comparison of single-objective optimization and multi-objective optimization results of maximum lower olefin selectivity and minimum H2O equilibrium mole fraction |
本文针对二氧化碳氢化合成低碳烯烃反应进行了热力学分析和优化,使用Gibbs自由能最小化方法建立了反应体系的平衡态热力学模型;基于统计学理论建立了CO2平衡转化率、低碳烯烃选择性和H2O平衡摩尔分数的回归函数模型,并利用模拟计算的数据对模型参数进行了拟合;最后结合NSG A-Ⅱ多目标优化算法,分别以CO2平衡转化率最大和H2O平衡摩尔分数最小、低碳烯烃选择性最大和H2O平衡摩尔分数最小为优化目标对反应系统进行了优化,得到相应的Pareto最优前沿。主要结论如下:
(1) CO2平衡转化率随着反应温度的升高先减小后增大;不同反应压力条件下,低碳烯烃选择性随温度的升高先缓慢变化后快速减小,在高温条件下,低碳烯烃选择性随压力的增大单调递增;H2O的平衡摩尔分数随着反应温度的升高先快速减小后缓慢增加。
(2) 多目标最优方法能够折中考虑多个相互矛盾的目标,使反应系统协同达到最优。反应系统经过多目标优化后,相比仅考虑反应效率的单目标优化结果,H2O的平衡摩尔分数从47.2%和51.1%分别减少到24.9%和18.7%;相比仅考虑催化剂水解失活风险的单目标优化结果,CO2平衡转化率和低碳烯烃选择性从64.9%和8.7%分别增加到72.9%和58.6%。
| [1] |
高鹏, 崔勖, 钟良枢, 等. CO/CO2加氢高选择性合成化学品和液体燃料[J]. 化工进展, 2019, 38(1): 183-195. GAO P, CUI X, ZHONG L S, et al. CO/CO2 hydrogenation to chemicals and liquid fuels with high selectivity[J]. Chemical Industry and Engineering Progress, 2019, 38(1): 183-195. (in Chinese) |
| [2] |
梁兵连, 段洪敏, 侯宝林, 等. 二氧化碳加氢合成低碳烯烃的研究进展[J]. 化工进展, 2015, 34(10): 3746-3754. LIANG B L, DUAN H M, HOU B L, et al. Progress in the catalytic hydrogenation of carbon dioxide to light olefines[J]. Chemical Industry and Engineering Progress, 2015, 34(10): 3746-3754. (in Chinese) |
| [3] |
邵斌, 孙哲毅, 章云, 等. 二氧化碳转化为合成气及高附加值产品的研究进展[J]. 化工进展, 2022, 41(3): 1136-1151. SHAO B, SUN Z Y, ZHANG Y, et al. Recent progresses in CO2 to syngas and high value-added products[J]. Chemical Industry and Engineering Progress, 2022, 41(3): 1136-1151. (in Chinese) |
| [4] |
向航, 李静, 曹建新, 等. CO2绿色化合成低碳烯烃Fe基催化剂研究进展[J]. 现代化工, 2015, 35(2): 27-31, 33. XIANG H, LI J, CAO J X, et al. Recent progress in Fe-based catalysts for green synthesis of light olefins from carbon dioxide[J]. Modern Chemical Industry, 2015, 35(2): 27-31, 33. (in Chinese) |
| [5] |
苏春彦, 檀建群, 王承学. 铁基催化剂上二氧化碳加氢合成低碳烯烃的研究[J]. 天然气化工(C1化学与化工), 2013, 38(3): 34-38, 47. SU C Y, TAN J Q, WANG C X. Study on CO2 hydrogenation to light olefins over iron-based catalysts[J]. Natural Gas Chemical Industry, 2013, 38(3): 34-38, 47. (in Chinese) |
| [6] |
刘业奎, 王黎, 侯栋, 等. 二氧化碳加氢合成低碳烯烃反应平衡体系热力学研究[J]. 催化学报, 2004, 25(3): 210-218. LIU Y K, WANG L, HOU D, et al. Study on thermodynamics of balanceable reaction system for hydrogenation of carbon dioxide to light alkenes[J]. Chinese Journal of Catalysis, 2004, 25(3): 210-218. (in Chinese) DOI:10.3321/j.issn:0253-9837.2004.03.011 |
| [7] |
张磊, 陈林根, 夏少军, 等. CO2加氢合成低碳烯烃反应热力学分析[J]. 工程热物理学报, 2017, 38(6): 1135-1143. ZHANG L, CHEN L G, XIA S J, et al. Thermodynamics analyses of hydrogenation of carbon dioxide to light olefins[J]. Journal of Engineering Thermophysiscs, 2017, 38(6): 1135-1143. (in Chinese) |
| [8] |
TORRENTE-MURCIANO L, MATTIA D, JONES M D, et al. Formation of hydrocarbon via CO2 hydrogenation: a thermodynamic study[J]. Journal of CO2 Utilization, 2014, 6: 34-39. DOI:10.1016/j.jcou.2014.03.002 |
| [9] |
SWAPNESH A, SRIVASTAVA V C, MALL I D. Comparative study on thermodynamic analysis of CO2 utilization reactions[J]. Chemical Engineering Technology, 2014, 37(10): 1765-1777. DOI:10.1002/ceat.201400157 |
| [10] |
JIA G X, TAN Y S, HAN Y Z. A comparative study on the thermodynamics of dimethyl ether synthesis from CO hydrogenation and CO2 hydrogenation[J]. Industrial & Engineering Chemistry Research, 2006, 45(3): 1152-1159. |
| [11] |
TABRIZI F F, MOUSAVI S A H S, ATASHI H. Thermodynamic analysis of steam reforming of methane with statistical approaches[J]. Energy Conversion and Management, 2015, 103: 1065-1077. |
| [12] |
ATASHI H, GHOLIZADEH J, TABRIZI F F, et al. Thermodynamic analysis of carbon dioxide reforming of methane to syngas with statistical methods[J]. International Journal of Hydrogen Energy, 2017, 42(8): 5464-5471. |
| [13] |
高宠明, 叶昊天, 邹雄, 等. 考虑NOx排放的制氢操作参数多目标优化[J]. 大连理工大学学报, 2020, 60(3): 237-243. GAO C M, YE H T, ZOU X, et al. Multi-objective optimization of hydrogen production operation parameters considering NOx emission[J]. Journal of Dalian University of Technology, 2020, 60(3): 237-243. (in Chinese) |
| [14] |
WANG F Q, JING L, CHENG Z M, et al. Combination of thermodynamic analysis and regression analysis for steam and dry methane reforming[J]. International Journal of Hydrogen Energy, 2019, 44(30): 15795-15810. |
| [15] |
SHAHHOSSEINI H R, FARSI M, EINI S. Multi-objective optimization of industrial membrane SMR to produce syngas for Fischer-Tropsch production using NSG A-Ⅱ and decision makings[J]. Journal of Natural Gas Science and Engineering, 2016, 32: 222-238. |
| [16] |
DEHGHANI Z, RAHIMPOUR M R, SHARIATI A. Simulation and multi-objective optimization of a radial flow gas-cooled membrane reactor, considering reduction of CO2 emissions in methanol synthesis[J]. Journal of Environmental Chemical Engineering, 2021, 9(2): 104910. |
| [17] |
MCDONALD C M, FLOUDAS C A. Global optimization and analysis for the Gibbs free energy function using the UNIFAC, Wilson, and ASOG equations[J]. Industrial & Engineering Chemistry Research, 1995, 34(5): 1674-1687. |
| [18] |
SOAVE G. Equilibrium constants from a modified Redlich-Kwong equation of state[J]. Chemical Engineering Science, 1972, 27(6): 1197-1203. |
| [19] |
YAWS C L. Chemical properties handbook[M]. New York: McGraw-Hill, 1999.
|







