2. 北京化工大学 智能过程系统工程教育部工程研究中心, 北京 100029
2. Engineering Research Center of Intelligent Process Systems Engineering, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
随着科学技术的不断发展,化工过程控制系统越来越集成化、精细化、自动化,复杂化工生产过程的安全性和可靠性也越来越需要加以重视。在生产过程中,当化工系统某一环节发生故障时,不及时的处理可能会造成故障扩大,进而导致重大事故的发生。因此,对于复杂化工生产过程的监控是十分必要的。化工生产过程往往是一个动态系统,在这个过程中会产生大量过程数据,对化工生产过程数据进行故障诊断以及故障诊断技术的分析,当系统产生异常时,将有助于工作人员及时采取相应措施,将损失降至最低[1]。
化工过程的故障诊断主要用于判断化工生产过程中的参数、状态及其特征量是否都处于预定范围[2],如果所有化工过程参数都在预定范围内,且波动范围在正常范围内,则认为其运行正常,否则认为系统存在故障。研究者们基于化工过程数据信息开展了许多针对故障诊断的研究。文献[3]考虑过程系统数据变量之间的关系,使用复杂网络理论构建了故障诊断模型。文献[4]利用主成分分析算法对化工过程进行故障分析。文献[5]基于数据驱动的方法对田纳西-伊斯曼(Tennessee Eastman,TE)过程进行故障诊断与过程监控。然而,由于上述方法是将高维特征空间映射到低维特征空间,使得所得特征不再是原始特征,这导致了此类故障诊断模型不具有很好的可解释性。因此,为了提高故障诊断模型的可解释性,并保留原始数据的特征信息,文献[6]采用融合随机黑洞策略的灰狼优化算法进行工业控制系统的故障诊断,并在算法求解过程中保留了原始数据的特征信息。文献[7]基于数据驱动的方法对化工过程的故障诊断进行探讨,利用控制图法、定量知识法、多变量统计分析及规则变量分析等方法提升了模型的可解释性。文献[8]指出特征选择可以提升模型在面对体量大、维度高的数据时的表现,而且保持了原有特征。
拉斯维加斯包裹式(Las Vegas wrapper,LVW)方法是一种常用的包裹式特征选择方法[9]。目前, 包裹式特征选择方法在随机策略搜索特征子集中的应用相对较多。文献[10]采用基于权重分析的包裹式特征选择方法,可以有效减少特征的数量,达到提高准确性的目的。文献[11]基于LVW框架给出了一种新的无监督特征选择方法,使用随机策略来进行子集搜索,并以最终分类器的误差作为特征子集的评级准则。文献[12]采用一种基于LVW嵌入式算法特征提取器和集合学习的改进模型,提高了血液透析时机的预测精度。但是,传统的LVW的特征选择具有盲目性,找到最优特征组合的时间开销巨大。
遗传算法(genetic algorithm,GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型[13-15]。遗传算法是一种自适应全局优化搜索算法,在化工领域应用广泛[16-18]。由于GA具有高效的随机搜索能力,并且具备可扩展性,激发了国内外学者的研究兴趣。文献[19]使用并行遗传算法提高了化工过程系统中大规模优化问题的求解效率;文献[20]采用遗传算法进行分散常规控制系统结构设计的优化;文献[21]针对工艺过程数据的误差,使用遗传算法提高了数据校正方法的性能。
针对化工过程产生的大量过程数据,采用传统的特征提取算法进行训练迭代需要消耗大量的时间,并且算法的准确率不高。因此,本文提出一种结合GA的改进LVW特征选择算法(GA-LVW)。首先采用增强的LVW嵌入式算法,通过随机策略搜索特征子集,找到最有利于学习者性能的最佳特征组合,同时,结合GA在寻求最优解问题上的优势改进LVW搜索的盲目性,并直观地保留了原始特征,使得GA-LVW算法提升了故障诊断的精确度。然后,在TE过程基础上对温度异常进行故障诊断,实验结果表明,GA-LVW算法的检测准确率高于未改进的LVW算法。同时,结合不同分类器的GA-LVW算法使得故障诊断的准确率得到进一步提高,这保障了复杂化工生产过程的安全性和可靠性。
1 改进的GA-LVW算法 1.1 GA算法GA通过模拟自然进化过程,可用来搜索最优解,是一种启发式搜索方法,将其应用于特征选择[22]的具体步骤如下。
1) 编码 每一个特征选择是否用1或0表示,1表示选择该特征,0表示不选择该特征。第一代种群由随机函数随机生成。本文使用的随机函数是Python的random模块下的choice函数,用fr表示,它可以从序列中随机选取一个元素。
| $ f_r={random} {. choice }(0, 1) $ | (1) |
2) 适应度计算 计算个体i的适应度值fi,适应度值用于评价个体优劣,由适应度函数fitness计算得到。需要对每一代种群pop(t)中的每个个体i进行计算。
| $ f_i= { fitness }\left({pop}_i(t)\right) $ | (2) |
3) 选择 选择是一个优胜劣汰的过程,即从旧群体中以一定概率选择优良个体组成新的种群,以繁殖得到下一代个体。个体适应度值越高,被选择的机会就越大。本文使用随机竞争法,如式(3)所示,从种群中随机选取两个个体(random(popi),random(popj)),比较其适应度值大小,适应度值大的作为winner,用于交叉产生下一代种群。
| $ winner = max\{f_{random(pop_i)} , f_{random(pop_j)} \} $ | (3) |
4) 交叉 从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体。式(4)是交叉前的父代,式(5)是交叉后得到的两个新子代,i代表了交叉点的位置。
| $ \left\{\begin{array}{l} b_1 b_2 b_3 \cdots b_i \mid b_{i+1} b_{i+2} \cdots b_n \\ c_1 c_2 c_3 \cdots c_i \mid c_{i+1} c_{i+2} \cdots c_n \end{array}\right. $ | (4) |
| $ \left\{\begin{array}{l} b_1 b_2 b_3 \cdots c_i \mid b_{i+1} b_{i+2} \cdots b_n \\ c_1 c_2 c_3 \cdots b_i \mid c_{i+1} c_{i+2} \cdots c_n \end{array}\right. $ | (5) |
5) 变异 为了跳出局部最小并且加速算法的收敛,在搜索过程中需要对个体进行变异。选择一个较小的值作为变异率,对新种群中的一些个体基因随机选择一个进行反转。在实际应用中,主要采用单点变异的方法,又称位变异,即只需要对基因序列中的某一位进行变异。以二进制编码为例,即0变为1,而1变为0。个体变异过程如式(6)所示,其中个体的第5位发生变异。
| $ \begin{array}{l} 0111110110\\ 0111010110 \end{array} $ | (6) |
LVW算法是一种典型的包裹式特征选择方法,它在拉斯维加斯方法框架下使用随机策略来进行子集搜索,并以最终分类器的误差作为特征子集评价准则。同时,不同于过滤式特征选择将特征选择和学习训练分割开[23],LVW直接对指定学习器进行优化,因此最终的分类效果更好。LVW的具体步骤如下。
1) 给定数据集D,LVW通过随机搜索得到一个特征子集A′,进而形成由特征子集构成的子数据集DA′。将DA′划分为验证集和训练集,在指定的学习器ζ上进行k折交叉验证,得到交叉验证误差Ei,对交叉验证误差Ei进行k次累计求和得到平均误差Ei′。
| $ E_i = { CrossValidation }\left(\zeta\left(D^{A^{\prime}}\right)\right) $ | (7) |
| $ E_i^{\prime} =\frac{1}{k} \sum\limits_{i=1}^k E_i $ | (8) |
除将交叉验证的结果作为评价标准外,还可以使用测试数据集在训练模型上的泛化误差E′作为LVW的评价标准。
| $ E^{\prime}= { Generalization }\left(\zeta_{\text {train }}\left(D_{\text {test }}^{A^{\prime}}\right)\right) $ | (9) |
式中,DtestA′为特征子集构成的测试子数据集。
2) 当满足式(10)条件时,更新全局最小误差E、全局最优特征子集A*、特征子集数d′和全局最优特征数d。
| $ \left(E^{\prime}<E\right) \operatorname{or}\left(\left(E^{\prime}=E\right) \text { and }\left(d^{\prime}<d\right)\right) $ | (10) |
3) 重复执行上述两个步骤,直到满足某种设定的终止条件。
LVW每次搜索的结果都是不相关的,具有盲目性,如果可使下一次的搜索结果比当前搜索结果要好,就能够提升搜索的效率。因此将LVW中的随机搜索策略替换为智能搜索策略,以提升搜索算法性能。GA-LVW将GA的适应度函数设计为验证集在训练模型上交叉验证的平均误差或测试集在训练模型上的泛化误差,这不仅提升了搜索效率,又保留了LVW在特征选择的同时可以完成对指定学习器训练的特点。本文设置的适应度函数为
| $ { fitness }(i)=E_i(i) \text { or } E^{\prime}(i) $ | (11) |
首先,利用GA算法对特征种群进行编码与初始化;其次,LVW通过随机搜索得到一个特征子集,进而形成由特征子集构成的子数据集;然后,将特征子集划分为验证集和训练集,对选择、交叉、变异之后的种群个体适应度进行计算,将适应度大的种群特征予以保留,作为当前的最优种群,同时更新最优的特征子集。与此同时,根据个体的适应度,确定是否需要对个体进行交叉和/或变异,若确定不需要对个体进行交叉和/或变异,则输出目标特征集;最后,判断是否满足GA算法的结束条件,如果满足则输出训练模型与优化特征子集。GA-LVW算法流程如图 1所示。
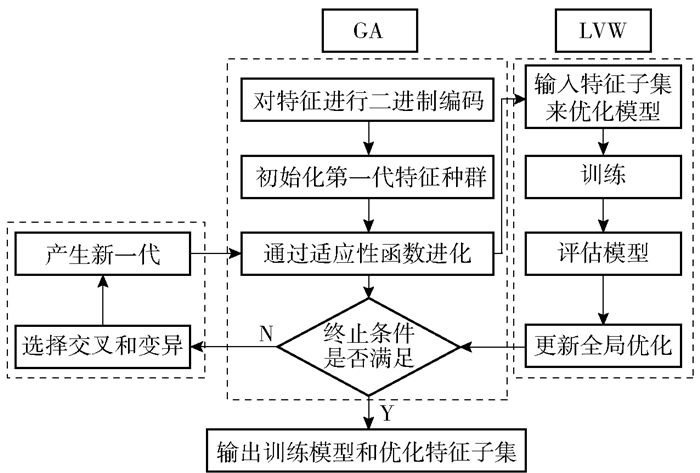
|
图 1 GA-LVW算法流程图 Fig.1 The GA-LVW algorithm flow chart |
TE过程为评价过程控制和监控方法提供了一个现实的工业过程,对一般化工过程具有一定的代表性[24]。利用在TE过程仿真中采集的数据来验证各种故障检测和诊断方法的有效性,已在故障诊断领域得到了广泛的应用[25-26]。
TE过程有4种气体反应物A、C、D和E,在经过化工流程反应后,最终生成3种产物G、H和F,其中G和H是目标气态产物,F是液态副产物,相应的反应方程式如下。
| $ \mathrm{A}+\mathrm{C}+\mathrm{D} \rightarrow \mathrm{G} $ | (12) |
| $ \mathrm{A}+\mathrm{C}+\mathrm{E} \rightarrow \mathrm{H} $ | (13) |
| $ \mathrm{A}+\mathrm{E} \rightarrow \mathrm{F} $ | (14) |
| $ 3 \mathrm{D} \rightarrow 2 \mathrm{F} $ | (15) |
产物G对温度有很高的要求,具有温度敏感性,反应过程中细微的温度偏差就会造成结果的巨大偏差,因此在整个TE过程中对温度的精确控制极其重要。TE过程分为5个单元,分别是反应器、冷凝器、循环压缩机、气液分离器和汽提塔。在反应器中催化剂的催化下气态反应物A、C、D和E发生化学反应,反应放热的气态产物经冷凝器后流入气液分离器,其中的气态部分经过循环压缩机返回至反应器继续参与反应,副产物和未参与反应的B经过排空回路排出,液态部分进入汽提塔进行分离,产物G和H从其底部流出。TE过程的工艺流程图如图 2所示。TE过程包含的变量多、耦合性强,共包含41个测量变量和12个操作变量[27]。
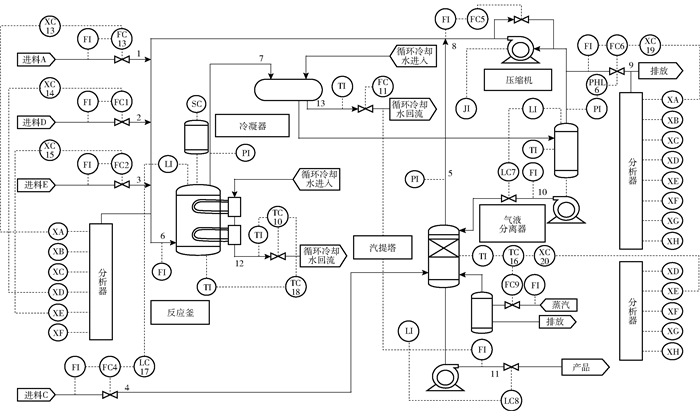
|
图 2 TE过程流程图 Fig.2 The TE process flow chart |
本文使用的数据来源是Ricker[28]提出的TE生产过程数据。TE过程每小时产生100组数据,通过50 h的运行,最终产生5 000组数据。为了模拟TE过程温度异常的故障诊断实验,采取偏置注入的方法使原始温度数据发生异常变化,并利用GA-LVW算法得到训练模型与优化特征子集。同时,由于支持向量机(SVM)[29]、K最近邻(KNN)[30]和朴素贝叶斯(NB)[31]等分类器具备无需训练、分类时间短、分类效果好等良好特性,利用这些分类器对这种温度扰动故障进行分类,进而对TE过程中出现的温度扰动故障进行准确诊断。
3.1 故障诊断实验通过模拟TE过程温度异常的故障诊断实验,验证GA-LVW算法的有效性。这种故障诊断的形式如式(16)所示。
| $ \tilde{a}_i(t)= \begin{cases}a_i(t)+b, & t \in T_i \\ a_i(t), & t \notin T_i\end{cases} $ | (16) |
式中,
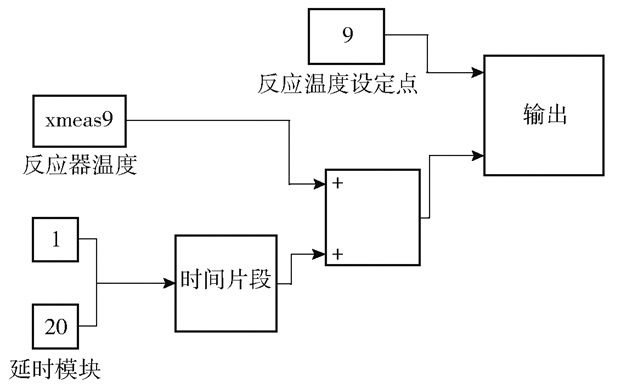
|
图 3 加入偏置注入的反应器温控回路 Fig.3 Reactor temperature control loop with bias injection |
在偏置注入信号b=1、0.1和0.05上进行实验,使用b=1的数据集进行模型训练,b=0.1和0.05的数据集进行泛化误差测试。将迭代次数设置为100,种群大小设置为10,变异率设为0.1。将SVM、KNN和NB这3种常用分类器分别嵌入GA-LVW,用于对温度扰动故障进行分类和诊断准确率计算。在实验过程中不同迭代次数下的准确率结果如图 4~6所示。
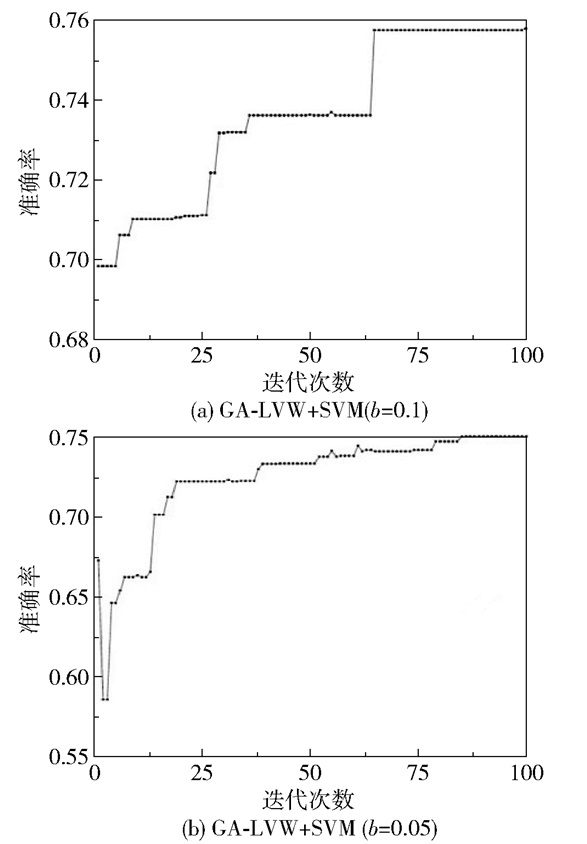
|
图 4 GA-LVW+SVM算法迭代过程 Fig.4 Iterative process of the GA-LVW+SVM algorithm |
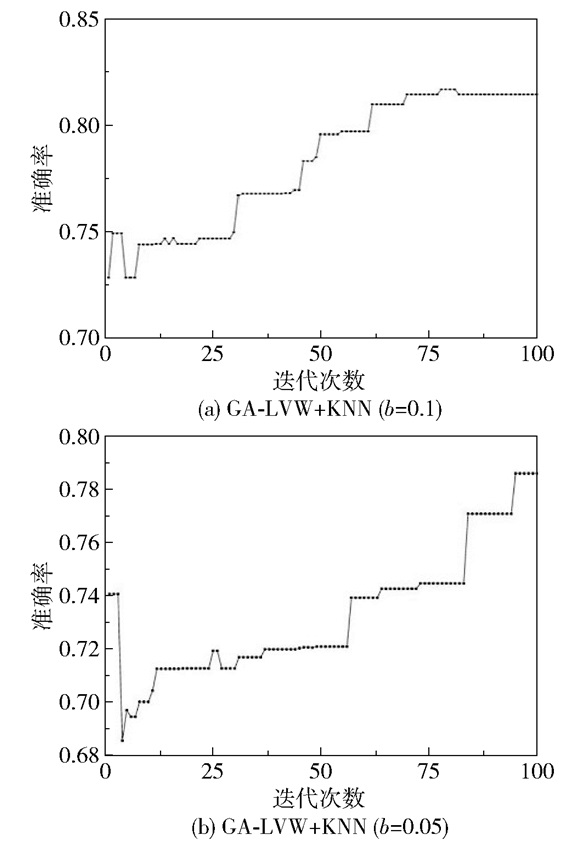
|
图 5 GA-LVW+KNN算法迭代过程 Fig.5 Iterative process of the GA-LVW+KNN algorithm |
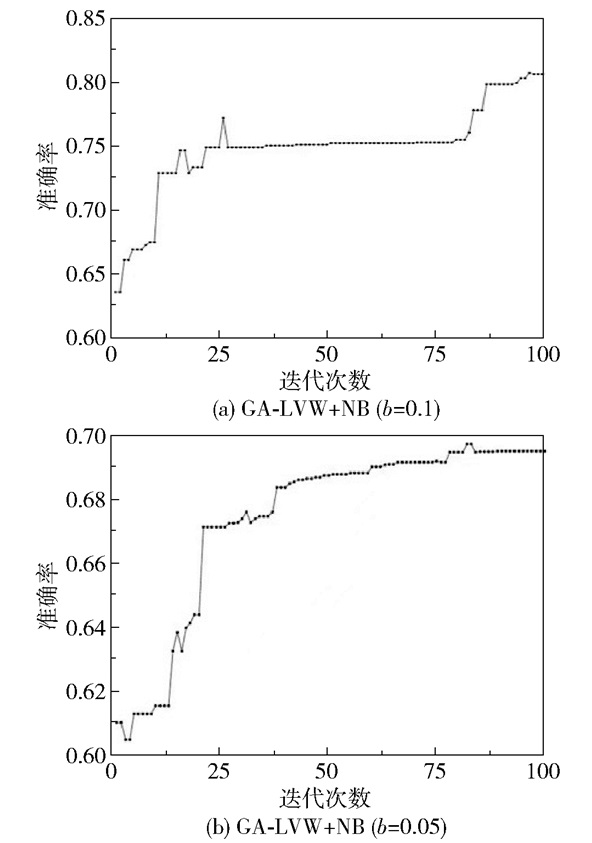
|
图 6 GA-LVW+NB算法迭代过程 Fig.6 Iterative process of the GA-LVW+NB algorithm |
由图 4~6的GA-LVW算法迭代结果分析可知,将GA-LVW算法用于特征选择可以不断优化特征子集。同时,由于SVM、KNN、NB分类器的特征选择机理不同,使得不同的分类器选择的特征类型也不相同,进而致使结合不同分类器的GA-LVW算法对故障诊断的检测准确率也不相同。
对比不同注入偏置下GA-LVW+SVM、GA-LVW+KNN、GA-LVW+NB算法的迭代结果,可以看出注入偏置为0.1时的故障诊断准确率高于注入偏置为0.05时的相应值。其中,算法迭代中出现的准确率的偶尔下降,主要是GA-LVW算法为了跳出局部最优而进行的新尝试。
3.2 实验结果表 1展示了3种改进后的算法GA-LVW+SVM、GA-LVW+KNN、GA-LVW+NB与未改进算法SVM、KNN、NB、LVW+SVM、LVW+KNN、LVW+NB的检测准确率对比结果。其中,LVW系列算法和GA-LVW系列算法都进行了100次迭代以比较在相同的迭代次数下分类器的检测性能;SVM算法使用高斯核函数,并将高斯核的带宽设置为0.01。从表 1结果可以得到以下两点:1)特征选择可以提升检测准确率,在相同迭代次数下,GA-LVW可以进一步提升LVW的检测准确率,从而提高搜索的稳定性和找到近似最优解的速度;2)GA-LVW+KNN算法在b=0.1和0.05时均取得了最好的效果,检测准确率分别达到0.817和0.786。此外,训练GA-LVW的时间开销主要依赖于其嵌入的学习器,在本文实验的数据量下,训练SVM需要0.12 s,而训练KNN仅需要0.06 s。
| 下载CSV 表 1 检测准确率对比 Table 1 Comparison of detection accuracy |
表 2是GA-LVW的特征选择结果,表中数字代表TE过程41个测量变量的编号,具体对应关系可见文献[27]。在表 2所列的特征选择结果中,存在一部分冗余特征,因此实验统计了3次特征选择中出现频率较高的特征。当b=0.1时,在3次特征选择中均出现的特征有1号特征(A物料流量)和29号特征(放空气体中A组分的色谱测量值)。当b=0.05时,在3次特征选择中均出现的特征有1号特征、7号特征(反应器压强)和37号特征(产品中D组分的色谱测量值)。因此,在实际场景中,操作人员可根据相关组分的流量、色谱测量值以及反应器的物理特征来检测温度的异常变化。
| 下载CSV 表 2 GA-LVW特征选择结果 Table 2 Feature selection results of the GA-LVW |
表 3对比了特征选择后的特征个数。实验中原始特征共有41个,从结果可以看出,经过特征选择后特征数量有所减少,并且本文所提的GA-LVW算法相比于未改进的LVW算法,特征数量进一步减少,这使得操作人员可以更加精准地定位问题所在,体现了所提算法的有效性。
| 下载CSV 表 3 不同算法下的特征个数对比 Table 3 Comparison of the number of features under different algorithms |
本文针对TE化工过程中温度异常变化的故障诊断,提出一种基于遗传算法改进的拉斯维加斯包裹式算法(GA-LVW)。首先,采用增强的LVW嵌入式算法进行特征子集随机搜索,找到最有利于学习器性能的特征子集。其次,利用GA的优点改进了LVW在特征选择时的盲目性,使得特征组合能够快速有效地收敛到近似最优,同时也保留了数据的原始特征,使得模型更具直观性。最后,实验结果表明,在迭代次数相同且减少特征数量的情况下,GA-LVW算法仍然保持了较高的检测准确率。当偏置值为0.1时,与KNN、LVW+KNN等算法相比,GA-LVW算法的故障诊断准确率分别提高了0.200 8、0.102 6,当偏置值为0.05时,与KNN、LVW+KNN等算法相比,GA-LVW算法的故障诊断准确率分别提高了0.147 2、0.079 2。此外,由于GA-LVW具有可扩展性,下一步计划将精英保留的遗传算法、加入灾变的遗传算法等搜索算法与GA-LVW算法进行结合,对此类算法在故障诊断中的应用作进一步研究。
| [1] |
黄启明, 钱宇, 林伟璐, 等. 化工过程故障诊断研究进展[J]. 化工自动化及仪表, 2000, 27(3): 1-5. HUANG Q M, QIAN Y, LIN W L, et al. Advances of fault diagnosis for chemical process[J]. Control and Instruments in Chemical Industry, 2000, 27(3): 1-5. (in Chinese) DOI:10.3969/j.issn.1000-3932.2000.03.001 |
| [2] |
李传坤, 赵东风, 王春利, 等. 一种化工过程故障诊断知识自动化方法研究[J]. 高校化学工程学报, 2018, 32(2): 393-400. LI C K, ZHAO D F, WANG C L, et al. Study on a knowledge automation method for fault diagnosis of chemical processes[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(2): 393-400. (in Chinese) DOI:10.3969/j.issn.1003-9015.2018.02.018 |
| [3] |
陈雨, 韩永明, 王尊, 等. 基于数据复杂网络理论的系统故障检测方法[J]. 化工学报, 2014, 65(11): 4503-4508. CHEN Y, HAN Y M, WANG Z, et al. System fault detection based on data-driven and complex networks theory[J]. CIESC Journal, 2014, 65(11): 4503-4508. (in Chinese) DOI:10.3969/j.issn.0438-1157.2014.11.041 |
| [4] |
蔡配配, 邓晓刚, 曹玉苹, 等. 基于WPRKPCA的非线性化工过程微小故障检测[J]. 化工进展, 2019, 38(12): 5247-5256. CAI P P, DENG X G, CAO Y P, et al. Incipient fault detection of nonlinear chemical processes based on weighted probability related KPCA[J]. Chemical Industry and Engineering Progress, 2019, 38(12): 5247-5256. (in Chinese) |
| [5] |
YIN S, DING S X, HAGHANI A, et al. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process[J]. Journal of Process Control, 2012, 22(9): 1567-1581. DOI:10.1016/j.jprocont.2012.06.009 |
| [6] |
耿志强, 曾荣甫, 徐园, 等. 融合灰狼优化算法在工控系统入侵检测中的应用[J]. 化工学报, 2020, 71(3): 1080-1087. GENG Z Q, ZENG R F, XU Y, et al. Intrusion detection of industrial control system based on grey wolf optimization integrated random black hole[J]. CIESC Journal, 2020, 71(3): 1080-1087. (in Chinese) |
| [7] |
李晗, 萧德云. 基于数据驱动的故障诊断方法综述[J]. 控制与决策, 2011, 26(1): 1-9. LI H, XIAO D Y. Survey on data driven fault diagnosis methods[J]. Control and Decision, 2011, 26(1): 1-9. (in Chinese) |
| [8] |
王艳丽, 梁静, 薛冰, 等. 基于进化计算的特征选择方法研究概述[J]. 郑州大学学报(工学版), 2020, 41(1): 49-57. WANG Y L, LIANG J, XUE B, et al. Research on evolutionary computation for feature selection[J]. Journal of Zhengzhou University(Engineering Science), 2020, 41(1): 49-57. (in Chinese) |
| [9] |
叶吉祥, 龚希龄. 一种快速的Wrapper式特征子集选择新方法[J]. 长沙理工大学学报(自然科学版), 2010, 7(4): 69-73. YE J X, GONG X L. A novel fast Wrapper for feature subset selection[J]. Journal of Changsha University of Science and Technology(Natural Science), 2010, 7(4): 69-73. (in Chinese) DOI:10.3969/j.issn.1672-9331.2010.04.012 |
| [10] |
HSU C N, HUANG H J, SCHUSCHEL D. The ANNIGMA-wrapper approach to fast feature selection for neural nets[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2002, 32(2): 207-212. DOI:10.1109/3477.990877 |
| [11] |
陈彤, 陈秀宏. 特征自表达和图正则化的鲁棒无监督特征选择[J]. 智能系统学报, 2022, 17(2): 286-294. CHEN T, CHEN X H. Feature self-representation and graph regularization for robust unsupervised feature selection[J]. CAAI Transactions on Intelligent Systems, 2022, 17(2): 286-294. (in Chinese) |
| [12] |
XIONG C Z, SU M L, JIANG Z T, et al. Prediction of hemodialysis timing based on LVW feature selection and ensemble learning[J]. Journal of Medical Systems, 2019, 43(1): 18. DOI:10.1007/s10916-018-1136-x |
| [13] |
KATOCH S, CHAUHAN S S, KUMAR V. A review on genetic algorithm: past, present, and future[J]. Multimedia Tools and Applications, 2021, 80(5): 8091-8126. DOI:10.1007/s11042-020-10139-6 |
| [14] |
WHITLEY D. A genetic algorithm tutorial[J]. Statistics and Computing, 1994, 4(2): 65-85. |
| [15] |
葛继科, 邱玉辉, 吴春明, 等. 遗传算法研究综述[J]. 计算机应用研究, 2008, 25(10): 2911-2916. GE J K, QIU Y H, WU C M, et al. Summary of genetic algorithms research[J]. Application Research of Computers, 2008, 25(10): 2911-2916. (in Chinese) DOI:10.3969/j.issn.1001-3695.2008.10.008 |
| [16] |
郑启富, 陈德钊. 优进遗传算法及其在化工数据处理中的应用[J]. 浙江大学学报(工学版), 2003, 37(3): 303-306, 313. ZHENG Q F, CHEN D Z. Eugenic evolution genetic algorithm and its application for chemical engineering data processing[J]. Journal of Zhejiang University(Engineering Science), 2003, 37(3): 303-306, 313. (in Chinese) DOI:10.3785/j.issn.1008-973X.2003.03.010 |
| [17] |
杨来顺, 王建星, 孙煜, 等. 基于遗传算法的管式除雾器多目标优化设计[J]. 高校化学工程学报, 2020, 34(3): 792-801. YANG L S, WANG J X, SUN Y, et al. Multi-objective optimization of a tube separator by genetic algorithm[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(3): 792-801. (in Chinese) DOI:10.3969/j.issn.1003-9015.2020.03.031 |
| [18] |
王江, 翟玉玲, 姚沛滔, 等. 基于多目标遗传算法的微通道结构优化[J]. 高校化学工程学报, 2020, 34(4): 1034-1043. WANG J, ZHAI Y L, YAO P T, et al. Structural optimization of microchannels based on multi-objective genetic algorithm[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(4): 1034-1043. (in Chinese) DOI:10.3969/j.issn.1003-9015.2020.04.025 |
| [19] |
康丽霞, 姜楠, 夏明星, 等. 基于OpenMP的并行GA加速求解换热网络设计[J]. 高校化学工程学报, 2016, 30(2): 431-438. KANG L X, JIANG N, XIA M X, et al. Parallel genetic algorithm for design of HEN based on OpenMP system[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(2): 431-438. (in Chinese) DOI:10.3969/j.issn.1003-9015.2016.02.026 |
| [20] |
李凡, 许锋, 罗雄麟. 分散常规控制系统结构设计的遗传算法求解[J]. 化工学报, 2018, 69(S2): 266-273. LI F, XU F, LUO X L. Control configuration design with genetic algorithm for decentralized control system[J]. CIESC Journal, 2018, 69(S2): 266-273. (in Chinese) |
| [21] |
YÉLAMOS I, MÉNDEZ C, PUIGJANER L. Enhancing dynamic data reconciliation performance through time delays identification[J]. Chemical Engineering and Processing, 2007, 46(12): 1251-1263. DOI:10.1016/j.cep.2006.10.013 |
| [22] |
ALI W, AHMED A A. Hybrid intelligent phishing website prediction using deep neural networks with genetic algorithm-based feature selection and weighting[J]. IET Information Security, 2019, 13(6): 659-669. DOI:10.1049/iet-ifs.2019.0006 |
| [23] |
KUMAR V, KUMAR D, KAUR M, et al. A novel binary seagull optimizer and its application to feature selection problem[J]. IEEE Access, 2021, 9: 103481-103496. DOI:10.1109/ACCESS.2021.3098642 |
| [24] |
苏鑫, 裴华健, 吴迎亚, 等. 应用经遗传算法优化的BP神经网络预测催化裂化装置焦炭产率[J]. 化工进展, 2016, 35(2): 389-396. SU X, PEI H J, WU Y Y, et al. Predicting coke yield of FCC unit using genetic algorithm optimized BP neural network[J]. Chemical Industry and Engineering Progress, 2016, 35(2): 389-396. (in Chinese) |
| [25] |
周乐, 刘昕明, 周鹤龄. CPSO-NP优化算法及其在TE过程中应用[J]. 测控技术, 2018, 37(7): 32-36, 41. ZHOU L, LIU X M, ZHOU H L. Chaotic particle swarm optimization with natural selection and predatory search(CPSO-NP) and its application in TE process[J]. Measurement and Control Technology, 2018, 37(7): 32-36, 41. (in Chinese) |
| [26] |
李宏光, 夏丽君. 改进的FP-growth算法及其在TE过程故障诊断中的应用[J]. 北京工业大学学报, 2016, 42(5): 697-706. LI H G, XIA L J. Improved FP-growth algorithm with applications in TE process fault diagnosis[J]. Journal of Beijing University of Technology, 2016, 42(5): 697-706. (in Chinese) |
| [27] |
WANG J, HE Q P. Multivariate statistical process monitoring based on statistics pattern analysis[J]. Industrial & Engineering Chemistry Research, 2010, 49(17): 7858-7869. |
| [28] |
RICKER N L. Decentralized control of the Tennessee Eastman challenge process[J]. Journal of Process Control, 1996, 6(4): 205-221. |
| [29] |
CHERKASSKY V, MA Y Q. Practical selection of SVM parameters and noise estimation for SVM regression[J]. Neural Networks, 2004, 17(1): 113-126. |
| [30] |
XING W C, BEI Y L. Medical health big data classification based on KNN classification algorithm[J]. IEEE Access, 2020, 8: 28808-28819. |
| [31] |
DOMINGOS P, PAZZANI M. On the optimality of the simple Bayesian classifier under zero-one loss[J]. Machine Learning, 1997, 29(2): 103-130. |








