2. 广东力劲塑机智造股份有限公司, 中山 528400
2. Zhong Shan LK Machinery Co., Ltd., Zhongshan 528400, China
宏观超分子组装是超分子化学中新兴的一个研究领域,其通过在微米级别的高分子基元表面进行官能团修饰,利用表面官能团间的弱相互作用,以界面组装的方式实现宏观超分子结构的构建[1]。
在宏观超分子组装的凝胶材料方面,Harada等[2]实现了从毫米到厘米尺度的宏观超分子组装。Ma等[3]通过合成具有热响应性的凝胶和pH-荧光响应的凝胶,不仅实现了宏观超分子组装,还能根据外界温度和pH值产生形状和荧光强弱的变化。在宏观超分子的组装策略方面,石峰等[4-6]提出了基于动态组装/解组装的自纠错策略,利用热力学亚稳态结构与稳态结构在盐溶液下的差异,实现了宏观超分子的精准组装。但是由于传统人工组装实验存在耗时长、标准不统一的问题,限制了宏观超分子组装的进一步发展,因此需要引入自动化技术,以解决上述问题。
现阶段,宏观超分子组装实验需要人眼去识别组装体的组装状态,并且若组装不符合要求,需人工更换溶液进行解组装。待解组装完毕,科研人员还需对其进行清洗,以保证后续的重新组装。这种以人工识别与人工操作实验为主的工作方法,存在实验强度大、效率低下、人力资源浪费、工业中难以标准化等问题。随着自动化技术的发展,越来越多的自动化设备运用于科研实验中,提高了科研效率和成果的重现率[7]。因此,本文设计了用于宏观超分子组装实验的自动化实验平台,以解决当前存在的强度大、效率低下等问题,为组装实验进一步的工业化奠定基础。
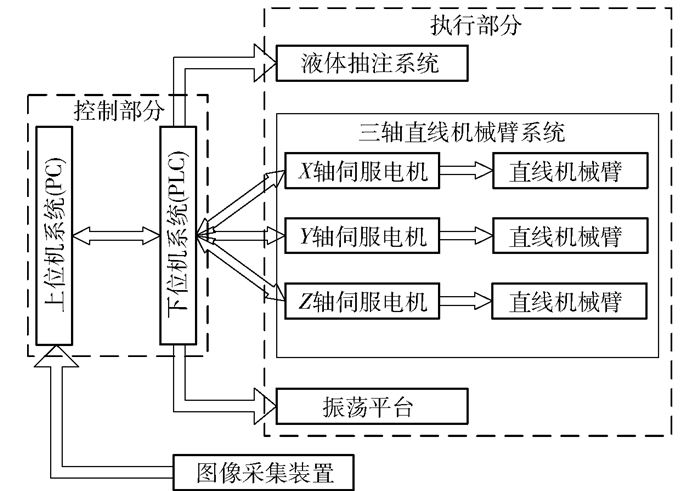
1 实验平台硬件方案设计本文设计基于机器视觉的宏观超分子组装实验平台,主要包括控制、图像采集和执行3个部分,各部分之间的关系如图 1所示。各部分的说明如下。
|
图 1 宏观超分子组装实验平台硬件结构图 Fig.1 Hardware structure diagram of the macroscopic supramolecular assembly experimental platform |
(1) 控制部分,包括上位机系统和下位机系统。上位机系统主要运行实验平台操作界面、处理和分析采集装置采集的图像、输出控制信息以及监控下位机系统和执行系统的运行状况。采用西门子200 SMART可编程控制器(PLC)作为下位机系统的控制中枢,通过以太网端口接收上位机控制信息并向上位机系统反馈设备运行状况,同时根据上位机控制信息与内置PLC程序控制执行设备的运行。
(2) 图像采集部分,主要硬件为图像采集装置。图像采集装置采集标识物以实现视觉定位和采集实验结果图像。其中超分子组装单体尺寸达到毫米级别(3 mm×3 mm×3 mm),因此选用迈德威视科技有限公司的MV-SUA 1600C-T工业相机,分辨率为1 600万像素,以及MV-LD-16-10M-J工业镜头,焦距为16 mm,相面尺寸为6.16 mm×4.62 mm。
(3) 执行部分,包括三轴直线机械臂系统、液体抽注系统和振荡平台。三轴直线机械臂系统由台达电子工业股份有限公司的台达B2伺服系统和滚珠丝杆副构成,负责将图像采集装置带到指定位置进行拍摄,和将液体抽注系统带到指定位置进行换液操作,系统控制精度达0.1 mm;液体抽注系统由蠕动泵、蠕动泵控制器、电磁阀和流量传感器构成,负责宏观超分子组装实验的组装阶段、解组装阶段和清洗阶段的换液操作;振荡平台由圆周式实验摇床构成,为宏观超分子组装实验的组装与解组装提供能量。
由于实验为液体环境,若增添外部垂直光照会形成镜面反射,导致采集图像过亮,并且实验室灯光条件已满足视觉系统的处理要求,因此本文实验不再增添外部光照系统。
2 视觉定位算法在宏观超分子组装实验结果的识别阶段,本文采用视觉识别确定每个实验烧杯的位置,需要先对相机进行标定以建立图像坐标与世界坐标的关系。由于振荡平台停止后存在平台位置不确定的现象,本文提出双标识物视觉定位算法以解决该问题。
2.1 相机标定 2.1.1 小孔成像模型相机标定的目的是将图像坐标系转换为相机坐标系,再转换为世界坐标系[8]。本文使用的工业相机是小孔成像模型相机,在该模型下图像坐标系与世界坐标系的关系可表示为
| $ \boldsymbol{Z}_c\left[\begin{array}{c} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{ccc} f_x & 0 & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cc} \boldsymbol{R} & \boldsymbol{T} \\ {\bf{0}}^{\mathrm{T}} & 1 \end{array}\right]\left[\begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array}\right] $ | (1) |
式中,(XW, YW, ZW)是世界坐标系下的某一点坐标,该点在图像坐标系下的坐标为(u, v);fx、fy为相机内参在x轴、y轴上的焦距,u0、v0为相机光轴在图像坐标系中的偏移量,R、T分别为相机坐标系变换到世界坐标系的旋转矩阵与平移矩阵。
由式(1)可知,为了进行图像坐标系到世界坐标系的转换,需要求取相机的参数。张氏标定法[9]作为标定相机内参的方法之一,具有标定时设备要求低、操作简单、精度高等优点,因此本文采用张氏标定法确定相机内参,具体过程可参考文献[9],本文不再过多赘述。
2.1.2 平面九点标定法求取相机外参的过程即为手眼标定[10],根据相机安装位置的不同,标定模型可分为眼在手上模型和眼在手外模型。由于本文中工业相机安装在直线机械臂上,因此手眼标定模型为眼在手上模型。常用的手眼标定方法有Tsai手眼标定两步法[11]和张氏手眼标定法[9],两种方法均需求出手眼矩阵中的旋转矩阵R,才能求出平移矩阵T。而本文所设计的三轴直线机械臂没有旋转自由度,即机械臂在任何情况下的姿态都是固定的,无法依据上述两种方法求出平移矩阵T,因此采用平面九点标定方法进行手眼标定[12]。
对式(1)进行简化,得到式(2),其中cendM代表相机坐标系到机械臂末端坐标系的转换矩阵,endbaseM代表机械臂末端坐标系到基座坐标系的转换矩阵。
| $ \boldsymbol{Z}_c\left[\begin{array}{c} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{ccc} f_x & 0 & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \end{array}\right]{_{\rm c}^{\text {end }}} \boldsymbol{M}{_{\text {end }}^{\text {base }} }\boldsymbol{M}\left[\begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array}\right] $ | (2) |
本文的三轴直线机械臂无旋转自由度,且机械臂末端坐标为(Xend,Yend,Zend),因此
| $ {_{\text {end }}^{\text {base }} }\boldsymbol{M}=\left[\begin{array}{cccc} 1 & 0 & 0 & X_{\text {end }} \\ 0 & 1 & 0 & Y_{\text {end }} \\ 0 & 0 & 1 & Z_{\text {end }} \\ 0 & 0 & 0 & 1 \end{array}\right] $ | (3) |
同时,可设
| $ {_{\rm c}^{\text {end }}} \boldsymbol{M}=\left[\begin{array}{llll} h_1 & h_2 & h_3 & h_4 \\ h_5 & h_6 & h_7 & h_8 \\ h_9 & h_{10} & h_{11} & h_{12} \end{array}\right] $ | (4) |
将式(3)、(4)代入式(2)中,可得
| $ \begin{aligned} & \boldsymbol{Z}_c\left[\begin{array}{c} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{ccc} f_x & 0 & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} h_1 & h_2 & h_3 & h_4 \\ h_5 & h_6 & h_7 & y_8 \\ h_9 & h_{10} & h_{11} & h_{12} \end{array}\right] . \\ & {\left[\begin{array}{cccc} 1 & 0 & 0 & X_{\text {end }} \\ 0 & 1 & 0 & Y_{\text {end }} \\ 0 & 0 & 1 & Z_{\text {end }} \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array}\right]} \end{aligned} $ | (5) |
由式(5)可知,存在12个未知量。在相机内参、机械臂末端坐标确定的情况下,已知1个点的像素坐标和世界坐标可求出3个未知量,因此至少需要4个点的实际坐标和像素坐标,才能求出12个未知量。为了提高精度,采集9个点的实际坐标和像素坐标进行标定,得到超定方程组,可采用最小二乘法求得cendM,如式(6)所示。
| $ _{\rm c}^{\text {end }} \boldsymbol{M}=\left[\begin{array}{cccc} 0.97507 & 0.03547 & 26.91241 & -1.12604 \\ -0.02492 & 0.99045 & 20.88145 & -0.87370 \\ -7.715 \mathrm{e}^{-16} & 9.4368 \mathrm{e}^{-16} & -16.9577 & 0.70952 \end{array}\right] $ | (6) |
为了检测实验平台的定位精度,随机采集8个点,每个点的实际坐标、计算坐标及误差如表 1所示。
| 下载CSV 表 1 随机8点的定位误差 Table 1 Positioning errors of random eight points |
在实验中圆杯直径为45 mm,液体抽注系统的抽注喷头直径为40 mm,允许定位误差为5 mm。由表 1可知,采用平面九点标定方法,实验平台的定位误差不超过0.5 mm,完全满足抽注喷头在圆杯内的定位精度。
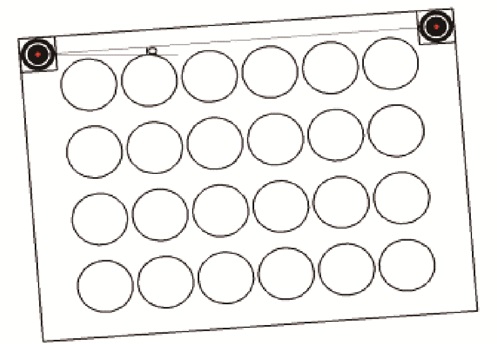
2.2 双标识物视觉定位算法本文采用图 2所示的双标识物,设计了一种基于双标识物的视觉定位算法。
|
图 2 基于双标识物的视觉定位 Fig.2 Visual localization based on double markers |
基于双标识物的视觉定位算法步骤如下。
1) 图像灰度化处理。将彩色标识物图像转化为单通道灰度图像,降低图像处理量。
2) 图像中值滤波。灰度图像中存在噪点,利用中值滤波方法去除噪点,且保留图像边缘细节。
3) 图像二值化分割。对图像进行二值化分割,将标识物从图像中分割出来,同时采用直方图双峰法对二值化阈值进行自适应,即先求图像的直方图,再对直方图进行多次平滑处理,直至形成具有双波峰单波谷结构的直方图。取波谷对应的灰度值作为二值化阈值,其中平滑处理函数为
| $ \left\{\begin{aligned} B[i] & =(A[i]+A[i]+A[i+1]) / 3, \\ i & =0 \\ B[i] & =(A[i-1]+A[i]+A[i+1]) / 3, \\ 0 & <i<255 \\ B[i] & =(A[i-1]+A[i]+A[i]) / 3, \\ i & =255 \end{aligned}\right. $ | (7) |
式中,数组A、B分别为平滑处理前后直方图分布情况,i为灰度值。
4) 改进Canny算法提取图像轮廓。采用Canny算法对图像轮廓进行提取,同时利用最小交叉熵理论对Canny算法的阈值实现自适应取值,高阈值取最优阈值t,低阈值取t/2,求取最优阈值t的相关公式如下。
| $ a=\frac{\sum\limits_{j=0}^{t-1} j g(j)}{\sum\limits_{j=0}^{t-1} g(j)}, b=\frac{\sum\limits_{j=t}^{N-1} j g(j)}{\sum\limits_{j=t}^{N-1} g(j)} $ | (8) |
| $ M(t)=\sum\limits_{t=0}^{t-1} j i(j) \lg \left(\frac{j}{a}\right)+\sum\limits_{j=t}^{N-1} j i(j) \lg \left(\frac{j}{b}\right) $ | (9) |
| $ t=\arg \min (M(t)) $ | (10) |
式中,g(j)为梯度幅值为j的个数,i(j)为j处对应的灰度值,N为梯度级数,一般取255。
5) 筛选标识物轮廓。由于相机与拍摄平面距离不变,即标识物轮廓面积不变,所以根据轮廓面积的取值范围进行筛选。以轮廓面积[80 000, 550 000]作为筛选条件,除去一部分不符合要求的轮廓区域,再根据标识物轮廓类似圆形、外接矩形长宽比约为1(即以外接矩形长宽比为[0.99, 1.01])作为筛选条件,筛选出标识物的所有轮廓。
6) 标识物中心坐标求取。对标识物轮廓进行求矩计算得出标识物的中心像素坐标,最后将中心像素坐标转换为世界坐标。中心像素坐标计算公式为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ (\bar{x}, \bar{y})=\left(\frac{\sum\limits_x \sum\limits_y x I(x, y)}{\sum\limits_x \sum\limits_y I(x, y)}, \frac{\sum\limits_x \sum\limits_y y I(x, y)}{\sum\limits_x \sum\limits_y I(x, y)}\right)= \\ \left(\frac{M_{10}}{M_{00}}, \frac{M_{01}}{M_{00}}\right) \end{array} $ | (11) |
式中,(x, y)为圆形标识物中心像素坐标,(x, y)为标识物边缘各点的像素坐标,I(x, y)为(x, y)处的像素值,M00、M10、M01分别为像素I(x, y)相对于图像中的点(0, 0)、(1, 0)、(0, 1)的矩。
7) 拍摄点坐标求取。若振荡平台与实验平台不平行,如图 2所示,即双标识物中心连线与实验平台X方向存在偏转角α,假设被拍摄点A的理想坐标为(X0, Y0),则其实际坐标为(X0′, Y0′)
| $ X_0^{\prime}=X_0 \cos \alpha-Y_0 \sin \alpha $ | (12) |
| $ Y_0^{\prime}=Y_0 \sin \alpha+X_0 \cos \alpha $ | (13) |
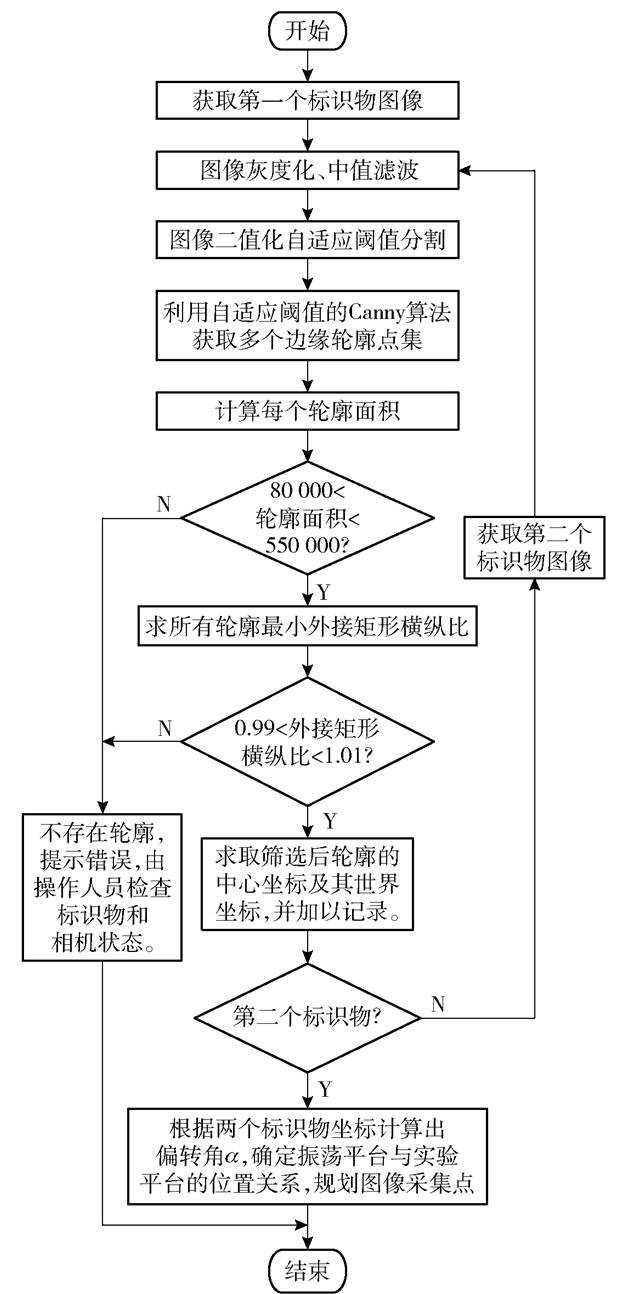
根据上述步骤,本文设计的基于双标识物的视觉定位算法流程如图 3所示。
|
图 3 视觉定位算法流程图 Fig.3 Flow chart of the visual positioning algorithm |
本文进行了标识物定位实验。分别拍摄左右标识物的图像,并利用所提出的视觉定位算法提取标识物轮廓,通过式(11)计算得到两标识物中心像素坐标与其世界坐标,如表 2所示,其中左侧标识物图像处理流程如图 4所示。
| 下载CSV 表 2 标识物几何中心的像素坐标与世界坐标 Table 2 Pixel coordinates and world coordinates of the geometric center of the marker |
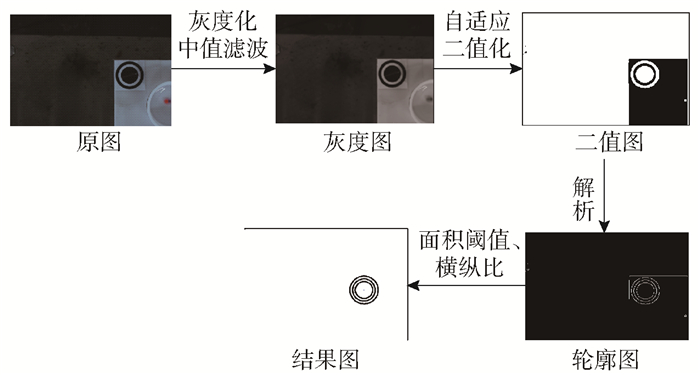
|
图 4 标识物轮廓提取结果 Fig.4 Results of marker contour extraction |
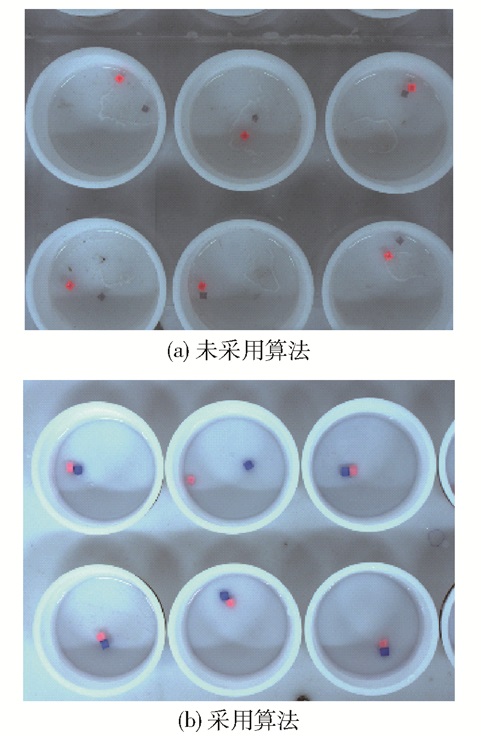
根据上述算法提取到两个标识物的轮廓中心点,计算得出双标识物中心连线与实验平台X方向存在的偏转角α为1.708°,并将其带入式(12)、(13)中,从而确定拍摄点的位置。取其中一个拍摄位置的拍摄效果,如图 5所示。可以看出,在对未采用本算法取得的拍摄点进行拍摄得到的图片中,6个烧杯无法完整出现在拍摄视野中(图 5(a));而在运用本算法取得的拍摄点上进行拍摄,得到的图片能够完整显示出6个烧杯的位置(图 5(b))。
|
图 5 采用基于双标识物的视觉定位算法前后效果对比 Fig.5 Comparison of effects before and after using the visual positioning algorithm based on double markers |
采集的实验结果图像由上位机系统进行图像处理,得到所有不合格实验烧杯的坐标,并传输给下位机系统,下位机系统控制机械臂末端带动液体抽注系统,对不合格实验烧杯进行换液操作。在此基础上,进一步优化机械臂末端运动路径。
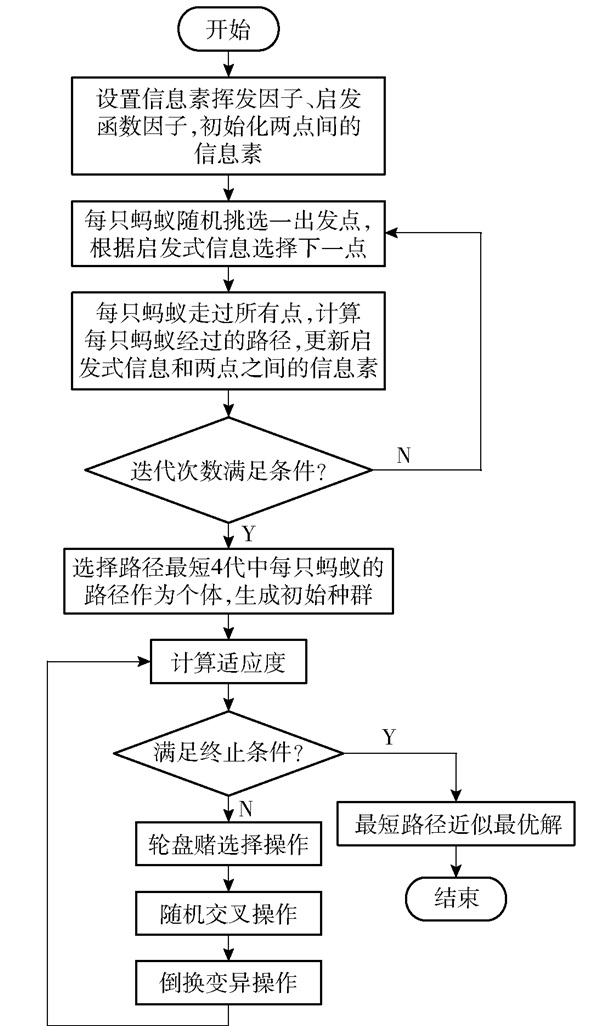
3.1 基于多代局部最优解的混合蚁群遗传算法遗传算法[13]是依据自然界进化规律设计的,蚁群算法[14]则是根据蚁群觅食规律提出的。遗传算法存在搜索时间长、收敛速度低和局部搜索能力差等缺点,而蚁群算法虽有较好的收敛速度,但容易陷入局部最优。本文综合遗传算法与蚁群算法各自的优点,提出基于多代局部最优解的混合蚁群遗传算法,算法流程如图 6所示。
|
图 6 基于多代最优解空间的混合蚁群遗传算法 Fig.6 Hybrid ant colony genetic algorithm based on multi generation optimal solution space |
从流程图可以看出,本文算法利用蚁群算法较高的收敛速度进行初始化计算,选择蚁群算法迭代过程中产生局部最优值的4代解空间作为初始种群,来优化遗传算法的初始种群。此算法综合了蚁群算法优秀的局部搜索能力和遗传算法强大的全局搜索能力,具有良好的综合搜索能力。
3.2 算法验证为了验证所提算法的性能,本文利用旅行商问题(TSP)标准数据集中的st70数据集[15]和本文实验中产生的坐标数据集(MAS数据集),对遗传算法、蚁群算法和本文算法进行仿真。本文算法所使用的参数如表 3所示。
| 下载CSV 表 3 混合蚁群遗传算法参数 Table 3 Parameters of hybrid ant colony genetic algorithm |
对于st70数据集,所得仿真结果如表 4所示。混合蚁群遗传算法迭代次数少,且在运行效率上,其运行时间相对于遗传算法和蚁群算法分别缩短了60.6%和61.8%;在最短路径值上,本文算法相对于遗传算法和蚁群算法分别缩短了2.05%和4.14%。
| 下载CSV 表 4 st70数据集下3种算法结果比较 Table 4 Comparison of results of three algorithms with the st70 dataset |
对于MAS数据集,所得仿真结果如表 5所示。在运行效率上,混合蚁群遗传算法运行时间相对于遗传算法和蚁群算法分别缩短了60.5%和34.6%;在最短路径值上,本文算法相对于遗传算法和蚁群算法分别缩短了4.35%和1.22%。
| 下载CSV 表 5 MAS数据集下3种算法结果比较 Table 5 Comparison of results of three algorithms with the MAS dataset |
基于机器视觉与PLC所设计的宏观超分子组装实验平台实物如图 7所示。

|
图 7 基于机器视觉与PLC的宏观超分子组装实验平台 Fig.7 The macroscopic supramolecular assembly experimental platform based on machine vision and PLC |
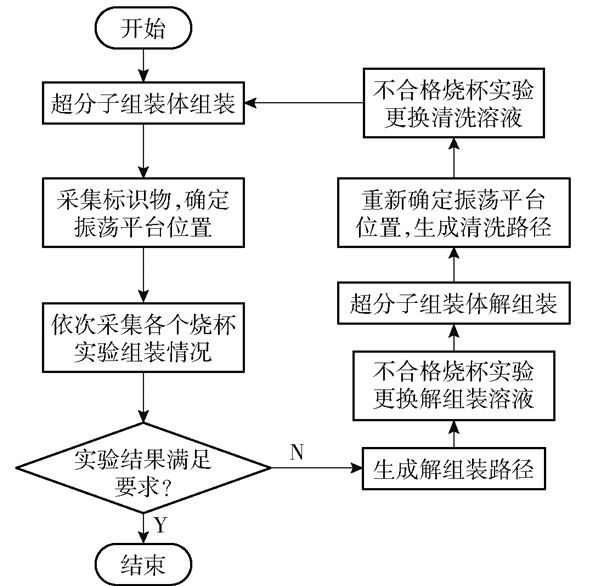
宏观超分子组装实验流程如图 8所示。受限于图像清晰度和视野范围,并且为了提高图像采集效率,图像采集装置一次采集6个实验烧杯。同时为防止识别误判,使识别结果更精准,每个实验周期采集3次组装图像且每次采集前振荡平台需振荡5 s以变更组装体位姿,当识别结果2次达到合格及以上,可判定该烧杯组装实验为合格。本文实验所用烧杯总数为72个,当水凝胶精准组装率达到90%,则表示整个组装实验成功。
|
图 8 宏观超分子组装实验流程 Fig.8 Experimental flow chart of macroscopic supramolecular assembly |
应用本文设计的实验平台进行宏观超分子组装实验,实验结果如图 9所示。

|
图 9 宏观超分子组装实验结果 Fig.9 Experimental results of macroscopic supramolecular assembly |
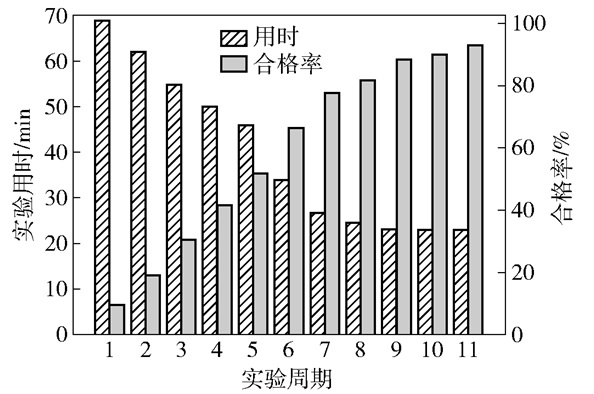
每个实验周期的用时与合格率如图 10所示。可以看出随着宏观超分子组装实验的进行,每个实验周期中的不合格组装数越来越少,实验合格率不断上升,实验周期用时不断减少。本次实验共进行了11个周期,实验总用时为442 min,相对人工手动实验用时减少8%,并且大大减少了人工操作。
|
图 10 每个实验周期用时与合格率情况 Fig.10 Time consumption and qualification rate of each experimental cycle |
为了验证实验平台的重复性,利用所设计的实验平台又进行了5次宏观超分子组装实验,每次实验的实验周期数、实验用时以及合格率情况如表 6所示。由表可知,实验合格率越高,实验的周期数越多,因此实验时间也会越长,但均比手工操作实验用时有所缩短。同时5次实验的合格率均大于90%,表明实验平台能够稳定地重复进行宏观超分子组装实验。
| 下载CSV 表 6 5次宏观超分子组装实验结果 Table 6 Results of five macroscopic supramolecular assembly experiments |
本文设计了基于机器视觉的宏观超分子组装实验平台,结合PLC编程技术与视觉识别技术,实现了宏观超分子组装实验的自动化运行;提出基于平面九点标定的双标识物视觉定位算法,解决了实验平台视觉定位精度差的问题;提出基于多代局部最优解的混合蚁群遗传算法,以优化机械臂末端运动路径,有效缩短了机械臂运动路径,减少了整个实验时间。
实际应用的实验结果表明,该平台可以重复、稳定地进行实验,能够解放科研人员的双手,有效解决人工组装实验存在的实验强度大、实验效率低下、人力资源浪费等问题,同时对宏观超分子精准组装实现快速、批量地工业化生产具有一定的实际意义。
| [1] |
谢佩辰. 基于宏观超分子组装的水下粘附界面作用机制研究[D]. 北京: 北京化工大学, 2019. XIE P C. Study on mechanism of underwater adhesion interface based on macro-supramolecular assembly[D]. Beijing: Beijing University of Chemical Technology, 2019. (in Chinese) |
| [2] |
HARADA A, KOBAYASHI R, TAKASHIMA Y, et al. Macroscopic self-assembly through molecular recognition[J]. Nature Chemistry, 2011, 3(1): 34-37. DOI:10.1038/nchem.893 |
| [3] |
MA C X, LU W, YANG X X, et al. Bioinspired anisotropic hydrogel actuators with on-off switchable and color-tunable fluorescence behaviors[J]. Advanced Functional Materials, 2018, 28(7): 1704568. DOI:10.1002/adfm.201704568 |
| [4] |
成梦娇, 石峰. 精准宏观超分子组装[J]. 高分子学报, 2020, 51(6): 598-608. CHENG M J, SHI F. Precise macro supramolecular assembly[J]. Acta Polymerica Sinica, 2020, 51(6): 598-608. (in Chinese) |
| [5] |
成梦娇, 张倩, 石峰. 宏观超分子组装——超分子材料制备新理念[J]. 中国科学: 化学, 2017, 47(7): 816-829. CHENG M J, ZHANG Q, SHI F. Macroscopic supramolecular assembly: new concept for the fabrication of supramolecular materials[J]. Scientia Sinica Chimica, 2017, 47(7): 816-829. (in Chinese) |
| [6] |
JU G N, GUO F L, ZHANG Q, et al. Self-correction strategy for precise, massive, and parallel macroscopic supramolecular assembly[J]. Advanced Materials, 2017, 29(37): 1702444. DOI:10.1002/adma.201702444 |
| [7] |
CHATTERJEE S, GUIDI M, SEEBERGER P H, et al. Automated radial synthesis of organic molecules[J]. Nature, 2020, 579: 379-384. DOI:10.1038/s41586-020-2083-5 |
| [8] |
顾璟琛. 基于单目视觉的机器人精密插件系统设计[D]. 上海: 上海交通大学, 2017. GU J C. Monocular vision-based autonomous manipulator insertion system[D]. Shanghai: Shanghai Jiao Tong University, 2017. (in Chinese) |
| [9] |
ZHANG Z Y. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. DOI:10.1109/34.888718 |
| [10] |
程麒, 潘丰, 袁瑜键. 基于3D视觉传感器的龙门架机器人手眼标定方法[J]. 光电工程, 2021, 48(4): 200239. CHENG L, PAN F, YUAN Y J. Hand-eye calibration method of gantry robot based on 3D vision sensor[J]. Opto-Electronic Engineering, 2021, 48(4): 200239. (in Chinese) |
| [11] |
TSAI R Y, LENZ R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration[J]. IEEE Transactions on Robotics and Automation, 1989, 5(3): 345-358. DOI:10.1109/70.34770 |
| [12] |
张立国, 杨曼, 金梅, 等. 基于改进九点标定的机器人投板方法[J]. 制造技术与机床, 2021(12): 7-14. ZHANG L G, YANG M, JIN M, et al. Robot board throwing algorithm based on improved nine point calibration[J]. Manufacturing Technology & Machine Tool, 2021(12): 7-14. (in Chinese) |
| [13] |
HOLLAND J H. Adaptation in natural and artificial systems[M]. Bradford: A Bradford Book, 1992.
|
| [14] |
COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]//Proceedings of ECAL91-European Conference on Artificial Life. Paris, 1991: 134-142.
|
| [15] |
赵鑫, 杨雄飞, 钱育蓉. 改进的蚁群优化算法求解旅行商问题[J]. 计算机工程与设计, 2022, 43(4): 962-968. ZHAO X, YANG X F, QIAN Y R. Improved ant colony optimization algorithm for TSP[J]. Computer Engineering and Design, 2022, 43(4): 962-968. (in Chinese) |








