2. 石河子大学 机械电气工程学院, 石河子 832003
2. College of Mechanical and Electrical Engineering, Shihezi University, Shihezi 832003, China
滚动轴承是旋转机械中广泛使用的一类关键部件,其运行状态会对设备的整体性能及使用寿命产生直接影响[1-3]。振动信号携带与设备健康状况有关的信息,当轴承发生故障时,其振动信号会表现出非线性和非平稳的特点,且早期故障特征较弱,极易淹没在背景噪声中,使得对故障类型的判断和故障位置的识别变得十分困难。因此开展从强噪声背景中提取微弱故障特征的研究,对于旋转机械设备早期的故障诊断、定期维护和工业生产安全都具有重要意义。
近年来,短时傅里叶变换(short-time Fourier transform,STFT)[4]、Wigner-Ville分布(Wigner-Ville distribution,WVD)[5]和小波变换(wavelet transform,WT)[6-7]等分析方法已经被广泛应用于轴承的故障诊断并取得了一定效果。然而,这些方法均具有各自的局限性,如短时傅里叶变换中窗口的大小和形状是固定的,不适合对非平稳信号进行分析;Wigner-Ville分布在处理多分量信号时会产生交叉项干扰;小波变换受Heisenberg准则和小波基函数的影响,在实际应用中很难找到合适的小波基函数,且一旦选定便不可更改,因此不具备自适应特性。针对上述方法的不足,研究者们相继提出一些适用于分析非线性非平稳信号的算法。高强等[8]提出一种基于经验模态分解(empirical mode decomposition,EMD)的滚动轴承故障诊断方法,用于处理具有内圈及外圈损伤的滚动轴承振动信号,可有效提取轴承故障特征。李常有等[9]应用独立分量分析(independent component analysis,ICA)将滚动轴承系统产生的声信号从传声器获取的声信号中分离出来,然后采用基于Morlet小波变换的包络分析降噪并获取特征信号。石瑞敏等[10]针对滚动轴承故障振动信号的多载波多调制特性,提出一种基于局部均值分解(local mean decomposition,LMD)能量特征的特征向量提取方法,并联合支持向量机用于提取滚动轴承不同工作状态下信号的故障特征,可有效识别故障类型。孟宗等[11]为了解决振动信号中所含噪声对故障诊断结果影响较大的问题,提出一种联合小波改进阈值法与希尔伯特-黄变换(Hilbert-Huang transform,HHT)的信号分析方法,仿真和实验结果验证了方法的有效性。马增强等[12]针对滚动轴承早期故障振动信号信噪比低和特征提取困难的问题,提出基于变分模态分解(variational mode decomposition,VMD)和能量算子集合的故障特征提取方法,该方法提高了信号的分解效率,降低了噪声影响,能够实现滚动轴承故障的精确诊断。
高阶同步压缩变换(FSSTH)是一种新近出现的自适应信号分析方法[13],其核心思想是构建高阶瞬时频率估计算子,通过提高时频面上每一点的瞬时频率精度来达到增强信号时频能量聚焦性的目的,同时具备较高的信号模态提取精度。鲁棒主成分分析(robust principal component analysis,RPCA)可以从噪声污染的稀疏观测数据中恢复出本质上低秩的数据。基于高阶同步压缩变换优良的稀疏表示性能和鲁棒主成分分析提取低秩数据的优势,本文联合高阶同步压缩变换和鲁棒主成分分析算法提出一种强噪声背景下轴承微弱故障冲击特征提取方法。该方法首先通过FSSTH将测量信号变换到稀疏子空间;然后基于RPCA算法将获得的稀疏时频数据分解成低秩矩阵和稀疏矩阵;最后通过逆FSSTH恢复降噪后的振动信号,并利用包络谱分析实现故障诊断。将所提方法应用于仿真信号和实验轴承故障信号,成功提取出了故障冲击特征。
1 高阶同步压缩变换与鲁棒主成分分析算法 1.1 高阶同步压缩变换高阶同步压缩变换是短时傅里叶同步压缩变换(short-time Fourier-based synchrosqueezing transform,FSST)的推广,其突破了FSST关于弱频率调制假设的限制,可用于分析更广泛的强调幅-调频(amplitude modulated-frequency modulated,AM-FM)信号。
一个AM-FM信号x定义为
| $ x(t)=A(t) \mathrm{e}^{\mathrm{i} 2 \pi \varphi(t)} $ | (1) |
式中,A(t)和φ(t)分别表示瞬时振幅和瞬时相位。
在窗函数g下信号x的短时傅里叶变换为
| $ V_x^g(t, \zeta)=\int x(\tau) g^*(\tau-t) \mathrm{e}^{-\mathrm{i} 2 \pi \zeta(\tau-t)} \mathrm{d} \tau $ | (2) |
式中,t和ζ分别表示时间和频率,g*为窗函数g的复共轭。
令wx(t, ζ)表示关于t和ζ的瞬时频率,则有
| $ w_x(t, \zeta)=\mathfrak{R}\left\{\frac{\partial_t V_x^g(t, \zeta)}{\mathrm{i} 2 \pi V^f g_x(t, \zeta)}\right\} $ | (3) |
式中,
因此,FSST定义为
| $ T_x^{g, \gamma}(t, w)=\frac{1}{g^*(0)} \int_{\left\{\zeta, \left|v_x^g(t, \zeta)\right|>\gamma\right\}} V_x^g(t, \zeta) \cdot \delta\left(w-w_x(t, \zeta)\right) \mathrm{d} \zeta $ | (4) |
式中,γ表示阈值,δ表示Dirac分布。
在式(1)中,信号x在τ的泰勒展开式为
| $ x(\tau)=\exp \left(\sum\limits_{k=0}^N \frac{(\lg A)^{(k)}(t)+\mathrm{i} 2 \pi \phi^{(k)}(t)}{k !} \cdot(\tau-t)^k\right) $ | (5) |
式中,Z(k)(t)表示Z关于t的k阶导数。
将式(5)代入式(2),得到
| $ \begin{aligned} & V_x^g(t, \zeta)=\int x(\tau+t) g^*(\tau) \mathrm{e}^{-\mathrm{i} 2 \pi \zeta \tau} \mathrm{d} \tau= \\ & \int \exp \left(\sum\limits_{k=0}^N \frac{(\lg A)^{(k)}(t)+\mathrm{i} 2 \pi \phi^{(k)}(t)}{k !} \tau^k\right) \cdot \\ & g^*(\tau) \mathrm{e}^{-\mathrm{i} 2 \pi \zeta \tau} \mathrm{d} \tau \end{aligned} $ | (6) |
同时,式(3)改写为
| $ \begin{gathered} w_x(t, \tau)=\frac{(\lg A)(t)}{\mathrm{i} 2 \pi}+\phi^{\prime}(t)+ \\ \sum\limits_{k=2}^N \frac{(\lg A)^{(k)}(t)+\mathrm{i} 2 \pi \phi^{(k)}(t)}{\mathrm{i} 2 \pi(k-1) !} \frac{V_x^{t^{k-1 g}}(t, \zeta)}{V_x^g(t, \zeta)} \end{gathered} $ | (7) |
引入频率调制算子qζ, x[k, N]
| $ q_{\eta, f}^{[k, N]}=\frac{(\lg A)^{(k)}(t)+\mathrm{i} 2 \pi \phi^{(k)}(t)}{\mathrm{i} 2 \pi(k-1) !} $ | (8) |
则N阶局部复瞬时频率ωζ, x[N]表示为
| $ w_{\zeta, x}^{[N]}(t, \zeta)=\\ \left\{\begin{array}{l} w_x(t, \zeta)+\sum\limits_{k=2}^N q_{\zeta, x}^{[k, N]}(\zeta, t)\left(-y_{k, 1}(t, \zeta)\right), \\ V_x^g(t, \zeta) \neq 0, \partial_\zeta x_{j, j-1}(t, \zeta) \neq 0(j \geqslant 2) \\ w_x(t, \zeta), \quad \text { otherwise } \end{array}\right. $ | (9) |
最后,将式(4)中的wx(t, ζ)替换为wζ, x[N](t, ζ),得到FSSTH的数学表达式为
| $ T_{N, x}^{g, \gamma}(t, w)=\frac{1}{g^*(0)} \int_{\left\{\zeta, \left|v_x^g(t, \zeta)\right|>\gamma\right\}} V_x^g(t, \zeta) \delta(w-\left.w_{\zeta, x}^{[N]}(t, \zeta)\right) \mathrm{d} \zeta $ | (10) |
同时,模态重构可以通过式(11)实现。
| $ s_i(t) \approx \int_{\left\{w, \left|w-\varphi_i(t)\right|<d\right\}} T_{N, x}^{g, \gamma}(t, w) \mathrm{d} w $ | (11) |
式中,d表示补偿因子,φi(t)是ϕ′i(t)的估计值。
1.2 鲁棒主成分分析使用RPCA算法分解含噪声稀疏时频数据D得到低秩矩阵L和稀疏矩阵S,这个过程描述为
| $ \boldsymbol{D}=\boldsymbol{L}+\boldsymbol{S} $ | (12) |
低秩矩阵L可以通过式(13)求解
| $ \min\;{rank}(\boldsymbol{L})+\mu\|\boldsymbol{S}\|_0 {, subject\;to\;} \boldsymbol{D}=\boldsymbol{L}+\boldsymbol{S} $ | (13) |
式中,rank(L)表示L的秩;‖·‖0表示计算矩阵的l0范数;μ是一个大于零的算子,用于平衡式(13)中两项的权重。
为了求解方程(13),通常将其转化成一个凸松弛最优化问题,即
| $ \min \|\boldsymbol{L}\|_*+\mu\|\boldsymbol{S}\|_1, {subject\;to\;} \boldsymbol{D}=\boldsymbol{L}+\boldsymbol{S} $ | (14) |
式中,‖·‖*和‖·‖1分别表示矩阵的核范数和l1范数。
使用精确的增广拉格朗日乘子算法求解方程(14),即
| $ F(\boldsymbol{L}, \boldsymbol{S}, Y, \sigma)=\|\boldsymbol{L}\|_*+\mu\|\boldsymbol{S}\|_1+\langle Y, \boldsymbol{D}-\boldsymbol{L}-\boldsymbol{S}\rangle+\frac{\sigma}{2}\|\boldsymbol{D}-\boldsymbol{L}-\boldsymbol{S}\|_F^2 $ | (15) |
式中,Y表示拉格朗日乘子;σ为惩罚项,用于确保方程(15)收敛;‖·‖F表示Frobenius范数。
在求解方程(15)过程中,首先固定Y和S,计算L,即
| $ \boldsymbol{L}_{k+1}=\arg \min\limits_{\boldsymbol{L}} F\left(\boldsymbol{L}, \boldsymbol{S}_{k+1}, Y_k, \sigma_k\right) $ | (16) |
然后,固定Y和L,计算S,即
| $ \boldsymbol{S}_{k+1}=\arg \min\limits_\boldsymbol{S} F\left(\boldsymbol{L}_{k+1}, \boldsymbol{S}, Y_k, \sigma_k\right) $ | (17) |
式中,k和k+1分别表示第k和k+1次迭代。
最后,Y和σ通过下式求解,即
| $ Y_{k+1}=Y_k+\boldsymbol{\sigma}\left(\boldsymbol{D}-\boldsymbol{L}_{k+1}-\boldsymbol{S}_{k+1}\right) $ | (18) |
| $ \sigma_{k+1}=\xi \sigma_k $ | (19) |
式中,ξ是一个常量且大于1。经过多次迭代后,方程(15)获得最小值,此时,L和S即为所求解。
1.3 算法流程经过FSSTH后,在时频域中信号和噪声均是稀疏的。RPCA算法将含噪声测量信号的时频数据分解成低秩矩阵和稀疏矩阵,然后对低秩矩阵施加逆FSSTH变换可恢复出降噪后的信号。算法流程如图 1所示,具体步骤如下:
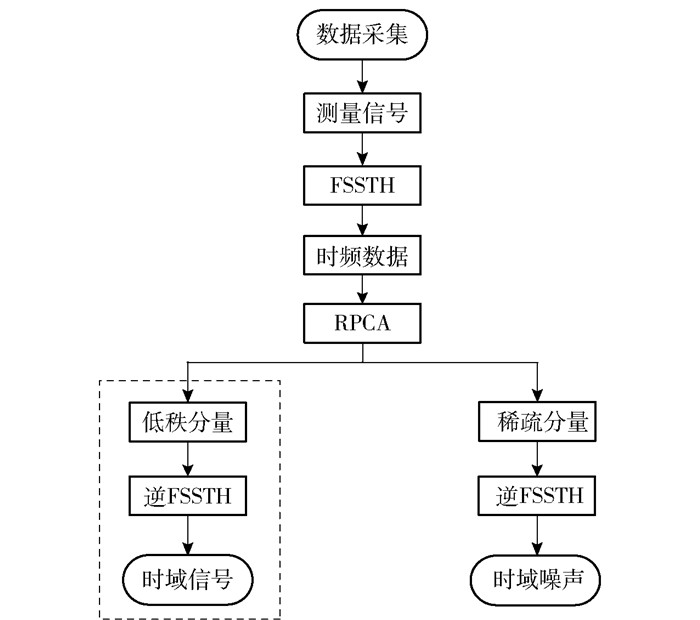
|
图 1 本文方法流程图 Fig.1 The flowchart of the proposed method |
1) 通过FSSTH变换得到含噪声测量信号的时频数据;
2) 从时频数据中提取振幅谱和相位谱;
3) 基于RPCA算法将振幅谱分解得到低秩矩阵和稀疏矩阵;
4) 对低秩矩阵施加逆FSSTH变换提取降噪后的振动信号。
2 仿真信号分析首先使用仿真信号验证所提方法的有效性。根据轴承发生故障时产生的冲击衰减信号构建仿真信号,其数学表达式如下。
| $ y=x * h $ | (20) |
式中,y表示合成信号;x表示脉冲序列;h表示一个滤波器;*表示卷积运算。具体而言,x的数学公式为
| $ x(n)=\sum\limits_{m=0}^{N_m} \delta\left(n-m D_T\right), n=1, 2, \cdots, N $ | (21) |
其中,δ(*)表示Dirac脉冲。h的Z变换为
| $ H(z)=\frac{1-z^{-1}}{1-2 \cos (2 \pi \cdot 0.2) r z^{-1}+r^2 z^{-2}} $ | (22) |
生成仿真信号的具体做法如下:①令N=10 000,DT=600,Nm=16,时间长度为1 s,采样频率为10 kHz,生成脉冲序列x;② x通过滤波器H(z)(r=0.95)合成瞬态信号y;③添加高斯噪声得到含噪声瞬态信号。
图 2所示为模拟得到的仿真信号。图 3为含噪声仿真信号(信噪比为-10 dB),噪声使得信号中的冲击特性变得微弱,通过时域波形已无法有效提取冲击特征。
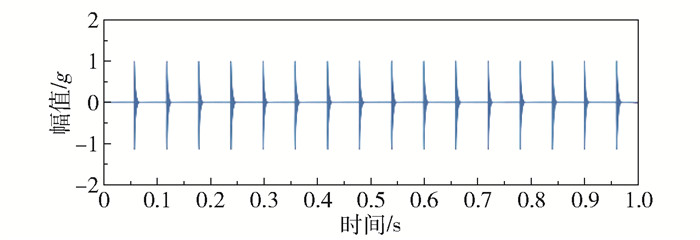
|
图 2 周期性瞬态信号 Fig.2 Periodic transient signal |
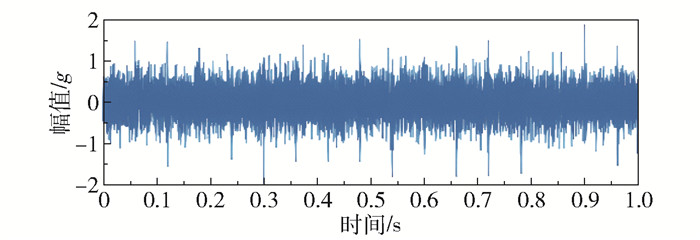
|
图 3 含噪声的瞬态信号 Fig.3 Transient signal with noise |
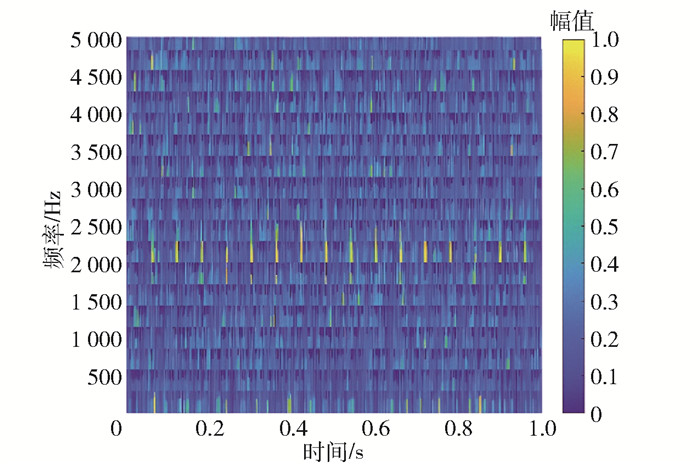
使用FSSTH变换(4阶)处理瞬态信号和含噪声的瞬态信号并提取振幅谱,得到的时频分布如图 4、5所示。从图中可以看出,经过处理后瞬态信号的特征能够被成功捕获(图 4),噪声分布在整个时频域(图 5)。这说明在时频域中瞬态信号的低秩部分不会发生较大变化,即瞬态信号的时频特征是低秩或近似低秩的,因此,可使用RPCA算法将含噪声瞬态信号的振幅谱分解成低秩分量和稀疏分量。
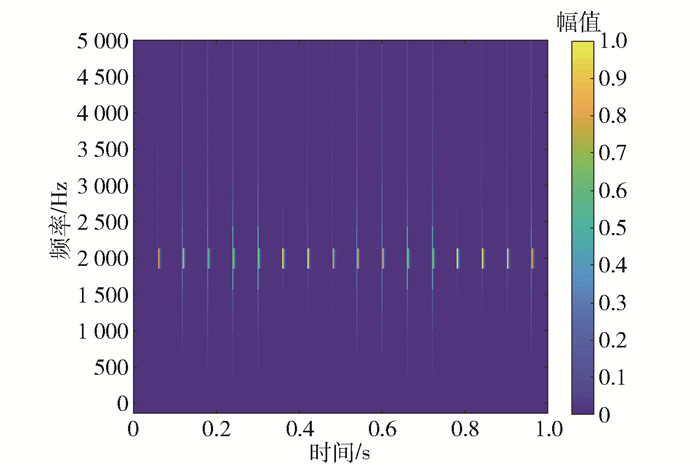
|
图 4 瞬态信号的时频分布 Fig.4 Time-frequency representation of a transient signal |
|
图 5 含噪声瞬态信号的时频分布 Fig.5 Time-frequency representation of a noisy transient signal |
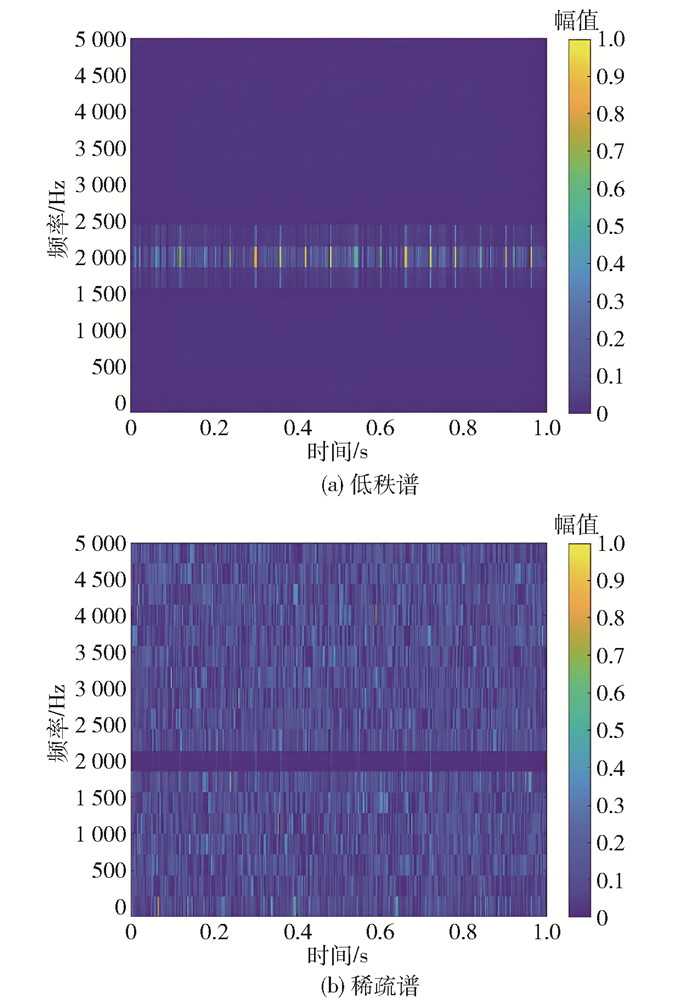
图 6(a)和(b)分别为含噪声瞬态信号的振幅谱经RPCA算法分解得到的低秩时频分布和稀疏时频分布,二者分别对应原始瞬态信号和噪声。值得注意的是原始瞬态信号的低秩时频分布(图 4)和RPCA算法分解得到的低秩时频分布(图 6(a))是有差异的,原因在于时频域中瞬态信号并非精确低秩,而是近似低秩,因此分解得到的低秩矩阵可以用来重构瞬态信号。
|
图 6 RPCA算法分解得到的低秩谱和稀疏谱 Fig.6 Low-rank and sparse spectrum decomposed by RPCA |
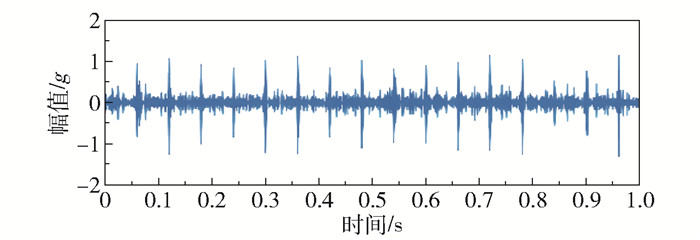
提取的低秩矩阵经逆FSSTH变换到时间域得到降噪后的瞬态信号,如图 7所示。可以看出,周期性瞬态信号几乎得到完全恢复。与含噪声瞬态信号(-10 dB)相比,重构信号的冲击特征更加明显,更有利于特征提取。这说明本文提出的方法能够实现强噪声背景下滚动轴承的微弱故障特征提取。
|
图 7 本文方法重构的周期性瞬态信号 Fig.7 Periodic transient signal reconstructed using the proposed method |
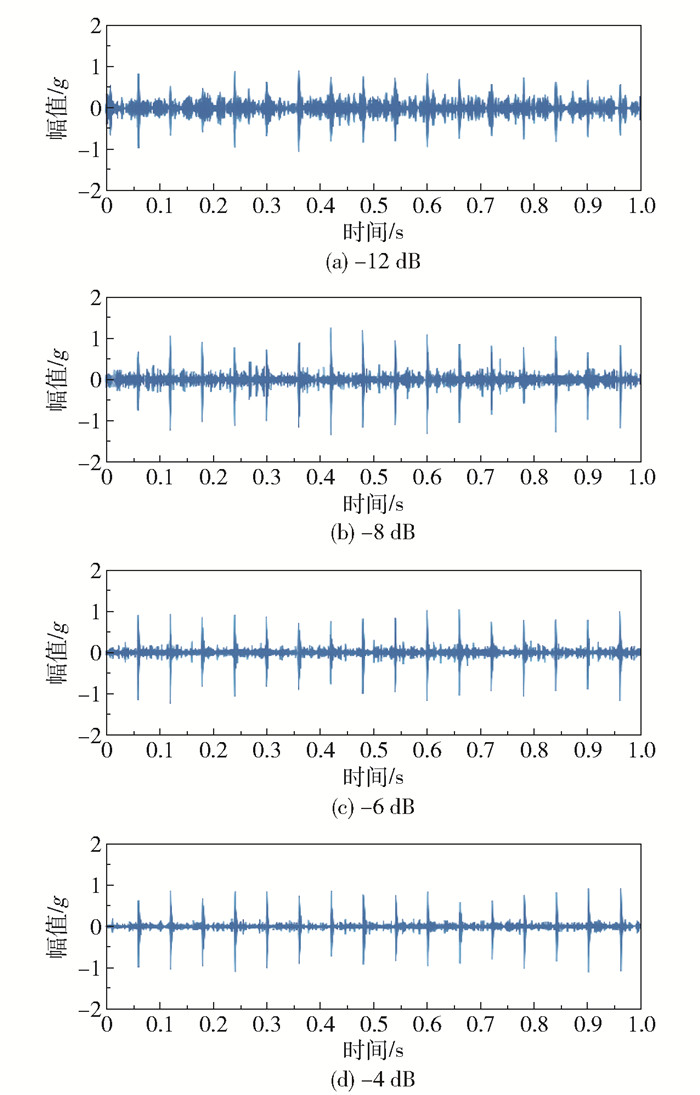
图 8显示了本文方法针对仿真信号在不同信噪比(-12、-8、-6 dB和-4 dB)下的重构结果对比。可以看出,周期性瞬态信号被成功恢复出来,且信噪比越高,故障特征提取效果越好。
|
图 8 本文方法在不同信噪比下的重构信号对比 Fig.8 Reconstructed signal comparison with different SNR using the proposed method |
将所提方法应用于实际滚动轴承故障的数据分析,进一步验证其应用效果。
3.1 实验信号数据实验数据来自美国凯斯西储大学(Case Western Reserve University,CWRU)轴承数据中心,轴承实验台如图 9所示。实验用轴承型号为SKF6205深沟球轴承,其内圈直径d为25 mm,外圈直径D为52 mm,滚动体直径为7.94 mm,节圆直径为39.04 mm,共有9个滚子,接触角α为0。分别在12 kHz和48 kHz的采样频率下采集数据,数据类型包括正常、内圈故障、外圈故障和滚动体故障,本文仅对内圈故障和外圈故障进行分析。使用内圈和外圈故障振动信号进行测试,其故障频率计算公式分别为
| $ f_{\mathrm{i}}=\frac{1}{2} z f_{\mathrm{r}}\left(1+\frac{d}{D} \cos \alpha\right) $ | (23) |
| $ f_{\mathrm{o}}=\frac{1}{2} z f_{\mathrm{r}}\left(1-\frac{d}{D} \cos \alpha\right) $ | (24) |

|
图 9 轴承实验台 Fig.9 Bearing test rig |
式中,z表示滚子个数,fr表示转频且fr=29.17 Hz。根据上述公式可以计算得到内圈故障频率fi=160.02 Hz,外圈故障频率fo=105.93 Hz。
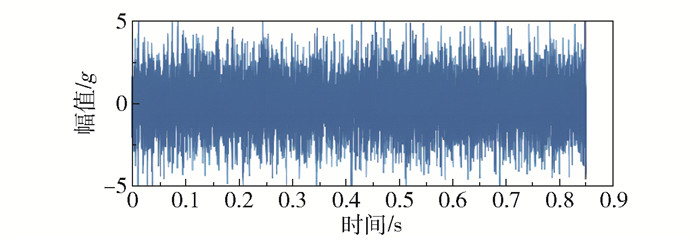
3.2 内圈故障分析图 10为含噪声(信噪比为-5 dB)的内圈故障振动信号时域波形图(采样频率为12 kHz,损伤深度为0.177 8 mm)。由图可见,噪声干扰使得内圈故障引起的冲击特征显得十分微弱。为了准确提取内圈故障引起的冲击特征,需要对该信号进行降噪处理。
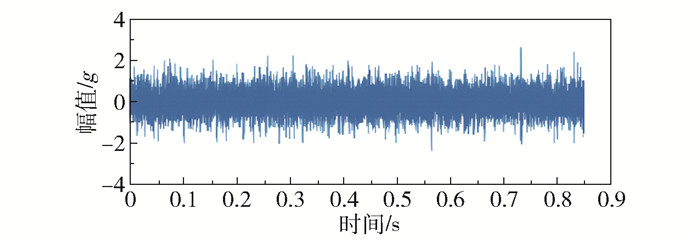
|
图 10 含噪声内圈故障振动信号波形图 Fig.10 Time-domain waveform of a noisy inner race fault signal |
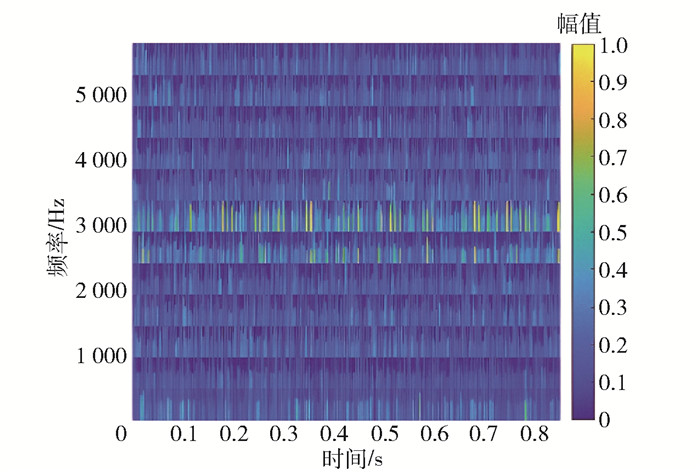
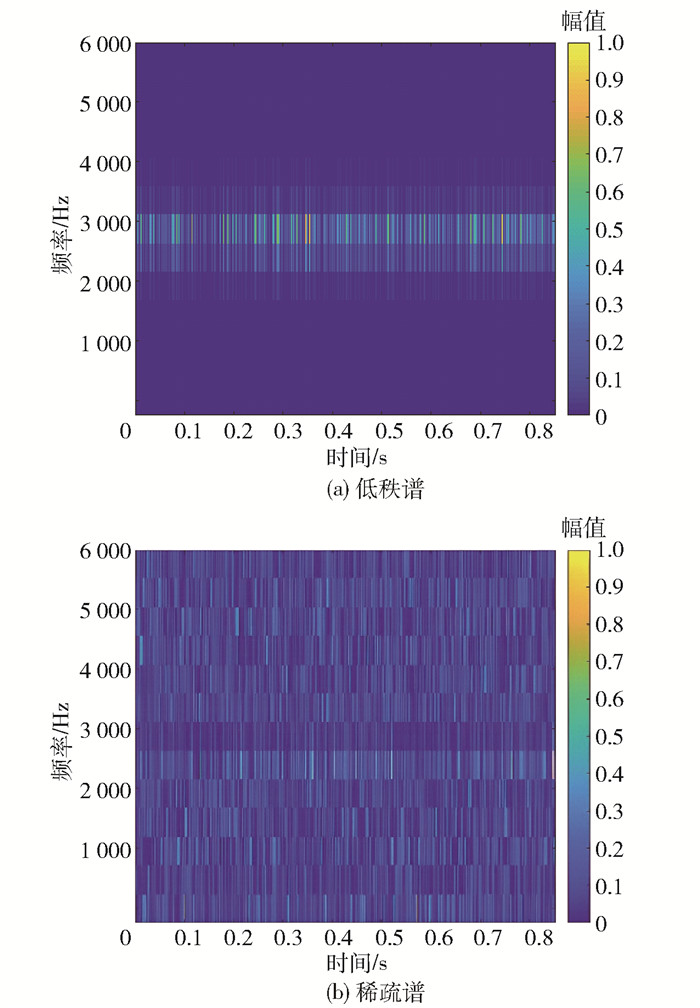
图 11为经FSSTH变换(4阶)得到的时频谱。采用RPCA算法对振幅谱分解得到低秩矩阵和稀疏矩阵,分别如图 12(a)、(b)所示,低秩谱主要反映内圈故障信号的特征,稀疏谱主要用来表征噪声。最后将低秩矩阵进行逆FSSTH变换得到降噪后的内圈故障信号,如图 13所示。由图可见,经过降噪处理后内圈故障信号的冲击特征更加明显,有利于微弱故障特征的提取。
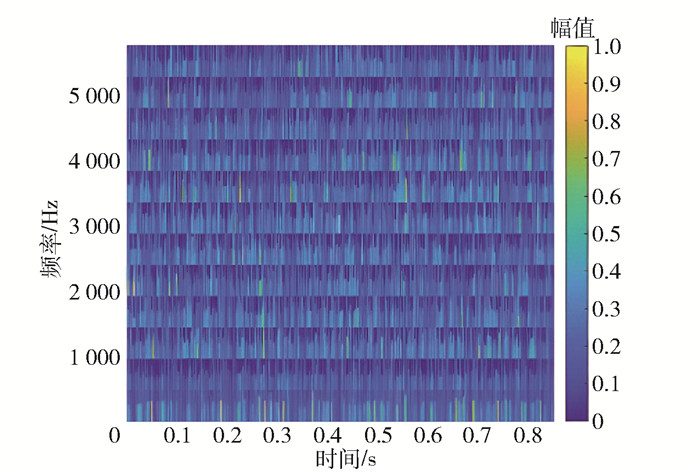
|
图 11 内圈故障信号经FSSTH变换后的时频谱 Fig.11 Time-frequency distribution of a noisy inner race fault signal |
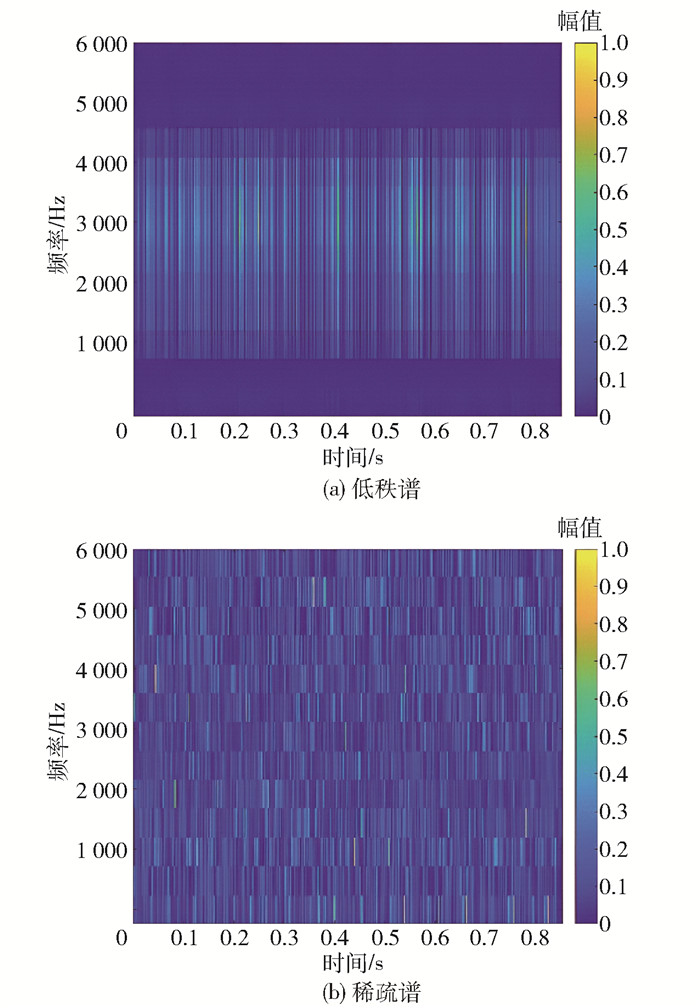
|
图 12 RPCA算法分解得到的低秩谱和稀疏谱 Fig.12 Low-rank and sparse spectrum decomposed by RPCA |
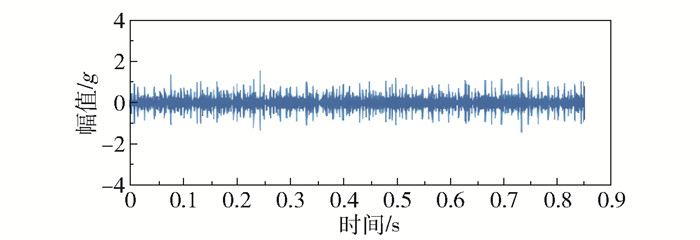
|
图 13 重构后的内圈故障信号 Fig.13 Reconstructed inner race fault signal |
图 14(a)~(c)分别为原始含噪声内圈故障信号包络谱、谱峭度方法处理后的内圈故障信号包络谱及本文方法处理后的内圈故障信号包络谱。从图 14(a)可以看出,原始内圈故障特征频率及其倍频成分十分微弱,难以进行可靠的故障模式识别。经谱峭度方法处理后,转频(fr)及故障频率(fi)有所显示,但是特征较为微弱。经过本文方法处理后,转频和内圈故障频率及其倍频(2fi)更加突出,更有利于内圈故障的识别。
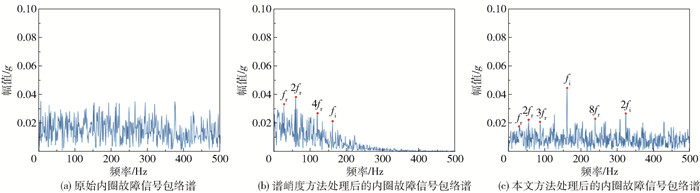
|
图 14 原始内圈故障信号和处理后的包络谱 Fig.14 Envelope spectra of the raw inner fault signals and after processing |
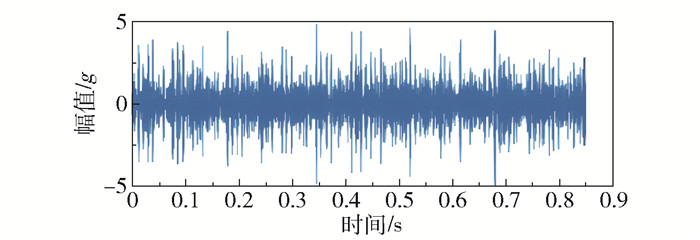
外圈故障振动信号时域波形如图 15所示(采样频率为12 kHz,信噪比为-5 dB,损伤深度为0.177 8 mm)。受背景噪声影响外圈故障引起的冲击特征显得微弱,从时域波形图难以直接获取信号的冲击特征。采用FSSTH变换(4阶)处理得到时频谱(图 16),然后基于RPCA算法对振幅谱分解得到低秩矩阵和稀疏矩阵,相应的低秩谱和稀疏谱如图 17(a)和(b)所示。最后对低秩矩阵进行逆FSSTH变换得到降噪后的外圈振动信号,如图 18所示。由图可见,经本文方法处理后的时域图中呈现出明显的有规律的冲击特征。
|
图 15 含噪声外圈故障振动信号波形图 Fig.15 Time-domain waveform of a noisy outer race fault signal |
|
图 16 外圈故障信号经FSSTH变换后的时频谱 Fig.16 Time-frequency distribution of a noisy outer race fault signal |
|
图 17 RPCA算法分解得到的低秩谱和稀疏谱 Fig.17 Low-rank and sparse spectrum decomposed by RPCA |
|
图 18 重构后的外圈故障信号 Fig.18 Reconstructed outer race fault signal |
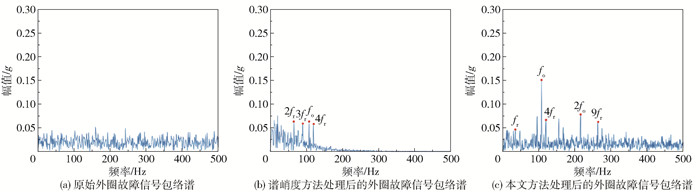
图 19(a)~(c)分别为原始含噪声外圈故障信号的包络谱、谱峭度方法处理后的外圈故障信号包络谱及本文方法处理后的外圈故障信号包络谱。由图 19(a)可见,原始包络谱中故障特征频率及其倍频成分较为微弱,无法有效指示轴承的状态。经谱峭度方法处理后,故障特征频率(fo)得以显示,但是仍然不够明显。经本文方法处理后,可提取丰富的特征信息,外圈故障频率(fo)及其倍频特征(2fo)更加突出,有利于外圈故障的识别。
|
图 19 原始外圈故障信号和处理后的包络谱 Fig.19 Envelope spectra of the raw outer fault signals and after processing |
针对周期性瞬态信号的低维模型,本文提出一种基于低秩-稀疏分解的轴承故障信号冲击特征提取方法,充分利用了高阶同步压缩变换优良的稀疏表示性能和鲁棒主成分分析可提取数据中低秩分量的优势。所提方法不需要对数据进行先验训练和提取其他特征。仿真信号和轴承实验数据测试结果表明,提出的方法可以有效识别故障信号中的冲击特征,能够实现强噪声背景下滚动轴承的微弱故障特征提取。此外,方法中参数的调整对故障特征提取结果具有一定的影响,如何快速、准确地获取所需参数是今后需要进一步深入研究的内容。
| [1] |
李富才, 何正嘉, 陈进. 小波域相关滤波法及其早期故障预示应用[J]. 振动工程学报, 2005, 18(2): 145-148. LI F C, HE Z J, CHEN J. Wavelet transform domain correlation filter and its application in incipient fault prognosis[J]. Journal of Vibration Engineering, 2005, 18(2): 145-148. (in Chinese) DOI:10.3969/j.issn.1004-4523.2005.02.003 |
| [2] |
高树成, 姚剑飞, 陈建, 等. 一种用于机床角度头故障诊断的双重降噪方法[J]. 北京化工大学学报(自然科学版), 2020, 47(5): 97-103. GAO S C, YAO J F, CHEN J, et al. A dual noise reduction method for angle head fault diagnosis[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2020, 47(5): 97-103. (in Chinese) |
| [3] |
江志农, 魏东海, 王磊, 等. 基于CART决策树的柴油机故障诊断方法研究[J]. 北京化工大学学报(自然科学版), 2018, 45(4): 71-75. JIANG Z N, WEI D H, WANG L, et al. Fault diagnosis of diesel engines based on a classification and regression tree (CART) decision tree[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2018, 45(4): 71-75. (in Chinese) |
| [4] |
LIU D D, CHENG W D, WEN W G. Rolling bearing fault diagnosis via STFT and improved instantaneous frequency estimation method[J]. Procedia Manufacturing, 2020, 49: 166-172. DOI:10.1016/j.promfg.2020.07.014 |
| [5] |
石林锁, 张亚洲, 米文鹏. 基于WVD的谱峭度法在轴承故障诊断中的应用[J]. 振动、测试与诊断, 2011, 31(1): 27-31. SHI L S, ZHANG Y Z, MI W P. Application of Wigner-Ville-distribution-based spectral kurtosis algorithm to fault diagnosis of rolling bearing[J]. Journal of Vibration, Measurement and Diagnosis, 2011, 31(1): 27-31. (in Chinese) DOI:10.3969/j.issn.1004-6801.2011.01.007 |
| [6] |
高立新, 殷海晨, 张建宇, 等. 第二代小波分析在轴承故障诊断中的应用[J]. 北京工业大学学报, 2009, 35(5): 577-581. GAO L X, YIN H C, ZHANG J Y, et al. An application of the second generation of wavelet transform in the fault diagnosis of rolling bearings[J]. Journal of Beijing University of Technology, 2009, 35(5): 577-581. (in Chinese) |
| [7] |
WANG X D, ZI Y Y, HE Z J. Multiwavelet denoising with improved neighboring coefficients for application on rolling bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2011, 25(1): 285-304. DOI:10.1016/j.ymssp.2010.03.010 |
| [8] |
高强, 杜小山, 范虹, 等. 滚动轴承故障的EMD诊断方法研究[J]. 振动工程学报, 2007, 20(1): 15-18. GAO Q, DU X S, FAN H, et al. An empirical mode decomposition based method for rolling bearing fault diagnosis[J]. Journal of Vibration Engineering, 2007, 20(1): 15-18. (in Chinese) |
| [9] |
李常有, 徐敏强, 高晶波, 等. 基于独立分量分析的滚动轴承故障诊断[J]. 哈尔滨工业大学学报, 2008, 40(9): 1363-1365. LI C Y, XU M Q, GAO J B, et al. Fault diagnosis for rolling element bearings based on independent component analysis[J]. Journal of Harbin Institute of Technology, 2008, 40(9): 1363-1365. (in Chinese) |
| [10] |
石瑞敏, 杨兆建. 基于LMD能量特征的滚动轴承故障诊断方法[J]. 振动、测试与诊断, 2015, 35(5): 832-836. SHI R M, YANG Z J. Fault diagnosis of rolling bearing based on energy feature of local mean decomposition[J]. Journal of Vibration, Measurement and Diagnosis, 2015, 35(5): 832-836. (in Chinese) |
| [11] |
孟宗, 李姗姗. 基于小波改进阈值去噪和HHT的滚动轴承故障诊断[J]. 振动与冲击, 2013, 32(14): 204-208. MENG Z, LI S S. Rolling bearing fault diagnosis based on improved wavelet threshold de-noising method and HHT[J]. Journal of Vibration and Shock, 2013, 32(14): 204-208. (in Chinese) |
| [12] |
马增强, 李亚超, 刘政, 等. 基于变分模态分解和Teager能量算子的滚动轴承故障特征提取[J]. 振动与冲击, 2016, 35(13): 134-139. MA Z Q, LI Y C, LIU Z, et al. Rolling bearings fault feature extraction based on variational mode decomposition and Teager energy operator[J]. Journal of Vibration and Shock, 2016, 35(13): 134-139. (in Chinese) |
| [13] |
PHAM D H, MEIGNEN S. High-order synchrosqueezing transform for multicomponent signals analysis—with an application to gravitational-wave signal[J]. IEEE Transactions on Signal Processing, 2017, 65(12): 3168-3178. |








