乙烯是石油化工行业中最重要的基础原料之一,石化生产中使用的大部分原料烃都用于生产烯烃和芳烃,因此,乙烯的生产能力可以用来衡量石油化工水平。目前大部分乙烯都由裂解炉生产[1],生产过程中会产生焦炭并附着在炉管内壁上,增加炉管热阻,还对生产安全造成影响[2]。当裂解炉管内壁上的焦炭积累到一定程度时,必须进行烧焦操作。Froment等[3]和Heynderickx等[4]对烧焦过程进行了数值模拟,模拟结果表明烧焦过快容易造成飞温,而烧焦温度控制是烧焦过程控制的核心。工业裂解炉通常有数十根炉管,所有炉管均由底部和侧部烧嘴加热,不同温度的炉管形成了温度场,而各炉管温度一般不同[5],因此形成的温度场分布并不均匀。
裂解炉烧焦过程为黑箱模型,炉管内壁温度无法测量,一般通过炉管出口温度(coil outlet temperature, COT)估计裂解炉内壁温度[6],因此现场通过对COT的控制来控制裂解炉内壁温度。目前工业领域最常用的烧焦方法为蒸汽-空气法。蒸汽-空气法的非平稳操作特征明显,COT分布的统计特征随时间改变,然而目前随机分布模型大多为线性模型[7-8],无法描述整个烧焦COT的分布变化情况。
在乙烯裂解炉烧焦的升温过程中,经常出现炉管温度分布分散的情况。温度过高的部分炉管会导致裂解炉管的使用寿命降低,且有烧穿的风险[9-11]。目前,工业实践中蒸汽-空气烧焦法仅通过串级比例积分微分(proportional integral derivative, PID)控制COT均值。仅控制COT的均值难以使整个裂解炉温度分布均衡,仍存在单根炉管过热的风险。为避免单根炉管过热,需对COT分布进行控制。将COT分布视为随机系统的输出分布,目前针对随机系统输出分布的控制方法较为成熟[12-13],如最小方差、概率密度函数(probability density function, PDF)形状控制等。
本文对乙烯烧焦过程COT分布控制进行研究,提出了烧焦过程COT随机分布模型辨识方法,并将烧焦过程根据主导反应划分为多个阶段,分别对各阶段的COT分布建模,再根据各个阶段COT分布模型特征将整个烧焦过程用Hammerstein模型表述,以此描述整个烧焦过程的COT分布变化。基于COT分布权值模型,本文提出了一种鲁棒最小方差协方差约束控制方法实现对权值的实时控制,进而控制COT分布。
1 烧焦过程COT分布PDF建模 1.1 烧焦各阶段线性模型烧焦过程会放出大量的热,COT分布控制不均衡容易造成裂解炉飞温,威胁生产安全[14-15],因此烧焦过程中对COT分布的控制非常重要。烧焦过程的基元反应如式(1)~(7)所示[16-17],可以看出各基元反应的反应热差别明显。
| $ {\rm{C}} + {{\rm{O}}_2} = {\rm{C}}{{\rm{O}}_2};\Delta H = - 393.5{\rm{kJ/mol}} $ | (1) |
| $ {\rm{CO}} + 0.5{{\rm{O}}_2} = {\rm{C}}{{\rm{O}}_2};\Delta H = - 283{\rm{kJ/mol}} $ | (2) |
| $ {\rm{CO}} + 3{{\rm{H}}_2} = {\rm{C}}{{\rm{H}}_4} + {{\rm{H}}_2}{\rm{O}};\Delta H = - 203{\rm{kJ/mol}} $ | (3) |
| $ {\rm{C}} + 0.5{{\rm{O}}_2} = {\rm{CO}};\Delta H = - 110.5{\rm{kJ/mol}} $ | (4) |
| $ {\rm{CO}} + {{\rm{H}}_2}{\rm{O}} = {\rm{C}}{{\rm{O}}_2} + {{\rm{H}}_2};\Delta H = - 41{\rm{kJ/mol}} $ | (5) |
| $ {\rm{C}} + {{\rm{H}}_2}{\rm{O}} = {\rm{CO}} + {{\rm{H}}_2};\Delta H = 131.5{\rm{kJ/mol}} $ | (6) |
| $ {\rm{C}} + {\rm{C}}{{\rm{O}}_2} = 2{\rm{CO}};\Delta H = 172.5{\rm{kJ/mol}} $ | (7) |
按照反应主导情况可将烧焦过程分为以下4个阶段:
1) 温升缓慢阶段该阶段裂解炉中几乎都是蒸汽,空气非常少,主要以反应(2)为主导,该阶段CO含量较少,CO2与空气含量几乎相同,烧焦温升较慢;
2) 温升快速阶段通入一定量的空气后,裂解炉内焦炭量依旧远大于氧气量,此时以反应(3)为主导,CO含量较多,CO2含量有所增加,烧焦温升快;
3) 温升较快阶段待空气量大于蒸汽量,表面焦炭反应完全,此时主导反应为反应(1),CO含量较少,CO2含量较多,烧焦温升较快;
4) 温度平稳阶段只通入空气后,裂解炉内发生的反应几乎只有反应(1),参与反应的焦炭为最深一层,此时几乎没有CO,CO2较少,烧焦温度平稳。
以某一阶段为例,将乙烯裂解炉COT分布的概率密度函数作为被控对象,分别对4个阶段的多炉管COT分布的概率密度函数利用小波神经网络逼近。选取多炉管COT的最大值Tmax和最小值Tmin,设单根炉管出口温度为T(t),以燃料气流量u(t)为T(t)分布的控制输入,则本文考虑的随机分布系统可表示为
| $ \{u(t)\} \rightarrow\{T(t)\}, t \in(0, +\infty) $ | (8) |
T(t)分布可以用累积概率分布函数F(y, u(t))来表述
| $ \begin{array}{l} \;\;\;\;\;\;\;F(y, u(t)) = P(T(t) < y\mid \mathit{u}(t)), y \in \left[ {{T_{\min }}, } \right.\\ \left. {{T_{\max }}} \right] \end{array} $ | (9) |
式中,P(T(t) < y|u(t))是当u(t)作用到随机系统上时,随机变量T(t)小于y的概率。则对应的概率密度函数γ为
| $ \;\;\;\;\;\;\;\gamma(y, u(t))=\frac{\mathrm{d} F(y, u(t))}{\mathrm{d} y} $ | (10) |
可以用小波神经网络建立PDF与权值之间的关系
| $ \begin{array}{l} \;\;\;\;\;\;\;\gamma (y, u(t)) = \sum\limits_{i = 1}^n {{\psi _i}} (y){g_i}(u(t)) + {e_0}, y \in \\ \left[ {{T_{\min }}, {T_{\max }}} \right] \end{array} $ | (11) |
式中,u(t)为控制输入,gi为相关权值,ψi(y)为预先选定的小波基函数,e0为逼近误差。通过对乙烯裂解炉COT的PDF使用小波神经网络逼近,得到权值。为方便计算概率密度函数,将随机分布系统离散化,忽略逼近误差,权值动态系统可描述为
| $ \begin{aligned} \;\;\;\;\;\;\;&\boldsymbol{x}(k+1)=\boldsymbol{A} \boldsymbol{x}(k)+\boldsymbol{B} u(k) \\ \;\;\;\;\;\;\;&\gamma(y, k)=\boldsymbol{C}(y) \boldsymbol{x}(k)+L(y) \end{aligned} $ | (12) |
式中,x(k)=[g1(k), …, gn-1(k)]T, A∈R(n-1)×(n-1), B∈R(n-1)×m, C(y)、L(y)分别为
| $ \;\;\;\;\;\;\;\boldsymbol{C}(y)=\boldsymbol{C}_\psi(y)-\frac{\psi_n(y)}{b_n} \boldsymbol{b}^{\mathrm{T}} \in R^{1 \times(n-1)} $ | (13) |
| $ \;\;\;\;\;\;\;L(y)=b_n^{-1} \psi_n(y) \in R^{1 \times 1} $ | (14) |
| $ \;\;\;\;\;\;\;b_i=\int_{T_{\min }}^{T_{\max }} \psi_i(x) \mathrm{d} y, \boldsymbol{b}^{\mathrm{T}}=\left[b_1, b_2, \cdots, b_{n-1}\right] \in R^{n-1} $ | (15) |
| $ \;\;\;\;\;\;\;\boldsymbol{C}_\psi(y)=\left[\psi_1(y), \psi_2(y), \cdots, \psi_{n-1}(y)\right] \in R^{n-1} $ | (16) |
PDF满足在整个区间积分为1的自然约束,即
| $ \;\;\;\;\;\;\;\int_{T_{\min }}^{T_{\max }} \gamma(y, k) \mathrm{d} y=1 $ | (17) |
由式(11)、(15)、(17)可得
| $ \;\;\;\;\;\;\;g_n(k)=\frac{1-\boldsymbol{b}^{\mathrm{T}} \boldsymbol{x}(k)}{b_n} $ | (18) |
以上即为建立某一阶段烧焦过程COT分布线性模型的方法。针对不同阶段建立线性模型,再设计控制器不失为一种COT分布控制方法。但由于目前某炼化烯烃部无法实时测量炉管出口的CO与CO2含量,难以准确在线识别烧焦所处阶段,不同阶段控制器的准确切换较为困难,因此该方法难以在实际工业现场应用。
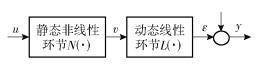
1.2 COT分布Hammerstein模型烧焦过程输入为燃料气流量,蒸汽-空气法烧焦时燃料气流量一般为阶跃变化,燃料气流量变化导致COT变化的稳态增益较易计算。不同阶段炉管内部反应热不同,燃料气流量变化导致COT变化的稳态增益也不同,因此烧焦过程的稳态增益变化为非线性。COT变化的动态过程为炉管传热过程,各阶段相似,可近似为线性动态过程。烧焦过程存在静态非线性和动态线性特性,因此采用如图 1所示的具有动态线性、静态非线性环节的Hammerstein模型对整个烧焦过程的COT分布变化进行描述。
|
图 1 Hammerstein模型结构 Fig.1 Hammerstein model structure |
将稳态非线性环节用f(·)表示,烧焦过程的Hammerstein模型可描述为
| $ \begin{aligned} \;\;\;\;\;\;\;&\boldsymbol{x}(k+1)=\boldsymbol{F} \boldsymbol{x}(k)+\boldsymbol{G} v(k) \\ \;\;\;\;\;\;\;&v(k)=f(u(k)) \\ \;\;\;\;\;\;\;&\gamma(y, k)=\boldsymbol{C}(y) \boldsymbol{x}(k)+L(y) \end{aligned} $ | (19) |
模型结构确定之后需要辨识模型参数。由于式(19)所示的Hammerstein模型输出方程中存在以y为自变量的函数,且C(y)、L(y)在小波神经网络逼近时已确定,因此需辨识的模型参数为F、G、f(·)。其中f(·)为非线性静态环节,F、G为线性动态环节参数。对于这些未知参数,一般可采用同步辨识法与分步辨识法计算。同步辨识法不需要对v(k)进行估计,直接计算非线性环节和线性环节的所有参数;分步辨识法则是将非线性环节与线性环节分离开辨识,一般需要估计中间变量v(k)。
对Hammerstein模型参数采用分步辨识,通过迭代法辨识F、G、f(·)。迭代法是固定一部分参数、辨识另一部分参数的辨识方法,该方法原理简单,辨识效率高[18],但初值不合适时可能会不收敛。
非线性稳态环节参数化较为困难,因此采用如式(20)所示的WaveARX神经网络描述。WaveARX神经网络是在小波神经网络基础上并列一个ARX模型,提高了对线性模型的逼近能力。
| $ \;\;\;\;\;\;\;f(u) \approx \sum\limits_{i=1}^N g_i^{\prime} \cdot \phi_i(u)+k u+k_0 $ | (20) |
式中,g′i为WaveARX神经网络的权重系数,
对于非线性静态环节f(·),使用WaveARX神经网络进行辨识。神经网络的输出为f(u),输入为u,非线性静态环节f(·)的逼近关系为[19]
| $ \;\;\;\;\;\;\;f(u)=\boldsymbol{\phi}(u) \cdot \boldsymbol{\omega}+k u+k_0 $ | (21) |
式中,ω=[g′1, g′2, …, g′N]T, ϕ(y)=[ϕ1(y), ϕ2(y), …, ϕN(y)]。
对于式(19)的Hammerstein模型,将非线性环节f(u)代入后,可得如下状态方程。
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{x}}(k + 1) = \mathit{\boldsymbol{Fx}}(k) + \mathit{\boldsymbol{G}} \cdot \boldsymbol{\phi} (u(k)) \cdot \mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{G}} \cdot k \cdot \\ u(k) + \mathit{\boldsymbol{G}} \cdot {k_0} \end{array} $ | (22) |
针对式(22)所示模型可定义准则函数为
| $ \begin{array}{l} \;\;\;\;\;\;\;J\left( {\mathit{\boldsymbol{\hat F}}, \mathit{\boldsymbol{\hat G}}, \mathit{\boldsymbol{\hat \omega }}, \hat k, {{\hat k}_0}} \right){\rm{ = argmin}}\frac{1}{M}\sum\limits_{k = 1}^M {\left[ {\mathit{\boldsymbol{x}}\left( {k + 1} \right) - } \right.} \\ {\left. {\mathit{\boldsymbol{\hat F}}\mathit{\boldsymbol{x}}(k) + \hat {\bf{G}}\boldsymbol{\phi} (u(k)) \cdot \mathit{\boldsymbol{\hat \omega }} + \mathit{\boldsymbol{\hat G}}\hat k \cdot u(k) + \mathit{\boldsymbol{\hat G}} \cdot {{\hat k}_0}} \right]^2} \end{array} $ | (23) |
其中,
| $ \;\;\;\;\;\;\;\left\{ {\begin{array}{*{20}{l}} {{{\left( {\mathit{\boldsymbol{\hat \omega }}, \hat k, {{\hat k}_0}} \right)}_j} = \mathop {{\mathop{\rm argmin}\nolimits} }\limits_{\left( {\mathit{\boldsymbol{\hat \omega }}, \hat k, {{\hat k}_0}} \right)} J\left( {{{(\mathit{\boldsymbol{\hat F}}, \mathit{\boldsymbol{\hat G}})}_{j - 1}}, \mathit{\boldsymbol{\hat \omega }}, \hat k, {{\hat k}_0}} \right)}\\ {{{(\mathit{\boldsymbol{\hat F}}, \mathit{\boldsymbol{\hat G}})}_j} = \mathop {{\mathop{\rm argmin}\nolimits} }\limits_{(\mathit{\boldsymbol{\hat F}}, \mathit{\boldsymbol{\hat G}})} J\left( {\mathit{\boldsymbol{\hat F}}, \mathit{\boldsymbol{\hat G}}, {{\left( {\mathit{\boldsymbol{\hat \omega }}, \hat k, \hat {{k_0}}} \right)}_{j - 1}}} \right)} \end{array}} \right. $ | (24) |
式中,j表示迭代次数。具体的迭代法求
1) 选择适当的小波基函数,使用小波神经网络逼近COT的PDF获得烧焦过程的权值变化数据;
2) 以COT与燃料气流量的稳态增益变化作为初始中间变量估计
3) 固定参数
4) 固定参数
5) 将最新的参数
通过迭代法求得模型参数后,为方便模型计算与控制器设计,将模型参数变换后可得以下状态方程。
| $ \;\;\;\;\;\;\;\boldsymbol{x}(k+1)=\boldsymbol{f}^{\prime}(u(k))+\boldsymbol{F} \boldsymbol{x}(k)+\boldsymbol{H} u(k)+\boldsymbol{c}_0 $ | (25) |
式中,
烧焦过程整体的非线性模型可描述为
| $ \begin{aligned} \;\;\;\;\;\;\;&\boldsymbol{x}(k+1)=\boldsymbol{G}(\boldsymbol{x}(k), u(k))+\boldsymbol{\zeta}_1(k) \\ \;\;\;\;\;\;\;&\gamma(y, k)=\boldsymbol{C}(y) \boldsymbol{x}(k)+L(y) \end{aligned} $ | (26) |
式中,x∈Rn-1为状态变量,u∈Rm为输入变量,γ为输出变量;非线性函数G: Rn-1×Rm→Rn-1,高斯白噪声向量ζ1(k)为n-1维。
| $ \;\;\;\;\;\;\;E\left[ {{\mathit{\boldsymbol{\zeta }}_1}(k)} \right] = 0 $ | (27) |
| $ \;\;\;\;\;\;\;E\left[ {{\mathit{\boldsymbol{\zeta }}_1}(k)\mathit{\boldsymbol{\zeta }}_1^{\rm{T}}(j)} \right] = {\mathit{\boldsymbol{V}}_1} $ | (28) |
式中,E(·)表示求均值运算,V1为对称正定矩阵。
基于WaveARX神经网络的真实最大逼近偏差ef为
| $ \begin{array}{l} \;\;\;\;\;\;\;{e_f} = \left\| {\mathit{\boldsymbol{G}}(\mathit{\boldsymbol{x}}(k), u(k)) - {\mathit{\boldsymbol{f}}^\prime }(u(k)) - \mathit{\boldsymbol{Fx}}(k) - } \right.\\ {\left. {\mathit{\boldsymbol{H}}\mathit{u}(k) - {\mathit{\boldsymbol{c}}_0}} \right\|_\infty } \end{array} $ | (29) |
其中向量[e1, e2, …, en-1]T的∞范数由式(30)定义
| $ \begin{array}{l} \;\;\;\;\;\;\;{\left\| {{e_1}, {e_2}, \cdots , {e_{n - 1}}} \right\|_\infty } = \max \left\{ {\left| {{e_1}} \right|, \left| {{e_2}} \right|, \cdots } \right.{\rm{, }}\\ \left. {\left| {{e_{n - 1}}} \right|} \right\} \end{array} $ | (30) |
建立烧焦过程COT分布模型,状态变量x为小波神经网络逼近PDF所得的权值,输入u为燃料气流量,γ为COT分布的概率密度函数,x、γ两者的关系如式(31)所示。
| $ \;\;\;\;\;\;\;\gamma(y)=\boldsymbol{C}(y) \boldsymbol{x}+L(y) $ | (31) |
定理1 若存在xg使得‖x-xg‖2→0,则
证明:若‖x-xg‖2→0,则
| $ \;\;\;\;\;\;\;\sum\limits_{i = 1}^{n - 1} {{C_i}} (y){\left( {{x_i} - {x_{gi}}} \right)^2} \to 0 $ | (32) |
Ci(y)为C(y)的第i个元素,由式(32)可得
| $ \;\;\;\;\;\;\;\sum\limits_{i = 1}^{n - 1} {{C_i}} (y)\left( {{x_i} - {x_{gi}}} \right) \to 0 $ | (33) |
由x、γ两者的关系式(式(31))可得
| $ \begin{array}{l} \;\;\;\;\;\;\;\int_{{T_{\min }}}^{{T_{\max }}} {{{\left( {\gamma (y) - {\gamma _g}(y)} \right)}^2}} {\rm{d}}y = \int_{{T_{\min }}}^{{T_{\max }}} {(\mathit{\boldsymbol{C}}(} y)(\mathit{\boldsymbol{x}} - \\ {\left. {\left. {{\mathit{\boldsymbol{x}}_g}} \right)} \right)^2}{\rm{d}}y = \int_{{T_{\min }}}^{{T_{\max }}} {{{\left( {\sum\limits_{i = 1}^{n - 1} {{C_i}} (y)\left( {{x_i} - {x_{gi}}} \right)} \right)}^2}} {\rm{d}}y \end{array} $ | (34) |
由此可得
建立烧焦过程COT随机分布系统模型,设计最小方差协方差约束控制器[20-22]。考虑到模型逼近偏差,基于WaveARX神经网络的非线性系统逼近可写为
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{x}}(k + 1) = {\mathit{\boldsymbol{f}}^\prime }(u(k)) + \mathit{\boldsymbol{Fx}}(k) + \mathit{\boldsymbol{H}}u(k) + {\mathit{\boldsymbol{c}}_0} + \\ {\mathit{\boldsymbol{E}}_f} + {\mathit{\boldsymbol{\xi }}_1}(k)\\ \;\;\;\;\;\;\;\mathit{\boldsymbol{Y}}(k) = \mathit{\boldsymbol{I}} \cdot \mathit{\boldsymbol{x}}(k) \end{array} $ | (35) |
其中I为单位矩阵,模型偏差Ef=G(x(k), u(k))-f′(u(k))-Fx(k)-Hu(k)-c0。
由定理1可知,当x趋近于目标值时,γ也趋近于目标PDF,因此可通过控制x趋近于目标值使得γ趋近于目标PDF。引入设定值r,r∈R(n-1)×1,对系统(式(35))进行控制,引入状态反馈矩阵K(k),令u(k)=-K(k)x(k)。
闭环状态空间方程为
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{x}}(k + 1) = {\mathit{\boldsymbol{f}}^\prime }(u(k)) + \mathit{\boldsymbol{Fx}}(k) + \mathit{\boldsymbol{H}}[ - \mathit{\boldsymbol{K}}(k) \cdot \\ \mathit{\boldsymbol{x}}(k)] + {\mathit{\boldsymbol{c}}_0} + {\mathit{\boldsymbol{E}}_f} + {\mathit{\boldsymbol{\xi }}_1}(k) \end{array} $ | (36) |
控制偏差为e(k)=Y(k)-r(k),e(k)∈Rn-1,为方便书写,令S(k)=F-HK(k),则
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{e}}(k + 1) = {\mathit{\boldsymbol{f}}^\prime }(u(k)) + \mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{e}}(k) + \mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + \\ {\mathit{\boldsymbol{c}}_0} + {\mathit{\boldsymbol{E}}_f} + {\mathit{\boldsymbol{\xi }}_1}(k) - \mathit{\boldsymbol{r}}(k) \end{array} $ | (37) |
取‖f′(u(k))‖∞=af,则控制偏差的协方差矩阵为
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{\rho }}(k + 1) = E\left\{ {\mathit{\boldsymbol{e}}(k + 1) \cdot {{[\mathit{\boldsymbol{e}}(k + 1)]}^{\rm{T}}}} \right\} = \\ E\left\{ {\left[ {{\mathit{\boldsymbol{e}}^\prime }(k + 1) + {\mathit{\boldsymbol{E}}_f}} \right] \cdot {{\left[ {{\mathit{\boldsymbol{e}}^\prime }(k + 1) + {\mathit{\boldsymbol{E}}_f}} \right]}^{\rm{T}}}} \right\} = E\left\{ {{\mathit{\boldsymbol{e}}^\prime }(k + } \right.\\ 1) \cdot {\left[ {{\mathit{\boldsymbol{e}}^\prime }(k + 1)} \right]^{\rm{T}}} + {\mathit{\boldsymbol{E}}_f}{\left[ {{\mathit{\boldsymbol{e}}^\prime }(k + 1)} \right]^{\rm{T}}} + {\mathit{\boldsymbol{e}}^\prime }(k + 1)\mathit{\boldsymbol{E}}_f^{\rm{T}} + \\ \left. {{\mathit{\boldsymbol{E}}_f} \cdot \mathit{\boldsymbol{E}}_f^{\rm{T}}} \right\} \end{array} $ | (38) |
其中,
| $ \begin{array}{l} \;\;\;\;\;\;\;E\left\{ {{\mathit{\boldsymbol{e}}^\prime }(k + 1) \cdot {{\left[ {{\mathit{\boldsymbol{e}}^\prime }(k + 1)} \right]}^{\rm{T}}}} \right\} = \mathit{E}\{ [\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + \\ \left. {{\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right] \cdot {\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]^{\rm{T}}} + {\mathit{\boldsymbol{f}}^\prime }(u(k)) \cdot \\ {\mathit{\boldsymbol{f}}^\prime }{(u(k))^{\rm{T}}} + \mathit{\boldsymbol{S}}(k) \cdot {\mathit{\boldsymbol{e}}^\prime }(k) \cdot {\mathit{\boldsymbol{e}}^\prime }{(k)^{\rm{T}}} \cdot \mathit{\boldsymbol{S}}{(k)^{\rm{T}}} + \\ {\mathit{\boldsymbol{f}}^\prime }(u(k)) \cdot {\mathit{\boldsymbol{e}}^\prime }{(k)^{\rm{T}}} \cdot \mathit{\boldsymbol{S}}{(k)^{\rm{T}}} + \mathit{\boldsymbol{S}}(k) \cdot {\mathit{\boldsymbol{e}}^\prime }(k) \cdot {\mathit{\boldsymbol{f}}^\prime }{(u(k))^{\rm{T}}} + \\ \mathit{\boldsymbol{S}}(k) \cdot {\mathit{\boldsymbol{e}}^\prime }(k) \cdot {\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]^{\rm{T}}} + \\ \left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]{\mathit{\boldsymbol{e}}^\prime }{(k)^{\rm{T}}}\mathit{\boldsymbol{S}}{(k)^{\rm{T}}} + [\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + \\ \left. {{\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right] \cdot {\mathit{\boldsymbol{f}}^\prime }{(u(k))^{\rm{T}}} + {\mathit{\boldsymbol{f}}^\prime }(u(k)) \cdot [\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + \\ \left. {{{\left. {{\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]}^{\rm{T}}} + {\mathit{\boldsymbol{\xi }}_1}(k) \cdot {{\left[ {{\mathit{\boldsymbol{\xi }}_1}(k)} \right]}^{\rm{T}}}} \right\} \end{array} $ | (39) |
定义1 S1,S2为同阶实对称阵,假如S1-S2为半正定阵,记为S1-S2≥0,则称S1≥S2。
引理1 d∈Rn为列向量,I为单位阵,由定义1可得:①ddT为半正定阵,即ddT≥0;②dTdI-dd为半正定阵,即dTdI≥ddT。
由引理1可得以下6个不等式:
| $ \begin{array}{l} \;\;\;\;\;\;\;E\left\{ {{\mathit{\boldsymbol{E}}_f}\mathit{\boldsymbol{E}}_f^{\rm{T}}} \right\} \le ne_f^2\mathit{\boldsymbol{I}}\\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{E}}_\mathit{f}}{\left[ {{\mathit{\boldsymbol{e}}^\prime }(k + 1)} \right]^{\rm{T}}} + {\mathit{\boldsymbol{e}}^\prime }(k + 1)\mathit{\boldsymbol{E}}_f^{\rm{T}} \le {\mathit{\boldsymbol{e}}^\prime }(k + 1) \cdot \\ {\left[ {{\mathit{\boldsymbol{e}}^\prime }(k + 1)} \right]^{\rm{T}}} + {\mathit{\boldsymbol{E}}_f} \cdot \mathit{\boldsymbol{E}}_f^{\rm{T}}\\ \;\;\;\;\;\;\;\mathit{E}\left\{ {{\mathit{\boldsymbol{f}}^\prime }(u(k)) \cdot {{\left[ {{\mathit{\boldsymbol{f}}^\prime }(u(k))} \right]}^{\rm{T}}}} \right\} \le na_f^2\mathit{\boldsymbol{I}}\\ \;\;\;\;\;\;\;\mathit{E}\left[ {{\mathit{\boldsymbol{f}}^\prime }\mathit{\boldsymbol{e}}{{(k + 1)}^{\rm{T}}}\mathit{\boldsymbol{S}}{{(k)}^{\rm{T}}} + \mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{e}}(k + 1){\mathit{\boldsymbol{f}}^{\prime {\rm{T}}}}} \right] \le n \cdot \\ a_f^2 \cdot \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{\rho }}(k)\mathit{\boldsymbol{S}}{(k)^{\rm{T}}}\\ \;\;\;\;\;\;\;\mathit{E}\left\{ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{e}}(k + 1){{\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]}^{\rm{T}}} + } \right.\\ \left. {\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]\mathit{\boldsymbol{e}}{{(k + 1)}^{\rm{T}}}\mathit{\boldsymbol{S}}{{(k)}^{\rm{T}}}} \right\} \le \\ \left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]{\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]^{\rm{T}}} + \\ \mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{\rho }}(k)\mathit{\boldsymbol{S}}{(k)^{\rm{T}}}\\ \;\;\;\;\;\;\;\mathit{E}\left\{ {{\mathit{\boldsymbol{f}}^\prime }(u(k)){{\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]}^{\rm{T}}} + } \right.\\ \left. {\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]{\mathit{\boldsymbol{f}}^\prime }{{(u(k))}^{\rm{T}}}} \right\} \le [\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + \\ \left. {{\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]{\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]^{\rm{T}}} + na_f^2\mathit{\boldsymbol{I}} \end{array} $ |
将上述6个不等式代入式(38),可得
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{\rho }}(k + 1) \le 6na_f^2\mathit{\boldsymbol{I}} + 6\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{\rho }}(k)\mathit{\boldsymbol{S}}{(k)^{\rm{T}}} + 2{\mathit{\boldsymbol{V}}_1} + \\ 2ne_f^2\mathit{\boldsymbol{I}} + 6\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - } \right.\\ \mathit{\boldsymbol{r}}(k){]^{\rm{T}}} \end{array} $ | (40) |
取P(0)≥ρ(0),令
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{P}}(k + 1) = 6na_f^2\mathit{\boldsymbol{I}} + 6\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{P}}(k)\mathit{\boldsymbol{S}}{(k)^{\rm{T}}} + 2{\mathit{\boldsymbol{V}}_1} + \\ 2ne_f^2\mathit{\boldsymbol{I}} + 6\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}(k)} \right]\left[ {\mathit{\boldsymbol{S}}(k)\mathit{\boldsymbol{r}}(k) + {\mathit{\boldsymbol{c}}_0} - } \right.\\ \mathit{\boldsymbol{r}}(k){]^{\rm{T}}} \end{array} $ | (41) |
由式(40)、(41)可得P(k+1)-ρ(k+1)≥6S(k)·[P(k)-ρ(k)]·S(k)T,当取P(0)≥ρ(0)时,不等式右侧为半正定矩阵,由引理1可得,P(k+1)≥ρ(k+1),即P(k+1)是ρ(k+1)的上限估计。当P(k+1)取极小值时,ρ(k+1)将收敛于一个更小的范围。考虑到系统输入输出有一定的约束,使用线性矩阵不等式求解K(k)。
控制目标为偏差e的方差上限最小,性能指标可写为
| $ \begin{array}{l} \;\;\;\;\;\;\;J = \mathop {\lim }\limits_{k \to \infty } \left\{ {\mathit{E}\left[ {\mathit{\boldsymbol{e}}{{(k)}^{\rm{T}}}\mathit{\boldsymbol{Qe}}(k) + \mathit{\boldsymbol{u}}{{(k)}^{\rm{T}}}\mathit{\boldsymbol{Ru}}(k)} \right]} \right\} \le \\ \mathop {\lim }\limits_{k \to \infty } \left\{ {\sum\limits_{i = 1}^p {{q_i}} P(k) + \sum\limits_{j = 1}^m {{r_j}} U(k)} \right\} \le \sum\limits_{i = 1}^p {{q_i}} {P_i} + \\ \sum\limits_{j = 1}^m {{r_j}} {U_j} \end{array} $ | (42) |
式中,p和m分别为输出维数和输入维数,qi、rj分别为偏差方差与输入方差加权值,Pi为P对角线上的第i个元素,Uj为输入协方差矩阵U对角线上的第j个元素。
根据式(42),令目标函数为
| $ \;\;\;\;\;\;\;\mathop {\min }\limits_{\mathit{\boldsymbol{K}}, {P_i}, {U_j}} J = \mathop {\min }\limits_{\mathit{\boldsymbol{K}}, {P_i}, {U_j}} \sum\limits_{i = 1}^p {{q_i}} {P_i} + \sum\limits_{j = 1}^m {{r_j}} {U_j} $ | (43) |
输入输出的方差约束为
| $ \;\;\;\;\;\;\;{\mathit{\Sigma }_{yi}} = {\boldsymbol{\phi} _i}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_x}\boldsymbol{\phi} _i^{\rm{T}} $ | (44) |
| $ \;\;\;\;\;\;\;{\mathit{\Sigma} _{uj}} = {\boldsymbol{\phi} _j}{\mathit{\boldsymbol{K}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_x}{{\mathit{\boldsymbol{K}}}^{\rm{T}}}\boldsymbol{\phi} _j^{\rm{T}} $ | (45) |
| $ \;\;\;\;\;\;\;{\mathit{\Sigma }_{yi}} < \bar y_i^2,i = 1,2, \cdots ,p $ | (46) |
| $ \;\;\;\;\;\;\;{\mathit{\Sigma }_{uj}} < \bar u_j^2,j = 1,2, \cdots ,m $ | (47) |
其中,Σu与Σy为系统稳态输入与输出的协方差矩阵,Σuj和Σyi分别为Σu和Σy的矩阵对角线上第j个和第i个值,Σx是系统状态变量的协方差矩阵,ϕi和ϕj分别为单位阵第i、j行。
对于式(28)所示系统,若存在状态反馈控制律K使得控制偏差方差上限最小,输入方差最小,则控制律K需满足以下条件。
| $ \;\;\;\;\;\;\;\mathop {\min }\limits_{\mathit{\boldsymbol{K}}, {P_i}, {U_j}} \sum\limits_{i = 1}^p {{q_i}} {P_i} + \sum\limits_{j = 1}^m {{r_j}} {U_j} $ | (48) |
| $ \;\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}} { - 3{\mathit{\boldsymbol{P}}^{ - 1}}}&{{\mathit{\boldsymbol{S}}^{\rm{T}}}}&0\\ \mathit{\boldsymbol{S}}&{3na_f^2\mathit{\boldsymbol{I}} + ne_f^2\mathit{\boldsymbol{I}} - \frac{1}{3}\mathit{\boldsymbol{P}}}&{\mathit{\boldsymbol{Sr}} + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}}\\ 0&{{{\left( {\mathit{\boldsymbol{Sr}} + {\mathit{\boldsymbol{c}}_0} - \mathit{\boldsymbol{r}}} \right)}^{\rm{T}}}}&{ - \frac{1}{3}\mathit{\boldsymbol{I}}} \end{array}} \right) < 0 $ | (49) |
| $ \;\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}} { - {U_i}}&{\boldsymbol{\phi} \mathit{\boldsymbol{Kx}}}\\ {{{(\mathit{\boldsymbol{Kx}})}^{\rm{T}}}\boldsymbol{\phi} _i^{\rm{T}}}&{ - \mathit{\boldsymbol{I}}} \end{array}} \right) < 0 $ | (50) |
| $ \;\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}} { - {Y_j}}&{{\boldsymbol{\phi} _j}\mathit{\boldsymbol{x}}}\\ {{\mathit{\boldsymbol{x}}^{\rm{T}}}\boldsymbol{\phi} _j^{\rm{T}}}&{ - \mathit{\boldsymbol{I}}} \end{array}} \right) < 0 $ | (51) |
| $ \;\;\;\;\;\;\;{Y_i} < \bar y_i^2,i = 1,2, \cdots ,p $ | (52) |
| $ \;\;\;\;\;\;\;{U_j} < \bar u_j^2,j = 1,2, \cdots ,m $ | (53) |
运用Schur补引理可将式(41)、(44)、(45)转换成矩阵不等式即式(49)、(50)、(51),其中Y为输出协方差矩阵。
对于式(48)~(53),可使用LMI工具箱求解控制律K。
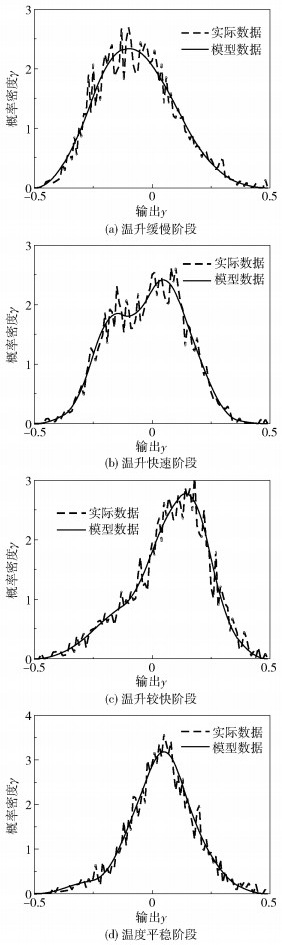
3 实验仿真与工业应用 3.1 模型辨识结果根据离线CO和CO2数据将烧焦过程分为4个阶段,使用式(10)计算出各阶段概率密度函数,以COT的PDF为研究对象,对PDF进行逼近,得到烧焦各阶段权值的变化,再以权值为状态变量,建立烧焦过程各阶段COT分布模型,结果如图 2所示。
|
图 2 烧焦4个阶段的PDF模型 Fig.2 PDF models of the four stages of decoking |
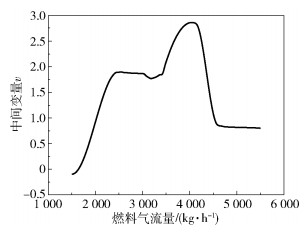
4个阶段的模型稳态增益均不相同,而线性动态过程较为相似,因此使用Hammerstein模型描述整个烧焦过程的权值变化情况。将采用小波神经网络逼近概率密度函数所得权值作为系统的状态变量,燃料气流量作为系统输入,使用迭代法求解Hammerstein模型参数,非线性环节辨识结果如图 3所示,线性环节辨识结果如图 4所示。
|
图 3 非线性环节辨识结果 Fig.3 Identification results for nonlinear static links |
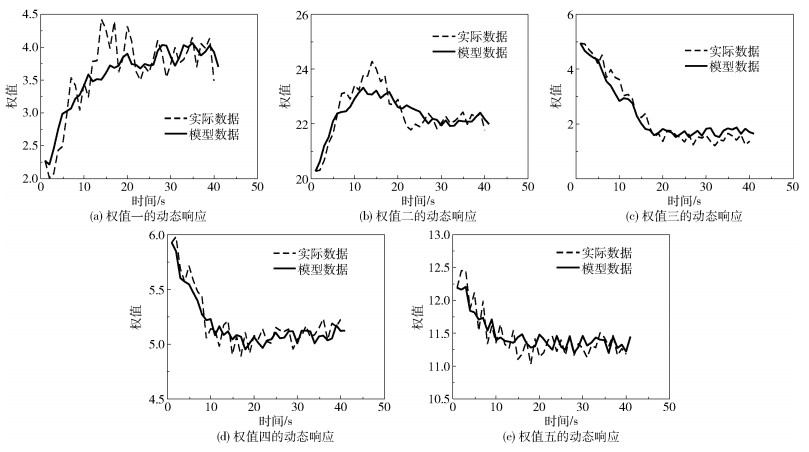
|
图 4 线性环节辨识结果 Fig.4 Identification results for linear dynamic links |
从非线性环节辨识结果可以看出,燃料气流量不同时,中间变量v的变化率也不同,甚至变化方向相反,表明不同阶段COT分布的变化速率不同,甚至变化方向相反。
3.2 PDF权值控制器仿真对比针对Hammerstein模型提出一种针对权值的控制方法。根据定理1,一旦权值接近目标权值,COT的PDF也会接近目标PDF。通过计算得出控制偏差的协方差矩阵上限P(k+1)的迭代方程。为使得P(k+1)在约束范围内最小,使用LMI求解K(k)。本次控制目标权值为(0.5, 1, 27, 29, 2),期望概率密度函数为N(0, 0.01)。
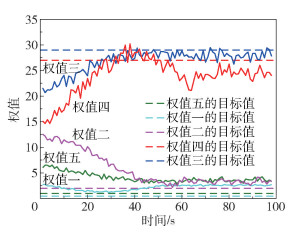
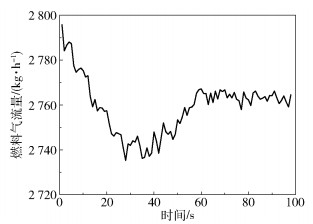
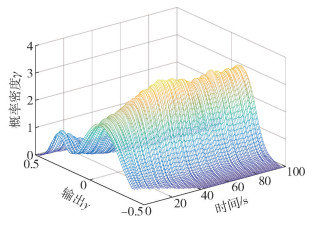
图 5显示了控制后权值的变化情况,5个权值由控制前的(2.7, 12, 21, 15, 6)改变至控制后的(2.5, 3, 27, 24, 3),可以看出在控制器的作用下,权值在接近目标值。图 6为控制器作用下的输入变化情况。由图 5、6可以看出,控制器可通过改变输入控制权值来接近目标值。由定理1可知,在控制器的作用下实际PDF接近目标PDF。控制前后PDF的变化情况如图 7所示,可以看出控制器能够使得COT分布更加集中。
|
图 5 控制后权值的变化情况 Fig.5 Weight changes after control |
|
图 6 输入变化情况 Fig.6 Input changes |
|
图 7 控制前后的PDF变化 Fig.7 PDF changes before and after control |
上述控制结果表明,所得控制器可通过控制燃料气流量来控制COT分布的PDF,使得COT分布更加集中。
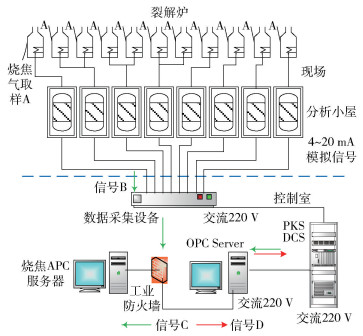
3.3 工业应用测试选取某炼化公司的大型乙烯工业裂解炉烧焦过程为测试对象,使用OPC(OLE for process control)连接集散型控制系统(distributed control system, DCS),完成软件与DCS的数据交换。在实际烧焦过程中投用该控制器,系统结构如图 8所示。
|
图 8 烧焦控制系统结构 Fig.8 Structure of the decoking control system |
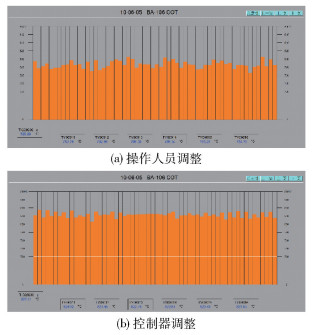
图 9为自动烧焦程序DCS画面。在实际烧焦过程中投用COT分布控制器,对COT的设定值进行调整,画面左下角记录调整后的数值。图 10(a)、(b)分别是通过人工和控制器调整COT后某一时刻炉管COT的DSC画面,可以看出控制器调整后的COT分布更加集中,控制器投用效果符合预期。表 1为烧焦各阶段操作人员调整与控制器调整后的COT方差对比,可以看出控制器调整后相较于人工调整后的COT方差降低20.93%,COT最大偏差降低22.04%,表明控制器的控制效果相较于操作人员调整有一定的提升。
|
图 9 自动烧焦程序DCS画面 Fig.9 DCS screen of auto decoking program |
|
图 10 操作人员调整和控制器调整后的DCS画面 Fig.10 DCS screen after operator adjustment and controller adjustment |
| 下载CSV 表 1 操作人员调整与控制器调整统计量对比 Table 1 Statistical comparison between operator adjustment and controller adjustment |
本文针对乙烯裂解炉烧焦过程的COT控制问题提出了一种COT分布控制方法。使用概率密度函数描述COT分布情况,采用小波神经网络逼近概率密度函数得到相应权值。以燃料气流量为系统输入,概率密度函数为系统输出,权值为状态变量,建立烧焦各阶段的模型。使用静态非线性、动态线性的Hammerstein模型描述整个烧焦过程的COT分布变化,并采用迭代法求解模型参数。针对烧焦过程COT的Hammerstein模型,设计了一个鲁棒最小方差协方差约束控制器,并利用LMI求解。采用实际工业数据进行仿真,建立整个烧焦过程COT分布的变化模型,使用控制器对模型进行控制,实验结果表明控制器能使得实际COT分布接近目标COT分布。并将所提控制方法在工业裂解炉上投用,测试结果表明与人工调整相比,控制器降低了COT的方差与最大偏差,有良好的控制效果。
| [1] |
徐海丰. 2019年世界乙烯行业发展状况与趋势[J]. 国际石油经济, 2020, 28(5): 48-54. XU H F. Global ethylene industry in 2019 and its development trend[J]. International Petroleum Economics, 2020, 28(5): 48-54. (in Chinese) |
| [2] |
KHODAMORAD S H, FATMEHSARI D H, REZAIE H, et al. Analysis of ethylene cracking furnace tubes[J]. Engineering Failure Analysis, 2012, 21: 1-8. DOI:10.1016/j.engfailanal.2011.11.018 |
| [3] |
SCHOOLS E M, FROMENT G F. Simulation of decoking of thermal cracking coils by steam/air-mixtures[J]. AIChE Journal, 1997, 43(1): 118-126. DOI:10.1002/aic.690430114 |
| [4] |
HEYNDERICKX G J, SCHOOLS E M, MARIN G B. Optimization of the decoking procedure of an ethane cracker with a steam/air mixture[J]. Industrial & Engineering Chemistry Research, 2006, 45(22): 7520-7529. |
| [5] |
陈德坤. 大型乙烯裂解炉烧焦过程中COT随机分布系统建模与控制研究[D]. 北京: 北京化工大学, 2021. CHEN D K. Study on modeling and control of COT stochastic distribution system during coke burning in large ethylene cracking furnace[D]. Beijing: Beijing University of Chemical Technology, 2021. (in Chinese) |
| [6] |
谢磊, 员鑫. COT温度先进控制在乙烯裂解炉中的应用[J]. 化工自动化及仪表, 2021, 48(2): 193-196. XIE L, YUN X. Application of COT advanced temperature control in ethylene cracking furnace[J]. Control and Instruments in Chemical Industry, 2021, 48(2): 193-196. (in Chinese) DOI:10.3969/j.issn.1000-3932.2021.02.019 |
| [7] |
周靖林. PDF控制及其在滤波中的应用[D]. 北京: 中国科学院自动化研究所, 2005. ZHOU J L. PDF control and its application in filtering[D]. Beijing: Institute of Automation, Chinese Academy of Sciences, 2005. (in Chinese) |
| [8] |
REN M F, ZHANG Q C, ZHANG J H. An introductory survey of probability density function control[J]. Systems Science & Control Engineering, 2019, 7(1): 158-170. |
| [9] |
王冬伟. 乙烯裂解炉的结焦原因及防控技术[J]. 化工管理, 2018(2): 99. WANG D W. Causes of coking in ethylene cracking furnaces and prevention and control techniques[J]. Chemical Enterprise Management, 2018(2): 99. (in Chinese) |
| [10] |
张永军, 万书宝, 郭英爽, 等. 乙烯裂解炉的结焦及其抑制措施[J]. 化学工业, 2011, 29(12): 46-51. ZHANG Y J, WAN S B, GUO Y S, et al. Coke formation and coke inhibition measures of ethylene cracking furnace[J]. Chemical Industry, 2011, 29(12): 46-51. (in Chinese) DOI:10.3969/j.issn.1673-9647.2011.12.011 |
| [11] |
ACU A M, BAŞCANBAZ-TUNCA G, RASA I. Information potential for some probability density functions[J]. Applied Mathematics and Computation, 2021, 389: 125578. DOI:10.1016/j.amc.2020.125578 |
| [12] |
YIN L P, ZHANG H Y, GUO L. Data driven output joint probability density function control for multivariate non-linear non-Gaussian systems[J]. IET Control Theory & Applications, 2015, 9(18): 2697-2703. |
| [13] |
LI L F, YAO L N. Discrete-time 2-order sliding mode fault-tolerant tracking control for non-Gaussian nonlinear stochastic distribution control systems with missing measurements[J]. Complexity, 2020, 2020: 9704861. |
| [14] |
HEYNDERICKX G J, SCHOOLS E M, MARIN G B. Simulation of the decoking of an ethane cracker with a steam/air mixture[J]. Chemical Engineering Science, 2006, 61(6): 1779-1789. DOI:10.1016/j.ces.2005.10.008 |
| [15] |
TARAFDER A, LEE B C S, RAY A K, et al. Multiobjective optimization of an industrial ethylene reactor using a nondominated sorting genetic algorithm[J]. Industrial & Engineering Chemistry Research, 2005, 44(1): 124-141. |
| [16] |
朱磊, 赵众. 基于工况识别的乙烯裂解炉清焦控制系统[J]. 化工自动化及仪表, 2019, 46(7): 513-518. ZHU L, ZHAO Z. Decoking control system for ethylene cracking furnace based on operating region recognition[J]. Control and Instruments in Chemical Industry, 2019, 46(7): 513-518. (in Chinese) DOI:10.3969/j.issn.1000-3932.2019.07.001 |
| [17] |
智茂轩. 乙烯装置裂解炉的烧焦过程模拟[J]. 乙烯工业, 2020, 32(2): 34-37. ZHI M X. Simulation of coking process in the cracking furnace of ethylene plant[J]. Ethylene Industry, 2020, 32(2): 34-37. (in Chinese) DOI:10.3969/j.issn.1671-7120.2020.02.011 |
| [18] |
贾立, 李训龙. Hammerstein模型辨识的回顾及展望[J]. 控制理论与应用, 2014, 31(1): 1-10. JIA L, LI X L. Identification of Hammerstein model: review and prospect[J]. Control Theory & Applications, 2014, 31(1): 1-10. (in Chinese) |
| [19] |
赵众, 顾幸生, 蒋慰孙. 基于WaveARX神经网络的非线性动态过程故障检测[J]. 华东理工大学学报, 1998, 24(3): 347-353. ZHAO Z, GU X S, JIANG W S. Fault detection of nonlinear dynamic process based on WaveARX neural network[J]. Journal of East China University of Science and Technology, 1998, 24(3): 347-353. (in Chinese) |
| [20] |
LI G, ZHAO Q. Adaptive fault-tolerant shape control for nonlinear Lipschitz stochastic distribution systems[J]. Journal of the Franklin Institute, 2017, 354(10): 4013-4033. |
| [21] |
SKELTON R E, IWASAKI T. Liapunov and covariance controllers[J]. International Journal of Control, 1993, 57(3): 519-536. |
| [22] |
QIN Z, LIANG Y G. Sensor management of LEO constellation based on covariance control[J]. Journal of Systems Engineering and Electronics, 2019, 30(2): 393-401. |








