大型储罐作为能源系统的重要组成部分,在军事、交通、航空和石化等行业中有着非常广泛的应用。储罐是石油、化工等行业必不可少的、重要的基础设施,使用中在各种气液腐蚀及应力变化作用下会出现形变、泄露等现象。由于罐区储罐数量多且密集, 其间各种输油管道又错综复杂, 个别储罐储存的可燃物如汽油、天然气等储存量大、易燃、易爆甚至有毒,一旦发生泄漏, 轻则造成资源浪费, 重则可能引起火灾、爆炸、中毒等事故,造成巨大损失,因此对储罐的检测和数据采集很有必要[1-3]。随着石化行业的蓬勃发展,大型储罐的建造逐渐兴起,而对其容积的测量一直是储罐运行的一大难题。三维激光扫描仪的出现解决了储罐的容积测量问题[2-5]。近十几年来,迅速发展起来的三维激光扫描技术以其非接触、高精度、数字化、自动化等特点应用于储罐罐体的三维扫描,克服了传统测量方法测量精度不高的问题,同时还提高了检测效率。然而尽管扫描仪的高速性和高采样率可以快速地对储罐内外部进行三维点云数据的采集,但此方法获取的三维点云数据存在数据量庞大、包含大量的冗余点以及数据散乱等问题,会对后续的三维建模和容积测量造成严重影响,因此需要对三维点云数据作精简处理。
传统的点云精简算法主要包括基于网格的精简算法、基于曲率的精简算法、聚类精简算法等。基于网格的精简算法主要通过先构建多边形网络(如三角形网络、四边形网络等),再依据特定的规则对这些网络的重要性进行筛选,以删去其中的冗余网络[6-8]。这种方法易于实现,但耗费时间较长,而且网格中心点可能不是原始点云数据,会带来特征信息丢失等问题。基于曲率的精简算法[9-10]和聚类精简算法[11-13]都是直接对点数据进行精简,不需要构建网络。其中基于曲率的精简算法对封闭曲面的点云精简能获得较满意的效果,但对于非封闭曲面会丢失部分边界信息;而聚类精简算法可有效地保持原始数据的整体轮廓、局部细节特征且避免出现数据空洞,但对噪声敏感。很多学者结合以上几种方法的特点提出了改进的点云精简方法。陈辉等[14]提出一种基于动态网格k邻域搜索的点云精简方法,该方法将特征提取与二次精简方法相结合,既保留了点云的几何特征,又避免了空洞的产生。林松等[15]利用点云局部邻域协方差矩阵的3个特征值构造的维度特征,构建局部邻域信息熵函数,并依据局部熵值最小原则确定最优邻域,从而实现了三维点云的精简。袁小翠等[10]提出一种基于高斯球的点云自适应聚类精简算法,该方法的特征保持效果较好,但在平坦区域易造成数据空洞。兰渐霞等[16]提出一种基于两阶非均匀划分的点云精简算法,该方法在保证精度的情况下具有很高的精简率和运算效率。随着可以快速获取储罐点云数据的三维扫描技术的迅速发展,基于激光扫描的3D点云大型储罐容积测量方法得到了许多研究人员的关注[2-5]。大型储罐的三维点云由于数据量庞大,在对其进行计算机显示和容积测量时易存在耗时过长、计算效率低等问题,因此需要在保留特征信息的基础上,对大型储罐点云数据进行精简处理。
为了解决三维点云的精简率和特征信息保留难以兼顾的问题,本文提出了一种改进的储罐三维点云精简方法, 通过随机抽样一致(random sample consensus,RANSAC)算法对栅格内点云数据建立球模型,以达到在取得高精简率的同时保留特征数据的效果。
1 储罐三维点云精简方法 1.1 储罐点云数据获取基于三维激光扫描技术的储罐点云获取通常是以激光扫描设备中心为原点O、铅垂线为Z轴、水平度盘零方向为X轴建立三维坐标系[4],则储罐罐体上的任意一个点P(Xp, Yp, Zp)可以表示为
| $ \left\{\begin{array}{l} X_p=r_p \cdot \cos \beta \cdot \cos \alpha \\ Y_p=r_p \cdot \cos \beta \cdot \sin \alpha \\ Z_p=r_p \cdot \sin \beta \end{array}\right. $ | (1) |
式中,rp为点P到坐标系原点O的距离,α为OP与X轴方向的夹角,β为OP与Y轴方向的夹角。
1.2 改进的三维点云精简算法本文改进的点云精简算法主要思路如下:先应用均匀网格法构建立体包围盒并分割成若干小栅格,使得每个小的栅格内包含有限点云数量;然后,对每个栅格内的点云数据使用RANSAC算法建模,选择模型上具有代表性的点作为点云数据的特征点,滤除冗余点;最后,对所有小栅格内精简过的点云数据进行拼接,得到最终的精简结果。改进的算法框图如图 1所示。
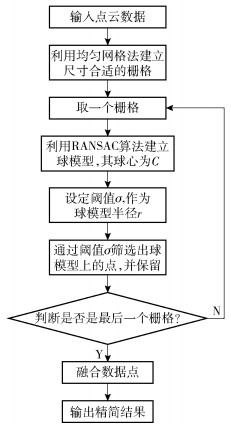
|
图 1 改进的点云精简算法流程图 Fig.1 Flowchart of the improved point cloud simplification algorithm |
在栅格内建立球模型S,首先随机选取一点C,其坐标为(a, b, c),作为球模型上的中心点。对于栅格内的任一点(xi, yi, zi),i=0, 1, 2, …, n,其中n为栅格内所有点的数目,其到中心点C的欧氏距离为
| $ D_i=\sqrt{\left(x_i-a\right)^2+\left(y_i-b\right)^2+\left(z_i-c\right)^2} $ | (2) |
设定阈值σ,也即球模型的半径,将所求的距离Di与阈值σ比较,当Di < σ时,可认为该点为球模型上的局内点,反之则该点为误差点,应当滤除。记录符合要求的局内点数目m,以及局内点对应的点云数据。设定初始期望局内点数目M,通过与实验记录的局内点数目m比较,来判断此模型是否是最佳模型。若m>M,则更新期望局内点数目使得M=m,并更新输出的点云数据。
设p是所有n个点均为局内点的概率,则1-p是n个点中至少有一个点为局外点的概率;设w表示每次从数据集中选取一个局内点的概率,则有w=m/n。通常情况下,事先并不知道w的值,但是可以给出一些期望的值。则迭代k次,每次都至少采样一个外点的概率为(1-wn)k,由此得到等式(3)。
| $ 1-p=\left(1-w^n\right)^k $ | (3) |
式(3)两边取对数,则可以由式(4)计算得到k的值。
| $ k=\frac{\lg (1-p)}{\lg \left(1-w^n\right)} $ | (4) |
若m < M, 重新随机抽取新的S, 重复以上过程,直到建立最佳的球模型。
在本文算法中,阈值σ的选取需要根据栅格大小的不同而调整,从而提高对栅格内球模型建模的准确性以及滤除冗余点的效率。
综上所述,改进的储罐点云精简算法的主要步骤如下:
1) 输入储罐三维点云数据,建立体包围盒,并将体包围盒分成尺寸均匀的小栅格;
2) 取一个小栅格,判断栅格内是否有点云数据,若没有相应数据,则删除空栅格,反之进入步骤3);
3) 使用RANSAC算法对栅格内的点云数据建立球模型,设定相应的阈值,比较点数据到球中心点的距离是否小于阈值,若是,则保留点数据,反之则删除该冗余点;
4) 判断此栅格是否是最后一个栅格,若是,则整合数据点,并输出精简结果,反之回到步骤2)。
2 实验结果与分析本文实验应用的点云数据集为ModelNet40数据集[17]中的飞机数据集和大型储罐扫描数据集[5]。飞机数据集中包含的三维点数量为10 000,大型储罐扫描数据集中包含的三维点数量为600 000。算法的主要评价指标包括精简率、运行时间和特征保持情况。其中,精简率以滤除的点云数量占原始点云数量的分数来表征。通过对均匀网格法、非均匀网格法以及本文算法的精简率和特征保持情况比较,可以得出各算法在滤除冗余点、保留特征信息方面的效果优劣。
2.1 飞机数据集首先,对飞机数据集进行改进的点云精简算法验证实验。精简飞机数据集时设定的栅格尺寸为0.04。在对栅格点云数据建立拟合球模型时,设定希望抽取的特征点均为内点的概率p=0.9。验证实验结果如图 2所示。

|
图 2 点云精简算法验证实验对比 Fig.2 Comparison of experiments to verify the point cloud reduction algorithm |
由图 2的实验结果可以看到,无论是使用均匀网格法还是非均匀网格法进行精简,都不可避免地会产生数据空洞问题,而改进的算法并没有出现该问题。另外,在红色虚线椭圆标记处,改进算法保留的轮廓信息更接近原始数据。
此外,实验中还计算了各算法在飞机数据集上的精简率和运行时间,具体结果如表 1所示。可以看出,本文算法的精简率相较于均匀网格法略低,高于非均匀网格法。结合图 2和表 1的实验结果,本文算法可使得点云数目得到较大比率的精简,同时特征仍然获得较好的保持。
| 下载CSV 表 1 飞机数据集精简实验精简率以及运行时间结果 Table 1 Aircraft data set reduction experimental reduction rate and running time results |
其次,改变本文算法中设定的阈值,对飞机数据集进行精简,所得结果如图 3所示, 精简率和运行时间见表 2。
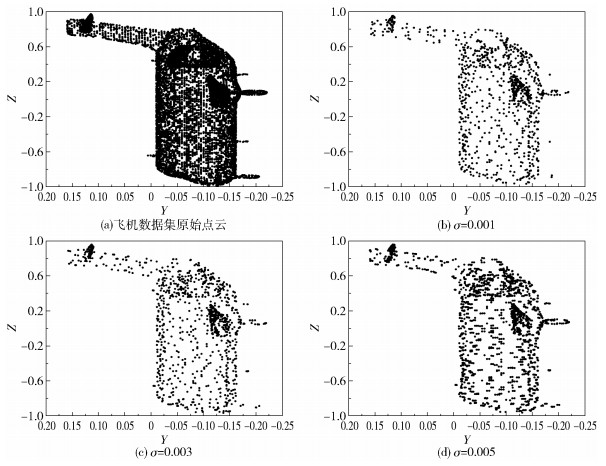
|
图 3 不同阈值下精简结果对比 Fig.3 Comparison of simplified results for different thresholds |
| 下载CSV 表 2 飞机数据集在不同阈值下的精简率及运行时间 Table 2 Reduction rate and running time of aircraft data sets under different thresholds |
由图 3和表 2的实验结果可以看出设定阈值大小对精简结果和精简率的影响。阈值越大,栅格内使用RANSAC算法建立的球模型越大,相应的迭代次数越少,运行时间越短,保留的数据点越多,精简效果越差,精简率就越低;阈值越小,栅格内使用RANSAC算法建立的球模型越小,相应的迭代次数越多,运行时间越长,精简效果越好,精简率也越高。
2.2 大型储罐扫描数据集由于立式罐的空间尺寸较大,使用三维激光扫描仪获取的点云数据数量级较大,存在较多的冗余点,因此同样需要进行点云精简。使用本文算法对立式罐三维点云数据进行精简,栅格大小设定为0.01,原始的点云数目为600 000,经过精简后的点云数据有131 638,精简率达到78.06%,特征保持效果也较好,只是运行时间较长(见表 3)。同时,使用均匀网格法和非均匀网格法对储罐原始点云进行精简,并将所得结果与本文算法的精简结果作比较,结果如图 4、5所示,其中图 4为罐壁部分数据集,图 5为罐内附件部分数据集。
| 下载CSV 表 3 立式罐数据集精简实验的精简率及运行时间 Table 3 Reduction rate and running time of vertical tank data set reduction experiments |
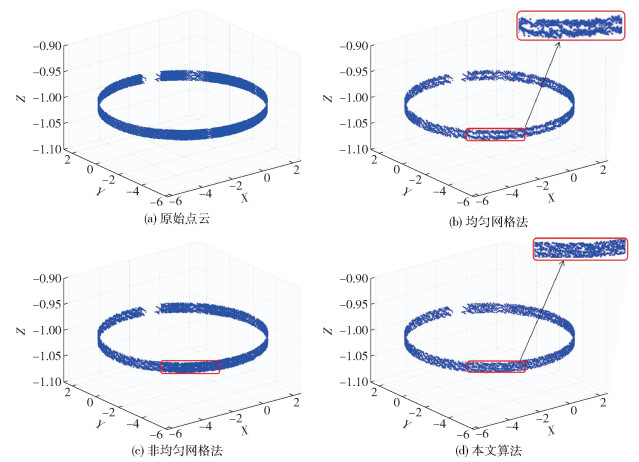
|
图 4 立式罐罐壁数据集点云精简算法实验结果对比 Fig.4 Comparison of experimental results of point cloud reduction algorithms for vertical tank wall data sets |
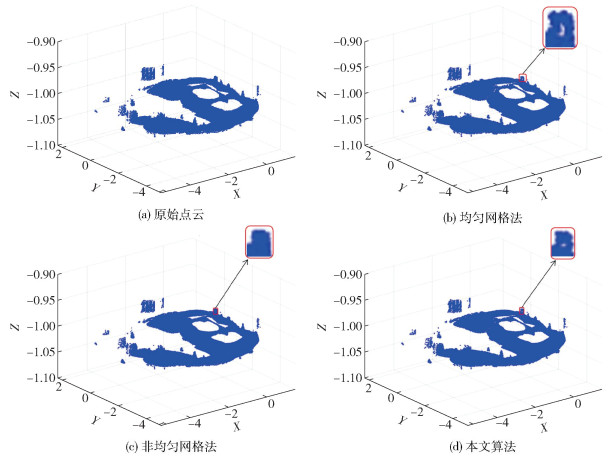
|
图 5 立式罐罐内附件数据集点云精简算法实验结果对比 Fig.5 Comparison of experimental results of point cloud reduction algorithms for data sets of vertical tank accessories |
与均匀网格法和本文算法相比,非均匀网格法对点云的精简率较低,因此,图 4中主要对比了均匀网格法和本文算法精简后罐壁处的结果。从图中红色椭圆内罐壁精简点云放大的部分中可以看出,使用均匀网格法精简后的罐壁处有许多空洞出现,特征保持效果明显不如本文算法精简后的点云结果分布匀称。
同样,图 5给出了罐内附属部件的点云精简结果对比,并放大了管道口的点云精简结果。在使用均匀网格法的精简结果中,罐内红色椭圆标注的管道处空洞现象比其他两种方法更明显,且罐内其他附件点云精简后结果的特征轮廓与原始点云相比出现差异,总体特征保持效果不如非均匀网格法和本文算法。
最后,在实验中计算了立式储罐点云数据集的精简率和运行时间,具体结果如表 3所示。可以看出,本文算法的精简率略低于均匀网格法,高于非均匀网格法,运行时间也远低于非均匀网格法,略高于均匀网格法。
此外,分别使用均匀网格法、非均匀网格法以及本文算法对立式储罐数据进行精简,并根据精简后的点云进行了储罐容积的估计,结果如表 4所示。
| 下载CSV 表 4 立式罐三维点云数据集精简实验所得容积结果 Table 4 Volume results of vertical tank 3D point cloud data set reduction experiments |
从表 4中结果可以看出,使用本文算法精简结果估计的储罐容积相较于均匀网格法和非均匀网格法相对误差最小,更接近原始点云的储罐容积。
3 结论本文研究了一种大型储罐三维点云的精简方法,通过特征数据建模的手段解决了点云精简过程中特征丢失和数据空洞的问题。该方法在保留了均匀网格法精简率高的优点的同时,还提高了特征保持效果,克服了均匀网格法在特征信息保留方面的不足;此外,还可以通过调整栅格的阈值大小来取得不同的精简率。对飞机数据集和立式罐数据集的实验结果表明,与传统的均匀网格法和非均匀网格法相比,本文方法精简率高,特征保持效果更好。
| [1] |
王旭, 廖柯熹, 张志坚, 等. 基于FLACS的汽油储罐可燃气体泄漏的流场分析[J]. 北京化工大学学报(自然科学版), 2022, 49(2): 31-38. WANG X, LIAO K X, ZHANG Z J, et al. Flow field analysis of combustible gas leakage in gasoline storage tank based on FLACS[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2022, 49(2): 31-38. (in Chinese) |
| [2] |
CHEN X L, SHI H L, HAO H D, et al. Research on algorithm of cross-section area of oil storage tank capacity based on point cloud data[C]//Proceedings of 2019 14th IEEE International Conference on Electronic Measurement & Instruments. Changsha, 2019: 567-572.
|
| [3] |
王金涛, 刘子勇, 张珑, 等. 大型油罐容量计量中3D空间建模方法研究与比对试验分析[J]. 仪器仪表学报, 2010, 31(2): 421-425. WANG J T, LIU Z Y, ZHANG L, et al. Research on 3D laser scanning method for tank volume metrology and its comparison experiment analysis[J]. Chinese Journal of Scientific Instrument, 2010, 31(2): 421-425. (in Chinese) DOI:10.19650/j.cnki.cjsi.2010.02.030 |
| [4] |
庄正杰, 王立光, 龚应忠, 等. 基于三维激光扫描及凸包算法的油罐底部排量快速测量[J]. 计量学报, 2018, 39(6): 852-856. ZHUANG Z J, WANG L G, GONG Y Z, et al. Rapid volume measurement for oil tank displacement based on 3D laser scanning and convex hull algorithm[J]. Acta Metrologica Sinica, 2018, 39(6): 852-856. (in Chinese) DOI:10.3969/j.issn.1000-1158.2018.06.19 |
| [5] |
王金涛, 刘翔, 佟林, 等. 用于油库安全监控的立式储罐钢板变形激光测量方法[J]. 计量学报, 2018, 39(2): 217-221. WANG J T, LIU X, TONG L, et al. Method of deformation measurement for vertical tank based on 3D laser scanning method for production safety oil depot[J]. Acta Metrologica Sinica, 2018, 39(2): 217-221. (in Chinese) DOI:10.3969/j.issn.1000-1158.2018.02.16 |
| [6] |
李仁忠, 杨曼, 刘阳阳, 等. 一种散乱点云的均匀精简算法[J]. 光学学报, 2017, 37(7): 89-97. LI R Z, YANG M, LIU Y Y, et al. An uniform simplification algorithm for scattered point cloud[J]. Acta Optica Sinica, 2017, 37(7): 89-97. (in Chinese) |
| [7] |
常鑫, 郎锐, 董建业. 基于移动网格点云精简算法的研究[J]. 测绘工程, 2018, 27(5): 17-22. CHANG X, LANG R, DONG J Y. Algorithm of point cloud simplification based on moving grid mesh[J]. Engineering of Surveying and Mapping, 2018, 27(5): 17-22. (in Chinese) |
| [8] |
LEE K H, WOO H, SUK T. Point data reduction using 3D grids[J]. The International Journal of Advanced Manufacturing Technology, 2001, 18(3): 201-210. DOI:10.1007/s001700170075 |
| [9] |
YAO Z W, ZHAO Q X, LI X F, et al. Point cloud registration algorithm based on curvature feature similarity[J]. Measurement, 2021, 177(11): 109274. |
| [10] |
袁小翠, 吴禄慎, 陈华伟. 特征保持点云数据精简[J]. 光学精密工程, 2015, 23(9): 2666-2676. YUAN X C, WU L S, CHEN H W. Feature preserving point cloud simplification[J]. Optics and Precision Engineering, 2015, 23(9): 2666-2676. (in Chinese) |
| [11] |
SHI B Q, LIANG J, LIU Q. Adaptive simplification of point cloud using k-means clustering[J]. Computer-Aided Design, 2011, 43(8): 910-922. |
| [12] |
CHEN N, LU X J. A novel point cloud simplification method with integration of multiple-feature fusion and density uniformity[J]. Measurement Science and Technology, 2021, 32(12): 125211. |
| [13] |
李健, 曹垚, 王宗敏, 等. 融合k-means聚类和Hausdorff距离的散乱点云精简算法[J]. 武汉大学学报·信息科学版, 2020, 45(2): 250-257. LI J, CAO Y, WANG Z M, et al. Scattered point cloud simplification algorithm integrating k-means clustering and Hausdorff distance[J]. Geomatics and Information Science of Wuhan University, 2020, 45(2): 250-257. (in Chinese) |
| [14] |
陈辉, 黄晓铭, 刘万泉. 基于动态网格k邻域搜索的激光点云精简算法[J]. 控制与决策, 2020, 35(12): 2986-2992. CHEN H, HUANG X M, LIU W Q. Laser point cloud simplification algorithm based on dynamic grid k-nearest neighbors searching[J]. Control and Decision, 2020, 35(12): 2986-2992. (in Chinese) |
| [15] |
林松, 田林亚, 毕继鑫, 等. 基于最优邻域局部熵的点云精简算法[J]. 测绘工程, 2021, 30(5): 12-17. LIN S, TIAN L Y, BI J X, et al. Point cloud simplification algorithm based on local entropy of optimal neighborhood[J]. Engineering of Surveying and Mapping, 2021, 30(5): 12-17. (in Chinese) |
| [16] |
兰渐霞, 王泽勇, 李金龙, 等. 基于非均匀划分的机车走行部三维点云精简[J]. 光电工程, 2019, 46(2): 180269. LAN J X, WANG Z Y, LI J L, et al. Simplification of locomotive running gear three-dimensional point cloud based on non-uniform division[J]. Opto-Electronic Engineering, 2019, 46(2): 180269. (in Chinese) |
| [17] |
WU Z R, SONG S R, KHOSLA A, et al. 3D ShapeNets: a deep representation for volumetric shapes[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, 2015: 1912-1920.
|








