2. 中国纺织科学研究院有限公司 生物源纤维制造技术国家重点实验室, 北京 100025
2. State Key Laboratory of Biobased Fiber Manufacturing Technology, China Textile Academy Co., Ltd., Beijing 100025, China
在合成纤维工业中,熔融纺丝是常用的纺丝成型工艺之一,具有可适用于多组分体系、加工过程中无需溶剂、环境安全性高等特点[1]。聚合物熔体通过纺丝组件顶部的扩散板进入组件后,在上游输送泵提供的压力下依次通过砂腔、分配板、导流板,并在喷丝板挤压下形成丝条,最后经冷却、卷绕、拉伸等工艺形成纤维[2]。
在纺丝成型过程中,纺丝组件常出现出丝不均匀的问题,主要原因是纺丝组件内物料流动和分配不均匀。针对以上问题,研究者对影响纺丝组件内流场的因素进行了研究。Pervadchuk等[3]研究了聚己内酰胺熔体在喷丝孔中的流动,发现喷丝孔的几何形状对熔体流动有影响。Tzeng[4]利用甘油作为涤纶树脂的模拟介质进行冷态实验,研究了不同雷诺数、喷嘴尺寸等因素对流体流经喷丝板时流场的影响。顾家耀[5]经研究发现,当纺丝组件内的床层孔隙率较大时,喷丝板出丝不均匀;当床层孔隙率较小、压力较大时,喷丝板出丝较为均匀。Xia等[6]采用数值模拟的方法研究了喷丝孔的出口长度、导角和直径对喷丝孔内的径向与轴向速度、剪切速率和压力分布的影响,结果表明导角减小会消除喷丝板内涡流,出口长度增加会使喷丝板内压降增大。由于聚合物熔体的流动状态与最终成型的纤维品质密切相关,而熔体的流动状态与其流变特性的关系紧密[7],因此研究聚合物熔体的流变特性及其对纺丝组件内流场的影响十分重要。目前,对纺丝组件内熔体流动的研究主要集中在组件结构对内部流场的影响,而缺乏针对聚合物熔体流变特性与纺丝组件内流场之间关系的相关研究。为此,本文测定了聚对苯二甲酸乙二醇酯(PET)、常压阳离子染料可染聚合物(ECDP)熔体的流变特性,采用计算流体力学方法研究了具有不同流变特性的聚合物熔体在纺丝组件内的流动行为,分析了熔体在纺丝组件内的流场规律,以期为纺丝组件结构的优化提供指导。
1 聚合物熔体流变特性 1.1 实验材料PET,特性黏度0.72 dL/g,熔点240 ℃,中国石化仪征化纤有限公司;ECDP-1,特性黏度0.601 dL/g,熔点236 ℃,中国纺织科学研究院有限公司;ECDP-2,特性黏度0.574 dL/g,熔点240 ℃,绍兴九洲化纤有限公司。
1.2 流变特性测定采用毛细管流变仪(RHEOGRAPH25型,德国Goettfert公司)测量以上3种聚合物熔体的流变特性。毛细管长径比为40∶1,测试温度为270、280、290 ℃。为了避免聚酯切片吸收空气中的水分而影响实验结果,样品需要经过预结晶、干燥等过程,并且测试过程中不断注入高纯氮气。
1.3 本构方程纺丝组件中的流体为聚合物熔体,采用幂律方程(式(1))表示其流变行为。
| $ \tau=K \dot{\gamma}^n $ | (1) |
式中:τ为剪切应力,Pa;K为稠度系数,是黏度的量度,Pa·sn;
图 1为不同温度下聚合物熔体的流变曲线。对图 1中的流变曲线进行线性拟合,得到聚合物熔体的稠度系数K和流变指数n,结果如表 1所示。由表 1可知,在270~290 ℃的温度范围内,PET、ECDP-1和ECDP-2的流变指数n均小于1,说明熔融状态下这3种聚合物都属于假塑性流体。此外,三者的n值都随着温度的升高而增大并接近1,表明聚合物熔体的假塑性随着温度的升高而减弱。
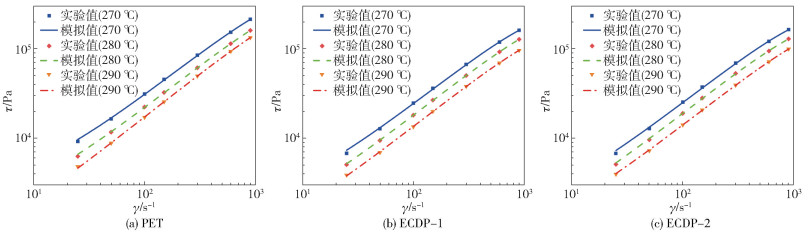
|
图 1 不同温度下聚合物熔体的流变曲线 Fig.1 Rheological curves of polymer melts at different temperatures |
| 下载CSV 表 1 不同温度下聚合物熔体的稠度系数K和流变指数n Table 1 Consistency coefficient K and rheological index n of polymer melts at different temperatures |
图 2为不同温度下聚合物熔体的黏度μ与剪切速率γ的关系。由结果可知,3种聚合物熔体的黏度随着剪切速率的增大而减小。聚合物熔体中含有缠结、环状的长链分子,当静止时,这些长链分子将维持内部的不规则次序,熔体具有相当高的内部阻力,因此黏度较高;当熔体在剪切力的作用下开始流动时,内部的长链分子将沿流动方向解缠绕、拉伸和取向,排列后的分子线团更易流动,因此黏度降低[8]。在熔体纺丝过程中,可以通过施加适当的剪切速率使熔体具有更好的流动性。
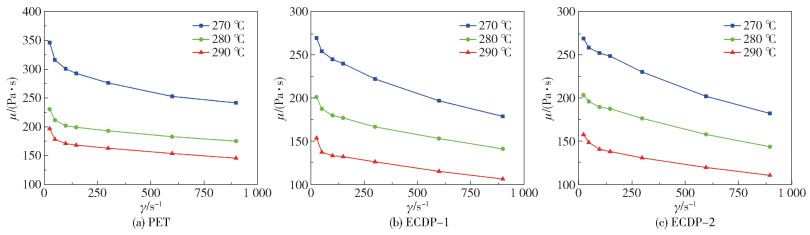
|
图 2 不同温度下聚合物熔体的黏度μ随剪切速率γ的变化 Fig.2 Viscosity of polymer melt as a function of shear rate at different temperatures |
从聚合物熔体的流变特性中可以看到,其稠度系数K的范围为229~525 Pa·sn,流变指数n的范围为0.848~0.910。在本文的数值模拟中,为了覆盖更广泛的流变特性,取K的范围为50~500 Pa·sn,n的范围为0.4~1.0。
2 数值模拟方法 2.1 模拟域本文使用Solidworks软件绘制纺丝组件的几何模型,采用Fluent软件进行数值模拟。图 3为纺丝组件的结构模型示意图。该结构模型由熔体入口、扩散板、压盖、砂腔、分配板、导流板和喷丝板等结构组成。压盖连接扩散板和砂腔,起密封作用;砂腔中含有过滤层与过滤网,用于过滤熔体中的杂质并对熔体进行剪切升温。纺丝组件的流道可以看作是由多个圆管及平板构成的组合流道,同时考虑到聚合物熔体的高黏度特性,因此熔体在纺丝组件内的流动可以看作是其流经多个圆管及多个平板的复杂层流流动。本文在构建纺丝组件的结构模型时,考虑到纺丝组件结构的轴对称性,采取组件结构的1/12作为模拟域进行计算,模拟域及网格如图 4所示。
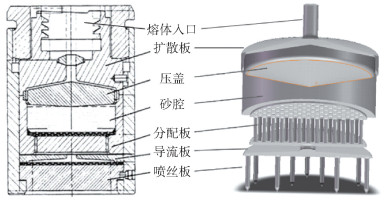
|
图 3 纺丝组件的结构模型示意图 Fig.3 Schematic diagram of the structural model of the spinning assembly |
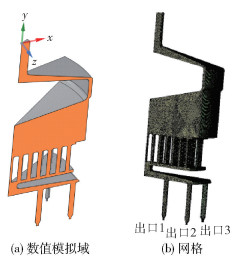
|
图 4 数值模拟域及网格示意图 Fig.4 Schematic diagrams of the numerical simulation domain and grid |
对纺丝组件进行三维数值模拟时,对组件内熔体流动进行了如下假设:
(1) 聚合物熔体为不可压缩的假塑性流体,且在流动过程中充满纺丝组件;
(2) 聚合物熔体在纺丝组件内的流动为稳态流动;
(3) 由于聚合物熔体的黏度极高,重力等体积力远小于黏性力,因此数值模拟中只考虑黏性力,忽略流动过程中的重力。
流体在纺丝组件内流动的模拟过程遵循连续性方程(式(2))和动量方程(式(3)~(5))。
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0 $ | (2) |
| $ \frac{{\partial p}}{{\partial x}} + \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} = 0 $ | (3) |
| $ \frac{{\partial p}}{{\partial y}} + \frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\tau _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}} = 0 $ | (4) |
| $ \frac{{\partial p}}{{\partial z}} + \frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}} = 0 $ | (5) |
式中:u、v、w分别为流体在x、y、z方向上的分速度,τij为流体在不同方向上受到的剪切应力,τii为法向应力,p为流体所受的压力。
2.3 边界条件使用层流模型描述流动过程,并且考虑非牛顿流体的本构方程,纺丝组件的入口设置为速度入口,出口设置为压力出口。本文选取纺丝组件的1/12作为模拟域,将两侧壁面设置为对称边界,其余壁面设置为无滑移壁面;砂腔内设置为多孔介质模型,其黏性阻力系数为4×106 m-2。
2.4 网格无关性分析模拟域中的网格尺寸与模拟结果的关系密切。本文选择3种尺寸的网格进行无关性验证,如表 2所示。
| 下载CSV 表 2 不同模拟网格的尺寸及数量 Table 2 Size and number of different simulation grids |
网格无关性分析结果如图 5所示。取z=0平面内不同位置的速度进行对比,由图 5(a)~(c)可以看出,在最大网格尺寸为0.25 mm(Case2)与0.15 mm(Case3)时纺丝组件内流体的速度分布几乎无差别。在喷丝板前(y/H=-0.80),最大网格尺寸为0.5 mm(Case1)时纺丝组件内流体速度与其他两种网格尺寸下的流体速度相差较大。因此,本文采取第二种尺寸的网格(Case2)进行模拟计算。
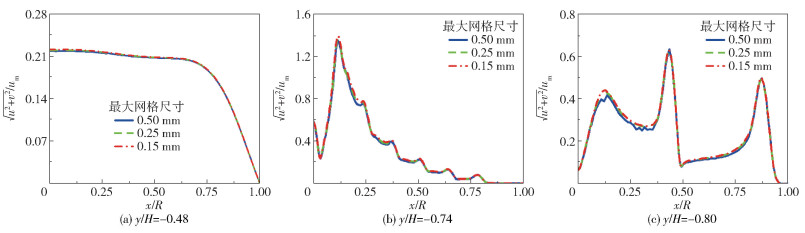
|
um—纺丝组件入口流速; |
为了验证计算流体力学方法的准确性,本文将数值模拟结果与粒子图像测速(PIV)实验结果进行对比。由于纺丝组件砂腔具有高度对称的结构,因此选择砂腔内一侧进行PIV实验。
实验中使用的主要物料为:麦芽糖浆,固含量82%(质量分数),葡萄糖当量(DE)为42,密度1 350 kg/m3,北京广盛源生物科技有限公司;空心玻璃珠(直径8~12 μm),型号MD8-12LTR,密度1 500 kg/m3,美国TSI公司。选择78.9%麦芽糖浆的水溶液进行折射率匹配,溶液温度为20 ℃,黏度为20 Pa·s。
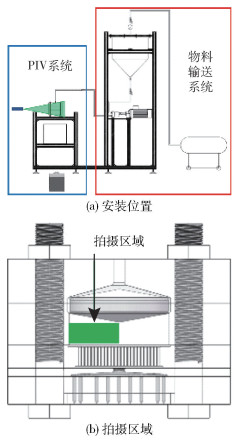
PIV系统的安装位置及拍摄区域如图 6所示。2D-PIV系统包括:高分辨率CCD相机(PowerView Plus 11M型,美国TSI公司);激光发射器(Beamtech Vlite-200,北京镭宝光电技术有限公司,能量200 mJ,厚度1 mm);同步器(美国TSI公司),用于控制激光发射与相机拍摄同步进行。实验过程中脉冲激光发射的时间间隔Δt设置为232 μs。
|
图 6 PIV系统的安装位置和拍摄区域 Fig.6 Installation location and shooting area of the PIV system |
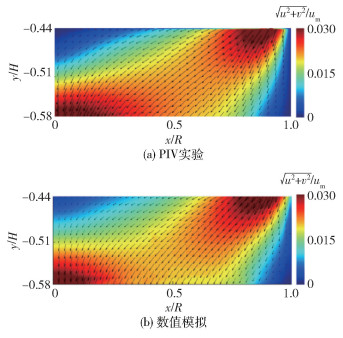
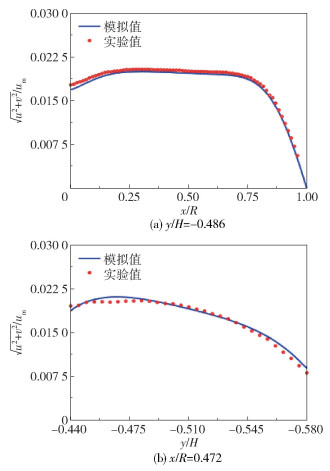
图 7为PIV实验与数值模拟的速度分布云图,图 8为流体在砂腔内不同位置的速度分布的实验与模拟结果。可以看出数值模拟与PIV实验的结果吻合良好,同时也进一步证明了所选网格尺寸方案的合理性。
|
图 7 PIV实验与数值模拟的速度分布云图 Fig.7 Velocity distribution contours of the PIV experiment and numerical simulation |
|
图 8 流体在砂腔内不同位置的速度分布的实验与模拟结果 Fig.8 Experimental and simulation results of the fluid velocity distribution at different positions in the sand cavity |
在幂律方程中,稠度系数K为流体黏度的量度,流体黏度越高,稠度系数K越大,并且K与剪切速率无关。在保持流变指数n=0.8不变和入口流速um为0.05 m/s的情况下,考察稠度系数对纺丝组件内流体流动的影响。
3.1.1 压力分布图 9为z=0平面内不同稠度系数K下纺丝组件内的压力分布云图,表 3为不同稠度系数K下纺丝组件的入口压力。可以看出稠度系数K对组件内压力分布的影响较为明显,随着K的增大,纺丝组件的入口压力相应增大,并且与K值近似成正比。
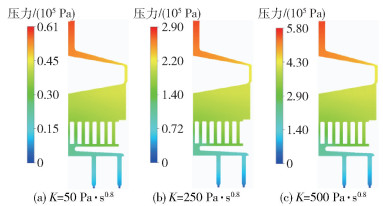
|
图 9 不同稠度系数下纺丝组件的压力分布云图 Fig.9 Pressure distribution contours in the spinning assembly with different consistency coefficients |
| 下载CSV 表 3 不同稠度系数K下纺丝组件的入口压力 Table 3 Inlet pressure of the spinning assembly with different consistency coefficients |
图 10和图 11分别为z=0平面内不同稠度系数的流体在纺丝组件内的速度分布云图和基于入口速度的无因次化速度分布曲线。由结果可以看出,纺丝组件内流场分布趋势并不随稠度系数的变化而变化,因此稠度系数对纺丝组件内的速度场几乎没有影响。
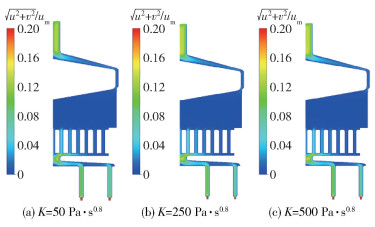
|
图 10 不同稠度系数的流体在纺丝组件内的速度分布云图 Fig.10 Velocity distribution contours of fluids with different consistency coefficients in the spinning assembly |
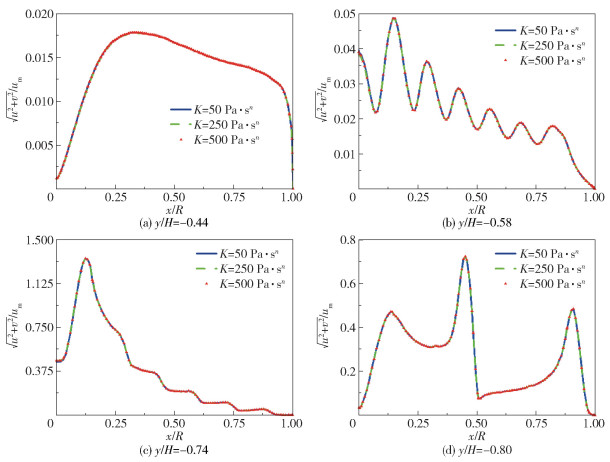
|
图 11 不同稠度系数的流体在纺丝组件内的无因次化速度分布 Fig.11 Dimensionless velocity distribution of fluids with different consistency coefficients in the spinning assembly |
在入口流速um=0.05 m/s、稠度系数K=250 Pa·sn的条件下,分别从压力和速度分布两方面分析流变指数n对纺丝组件内流场的影响。
图 12为不同流变指数的流体在纺丝组件z=0平面内的压力分布云图,表 4为不同流变指数下纺丝组件的入口压力。由结果可以看到,不同流变指数的流体在纺丝组件内的压力分布趋势非常相似,入口处的压力最大,随着聚合物向下流动,压力逐渐减小;入口压力随着流变指数n的增大而增大,这是由于在n<1的情况下,流体的表观黏度随着n的增大而增大,当流速保持不变时,流体流动的阻力增加,因此入口压力增大以克服流动阻力。
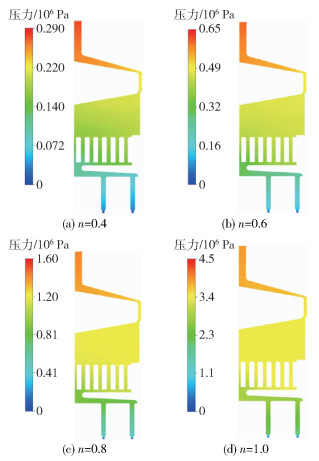
|
图 12 不同流变指数下纺丝组件内的压力分布云图 Fig.12 Pressure distribution contours of the spinning assembly for different rheological indexes |
| 下载CSV 表 4 不同流变指数下纺丝组件的入口压力 Table 4 Inlet pressure of the spinning assembly for different rheological indexes |
图 13为不同流变指数的流体在纺丝组件z=0平面内的速度分布云图。可以看出,不同流变指数的流体的入口流速有较大差别,入口流速随着流变指数的增大而增大;聚合物熔体在砂腔等横截面积较大的位置处速度相对较小,而在组件入口、导流板等横截面积较小的位置处速度相对较大。
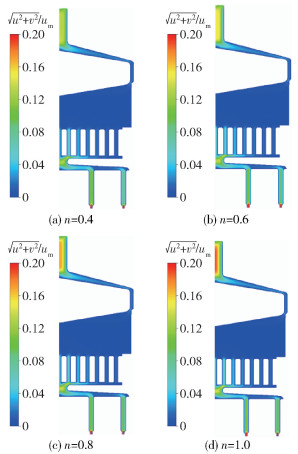
|
图 13 不同流变指数的流体在纺丝组件内的速度分布云图 Fig.13 Velocity distribution contours of fluids with different rheological indexes in the spinning assembly |
图 14为不同流变指数的流体在砂腔内z=0平面上的速度分布云图,图 15为不同流变指数的流体在z=0平面内不同位置的速度分布。从图 14中可以看出,不同流变指数的流体在砂腔内的流动速度较小但分布相对均匀,这是由砂腔内过滤砂的存在引起的。砂腔上游压盖的存在使得流体从压盖四周流入砂腔,导致压盖下方外侧的速度较大而下方中心处的速度较小(图 15(a)),砂腔中部的流体在砂腔内形成滞留区,流体在纺丝组件内的停留时间不均匀,处于压盖下方中部的聚合物熔体可能会由于在纺丝组件内停留时间过长而发生降解,最终出现喷丝孔出丝不均匀以及断丝等问题。同时,砂腔下游的导流板结构使得流体在砂腔内向下流动时向中心汇聚,造成砂腔底部中心处的流速较大(图 15(b))。此外,由图 15(a)还可以看出,在砂腔上游(y/H=-0.44)处,流变指数越大,流体在砂腔内的流速也越大。

|
图 14 不同流变指数的流体在砂腔内z=0平面上的速度分布云图 Fig.14 Velocity distribution contours of fluids with different rheological indexes on the z=0 plane in the sand cavity |
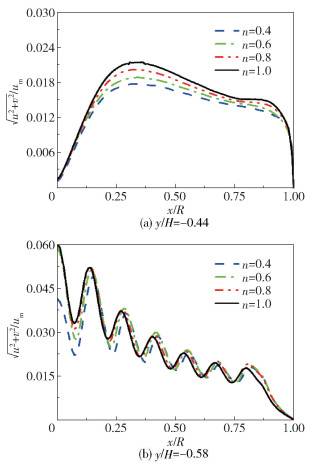
|
图 15 不同流变指数的流体在砂腔内z=0平面上不同位置的速度分布 Fig.15 Velocity distribution of fluids with different rheological indexes at different positions on the z=0 plane in the sand cavity |
图 16为不同流变指数的流体在分配板、导流板和喷丝板内z=0平面上的速度分布云图。可以看出,聚合物熔体在分配板内圈的流速较大,沿外圈方向流速逐渐减小,并且流变指数对分配板流场的影响不显著。图 17(a)为不同流变指数的聚合物熔体在导流板前方的速度分布,由于导流板中心存在开口为8 mm的导孔,所以会导致靠近导流板中部的流速大于外侧的流速;同时还可以看出不同流变指数的聚合物熔体经过导流板时流速相差并不大。图 17(b)为聚合物熔体流入喷丝板后的速度分布,喷丝板为具有内外两圈的开孔结构(图 18),可以看出聚合物熔体在内外两圈的流速并不均匀,内圈喷丝孔的流速大于外圈,并且不同流变指数的流体在流经喷丝板时速度差异明显。
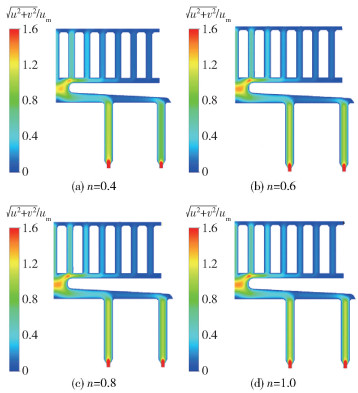
|
图 16 不同流变指数的流体在分配板、导流板和喷丝板内z=0平面上的速度分布云图 Fig.16 Velocity distribution contours of fluids with different rheological indexes on the z=0 plane in the distribution plate, guide plate and spinneret |
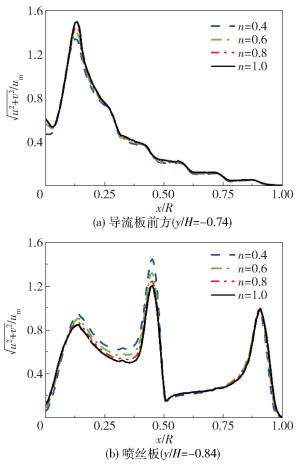
|
图 17 不同流变指数的流体在导流板前方和喷丝板内z=0平面上的速度分布 Fig.17 Velocity distribution of fluids with different rheological index on the z=0 plane in front of the guide plate and inside the spinneret |
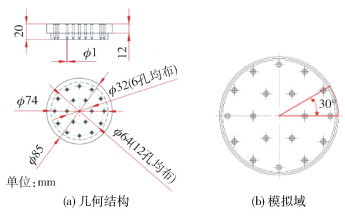
|
图 18 喷丝板的几何结构与模拟域 Fig.18 Geometric structure and simulation domain of the spinneret |
图 19为不同流变指数的流体在喷丝板前方(y/H=-0.84)的速度分布云图。可以看出,聚合物熔体在喷丝板处由内圈向外圈流动时速度逐渐减小,并且在外圈的两喷丝孔之间速度达到最小,形成滞留区;流变指数越大,滞留区越小,内外圈的流速差异越小。
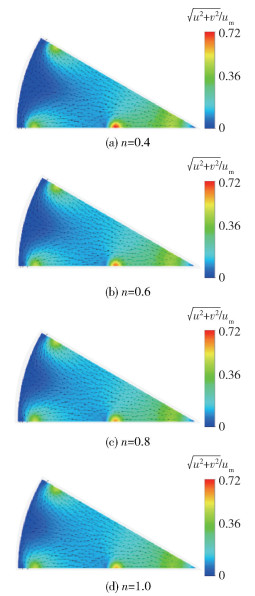
|
图 19 不同流变指数的流体在喷丝板前方(y/H=-0.84)的速度分布云图 Fig.19 Velocity distribution contours of fluids with different rheological indexes in front of the spinneret(y/H=-0.84) |
为了量化纺丝组件中喷丝板出丝的均匀性,定义各喷丝孔的流量与平均流量之间的相对偏差为η。
| $ \eta=\left|\frac{q_{\mathrm{m} i}-\bar{q}_{\mathrm{m}}}{\bar{q}_{\mathrm{m}}}\right| \times 100 \% $ | (6) |
式中:qmi为单个喷丝孔的质量流量,g/s;qm为所有喷丝孔的平均质量流量,g/s。不同流变指数的流体在各喷丝孔出口的质量流量及相对偏差如表 5所示。由结果可知,在流体的流变特性相同时,喷丝板各喷丝孔处的出口流量有所不同,内圈喷丝孔(outlet 1)的流量大于外圈喷丝孔(outlet 2和outlet 3),这是因为来自导流板的流体更易从中心进入喷丝板,同时在喷丝板前流体由内圈向外圈流动时,在流动过程中存在能量损失,使得内圈喷丝孔内熔体的流速大于外圈喷丝孔。此外,随着流体流变指数的增大,各喷丝孔流量的相对偏差η逐渐减小,喷丝孔内外圈流量分配的均一性提高。
| 下载CSV 表 5 不同流变指数的流体在各出口的质量流量及其相对偏差 Table 5 Mass flow and relative deviation of fluids with different rheological indexes at each outlet |
(1) 在270~290 ℃的温度范围内,PET、ECDP-1、ECDP-2的流变指数n均小于1,且n值均随着温度的升高而增大并接近1;聚合物熔体的黏度随着剪切速率的增大而减小,表现为假塑性流体。
(2) 流体的稠度系数对组件内的压力分布影响较大,组件入口压力随着K的增大而增大,且二者近似呈线性关系;稠度系数对纺丝组件内的速度场几乎无影响。
(3) 流体的流变指数对纺丝组件内的速度与压力分布有影响,组件内入口压力和入口流速随着流变指数的增大而增大;流体在砂腔内的流速较小但分布较为均匀,在砂腔上游,流变指数越大,流体流速越大;不同流变指数的流体在经过分配板和导流板时流速差异不明显;聚合物熔体在喷丝板外圈的喷丝孔之间形成滞留区,并且流变指数越大,滞留区越小,喷丝孔内外圈流量分配越均匀。
| [1] |
PERSANO L, CAMPOSEO A, TEKMEN C, et al. Industrial upscaling of electrospinning and applications of polymer nanofibers: a review[J]. Macromolecular Materials and Engineering, 2013, 298(5): 504-520. |
| [2] |
宣志强. 新型扣压式纺丝组件的研究和开发[J]. 合成纤维, 2010, 39(4): 23-26. XUAN Z Q. The development of a new type screw conjugate spinpack[J]. Synthetic Fiber in China, 2010, 39(4): 23-26. (in Chinese) |
| [3] |
PERVADCHUK V P, GLOT I O, YANKOV V I, et al. Flow of a polycaprolactam melt in standard spinneret holes[J]. Fibre Chemistry, 1984, 16(2): 94-96. DOI:10.1007/BF00555878 |
| [4] |
TZENG S C. Behaviors of flow mechanisms and heat transfer of non-Newtonian fluids through a spinneret[J]. Heat and Mass Transfer, 2004, 40(8): 603-613. |
| [5] |
顾家耀. POY条干不匀率影响因素的探讨[J]. 合成纤维工业, 1993, 16(1): 53-56. GU J Y. Discussion on influencing factors of POY strip unevenness[J]. China Synthetic Fiber Industry, 1993, 16(1): 53-56. (in Chinese) |
| [6] |
XIA X L, WANG J N, WANG H P, et al. Numerical investigation of spinneret geometric effect on spinning dynamics of dry-jet wet-spinning of cellulose/[BMIM]Cl solution[J]. Journal of Applied Polymer Science, 2016, 133(38): 43962.
|
| [7] |
金日光, 马秀清. 高聚物流变学[M]. 上海: 华东理工大学出版社, 2012. JIN R G, MA X Q. Polymer rheology[M]. Shanghai: East China University of Science and Technology Press, 2012. (in Chinese) |
| [8] |
施拉姆. 实用流变测量学[M]. 李晓晖, 译. 北京: 石油工业出版社, 1998. SCHRAMM G. A practical approach to rheology and rheometry[M]. LI X H, trans. Beijing: Petroleum Industry Press, 1998. (in Chinese) |








