高性能碳纤维复合材料具有抗拉强度高、模量大、耐高温等优点,广泛应用于航空、军事、汽车、民用建筑和能源开发等领域。温度作为碳纤维石墨化过程的主要影响因素,对材料的微晶结构、力学性能等有较大的影响[1-2],因此制备高性能碳纤维的关键要素之一是保证稳定的温度条件。传统的比例-积分-微分(proportional integral differential,PID)温度控制系统最初应用于线性控制系统,其基于准确的数学模型对温度进行控制,并且PID控制器的3个参数(比例系数kp、积分系数ki和微分系数kd)主要依据经验获取。而实际工业中大多数温度控制系统具有非线性、时变性、大惯性等特点,因此采用传统PID控制方法难以达到工业要求。为此,人们对温度控制策略进行了改进,从传统PID控制转变为PID与智能算法相结合的优化控制。高晓冬[3]针对大型预氧化炉非线性、大迟滞及高控制精度要求的特点,采用模糊自适应的PID控制算法取代传统PID控制方法对预氧化炉的炉内温度进行控制,并在MATLAB平台上进行了仿真研究,结果表明该算法控温准确,抗干扰能力强。熊昌炯等[4]通过分析PID算法的特点,设计了一种应用于炉温控制的不完全微分模糊自适应PID控制算法,与传统PID控制相比,该算法具有超调量小、响应速度快和稳态误差小的优点。采用模糊控制对传统PID进行优化,无需精确的数学模型,并且鲁棒性好,超调量小[5-6]。但是模糊控制本身也存在一定的局限性,在模糊自适应PID算法中,主要根据已有经验和相关理论制定kp、ki和kd的模糊控制规则,制定的规则对控制效果有较大影响;同时,模糊规则表的制定存在很大的主观性,依据前人对项目主观经验的积累所形成的控制结果输出不一定是最佳的,故难以保证其控制效果达到最优。
为了解决以上问题,人们尝试将遗传算法与模糊控制相结合,以改善温度控制系统的性能[7-10]。吕晓娟等[11]将遗传算法优化的模糊控制器应用到过热汽温控制系统中,控制效果及精度优于传统PID控制。Li等[12]采用遗传算法对PID控制器中的关键参数进行选择和优化,并基于参考控制场景对温控系统进行评估,研究结果表明,该优化方法在散裂目标系统的温度控制中具有适用性和可行性。为了解决套筒窑燃烧控制系统燃烧效率低、所生产石灰活性低的问题,Li等[13]引入改进遗传算法优化模糊控制的隶属函数参数,提出一种模糊PID智能控制燃烧室温度的策略,仿真结果表明,相较于传统控制策略,该方法能够有效控制烟气中的含氧量,提高燃烧效率。近年来,基于遗传算法的模糊PID控制策略日趋成熟,但是将其应用于碳纤维激光石墨化炉温度控制的研究鲜有报道。
为了制备高性能碳纤维复合材料,本课题组在前期工作中设计改良了碳纤维石墨化炉的结构,提出一种以激光作为热源的激光隧道全反射轴心聚焦碳纤维石墨化炉,这种石墨化炉可以在短时间内迅速升温至3 000 ℃以满足加热要求[14]。在此基础上,本课题组又提出了一种碳纤维可控激光式超高温石墨化装置,采用控制器实时控制收放丝的速度和可控激光器的功率[15]。为了使加热区域的温度保持动态平衡,本文以该石墨化装置为研究对象,提出了一种基于遗传算法的模糊控制器设计策略,对PID参数kp、ki和kd的模糊规则表寻找全局最优解,并进行了仿真实验,结果表明该算法可行有效,对实际应用具有一定的指导意义。
1 基于遗传算法的模糊控制器设计 1.1 模糊控制器结构在工业生产过程中常使用PID控制方法对温度进行控制,该方法具有原理简单、易于操作和鲁棒性好等特点,其数学表达式如式(1)所示。
| $ u(t)=k_{\mathrm{p}} e(t)+k_{\mathrm{i}} \int_0^{\infty} e(t) \mathrm{d} t+k_{\mathrm{d}} \frac{\mathrm{d} e(t)}{\mathrm{d} t} $ | (1) |
式中:u(t)为控制器输出,e(t)为偏差,t为时间。
鉴于模糊控制无需精确的数学模型即可进行系统控制,故针对所求数学模型采用模糊算法对PID控制进行参数优化。碳纤维激光石墨化炉模糊控制器主要由模糊化、模糊规则库、模糊推理及解模糊化几个部分组成,其控制框图如图 1所示。
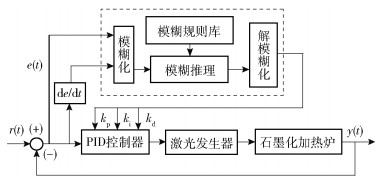
|
r(t)为预设值,y(t)为实际输出值。 图 1 自适应模糊PID控制系统结构 Fig.1 Structure of the adaptive fuzzy PID control system |
将偏差e(t)和偏差变化率de/dt(可简写为ec(t)) 传到模糊控制器中,通过模糊控制器的正常流程解析和输出之后,将求解出的参数Δkp、Δki和Δkd分别送到PID控制器中,然后通过式(2)~(4)进行在线的实时参数自整定。
| $ k_{\rm{p}}^\prime = {k_{{\rm{p}}0}} + \Delta {k_{\rm{p}}} $ | (2) |
| $ k_{\rm{i}}^\prime = {k_{{\rm{i}}0}} + \Delta {k_{\rm{i}}} $ | (3) |
| $ k_{\rm{d}}^\prime = {k_{{\rm{d}}0}} + \Delta {k_{\rm{d}}} $ | (4) |
式中:kp0、ki0和kd0为3个参数的初始值,k′p、k′i和k′d为优化后的参数值。
在模糊控制器中,控制规则表与控制效果息息相关。输入量e(t)、ec(t)的变化范围可以划分为:负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)和正大(PB)这7种情况,e(t)和ec(t)自由组合可得到49条规则,每条规则分别给出kp、ki、kd这3个参数的模糊量,包括8种情况:负大(NB)、负中(NM)、负小(NS)、负零(NZ)、正零(PZ)、正小(PS)、正中(PM)和正大(PB)。本文以如下规则作为示例。
If e(t) is NS and ec(t) is Z, then kp is PZ and ki is PZ and kd is PS. (若偏差e(t)为负小且偏差变化率ec(t)为零,则kp为正零,ki为正零,kd为正小。)
碳纤维激光石墨化炉的传递函数G(s)为一阶惯性加迟滞系统,如式(5)所示。
| $ G(s) = \frac{{K{{\rm{e}}^{ - \tau s}}}}{{Ts + 1}} $ | (5) |
式中:K为放大系数,T为时间常数,τ是纯滞后时间,e是自然对数的底,s为拉氏变换后的复变量。
根据本课题组的前期研究[16-17],同时参考文献[18],通过数学建模并对激光功率P分别为50、100、150、200、250 W和300 W情况下得到的温度数据进行分析处理,求取K、T、τ,最终得到如式(6)所示的数学模型。
| $ G(s)=\frac{17.02 \mathrm{e}^{-0.09 s}}{0.185 s+1} $ | (6) |
借助Simulink环境对模糊控制系统进行搭建并仿真,仿真系统如图 2所示。针对纯滞后环节带来的震荡效应,常采用史密斯预估器对其进行补偿[19-20],补偿结构如图 2中的虚线框所示。

|
图 2 基于Simulink的模糊PID控制仿真系统 Fig.2 Simulation system of the fuzzy-PID control based on Simulink |
仿真结果如图 3所示,其中:“step”曲线代表阶跃信号,“PID”曲线代表传统PID整定曲线,“fuzzy-PID”曲线代表传递函数为一阶惯性系统的模糊PID控制,“fuzzy-Delay”曲线代表传递函数为一阶惯性加迟滞系统的模糊PID控制。
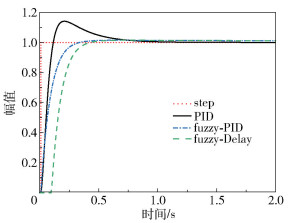
|
图 3 不同控制方法的仿真结果 Fig.3 Simulation results of different control methods |
由图 3可知,对于无论是否有迟滞环节的模糊PID控制(fuzzy-PID和fuzzy-Delay),除了因迟滞环节产生响应时间差之外,其整体曲线相同,并且两者的控制效果均优于传统PID,响应时间和超调量均大幅度减少。
在本文提出的模糊PID控制系统中,规则表的制定直接影响3个参数的输出,最终影响控制精度。在实际生产中,依赖经验所得的规则表并不一定是最佳规则,故PID参数并非最好。为此,本文尝试引入遗传算法对规则表进行全局寻优,以提高规则表的精准性,改善控制效果。
1.2 遗传算法优化编码优化参数为PID的3个参数kp、ki和kd,根据模糊控制规则表,每个参数有49种条件,故一组参数有147种组合。二进制具有计算简单快速的特点,通过改变“0”、“1”即可实现基因变化,故采用二进制编码,“000~111”分别代表十进制中0~7这8个数,在编码并进行二进制转十进制后分别加1,得到1~8共8个数,分别代表:负大(NB)、负中(NM)、负小(NS)、负零(NZ)、正零(PZ)、正小(PS)、正中(PM)和正大(PB)这8种情况。故一条染色体含有441个基因,包含一组完整的kp、ki和kd参数信息,被视作一个“个体”。图 4为一个个体的二进制编码示意图。
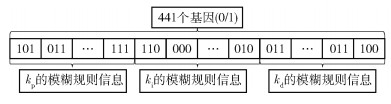
|
图 4 个体编码示例 Fig.4 Example of individual coding |
通过遗传算法进行全局寻优,解码情况如图 5所示,其代表一个参数(如kp)的完整规则表。将其投入到模糊控制器,由式(2)~(4)可知,模糊控制器输出此时最佳的参数增量,计算得到kp、ki和kd的更新值,进而实现PID控制,直到迭代次数结束,保留最佳参数组合作为最优解。
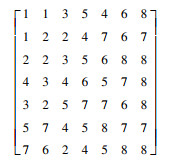
|
图 5 一个参数的解码规则表示例 Fig.5 Example of a decoding rule table for one parameter |
适应度函数常用目标函数作为控制系统的性能标准。积分性能指标ITAE可以用于评价控制系统的响应时间、超调量等动态和静态性能,其计算公式如式(7)所示。J(ITAE)越小,说明响应时间t越短,偏差绝对值|e(t)|越小,精度越高。在遗传算法中,为了便于计算,可将目标函数进行适当变换,得到适应度函数f,如式(8)所示。适应度值越大,遗传寻优效果越好,这样可以根据适应度值确定搜索方向和范围。为了便于计算机计算,将积分函数进行离散化,得到ΔJ=t|e(t)|ΔT(ΔT为采样时间间隔)。
| $ J(ITAE) = \int_0^\infty t |e(t)|{\rm{d}}t $ | (7) |
| $ f = \frac{1}{{1 + J(ITAE)}} $ | (8) |
种群初始化初始种群可以随机生成,为了保证种群具有较好的多样性,个体数一般在30~100之间。同理,代数的选择也需适当,代数过少,则无法寻到最优目标;代数过多,则计算时间太长,故代数一般为30~100。
选择从当前群体中根据一定标准进行优胜劣汰的过程称为选择,旨在选出优良的个体,使它们有机会作为父代繁殖子孙。选择算子的选择方式有多种,例如精英策略、轮盘赌算法或适应度值排名等,为防止种群过早成熟,同时提高迭代速率,本文采用精英策略和适应度值排名相结合的选择方式。
交叉种群中两个个体基因发生互换的过程称为交叉,可分为单点交叉、两点交叉和多点交叉。交叉算子Pc(也称交叉概率)决定着全局寻优的能力,一般在0.3~1之间。
变异种群中某个个体的某处基因发生改变的过程称为变异。变异算子Pm(也称变异概率)决定着算法局部寻优的能力,一般在0.01~0.1之间。
2 仿真分析设置遗传算法参数如下:代数n=30,个体基因数Bitlength=441,初始种群数popsize=20,交叉算子Pc=0.9,变异算子Pm=0.07。采用MATLAB进行模拟仿真,以全代码形式对PID控制、模糊控制和遗传算法进行编程仿真,输入信号幅值为1的阶跃函数。
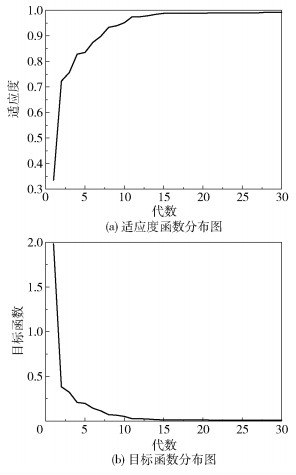
图 6(a)为适应度函数分布图,可以看出,适应度值随着迭代次数的增加而增大,最终适应度值为0.996 8,数值越接近1,说明该种群越优,越符合目标函数的最优解。图 6(b)为目标函数值分布图,可以看出,目标函数值分布趋势与适应度函数分布趋势相反,目标函数值随着迭代次数的增加而减小,第10代时目标函数曲线收敛至0附近,第10代以后目标函数值几乎为0,即积分性能指标J(ITAE)趋于0,控制效果优越。
|
图 6 性能指标函数曲线 Fig.6 Curves of performance indicator function |
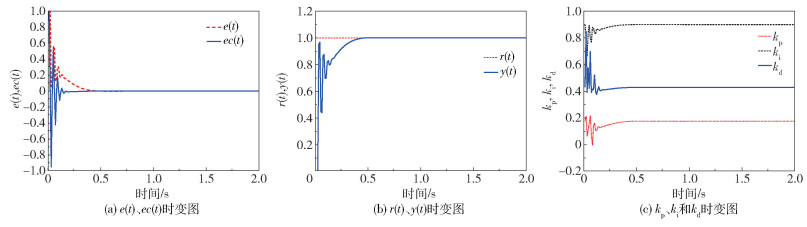
为了验证上述算法的可靠性,对适应度函数最佳的个体进行解码,得到模糊控制规则表,并投入模糊PID控制器,得到的运行结果如图 7所示。图 7(a)为偏差e(t)和偏差变化率ec(t)随时间的变化曲线,e(t)、ec(t)值由1逐渐趋于0,表明该控制系统的控制精度达到较高的标准。图 7(b)为阶跃信号r(t)和控制系统输出量y(t)随时间的变化曲线,y(t)在1 s附近达到稳定。图 7(c)为PID的参数kp、ki和kd随时间的变化曲线,由图可知,当优化效果较好时,该组参数为:kp=0.173,ki=0.889,kd=0.429。
|
图 7 最优个体的控制参数图 Fig.7 Control parameter diagram of the optimal individual |
为了进一步比较3种控制方法(传统PID、模糊PID和基于遗传算法的模糊PID)的整定效果,以上升时间、调节时间和超调量作为阶跃响应的性能指标参数进行对比,结果如表 1所示。由结果可知,传统PID的上升时间和调节时间较短,但超调量较大;与传统PID相比,模糊PID大大减少了超调量;基于遗传算法的模糊PID控制方法实现了无超调量,与模糊PID相比,上升时间缩短了45.65%,调节时间缩短了30.15%。
| 下载CSV 表 1 3种方法的控制效果对比 Table 1 Comparison of control effects for three methods |
综上,基于遗传算法的模糊PID控制算法的响应时间短,无超调量,偏差小,控制精度高。结果表明借助遗传算法对模糊规则表寻优是可行有效的,可以替代传统人工迭代过程中的经验选择以改善系统性能。
3 结论本文针对碳纤维激光石墨化炉的温度控制系统进行优化设计,引入遗传算法对模糊控制器中的模糊规则表进行全局寻优,借助MATLAB和Simulink环境进行编程仿真,结果表明,基于遗传算法的模糊PID控制效果在整体上优于模糊PID控制和传统PID控制,其响应时间短,控制精度高,无超调量,可用于碳纤维激光石墨化炉的温度控制系统设计。
| [1] |
张政和, 杨卫民, 谭晶, 等. 碳纤维石墨化技术研究进展[J]. 化工进展, 2019, 38(3): 1434-1442. ZHANG Z H, YANG W M, TAN J, et al. Research progress of graphitization of carbon fibers[J]. Chemical Industry and Engineering Progress, 2019, 38(3): 1434-1442. (in Chinese) |
| [2] |
姜鹏飞. 进口中间相沥青碳纤维超高温石墨化处理后的特性分析[J]. 化学通报, 2022, 85(1): 127-131. JIANG P F. Characteristics analysis of commercial mesophase pitch-based carbon fibers after ultra-high temperature graphitization[J]. Chemistry, 2022, 85(1): 127-131. (in Chinese) |
| [3] |
高晓冬. 碳纤维生产控制系统开发及优化[D]. 济南: 山东大学, 2012. GAO X D. The control system development and optimization for carbon fiber production[D]. Jinan: Shandong University, 2012. (in Chinese) |
| [4] |
熊昌炯, 王春荣, 夏尔冬. 基于改进PID算法的加热炉温度控制研究[J]. 中国设备工程, 2022(12): 101-102. XIONG C J, WANG C R, XIA E D. Research on temperature control of heating furnace based on improved PID algorithm[J]. China Plant Engineering, 2022(12): 101-102. (in Chinese) |
| [5] |
李智芳. 模糊控制器在高温窑炉计算机控制系统中应用与实现[J]. 微型电脑应用, 2000, 16(10): 34-38. LI Z F. Application and implementation of the fuzzy controller in a computerized control system for the high-temperature furnace[J]. Microcomputer Applications, 2000, 16(10): 34-38. (in Chinese) DOI:10.3969/j.issn.1007-757X.2000.10.011 |
| [6] |
闫茂里, 李肖, 王伟, 等. 模糊PID控制器在浸出车间石蜡加热器温度闭环控制中的应用[J]. 中国油脂, 2022, 47(7): 98-102, 120. YAN M L, LI X, WANG W, et al. Application of fuzzy PID controller in temperature closed-loop control of para-ffin heater in leaching workshop[J]. China Oils and Fats, 2022, 47(7): 98-102, 120. (in Chinese) |
| [7] |
李璀璀, 易文俊, 管军, 等. 基于遗传算法的电动舵机系统模糊PID控制[J]. 兵器装备工程学报, 2021, 42(3): 162-167. LI C C, YI W J, GUAN J, et al. Fuzzy PID control of electric steering system based on genetic algorithm[J]. Journal of Ordnance Equipment Engineering, 2021, 42(3): 162-167. (in Chinese) DOI:10.11809/bqzbgcxb2021.03.030 |
| [8] |
CHEN C C, LUO J. Hybrid optimal control of robot motor based on improved genetic algorithm and fuzzy logic[C]//2017 International Conference on Robotics and Automation Sciences. Hongkong, 2017: 53-57.
|
| [9] |
ZHOU Y, WANG Z, YANG L. Application of fuzzy PID control based on GA in control valve[J]. Applied Mechanics and Materials, 2014, 668-669: 445-449. DOI:10.4028/www.scientific.net/AMM.668-669.445 |
| [10] |
ELAWADY W M, LEBDA S M, SARHAN A M. An optimized fuzzy continuous sliding mode controller combined with an adaptive proportional-integral-derivative control for uncertain systems[J]. Optimal Control Applications and Methods, 2020, 41(3): 980-1000. DOI:10.1002/oca.2580 |
| [11] |
吕晓娟, 梁东义, 李玉娜. 基于遗传算法的模糊控制在过热汽温控制系统优化中的应用[J]. 电子制作, 2019(16): 23-24, 40. LV X J, LIANG D Y, LI Y N. Application of fuzzy control based on genetic algorithm in optimization of superheated steam temperature control system[J]. Practical Electronics, 2019(16): 23-24, 40. (in Chinese) |
| [12] |
LI J Y, DAI Y, GU L, et al. Genetic algorithm based temperature control of the dense granular spallation target in China initiative accelerator driven system[J]. Annals of Nuclear Energy, 2021, 154: 108127. |
| [13] |
LI S M, YANG P, YANG F, et al. Research on lime kiln temperature system based on fuzzy PID algorithm and optimal control[C]//The 26th China Control and Decision Conference. Changsha, 2014: 5141-5144.
|
| [14] |
杨卫民, 王晗, 阎华, 等. 一种激光隧道全反射轴心聚焦碳纤维石墨化炉: CN 104760953A[P]. 2015-07-08. YANG W M, WANG H, YAN H, et al. A carbon fiber graphitization furnace with laser tunnel total reflection axis focusing: CN 104760953A[P]. 2015-07-08. (in Chinese) |
| [15] |
谭晶, 黎三洋, 丁玉梅, 等. 一种碳纤维可控激光式超高温石墨化装置: CN 106521712B[P]. 2019-04-30. TAN J, LI S Y, DING Y M, et al. An ultra-high temperature graphitization device controlled by laser for carbon fiber: CN 106521712B[P]. 2019-04-30. (in Chinese) |
| [16] |
张欢雷, 程礼盛, 张政和, 等. 激光与微波协同加热碳纤维的温度与热应力分布规律[J]. 化工进展, 2020, 39(增刊1): 195-199. ZHANG H L, CHENG L S, ZHANG Z H, et al. Insights into the distribution regularity of temperature and thermal stress for the co-heating process of carbon fibers via laser and microwave[J]. Chemical Industry and Engineering Progress, 2020, 39(S1): 195-199. (in Chinese) |
| [17] |
黄灿, 杨卫民, 程礼盛, 等. 激光辐照碳纤维石墨化的径向均匀性[J]. 材料热处理学报, 2019, 40(10): 166-173, 180. HUANG C, YANG W M, CHENG L S, et al. Radial uniformity of carbon fiber graphitization by laser irradiation[J]. Transactions of Materials and Heat Treatment, 2019, 40(10): 166-173, 180. (in Chinese) |
| [18] |
吴浩玚. 小型焚烧炉智能测控系统设计与研究[D]. 北京: 北京石油化工学院, 2020. WU H Y. Design and research of intelligent measurement and control system for small incinerator[D]. Beijing: Beijing Institute of Petrochemical Technology, 2020. (in Chinese) |
| [19] |
焦健. 基于史密斯预估补偿及自整定PID的过热汽温控制方案[J]. 山西电力, 2020(2): 41-44. JIAO J. The control scheme of overheating steam temperature based on Smith predictive compensation and self-adjusting PID[J]. Shanxi Electric Power, 2020(2): 41-44. (in Chinese) |
| [20] |
王淏, 程慧, 刘强, 等. Smith预估模糊PID控制算法及其在温度控制中的应用[J]. 软件, 2022, 43(6): 168-170. WANG H, CHENG H, LIU Q, et al. Smith predictive fuzzy PID control algorithm and its application in temperature control[J]. Software, 2022, 43(6): 168-170. (in Chinese) |








