引言

鲁棒主成分分析(RPCA)是低秩恢复问题的一种。Candès等^[1]提出基于矩阵的RPCA方法(matrix RPCA, MRPCA), 能够从被稀疏大噪声损坏的观测数据中恢复出隐含的低秩分量；MRPCA将观测数据分解为低秩分量和稀疏分量，用矩阵核范数约束低秩分量，矩阵范数约束稀疏分量。该模型简单且易于求解，被广泛应用在视觉处理任务中，如图像恢复和背景建模^[1-2]。但是MRPCA方法会将观测数据矩阵化，这样的预处理步骤会导致不必要的信息损失，带来次优的恢复结果。针对此问题，许多基于张量的RPCA方法被相继提出，如基于Tucker分解^[3]的求和核范数(sum nuclear norm, SNN)模型^[4]、基于张量火车分解^[5]的张量火车核范数(tensor train nuclear norm, TTNN)模型^[6]和基于张量环(tensor ring, TR)分解的鲁棒张量环补全(robust tensor ring completion, RTRC)模型^[7]等。为了刻画张量不同模型之间的相关性，研究者们在SNN、TTNN和RTRC中通过特殊的矩阵化策略将张量展开为一组矩阵，提出了可用交替方向乘子算法(ADMM)求解的张量鲁棒主成分分析(tensor-RPCA, TRPCA)模型。Kilmer等^[8]提出了一种新的张量乘法t积(tensor-tensor product)和张量奇异值分解(tensor singular value decomposition, t-SVD)策略。在t积和t-SVD的张量框架下，Lu等^[2]提出了张量核范数(tensor nuclear norm, TNN)概念，Zhou等^[9]提出了张量低秩表示(low rank tensor representation, LRTR)模型。在TNN和LRTR模型中，以基于t积的张量核范数t-TNN作为tubal秩的凸包络，t-TNN等价于张量的所有前切片组成的块循环矩阵的核范数或者张量按模3方向作离散傅里叶变换所得张量的所有前切片组成的块对角矩阵的核范数，因此t-TNN可以看作一种特殊的矩阵化方式，用来刻画张量的空间信息和第三通道的相关性。此外，t-SVD可以利用快速傅里叶变换加速计算，并且tubal秩可以描述张量子空间结构。上述模型在图像恢复和背景建模中取得了较好的效果，但是对输入数据低秩结构的强依赖性问题仍然没有得到解决。

针对上述问题，本文在t积和t-SVD的张量框架下提出一个增强的张量鲁棒主成分分析模型(E-TRPCA)用于图像恢复和背景建模。首先学习得到一个字典张量，并构造了一个增强的张量核范数(E-TNN)正则项；其次，在低秩张量表示的基础上，提出了一个去随机噪声的模型；最后，设计了一个高效的交替方向乘子算法来解决所提出的问题。在图像恢复和背景建模上的实验证明了所提方法的优越性。

1 张量奇异值分解框架 1.1 符号说明

给定张量$\mathscr{A} \in \mathbb{R}^{h \times w \times s} $，$\mathscr{A} $_{(1, : , : )}、$\mathscr{A} $_{(: , 1，: )}以及$\mathscr{A} $_{(: , : , 1)}分别是$\mathscr{A} $的第一个横切片、第一个侧切片和第一个前切片，$\mathscr{A} $_{i, j, k}是$\mathscr{A} $在(i, j, k)位置的元素。unfold()运算将张量展开为矩阵, old()运算是其逆运算。

$ \operatorname{unfold}(\mathscr{A})=\left[\begin{array}{c} \mathscr{A}_{(:, :, 1)} \\ \mathscr{A}_{(:, :, 2)} \\ \vdots \\ \mathscr{A}_{(:, :, s)} \end{array}\right], \text { fold }\left(\left[\begin{array}{c} \mathscr{A}_{(:, :, 1)} \\ \mathscr{A}_{(:, :, 2)} \\ \vdots \\ \mathscr{A}_{(:, :, s)} \end{array}\right]\right)=\mathscr{A} $

$\bar{\mathscr{A}} $=fft($\mathscr{A} $, [], 3)记为对$\mathscr{A} $的每个管道的离散傅里叶变换。

bdiag()运算将张量$\bar{\mathscr{A}} $变为块对角矩阵A

$ \mathit{\boldsymbol{\bar A}} = {\mathop{\rm bdiag}\nolimits} (\bar{\mathscr{A}}) = \left[ {\begin{array}{*{20}{l}} {{{\bar{\mathscr{A}}}_{(:, :, 1)}}}&{}&{}&{}\\ {}&{{{\bar{\mathscr{A}}}_{(:, :, 2)}}}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{{\bar{\mathscr{A}}}_{(:, :, s)}}} \end{array}} \right] $

bcirc()运算是将张量$\mathscr{A} $变为块循环矩阵的运算

$ \operatorname{bcirc}(\mathscr{A})=\left[\begin{array}{cccc} \mathscr{A}_{(:, :, 1)} & \mathscr{A}_{(:, :, s)} & \cdots & \mathscr{A}_{(:, :, 2)} \\ \mathscr{A}_{(:, :, 2)} & \mathscr{A}_{(:, :, 1)} & \cdots & \mathscr{A}_{(:, :, 3)} \\ \vdots & \vdots & \ddots & \vdots \\ \mathscr{A}_{(:, :, s)} & \mathscr{A}_{(:, :, s-1)} & \cdots & \mathscr{A}_{(:, :, 1)} \end{array}\right] $

1.2 t积和张量奇异值分解

定义1(t积)   给定张量$\mathscr{A} \in \mathbb{R}^{h \times l \times s}$, $\mathscr{B} \in \mathbb{R}^{l \times w \times s}$，则t积定义为^[8]

$ \mathscr{A} * \mathscr{B}=\text { fold }(\operatorname{bcirc}(\mathscr{A}) \operatorname{unfold}(\mathscr{B})) $

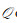
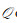
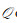
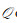
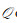
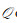
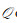
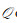
定义2(正交张量)   如果$ \in \mathbb{R}^{n \times n \times l} $满足^T* = * ^T= $\mathscr{T} \in \mathbb{R}^{n \times n \times l}$，则为正交张量。进一步，如果$ \in \mathbb{R}^{p \times q \times l}$满足^T* = $\mathscr{T} \in \mathbb{R}^{q \times q \times l}$，则为部分正交张量。

定义3(张量奇异值分解)^[2]   给定张量$\mathscr{A} $∈$\mathbb{R}^{h \times w \times s} $，它可以分解为如下形式

$ \mathscr{A}=\mathscr{U} * \mathscr{S} * \mathscr{V}^{\mathrm{T}} $

式中，$\mathscr{U} \in \mathbb{R}^{h \times h \times s}$, $\mathscr{V} \in \mathbb{R}^{w \times w \times s}$是正交张量，$\mathscr{S} \in \mathbb{R}^{h \times w \times s}$是f-diagonal张量。

定义4(管道秩)   给定张量$\mathscr{A} \in \mathbb{R}^{h \times w \times s}$，则张量的管道秩为$\mathscr{S}$中非零管道的个数^[10]，记为rank_t($\mathscr{A}$)

$ \operatorname{rank}_t(\mathscr{\mathscr { A }})=\{i, \mathscr{S}(i, i, :) \neq 0\} $

式中，$\mathscr{A}=\mathscr{U} * \mathscr{S} * \mathscr{V}$^T是$\mathscr{A}$的t-SVD分解。

定义5(张量核范数)^[2]   $\mathscr{A}=\mathscr{U} * \mathscr{S} * \mathscr{V}$^T是$\mathscr{A}$的t-SVD，$\mathscr{A} \in \mathbb{R}^{h \times w \times s}$，则$\mathscr{A}$的核范数表示为

$ \|\mathscr{A}\|_*=\sum\limits_{i=1}^r \mathscr{S}_{(:, :, i)} $

其中, r=rank_t($\mathscr{A}$)。

引理1   张量$\mathscr{A} \in \mathbb{R}^{h \times w \times s}$，$\mathscr{B} \in \mathbb{R}^{w \times h \times s}$，令$\mathscr{F}$=$\mathscr{A} * \mathscr{B}$，则有：

① ‖$\mathscr{A}$‖_F²=$\frac{1}{s}\|\overline{\boldsymbol{A}}\|_F^2$，并且〈$\mathscr{A}, \mathscr{B}$〉=$\frac{1}{s}$〈$\overline{\boldsymbol{A}}, \overline{\boldsymbol{B}}$〉；

② $ \mathscr{F}=\mathscr{A} * \mathscr{B}$，则F =AB。

引理2^[11]   $ \forall \boldsymbol{A} \in \mathbb{R}^{m \times n}* \mathscr{B}$，则问题

$ \min\limits _{V V^{\mathrm{T}}=I}\langle\boldsymbol{A}, \boldsymbol{V}\rangle $

(1)

有全局解V^*= BC^T，A=BCD^T是A的奇异值分解。

根据引理1，本文给出了引理2的张量推广形式。

定理1   任给张量$\mathscr{A} \in \mathbb{R}^{h \times w \times s} $，问题

$ \min\limits _{\mathscr{V} \cdot \mathscr{V}^{\mathrm{T}}=\mathscr{I}}\langle\mathscr{A}, \mathscr{V}\rangle $

(2)

的全局解为$\mathscr{V}=\mathscr{B} * \mathscr{D}^{\mathrm{T}} $，$\mathscr{A}=\mathscr{B} * \mathscr{C}* \mathscr{D}^{\mathrm{T}} $是$\mathscr{A}$的t-SVD。

证明   由引理1以及B、C的块对角结构可知，问题(2)可以分解为以下子问题

$ \min\limits _{\bar{\mathscr{V}}_{(i, i, k)} \overline{\mathscr{V}}_{(i, i, k)}^{\mathrm{T}}=I}\left\langle\overline{\mathscr{A}}_{(i, i, k)}, \overline{\mathscr{V}}_{(i, i, k)}\right\rangle, k=1, 2, \cdots, s $

(3)

由引理2知，式(3)中各子问题的全局解存在，$\overline{\mathscr{V}}_{(:, :, k)} $=$\overline{\mathscr{B}}_{(:, :, k)} \overline{\mathscr{D}}_{(:, :, k)}^{\mathrm{T}} $, $\overline{\mathscr{A}}_{(:, :, k)}$=$\overline{\mathscr{B}}_{(:, :, k)} \overline{\mathscr{C}}_{(:, :, k)} \cdot$ $\overline{\mathscr{D}}_{(:, :, k)}^{\mathrm{T}}$是$ \overline{\mathscr{A}}_{(:, :, k)}$的t-SVD。由引理1中的$ \mathscr{F}$=$ \mathscr{A}*\mathscr{B}$, 则F =AB可知，$\overline{\mathscr{V}}=\overline{\mathscr{B}} * \overline{\mathscr{D}}^{\mathrm{T}} $, $\mathscr{V}=\mathscr{B} * \mathscr{D}^{\mathrm{T}}$。因此$\mathscr{A}=\mathscr{B} * \mathscr{C} * \mathscr{D}{ }^{\mathrm{T}}$是$\mathscr{A} $的t-SVD。

2 E-TRPCA方法 2.1 基于t-SVD的E-TRPCA模型

如图 1所示，矩阵可以分解为两个矩阵的积^[12]

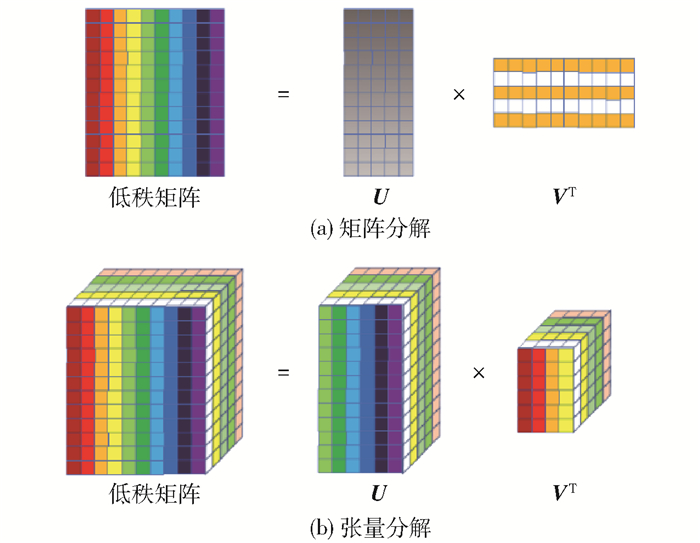
$ \boldsymbol{X}=\boldsymbol{U} \boldsymbol{V}^{\mathrm{T}}+\boldsymbol{S} $

(4)

借助t积，可以把矩阵的情形推广到张量情形

$ \mathscr{B}=\mathscr{L}+e=\mathscr{U} * \mathscr{V}^{\mathrm{T}}+ℯ $

(5)

事实上，如果对$ \mathscr{V}$施加一个正交约束，则有$ \mathscr{U}=\mathscr{L} * \mathscr{\mathscr { V }}$。与传统的核范数最小化(nuclear norm minimization，NNM)问题相同，对分量U施加低秩约束，则可以构造如下E-TNN正则项

$ \|\mathscr{L}\|_{\mathrm{E}-\mathrm{TNN}}=\min\limits _{\mathscr{V} \in \mathbb{R}^w \times r \times s}\|\mathscr{L} * \mathscr{V}\|_*\\ \text { s.t. }\|\mathscr{L} * \mathscr{V}\|_F=\|\mathscr{L}\|_F\\ \mathscr{V}{ }^{\mathrm{T}} * \mathscr{V}=\mathscr{T} $

(6)

第一个是约束在变换结果$ \mathscr{L} * \mathscr{V}$上的Frobenius范数，这有助于避免变换引起的信息损失；第二个是对$ \mathscr{V}$的正交约束，倾向于使变换后的结果$ \mathscr{L} * \mathscr{V}$尽可能保留低秩张量$ \mathscr{L}$的信息，此外它还可以帮助获得该变量的闭式解。由于不容易直接求解上述问题，因此将式(6)重新表述为以下等价问题

$ \|\mathscr{L}\|_{\text {E-TNN }}=\min\limits _{\mathscr{U}, \mathscr{V}}\|\boldsymbol{U}\|_*\\ \text { s.t. } \mathscr{L}=\mathscr{U} * \mathscr{V}^{\mathrm{T}}, \mathscr{V}^{\mathrm{T}} * \mathscr{V}=\mathscr{T}\\ \mathscr{U} \in \mathbb{R}^{h \times r \times s}, \mathscr{V} \in \mathbb{R}^{w \times r \times s} $

(7)

与TNN一样，E-TNN同样作用在分量$\mathscr{L} $上，不同之处在于E-TNN不直接约束$\mathscr{L} $本身，而是约束从$\mathscr{L} $中学习得到的一组基，这组基是$\mathscr{L} $的所有侧切面的一个线性表示^[9]。矩阵分解可以把矩阵分解为字典和稀疏矩阵的积，因此，借助上述张量工具，把分量$\mathscr{L} $分解为字典张量$\mathscr{U} $和投影张量$\mathscr{V} $的共轭转置的乘积。字典张量$\mathscr{U} $由分量$\mathscr{L} $经过正交变换得到: $\mathscr{U} $=$\mathscr{L} $*$\mathscr{V} $，$\mathscr{V} $是正交变换张量，维度为w×r×s, r < w。另外，字典张量$\mathscr{U} $的规模总是小于低秩分量$\mathscr{L} $，这使得它们受到噪声损坏的影响较小，从而可以获得更鲁棒的恢复效果。

将E-TNN正则项嵌入到TRPCA模型，得到如下低秩张量恢复模型

$ \;\;\;\;\;\;\;\;\;\min\limits _{\mathscr{U}, \mathscr{V}, \mathscr{X}, e}\|\mathscr{U}\|\left\|_*+\lambda\right\| ℯ \|_1\\ \text { s. t. } \mathscr{X}=\mathscr{L}+ℯ\\ \;\;\;\;\;\;\;\;\;\mathscr{L}=\mathscr{U} * \mathscr{V}^{\mathrm{T}}, \mathscr{V}^{\mathrm{T}} * \mathscr{V}=\mathscr{T}\\ \;\;\;\;\;\;\;\;\;\mathscr{U} \in \mathbb{R}^{h \times w \times s}, \mathscr{V} \in \mathbb{R}^{w \times r \times s} $

(8)

式中$\mathscr{X}, \mathscr{L}, ℯ \in \mathbb{R}^{h \times w \times s} $分别为观测张量、低秩张量和稀疏张量，l₁范数来约束稀疏张量，λ为超参数。

2.2 ADMM优化

本节中，通过ADMM算法^[13]求解模型(8)。由模型(8)得到以下增广拉格朗日函数。

$ \begin{array}{l} \;\;\;\;\;\mathscr{L}\left(\mathscr{U}, \mathscr{V}, \mathscr{L}, ℯ, \mathscr{Y}_1, \mathscr{Y}_2\right)=\|\mathscr{U}\|\left\|_*+\lambda\right\| ℯ \|_l+ \\ \frac{\mu}{2}\left\|\mathscr{X}-\mathscr{L}-ℯ+\frac{\mathscr{Y}_1}{\mu}\right\|_F^2+\frac{\mu}{2}\left\|\mathscr{L}-\mathscr{U} * \mathscr{V}^{\mathrm{T}}+\frac{\mathscr{Y}_1}{\mu}\right\|_F^2 \end{array} $

(9)

式中，μ为惩罚项系数。ADMM可以把上述问题分解为如下的5个子问题，在每一个子问题中，固定其余变量不变，只更新一个变量。

$\mathscr{L} $子问题  从式(9)中找出所有包含$\mathscr{L} $的项，得到如下更新公式

$ \mathscr{L}=-\frac{1}{2}\left(\mathscr{X}-e+\frac{\mathscr{Y}_1}{\mu}+\mathscr{U} * \mathscr{V}^{\mathrm{T}}-\frac{\mathscr{Y}_2}{\mu}\right) $

(10)

$\mathscr{U} $子问题  从式(9)中找出所有包含$\mathscr{U} $的项，得到如下问题

$ \;\;\;\;\;\;\;\mathscr{U}^*=\min\limits _{\mathscr{U}}\|\mathscr{U}\|_*+\frac{\mu}{2}\left\|\mathscr{L}-\mathscr{U} * \mathscr{V}^{\mathrm{T}}+\frac{\mathscr{Y}_2}{\mu}\right\|_F^2=\\ \min\limits _{\mathscr{U}}\|\mathscr{U}\|_*+\frac{\mu}{2}\left\|\mathscr{U}-\left(\mathscr{L}+\frac{\mathscr{Y} 2}{\mu}\right) \mathscr{V}\right\|_F^2 $

(11)

这个子问题可以通过张量奇异值阈值算子^[2]求解

$ \mathscr{U}_*=\mathscr{D}_{\frac{1}{\mu}}\left(\left(\mathscr{L}+\frac{\mathscr{Y} 2}{\mu}\right) \mathscr{V}\right) $

(12)

$\mathscr{V} $子问题  从式(9)中找出所有包含$\mathscr{V} $的项，令$\mathscr{P}=\mathscr{L}+\frac{\mathscr{Y}_2}{\mu} $，得到如下问题

$ \;\;\;\;\;\;\;\;\;\mathscr{V}^*=\min\limits _{\mathscr{V}} \frac{\mu}{2}\left\|\mathscr{L}-\mathscr{U} * \mathscr{V}^{\mathrm{T}}+\frac{\mathscr{Y}_2}{\mu}\right\|_F^2=\min\limits _{\mathscr{V}} \frac{\mu}{2}\langle\mathscr{U} *\\ \left.\mathscr{V}^{\mathrm{T}}-\mathscr{P}\left(\mathscr{U} * \mathscr{V}^{\mathrm{T}}-\mathscr{P}\right)^{\mathrm{T}}\right\rangle=\min\limits _{\mathscr{V}} tr\left(\mathscr{P}^{\mathrm{T}} * \mathscr{U} *\right.\\ \left.\mathscr{V}^{\mathrm{T}}\right)_{(:, :, 1)}=\min\limits _{\mathscr{V}}\left\langle\mathscr{P}^{\mathrm{T}} * \mathscr{U}, \mathscr{V}\right\rangle $

(13)

由定理1可知

$ \left\{\begin{array}{l} {[\mathscr{B}, \sim, \mathscr{C}]=\mathrm{t}-\mathrm{svd}\left(\mathscr{P}^{\mathrm{T}} * \mathscr{U}\right)} \\ \mathscr{V}^*=\mathscr{B} * \mathscr{C}^{\mathrm{T}} \end{array}\right. $

(14)

$ℯ $子问题  从式(9)中找出所有包含$ℯ $的项，得到如下问题

$ ℯ^*=\min\limits _ {ℯ}\|ℯ\|_1+\frac{\mu}{2}\left\|\mathscr{X}-\mathscr{L}-ℯ+\frac{y_1}{\mu}\right\|_F^2 $

(15)

这个子问题可以通过软阈值收缩算子^[14]来得到闭式解

$ ℯ^*=ℯ_{\frac{1}{\mu}}\left(\mathscr{X}-\mathscr{L}+\frac{ℯ_1}{\mu}\right) $

(16)

拉格朗日乘子$\mathscr{Y}_1 $, $\mathscr{Y}_2 $通过如下公式来更新

$ \left\{\begin{array}{l} \mathscr{Y}_1=\mathscr{Y}_1+\mu(\mathscr{X}-\mathscr{L}-ℯ) \\ \mathscr{y}_2=\mathscr{Y}_2+\mu\left(\mathscr{L}-\mathscr{U} \mathscr{V}^{\mathrm{T}}\right) \end{array}\right. $

(17)

综上所述，求解E-TRPCA模型(8)的ADMM算法(算法1)详细过程如下。

输入: $\mathscr{X} \in \mathbb{R}^{h \times w \times s} $，r, λ, μ=10^-2, μ_max=10⁶，p=1.3，$ℯ $=10⁷

输出: $\mathscr{L}, ℯ, \mathscr{U}, \mathscr{V} $

初始化参数: 初始化$\mathscr{L}, ℯ, \mathscr{Y}_1, \mathscr{Y}_2=0 \in \mathbb{R}^{h \times w \times s} $，$\mathscr{U} \in \mathbb{R}^{h \times w \times s} $, $\mathscr{V} \in \mathbb{R}^{w \times r \times s}$

1: while 不满足收敛条件

2:       通过式(10)更新$\mathscr{L} $

3:       通过式(12)更新$\mathscr{U} $

4:       通过式(14)更新$\mathscr{V} $

5:       通过式(16)更新$ℯ $

6:       检查收敛条件

$ \frac{\|\mathscr{X}-\mathscr{L}-ℯ\|_F^2}{\|\mathscr{X}\|_F^2} \leqslant ℯ, \left\|\mathscr{L}-\mathscr{U} * \mathscr{V}^{\mathrm{T}}\right\|_F^2 \leqslant ℯ $

7:       通过式(17)更新$ \mathscr{Y}_1$，$ \mathscr{Y}_2$

8: end while

2.3 复杂度分析

算法1以三阶张量$\mathscr{X} \in \mathbb{R}^{h \times w \times s} $作为输入，主要的计算成本是在更新$ \mathscr{U}$, $ \mathscr{V}$时产生的。更新$ \mathscr{U}$需要计算一个大小为h×w×s张量的t-SVD，更新$ \mathscr{V}$时需要计算一个大小为w×r×s张量的t-SVD, 那么算法1的时间复杂度为O(max(h, w)rslogs+(max(h, w)r²s))。

3 实验验证

以图像恢复作为仿真实验、背景建模作为真实实验来测试所提方法，并与RPCA方法^[1]、基于Tucker分解的SNN方法^[4]、基于t-SVD的TNN方法^[2]、基于张量火车分解的TTNN方法^[6]和基于张量环分解的RTRC方法^[7]这5种方法进行对比。其中，RTRC方法被用来解决张量补全问题，在本文中用于张量鲁棒主成分分析，记为TRNN(tensor ring nuclear norm)。图像恢复实验中的图片和背景建模中的视频分别用三阶张量和四阶张量存储，它们的值均被缩放到[0, 1]。

3.1 图像恢复

使用伯克利分割数据集^[15]中的彩色图像进行测试。图片的大小为321×481×3或481×321×3。RPCA、TNN、TRNN和本文方法可以直接处理三阶张量，TTNN方法在数据输入模型之前采用ketaugmentation (KA)技术作了数据增强处理，因此需要把图片大小调整为320×480×3，再利用KA方法将图片尺寸转化为[4×4×4×5×4×4×5×6×3]。

噪声模拟本文主要去除图像中的随机噪声，随机噪声比例p分别设为0.1、0.2、0.3，以p=0.1为例，即图像有10%的像素被设为区间[0, 1]之间的一个随机值，被破坏的像素的位置是随机的。

评价指标  为了评价比较方法去除随机噪声的性能，选取峰值信噪比(peak signal-to-noise ratio, PSNR)和结构相似度(structural similarity index, SSIM)作为评价指标^[16]，PSNR值和SSIM值越高，表示恢复结果越好。

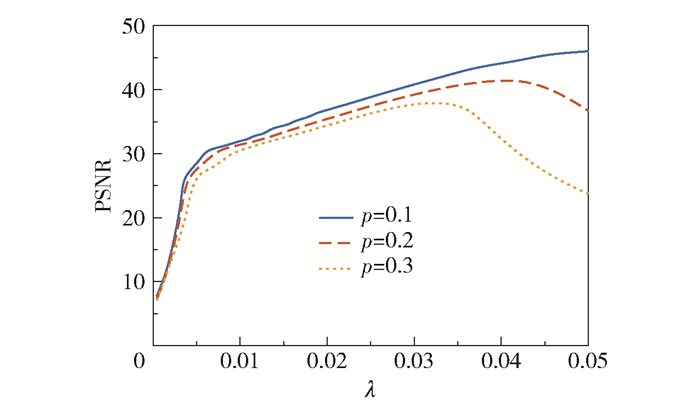
参数分析  本文提出的模型包含正则项参数λ和tubal秩r。正则项参数λ用来控制随机噪声对恢复结果的影响。由图 2知，当p=0.1时，在λ为0.045处PSNR取得最大值，p=0.2时，在λ为0.041处取得最大值，p=0.3时，在λ为0.032处取得最大值。p=0.1时，本文设定$\lambda=\frac{1}{\sqrt{\min (h, w)}} $, p=0.2, 0.3时，本文设定$\lambda=\frac{1}{\sqrt{\min (h, w) s}} $。

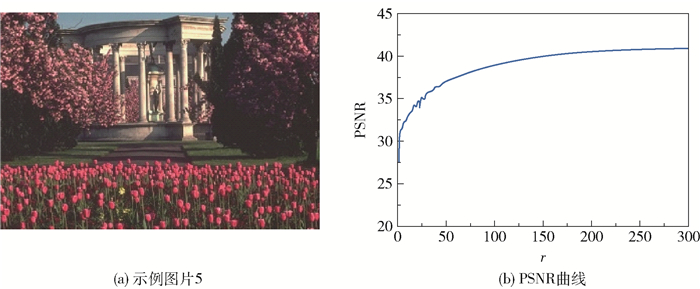
Tubal秩r用于刻画图像的低秩性。本文通过遍历r来分析tubal秩对PSNR的影响。由图 3(b)可知，随着r的增大，图像的恢复效果也越来越好。为了在效率和性能之间取得一个平衡，将r设为$\frac{\min (h, w)}{2} $。

1) 视觉效果比较

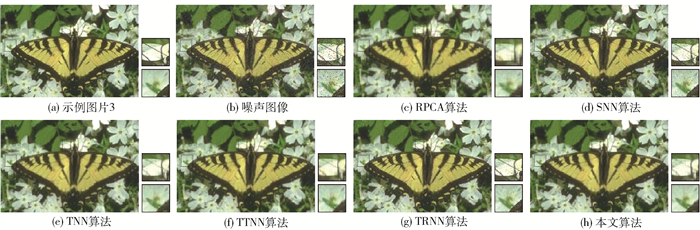
为了直观地对比图像的恢复结果，从伯克利分割数据集中选取了6张示例图片进行可视化展示。从图 4~9中可以看出，RPCA、SNN、TTNN和TRNN算法虽然能够去除图片中的随机噪声和椒盐噪声，但这4种方法不能很好地保留图像中的细节。图 4(h)~9(h)展示了本文所提模型的恢复结果，可以看到添加的噪声被去除，并且图像中的纹理和边缘也得到了很好的保留。这说明本文提出的E-TNN正则项要比t-SVD张量框架下的张量核范数更有效。

2) 定量结果比较

表 1~3分别是6张示例图片在不同随机噪声比例p=0.1、0.2、0.3下的PSNR值和SSIM值。可以看出，本文所提模型的PSNR评价指标在所有的噪声比例中都取得了最好的结果，而且在SSIM评价指标上也基本上取得了最优或次优的结果。

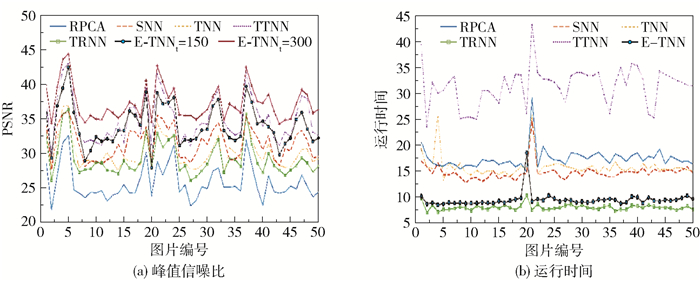
图 10给出了在p=0.1时伯克利分割数据集50张图片的PSNR值和运行时间的比较。可以看出，与其他几种算法相比，本文所提方法取得的PSNR值最高, 并且运行所需时间也仅次于TRNN方法，远低于其他方法。

此外，由表 1~3可知，在示例图片1和示例图片5中，所有方法都没有取得比较好的恢复效果，而示例图片4和示例图片6的恢复效果较好。

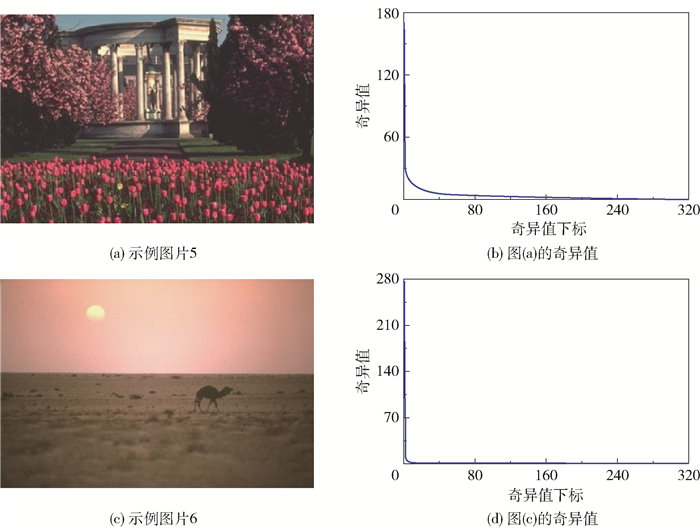
RPCA、SNN、TNN、TTNN、TRNN等方法都假设数据具有低秩结构，对低秩性有强依赖性。我们发现，对于结构比较复杂、纹理较为丰富的示例图片5(图 11(a))，其张量奇异值并没有迅速接近于0(图 11(b))，这表明其tubal秩相对较大，上述方法难以取得好的恢复效果。而在背景空旷的示例图片6(图 11(c))中, 其奇异值则迅速接近于0(图 11(d))，表明tubal秩较小，上述方法可以取得较好的恢复效果。对此，本文新增了一个参数r用于控制tubal秩对数据恢复效果的影响，E-TRPCA模型中的λ参数可以协调核范数正则项和l₁正则项，参数r则可以进一步控制核范数正则项。由图 3可知，当随机噪声比例p=0.1时，在不改变其他参数的情况下，r从0增加300，PSNR也从25增加到42，这为处理不同场景的图像提供了一个优化手段。

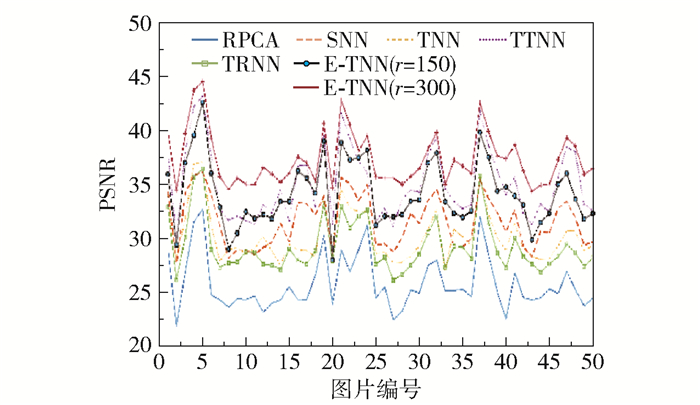
为了更好地评估本文模型的泛化性，图 12给出了r=150和r=300两种情况下本文方法与其他5种方法的PSNR值比较。从图中可以看出，当r取150和300时，本文所提方法取得的PSNR值都要高于RPCA、SNN、TNN、TTNN和TRNN方法，而且r=300时所得的结果要好于r=150时的结果。这说明在数据是否具有低秩性的先验信息未知的情况下，本文所提方法具有较好的泛化性。

3.2 背景建模

视频的前景和背景分离任务一直以来都是研究的热点。视频由连续的帧图像序列组成，其中结构稳定、变动很小的场景内容是视频的背景。由于背景之间的相关性，可以将其视作一个低秩分量，而在视频中所占像素较小且变动显著的物体，如汽车或行人，即为视频的前景，可以视为稀疏分量。本文选取了driverway(117帧)^[17]和shop(100帧)^[18]两个视频。在RPCA算法中，将视频张量h×w×3×f展开为矩阵hw×3f; 在SNN、TNN、TRNN算法中，将视频张量的大小转化为hw×3×f; 在本文所提方法中，将视频张量转化为hw×f×3，f表示视频的帧数。

表 4为RPCA、SNN、TNN、TRNN和本文方法运行时间的比较，图 13~16给出了5种方法在两个视频上的结果(TTNN方法难以找到一个合适的KA参数，故不参与比较)。可知5种方法都可以将运动的行人从背景中提取出来，但本文方法的用时最短。

3.3 去除高斯噪声

本文在原有模型的基础上新增了一个正则项$ \|\mathscr{N}\|$₂₁来刻画高斯噪声。通过最小化核范数、l₁范数和l₂₁的组合，分离出被混合噪声破坏的干净数据。

l₂₁范数定义如下。

$\|\boldsymbol{A}\|_{21}=\sum\limits_k^{n_3} \sum\limits_j^{n_2} \sqrt{\sum\limits_i^{n_1}\left|a_{i j k}\right|^2} $，这里A =(a_ijk)_n1×n2×n3。

此时，模型(8)可以改写为

$ \begin{array}{l} \min\limits _{\mathscr{U}, \mathscr{V}, \mathscr{X}, ℯ}\|\mathscr{U}\|_*+\lambda\|ℯ\|_1+\beta\|\mathscr{N}\|_{21} \\ \text { s. t. } \mathscr{X}=\mathscr{L}+ℯ+\mathscr{N} \\ \mathscr{L}=\mathscr{U} * \mathscr{V}^{\mathrm{T}}, \mathscr{V}^{\mathrm{T}} * \mathscr{V}=\mathscr{T} \\ \mathscr{U} \in \mathbb{R}^{h \times r \times s}, \mathscr{V} \in \mathbb{R}^{w \times r \times s} \end{array} $

(18)

模型(18)的增广拉格朗日函数为

$ \begin{array}{l} \;\;\;\;\;\;\mathscr{L}\left(\mathscr{U}, \mathscr{V}, \mathscr{L}, ℯ, \mathscr{Y}_1, \mathscr{Y}_2\right)=\|\mathscr{U}\| *+\lambda\|ℯ\|_1+ \\ \beta\|\mathscr{N}\|_{21}+\frac{\mu}{2}\left\|\mathscr{X}-\mathscr{L}-ℯ-\mathscr{N}+\frac{\mathscr{Y}_1}{\mu}\right\|_F^2+\frac{\mu}{2} \| \mathscr{L}- \\ \mathscr{U} * \mathscr{V}^{\mathrm{T}}+\frac{\mathscr{Y}_2}{\mu} \|_F^2 \end{array} $

(19)

式(19)依然采取ADMM算法求解，与算法1相比，求解模型(8)多出一个子问题，即求解‖ $\mathscr{N} $ ‖₂₁子问题, 该子问题可以写成如下格式。

$ \mathscr{N}^*=\min\limits _{\mathscr{N}}\|\mathscr{N}\|_{21}+\frac{\mu}{2}\left\|\mathscr{N}-\left(\mathscr{X}-\mathscr{L}-ℯ+\frac{\mathscr{Y}_1}{\mu}\right)\right\|_F^2 $

(20)

令$\mathscr{C}=\mathscr{X}-\mathscr{L}-ℯ+\frac{\mathscr{Y}_1}{\mu} $，则有

$ \left\{ {\begin{array}{*{20}{l}} {\frac{{{{\left\| {{{\cal \mathscr{C}}_{(:, j, k)}}} \right\|}_2} - \frac{\beta }{\mu }}}{{{{\left\| {{{\cal \mathscr{C}}_{(:, j, k)}}} \right\|}_2}}}{{\cal \mathscr{C}}_{(:, j, k)}}, }&{\frac{\beta }{\mu } < {{\left\| {{{\cal \mathscr{C}}_{(:, j, k)}}} \right\|}_2}}\\ {0, }&{其他} \end{array}} \right. $

(21)

本文将模型(18)应用于图片恢复。图 17给出了本文方法去除混合噪声的可视化结果。图 17(b)是添加了均值为0、方差为0.05的高斯噪声和随机噪声比例p=0.2的示例图片2。从图 17(c)~(e)可以看出，图像的低秩部分、随机噪声部分和高斯噪声部分都被很好地分离出来。

4 结束语

本文引入了增强的TNN正则项(E-TNN)，提出一种增强的TRPCA模型。与TNN相比，E-TNN能够在张量数据的子空间投影上计算低秩性，可刻画张量数据中各成分的相关性和差异，从而更真实地反映张量数据的潜在低秩结构。与张量鲁棒主成分分析方法相比，本文所提算法可以有效地恢复出被噪声破坏的图像, 并缩短运行所需时间。下一步可以基于不同维度的张量数据自动调整字典张量的维度。此外，基于广义线性变换的t积张量框架在张量低秩恢复问题中的应用将是未来的研究方向之一。