引言

随着现代工业的快速发展，工业生产的安全性与可靠性变得尤为重要。近年来，以故障检测为主导的过程监测技术与方法成为学术界和工业界的研究热点。目前的故障检测方法主要分为以下3类：基于数学模型的故障检测方法，基于定性知识的故障检测方法和基于数据驱动的故障检测方法。其中基于数据驱动的故障检测方法与基于数学模型的故障检测方法相比，不需要精准的系统模型，同时随着传感器技术的飞速发展，海量数据的获得也变得更加容易，因此基于数据驱动的故障检测方法扮演着愈加重要的角色^[1]。主成分分析(principal component analysis, PCA)作为一种基于数据驱动的故障检测算法，由于其简便的算法流程及对高维数据的高效处理能力而受到广泛的关注与研究^[2]，相关的拓展算法包括概率PCA (probability PCA)^[3]、核PCA (kernel PCA)^[4]、动态PCA (dynamic PCA)^[5]等。

尽管对于PCA算法的各种改进有很多，但针对其中主元的选取及后续的处理问题仍然需要更加深入的研究。传统的主元选取方法有累计方差贡献法(cumulative percent variance, CPV)^[6], 重构误差方差法(variance of the reconstruction error, VRE)^[7]和平均特征值法(average eigenvalue, AE)^[8]等。这些方法都是认为较大方差所对应的主元包含更多的信息，而较小的方差所对应的主元则常常被忽视。Jolliffe^[9]提出具有较小方差的主元和具有较大方差的主元同等重要，Togkalidou等^[10]指出具有较大方差的主元不一定具有最多的信息量。因此，仅凭方差的贡献度大小来确定主元的方法过于主观机械，有可能造成有用信息的丢失。同时，传统主元选取方法根据正常工况数据进行线下建模，没有考虑故障样本对建模的影响。上述问题都会导致故障检测性能的大幅下降。为此，陶阳等^[11]将RelifeF算法与PCA算法相结合，从故障特征角度出发，避免了主元选取时的主观性。Jiang等^[12]统计单个主元T²统计量的变化率，通过选取与监测敏感主元进行故障检测，但在选取主元阶段仍采用传统的CPV方法，导致有用信息丢失，从而影响检测效果。仓文涛等^[13]通过构造累计T²统计量的变化率来体现主元的变异程度，但是传统T²统计量要求数据变量服从正态分布，而实际工业流程中采集到的数据显然很难满足此限制条件。同时从几何角度来看，T²统计量实质上是一个椭圆形控制边界，误差较大。Song等^[14]提出全变量表达(full variable expression, FVE)的主元选取方法，选取对各个变量解释性最大的主元作为关键主元，保留了所有变量信息，取得了良好的故障检测效果。但该方法仍然是依据T²统计量的形式构造相应的统计量进行检测；其次，上述所有方法都是同等看待被选主元。实际上，故障发生时只有某些主元含有与故障相关的重要信息，这些主元在后续处理中需要加以突出。海林格距离(Hellinger distance, HD)是信息论中的一个概念，在统计学和概率学中用来衡量两个概率密度分布间的差异。在故障检测领域，Jiang等^[15]将HD用于变量块的划分，将拥有相似概率密度分布的变量归结到同一个分块进行故障检测；Harrou等^[16]将HD作为统计量，用来监测非线性投影产生残差的概率密度分布；Chen等^[17]将HD用于高速列车的故障检测，相关实验表明HD作为散度的一种，有着比Kullback-Leibler(K- L)散度更好的检测效果。

局部离群因子(local outlier factor, LOF) 由Breunig等^[18]提出，用于搜寻数据中的离群点。该方法利用样本点的局部离群因子值的大小来衡量其离群程度，对于样本数据的分布没有要求。故障样本相对于正常样本即可视为离群点，因此该算法已开始被研究者运用到故障检测领域。Lee等^[19]将LOF算法与独立元分析法相结合，用于解决数据高斯与非高斯混合分布情况下的故障检测问题，突破了传统独立元分析法对于非高斯分布数据的限制。Deng等^[20]利用双加权策略改进核主元分析法，并将其与LOF算法相结合，兼顾了工业过程的非线性特点以及数据的非高斯分布。冯立伟等^[21]提出基于时空近邻标准化(time-space nearest neighborhood standardization, TSNS)- LOF的故障检测方法，提高了对于多模态过程的故障检测能力。由以上文献可以看出，将LOF算法融入到故障检测方法中并且构建相应的统计量，有利于提高故障检测能力。

本文在FVE方法基础上，利用海林格距离变化率对故障的敏感性提出一种基于全变量表达和海林格距离的故障检测算法(Hellinger distance weighted full variable expression-Mahalanobis distance LOF, HDWFV E- MDLOF)。首先利用FVE的主元选取方法有效地保留了全部变量信息，之后提出基于海林格距离变化率的指标，突出故障相关主元；同时，考虑到数据变量的无特定分布以及尺度问题，将加权后的关键主元作为改进LOF算法的输入，构造相应统计量进行故障检测。数值仿真实例和带钢热连轧实际生产数据验证了所提方法的有效性与优越性。

1 PCA算法及海林格距离 1.1 PCA算法

PCA是一种用于多变量统计过程监控的基本方法，其具体实施步骤如下。给定一个原始数据矩阵X ∈ R^n×m, 其中n为样本数，m为变量数(传感器个数)，其协方差矩阵为

$ \mathit{\boldsymbol{S}} = \frac{1}{{n - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} $

(1)

接下来对协方差矩阵进行奇异值分解(SVD)

$ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{P \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{P}}^{\rm{T}}} $

(2)

其中，

$ \mathit{\boldsymbol{P}} = [{\mathit{\boldsymbol{P}}_{{\rm{pc}}}}{\mathit{\boldsymbol{P}}_{{\rm{res}}}}], \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{{\rm{pc}}}}}&0\\ 0&{{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{{\rm{res}}}}} \end{array}} \right] $

(3)

式中，Λ_pc=diag(λ₁, λ₂，…, λ_l)，Λ_res=diag(λ_l+1, λ_l+2，…, λ_m)，P为负载矩阵，Λ为特征值矩阵；l作为主元个数将负载矩阵划分成两部分，即主元空间的P_pc和残差空间的P_res。l由累计方差贡献率(CPV)确定

$ \frac{{\sum\limits_{i = 1}^l {{\lambda _i}} }}{{\sum\limits_{i = 1}^m {{\lambda _i}} }} \times 100\% \ge 85\% $

(4)

根据以上描述，样本X ∈ R ^n×m可以被分解为

$ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{\hat X}} + \mathit{\boldsymbol{\tilde X}} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{P}}_{{\rm{pc}}}} + \mathit{\boldsymbol{\tilde X}} $

(5)

式中，$ \mathit{\boldsymbol{\hat X}} \in {\mathit{\boldsymbol{R}}^{n \times m}}$为主成分矩阵，$ \mathit{\boldsymbol{\tilde X}} \in {\mathit{\boldsymbol{R}}^{n \times m}}$为残差矩阵，T ∈ R^n×l为得分矩阵。

在PCA分解后的两个空间里分别建立T²统计量与平方预测误差(squared prediction error, SPE)统计量

$ {T^2} = {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{{\rm{pc}}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}\mathit{\boldsymbol{P}}_{{\rm{pc}}}^{\rm{T}}\mathit{\boldsymbol{X}} $

(6)

$ {E_{{\rm{SPE}}}} = \mathit{\boldsymbol{X}}(\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}_{{\rm{pc}}}}\mathit{\boldsymbol{P}}_{{\rm{pc}}}^{\rm{T}}){\mathit{\boldsymbol{X}}^{\rm{T}}} $

(7)

T²统计量反映的是主元空间的变化，而SPE统计量反映的是残差空间的变化。关于T²和SPE这两个统计量的具体描述以及相应控制限的设定可以参考文献[22]，两个统计量中只要有任意一个超过其对应控制限，即可认定有故障发生。

1.2 海林格距离

HD作为一种度量两个概率密度分布差异的工具，已得到广泛应用^[23-25]。假设有两个连续的概率密度函数f(x)和g(x)，那么f(x)和g(x)之间的海林格距离可以由式(8)描述。

$ {D_{{\rm{HD}}}}\left( {f, g} \right) = \sqrt {\frac{1}{2}\int {{{\left( {\sqrt {f\left( x \right)} - \sqrt {g\left( x \right)} } \right)}^2}{\rm{d}}x} } $

(8)

f(x)和g(x)的差异越大，HD的数值就越大。因此HD能够用来衡量正常指标与异常指标之间的差异。同时，海林格距离是一个对称有界的距离，即0≤D_HD(f, g)=D_HD(g, f)≤1，根据勒贝格测度^[26]可以得到式(8)的平方变形形式

$ D_{{\rm{HD}}}^{^2}\left( {f, g} \right) = 1 - \int {\sqrt {f\left( x \right)g\left( x \right)} {\rm{d}}x} $

(9)

2 基于马氏距离的局部离群因子

对于任意样本x_i(i=1, 2, …, n)，在样本数据集X中以欧式距离为度量找寻x_i的k个近邻点组成局部近邻集N(x_i)={x_i¹, …x_i^f, …x_i^k}，f=1, 2, …, k，并通过式(10)计算样本x_i和它的局部近邻集成员x_i^f的马氏距离

$ \begin{array}{l} \;\;\;\;\;\;\;{d_{\rm{m}}}({\mathit{\boldsymbol{x}}_i}, x_{_i}^{^f}) = \\ \sqrt {\{ {\mathit{\boldsymbol{x}}_i} - {\bf{mean}}[N(x_{_i}^{^f})]\} \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{^{ - 1}}{{\{ {\mathit{\boldsymbol{x}}_i} - {\bf{mean}}[N(x_{_i}^{^f})]\} }^{\rm{T}}}} \end{array} $

(10)

式中，Σ为x_i^f的局部近邻集N(x_i^f)的协方差矩阵，mean [N(x_i^f)]为其均值向量。式(10)中利用mean [N(x_i^f)]替代x_i^f是为了在正常工况下减少关键主元可能受到的污染的影响^[27]。接着对每个样本的近邻按照式(10)进行排序并得到每个样本的领域半径k_distance_m(x_i)。

$ \begin{array}{l} {d_{\rm{m}}}({\mathit{\boldsymbol{x}}_i}, x_{_i}^1) \le \ldots \le {d_{\rm{m}}}({\mathit{\boldsymbol{x}}_i}, x_{_i}^{^f}) \ldots \le {d_{\rm{m}}}({\mathit{\boldsymbol{x}}_i}, x_{_i}^k)\\ k\_{\rm{distanc}}{{\rm{e}}_{\rm{m}}}({\mathit{\boldsymbol{x}}_i}) = {d_{\rm{m}}}({\mathit{\boldsymbol{x}}_i}, x_{_i}^k) \end{array} $

(11)

样本x_i与其近邻点x_i^f之间的可达距离表示为

$ \begin{array}{l} \;\;\;\;\;\;\;{\rm{reach}}\_d({\mathit{\boldsymbol{x}}_i}, x_{_i}^{^f}) = {\rm{max}}\{ k\_{\rm{distanc}}{{\rm{e}}_{\rm{m}}}({\mathit{\boldsymbol{x}}_i}), {d_{\rm{m}}}({\mathit{\boldsymbol{x}}_i}, \\ x_{_i}^{^f})\} \end{array} $

(12)

同时，定义样本x_i的局部可达密度为

$ {D_{{\rm{Ird}}}}({\mathit{\boldsymbol{x}}_i}) = \frac{k}{{\sum\limits_{f = 1}^k {{\rm{reach}}\_d({\mathit{\boldsymbol{x}}_i}, x_{_i}^{^f})} }} $

(13)

样本x_i的局部离群因子表示为x_i所有近邻的平均局部可达密度与样本点x_i的局部可达密度的比值

$ {R_{{\rm{LOF}}}}({\mathit{\boldsymbol{x}}_i}) = \frac{1}{k}\sum\limits_{f = 1}^k {\frac{{{D_{{\rm{Ird}}}}(x_{_i}^{^f})}}{{{D_{{\rm{Ird}}}}({\mathit{\boldsymbol{x}}_i})}}} $

(14)

3 基于HDWFV E- MDLOF的故障检测方法 3.1 HDWFV E- MDLOF算法

X ∈ R^n×m经过PCA分解后得到得分矩阵T =[t₁, t₂, …, t_m]∈ R^n×m，传统PCA算法根据正常工况下的样本建立相应的模型，如式(15)所示，主元可由所有变量线性表示

$ {\mathit{\boldsymbol{t}}_j} = {\mathit{p}_{j1}}{\mathit{\boldsymbol{x}}_1} + {p_{j2}}{\mathit{\boldsymbol{x}}_2} + \ldots + {p_{jm}}{\mathit{\boldsymbol{x}}_m} $

(15)

由式(15)可知，负载系数p_ji反映了主元t_j与变量x_i的相关性，因此可以定义相关性指标p_ji²，该指标值越大，说明t_j与x_i的相关性越大。若p_ji²在[p_1i², p_2i², …, p_mi²]中最大，那么主元t_j就被选为关键主元。对于每一个变量，都可以通过上述方法判断获取其对应的关键主元。统计量T²的表达式为

$ {T^2} = {\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{x}} $

(16)

式中，P =[p₁, p ₂, …, p_f]∈ R^m×f为所选关键主元对应的负载向量构成的负载矩阵，Λ =diag[λ₁, λ₂, …, λ_f]∈ R^f×f为关键主元对应的特征值构成的对角矩阵，f为关键主元的个数。相应的控制限参照PCA算法用于故障检测时T²的控制限

$ T_\alpha ^2 = \frac{{f({n^2} - 1)}}{{n\left( {n - f} \right)}}{F_{f, n - f;\alpha }} $

(17)

式中, n为样本个数，F_{f, n-f; α}为置信水平1-α下、自由度f和n-f的F分布临界值。关键主元的具体描述可以参考文献[14]。

一般情况下，当故障发生时，不同得分向量与故障之间的相关性是存在差异的。得分向量较正常工况变化幅度越大，说明其包含越多的信息量^[12]，与故障的发生也越紧密相关。因此，须根据得分向量与故障的相关性给予其不同的权重值。与故障相关性越大的得分向量，对后续故障检测的贡献度也越大，需赋予较大的权重。本文利用基于海林格距离的得分向量变化率对权重进行定义，并且给出了该指标对于故障敏感性的证明。从故障对得分向量产生的影响角度出发，文献[28]对加性故障和乘性故障有如下定义：加性故障指故障的发生只影响得分向量的均值，乘性故障指故障的发生只影响得分向量的方差。由文献[28]可知，传统T²统计量对于乘性故障的检测效果较差，这是由于T²统计量本身的定义是从加性故障的角度出发的。接下来，给出基于海林格距离变化率的统计量。

假设正常工况下的得分向量为t_j, j=1, 2, …, m，故障情况下的得分向量为$ {{\mathit{\boldsymbol{\tilde t}}}_j}$, j=1, 2, …, m，则基于海林格距离的统计量为

$ hd_j^{^2} = 1 - \int {\sqrt {f({\mathit{\boldsymbol{t}}_j})f({{\mathit{\boldsymbol{\tilde t}}}_j})} {\rm{d}}t} $

(18)

式中，f(t_j)和$ f({{\mathit{\boldsymbol{\tilde t}}}_j})$为对应的概率密度函数，可以通过核密度估计获得，核函数采用最常用的高斯核函数形式

$ \begin{array}{l} f\left( t \right) = \frac{1}{{nh\sqrt {2{\rm{ \mathit{ π} }}} }}\sum\limits_{i = 1}^n {{\rm{exp}} - \frac{{{{({\mathit{\boldsymbol{t}}_j} - {t_{ij}})}^2}}}{{2{h^2}}}} \\ {\rm{ }}f\left( {\tilde t} \right) = \frac{1}{{nh\sqrt {2{\rm{ \mathit{ π} }}} }}\sum\limits_{i = 1}^n {{\rm{exp}} - \frac{{{{({{\mathit{\boldsymbol{\tilde t}}}_j} - {{\tilde t}_{ij}})}^2}}}{{2{h^2}}}} \end{array} $

(19)

式中，n为样本数目，h为平滑参数，t_ij为得分向量t_j的第i个元素，$ {{{\tilde t}_{ij}}}$为得分向量$ {{{\mathit{\boldsymbol{\tilde t}}}_j}}$的第i个元素。

若$ f({\mathit{\boldsymbol{t}}_j}) \sim ({\mu _j}, {\lambda _j}), f({{\mathit{\boldsymbol{\tilde t}}}_j}) \sim ({{\tilde \mu }_j}, {{\tilde \lambda }_j}), $那么由式(18)可得

$ hd_j^{^2} = 1 - \left( {\frac{{2\sqrt {{\lambda _j}{{\tilde \lambda }_j}} }}{{{\lambda _j} + {{\tilde \lambda }_j}}}} \right){\rm{exp}}\left( { - \frac{{{{({{\tilde \mu }_j} - {\mu _j})}^2}}}{{4({\lambda _j} + {{\tilde \lambda }_j})}}} \right) $

(20)

文献[17]证明了当故障引起得分向量的均值和方差发生变化后，hd_j²与均值和方差的变化量正相关，即hd_j²对故障的发生十分敏感。参考文献[29]中的表示形式，海林格距离变化率可以表示成单个得分向量与所有得分向量平均值的海林格距离二次型与该统计量的平均值之比

$ Rhd_j^{^2} = hd_j^{^2}/\overline {hd_j^{^2}} $

(21)

式中，hd_j²为第j个得分向量的海林格距离的二次型统计量，$ \overline {hd_j^{^2}} $为所有得分向量海林格距离的二次型统计量的平均值，其中j=1, 2, …, m。多变量系统中的故障往往是由PCA模型中个别得分向量的异常引起的，因此，对于一个数据集中的海林格距离平均值，其受异常得分向量的影响很小，故可以把$ \overline {hd_j^{^2}} $视为常数c。为了体现所提基于海林格距离变化率的统计量对于故障发生的敏感性以及对于噪声的鲁棒性，进行如下证明。

假设故障发生时导致得分向量均值的变化为Δμ_j，方差变化为Δλ_j，当传感器发生加性故障，即故障的发生只改变了得分向量的均值时，有

$ \begin{array}{l} \;\;\;\;\;\;\;Rhd_j^{^2} = \frac{{hd_j^{^2}}}{{\overline {hd_j^{^2}} }} = \frac{1}{c} \times \left( {1 - {{\left( {\frac{{2\sqrt {{\lambda _j}{{\tilde \lambda }_j}} }}{{{\lambda _j} + {{\tilde \lambda }_j}}}} \right)}^{\frac{1}{2}}} \cdot } \right.\\ \left. {{\rm{exp}}\left( { - \frac{{{{({{\tilde \mu }_j} - {\mu _j})}^2}}}{{4({\lambda _j} + {{\tilde \lambda }_j})}}} \right)} \right) = \frac{1}{c} \times \left( {1 - {\rm{exp}}\left( { - \frac{{\Delta \mu _{_j}^{^2}}}{{8{\lambda _j}}}} \right)} \right) \end{array} $

(22)

将式(22)中的Rhd_j²对Δμ_j求导得

$ \frac{{\partial Rhd_j^{^2}}}{{\partial \Delta {\mu _j}}} = \frac{1}{{4c{\lambda _j}}} \times {e^{\frac{{\Delta \mu _{_j}^{^2}}}{{8\lambda }}}} \times \Delta {\mu _j} $

(23)

式中，当Δμ_j>0时，$ \frac{{\partial Rhd_j^{^2}}}{{\partial \Delta {\mu _j}}}$ >0，即统计量Rhd_j²(Δμ_j)单调递增。

当传感器发生乘性故障，即故障的发生只改变得分向量的方差时，有

$ Rhd_j^{^2} = \frac{{hd_j^{^2}}}{{\overline {hd_j^{^2}} }} = \frac{1}{c} \times \left( {1 - {{\left( {\frac{{2\sqrt {{\lambda _j}({\lambda _j} + \Delta {\lambda _j})} }}{{2{\lambda _j} + \Delta {\lambda _j}}}} \right)}^{\frac{1}{2}}}} \right) $

(24)

将式(24)中的Rhd_j²对Δλ_j求导得

$ \begin{array}{l} \;\;\;\;\;\;\;\frac{{\partial Rhd_j^{^2}}}{{\partial \Delta {\lambda _j}}} = - \frac{1}{c} \times \\ \frac{{{\lambda _j}{{(\lambda _j^{^2} + {\lambda _j}\Delta {\lambda _j})}^{ - \frac{1}{2}}}(2{\lambda _j} + \Delta {\lambda _j}) - 2{{(\lambda _j^{^2} + \Delta {\lambda _j}{\lambda _j})}^{\frac{1}{2}}}}}{{{{(2{\lambda _j} + \Delta {\lambda _j})}^2}}} \end{array} $

(25)

式中，当Δλ_j>0时，$ \frac{{\partial Rhd_j^{^2}}}{{\partial \Delta {\lambda _j}}}$ >0，即统计量Rhd_j²(Δλ_j)单调递增。

当传感器上加性故障与乘性故障并存，即故障的发生既改变了得分向量的均值，又改变了得分向量的方差时，有

$ \begin{array}{l} \;\;\;\;\;\;\;Rhd_j^{^2} = \frac{{hd_j^{^2}}}{{\overline {hd_j^{^2}} }} = \frac{1}{c} \times \left( {1 - \left( {\frac{{2\sqrt {{\lambda _j}({\lambda _j} + \Delta {\lambda _j})} }}{{2{\lambda _j} + \Delta {\lambda _j}}}} \right)} \right)\cdot\\ {\rm{exp}}\left( { - \frac{{\Delta \mu _j^2}}{{4(2{\lambda _j} + \Delta {\lambda _j})}}} \right) \end{array} $

(26)

将式(26)分别对Δλ_j和Δμ_j求偏导，由上述两种情况可知，Rhd_j²随着Δλ_j和Δμ_j的增大而增大。综合以上3种情况的证明可知，基于海林格距离的变化率对于故障的发生十分敏感。另一方面，噪声对于系统的影响也需要考虑。

假设λ_j=λ_j^*+ν，其中λ_j^*表示无故障无噪声情况下的第j个方差，ν为噪声，对此有

$ \begin{array}{l} \;\;\;\;\;\;\;Rhd_j^{^2} = \frac{{hd_j^{^2}}}{{\overline {hd_j^{^2}} }} = \frac{1}{c} \times \left( {1 - \left( {\frac{{2\sqrt {(\lambda _j^{^*} + \nu ){{\tilde \lambda }_j}} }}{{\lambda _j^{^*} + \nu + {{\tilde \lambda }_j}}}} \right)} \right)\cdot\\ {\rm{exp}}\left( { - \frac{{{{({{\tilde \mu }_j} - {\mu _j})}^2}}}{{4(\lambda _j^{^*} + \nu + {{\tilde \lambda }_j})}}} \right) \end{array} $

(27)

对式(27)关于ν求偏导可得其sgn函数为

$ \begin{array}{l} \;\;\;\;\;\;\;{\rm{sgn}}\left( {\frac{{\partial Rhd_j^{^2}\left( \nu \right)}}{{\partial \nu }}} \right) = {\rm{sgn}}(\tilde \lambda _j^2 - {(\lambda _j^{^*})^2} + \\ {({{\tilde \mu }_j} - {\mu _j})^2}{\lambda _j}2\lambda _j^{^*}\nu - {\nu ^2}) \end{array} $

(28)

当ν=0时，式(28)的最大值为0，即

$ \left\{ {\begin{array}{*{20}{c}} {\frac{{\partial Rhd_j^{^2}\left( \nu \right)}}{{\partial \nu }}<0, \nu \ne 0}\\ {\frac{{\partial Rhd_j^{^2}\left( \nu \right)}}{{\partial \nu }} = 0, \nu = 0} \end{array}} \right. $

(29)

因此，Rhd_j²随着噪声ν的增大而减小，即Rhd_j²对噪声具有一定的鲁棒性。

综上可知采用Rhd_j²作为统计量对于故障的检测是有效的，该统计量反映了故障工况的偏离程度，Rhd_j²越大，说明第j个主元与该故障发生的相关性越大，因此赋予的权重值也越大。令

$ \alpha \prime = {\rm{exp}}\left( {\frac{{Rhd_j^{^2} - 1}}{\sigma }} \right) $

(30)

式中σ>0是可调参数。定义权重y_j^new如式(31)所示。

$ y_j^{{\rm{new}}} = \left\{ {\begin{array}{*{20}{c}} {1, }&{Rhd_j^{^2} \le \gamma }\\ {\alpha , }&{Rhd_j^{^2} > \gamma } \end{array}} \right. $

(31)

式中，γ为阈值，本文通过3σ法则来确定γ的数值。假设Rhd_j²的数值服从均值为M、标准差为η的高斯分布，那么阈值γ可由式(32)得到。

$ \gamma = M + L\eta $

(32)

式中，L为预警宽度，一般取值为3，即3σ法则。

那么，新的得分矩阵可表示为

$ \begin{array}{l} \;\;\;\;\;\;\;{\mathit{\boldsymbol{T}}_w} = {\mathit{\boldsymbol{T}}_{{\rm{key(new)}}}}\mathit{\boldsymbol{W}}{\rm{ }} = [{\rm{ }}{\mathit{\boldsymbol{t}}_{{\rm{1, new}}}}, {\rm{ }}{\mathit{\boldsymbol{t}}_{{\rm{2, new}}}}, \ldots , {\rm{ }}{\mathit{\boldsymbol{t}}_{f, {\rm{new}}}}]{\rm{ }}\cdot\\ \left[ {\begin{array}{*{20}{c}} {y_1^{{\rm{new}}}}& \ldots &0\\ \vdots & \ddots & \vdots \\ 0& \ldots &{y_f^{{\rm{new}}}} \end{array}} \right] = [y_1^{{\rm{new}}}{\mathit{\boldsymbol{t}}_{{\rm{1, new}}}}, y_2^{{\rm{new}}}{\mathit{\boldsymbol{t}}_{{\rm{2, new}}}}, \ldots , y_f^{{\rm{new}}}{\mathit{\boldsymbol{t}}_{f, {\rm{new}}}}] \end{array} $

(33)

式中，T_key(new)为故障工况下关键主元构成的得分矩阵，W为加权矩阵。

传统PCA在进行故障检测时，会设定如式(6)、(7)所示的统计量进行监测，这类根据数据间距离所设定的统计量要求采样数据满足正态分布，事实上在实际工业生产过程中，大部分采样数据没有特定的分布规律，这就导致了PCA用于故障检测时效果不佳。为此，本文利用基于密度的LOF构造了一个单一统计量，相较于T²和SPE，该统计量集中了故障对过程变量的影响。同时，LOF从密度的角度出发，依靠数据点的离散程度对故障进行检测，对于数据的分布没有特定的要求，避免了传统T²和SPE统计量要求数据服从正态分布的不足。除此之外，基于马氏距离的LOF与原始LOF算法相比，考虑了加权后的关键主元与其邻域子集之间的马氏距离对过程变量的影响，最终形成一种对数据分布具有鲁棒性的统计量。由于LOF统计量的分布情况无法准确获取，因此本文采用核密度估计法确定所构造LOF统计量的控制限。令正常工况下获得的LOF统计量构成集合Ω={R_{LOF, x1}, R_{LOF, x2}, …, R_{LOF, xn}}，对于LOF统计量进行核密度估计，如式(34)所示。

$ \hat f({R_{{\rm{LOF}},x}}) = \frac{1}{{n\theta }}\sum\limits_{i = 1}^n {K\left( {\frac{{{R_{{\rm{LOF}},x}} - {R_{{\rm{LOF}},{x_i}}}}}{\theta }} \right)} $

(34)

式中，K(·)为核函数，θ为核宽，LOF控制限R_LOF，limit在置信水平为α的情况下可由式(35)获得

$ \int_{ - \infty }^{{R_{{\rm{LOF, limit}}}}} {\hat f({R_{{\rm{LOF, }}x}}){\rm{d}}{R_{{\rm{LOF, }}x}} = 1 - \alpha } $

(35)

3.2 故障检测步骤

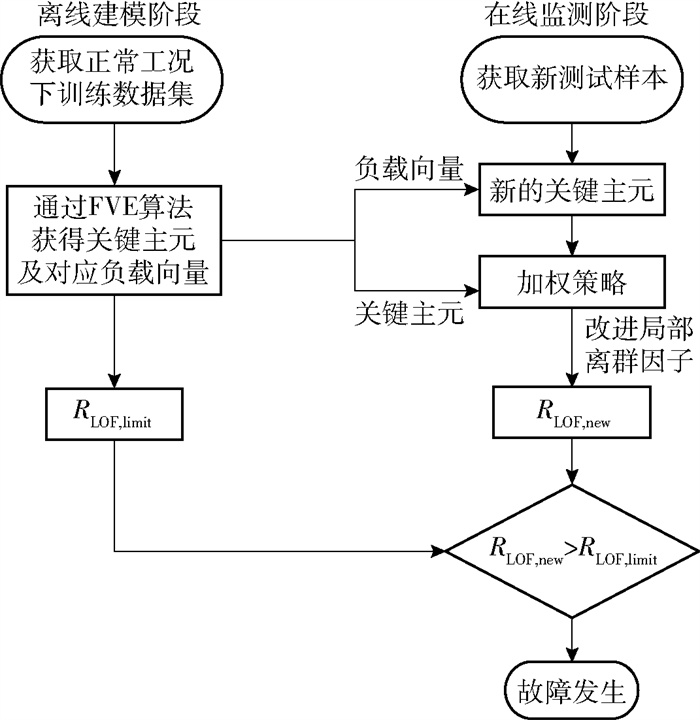
基于HDWFV E- MDLOF的故障检测流程如图 1所示。

离线建模阶段步骤如下。

1) 采集正常工况下的样本数据，标准化得到X ∈ R ^n×m。

2) 利用FVE得到f个关键主元t_j(j=1, 2, …, f)以及对应的负载向量$ {{\mathit{\boldsymbol{\bar p}}}_\mathit{j}}$；由关键主元构成的得分矩阵可以表示为T_key=[t₁, t₂, …, t_f]∈ R^n×f。

3) 将T_key=[t₁, t₂, …, t_f]∈ R^n×f作为改进LOF算法的输入，并利用核密度估计确定其控制限R_LOF，limit。

在线检测阶段步骤如下。

1) 采集异常工况下的样本数据，标准化得到X_new∈ R^n×m。

2) 对于新的数据x_new∈ R^m×1，关键主元由$ {{\bf{t}}_{j,{\rm{new}}}} = {\bf{\bar p}}_j^{\rm{T}}{{\bf{x}}_{{\rm{new}}}}$计算得到。

3) 通过式(20)、(21)计算Rhd_j²统计量并利用3σ法则计算其控制限γ，再根据式(30)~(32)赋予得分向量相应权重，根据式(33)形成新的加权后的得分矩阵T_w。

4) 将$ {\mathit{\boldsymbol{T}}_w} = [{\mathit{\boldsymbol{t}}_{{\rm{1, new}}}}, \mathit{\boldsymbol{t}}{\mathit{\boldsymbol{}}_{2, {\rm{new}}}}, \ldots , {\mathit{\boldsymbol{t}}_{f, {\rm{new}}}}] \in \mathit{\boldsymbol{R}}{^{n \times f}}$作为改进LOF算法的输入，求得统计量R_{LOF, new}，若R_{LOF, new}> R_{LOF, limit}，则说明有故障发生。

4 仿真分析 4.1 数值仿真实例

文献[30]中的数值实例被广泛应用于故障检测的仿真实验中，本文采用此数值实例验证所提方法的有效性。该数值例子表示结构如式(36)所示。

$ \begin{array}{l} \mathit{\boldsymbol{r}}\left( i \right) = \mathit{\boldsymbol{A}} \times \mathit{\boldsymbol{r}}\left( {i - 1} \right) + \mathit{\boldsymbol{B}} \times \mathit{\boldsymbol{u}}\left( {i - 1} \right)\\ \mathit{\boldsymbol{u}}\left( i \right) = \mathit{\boldsymbol{C}} \times \mathit{\boldsymbol{u}}\left( {i - 1} \right) + \mathit{\boldsymbol{D}} \times \mathit{\boldsymbol{h}}\left( {i - 1} \right)\\ \mathit{\boldsymbol{g}}\left( i \right) = \mathit{\boldsymbol{r}}\left( i \right) + \mathit{\boldsymbol{v}}\left( i \right) \end{array} $

(36)

式中，$ \begin{array}{l} \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {0.018}&{ - 0.191}&{0.287}\\ {0.847}&{0.264}&{0.943}\\ { - 0.333}&{0.514}&{ - 0.217} \end{array}} \right]{\rm{,}}\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 1&2\\ 3&{ - 4}\\ { - 2}&1 \end{array}} \right] {\rm{,}} \end{array}$ $ \begin{array}{l} \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {0.811}&{ - 0.226}\\ {0.477}&{0.415} \end{array}} \right],\mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {0.193}&{0.689}\\ { - 0.320}&{ - 0.749} \end{array}} \right]{\rm{,}} \end{array}$ h为一个在区间(-2, 2)内服从均匀分布的随机向量，v为一个服从均值为0、方差为0.1的正态分布的随机噪声向量，i为采样时刻。训练集X由200个正常采样点构成，x(i)=[g^T(i) u^T(i)]，测试集由包含故障的200个采样点构成，相关故障的设定及描述如下。

1) 故障1  变量h₁从第51个样本点开始直到200个样本点结束，增加一个幅值为3的单位阶跃故障。

2) 故障2  变量h₂从第51个样本点开始直到200个样本点结束，增加一个0.06(i-50)的斜坡故障。

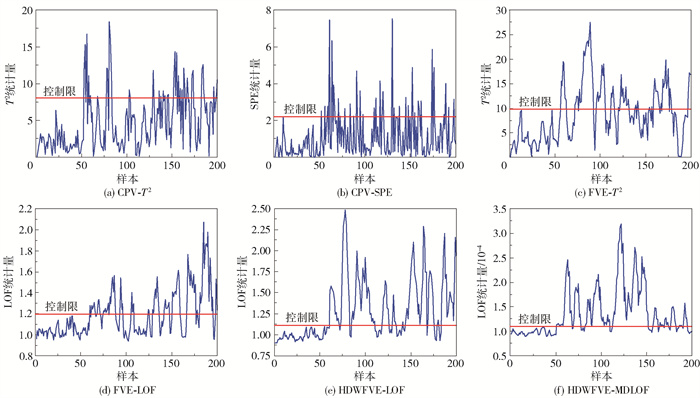
在运用FVE方法进行主元选取时，特征空间包含了几乎所有原始变量的信息，残差空间中几乎不包含有用信息，因此只需构建反映特征空间的T²统计量进行监测。运用本文所提方法与CPV- T²、CPV-SPE、FVE-T²、FVE-LOF以及HDWFVE-LOF进行仿真对比实验。其中CPV的贡献度设定为85%，控制限采用95%的置信度；LOF中的k值设定为15, 核宽设为500m(m为变量个数)。在CPV主元选取方法中，前3个主元的累计方差贡献率超过了85%，因此按照方差从大到小的顺序选取PC₁、PC₂、PC₃为主元，而在FVE的主元选取方法中，各变量对应的关键主元如表 1所示，PC₂、PC₃、PC₄、PC₅被选为主元。表 2为各个方法对于数值实例中故障1和故障2的漏报率与误报率。各个方法对故障1的检测结果如图 2所示。图 2(a)、(b)为传统PCA算法利用CPV主元选取方法所构建的基于T²和SPE统计量的故障检测结果，结合表 2可知，其中T²统计量的漏报率为74%，检测效果不佳，SPE统计量的漏报率达到75%，表明该统计量基本无法检测到故障的发生。图 2(c)为利用FVE主元选取方法进行故障检测的结果，结合表 2可知，T²统计量的漏报率降低为48.7%。图 2(d)为FVE主元选取法利用LOF作为统计量的故障检测结果，由表 2知其漏报率为46%，漏报率的降低是因为该方法从数据密度大小出发来搜寻故障点。图 2(e)给出了HDWFVE-LOF的故障检测结果，得益于对故障相关主元的合理加权，由表 2可知其漏报率为28%，得到大幅降低。图 2(f)为本文所提方法的故障检测结果，可以看出基于马氏距离的LOF算法起到了很好的效果，相比于其他方法，本文所提方法的漏报率最低，为20.8%。

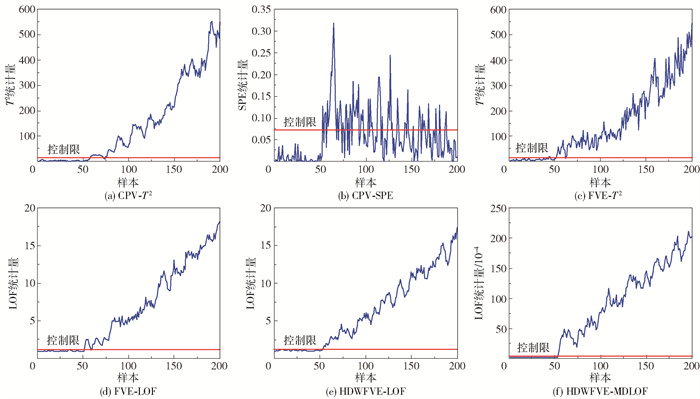
图 3给出了不同方法对故障2的检测结果。结合表 2的结果，总体上，除了传统PCA利用CPV的主元选取法将SPE作为统计量的漏报率较高外，其余方法均能够保持较低的故障漏报率。其中，本文所提方法最早检测到故障的发生，并且在检测到故障发生后依然保持着很好的稳定性，统计量曲线始终位于控制限上方，而其他方法在检测到故障发生后，统计量曲线有回落到控制限的现象(图 3(a)、(b)、(c)、(d))，引起漏报。

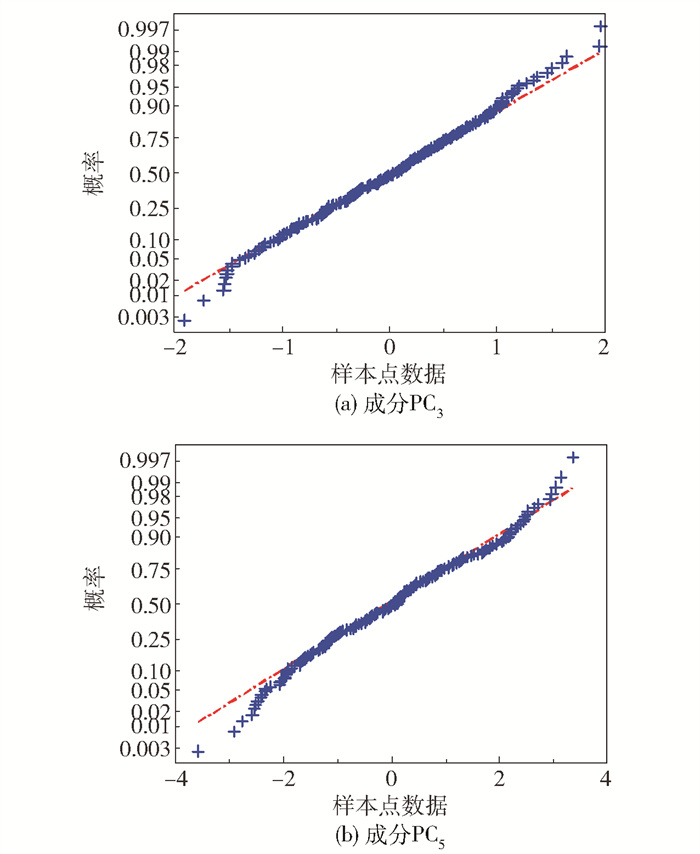
为了进一步体现LOF作为统计量的优越性，图 4(a)、(b)给出了故障2中运用本文方法加权后关键主元PC₃和PC₅的正态概率分布，其中横坐标为主成分样本点数据，纵坐标为先验概率。数据的分布越接近标准正态分布，相应图上散点的分布就越近似直线。由图 4可知，图中条形点的头部和尾部较直线还是有着较大的偏移，意味着这两个加权后的主元并不服从正态分布，这也从另一个角度说明了利用LOF构建统计量的必要性。综上，数值仿真结果体现了本文所提方法的有效性与优越性。

4.2 带钢热连轧过程验证

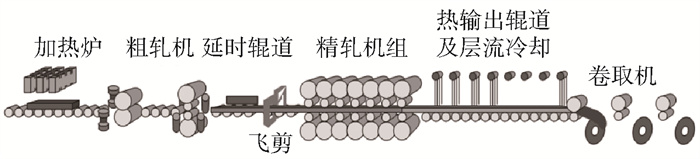
带钢热连轧过程(hot strip mill process, HSMP)是工业生产中的一个重要工序，其生产流程如图 5所示。由于HSMP在运行过程中有高温度、高速度、多阶段的特征，导致其变量具有高耦合的特点。对此，本文将该过程用于故障检测的研究。在带钢热连轧现场(鞍钢集团1 700 mm带钢热连轧生产线)收集能够反映生产过程的数据，相关的20个过程变量的具体描述如表 3所示。

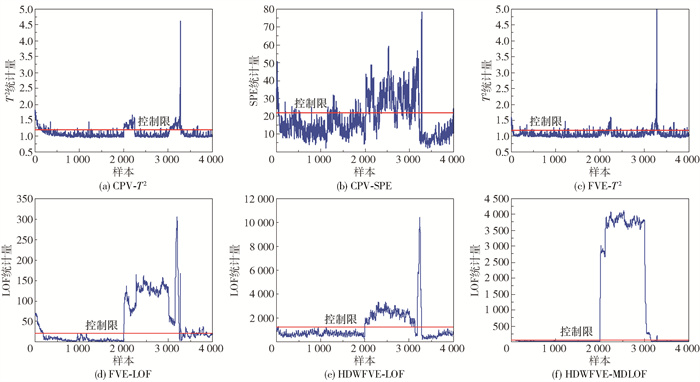
首先选取4 000个正常工况下带钢热连轧过程样本数据进行离线建模，再收集4 000个带有故障的样本数据进行在线检测，其中故障产生时间为样本点2 001到3 000，故障原因为第5机架的弯辊力测量传感器故障。LOF算法中近邻数k设置为150。利用KDE进行控制限计算时，核宽θ设置为500m(m为变量数)。利用FVE得到的关键主元与变量的对应关系如表 4所示。各方法对于该故障的检测结果如图 6所示，具体结果列于表 5。图 6(a)、(b)为PCA利用传统CPV方法对于该故障的检测结果，T²和SPE统计量的漏报率分别为74.2%和90.2%，数值都较高，尤其是SPE统计量，基本无法检测到故障的发生。图 6(c)为FVE方法选取关键主元后构建T²统计量的故障检测结果，关键主元的选取使得故障漏报率大大降低，且故障误报率没有出现较大的增加。对比图 6(d)、(e)、(f)可以得出，本文所提方法在检测出所有故障的同时，还获得了最低的故障误报率。

表 6给出了Relief F- PCA算法^[11]、敏感主成分分析(SPCA)算法^[12]、故障相关- 贝叶斯推断主成分分析(FBPCA)算法^[31]以及敏感主元多块主成分分析(MBSPCA)算法^[32]对于第5机架的弯辊力测量传感器故障的检测漏报率和误报率。其中MBSPCA算法中ω取值0.2，即敏感主元阈值ε_limit为0.003 9，所有方法的置信度均为95%。由表 6的数据对比可发现，本文所提方法的漏报率与误报率均为最低。综上可说明本文所提HDWFV E- MDLOF算法的有效性与优越性。

5 结论

本文提出一种基于HDWFV E- MDLOF的故障检测算法，在PCA框架下的主元选取阶段利用FVE方法获取关键主元，保留了全部变量信息，并利用海林格距离变化率对关键主元中的故障相关主元进行加权突出，有效地降低了故障漏报率；利用改进的LOF构造统计量，突破了传统统计量对于数据分布的限定。数值实例及带钢热连轧实际生产数据结果表明，与Relief F- PCA、SPCA、FBPCA以及MBSPCA等算法相比，本文所提算法的漏报率及误报率均为最低，证明了所提方法的有效性与优越性。