2. 北京东方雨虹防水技术股份有限公司,北京 100123
2. Beijing Oriental Yuhong Waterproof Technology Co. , Ltd. , Beijing 100123, China
沥青是由不同分子量的碳氢化合物及其非金属衍生物组成的黑褐色复杂混合物[1]。在高于一定温度时,其黏度受剪切速率的影响变小,表现为牛顿流体特性[2]。沥青具有防水性能高、抗老化性能好等优点,广泛应用于工业与民用建筑防水领域[3]。沥青通常被加工成薄层防水带状材料,常用的加工方法有冷却辊流延工艺和平板流延工艺。这些流延工艺使用冷却辊或冷却板冷却熔融的沥青,再经过自然冷却与喷淋降温,待沥青冷却至一定温度后覆膜包装,完成沥青防水带材的生产。由于覆膜与包装对温度有一定的要求,沥青在冷却辊覆膜冷却时,大量的高温熔融沥青需要将热量导出,因此流延工艺中沥青的温度控制对于提高产品质量及安全生产具有重要意义。
近年来,众多国内外学者致力于运用计算流体力学(computational fluid dynamics,CFD)方法研究流延过程中流动与传热问题,并考虑多种因素对流延工艺冷却效果的影响。Pagnola等[4]使用Open-FOAM软件模拟了无定形带材通过熔体旋转法冷却的过程,分析了毕渥数(Bi)对冷块熔融纺丝过程的影响。Sowjanya等[5]利用2D数值模拟,分析了Finemet合金熔融纺丝过程中辊速、压力、间隙以及狭缝的宽度和厚度对熔池的稳定性与带材厚度的影响。Xie等[6]对半固态镁合金带材连续流延过程进行了数值模拟,分析了入口温度、轧辊与熔融合金之间的传热、流延速度、凝固终点位置对带材质量的影响。李福森等[7]使用Fluent软件对塑料薄膜在流延辊筒上的冷却过程进行了数值模拟,分析了塑料薄膜在流延辊筒上的传热过程,得到了薄膜及辊面温度的变化规律。郭茜等[8]对平板流铸工艺中的冷却辊筒进行了温度场数值模拟,分析了辊速、辊外径、辊厚度对辊面传热性能的影响。马文鑫等[9]将固体胶片设定成流体,应用Fluent软件建立了胶片- 冷却鼓三维耦合换热模型,得到了胶片及各冷却鼓的温度分布规律。
综上所述,虽然很多学者利用CFD方法对流延工艺进行了数值模拟,但是很少对沥青的流延冷却过程进行数值模拟。为了更好地了解沥青流延过程的冷却机理,同时为沥青防水卷材的生产制造提供一定的理论基础,本文将沥青带材的流延加工过程等效成2D的高黏度流体流动过程,建立了多层沥青带材- 冷却辊筒二维模型,运用CFD方法,分析带材厚度、进料点位置、辊筒直径对沥青冷却过程的影响,期望研究结果为沥青延流工艺的温度控制提供科学指导。
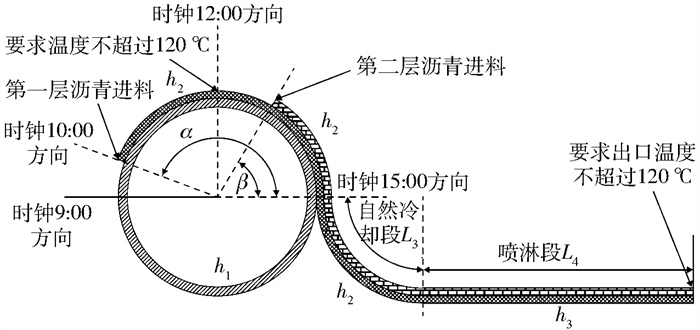
1 数学物理模型本文以某型复合沥青防水带材为例,该带材结构为聚对苯二甲酸乙二醇酯/聚乙烯复合膜(PET/PE)薄膜材料中间裹覆两层沥青材料,其流延工艺如图 1所示。首先在冷却辊筒的时钟9:00位置处覆第一层PET/PE薄膜,在时钟10:00位置处流延第一层沥青,沥青经过辊筒冷却后,在时钟12:00位置处覆第二层PET/PE薄膜(覆膜温度不超过120 ℃),带材继续被冷却后,再进行第二次沥青延流,经过两次沥青延流的带材继续被冷却辊筒冷却,直至带材离开辊筒,进入自然冷却阶段和喷淋冷却阶段,待带材风冷干燥后覆第三层PET/PE薄膜。
|
α、β—第一层、第二层沥青进料与时钟15:00方向的夹角;h1、h2、h3—辊筒内部、空气自然冷却段、喷淋段的对流换热系数;L3、L4—自然冷却段、喷淋段的换热面特征长度。 图 1 复合沥青防水带材的流延工艺 Fig.1 Casting process of composite asphalt waterproof strip |
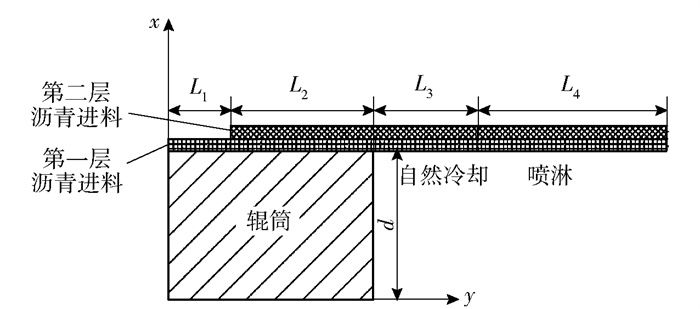
在实际流延生产工艺中,由于冷却辊筒直径较大,而每层沥青不足1 mm,故忽略冷却辊筒的曲率方向变化以简化计算模型,简化的模型如图 2所示。其中,L1为简化后的第一层沥青前端与第二层沥青前端的距离,L2为简化后的第二层沥青前端与辊筒末端的距离,其计算公式如下。
| $ {L_1} = \frac{{\alpha - \beta }}{{360}}{\rm{ \mathsf{ π} }}d, {L_2} = \frac{\beta }{{360}}{\rm{ \mathsf{ π} }}d $ |
|
图 2 简化的计算模型 Fig.2 Simplified calculation model |
式中:d为简化后的辊筒厚度。
为了便于计算和设置边界条件,在不失流延工艺本征的基础上,假设原本旋转的冷却辊筒处于静止状态,沥青处于层流的流体流动状态[10],冷却辊筒外壁与膜层材料完全直接接触,忽略空气夹层带来的空气热阻及PET/PE薄膜热阻,并且压力和密度也不随时间变化,因此可将上述模型简化为二维稳态定常流动与传热问题。
连续性方程为
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} = 0 $ | (1) |
式中:u为x方向的速度,v为y方向的速度。
动量守恒方程为
| $ \rho \left( {u\frac{{\partial u}}{{\partial x}} + u\frac{{\partial u}}{{\partial y}}} \right) = \rho {f_x} - \frac{{\partial p}}{{\partial x}} + \mu \left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right) $ | (2) |
| $ \rho \left( {u\frac{{\partial u}}{{\partial x}} + u\frac{{\partial u}}{{\partial y}}} \right) = \rho {f_y} - \frac{{\partial p}}{{\partial y}} + \mu \left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right) $ | (3) |
式中:ρ为密度,fx为x方向的体积力,fy为y方向的体积力,p为压力,μ为流体的动力黏度。
能量守恒定律是包含热交换的流动系统必须满足的基本定律,式(4)是以温度T为变量的能量守恒方程。
| $ \frac{{\partial \left( {\rho T} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho uT} \right) = {\rm{div}}\left( {\frac{k}{{{c_p}}}{\rm{grad}}T} \right) + {S_T} $ | (4) |
式中:cp是比热容,k为流体的传热系数,ST为黏性耗散项。
对于流动边界,两层沥青流动的速度值均为冷却辊筒旋转外壁线速度。对于第一层沥青的入口速度,边界条件为
| $ {\mathit{u}_{{\rm{x = 0}}}}{\rm{ = }}{\mathit{u}_{\rm{0}}} $ | (5) |
对于传热边界,冷却水与辊筒内壁采用第三类边界条件[11],边界条件为
| $ - \mathit{\lambda }\frac{{\partial t}}{{\partial y}}\left| {_{y = 0}} \right. = {h_1}({t_{y = 0}} - {t_1}) $ | (6) |
式中:λ为导热系数,t1为冷却水温度。
一般来说,对流传热系数h可以根据努塞尔数
| $ N{u_1} = 0.023Re_{\rm{l}}^{^{0.8}}Pr_{\rm{l}}^{^{0.4}} $ | (7) |
式中:Rel为辊筒内部冷却水的雷诺数,Prl为辊筒内部冷却水的普朗特数。
对于空气自然冷却阶段,采用横掠圆管Nu关联式[12]计算Nu。
| $ N{u_2} = 0.644Re_{\rm{g}}^{^{0.5}}Pr_{\rm{g}}^{^{1/3}} $ | (8) |
式中:Reg为空气自然冷却的雷诺数,Prg为空气自然冷却的普朗特数。
对于喷淋冷却阶段,采用喷嘴冲击射流实验Nu关联式[13]计算Nu。
| $ \begin{array}{l} N{u_3} = 2Re_\mathit{D}^{^{0.5}}Pr_{\rm{l}}^{^{0.42}}{(1 + Re_\mathit{D}^{^{0.55}})^{^{0.5}}} \times {\rm{ }}\\ \frac{{1 - 1.1D/r}}{{1 + 0.1\left( {\frac{H}{D} - 6} \right)D/r}}\frac{D}{r} \end{array} $ | (9) |
式中:ReD为冲击冷却时水的雷诺数,D为冲击孔直径,r为射流滞止区半径,H为冲击孔与表面的距离。
本文采用Fluent软件进行数值模拟,取沥青固定熔点为120 ℃,沥青进料温度为165 ℃,辊筒厚度为25 mm,冷却辊筒中水的温度为10 ℃,喷淋水的温度为10 ℃。为了便于储存并防止热量堆积,该沥青带材的最终温度在40 ℃以下。
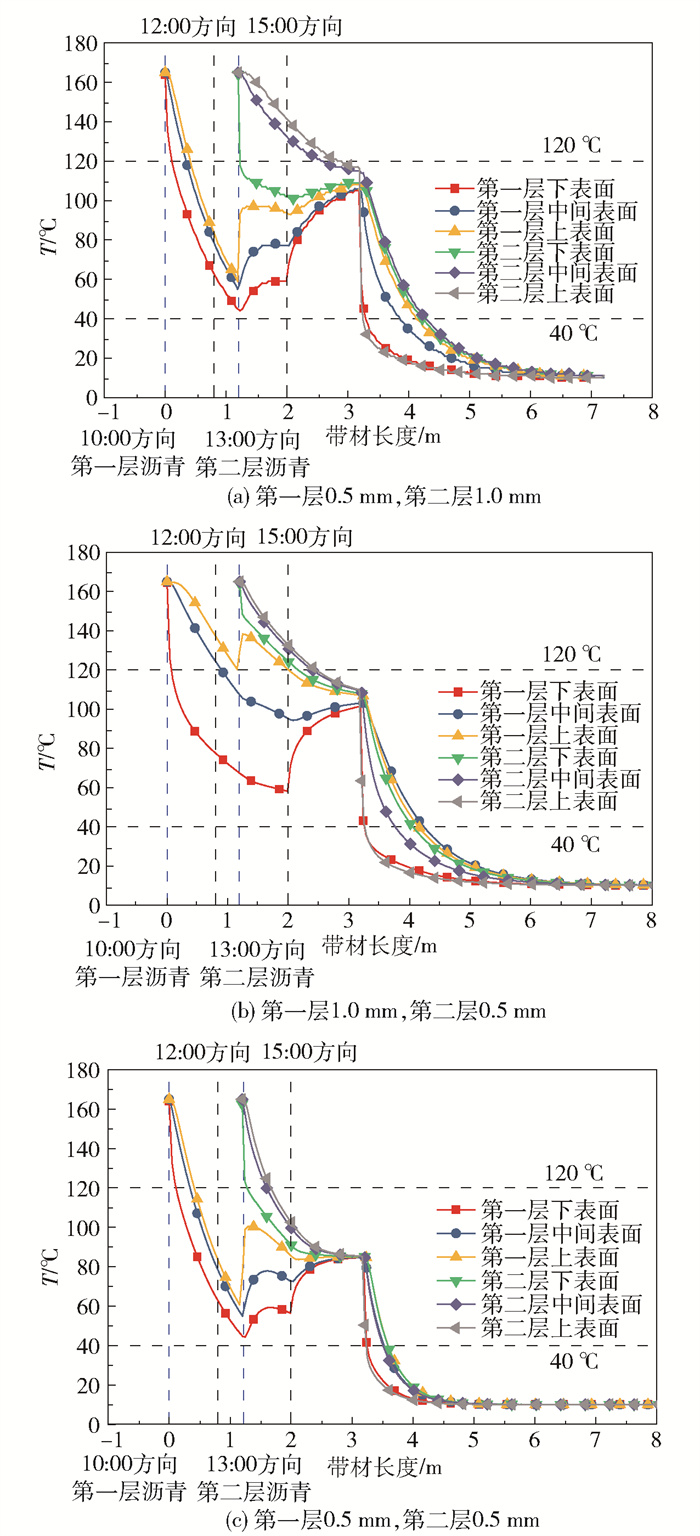
2 计算结果分析 2.1 沥青层厚度对传热过程的影响建立不同厚度的沥青层网格模型,通过数值模拟分析沥青层厚度对流延工艺沥青降温冷却过程的影响,结果如图 3所示。从图 3(a)和3(c)可以看出,在时钟15:00方向,厚度为1 mm的第二层沥青上表面温度比厚度为0.5 mm的第二层沥青上表面高出40 ℃。从图 3(b)和3(c)可以看出,在辊筒冷却段(0~2 m区间),在时钟12:00方向,厚度为1 mm的第一层沥青上表面温度比厚度为0.5 mm的第一层沥青上表面高出60 ℃。结果表明,沥青层厚度对辊筒冷却段的降温过程影响显著,第一层流延沥青越薄,底层热阻越小,辊筒对其冷却效果越好,越有利于第二层覆膜。在喷淋冷却段(3~7 m区间),图 3(a)与3(b)沥青带材的整体降温趋势接近,都在7 m之后沥青带材的整体温度接近室温,而图 3(c)中沥青在5 m之后就已经达到室温。
|
图 3 沥青层厚度对传热过程的影响 Fig.3 Effect of asphalt layer thicknesses on heat transfer process |
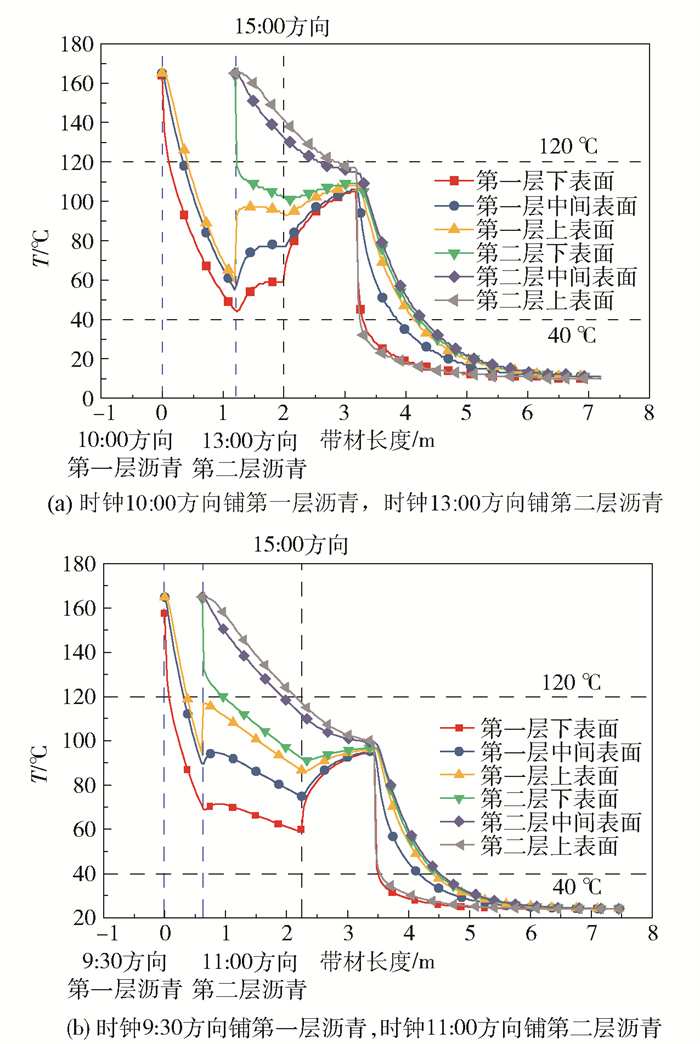
在冷却辊筒的不同方位上,建立沥青带材不同进料位置的网格模型,通过数值模拟分析了进料位置对整体沥青层降温冷却过程的影响,结果如图 4所示。与图 4(a)相比,图 4(b)的进料位置更靠前,并且两层沥青带材的间距更短,亦即两层沥青带材在辊筒冷却段的冷却时间更长。尽管总体上在这两种情况下沥青带材在7 m之后均冷却至相同温度,喷淋段对于整体的冷却过程贡献更加明显,使得图 4(a)和(b)中喷淋段的温度差别较小,但是在自然冷却段容易看出,图 4(b)的进料位置的降温作用比图 4(a)更明显。沥青流延位置前移,使得第一层流延沥青单独冷却的距离变短,到第二层延流沥青进料口前温度的降低量减少,但是在该工艺条件下,第二层沥青在离开辊筒前温度降低较为显著,因此在保证第二次PET/PE薄膜的覆膜温度不超过120 ℃的条件下,适当前移延流沥青的进料点,并且缩短两次流延沥青进料的间距,可以有效发挥辊筒的冷却作用。
|
图 4 进料位置对传热过程的影响 Fig.4 Effect of feeding positions on the heat transfer process |
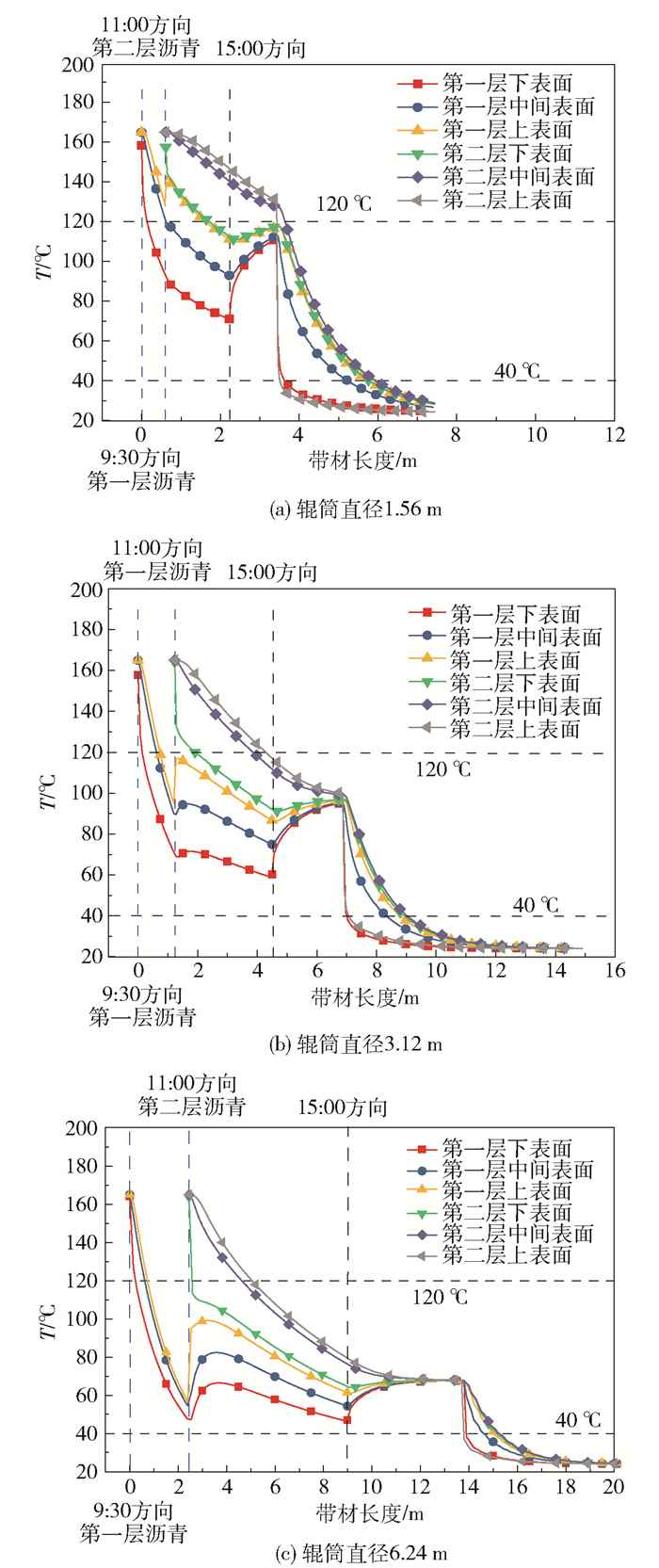
冷却辊筒兼具覆膜、流延和冷却的作用,调整辊筒直径,亦即调整辊筒冷却段的长度,可以为调整流延工艺覆膜及流延位置提供操作空间。建立沥青带材的不同辊筒直径,亦即辊筒冷却段长度的网格模型,通过数值模拟分析不同辊筒直径对沥青带材降温冷却过程的影响,结果如图 5所示。当辊筒直径从1.56 m增加到6.24 m时,第一层沥青上表面在时钟10:00方向的温度由155 ℃下降至120 ℃;第二层沥青上表面在时钟15:00方向的温度由150 ℃下降至约80 ℃。随着辊筒直径增大,冷却长度增加,沥青在冷却辊筒上的降温效果增强,并且时钟15:00方向比时钟10:00方向的降温更明显。
|
图 5 辊筒直径对传热过程的影响 Fig.5 Effect of steel cylinder diameters on the heat transfer process |
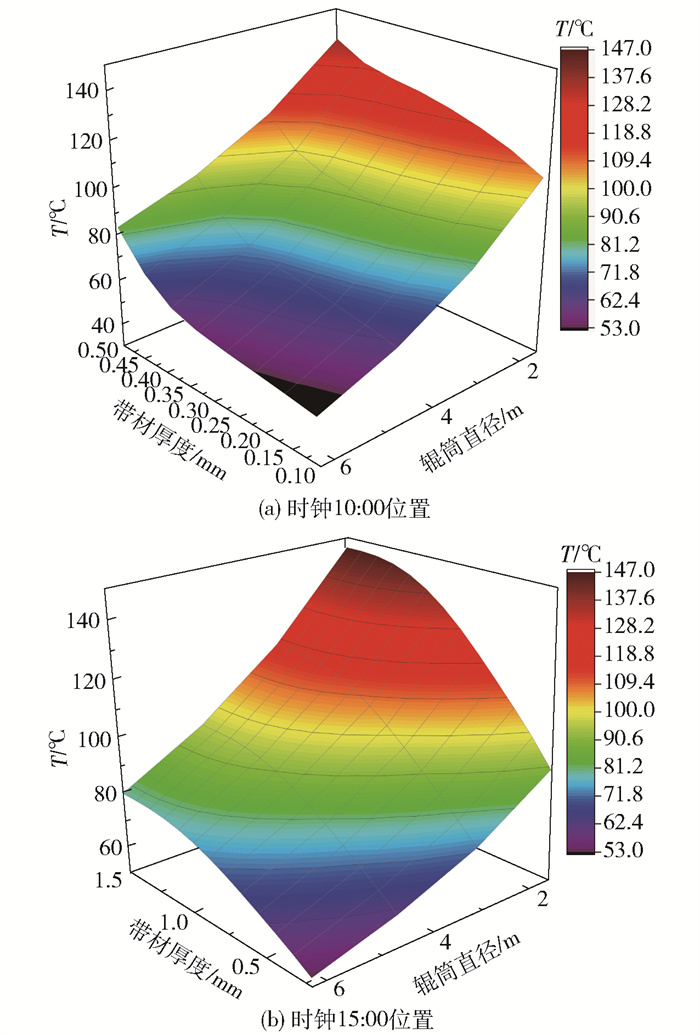
图 6为辊筒直径对沥青带材在时钟10:00和15:00位置沿带材厚度方向的温度分布的影响。从图中可以看出,无论在时钟10:00还是15:00位置,辊筒直径越大,沥青带材的整体温度越低。当辊筒直径为1.56 m时,在第二层沥青进料之前,第一层沥青的上表面温度均已经超过120 ℃,因此当辊筒直径较小时,沥青带材上表面得不到有效冷却,从而影响第二层覆膜工艺。随着辊筒直径的增大,第一层沥青的单独冷却时间更长,可适当前移第二次流延沥青的位置。
|
图 6 在时钟10:00和15:00位置辊筒直径沿带材厚度方向对传热过程的影响 Fig.6 Effect of steel cylinder diameters along the strip thickness direction on the heat transfer process at the 10:00 and 15:00 clock positions |
本文通过CFD数值模拟,将沥青带材的流延加工过程简化为2D高黏度流体与传热过程,建立了多层沥青带材- 冷却辊筒流动与传热数学模型,分析了带材厚度、进料点位置、辊筒直径对流延沥青冷却过程的影响,得到如下结论:
(1) 沥青厚度对辊筒冷却段的降温过程影响显著,第一层流延沥青越薄,底层热阻越小,辊筒对其冷却效果越好,越有利于第二层覆膜。
(2) 在有限的冷却长度范围内,适当前移第一次沥青流延的进料位置,并且缩短两次进料的间距,能够改善辊筒的冷却效果。
(3) 增大冷却辊筒直径,即增加沥青带材在辊筒上的冷却时间,可以保证流延沥青的充分冷却,为覆膜及流延工艺调整提供较大的操作空间,但冷却辊筒直径的增加会增加设备成本。
上述研究结果可以为类似沥青流延工艺的设计和工艺优化提供一定的理论指导,具有一定的工程应用价值。
| [1] |
陈中华, 廖前兵, 陈剑华, 等. 水性沥青防腐涂料的制备[J]. 电镀与涂饰, 2017, 36(22): 1167-1171. CHEN Z H, LIAO Q B, CHEN J H, et al. Preparation of waterborne asphalt anticorrosive coatings[J]. Electroplating & Finishing, 2017, 36(22): 1167-1171. (in Chinese) |
| [2] |
刘丽, 郝培文. 沥青胶浆粘度特性分析[J]. 河北工业大学学报, 2006, 35(2): 109-113. LIU L, HAO P W. Analysis on viscosity character of asphalt mortar[J]. Journal of Heibei University of Techno-logy, 2006, 35(2): 109-113. (in Chinese) DOI:10.3969/j.issn.1007-2373.2006.02.024 |
| [3] |
龚春平, 袁志欣, 邢铭琪. 沥青防水卷材耐热性检测技术分析[C]//国检集团第一届检验检测人员岗位能力提升论文集. 北京: 中国建材科技杂志社, 2020. GONG C P, YUAN Z X, XING M Q. Detection technology analysis of flow resistance at elevated temperature for asphalt waterproofing membrane[C]//Proceedings of the First Session of the National Inspection Group on Improving the Post Ability of Inspection and Testing Personnel. Beijing: China Building Materials Science and Technology Magazine, 2020. (in Chinese) |
| [4] |
PAGNOLA M, MALMORIA M, BARONE M. Biot number behaviour in the Chill Block Melt Spinning (CBMS) process[J]. Applied Thermal Engineering, 2016, 103: 807-811. DOI:10.1016/j.applthermaleng.2016.04.077 |
| [5] |
SOWJANYA M, KISHEN K R T. Obtaining stable puddle and thinner ribbons during planar flow melt spinning process[J]. Materials Today: Proceedings, 2017, 4(2): 890-897. DOI:10.1016/j.matpr.2017.01.100 |
| [6] |
XIE S S, YANG H Q, LI L, et al. Numerical simulation of semi-solid magnesium alloy in continuous roll-casting process[J]. Solid State Phenomena, 2006, 116-117: 583-586. DOI:10.4028/www.scientific.net/SSP.116-117.583 |
| [7] |
李福森, 王栓虎, 李欣兴, 等. 塑料薄膜在流延辊上冷却过程的数值模拟[J]. 塑料科技, 2011, 39(2): 35-38. LI F S, WANG S H, LI X X, et al. Numerical simulation of cooling process of plastic film on casting roller[J]. Plastics Science and Technology, 2011, 39(2): 35-38. (in Chinese) DOI:10.3969/j.issn.1005-3360.2011.02.002 |
| [8] |
郭茜, 严密. 平板流铸工艺中冷却辊的温度场数值模拟[J]. 稀有金属材料与工程, 2015, 44(8): 2048-2052. GUO X, YAN M. Thermal analysis for cooling rolls in planar-flow melt spinning[J]. Rare Metal Materials and Engineering, 2015, 44(8): 2048-2052. (in Chinese) |
| [9] |
马文鑫, 于洪杰, 刘云云, 等. 压延胶片与冷却鼓传热过程的数值模拟[J]. 北京化工大学学报(自然科学版), 2020, 47(3): 84-92. MA W X, YU H J, LIU Y Y, et al. Numerical simulation of the heat transfer between a rolling rubber-film and cooling-drums[J]. Journal of Beijing University of Che-mical Technology(Natural Science), 2020, 47(3): 84-92. (in Chinese) |
| [10] |
张兆顺, 崔桂香. 流体力学[M]. 3版. 北京: 清华大学出版社, 2015. ZHANG Z S, CUI G X. Fluidmechanics[M]. 3rd ed. Beijing: Tsinghua University Press, 2015. (in Chinese) |
| [11] |
陶文铨. 传热学[M]. 5版. 北京: 高等教育出版社, 2019. TAO W Q. Heat transfer[M]. 5th ed. Beijing: Higher Education Press, 2019. (in Chinese) |
| [12] |
CENGEL Y A. Heat transfer: a practical approach[M]. 2nd ed. New York: McGraw-Hill, 2003.
|
| [13] |
MARTIN H. Heat and mass transfer between impinging gas jets and solid surfaces[J]. Advances in Heat Transfer, 1977, 13: 1-60. |







