2. 国家管网集团西气东输分公司,上海 200122;
3. 国家管网集团西气东输山西输气分公司,太原 030000
2. National Pipeline Network West-East Gas Transmission Branch, Shanghai 200122;
3. National Pipeline Network West-East Shanxi Gas Transmission Branch, Taiyuan 030000, China
近年来,许多石化企业为高转速往复式压缩机加装了可变负荷的气量调节系统,为企业节省了大量的电能。基于部分行程顶开进气阀的无级气量调节系统因其安装方便、调控范围广、运行稳定等优势而引起大量关注,如贺尔碧格公司开发的Hydro-COM系统和国内一些厂家开发的无级气量调节系统都取得了较好的应用效果[1-2],其原理是在高压力的液压油作用下,执行油缸中的顶杆将进气阀强制开启,进而使得已经吸入压缩机气缸中的多余气体回流至进气管道[3]。高转速往复式压缩机的调控周期通常以毫秒为单位,对执行器的快速响应能力和参数稳定性有很精确的要求,因此执行器的性能对整个系统的稳定运行起着至关重要的作用。然而,在系统实际运行的过程中,由于电磁铁线圈老化、顶杆磨损、油站泄漏等因素可能会导致执行器发生失效、偏移、卡死等故障,严重影响系统的正常运行。因此,探索一种执行器故障情况下的无级气量调节系统自愈调控方法具有重要意义。
容错控制因具有在元部件出现故障时仍能保障系统稳定运行的能力,引起了很多学者的关注[4]。目前,容错控制在线性系统中的应用相对较多。文献[5]针对一类不确定线性系统,提出一种执行器故障情况下的自适应容错补偿控制策略。文献[6]基于Lyapunov-Krasovskii定理,将广义系统的稳定性问题转化为线性矩阵不等式求解问题,提出一种针对线性时滞系统的轨迹跟踪的主动容错控制方法。文献[7]提出一种基于二阶卡尔曼滤波器的线性二次最优容错控制器,并成功应用于四旋翼无人机。
从控制科学的角度来看,压缩机的各级排气压力与工作负荷之间的关系并不是线性的,每一级工作负荷的改变都会影响与之相邻的缓冲罐内的压力,因此这是一类多输入多输出耦合非线性系统。针对非线性系统的容错控制常见的控制方法有控制律重新调度、控制律重构、模型跟踪重组以及自适应容错控制等[8-11]。其中,自适应容错控制不依赖故障诊断机构提供的精准的故障信息,能够自适应地对故障及时地重组控制律,在算法上对故障作出补偿。因其具有良好的非线性系统跟踪能力和稳定的控制性能,自适应滑模容错控制方法激发了国内外学者的研究兴趣[12]。文献[13]应用终端滑模变结构控制方法为航天器编队飞行控制问题提出一种自适应变结构控制策略。文献[14]针对挠性航天器姿态控制中存在的反作用轮、执行器故障、外部干扰和时变惯性参数不确定性等问题,提出一种基于滑动模态的鲁棒自适应容错跟踪控制方法。文献[15]基于反步滑模控制,设计了一种不依赖故障检测和隔离机制的自适应容错控制方法,在执行器部分失效或完全失效的情况下,可以成功地实现飞行器的高精度控制和振动抑制。
基于故障主动自愈的思想,针对往复式压缩机无级气量调节系统执行机构故障和外界噪声干扰等问题,本文设计了一种自适应滑模容错控制策略。当故障发生时,执行机构的控制参数能够自适应地作出调节,对故障进行补偿,达到调控性能自愈的目的。实验结果证明了本文方法的有效性。
1 无级气量调节系统模型 1.1 气量调节系统机理模型在气量调节工况下,压缩机的一个工作周期分为膨胀过程、吸气过程、压缩过程、排气过程和回流过程。气体经压缩后会被排入缓冲罐以减小压力脉冲对设备的影响。将被压缩气体视为理想气体,则缓冲罐内的气体满足
| $ \mathit{pV}{\rm{ = }}\mathit{mRT} $ | (1) |
式中,p为缓冲罐压力,V为缓冲罐体积,m为缓冲罐内气体质量,R为气体常数,T为缓冲罐内气体温度。
本文研究对象为一台如图 1所示的2D型双缸双作用往复式压缩机,其主要结构参数如表 1所示。气体经一级气缸压缩后被排出至中间级缓冲罐;随后二级气缸从中间级缓冲罐吸入相应的气体量进行压缩并将其排出至末级缓冲罐。通常,末级缓冲杆会与下游的管路连接进行下一步的工艺过程。

|
图 1 2D型往复式压缩机实验台 Fig.1 Test bench of the 2D reciprocating compressor |
| 下载CSV 表 1 压缩机的主要结构参数 Table 1 Main structural parameters of the compressor |
在任意一个工作周期内,一级出口缓冲罐的气体质量变化为一级气缸排气质量与二级气缸吸气质量之差,二级出口缓冲罐的气体质量变化为二级气缸的排气质量与流出二级出口缓冲罐的气体质量之差。在加入无级气量调节系统后,二级气缸回流过程的气体质量变化也应该被考虑在内,于是有
| $ \left\{ {\begin{array}{*{20}{c}} {\frac{{{\rm{d}}{m_1}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}m_{_{{\rm{dvo}}}}^{^1}}}{{{\rm{d}}t}} - \frac{{{\rm{d}}m_{_{{\rm{svi}}}}^{^2}}}{{{\rm{d}}t}} + \frac{{{\rm{d}}m_{_{{\rm{svb}}}}^{^2}}}{{{\rm{d}}t}}}\\ {\frac{{{\rm{d}}{m_2}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}m_{{\rm{dvo}}}^2}}{{{\rm{d}}t}} - \frac{{{\rm{d}}{m_v}}}{{{\rm{d}}t}}} \end{array}} \right. $ | (2) |
式中,m1、m2分别为一、二级排气缓冲罐中的气体质量,mdvo1、mdvo2分别为一、二级气缸排气质量,msvi2为二级气缸吸气质量,msvb2为二级气缸回流气体质量,mv为通过二级缓冲罐出口阀的气体质量。
从式(2)可以看出,缓冲罐内气体质量的变化与吸气过程、回流过程和压缩过程都有关。结合文献[16]给出的上述3个过程的数学描述并代入压缩机主要结构参数,可以得到如式(3)所示的无级气量调节系统负荷与压力的微分方程表达式为
| $ \left\{ {\begin{array}{*{20}{c}} {\frac{{{\rm{d}}{p_1}}}{{{\rm{d}}t}} = - 0.08{p_1} + 0.01{p_2} + 5{\rm{ }}547.82 + }\\ {29{\rm{ }}422{u_1} - 0.275{p_1}{u_2}}\\ {\frac{{{\rm{d}}{p_2}}}{{{\rm{d}}t}} = 0.01{p_1} - 0.02{p_2} + 0.06{p_1}{u_2}} \end{array}} \right. $ | (3) |
式中,p1和p2分别为压缩机的一级和二级压力;u1和u2分别为压缩机的一级和二级工作负荷,调节范围为0~100%。
将式(3)写成一般仿射非线性系统形式
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}}\left( t \right)}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{x}} \right)} \end{array}} \right. $ | (4) |
式中,状态变量为x =[p1, p2]T,控制变量为u =[u1, u2]T,输出变量为y =[p1, p2]T,d (t)为外部扰动且满足| d (t)|≤D,其中D为有界常数。
联立式(3)和式(4)可得
| $ \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) = \left[ {\begin{array}{*{20}{c}} { - 0.08{x_1} + 0.014{\rm{ }}2{x_2} + 5{\rm{ }}547.82}\\ {0.010{\rm{ }}6{x_1} - 0.021{\rm{ }}1{x_2}} \end{array}} \right] $ | (5) |
| $ \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{x}} \right) = \left[ {\begin{array}{*{20}{c}} {29{\rm{ }}422}&{ - 0.275{x_1}}\\ 0&{0.057{x_1}} \end{array}} \right] $ | (6) |
| $ \mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{x}} \right) = {[{x_1}, {x_2}]^{\rm{T}}} $ | (7) |
气量调节系统的执行机构由电磁阀和油缸组成。电磁阀一般只有打开和关闭两种状态,其动作的时刻由控制器确定。在电磁阀开启后高压油快速进入油缸,将顶杆顶出并保持最大位移。常见的执行器故障形式有两种:1)电磁阀断路导致阀芯锁死、油路阻断,此时系统无法正常运行,必须停机检修或者启用备用电磁阀;2)因电磁铁线圈老化或者阀芯摩擦增大而导致的电磁铁性能退化,此时阀芯无法达到最大位移,流经电磁铁的高压油流量减少,进而影响顶杆的顶出时间。因此,从流量的角度出发,将执行器的故障分为卡死和偏移两种情况。
执行器故障情况下的气量调节系统非线性方程可写为
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}}\left( t \right) $ | (8) |
当第i个执行器发生故障时可以表示为
| $ {u_i} = {\sigma _i}{u_{ci}} + {{\bar u}_i} $ | (9) |
式中,u为控制器的实际输出,uc为控制器的理想输出,σ(0≤σ≤1)为执行器发生偏移故障时的偏移程度,u (0≤u≤1)为执行器卡死故障的位置,下标i表示第i个执行器。
为便于表述,将执行器故障形式进行分类,如表 2所示。
| 下载CSV 表 2 执行器故障类型 Table 2 Failure types of the actuator |
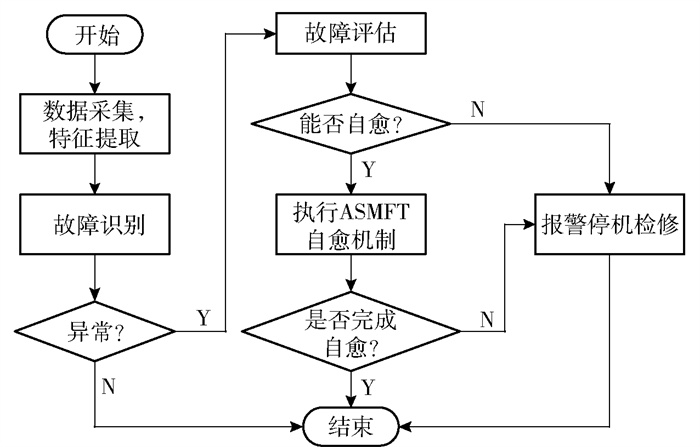
往复式压缩机无级气量调节是一类非线性、强耦合的控制系统。本文的目标是设计一种自愈控制器,在执行器发生故障的情况下,保证气量调节系统的排气量调节性能。自适应滑模自愈补偿策略的设计思想是在故障发生后重新调整控制器参数,以补偿故障对系统造成的影响。实时对复杂机器系统的运行状态及工况进行在线监测,分析可能产生故障的条件,采用对比甄别、诊断预测、自愈决策和主动控制等方法,使其不具备产生使用故障的条件,必要时将故障抑制在初始阶段,达到不引发故障或在不停机状态下将机器恢复至正常状态、保障机器健康运行的目的[17]。图 2为本文所提出的基于自适应滑模容错(adaptive sliding mode fault tolerant,ASMFT)的自愈控制流程图。
|
图 2 ASMFT自愈控制流程图 Fig.2 Flow chart of ASMFT self-healing control |
取滑模面为
| $ \mathit{\boldsymbol{s}}{\rm{ = }}\mathit{\boldsymbol{e}} $ | (10) |
式中,e为跟踪误差,当参考输入为xd时有e = x - xd。
于是
| $ \begin{array}{l} \mathit{\boldsymbol{\dot s}} = \mathit{\boldsymbol{\dot e}} = \mathit{\boldsymbol{\dot x}} - {{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} = \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}}\left( t \right){\rm{ }}{{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} = \\ \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) + {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\mathit{\boldsymbol{u}}_1} + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\mathit{\boldsymbol{u}}_2} + \mathit{\boldsymbol{d}}\left( t \right) - {{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} = \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right) + \\ {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right)({\sigma _1}{u_{c1}} + {{\bar u}_1}) + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right)({\sigma _2}{u_{c2}} + {{\bar u}_2}) + \mathit{\boldsymbol{d}}\left( t \right) - \\ {{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} \end{array} $ | (11) |
设σ =diag[σ1, σ2],u =[u1, u2]T,uc=[uc1, uc2]T,以及
| $ \mathit{\boldsymbol{\alpha }} = \mathit{\boldsymbol{ks}} + \mathit{\boldsymbol{\eta }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right)\mathit{ - }{{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} $ | (12) |
式中,k =[k1, k2]为可调节的控制器系数, η =[η1, η2]为可调节的符号函数系数。
由式(12)可得
| $ \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{x}} \right)\mathit{ - }{{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} = \mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{ks}} - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) $ | (13) |
联立式(11)~(13)可得
| $ \mathit{\boldsymbol{\dot s}} = \mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{ks}} - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{\bar u}} + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{\sigma }}{{\mathit{\boldsymbol{\bar u}}}_{\rm{c}}} + \mathit{\boldsymbol{d}}\left( t \right) $ | (14) |
接下来将根据故障信息的不同获知程度,对故障信息已知和故障信息未知这两种情况的自愈控制策略进行设计。
2.1.1 故障信息已知当故障信息已经准确获取,即σ和u都已知时,可将控制律设计为
| $ \left\{ {\begin{array}{*{20}{c}} {{u_{{\rm{c1}}}} = - {\mathit{\boldsymbol{\lambda }}_{11}}\mathit{\boldsymbol{\alpha }} - {\mathit{\boldsymbol{\lambda }}_{12}}}\\ {{u_{{\rm{c2}}}} = - {\mathit{\boldsymbol{\lambda }}_{21}}\mathit{\boldsymbol{\alpha }} - {\lambda _{22}}} \end{array}} \right. $ | (15) |
式中,λ11、λ21、λ12、λ22均为可调的控制器参数。
将式(15)代入式(14)可得
| $ \begin{array}{l} \;\;\;\;\;\;\mathit{\boldsymbol{\dot s}} = \mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{ks}} + ({\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){{\bar u}_1} + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){{\bar u}_2}) - ({\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right)\\ {\sigma _1}{\mathit{\boldsymbol{\lambda }}_{11}}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{\lambda _{12}}) - ({\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{\mathit{\boldsymbol{\lambda }}_{21}}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right)\\ {\sigma _2}{\lambda _{22}}) - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{d}}\left( t \right) = \mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{ks}} + ({\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){{\bar u}_1} + \\ {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){{\bar u}_2}) - \mathit{\boldsymbol{\alpha }}({\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{\mathit{\boldsymbol{\lambda }}_{11}} + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{\mathit{\boldsymbol{\lambda }}_{21}}) - {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right)\\ {\sigma _1}{\lambda _{12}} - {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{\lambda _{22}} - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{d}}\left( t \right) \end{array} $ | (16) |
如果控制器参数满足下述条件
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{\mathit{\boldsymbol{\lambda }}_{11}} + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{\mathit{\boldsymbol{\lambda }}_{21}} = 1}\\ {{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){{\bar u}_1} + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){{\bar u}_2} = {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{\lambda _{12}} + }\\ \;\;\;\;\;\;{{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{\lambda _{22}}} \end{array}} \right. $ | (17) |
则式(16)可以简化为
| $ \mathit{\boldsymbol{\dot s}} = - \mathit{\boldsymbol{ks}} - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{d}}\left( t \right) $ | (18) |
取Lyapunov函数为
| $ \mathit{\boldsymbol{V}}{\rm{ = }}\frac{1}{2}{\mathit{\boldsymbol{s}}^2} $ | (19) |
则
| $ \mathit{\boldsymbol{\dot V}} = \mathit{\boldsymbol{s\dot s}} = - \mathit{\boldsymbol{k}}{\mathit{\boldsymbol{s}}^2} - \mathit{\boldsymbol{\eta }}\left| s \right| + \mathit{\boldsymbol{sd}}\left( t \right) \le - \mathit{\boldsymbol{k}}{\mathit{\boldsymbol{s}}^2} \le 0 $ | (20) |
由于V ≥0,
2.1.1节讨论的是基于故障检测模块的输出信号,如果故障检测模块本身发生误报、漏报、延时等情况,将对后续的自愈控制方案产生很大的影响。并且考虑在故障发生后,故障信息难以在短时间内快速获知,即σ和u都未知,在这种情况下,将控制律设计为
| $ \left\{ {\begin{array}{*{20}{c}} {{u_{{\rm{c1}}}} = - {{\mathit{\boldsymbol{\hat \lambda }}}_{11}}\mathit{\boldsymbol{\alpha }} - {{\mathit{\hat \lambda }}_{12}}}\\ {{u_{{\rm{c2}}}} = - {{\mathit{\boldsymbol{\hat \lambda }}}_{21}}\mathit{\boldsymbol{\alpha }} - {{\mathit{\hat \lambda }}_{22}}} \end{array}} \right. $ | (21) |
式中,
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{\dot s}} = \mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{ks}} + ({\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){{\bar u}_1} + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){{\bar u}_2}) - ({\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right)\\ {\sigma _1}{{\mathit{\boldsymbol{\hat \lambda }}}_{11}}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\hat \lambda }_{12}}) - ({\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{{\mathit{\boldsymbol{\hat \lambda }}}_{21}}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right)\\ {\sigma _2}{{\hat \lambda }_{22}}) - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{d}}\left( t \right) \end{array} $ | (22) |
将式(17)代入式(22)有
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{\dot s}} = \mathit{\boldsymbol{\alpha }}({\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{\mathit{\boldsymbol{\lambda }}_{11}} + {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{\mathit{\boldsymbol{\lambda }}_{21}} - 1) + \mathit{\boldsymbol{\alpha }} + \\ {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{\mathit{\lambda }_{12}} + {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{\mathit{\lambda }_{22}} - \mathit{\boldsymbol{ks}} - ({\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\boldsymbol{\hat \lambda }}}_{11}}\mathit{\boldsymbol{\alpha }} + \\ {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\hat \lambda }}_{12}}) - \left( {{\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{{\mathit{\boldsymbol{\hat \lambda }}}_{21}}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{{\mathit{\hat \lambda }}_{22}}} \right) - \\ \mathit{\boldsymbol{\eta }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{d}}\left( t \right) = \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{\mathit{\boldsymbol{\lambda }}_{11}} + \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{\mathit{\boldsymbol{\lambda }}_{21}} + \\ {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{\mathit{\lambda }_{12}} + {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{\mathit{\lambda }_{22}} - \mathit{\boldsymbol{ks}} - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\boldsymbol{\hat \lambda }}}_{11}} - \\ {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\hat \lambda }}_{12}} - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{{\mathit{\boldsymbol{\hat \lambda }}}_{21}} - {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{{\mathit{\hat \lambda }}_{22}} - \mathit{\boldsymbol{\eta }} \cdot \\ {\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{d}}\left( t \right) = \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}\left( {{\mathit{\boldsymbol{\lambda }}_{11}} - {{\mathit{\boldsymbol{\hat \lambda }}}_{11}}} \right) + \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}) \cdot \\ {\sigma _2}\left( {{\mathit{\boldsymbol{\lambda }}_{21}} - {{\mathit{\boldsymbol{\hat \lambda }}}_{21}}} \right) + {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}\left( {{\mathit{\lambda }_{12}} - {{\mathit{\hat \lambda }}_{12}}} \right) + {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}\left( {{\mathit{\lambda }_{22}}} \right. - \\ \left. {{{\mathit{\hat \lambda }}_{22}}} \right) - \mathit{\boldsymbol{ks}} - \mathit{\boldsymbol{\eta }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{d}}\left( t \right) \end{array} $ | (23) |
令
| $ \mathit{\boldsymbol{\dot s}} = - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\boldsymbol{\tilde \lambda }}}_{11}} - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{{\mathit{\boldsymbol{\tilde \lambda }}}_{21}} - {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\boldsymbol{\tilde \lambda }}}_{12}} - {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{{\mathit{\boldsymbol{\tilde \lambda }}}_{22}} $ | (24) |
对本文所提出的控制器的稳定性进行理论分析,以证明系统的各个信号是有界且收敛的。设计Lyapunov函数为
| $ \mathit{\boldsymbol{V}} = \frac{1}{2}{\mathit{\boldsymbol{s}}^2} + \frac{{|{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right)|{\sigma _1}}}{{2{\gamma _1}}}({\rm{ }}{{\mathit{\boldsymbol{\tilde \lambda }}}^2}_{11} + \mathit{\tilde \lambda }_{12}^2) + \frac{{|{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right)|{\sigma _2}}}{{2{\gamma _2}}}({{\mathit{\boldsymbol{\tilde \lambda }}}^2}_{21} + \mathit{\tilde \lambda }_{22}^2) $ | (25) |
式中,γ1、γ2为自适应系数,且有γ1>0, γ2>0。
于是
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{\dot V}} = \mathit{\boldsymbol{s\dot s}} + \frac{{|{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right)|{\sigma _1}}}{{{\gamma _1}}}({{\mathit{\boldsymbol{\tilde \lambda }}}_{11}}{{\mathit{\boldsymbol{\hat \lambda }}}_{11}} + {{\mathit{\tilde \lambda }}_{12}}{{\mathit{\hat \lambda }}_{12}}) + \\ \frac{{|{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right)|{\sigma _2}}}{{{\gamma _2}}}({{\mathit{\boldsymbol{\tilde \lambda }}}_{21}}{{\mathit{\boldsymbol{\hat \lambda }}}_{21}} + {{\mathit{\tilde \lambda }}_{22}}{{\mathit{\hat \lambda }}_{22}}) \le \mathit{\boldsymbol{s}}( - \mathit{\boldsymbol{ks}} - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}\\ {{\mathit{\boldsymbol{\tilde \lambda }}}_{11}} - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{{\mathit{\boldsymbol{\tilde \lambda }}}_{21}} - {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\boldsymbol{\tilde \lambda }}}_{12}} - {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{{\mathit{\boldsymbol{\tilde \lambda }}}_{22}} + \\ \frac{{|{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right)|{\sigma _1}}}{{{\gamma _1}}}({{\mathit{\boldsymbol{\tilde \lambda }}}_{11}}{{\mathit{\boldsymbol{\hat \lambda }}}_{11}} + {{\mathit{\tilde \lambda }}_{12}}{{\mathit{\hat \lambda }}_{12}}) + \frac{{|{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right)|{\sigma _2}}}{{{\gamma _2}}}({{\mathit{\boldsymbol{\tilde \lambda }}}_{21}}{{\mathit{\boldsymbol{\hat \lambda }}}_{21}} + \\ {{\mathit{\tilde \lambda }}_{22}}{{\mathit{\hat \lambda }}_{22}}) \end{array} $ | (26) |
设计自适应律为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat \lambda }}}_{11}} = {\gamma _1}\mathit{\boldsymbol{s\alpha }}{\rm{sgn}}({\mathit{G}_1}\left( \mathit{\boldsymbol{x}} \right))\\ {{\mathit{\hat \lambda }}_{12}} = {\gamma _1}\mathit{\boldsymbol{s}}{\rm{sgn}}({\mathit{G}_1}\left( \mathit{\boldsymbol{x}} \right))\\ {{\mathit{\boldsymbol{\hat \lambda }}}_{21}} = {\gamma _2}\mathit{\boldsymbol{s\alpha }}{\rm{sgn}}({\mathit{G}_2}\left( \mathit{\boldsymbol{x}} \right))\\ {{\mathit{\hat \lambda }}_{22}} = {\gamma _2}\mathit{\boldsymbol{s}}{\rm{sgn}}({\mathit{G}_2}\left( \mathit{\boldsymbol{x}} \right)) \end{array} $ | (27) |
将式(27)代入式(26)得
| $ \begin{array}{l} \;\;\;\;\;\;\;\mathit{\boldsymbol{\dot V}} \le {\rm{ }}\mathit{\boldsymbol{s}}{\rm{ }}( - {\rm{ }}\mathit{\boldsymbol{ks}} - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\boldsymbol{\tilde \lambda }}}_{11}} - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{{\mathit{\boldsymbol{\tilde \lambda }}}_{21}} - \\ {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\tilde \lambda }}_{12}} - {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{{\mathit{\tilde \lambda }}_{22}} + \frac{{|{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right)|{\sigma _1}}}{{{\gamma _1}}}\left( {{{\mathit{\boldsymbol{\tilde \lambda }}}_{11}}} \right.\\ \left. {{\gamma _1}\mathit{\boldsymbol{s\alpha }}{\rm{sgn}}({\mathit{G}_1}\left( \mathit{\boldsymbol{x}} \right)) + {{\mathit{\tilde \lambda }}_{12}}\;{\gamma _1}\mathit{\boldsymbol{s}}{\rm{sgn}}({\mathit{G}_1}\left( \mathit{\boldsymbol{x}} \right))} \right) + \\ \frac{{|{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right)|{\sigma _2}}}{{{\gamma _2}}}({{\mathit{\boldsymbol{\tilde \lambda }}}_{21}}\;{\gamma _2}\mathit{\boldsymbol{s\alpha }}{\rm{sgn}}({\mathit{G}_2}\left( \mathit{\boldsymbol{x}} \right)) + {{\mathit{\tilde \lambda }}_{22}}\;{\gamma _2}\mathit{\boldsymbol{s}} \cdot \\ {\rm{sgn}}({\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right)) = \mathit{\boldsymbol{s}}{\rm{ }}( - {\rm{ }}\mathit{\boldsymbol{ks}} - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\boldsymbol{\tilde \lambda }}}_{11}} - \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{{\mathit{\boldsymbol{\tilde \lambda }}}_{21}} - \\ \left. {{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\tilde \lambda }}_{12}} - {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{x}}){\sigma _2}{{\mathit{\boldsymbol{\tilde \lambda }}}_{22}}} \right) + \left( {{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\boldsymbol{\tilde \lambda }}}_{11}}} \right.\mathit{\boldsymbol{s\alpha }} + \\ {\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{x}} \right){\sigma _1}{{\mathit{\tilde \lambda }}_{12}}\mathit{s} + \left( {{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{{\mathit{\boldsymbol{\tilde \lambda }}}_{21}}\mathit{\boldsymbol{s\alpha }} + {\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{x}} \right){\sigma _2}{{\mathit{\tilde \lambda }}_{22}}\mathit{s}} \right) \le \\ - \mathit{\boldsymbol{k}}{\mathit{\boldsymbol{s}}^2} \le 0 \end{array} $ | (28) |
由于V ≥0,
| $ \int_{\rm{o}}^t {\mathit{\boldsymbol{\dot V}}{\rm{d}}t} = - \mathit{\boldsymbol{k}}\int_{\rm{o}}^t {{s^2}{\rm{d}}t} $ | (29) |
即
| $ \mathit{\boldsymbol{V}}\left( \infty \right) - \mathit{\boldsymbol{V}}\left( 0 \right) = - \mathit{\boldsymbol{k}}\int_{\rm{o}}^\infty {{s^2}{\rm{d}}t} $ | (30) |
则由V有界可知,s和
本文利用Matlab/Simulink平台开展数值仿真研究,将所提的ASMFT自愈调控方法与比例微分积分(proportion integration differentiation, PID)控制方法进行实验对比,以验证所设计自愈调控方法的有效性和优越性。将ASMFT自愈控制器初始值设置为x =[p1, p2]=[200, 300],λ11(0)= λ21(0)=[0, 0],λ12(0)=λ22(0)=0,经过多次实验得到最优控制参数为γ =1×10-11×[1, 100],k =[0.05, 1×10-7],η =[10, 10]。排气压力设定值如下:在t=20 s和120 s时,一级压力发生+20 kPa的阶跃变化;在t=220 s和320 s时,二级压力发生+20 kPa的阶跃变化。为了防止抖震,将符号函数sgn (s)用饱和函数sat(s)代替,取Δ=1×10-6。
实际的工程应用中当执行器出现卡死故障时会造成气量调节系统失效甚至安全事故,应该立即停机检修,所以本文只考虑部分或者全部执行器发生偏移的故障类型,设置故障情况如下。
情况1 执行器正常,即σ =[1, 1],u =[0, 0]。
情况2 一级执行器偏移,二级执行器正常,即σ =[0.2, 1],u =[0, 0]。
情况3 一级执行器正常,二级执行器偏移,即σ =[1, 0.5],u =[0, 0]。
情况4 执行器全部偏移,即σ =[0.2, 0.5],u = [0, 0]。
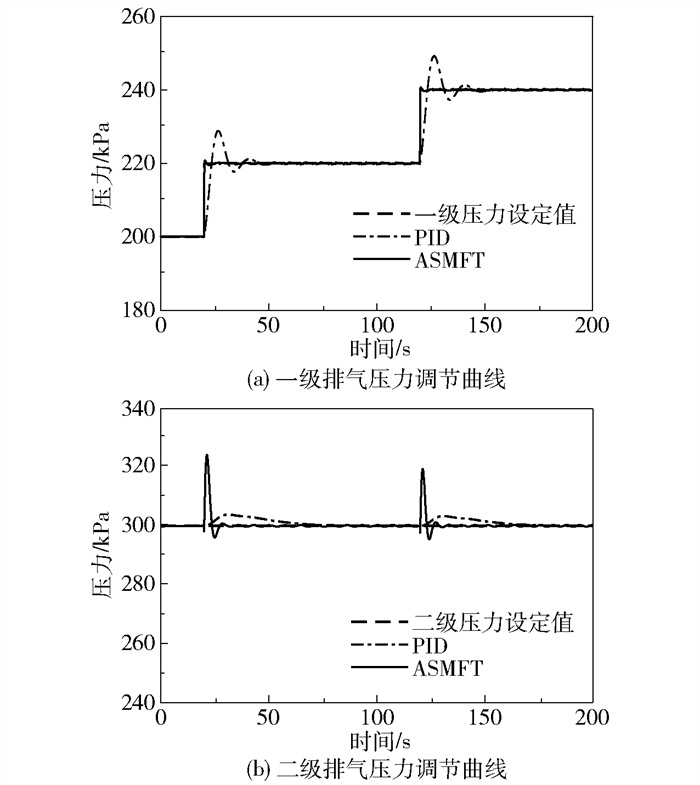
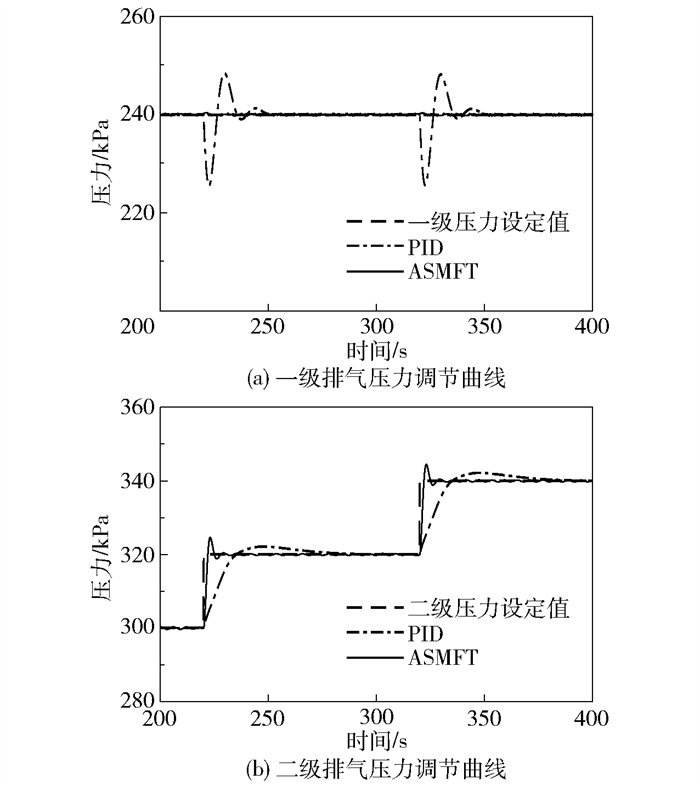
3.1 单个执行器故障单个执行器故障情况下的阶跃响应性能对比如图 3、4所示。可以看出ASMFT方法几乎不受执行器故障的影响,保持着良好的设定值跟踪性能;而PID方法却出现了较大的超调,调节时间较长。表明ASMFT方法具有更好的自愈调控性能。
|
图 3 改变一级排气压力设定值下单个执行器故障时的排气压力调节曲线 Fig.3 Exhaust pressure adjustment curve with an individual actuator failing when changing the first-stage exhaust pressure setpoint |
|
图 4 改变二级排气压力设定值下单个执行器故障时的排气压力调节曲线 Fig.4 Exhaust pressure adjustment curve with an individual actuator failing when changing the second-stage exhaust pressure setpoint |
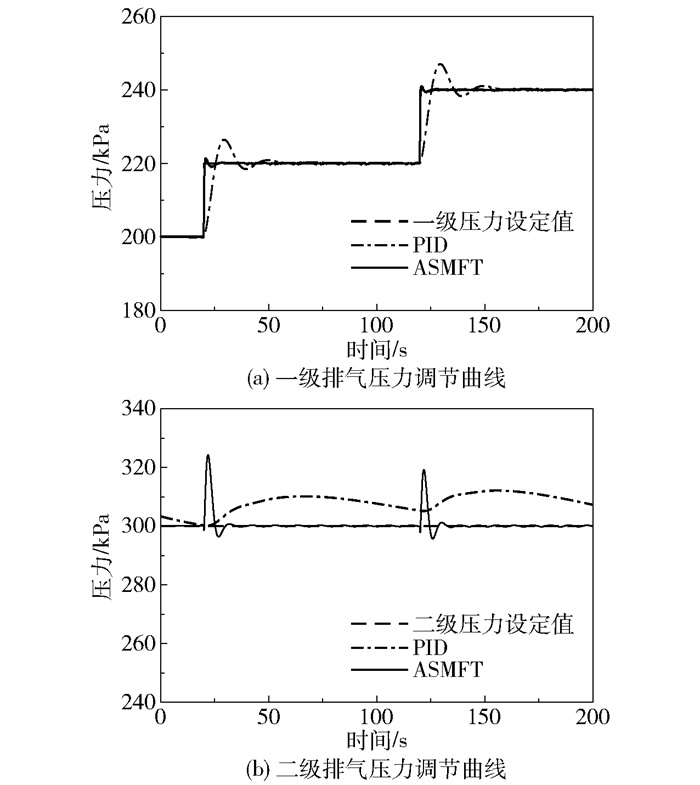
对全部执行器都出现偏移故障时两种调控方法的性能进行对比,结果如图 5、6所示。
|
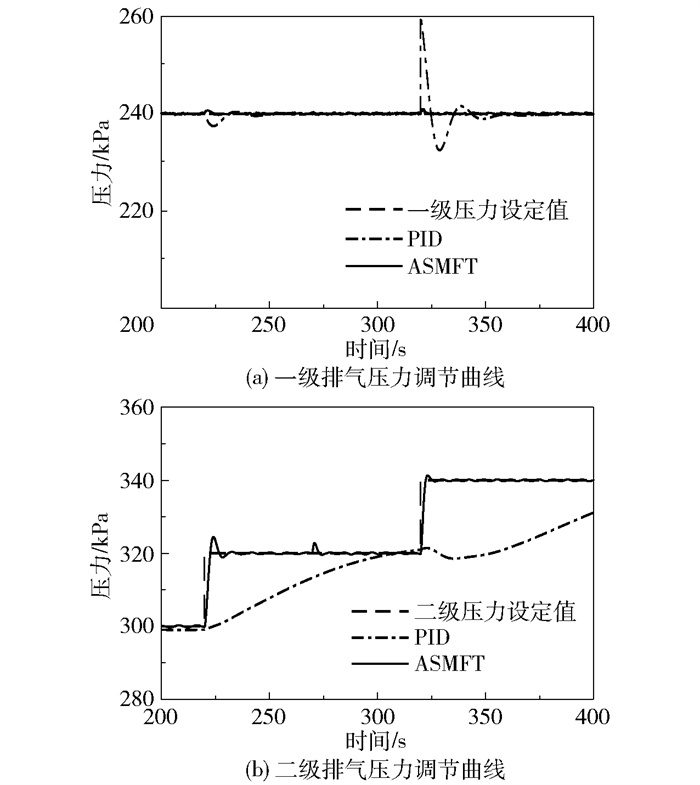
图 5 改变一级排气压力设定值下全部执行器故障时的排气压力调节曲线 Fig.5 Exhaust pressure adjustment curve with all actuators failing when changing the first-stage exhaust pressure setpoint |
|
图 6 改变二级排气压力设定值下全部执行器故障时的排气压力调节曲线 Fig.6 Exhaust pressure adjustment curve with all actuators failing when changing the second-stage exhaust pressure setpoint |
从图 5、6可以看出,虽然全部执行器出现故障时ASMFT方法的调节时间比单个执行器发生故障时所需时间稍微变长,但随后各级排气压力很快地收敛至设定值。然而PID调节方法在规定时间内几乎已经丧失了设定值跟踪性能,各级压力与设定值之间始终存在较大的偏差,此时可以认为PID调节方法已经失效。通过以上对比实验可以看出本文所提调控方法在应对执行器故障时具有较好的自愈性能。
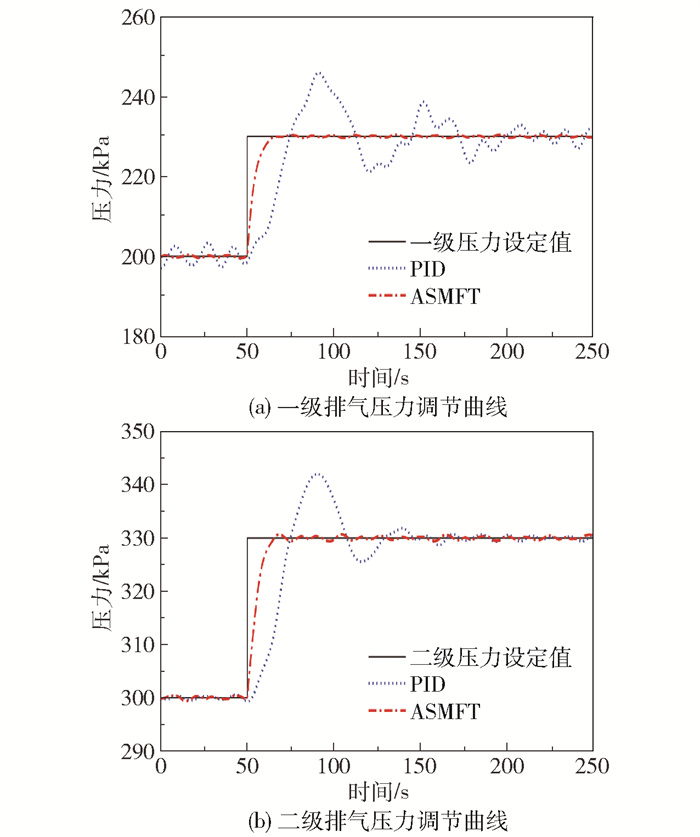
4 工程验证实验为了验证本文提出的ASMFT自愈调控策略的实际效果,在图 1所示的2D型压缩机实验台上对执行器故障的无级气量调节系统开展了对比实验研究。该压缩机一级气缸和二级气缸分别配置有4个和2个执行器,将每级一半的执行器用已老化的出现漂移故障的执行器替换。在压力稳定后,分别对一、二级负荷施加30 kPa的正阶跃信号,实验结果如图 7所示。
|
图 7 压缩机实验台排气压力调节曲线 Fig.7 Exhaust pressure adjustment curve of the compressor test bench |
从图 7可以看出,本文所提的ASMFT自愈调控方法相较PID控制方法具有更好的设定值跟踪性能,超调量和调节时间都更为优异,在执行器故障的情况下能够让设备性能实现自愈,较好地完成了调控任务。
5 结论(1) 本文提出的ASMFT自愈方案引入了自适应控制参数,有效地减少了系统对被控系统数学模型的依赖,简化了调整控制参数的工作量,保证了闭环故障系统的稳定性。
(2) 仿真实验和工程实验结果表明在部分或者全部执行器故障的情况下气量调节系统在本文提出的ASMFT自愈方案作用下都能保持稳定的调控性能,验证了所提方法的有效性,具有在工业现场应用的潜力。
| [1] |
赖朝喜. HydroCOM系统在加氢裂化装置新氢压缩机上的应用[J]. 压缩机技术, 2019, 5: 44-49. LAI C X. Application of HydroCOM system on new hydrogen compressor in hydrocracking unit[J]. Compressor Technology, 2019, 5: 44-49. (in Chinese) |
| [2] |
孙泽胜, 李旭. 无级气量调节系统在空气往复压缩机上的应用[J]. 氮肥与合成气, 2020, 48(3): 14-16, 23. SUN Z S, LI X. Application of stepless gas flow regulation system on air reciprocating compressor[J]. Nitrogenous Fertilizer & Syngas, 2020, 48(3): 14-16, 23. (in Chinese) |
| [3] |
王瑶, 张进杰, 周超, 等. 基于逐级递推回流控制的压缩机负荷连续调节系统研究[J]. 北京化工大学学报(自然科学版), 2018, 45(3): 84-89. WANG Y, ZHANG J J, ZHOU C, et al. A continuous capacity regulation system for a reciprocating compressor based on stage-by-stage recursive backflow control[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2018, 45(3): 84-89. (in Chinese) |
| [4] |
ASHAYERI L, DOUSTMOHAMMADI A, SABERI F F. Fault-tolerant control of flexible satellite with infinite-dimensional model[J]. Advances in Space Research, 2021, 68(7): 3080-3092. DOI:10.1016/j.asr.2021.07.009 |
| [5] |
郝立颖, 杨光红. 不确定线性系统的滑模容错控制[J]. 中国科技论文, 2013, 8(1): 62-66. HAO L Y, YANG G H. Robust fault-tolerant control based on sliding mode method for uncertain linear systems[J]. China Sciencepaper, 2013, 8(1): 62-66. (in Chinese) |
| [6] |
赵石磊, 郭红, 刘宇鹏. 基于轨迹跟踪的线性时滞系统容错控制[J]. 信息与控制, 2015, 44(4): 469-473. ZHAO S L, GUO H, LIU Y P. Fault tolerant control for linear time-delay system based on trajectory tracking[J]. Information and Control, 2015, 44(4): 469-473. (in Chinese) |
| [7] |
王君, 尹雄东. 四旋翼无人机的自适应容错控制[J]. 空间控制技术与应用, 2019, 45(1): 32-38. WANG J, YIN X D. Adaptive fault-tolerant control for quadrotor UAV[J]. Aerospace Control and Application, 2019, 45(1): 32-38. (in Chinese) |
| [8] |
LAWRENCE D A, RUGH W J. Gain scheduling dynamic linear controllers for a nonlinear plant[J]. Automatica, 1995, 31(3): 381-390. |
| [9] |
HAN Y, BIGGS J D, CUI N G. Adaptive fault-tolerant control of spacecraft attitude dynamics with actuator failures[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(10): 2033-2042. |
| [10] |
CAO T, GONG H J, HAN B. Sliding mode fault tolerant attitude control scheme for spacecraft with actuator faults[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2019, 36(1): 119-127. |
| [11] |
QIAN M S, JIANG B, LIU H H T. Dynamic surface active fault tolerant control design for the attitude control systems of UAV with actuator fault[J]. International Journal of Control, Automation and Systems, 2016, 14(3): 723-732. |
| [12] |
刘金琨. 滑模变结构控制MATLAB仿真: 基本理论与设计方法[M]. 4版. 北京: 清华大学出版社, 2019. LIU J K. Sliding mode control design and MATLAB simulation: the basic theory and design method[M]. 4th ed. Beijing: Tsinghua University Press, 2019. (in Chinese) |
| [13] |
GODARD, KUMAR K D. Fault tolerant reconfigurable satellite formations using adaptive variable structure techniques[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(3): 969-984. |
| [14] |
MAO Z H, YAN X G, JIANG B, et al. Adaptive fault-tolerant sliding-mode control for high-speed trains with actuator faults and uncertainties[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(6): 2449-2460. |
| [15] |
JIANG Y, HU Q L, MA G F. Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures[J]. ISA Transactions, 2010, 49(1): 57-69. |
| [16] |
江志农, 周超, 张进杰, 等. 往复压缩机气量调节控制失稳自愈调控方法研究[J]. 机械工程学报, 2020, 56(22): 131-141. JIANG Z N, ZHOU C, ZHANG J J, et al. Research on self-healing control method of reciprocating compressor capacity control instability[J]. Journal of Mechanical Engineering, 2020, 56(22): 131-141. (in Chinese) |
| [17] |
高金吉. 机器故障诊治与自愈化[M]. 北京: 高等教育出版社, 2012. GAO J J. Machines fault diagnosis and self-recovery[M]. Beijing: Higher Education Press, 2012. (in Chinese) |








