欠驱动系统是指控制输入自由度小于被控输出自由度的一类系统,如柔性机械臂的设计是通过一个伺服电机驱动机械臂产生位移,并抑制机械臂在移动过程中的弹性形变。欠驱动机械系统在机器人、航空航天、船舶等工业领域具有重要的研究意义和广泛的工程应用前景。针对欠驱动机械系统的控制,目前学者们已经提出了许多基于模型的设计方法,如反馈线性化、反演控制、内模控制、滑模控制等,以这类方法设计控制器时需要掌握被控系统的准确的数学模型[1]。常用的建模方法往往基于一定的假设或在对系统部分次要模态的忽略下进行;同时,当被控系统具有模型不确定、未建模动态或随机环境干扰时,一些传统方法会出现控制性能和鲁棒性变差等现象。为解决此类问题,数据驱动控制方法被提出并得到推广。数据驱动控制理论利用大量的数据和知识,在难于建立受控系统较准确机理模型的条件下, 实现对生产过程和设备的优化控制、预报和评价,具有重要的理论与现实意义[2]。
迭代学习控制是一种基于数据驱动的无模型控制方法,通过上一次迭代时的控制输入及本次(或上一次系统)的真实输出与参考轨迹的偏差信号,来提前修正学习下一次迭代的控制输入信号,使得系统在同一重复任务中的控制输入不断趋近于最优控制输入,最终使系统的输出收敛到参考轨迹上,实现系统的准确跟踪。由于其控制结构简单清晰,在重复性运动控制中性能高效精准,从而得到了广泛的研究与应用。傅勤[3]采用适用于非正则系统的微分型学习律设计优化的迭代学习控制器,借助泛函分析理论证明了闭环系统的收敛性;Liu等[4]针对柔性机械臂系统,利用比例-微分(proportional-derivative,PD)的反馈结构和迭代项构造自适应方案,进行轨迹跟踪并抑制扰动;王晶等[5]研究了对批次长度随机变化的反馈辅助比例-微分型量化迭代学习控制问题,量化了跟踪误差信号和控制输入信号,放宽了经典迭代学习控制中的限制要求。
然而,经典的迭代学习控制往往需要进行多次学习与迭代,迭代速率较低,并且对于重复性干扰的抑制能力较弱。Arimoto等[6]提出一种带有自适应性因子即遗忘因子的新型迭代学习控制律,研究表明遗忘因子的加入可以有效提高系统的抗干扰能力,并且在一定程度上增加收敛速度。戴宝林等[7]提出了基于最优增益方法的遗忘因子迭代学习控制算法,提高了系统的鲁棒性并改善了系统的输出性能。万鹏等[8]使用遗忘因子自适应性迭代学习控制器,实现了混联机械臂系统的角同步控制,提高了同步精度并加快了动态响应。李佳伟等[9]提出一种基于遗忘因子的数据驱动最优迭代学习控制算法,并应用于重复运动的非线性非仿射系统,提高了控制的灵活性。上述研究表明遗忘因子的加入可抑制系统中出现的重复性干扰,但当环境中出现的干扰具有非重复特性时,系统的控制性能会大大降低。
本文针对非线性欠驱动机械系统,设计了一种基于卡尔曼滤波器的遗忘因子迭代学习控制律。在迭代学习控制律中引入自适应性遗忘因子,以降低重复性干扰在迭代过程中的累加,增强系统在重复干扰信号下的鲁棒性。卡尔曼观测器通过比较滤波器输出和实际输出的残差,计算得到最小方差指标下的最优状态估计值,以减小非重复性高斯噪声干扰对系统状态的影响。
1 柔性尺动力学模型本文研究了一类由一个控制输入控制两个被控输出的欠驱动机械系统。作为典型的非线性欠驱动控制研究对象,柔性尺常用来进行柔性环节的理论研究和非线性控制的方法验证。以Quanser公司生产的柔性尺平台为实际研究对象,其组成结构如图 1所示。

|
图 1 柔性尺连杆结构模型 Fig.1 Flexible ruler link structure model |
如图 1所示,柔性尺由轻质不锈钢连杆、旋转伺服直流电动机、光电编码器等组成。其中,连杆上的应变片用来测量柔性尺偏转角,伺服电机驱动柔性连杆转动,光电编码器测量角度信号值。
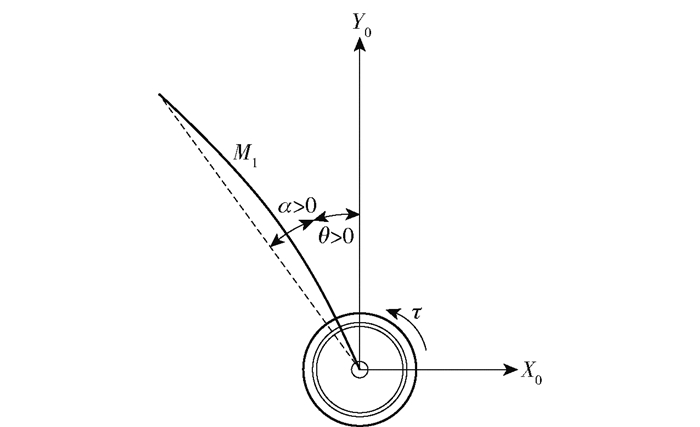
对柔性尺进行动力学分析,其物理模型如图 2所示。
|
图 2 柔性尺运动原理 Fig.2 Motion principle of flexible ruler |
柔性尺的控制目标是伺服角θ,其随伺服电机驱动而逆时针转动。在给定参考轨迹下,伺服电机的负载齿轮上产生一个扭矩τ,驱动柔性尺追踪目标角度θr,同时应保持柔性尺的弹性形变角α趋近于0(理想状况下为0),允许其在微小范围内波动,使弹性形变对伺服角追踪效果的影响降至最低。
通过牛顿-拉格朗日方法对柔性尺系统建模,得到柔性尺非线性动力学模型为[10]
| $ \begin{aligned} &\ \ \ \ \ \ \ \ \ddot{\theta}=\left(-\frac{B_{\mathrm{eq}}}{J_{\mathrm{eq}}}-\frac{\eta_{\mathrm{g}} K_{\mathrm{g}}^{2} \eta_{\mathrm{m}} K_{\mathrm{t}} K_{\mathrm{m}}}{J_{\mathrm{eq}} R_{\mathrm{m}}}\right) \dot{\theta}+\frac{K_{\mathrm{s}}}{J_{\mathrm{eq}}} \alpha+\frac{\eta_{\mathrm{g}} K_{\mathrm{g}} \eta_{\mathrm{m}} K_{\mathrm{t}}}{J_{\mathrm{eq}} R_{\mathrm{m}}} \cdot \\ &u+\varepsilon \frac{K_{\mathrm{s}}}{J_{\mathrm{eq}}} \alpha^{3} \\ &\ \ \ \ \ \ \ \ \ddot{\alpha}=\left(\frac{B_{\mathrm{eq}}}{J_{\mathrm{eq}}}+\frac{\eta_{\mathrm{g}} K_{\mathrm{g}}^{2} \eta_{\mathrm{m}} K_{\mathrm{t}} K_{\mathrm{m}}}{J_{\mathrm{eq}} R_{\mathrm{m}}}\right) \dot{\theta}-\frac{K_{\mathrm{s}}\left(J_{\mathrm{l}}+J_{\mathrm{eq}}\right)}{J_{\mathrm{eq}} J_{\mathrm{l}}} \alpha- \\ &\frac{\eta_{\mathrm{g}} K_{\mathrm{g}} \eta_{\mathrm{m}} K_{\mathrm{t}}}{J_{\mathrm{eq}} R_{\mathrm{m}}} u-\varepsilon \frac{K_{\mathrm{s}}\left(J_{\mathrm{l}}+J_{\mathrm{eq}}\right)}{J_{\mathrm{eq}} J_{\mathrm{l}}} \alpha^{3} \end{aligned} $ | (1) |
其中ε为建模系数,线性化后此部分的非线性项为0。定义状态变量
| $ \alpha^{3}=0 $ | (2) |
由此可以得到柔性尺的近似线性化数学模型,控制输入为u,整理可得系统对应的状态空间方程为
| $ \begin{aligned} &\dot{\boldsymbol{x}}=\boldsymbol{A}_{\text {ruler }} \boldsymbol{x}+\boldsymbol{B}_{\text {ruler }} u \\ &\boldsymbol{y}=\boldsymbol{C}_{\text {ruler }} \boldsymbol{x}+\boldsymbol{D}_{\text {ruler }} u \end{aligned} $ | (3) |
其模型参数为
| $ \boldsymbol{A}_{\text {ruler }}=\left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & \frac{K_{\mathrm{s}}}{J_{\mathrm{eq}}} & -\frac{B_{\mathrm{eq}}}{J_{\mathrm{eq}}}-\frac{\eta_{\mathrm{g}} K_{\mathrm{g}}^{2} \eta_{\mathrm{m}} K_{\mathrm{t}} K_{\mathrm{m}}}{J_{\mathrm{eq}} R_{\mathrm{m}}} & 0 \\ 0 & -K_{\mathrm{s}}\left(\frac{J_{\mathrm{l}}+J_{\mathrm{eq}}}{J_{\mathrm{eq}} J_{\mathrm{l}}}\right) & \frac{B_{\mathrm{eq}}}{J_{\mathrm{eq}}}+\frac{\eta_{\mathrm{g}} K_{\mathrm{g}}^{2} \eta_{\mathrm{m}} K_{\mathrm{t}} K_{\mathrm{m}}}{J_{\mathrm{eq}} R_{\mathrm{m}}} & 0 \end{array}\right] $ |
| $ \boldsymbol{B}_{\text {ruler }}=\left[\begin{array}{c} 0 \\ 0 \\ \frac{\eta_{\mathrm{g}} K_{\mathrm{g}} \eta_{\mathrm{m}} K_{\mathrm{t}}}{J_{\mathrm{eq}} R_{\mathrm{m}}} \\ -\frac{\eta_{\mathrm{g}} K_{\mathrm{g}} \eta_{\mathrm{m}} K_{\mathrm{t}}}{J_{\mathrm{eq}} R_{\mathrm{m}}} \end{array}\right] $ |
| $ \boldsymbol{C}_{\text {ruler }}=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right] $ |
| $ \boldsymbol{D}_{\text {ruler }}=\left[\begin{array}{l} 0 \\ 0 \end{array}\right] $ |
采用线性化后的近似模型便于卡尔曼观测器的设计,从而计算卡尔曼增益。
Quanser柔性尺动力学模型参数如表 1所示。
| 下载CSV 表 1 柔性尺模型参数 Table 1 Parameter of flexible ruler model |
在随机噪声或不确定干扰环境下,卡尔曼观测器可以实现对系统真实状态的最优估计。卡尔曼观测包括预测与更新两步:预测是指通过模型参数与当前时刻的测量数据对下一时刻进行先验估计,并进行不确定性的传递,以估计先验误差协方差;更新则是对状态进行修正,更新误差,结合先验估计值进行后验估计,得到最优状态估计值。
考虑线性化后受扰动的柔性尺系统
| $ \begin{aligned} &\dot{\boldsymbol{x}}_{k}(t)=\boldsymbol{A}_{\text {ruler }} \boldsymbol{x}_{k}(t)+\boldsymbol{B}_{\text {ruler }} u_{k}(t)+\boldsymbol{p}_{k}(t) \\ &\boldsymbol{y}_{k}(t)=\boldsymbol{C}_{\text {ruler }} \boldsymbol{x}_{k}(t)+\boldsymbol{o}_{k}(t) \end{aligned} $ | (4) |
式中,xk(t)是系统的状态,u是控制输入,yk(t)是系统输出,pk(t)是系统的过程噪声,ok(t)是系统的观测噪声。假设pk(t)和ok(t)是高斯分布的白噪声且不相关
| $ \begin{aligned} &\boldsymbol{Q}_{\boldsymbol{p}}=E\left[\boldsymbol{p}, \boldsymbol{p}^{\mathrm{T}}\right] \\ &\boldsymbol{R}_{\boldsymbol{o}}=E\left[\boldsymbol{o}, \boldsymbol{o}^{\mathrm{T}}\right] \\ &E\left[\boldsymbol{p}, \boldsymbol{o}^{\mathrm{T}}\right]=0 \end{aligned} $ | (5) |
其中E为期望算子。
2.1.1 状态预测首先根据系统的状态空间得到预估状态
| $ \hat{\overline{\boldsymbol{x}}}_{k}=\boldsymbol{A}_{\text {ruler }} \hat{\overline{\boldsymbol{x}}}_{k-1}+\boldsymbol{B}_{\text {ruler }} u_{k-1} $ | (6) |
根据定义得到状态估计误差
| $ \overline{\boldsymbol{e}}_{k}=\boldsymbol{x}_{k}-\hat{\overline{\boldsymbol{x}}}_{k} $ | (7) |
由式(7)得到误差协方差
| $ \overline{\boldsymbol{P}}_{k}=E\left[\overline{\boldsymbol{e}}_{k} \overline{\boldsymbol{e}}_{k}^{\mathrm{T}}\right] $ | (8) |
根据式(5)和式(8)得到误差协方差
| $ \overline{\boldsymbol{P}}_{k}=\boldsymbol{A}_{\text {ruler }} \boldsymbol{P}_{k-1} \boldsymbol{A}_{\text {ruler }}^{\mathrm{T}}+\boldsymbol{Q}_{\boldsymbol{p}} $ | (9) |
在卡尔曼滤波中关键参数为卡尔曼增益K,卡尔曼增益起到校正的作用。卡尔曼增益的含义在于利用相关性在系统执行控制的过程中根据误差动态调整预测模型和观测模型的权重,来决定更偏向于选择估计值还是观测值,从而起到关键滤波抗噪的作用。根据迹的定义可得
| $ \begin{aligned} &\ \ \ \ \ \ \ \ {tr}\left(\boldsymbol{P}_{k}\right)={tr}\left(\overline{\boldsymbol{P}}_{k}\right)-2 {tr}\left(\boldsymbol{K} \boldsymbol{C}_{\text {ruler }} \overline{\boldsymbol{P}}_{k}\right)+{tr}\left(\boldsymbol{K} \boldsymbol{C}_{\text {ruler }}\right. \\ &\left.\overline{\boldsymbol{P}}_{k} \boldsymbol{C}_{\text {ruler }}^{\mathrm{T}} \boldsymbol{K}^{\mathrm{T}}\right)+{tr}\left(\boldsymbol{K} \boldsymbol{R}_{\boldsymbol{o}} \boldsymbol{K}^{\mathrm{T}}\right) \end{aligned} $ | (10) |
利用误差协方差的迹对卡尔曼增益求导即
| $ \frac{\mathrm{d} {tr}\left(\boldsymbol{P}_{k}\right)}{\mathrm{d} \boldsymbol{K}}=0 $ | (11) |
根据式(10)和式(11)可得卡尔曼增益表达式
| $ \boldsymbol{K}=\frac{\overline{\boldsymbol{P}}_{k} \boldsymbol{C}_{\text {ruler }}^{\mathrm{T}}}{\boldsymbol{C}_{\text {ruler }} \overline{\boldsymbol{P}}_{k} \boldsymbol{C}_{\text {ruler }}^{\mathrm{T}}+\boldsymbol{R}_{\boldsymbol{o}}} $ | (12) |
将先验估计值和卡尔曼增益下的残差作为修正项对先验估计进行修正,得到后验估计值
| $ \hat{\boldsymbol{x}}_{k}=\hat{\overline{\boldsymbol{x}}}_{k}+\boldsymbol{K}\left(\boldsymbol{y}_{k}-\boldsymbol{C}_{\mathrm{ruler}} \hat{\overline{\boldsymbol{x}}}_{k}\right) $ | (13) |
将式(13)代入式(8)对误差进行更新得到
| $ \boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K} \boldsymbol{C}_{\text {ruler }}\right) \overline{\boldsymbol{P}}_{k} $ | (14) |
其中I为单位矩阵。由以上推导可知采用卡尔曼滤波递推算法可以不断修正观测值和实际值之间的残差,从而得到最优估计状态值。当存在高斯噪声时,可以通过这种方法对噪声进行平滑滤波,增强系统的鲁棒性。
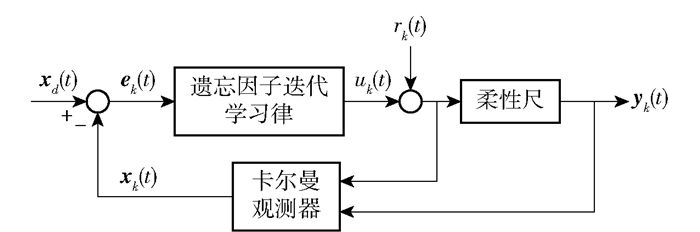
2.2 基于卡尔曼滤波器的遗忘因子迭代学习利用所设计的卡尔曼观测器,可以得到系统实时最优状态预测数据。通过被控系统的实时输出数据,参考其与目标轨迹的误差,设计基于卡尔曼观测器的遗忘因子比例-积分-微分(proportional-integral-derivative,PID)型迭代学习控制器,简称为遗忘因子型迭代学习控制,其控制结构如图 3所示。
|
图 3 控制系统结构 Fig.3 Control system structure |
PID型迭代学习控制律设计如下。
| $ \begin{aligned} &u_{k+1}(t)=(1-f f) u_{k}(t)+f f u_{0}+K_{\mathrm{p}} z_{k+1}(t)+ \\ K_{\mathrm{D}} &\dot{z}_{k+1}(t)+K_{\mathrm{I}} \int_{0}^{t} z_{k+1}(\tau) \mathrm{d} \tau \end{aligned} $ | (15) |
式中,zk+1为第k+1时刻参考轨迹与输出状态的追踪误差,ff∈[0, 1)为自适应项即遗忘因子,在迭代过程中动态变化,u0为初始控制值,ffu0为初始修正项。
遗忘因子型迭代学习控制在迭代初期通过初始修正项快速达到要求的参考值,增大收敛速度,并避免系统出现大幅度的超调及不必要的摆动;在迭代过程中动态减小遗忘因子的值直至0, 使系统受初始修正项的影响逐渐减小,而更多依赖于前次迭代时的控制输入信号,最终获得准确的控制输入信号序列。
3 数值仿真 3.1 理想环境中的迭代学习控制针对柔性尺非线性模型(式(1)),在Matlab2016 simulink上进行数值仿真。设定参考轨迹为yd=0.017 5sin(3πt),设置仿真时间为4 s,迭代次数为68次,初始控制输入u0=0.6,PID型学习律参数设置为KP=0.2,KI=0,KD=0.15。
设计两个性能指标,即运行时间内控制消耗J(式(16))以及误差绝对值的积分I(IAE)(式(17)),来定量衡量控制方法对应的系统性能。在本文中,需要分别讨论伺服角和形变角的性能指标IAEθ和IAEα。
| $ J=\int_{0}^{t} u \mathrm{d} t $ | (16) |
| $ I=\int_{0}^{t}|e| \mathrm{d} t $ | (17) |
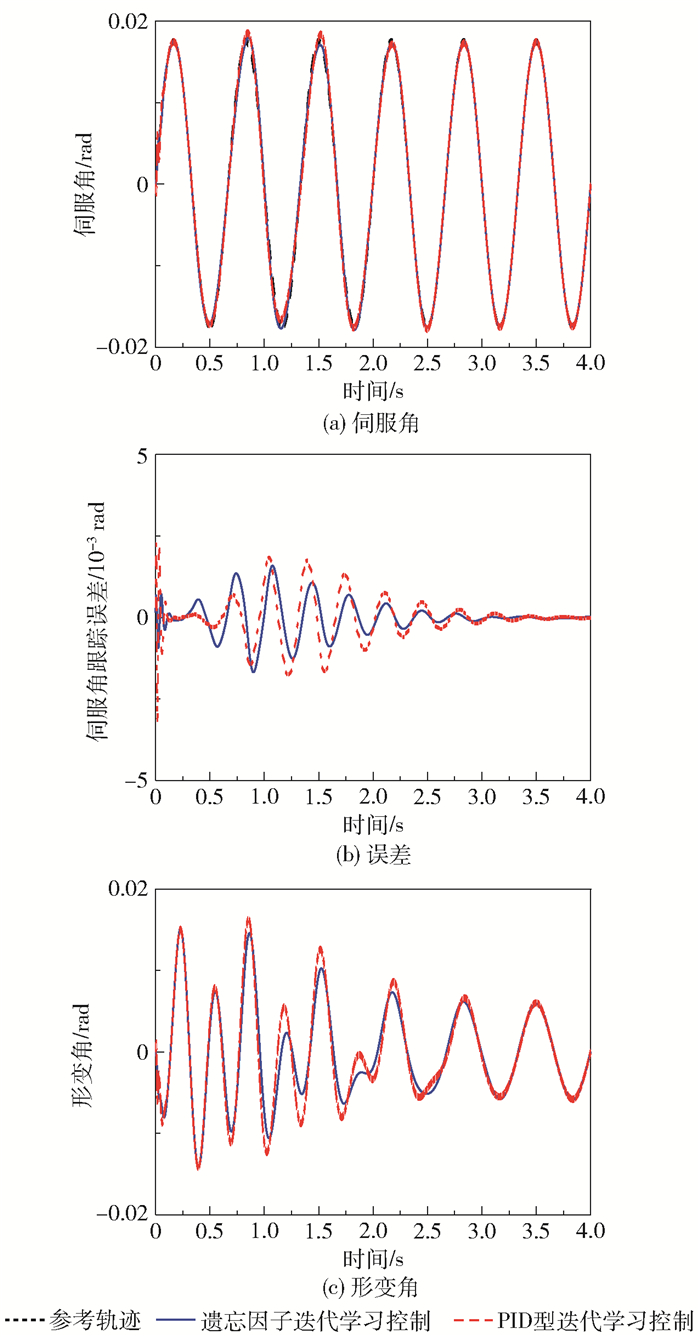
将含遗忘因子的PID型迭代学习控制与传统PID型迭代学习控制进行对比,设定遗忘因子ff=0.95,随着迭代次数的增加,遗忘因子在每次迭代时自动减去0.05直至减为0。设定参考轨迹yd=0.017 5sin(3πt),所得结果如图 4所示。
|
图 4 控制效果对比 Fig.4 Comparison of control effects |
从图 4可以看出两种迭代学习控制下,伺服角的性能表现总体相差不大,但PID型迭代学习控制前期的波动大于遗忘因子迭代学习控制。而在追踪误差分析上,传统PID型迭代学习控制的伺服角误差大于基于遗忘因子迭代学习控制的伺服角误差。对于形变角,PID型迭代学习控制的输出振荡剧烈,且偏差较大,而遗忘因子迭代学习控制器明显抑制了系统形变角的输出振荡,初始偏差也更小,收敛更快。同时,遗忘因子迭代学习控制比传统PID型迭代学习控制有更强的抑制形变的能力。
通过表 2的3个性能指标进行定量分析,对比得出遗忘因子迭代学习控制的控制消耗、伺服角及形变角的误差绝对值积分都更小,具有更加稳定、精准的控制性能。
| 下载CSV 表 2 不同迭代学习控制效果对比 Table 2 Comparison of different iterative learning control effects |
综上,遗忘因子的加入增强了系统的自适应性,并且可以加大收敛速度,抑制形变,优于传统PID型迭代学习控制效果。
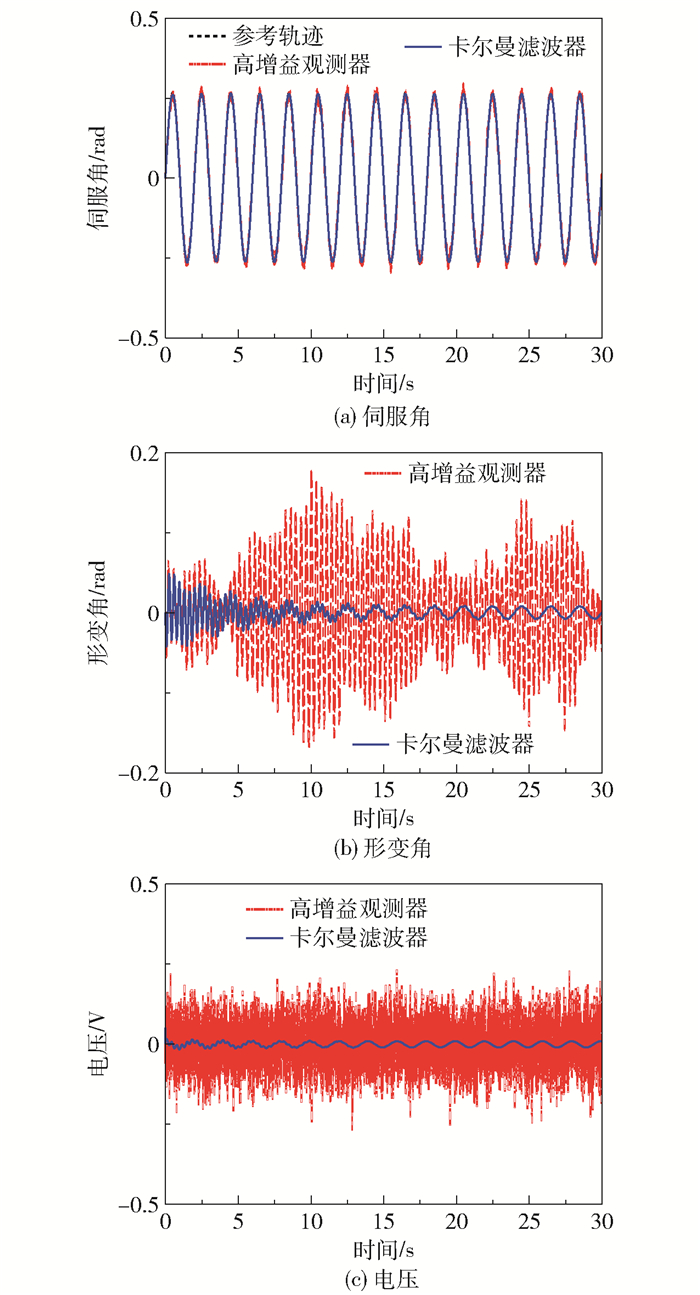
3.2 随机噪声环境中的迭代学习控制为了验证在随机噪声环境中本文控制设计的可行性,进行如下仿真。对比卡尔曼观测器与常用的高增益观测器下系统的控制表现,在两种观测器环境中均加入同样大小的高斯白噪声作为随机噪声,设置幅值为0.1,设定卡尔曼观测器参数Q=diag[ 0.001 0.001 0.001 0.001],R=diag[1 1]。数值仿真结果如图 5所示。
|
图 5 基于两种观测器的控制系统性能对比 Fig.5 Comparison of the system performance under the proposed control method based on two observers |
从图 5可见,在伺服角追踪过程中,基于两种观测器的控制设计的系统输出均能迅速逼近目标值,追踪性能良好。其中,在基于高增益观测器的控制设计下,噪声干扰仍会对系统伺服角产生一定程度的影响,系统输出与目标值之间的误差相对较大;而卡尔曼滤波器最大限度地降低了噪声影响,闭环系统伺服角的追踪性能良好。对于形变角,在基于高增益观测器的控制设计下,噪声干扰影响明显,形变角输出波动较大,柔性尺抖动剧烈,严重影响了闭环系统性能;而基于卡尔曼滤波器的控制设计有效抑制了噪声干扰,基于最小方差准则可得到系统最优估计状态,使形变角输出逼近理想状态,其值在0附近小范围波动。对于控制输入u,由图 5可知,基于高增益观测器的控制方法由于仅依据数学模型进行状态观测,缺少有效的噪声抑制设计,因而严重影响了控制输入和闭环系统性能;而基于卡尔曼滤波器的设计得到的状态数据保证了控制输入中的噪声影响最小,闭环系统整体稳定,且稳态误差较小。
通过表 3中的3个性能指标进行定量对比分析,可以得出卡尔曼滤波器下,本文提出的遗忘因子型迭代学习控制的控制消耗、伺服角及形变角的误差绝对值积分都更小,说明其控制性能更好。
| 下载CSV 表 3 两种观测器下遗忘因子型迭代学习控制效果对比 Table 3 Comparison of forgetting factor iterative learning control with two kinds of observer |
由以上分析可知,卡尔曼滤波器作为观测器可有效减小高斯噪声对系统的影响,使输出值更接近真实值,误差更小,具有更好的鲁棒性。
4 实物实验 4.1 实验平台为验证本文所设计方案的可行性,在Quanser公司设计的柔性尺系统实物平台(图 6)上进行实验验证。该平台由轻质不锈钢连杆、旋转伺服单元、旋转伺服直流电动机、光电编码器等组成。所有实物实验均在图 6所示的环境中进行。

|
图 6 柔性尺平台实物图 Fig.6 View of the flexible ruler platform |
在图 6所示的柔性尺平台上进行实物实验验证,参考轨迹设定为正弦曲线,频率为0.5 Hz,幅值为0.523 6 rad。迭代次数设定为60次,PID型学习参数设定为KP=8.5,KI=0,KD=0.07;初始控制输入u0=0.2,遗忘因子ff=0.95。
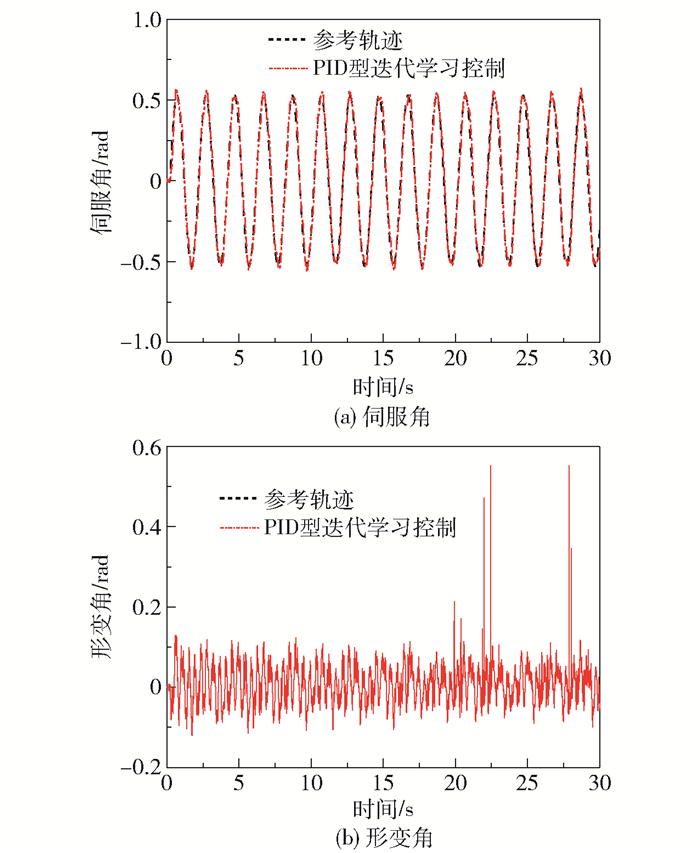
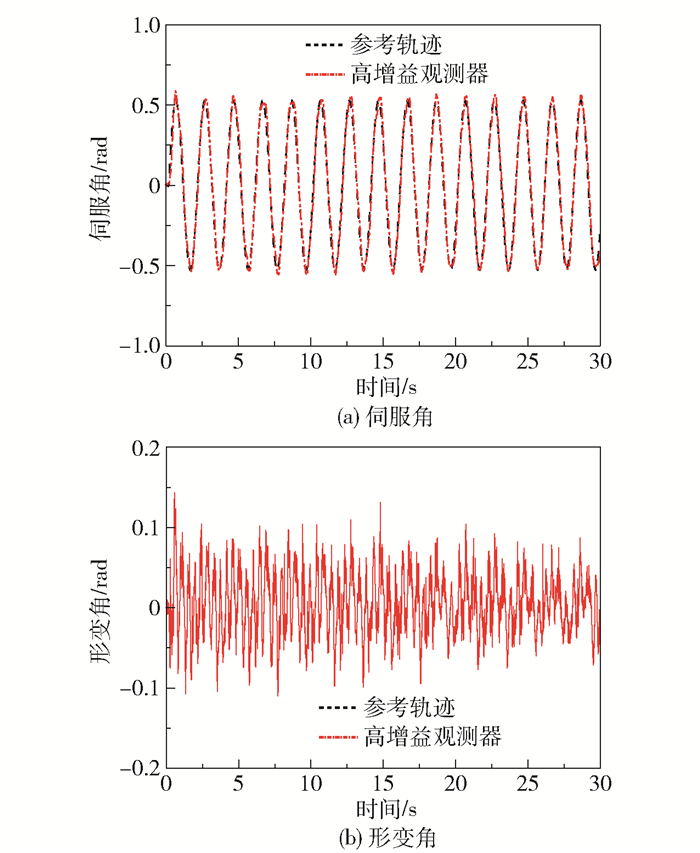
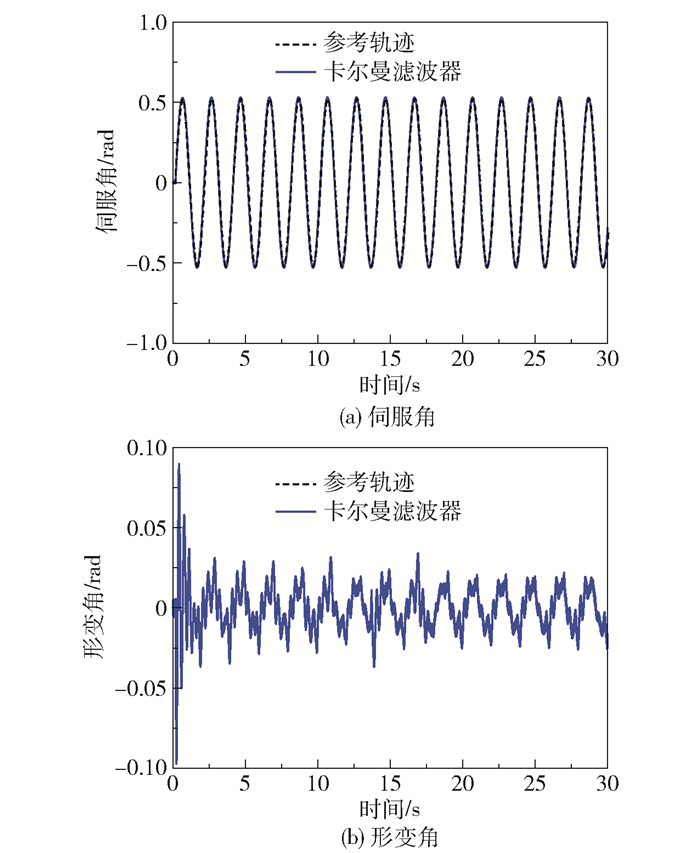
在实物仿真环境中加入幅值为0.1的输入高斯白噪声,分别对比基于高增益观测器的传统PID型迭代学习控制、基于高增益观测器的遗忘因子迭代学习控制和基于卡尔曼观测器的遗忘因子迭代学习控制的效果,结果如图 7~9所示。
|
图 7 基于高增益观测器的PID型迭代学习控制效果 Fig.7 Effect of PID iterative learning control based on a high gain observer |
|
图 8 基于高增益观测器的遗忘因子迭代学习控制效果 Fig.8 Effect of forgetting factor iterative learning control based on a high gain observer |
|
图 9 基于卡尔曼滤波器的遗忘因子迭代学习控制效果 Fig.9 Iterative learning control effect of forgetting factor based on a Kalman filter |
从图 7~9中伺服角的实际输出控制效果可以看出,基于高增益观测器的迭代学习控制在高斯白噪声的干扰下输出波形有明显失真,而基于卡尔曼观测器的遗忘因子迭代学习控制的跟踪效果更强且估计值更接近实际输出,噪声对系统的影响明显小于高增益观测器下的系统。从图 7~9中的形变角变化可知,基于卡尔曼观测器的遗忘因子迭代学习控制相比于其他两种迭代学习控制形变角更小,柔性尺抖振现象得到改善。
为了对比不同观测器下的迭代学习控制效果,对高增益观测器-PID迭代学习控制、高增益观测器-遗忘因子迭代学习控制和卡尔曼滤波器-遗忘因子迭代学习控制这3种设计分别进行了性能指标的定量分析,结果见表 4。可以看出遗忘因子的加入可以减小控制消耗、伺服角及形变角的误差绝对值积分,而卡尔曼滤波器可以更好地抑制形变角及伺服角的误差绝对值指标,控制性能更好。
| 下载CSV 表 4 两种观测器下的迭代学习控制效果对比 Table 4 Comparison of the effects of iterative learning control with two kinds of observers |
上述物理实验验证及性能定量分析的结果表明,在随机噪声环境下,相比于无遗忘因子、基于普通高增益观测器的控制设计,本文所提的基于卡尔曼滤波器的遗忘因子迭代学习控制设计在柔性尺平台上具有更强的鲁棒性和抗噪能力。
5 结论本文针对一类欠驱动机械系统设计了一种基于卡尔曼滤波器的遗忘因子PID型迭代学习控制策略,数值仿真实验验证了该方法对于欠驱动机械系统(柔性尺)可以获得稳定的控制。与无遗忘因子的普通高增益观测器的迭代学习控制方法相比,本文所提方法的控制性能更好,鲁棒性更强。同时,在实物上的实际控制实验也验证了本文所提方法的有效性;在重复性干扰和随机噪声等非重复性干扰的环境下,本文方法具有更强的鲁棒性。
| [1] |
张雪莲, 潘铁强. 柔性机械臂控制方法的研究[J]. 科技信息(学术研究), 2006(9): 89-90. |
| [2] |
侯忠生, 许建新. 数据驱动控制理论及方法的回顾和展望[J]. 自动化学报, 2009, 35(6): 650-667. HOU Z S, XU J X. On data-driven control theory: the state of the art and perspective[J]. Acta Automatica Sinica, 2009, 35(6): 650-667. (in Chinese) |
| [3] |
傅勤. 非正则分布参数系统的迭代学习控制[J]. 控制与决策, 2016, 31(1): 114-122. FU Q. Iterative learning control for irregular distributed parameter systems[J]. Control and Decision, 2016, 31(1): 114-122. (in Chinese) |
| [4] |
LIU Z J, LIU J K, HE W. An adaptive iterative learning algorithm for boundary control of a flexible manipulator[J]. International Journal of Adaptive Control and Signal Processing, 2017, 31(6): 903-916. DOI:10.1002/acs.2737 |
| [5] |
王晶, 周楠, 王森, 等. 随机变批次长度的反馈辅助PD型量化迭代学习控制[J]. 控制与决策, 2021, 36(10): 2569-2576. WANG J, ZHOU N, WANG S, et al. Feedback-assisted PD-type quantized iterative learning control with randomly iteration varying lengths[J]. Control and Decision, 2021, 36(10): 2569-2576. (in Chinese) |
| [6] |
ARIMOTO S, KAWAMURA S, MIYAZAKI F. Bettering operation of robots by learning: a new control theory for servomechanism or mechatronics systems[C]//The 23rd IEEE Conference on Decision and Control. Las Vegas, 1984: 1064-1069.
|
| [7] |
戴宝林, 龚俊, 李翠明. 带遗忘因子迭代学习控制最优增益研究[J]. 西北工业大学学报, 2019, 37(5): 1077-1084. DAI B L, GONG J, LI C M. Optimal gain for iterative learning control with forgetting factors[J]. Journal of Northwestern Polytechnical University, 2019, 37(5): 1077-1084. (in Chinese) DOI:10.3969/j.issn.1000-2758.2019.05.028 |
| [8] |
万鹏, 田汪洋, 周吉, 等. 混联机械臂系统带遗忘因子的迭代学习角同步控制[J]. 东莞理工学院学报, 2020, 27(3): 109-113. WAN P, TIAN W Y, ZHOU J, et al. Synchronization control of hybrid manipulator system[J]. Journal of Dongguan University of Technology, 2020, 27(3): 109-113. (in Chinese) |
| [9] |
李佳伟, 林娜, 池荣虎. 基于遗忘因子的数据驱动最优迭代学习控制算法研究[J]. 南京信息工程大学学报(自然科学版), 2021, 13(5): 582-588. LI J W, LIN N, CHI R H. Forgetting factor based data-driven optimal iterative learning control[J]. Journal of Nanjing University of Information Science & Technology, 2021, 13(5): 582-588. (in Chinese) |
| [10] |
Quanser Inc. . Srv02 rotary flexible link user manual[EB/CD]. Markham: Quanser Inc., 2011.
|








