2. 山东美陵化工设备股份有限公司,淄博 255000
2. Shandong Meiling Chemical Equipment Co., Zibo 255000, China
管壳式换热器是目前应用最为广泛的一种换热设备,这种换热器结构简单、制造成本低、流体流动截面宽、水垢清洗方便,有着广泛的适用范围,因此在高温、高压领域占据极其重要的地位。然而传热效率低是管壳式换热器最大的一个缺点,因此针对传统换热器设备的传热强化逐渐成为研究的主流,并主要集中于两个方向:一是开发换热效率更高的新型换热器;二是采用异形强化管来代替传统的光滑管从而达到强化传热的效果。前人的研究表明,与传统的直管通道相比,波纹形通道的换热能力有所提高[1-2]。根据此原理,研究人员开发出一种新的传热设备—波纹管换热器[3]。随后的研究表明,与传统管壳式换热器相比,波纹管结构换热器的综合性能有显著提高[4-6]。近年来,波纹管换热器已被广泛应用于化工、石油和动力等工业领域。众多学者也对波纹管进行了更进一步的研究。张国钊[7]对基管外径为25 mm的波纹管和光滑管进行了传热性能的对比实验,实验结果表明波纹管的传热性能高于传统的光滑管,在实验范围内其总传热系数是光滑管的1.1~1.2倍。昝永超等[8]利用计算流体力学软件Fluent模拟了波纹管的流动与传热特性,发现在所模拟的工况范围内,波纹管的传热特性相比于光滑管最多提高1.83倍。陈瑶等[9]利用Fluent对正弦形波纹管进行了模拟,对湍流状态下的流体流动与传热特性进行了研究,结果表明正弦形波纹管内流体的平均努塞尔数是其当量直径光滑管的1.65~2.67倍。肖金花[10]通过有限元模拟和实验对圆弧形波纹管的流动和传热特性进行了分析研究,发现波纹管的波峰内出现的“涡”是其发挥强化传热作用的关键因素,且在波纹管内的波峰下游处出现局部对流传热系数的最大值。针对这一发现,本课题组前期提出一种新型波纹管—圆弧切线波纹管(或称为锥纹管),锥纹管在传统圆弧形波纹管的基础上增加了强化区间,通过在波纹管的波峰下游处添加一部分直线段来延长波峰下游的长度,从而达到强化传热的效果[11]。随后,还对锥纹管的管内流动与传热特性进行了数值模拟研究[12],结果表明,锥纹管的传热效果和流动阻力性能都优于圆弧形波纹管,有较高的应用推广价值。
本文以水和32#液压油为传热介质,对锥纹管弓形折流板换热器的传热性能和压力降进行实验研究,将其与光滑管弓形折流板换热器进行对比,并在传热介质为水时对锥纹管弓形折流板换热器的管程及壳程传热准则关联式进行拟合,为新型高效管壳式换热器的开发和应用提供参考。
1 换热器结构本文实验所用锥纹管弓形折流板换热器管束结构如图 1所示,管束结构放大图见图 2(a),为进行对比,本文还针对传统光滑管弓形折流板换热器开展了实验,其管芯结构放大图见图 2(b)。实验用换热器为双管程浮头式换热器,由内径为300 mm的壳体,2个管箱以及包含2块管板、13块折流板和32根换热管的管束组成。壳体材料为Q345R钢,管体材料为10#钢,折流板材料为Q235B钢。管子排列方式为转置正方形。

|
图 1 锥纹管弓形折流板换热器管束结构 Fig.1 Tube bundle structure of the conically-corrugated tube heat exchanger with a segmental baffle |

|
图 2 管束结构局部放大图 Fig.2 Partial enlarged view of the tube bundle structure |
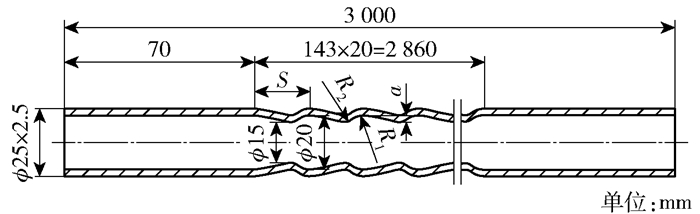
所用光滑管为Ф25 mm×2.5 mm的钢管。所用锥纹管结构见图 3。锥纹管由钢管挤压加工而成,管长L=3 000 mm,波峰圆弧半径R1=6 mm,波谷圆弧半径R2=5 mm,波深a=2.5 mm,波距S=20 mm,每根波纹管包含两个长度为70 mm的光滑管段及143个波纹段。
|
图 3 锥纹管结构示意图 Fig.3 Schematic structure of a conically-corrugated tube |
实验装置主要包括实验用换热器、冷水箱、热水箱(油箱)、冷却塔风机、冷水泵和热水(热油)泵以及中央控制台。图 4为实验用换热器及测试系统实物图。

|
图 4 实验用换热器及测试系统 Fig.4 Experimental heat exchanger and test system |
以管壳程介质均是水为例,实验过程如下:热水从热水箱流出,通过调节阀,由水泵提供动力依次流经流量计、压差计、温度传感器后,通过换热器壳程入口进入到壳程中,再从壳程出口流出,经过温度传感器后,流回热水箱;冷水从冷水箱流出,经过调节阀、水泵、流量计、压差计、温度传感器后,通过换热器管程入口进入管程,再从管程出口流出,经过温度传感器后,通过冷却塔风机将加热后的流体冷却,然后流回冷水箱。如此往复,形成循环,完成本次实验。
2.2 实验方案本文实验分为两组,第一组实验是管程介质为水、壳程介质为水的工况,第二组实验是管程介质为水、壳程介质为32#液压油的工况。具体实验方案如下。
1) 管程介质为水,壳程介质为水
步骤1 热水走壳程,冷水走管程。
步骤2 给定壳程流量Vo=45.00 m3/h(管间流速uo=0.984 3 m/s),管程进口温度为30 ℃,壳程进口温度为70 ℃,分别调整管程流量Vi(m3/h)为1.80、3.96、6.12、8.28、10.44、12.60、14.76、16.92、19.08、21.24、23.4、26.30。待温度和压力稳定后测量管程和壳程的实际流量、进口实际温度、出口温度以及压力降。每个测点测量4次。
步骤3 给定管程流量Vi=26.30 m3/h(管内流速ui=0.796 m/s),管程进口温度为30 ℃,壳程进口温度为70 ℃,分别调整壳程流量Vo(m3/h)为1.80、6.12、10.44、14.76、19.08、23.40、27.72、32.04、36.36、40.68、45.00。待温度和压力稳定后测量管程和壳程的实际流量和进口实际温度、管程和壳程出口温度以及管程和壳程压力降。每个测点测量4次。
分别对光滑管弓形折流板换热器、锥纹管弓形折流板换热器进行上述实验。
2) 管程介质为水,壳程介质为32#液压油
步骤1 热油走壳程,冷水走管程。
步骤2 给定壳程流量Vo=36.00 m3/h(管间流速uo=0.787 4 m/s),管程进口温度为30 ℃,壳程进口温度为70 ℃,分别调整管程流量Vi(m3/h)为1.80、3.96、6.12、8.28、10.44、12.60、14.76、16.92、19.08、21.24、23.4、26.30。待温度和压力稳定后测量管程和壳程的实际流量、进口实际温度、出口温度以及压力降。每个测点测量4次。
步骤3 给定管程流量Vi=26.30 m3/h(管内流速ui=0.796 m/s),管程进口温度为30 ℃,壳程进口温度为70 ℃,分别调整壳程流量Vo(m3/h)为18.0、19.8、21.6、23.4、25.2、27.0、28.8、30.6、32.4、34.2、36.0。待温度和压力稳定后测量管程和壳程的实际流量、进口实际温度、出口温度以及压力降。每个测点测量4次。
分别对光滑管弓形折流板换热器、锥纹管弓形折流板换热器进行上述实验。
2.3 数据处理将总传热系数K(单位W/(m2 ·K))作为换热器传热效率的评价标准,其计算式见式(1)[13]。
| $ K=\frac{Q}{A \Delta t_{\mathrm{m}}} $ | (1) |
式中,Q为平均换热量,W,取冷热介质热流量的算术平均值;A为换热面积,m2;Δtm为平均传热温差,℃。式(1)中,
| $ Q=\frac{Q_{\mathrm{c}}+Q_{\mathrm{h}}}{2} $ | (2) |
式中,Qc(h)=Vc(h)ρc(h)cp,c(h)Δtc(h),其中,Vc(h)为流量,m3/h;ρc(h)为流体密度,kg/m3;cp, c(h)为比热容,J/(kg ·K);Δtc(h)为冷(热)流体进出口温差,℃;下标c、h分别代表冷、热流体。
| $ A=n {\rm{ \mathsf{ π} }} d_{\mathrm{o}} L_{\mathrm{e}} $ | (3) |
其中,n为换热管根数;do为换热管外径,m;Le为换热管有效长度,m。
| $ \Delta t_{\mathrm{m}}=\frac{\Delta t_{1}+\Delta t_{2}}{2} $ | (4) |
式中,Δt1为管程流体进出口温差,Δt2为壳程流体进出口温差,℃。
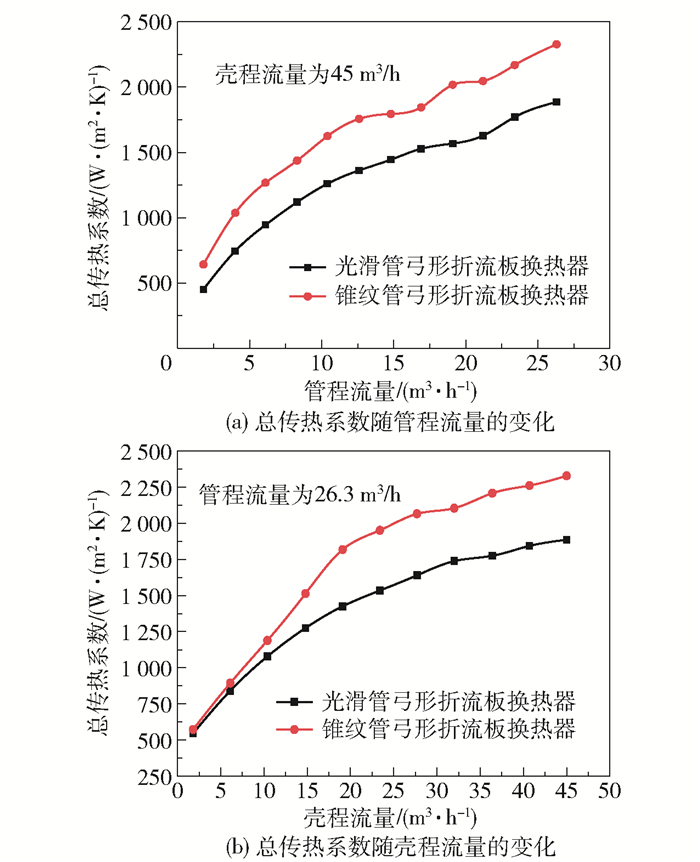
3 实验结果与分析 3.1 总传热系数图 5(a)、(b)分别为光滑管弓形折流板换热器与锥纹管弓形折流板换热器在管壳程介质均为水时,总传热系数随管程流量以及壳程流量的变化趋势。从图中可以看出,与光滑管弓形折流板换热器相比,锥纹管弓形折流板换热器的总传热系数在所测定的管程流量范围内提高了20%~40%,在所测定的壳程流量范围内提高了5%~28%。
|
图 5 管壳程介质均为水时,总传热系数随入口流量的变化 Fig.5 Variation of the total heat transfer coefficient with the inlet flow rate when the media in both shell and tube sides are water |
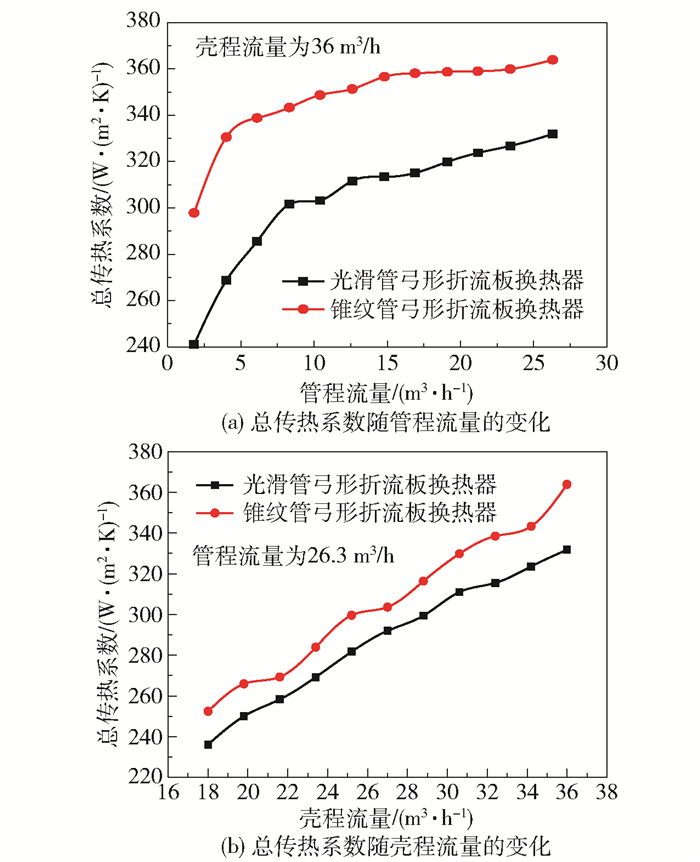
图 6(a)、(b)分别为光滑管弓形折流板换热器与锥纹管弓形折流板换热器在管程介质为水、壳程介质为32#液压油时,总传热系数随管程流量以及壳程流量的变化趋势。由图可知,与光滑管弓形折流板换热器相比,锥纹管弓形折流板换热器的总传热系数在所测定的管程流量范围内提高了10%~20%,在所测定的壳程流量范围内提高了5%~10%,这是由于锥纹管可起到双边强化作用。
|
图 6 管程介质为水、壳程介质为32#液压油时总传热系数随入口流量的变化 Fig.6 Variation of the total heat transfer coefficient with the inlet flow rate when the medium in the tube side is water and the medium in the shell side is 32# hydraulic oil |
管程压力降主要反映换热管内流体流动的阻力大小。图 7(a)、(b)所示为管程介质为水、壳程介质分别为水和32#液压油时,光滑管弓形折流板换热器与锥纹管弓形折流板换热器的管程压力降随管程流量的变化趋势。可以看出,锥纹管的管程压力降明显高于光滑管,当壳程介质为水时,在所测试管程流量范围内锥纹管的压力降增幅约为20%~70%,且随着流量的升高,两者之间的差距增大。当壳程介质为32#液压油时,可得到类似的结果。随着锥纹管传热性能的提高,其管内流体的流动压力降也会增加,这是由于壁面锥纹的存在会造成流体扰动,使流动阻力增加。

|
图 7 管程压力降随管程流量的变化 Fig.7 Variation of tube side pressure drop with tube side flow rate |
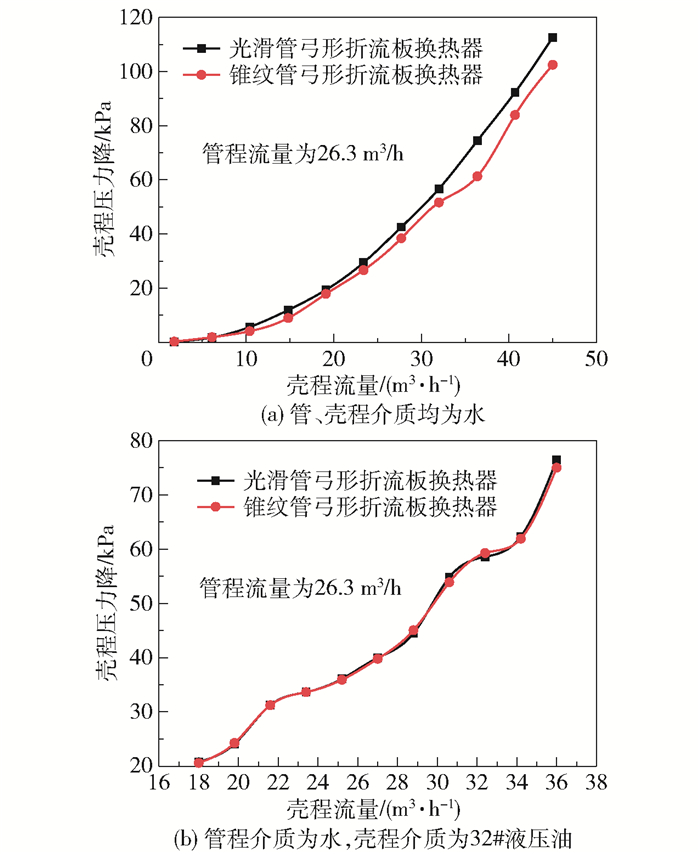
图 8(a)、(b)所示为管程介质为水、壳程介质分别为水和32#液压油时,光滑管弓形折流板换热器与锥纹管弓形折流板换热器的壳程压力降随壳程流量的变化趋势。由图 8(a)可以看出,当管、壳程介质均为水时,在所测试壳程流量范围内锥纹管换热器的壳程压力降比光滑管换热器的要低,降幅最高可达10%。与光滑管换热器相比,锥纹管换热器的折流板孔与锥纹管间缝隙较大,因此锥纹管换热器的壳程流通面积较大,壳程流速较低,致使其壳程压力降较低。由图 8(b)可以看出,当管程介质为水,壳程介质为32#液压油时,由于壳程流动介质黏度较大,壳程流速较低,漏流程度低,因此两台换热器的壳程压力降无明显差别。
|
图 8 壳程压力降随壳程流量的变化 Fig.8 Variation of shell side pressure drop with shell side flow rate |
在管程入口温度为30 ℃,壳程入口温度为70 ℃,管、壳程传热介质均为水的条件下,基于数值模拟结果和实验,对锥纹管弓形折流板换热器的管程及壳程传热准则关联式进行拟合及验证。
4.1 管程数值模拟及传热准则关联式 4.1.1 管程数值模拟选择水作为数值模拟时的流体介质。由于水的物性参数不会随温度的变化产生大幅度改变,因此认为在模拟过程中水的物性参数恒定不变,并选取温度为30 ℃时来计算,此时水的物性参数如表 1所示。
| 下载CSV 表 1 30 ℃时水的物性参数 Table 1 Physical properties of the medium(water) at 30 ℃ |
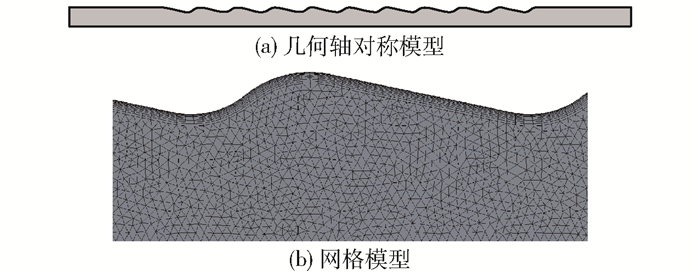
建立锥纹管内流体域有限元模型,锥纹管结构参数如表 2所示,几何轴对称模型和网格模型如图 9所示。
| 下载CSV 表 2 锥纹管结构参数 Table 2 Structural parameters of conically-corrugated tubes |
|
图 9 几何轴对称模型和网格模型 Fig.9 Geometric axisymmetric model and mesh model |
为了消除数值模拟时换热管的进出口段对管内流动和传热效果的影响,建立锥纹管模型时在波纹段两端的进出口分别设置长度为50 mm的直管段。波纹段共包含10个波距。模型是以X轴为对称轴的二维轴对称模型。
入口雷诺数范围为5 000~60 000,计算选用基于压力的隐式求解方式。湍流模型采用重整化群(RNG) k-ε模型,壁面函数选择Scalable Wall Functions,动量、能量、湍流动能、湍流耗散项都采用二阶迎风格式离散方程,压力与速度耦合采用Coupled算法。
入口边界条件:流体入口温度为30 ℃(303.15 K);采用速度入口边界条件,在波纹管入口处施加轴向速度分量,并假设其在横截面上均匀分布,径向速度分量为零;入口湍流动能和耗散率采用Fluent程序默认值。
出口边界条件:参考压力为外界大气压,因此出口边界设置为压力出口,且相对压力为0。
壁面边界条件:壁面采用无滑移边界条件,即在各个方向上的速度分量都等于0;管壁温度设置为恒定的70 ℃(343.15 K)。
4.1.2 管程传热准则关联式拟合在本文中认为锥纹管与光滑管的传热性能间存在相似关系,因此基于传统光滑管的传热准则关联式对锥纹管传热准则关联式进行拟合,关联式的基本形式如下。
| $ N u_{\mathrm{i}}=C {Re}_{\mathrm{i}}^{m} {Pr}_{\mathrm{i}}^{0.3} $ | (5) |
式中,Nui为努塞尔数;Rei为雷诺数;Pri为流体介质的普朗特数;下标i表示锥纹管内;C、m为参数。
对建立的有限元模型进行数值模拟,得到5 000≤Re≤60 000范围内的锥纹管管内努塞尔数,通过拟合可得关联式
| $ N u_{\mathrm{i}}=0.03 R e_{\mathrm{i}}^{0.878} {Pr}_{\mathrm{i}}^{0.3} $ | (6) |
或
| $ \alpha_{\mathrm{i}}=0.03 \frac{\lambda}{d_{\mathrm{i}}} {Re}_{\mathrm{i}}^{0.878} {Pr}_{\mathrm{i}}^{0.3} $ | (7) |
式中,αi为锥纹管管内传热系数,W/(m2 ·K);di为锥纹管基管内径,m。
数值模拟结果和关联式(6)计算结果的比较见表 3。从表中的相对误差可以看出,在5 000≤Re≤60 000范围内,拟合的关联式能够较好地表达锥纹管的传热特性。
| 下载CSV 表 3 数值模拟与关联式计算结果比较 Table 3 Comparison of numerical simulation and correlation calculation results |
总传热系数还可以按照式(8)计算[13]:
| $ \frac{1}{K}=\frac{1}{\alpha_{\mathrm{o}}}+R_{\mathrm{so}}+\frac{b}{\lambda_{\mathrm{b}}} \frac{d_{\mathrm{o}}}{d_{\mathrm{m}}}+R_{\mathrm{si}}+\frac{d_{\mathrm{o}}}{\alpha_{\mathrm{i}} d_{\mathrm{i}}} $ | (8) |
式中,αo为壳程传热系数,W/(m2 ·K);b为管壁的厚度,m;λb为换热管的导热系数,W/(m ·K);dm为换热管对数平均直径,m,
由于实验所用换热器为全新设备,因此换热管内、外表面的污垢热阻值可忽略不计。于是式(8)可简化为
| $ \frac{1}{K}=\frac{1}{\alpha_{\mathrm{o}}}+\frac{b}{\lambda_{\mathrm{b}}} \frac{d_{\mathrm{o}}}{d_{\mathrm{m}}}+\frac{d_{\mathrm{o}}}{\alpha_{\mathrm{i}} d_{\mathrm{i}}} $ | (9) |
联立式(7)和式(9)可得到壳程传热系数计算式
| $ \alpha_{\mathrm{o}}=\frac{1}{\frac{1}{K}-\frac{b}{\lambda_{\mathrm{b}}} \frac{d_{\mathrm{o}}}{d_{\mathrm{m}}}-\frac{d_{\mathrm{o}}}{\alpha_{\mathrm{i}} d_{\mathrm{i}}}} $ | (10) |
对于弓形缺口为25%的光滑管弓形折流板换热器,其壳程传热准则关联式为
| $ N u_{\mathrm{o}}=0.36 {Re}_{\mathrm{o}}^{0.55} {Pr}_{\mathrm{o}}^{0.33}\left(\frac{\mu_{\mathrm{f}}}{\mu_{\mathrm{w}}}\right)^{0.14} $ | (11) |
或
| $ \alpha_{\mathrm{o}}=0.36 \frac{\lambda}{d_{\mathrm{e}}} {Re}_{\mathrm{o}}^{0.55} {Pr}_{\mathrm{o}}^{0.33}\left(\frac{\mu_{\mathrm{f}}}{\mu_{\mathrm{w}}}\right)^{0.14} $ | (12) |
式中,Reo为壳程雷诺数;Pro为壳程流体普朗特数;
| $ R e_{\mathrm{o}}=\frac{\rho u_{\mathrm{o}} d_{\mathrm{e}}}{\mu} $ | (13) |
其中,de为壳程当量直径,m,对于三角形排列de=
对于工程问题,当流体被加热时,
类比光滑管弓形折流板换热器壳程传热准则关联式,设定锥纹管弓形折流板换热器壳程传热准则关联式形式为
| $ N u_{\mathrm{o}}=C R e_{\mathrm{o}}^{m} {Pr}_{\mathrm{o}}^{0.33} $ | (14) |
根据式(10)对实验数据进行处理,对计算所得壳程传热系数进行拟合,得到该锥纹管换热器在本文实验条件下,管、壳程介质均为水时的壳程传热准则关联式为
| $ N u_{\mathrm{o}}=0.255 {Re}_{\mathrm{o}}^{0.566} {Pr}_{\mathrm{o}}^{0.33} $ | (15) |
或
| $ \alpha_{\mathrm{o}}=0.255 \frac{\lambda}{d_{\mathrm{e}}} {Re}_{\mathrm{o}}^{0.566} {Pr}_{\mathrm{o}}^{0.33} $ | (16) |
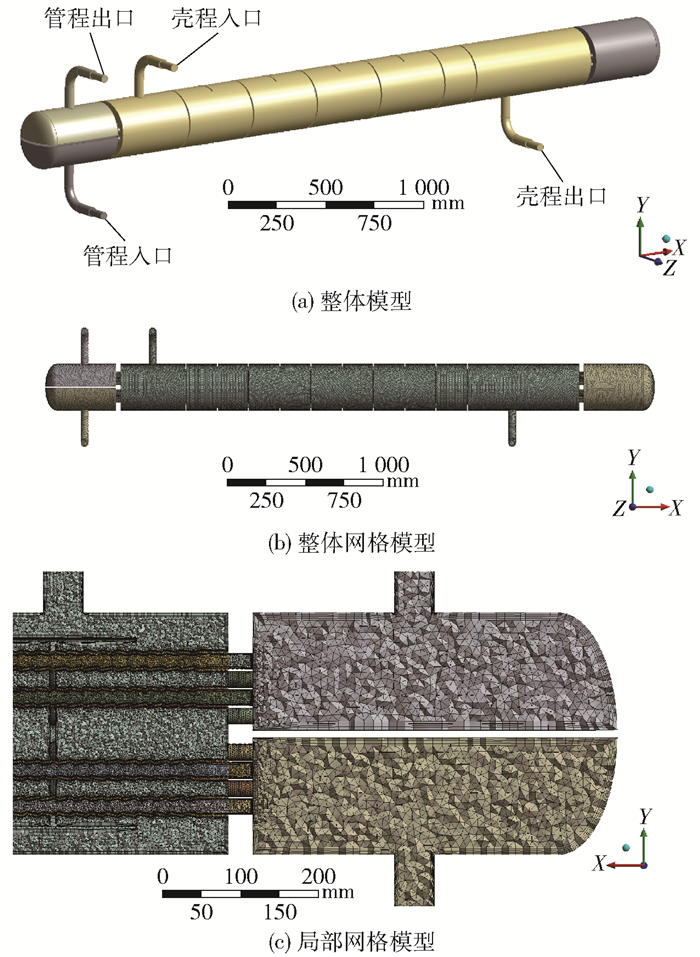
建立锥纹管换热器整体有限元模型,包括管程流体、换热管和壳程流体,结构参数与实验所用换热器相同。由于换热器整体结构复杂,因此采用非结构化网格进行离散,并对边界处网格进行细化。换热器整体模型和网格模型如图 10所示。
|
图 10 换热器整体模型和网格模型 Fig.10 Overall model and grid model of the heat exchanger |
在数值模拟过程中,忽略重力场的影响,入口边界设置为速度入口,速度范围与2.2节中实验方案一致。管程流体介质温度为30 ℃,壳程流体介质温度为70 ℃。出口边界设置为压力出口。求解采用基于压力的隐式求解器,压力与速度耦合采用SIMPLEC算法,湍流模型采用Realizable k-ε两方程模型。换热管壁面采用耦合壁面边界条件,其余固体壁面均采用无滑移绝热壁面。
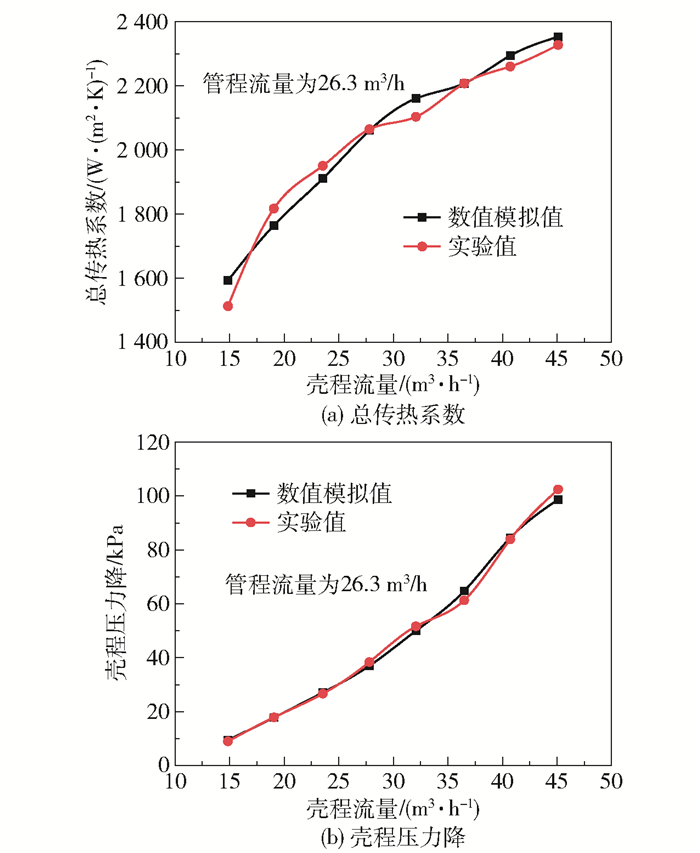
为验证数值模拟的准确性,将数值模拟结果与实验结果进行比较,结果如图 11所示。总传热系数和壳程压力降的最大相对误差分别为5.28%和5.67%,数值模拟与实验相差不大,表明数值模拟结果是可信的。
|
图 11 数值模拟结果验证 Fig.11 Verification of numerical simulation results |
将数值模拟值与拟合得到的传热准则关联式计算结果进行对比验证,具体如表 4所示。数值验算结果表明,关联式(15)与数值模拟的相对误差在15%以内。
| 下载CSV 表 4 壳程传热准则关联式验证 Table 4 Correlation verification of the shell side heat transfer criterion |
对于本文的实验和数值模拟,由于实际加工出的锥纹管及整个换热器与理想或数值模拟的模型在结构细节上可能有差异,会使得实验与计算结果之间存在一定误差;另外,由于换热量大,实验过程中温度的波动也会造成一些误差。
5 结论(1) 与光滑管弓形折流板换热器相比,锥纹管换热器的总传热系数明显提高,当管壳程介质均为水时,在所测试管程流量范围内增幅为20%~40%,在所测试壳程流量范围内增幅为5%~28%;当管程介质为水,壳程介质为32#液压油时,在所测试管程流量范围内增幅为10%~20%,在所测试壳程流量范围内增幅为5%~10%。
(2) 与光滑管弓形折流板换热器相比,在所测试壳程流量范围内,当壳程介质为水时,锥纹管换热器的壳程压力降降幅最大为10%;当壳程介质为32#液压油时,锥纹管换热器的壳程压力降与光滑管换热器相近,而在所测试管程流量范围内锥纹管的管程压力降提高了20%~70%。
(3) 在实验和模拟的基础上,对本文实验所用结构的锥纹管换热器在传热介质为水时的管壳程传热准则关联式进行了拟合,数值验算结果表明,所得关联式可以满足工程设计的精度要求(相对误差小于15%)。
虽然锥纹管弓形折流板换热器的管程压力降明显高于光滑管弓形折流板换热器,但综合考虑传热强化性能和较低的壳程阻力损失,锥纹管弓形折流板换热器仍具有良好的工程应用前景。
| [1] |
SUNDÉN B, SKÖLDHEDEN T. Heat transfer and pressure drop in a new type of corrugated channels[J]. International Communications in Heat and Mass Transfer, 1985, 12(5): 559-566. DOI:10.1016/0735-1933(85)90079-X |
| [2] |
SUDEN B, TROLLHEDEN S. Periodic laminar flow and heat transfer in a corrugated two-dimensional channel[J]. International Communications in Heat and Mass Transfer, 1989, 16(2): 215-225. DOI:10.1016/0735-1933(89)90023-7 |
| [3] |
邱广涛, 丰艳春. 波纹管式换热器(一)——起源、现状与发展[J]. 管道技术与设备, 1998(1): 43-45. QIU G T, FENG Y C. Corrugated tube heat exchanger(Ⅰ)—origin, present situation and development[J]. Pipeline Technique and Equipment, 1998(1): 43-45. (in Chinese) |
| [4] |
刘久逸. 管壳式换热器强化传热及管板强度研究[D]. 北京: 北京化工大学, 2017. LIU J Y. Heat transfer enhancement and tubesheet strength study of shell and tube heat exchanger[D]. Beijing: Beijing University of Chemical Technology, 2017. (in Chinese) |
| [5] |
张亮, 原亚东, 孙志强, 等. 波纹管对管壳式换热器内流体传热及流动特性的影响[J]. 热能动力工程, 2019, 34(4): 73-78. ZHANG L, YUAN Y D, SUN Z Q, et al. Effects of corrugated tube on heat transfer and flow characteristics of fluid in shell heat exchanger[J]. Journal of Engineering for Thermal Energy and Power, 2019, 34(4): 73-78. (in Chinese) |
| [6] |
胡卫朋, 梁才航, 莫家国, 等. 用于海鲜酱杀菌的折流板波纹管换热器传热与流动性研究[J]. 热科学与技术, 2019, 18(2): 115-120. HU W P, LIANG C H, MO J G, et al. Experimental studies of heat transfer and fluid flow in helical baffle corrugated tube heat exchanger used in hoisin sterilization[J]. Journal of Thermal Science and Technology, 2019, 18(2): 115-120. (in Chinese) |
| [7] |
张国钊. 波纹管传热及阻垢性能实验[J]. 重庆工学院学报(自然科学), 2009, 23(3): 116-120. ZHANG G Z. Experiment on heat transfer and fouling characteristics of corrugated tube[J]. Journal of Chongqing Institute of Technology (Natural Science), 2009, 23(3): 116-120. (in Chinese) |
| [8] |
昝永超, 李永华. 波纹管流动和传热特性的数值模拟[J]. 节能, 2018, 37(10): 58-62. ZAN Y C, LI Y H. Numerical simulation of flow and heat transfer characteristics of bellows[J]. Energy Conservation, 2018, 37(10): 58-62. (in Chinese) |
| [9] |
陈瑶, 顾伯勤, 周剑锋, 等. 正弦型波纹管强化传热机制的数值分析[J]. 南京工业大学学报(自然科学版), 2014, 36(4): 58-63. CHEN Y, GU B Q, ZHOU J F, et al. Numerical simulation of enhanced heat transfer mechanism in sinusoidal corrugated tubes[J]. Journal of Nanjing Tech University (Natural Science Edition), 2014, 36(4): 58-63. (in Chinese) |
| [10] |
肖金花. 波纹管传热强化及其轴向承载能力研究[D]. 北京: 北京化工大学, 2006. XIAO J H. Study of heat transfer enhancement and axial load-bearing capability of corrugated tubes[D]. Beijing: Beijing University of Chemical Technology, 2006. (in Chinese) |
| [11] |
杨秀杰, 钱才富. 圆弧切线波纹换热管内流动与传热性能的数值模拟[J]. 化工机械, 2008(3): 152-155. YANG X J, QIAN C F. Numerical simulation of the fluid flow and heat transfer in the arc-tangent corrugated heat exchange tubes[J]. Chemical Machinery, 2008(3): 152-155. (in Chinese) |
| [12] |
杨秀杰. 圆弧切线波纹换热管传热强化性能和轴向刚度研究[D]. 北京: 北京化工大学, 2008. YANG X J. Study of heat transfer enhancement and axial stiffness of arc-tangent corrugated tubes[D]. Beijing: Beijing University of Chemical Technology, 2008. (in Chinese) |
| [13] |
杨祖荣, 刘丽英, 刘伟. 化工原理[M]. 3版. 北京: 化学工业出版社, 2014: 141-145. YANG Z R, LIU L Y, LIU W. Principles of chemical engineering[M]. 3rd ed. Beijing: Chemical Industry Press, 2014: 141-145. (in Chinese) |








