图像的传输、储存和收集过程易受到外界各种有害噪声的干扰,从而影响图像的视觉质量,使之与原始图像之间产生较大的偏差。因此在对图像作进一步的分析之前,需要有关键的预处理步骤,如图像去噪、图像增强等[1]。磁共振成像(MRI)脑图像受外界影响产生的噪声主要为以加性噪声形式存在的高斯噪声,这些噪声具有随机性,且较难消除。为提高图像质量,研究者们提出了多种噪声消除方法。
小波变换具有局部时频变化和多分辨率的特征,去噪效果较好,因而得到广泛运用。其中最常见的是阈值去噪法,但由于硬阈值函数的不连续性以及软阈值函数存在恒定偏差,传统的阈值函数去噪并不能得到很好的效果。因此研究者们对传统阈值函数提出了一些改进。如邢国泉等[2]针对小于阈值的部分提出新的改进阈值函数对图像进行去噪,但由于大于阈值的部分直接保留原始信号,造成了较大偏差,从而影响去噪效果。杨铮等[3]和Yang等[4]针对大于阈值的部分提出新的改进阈值函数,分别用于轴承信号和伽马射线谱降噪,但改进阈值函数在小于阈值部分未能保留原始信号,使得去噪效果不太理想。陈竹安等[5]和葛佳悦等[6]针对传统阈值函数的不足对阈值两端整体作出改进,并将改进阈值函数分别用于遥感图像和信号的去噪,取得了较好的效果。
针对现有阈值函数在小波系数间依然存在恒定偏差的不足,本文提出一种改进的阈值函数去噪算法。首先证明了所提阈值函数的连续性和渐近性,其次通过图像去噪模拟实验选取合适的小波基,并得出在参数a=2、b=30时的去噪效果最优。最后通过实验模拟验证了本文方法在脑图像相似性评价标准上优于其他阈值函数。
1 小波阈值去噪 1.1 噪声模型通过小波变换对噪声信号进行处理后,噪声集中在小波的高阶部分,只有少量噪声存在于低阶部分。将大小为M×N的图像(M为图像的宽度,N为图像的高度)添加高斯噪声,此时含有高斯噪声的二维图像模型为
| $ g(i, j)=f(i, j)+\varepsilon(i, j) $ | (1) |
式中,g(i, j)表示含噪图像,f(i, j)表示原图像,ε(i, j)表示服从正态分布N(0, δ2)的高斯白噪声,δ为标准差。去噪的实质问题是从噪声图像g(i, j)中得到真实信号f(i, j)的近似值,尽可能地分离原始图像和噪声以达到去噪的目的。
1.2 传统阈值函数小波去噪的主要方法有基于奇异性检测的去噪、空间相关去噪和小波阈值去噪。其中小波阈值去噪使用小波变换来使相邻标度之间具有强的相关性以过滤图像中的高斯噪声,从而达到恢复图像的目的。考虑到小波具有相关性,在小波变换后具有较大振幅的主要为信号,较小振幅的为噪声,基于此设定适当的阈值函数进行去噪。
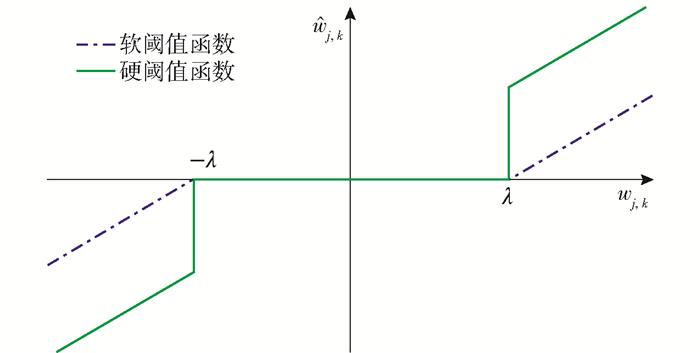
Donoho[7]设定的硬、软阈值函数图像如图 1所示。硬阈值函数为
| $ \hat{w}_{j, k}= \begin{cases}w_{j, k}, & \left|w_{j, k}\right| \geqslant \lambda \\ 0, & \left|w_{j, k}\right|<\lambda\end{cases} $ | (2) |
|
图 1 传统阈值函数的图像 Fig.1 Image of the traditional threshold function |
软阈值函数为
| $ \hat{w}_{j, k}= \begin{cases}\operatorname{sgn}\left(w_{j, k}\right)\left(w_{j, k}-\lambda\right), & \left|w_{j, k}\right| \geqslant \lambda \\ 0, & \left|w_{j, k}\right|<\lambda\end{cases} $ | (3) |
式中,
| $ \operatorname{sgn}\left(w_{j, k}\right)= \begin{cases}1, & w_{j, k}>0 \\ 0, & w_{j, k}=0 \\ -1, & w_{j, k}<0\end{cases} $ |
λ为阈值,wj, k为小波系数,
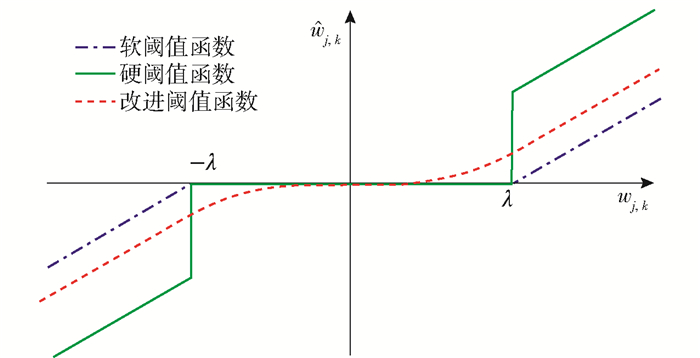
针对软阈值函数存在偏差的问题, 陈竹安等[5]对阈值λ的两端作出改进,提出了一种改进的阈值函数(式(4)),其图像如图 2所示。
| $ \hat{w}_{j, k}= \begin{cases}\operatorname{sgn}\left(w_{j, k}\right)\left(\left|w_{j, k}\right|-\lambda+\frac{\lambda}{2 k+1}\right), & \left|w_{j, k}\right| \geqslant \lambda \\ \frac{w_{j, k}^{2 k+1}}{(2 k+1) \lambda^{2 k}}, & \left|w_{j, k}\right|<\lambda\end{cases} $ | (4) |
|
图 2 阈值函数(4)的图像 Fig.2 Image of threshold function (4) |
阈值函数去噪方法的基本思想是尽可能去除振幅较小的小波系数,保留振幅较大的小波系数。文献[5]中改进的阈值函数虽然具有良好的连续性,但是小波系数在|wj, k|≥λ部分不具备渐近性,会使得小波系数间存在恒定偏差,从而影响最终的去噪效果。
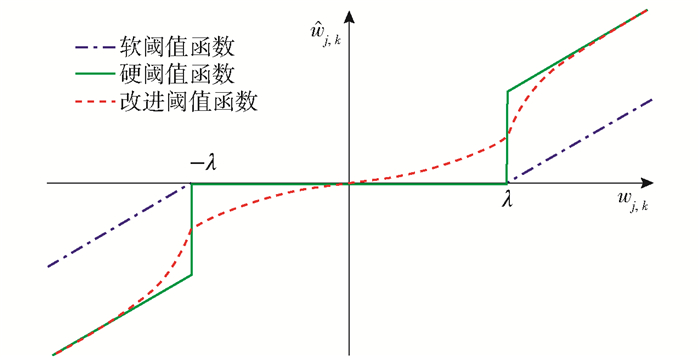
2 具有调节性的新改进阈值函数 2.1 新阈值函数的提出本文的改进阈值函数在0 < |wj, k| < λ部分添加了一个平滑的过渡区,在|wj, k|≥λ部分构造了一个具有渐近性的函数,并将这两段在阈值λ处连接,函数图像如图 3所示,具体表达式如下。
| $ \hat{w}_{j, k}= \begin{cases}w_{j, k}-\frac{w_{j, k}}{2} \frac{\mathrm{e}^{\lambda}+\mathrm{e}^{-\lambda}}{\mathrm{e}^{w_{j, k}}+\mathrm{e}^{-w_{j, k}}}, & \left|w_{j, k}\right| \geqslant \lambda \\ \frac{w_{j, k}}{2} \mathrm{e}^{\left|w_{j, k} / \lambda\right|-1}, & \left|w_{j, k}\right|<\lambda\end{cases} $ | (5) |
|
图 3 阈值函数(6)的图像 Fig.3 Image of threshold function (6) |
添加调节参数后的阈值函数为
| $ \hat{w}_{j, k}= \begin{cases}w_{j, k}-\frac{w_{j, k}}{2} \frac{b^{\lambda}+b^{-\lambda}}{b^{w_{j, k}}+b^{-w_{j, k}}}, & \left|w_{j, k}\right| \geqslant \lambda \\ \frac{w_{j, k}}{2} a^{\left|w_{j, k} / \lambda\right|-1}, & \left|w_{j, k}\right|<\lambda\end{cases} $ | (6) |
式中,a、b为调节参数,可以通过调节参数a、b的大小来降低估计小波系数与原小波系数间的恒定偏差,从而得到更好的去噪效果。
2.2 新阈值函数的连续性当wj, k→λ+时,式(6)第一个式子可以写为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \lim \limits_{w_{j, k} \rightarrow \lambda^{+}}\left(w_{j, k}-\frac{w_{j, k}}{2} \frac{b^{\lambda}+b^{-\lambda}}{b^{w_{j, k}}+b^{-w_{j, k}}}\right)=\lambda^{+}-\frac{\lambda^{+}}{2} \\ \frac{b^{\lambda}+b^{-\lambda}}{b^{\lambda^{+}}+b^{-\lambda^{+}}}=\frac{\lambda}{2} \end{array} $ | (7) |
当wj, k→λ-时,式(6)第二个式子可以写为
| $ \lim \limits_{w_{j, k} \rightarrow \lambda^{-}}\left(\frac{w_{j, k}}{2} a^{\left|w_{j, k} / \lambda\right|-1}\right)=\frac{\lambda^{-}}{2} a^{|\lambda-/ \lambda|-1}=\frac{\lambda}{2} $ | (8) |
当wj, k→-λ-时,式(6)第一个式子可写为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \lim \limits_{w_{j, k} \rightarrow-\lambda^{-}}\left(w_{j, k}-\frac{w_{j, k}}{2} \frac{b^{\lambda}+b^{-\lambda}}{b^{w_{j, k}}+b^{-w_{j, k}}}\right)=-\lambda^{-}-\frac{-\lambda^{-}}{2} \\ \frac{b^{\lambda}+b^{-\lambda}}{b^{-\lambda^{-}}+b^{\lambda^{-}}}=-\frac{\lambda}{2} \end{array} $ | (9) |
当wj, k→-λ+时,式(6)第二个式子可写为
| $ \begin{aligned} &\ \ \ \ \ \ \ \ \lim \limits_{w_{j, k} \rightarrow-\lambda^{+}}\left(\frac{w_{j, k}}{2} a^{\left|w_{j, k} \lambda\right|-1}\right)=\frac{-\lambda^{+}}{2} a^{\mid-\lambda^{+}/ \lambda \mid-1}= \\ &-\frac{\lambda}{2} \end{aligned} $ | (10) |
改进的阈值函数在阈值±λ处连续,且在式(6)中,当a, b→+∞时,阈值函数图像接近于硬阈值函数。在参数a、b的调节过程中,函数图像介于硬阈值函数和软阈值函数图像之间。
2.3 新阈值函数的渐近性当wj, k→-∞或wj, k→+∞时,有
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \lim \limits_{w_{j, k} \rightarrow-\infty} \frac{\hat{w}_{j, k}}{w_{j, k}}=\lim \limits_{w_{j, k} \rightarrow+\infty} \frac{\hat{w}_{j, k}}{w_{j, k}}=\lim \limits_{w_{j, k} \rightarrow \infty} \\ \frac{w_{j, k}-\frac{w_{j, k}}{2} \frac{b^{\lambda}+b^{-\lambda}}{b^{+\infty}+b^{-\infty}}}{w_{j, k}}=\lim \limits_{w_{j, k} \rightarrow \infty} \frac{w_{j, k}}{w_{j, k}}=1 \end{array} $ | (11) |
可以得出,改进的阈值函数以
在小波阈值去噪的过程中,阈值的选取非常关键,它影响着最终的去噪效果。Donoho等[8]提出一
种通用阈值
| $ \lambda=\delta_{n} \sqrt{2 \ln M \cdot N} $ | (12) |
由于噪声主要集中于小波系数的高频部分,并随着小波分解尺度的增加而减少,因此本文提出一种随着分解尺度的增加而降低的改进阈值
| $ \lambda=\delta_{n} \sqrt{2 \ln M \cdot N} / \lg \left(2^{j+1}+6\right) $ | (13) |
式中,lg (2j+1+6)为收缩因子,j为小波分解层数,δn为噪声的标准差,表示为
| $ \delta_{n}=\frac{{median}\left[\left|d_{j}(k)\right|\right]}{C} $ | (14) |
式中,dj(k)为小波细节,median表示中值运算,且C=0.674 5。
3 实验仿真 3.1 评价指标为了验证本文阈值函数相对其他阈值函数在医疗图像上去噪的优越性,使用图像相似度评价指标—均方误差EMS(MSE)和峰值信噪比RPSN(PSNR)来描述去噪效果。
均方误差定义为
| $ E_{\mathrm{MS}}=\frac{1}{M \cdot N} \sum\limits_{i=0}^{M} \sum\limits_{j=0}^{N}[f(i, j)-g(i, j)]^{2} $ | (15) |
峰值信噪比定义为
| $ R_{\mathrm{PSN}}=10 \lg \left(\frac{255^{2}}{E_{\mathrm{MS}}}\right) $ | (16) |
均方误差值越小,峰值信噪比值越大,表明去噪图像与原始图像的相似度越高,去噪效果越好。
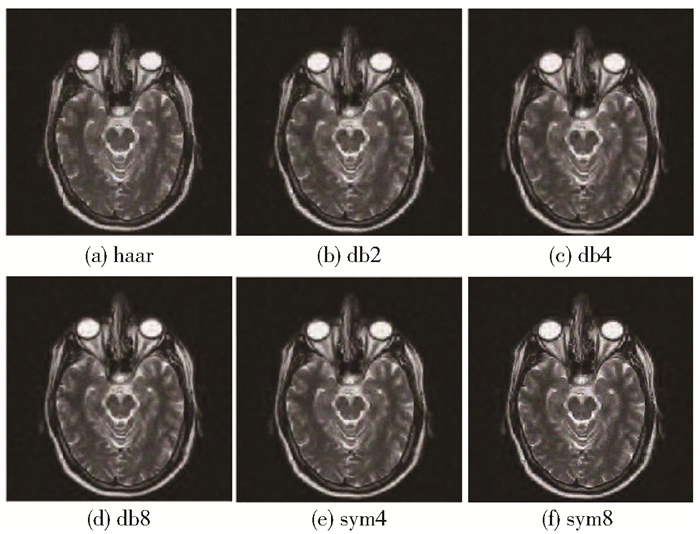
3.2 小波基的选取本文实验在Matlab(2014)中编程完成。对MRI脑图像A加入均值为0、对应标准差为30的高斯噪声,分别采用6种不同的小波基haar、db2、db4、db8、sym4、sym8对图像进行三层分解重构,改进阈值函数参数选取为a=2, b=30。经不同小波基去噪后的图像如图 4所示。由表 1的实验结果可知,选择sym8作为小波基时的去噪效果最好。
|
图 4 不同小波基对MRI图像A的去噪效果 Fig.4 Denoising effect of MRI image A with different wavelet bases |
| 下载CSV 表 1 不同小波基对MRI图像A的去噪数据 Table 1 MRI image A denoising data of different wavelet bases |
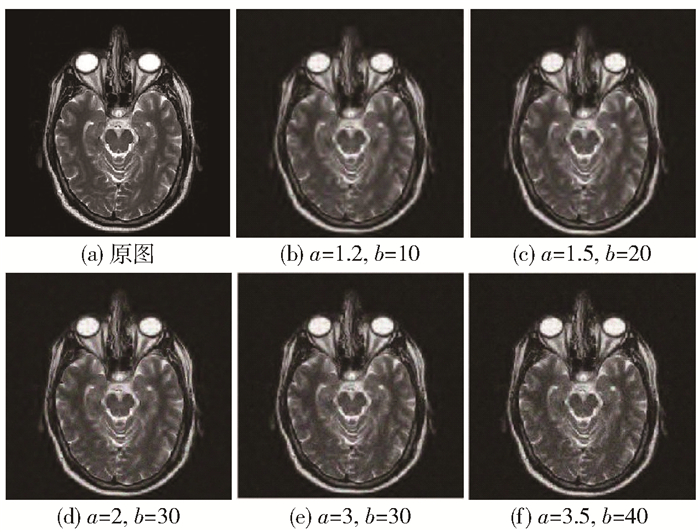
选取小波基为sym8,设定噪声标准差为30,讨论本文改进阈值函数中两个调节参数a、b对MRI图像A去噪效果的影响。从图 5可以看出,当a=3.5, b=40时所得图像中会残留部分噪声,其余参数下所得图像的视觉效果差别不大。根据表 2的去噪数据,当a=2, b=30时可获得最优的去噪效果。
|
图 5 不同参数下MRI图像A的去噪效果 Fig.5 Denoising effect of MRI image A with different parameters |
| 下载CSV 表 2 MRI图像A在不同参数下的去噪数据 Table 2 MRI image A denoising data with different parameters |
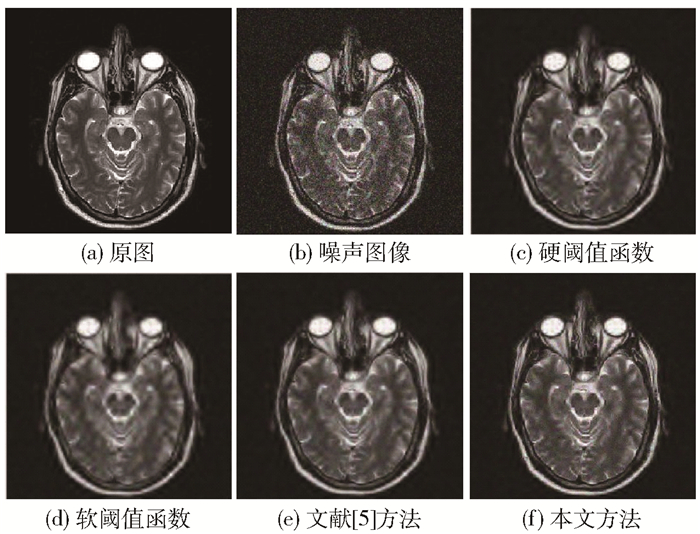
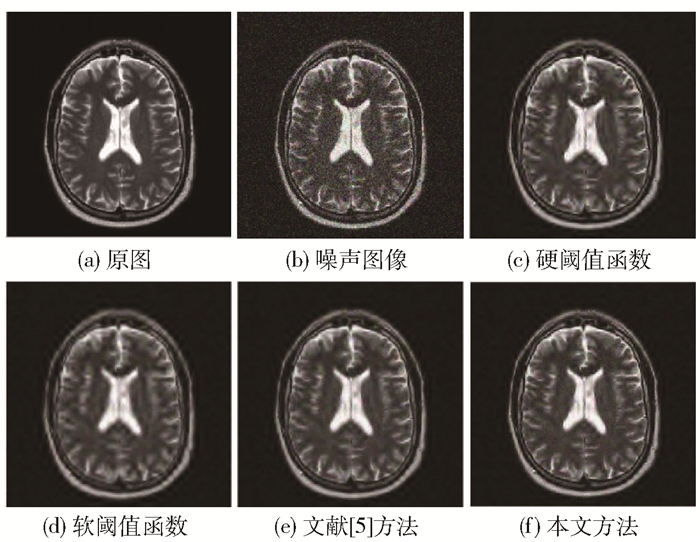
为验证改进阈值函数去噪的优越性,对两种MRI脑图像A、B分别采用传统阈值函数、文献[5]中的方法和本文改进阈值函数进行对比实验。在图像中加入均值为0,对应标准差分别为20、25、30的高斯噪声,选取sym8作为小波基并且设定最优参数为a=2, b=30。将图像分解之后进行阈值处理,最后重构获得去噪后的图像。不同标准差下硬、软阈值函数去噪所得图像的质量均不理想,文献[5]的改进阈值函数去噪所得图像的质量有一定的提高,本文方法去噪所得图像的视觉效果最好,其中标准差30下的去噪图像如图 6、7所示,20、25、30这3种不同标准差下的去噪数据如表 3、4所示。
|
图 6 不同方法对MRI图像A的去噪效果 Fig.6 Denoising effect of MRI image A with different methods |
|
图 7 不同方法对MRI图像B的去噪效果 Fig.7 Denoising effect of MRI image B with different methods |
| 下载CSV 表 3 不同方法对MRI图像A的去噪数据 Table 3 Denoising data of MRI image A with different methods |
| 下载CSV 表 4 不同方法对MRI图像B的去噪数据 Table 4 Denoising data of MRI image B with different methods |
从图 6和图 7可以看出,对两种MRI图像进行去噪处理,硬阈值函数所得图像有明显的振荡和伪吉布斯效应;软阈值函数所得图像明显失真,丢失了部分原图像的有用信息;文献[5]相对于传统阈值函数有一定程度的提高,所得去噪图像的清晰度更好,同时保留了更多的图像细节信息;然而相比之下,本文改进方法去噪所得图像的清晰度更高,去噪效果最佳。
表 3和表 4的实验数据表明,硬阈值函数的去噪效果要优于软阈值函数。文献[5]提出的改进阈值函数相比于硬阈值函数和软阈值函数具有更高的PSNR和更低的MSE,说明去噪效果得到了提高。本文所提方法在不同噪声标准差下都具有最大的PSNR和最小的MSE,因而无论是从视觉效果还是图像相似度评价标准来看,结果都可以表明本文改进的阈值去噪算法性能更为优越。
4 结束语基于硬阈值函数的不连续性和软阈值函数存在恒定偏差的不足,本文提出一种新的具有连续性、渐近性和灵活调节性的改进阈值函数。首先选取改进的固定阈值并通过实验选择合适的小波基,即sym8,随后得出改进阈值函数在参数a=2、b=30时的去噪效果达到最佳。采用不同阈值函数针对两种MRI脑图像进行去噪实验的对比结果表明,本文方法具有最佳的图像相似度评价指标,即PSNR最大,MSE最小。
| [1] |
GOLILARZ N A, GAO H, DEMIREL H. Satellite image de-noising with Harris hawks meta heuristic optimization algorithm and improved adaptive generalized Gaussian distribution threshold function[J]. IEEE Access, 2019, 7: 57459-57468. DOI:10.1109/ACCESS.2019.2914101 |
| [2] |
邢国泉, 叶华山, 张玉霞, 等. 基于一种新的阈值函数的小波图像去噪方法[J]. 生物医学工程学杂志, 2013, 30(4): 743-747. XING G Q, YE H S, ZHANG Y X, et al. A new wavelet image de-noising method based on new threshold function[J]. Journal of Biomedical Engineering, 2013, 30(4): 743-747. (in Chinese) |
| [3] |
杨铮, 霍迎科. 基于改进小波算法的轴承信号降噪研究[J]. 中国工程机械学报, 2020, 18(1): 40-44. YANG Z, HUO Y K. Denoising of roll bearing signal based on improved wavelet algorithm[J]. Chinese Journal of Construction Machinery, 2020, 18(1): 40-44. (in Chinese) |
| [4] |
YANG G F, DAI J C, LIU X J, et al. Denoising of Gamma-ray spectrum by optimized wavelet thresholding based on modified genetic algorithm in carbon/oxygen logging[J]. Journal of Radioanalytical and Nuclear Chemistry, 2019, 320(2): 351-359. DOI:10.1007/s10967-019-06477-x |
| [5] |
陈竹安, 胡志峰. 小波阈值改进算法的遥感图像去噪[J]. 测绘通报, 2018(4): 28-31. CHEN Z A, HU Z F. Remote sensing image denoising based on improved wavelet threshold algorithm[J]. Bulletin of Surveying and Mapping, 2018(4): 28-31. (in Chinese) |
| [6] |
葛佳悦, 唐春晖. 基于改进阈值函数的小波去噪算法研究[J]. 软件导刊, 2020, 19(6): 61-65. GE J Y, TANG C H. Research on wavelet denoising algorithm based on improved threshold function[J]. Software Guide, 2020, 19(6): 61-65. (in Chinese) |
| [7] |
DONOHO D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [8] |
DONOHO D L, JOHNSTONE I M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455. DOI:10.1093/biomet/81.3.425 |








