在工业生产中,管道广泛应用于输气、供水和运油等领域。由于管道长期处于高温高压的工作状态,在使用过程中容易造成内壁的腐蚀、脱落,甚至产生污垢黏连附着在内壁上导致出现内壁增厚等现象,这些缺陷的存在成为安全生产和使用的潜在隐患[1]。因此,对管道内壁缺陷的检测具有重要意义[2-3]。
导热反问题(inverse heat conduction problem,IHCP)已在很多工程领域中得到广泛应用[4]。导热反问题常用于计算反演边界条件[5-9]、热物性参数[10]、物体内部热源[11]及初始条件等未知项,也可用于物体内部缺陷[12-15]和内壁缺陷的识别。Chen等[16-17]采用共轭梯度法估计了管道外壁的未知霜层边界形状和管道内壁上的未知污垢边界形状,但只单一讨论了沿管道轴向变化的霜层或污垢分布情况;文献[18-19]对双层炉膛内壁的边界形状进行了反演,但没有探讨初始值及测点数目对反演结果精确度的影响;文献[20-24]应用共轭梯度法对管道内壁面的边界形状进行了稳态或瞬态的识别,并分别对所建反演模型的可行性进行了探究;张林等[25]在改进的一维修正算法基础上提出一维加权法,对二维圆管交界面形状进行了定量识别,提高了识别效率;Mohasseb等[26]采用遗传算法作为非适定导热反问题的计算方法,求解了方形板的热流密度边界,但算法的稳定性与收敛速度有待提高;文献[3]、[27-30]均采用列文伯格-马夸尔特(Levenberg- Marquardt,L-M)算法对未知参数进行了计算,算例验证了算法的有效性和优越性。在众多求解导热反问题的数值计算方法中,属于梯度类算法的L-M算法因具有稳定性好、构造思路简单、收敛快等优势而被广泛应用。
当前的大多数研究都只对管道内壁腐蚀减薄缺陷进行单一的讨论,涉及管道内壁污垢增厚缺陷识别的相对较少,因此本文提出基于有限元法和L-M算法构建反问题数学模型,利用COMSOL与MATLAB联合仿真稳定、快速的优势,将管道内径作为反演参数,分别对管道内壁腐蚀减薄缺陷与污垢增厚缺陷进行定量识别,并构造数值实验对反演结果的精确性和稳定性进行分析。
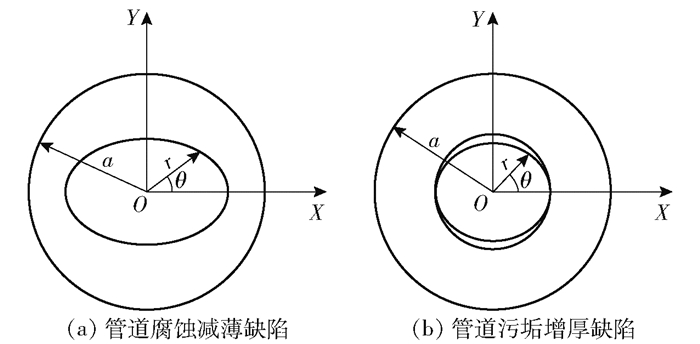
1 二维圆管物理模型二维圆管物理模型如图 1所示。管道外径a=0.3 m,壁厚d=25 mm。管道的导热系数λ1=17.60 W/(m·K),污垢的导热系数λ2=3.14 W/(m·K),外壁面对流换热系数hout=10 W/(m2·K),环境温度Ta=25 ℃,内壁面对流换热系数hin=1 000 W/(m2·K),管内流体温度Tf=200 ℃,θ为极角,r为出现缺陷后管道的内壁面极径。
|
图 1 管道两类缺陷的物理模型 Fig.1 Physical model of two types of defects in pipelines |
由于所研究内容为二维圆管内壁面缺陷的稳态识别,基于此作如下合理假设:1)管道忽略轴向导热的影响;2)管道导热系数和管内外的对流换热系数均为常数。
2.1.1 管道增厚缺陷圆管的导热偏微分方程为
| $ \frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}=0 $ | (1) |
假设给定内壁面和外壁面均为第三类边界条件,则边界条件为
| $ -\lambda_{1}\left(\frac{\partial T_{1}}{\partial n_{\text {out }}}\right)=h_{\text {out }}\left(T_{\text {out }}-T_{\mathrm{a}}\right) $ | (2) |
| $ -\lambda_{2}\left(\frac{\partial T_{2}}{\partial n_{\text {in }}}\right)=h_{\text {in }}\left(T_{\text {in }}-T_{\mathrm{f}}\right) $ | (3) |
污垢增厚缺陷存在着交界面Γ,在此处
| $ T_{1}=T_{2} $ | (4) |
| $ -\lambda_{1}\left(\frac{\partial T_{1}}{\partial n_{\mathrm{int}, 1}}\right)=-\lambda_{2}\left(\frac{\partial T_{2}}{\partial n_{\mathrm{int}, 2}}\right) $ | (5) |
式中,下标1代表管壁区域Ω1,下标2代表污垢区域Ω2;下标in、out分别为圆管内壁面和外壁面;n代表法线方向;下标int代表圆管与污垢交界面边界。
2.1.2 管道减薄缺陷管道减薄缺陷只存在于管壁区域Ω1,将式(3)进行修改可得式(6)。
| $ -\lambda_{1}\left(\frac{\partial T_{1}}{\partial n_{\mathrm{in}}}\right)=h_{\mathrm{in}}\left(T_{\mathrm{in}}-T_{\mathrm{f}}\right) $ | (6) |
式(6)与式(1)、式(2)共同构成了管道减薄缺陷导热正问题的数学描写。
2.2 导热反问题导热正问题是一个定解问题,而导热反问题则是一个最优化问题。
2.2.1 L-M算法L-M算法是非线性回归中回归参数最小二乘估计的一种方法,L-M算法将最速下降法和线性化方法相结合,从而较快地找到最优值。
对于两类内壁面缺陷的反演,内壁面几何边界都是未知的,可由极坐标向量R(θ)描述
| $ \boldsymbol{R}(\theta)=\left[r_{1}, r_{2}, \cdots, r_{n}, \cdots, r_{N}\right]^{\mathrm{T}} $ | (7) |
式中,r为极半径;N为内壁面离散节点个数。
数学偏微分方程组(式(1)~(5)以及式(1)、(2)、(6))需要获得外壁面测点温度以满足其封闭性,离散后的外壁面温度测量值记为
| $ \boldsymbol{Y}=\left[Y_{1}, Y_{2}, \cdots, Y_{m}, \cdots, Y_{M}\right]^{\mathrm{T}} $ | (8) |
式中,M为外壁面测点数。
进一步构建该最优化问题的目标函数为
| $ S(\boldsymbol{R})=[\boldsymbol{Y}-\boldsymbol{T}(\boldsymbol{R})]^{\mathrm{T}}[\boldsymbol{Y}-\boldsymbol{T}(\boldsymbol{R})] $ | (9) |
式中,T(R)为根据R(θ)所求得的外壁面温度的计算值,表示为
| $ \boldsymbol{T}(\boldsymbol{R})=\left[T_{1}, T_{2}, \cdots, T_{m}, \cdots, T_{M}\right]^{\mathrm{T}} $ | (10) |
通过式(9)对未知参量R(θ)求偏导得到目标函数梯度的最小化条件为
| $ \nabla S(\boldsymbol{R})=-2 \boldsymbol{J}^{\mathrm{T}}(\boldsymbol{R})[\boldsymbol{Y}-\boldsymbol{T}(\boldsymbol{R})]=0 $ | (11) |
式中,J(R)为敏度系数矩阵,表示为
| $ \boldsymbol{J}(\boldsymbol{R})=\left[\frac{\partial \boldsymbol{T}^{\mathrm{T}}(\boldsymbol{R})}{\partial \boldsymbol{R}}\right]^{\mathrm{T}} $ | (12) |
对式(11)的T(R)进行泰勒级数展开舍去高阶项,并加入衰减参数μLMk来调节迭代速度,得到迭代式
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \boldsymbol{R}^{k+1}=\boldsymbol{R}^{k}+\left[\left(\boldsymbol{J}^{k}\right)^{\mathrm{T}} \boldsymbol{J}^{k}+\mu_{\mathrm{LM}}^{k} \boldsymbol{\varOmega}^{k}\right]^{-1}\left(\boldsymbol{J}^{k}\right)^{\mathrm{T}}[\boldsymbol{Y}- \\ \left.\boldsymbol{T}\left(\boldsymbol{R}^{k}\right)\right] \end{array} $ | (13) |
式中,k为迭代次数;Ωk为一对角矩阵,表示为
| $ \boldsymbol{\varOmega}^{k}=\operatorname{diag}\left[\left(\boldsymbol{J}^{k}\right)^{\mathrm{T}} \boldsymbol{J}^{k}\right] $ | (14) |
迭代开始采用最速下降法以较大的μLMk进行计算,后来降低μLMk通过高斯牛顿法得到最终反演值。
根据偏差原理给出收敛条件为
| $ S(\boldsymbol{R})<\varepsilon $ | (15) |
式中,ε在不考虑测量误差时为一小正数。
2.2.2 数值计算过程MATLAB使用mphload函数加载COMSOL的mph文件,通过mphinterp函数便可读取数据,无需使用输入/输出文件。COMSOL在被调用时可以自动构建几何模型、更新网格和求解计算,有效提高了反演效率。
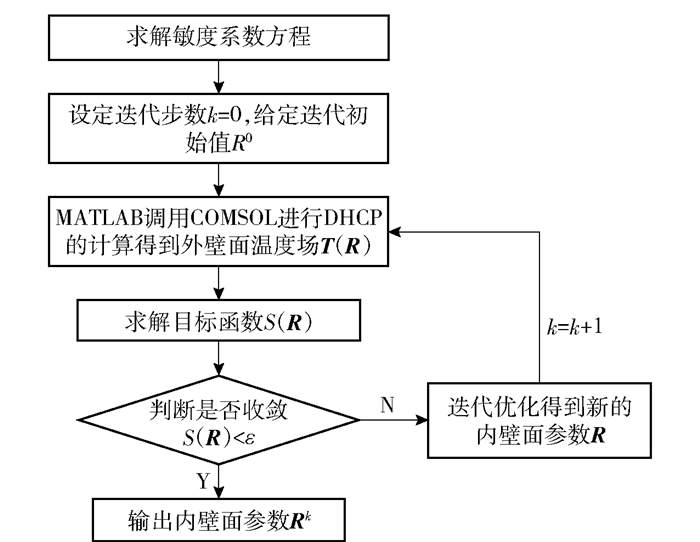
利用L-M算法求解导热反问题的流程图如图 2所示。
|
图 2 反演流程图 Fig.2 Chart of inversion progress |
为验证反演结果对引入测量误差的敏感性,在由导热正问题计算得到的外壁面精确值的基础上引入随机误差,来模拟实际的测量值。
| $ T_{\text {mea }}=T_{\text {exact }}+\sigma \omega $ | (16) |
式中,Tmea为外壁面温度测量值;Texact为外壁面温度精确值;σ为标准偏差;ω为区间[-2.576, 2.576]内服从标准正态分布的随机数,该区间能达到99%的测量可靠度。
当考虑实际测温误差时,收敛标准ε写成
| $ \boldsymbol{\varepsilon}=\sum\limits_{m=1}^{M} \sigma_{m}^{2}=M \boldsymbol{\sigma}^{2} $ | (17) |
为了表征反演值与精确值的偏离程度,定义平均相对误差为
| $ E_{\mathrm{RR}}=\frac{1}{N} \sum\limits_{n=1}^{N}\left|\frac{r_{n, \text { exact }}-r_{n, \text { est }}}{r_{n, \text { exact }}}\right| \times 100 \% $ | (18) |
式中,rn, exact为内径精确值;rn, est为内径反演值。
3 计算结果与分析通过运行程序进行数值计算,以验证管道减薄缺陷与增厚缺陷导热反问题反演的精确性。首先设定内壁面缺陷形状,由导热正问题得出外壁面温度模拟的实际测量值,为导热反问题提供输入数据;所设定的内壁面缺陷形状参数作为校验数据。为验证程序的稳定性和抗噪性,分别探讨初值、测温点数目及测量误差对反演结果的影响。
3.1 管道减薄缺陷对于管道减薄缺陷,在外壁面上均匀设置36个测点,内壁面由36个均匀分布的离散节点拟合得到。设定沿周向变化的内壁面几何形状为阶跃式函数、锲形函数和正弦函数,分别探讨这3种不同工况下的导热反问题。
3.1.1 阶跃式函数设定内壁面边界形状按阶跃式变化,即Case 1。
| $ R(\theta)= \begin{cases}0.275, & \theta \in[0,5 {\rm{ \mathsf{ π} }} / 6) \cup(7 {\rm{ \mathsf{ π} }} / 6,2 {\rm{ \mathsf{ π} }}] \\ 0.287\ 5, & \theta \in[5 {\rm{ \mathsf{ π} }} / 6,7 {\rm{ \mathsf{ π} }} / 6]\end{cases} $ | (19) |
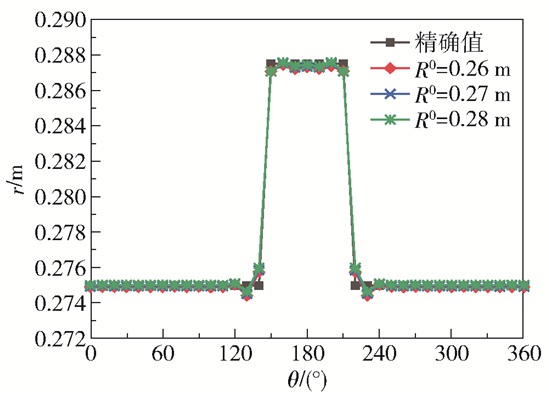
根据式(19)验证内壁面几何边界呈阶跃式规律变化下的反演结果,并探讨不同初值R0对反演结果的影响。由图 3可以看出,当R0取不同值时,反演曲线与精确曲线的走向基本趋于一致,靠近阶跃边界处的识别效果相对较差,但程序仍可较好地识别出管道内壁的边界形状。由表 1可以进一步得出,3种初始边界假设下,反演结果的平均相对误差最大仅相差0.015%,说明初始边界假设对内壁面几何边界的反演几乎没有影响;此外,3种初值下得出计算结果的平均相对误差均不超过0.1%,验证了程序反演的精确性。
|
图 3 不同初值下阶跃式几何边界的反演值与精确值 Fig.3 Inversion and exact values for a stepped geometrical boundary with different initial values |
| 下载CSV 表 1 Case1~Case3平均相对误差值 Table 1 Mean relative error values of Case1 to Case3 |
设定内壁面几何边界形状以锲形函数变化,即Case 2。
| $ R(\theta)= \begin{cases}0.275, & \theta \in[0, {\rm{ \mathsf{ π} }}) \cup({\rm{ \mathsf{ π} }}, 2 {\rm{ \mathsf{ π} }}] \\ 0.287\ 5, & \theta={\rm{ \mathsf{ π} }}\end{cases} $ | (20) |
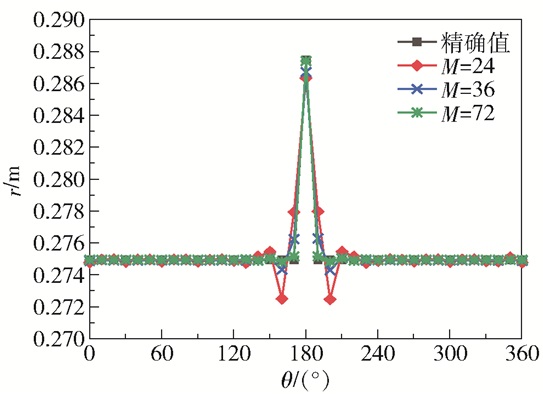
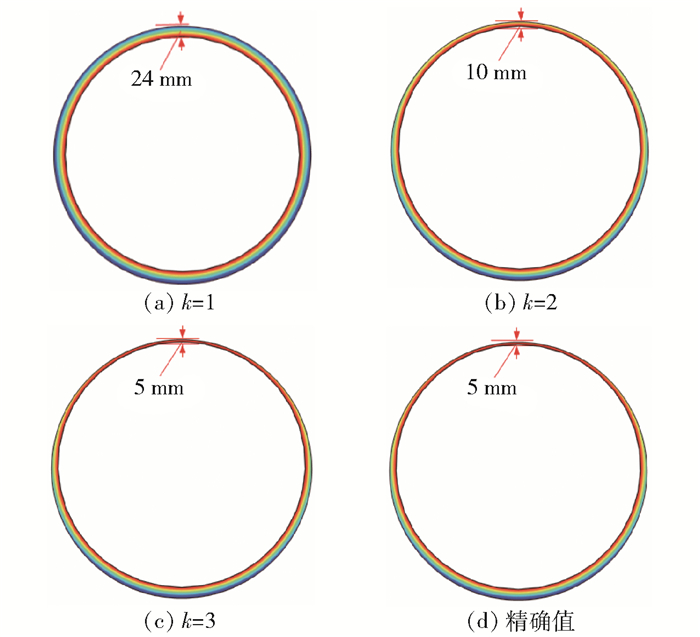
在式(20)所示的内壁边界形状以锲形函数变化的条件下,研究不同外壁面温度测点数目对识别结果的影响。由图 4可以看出,当M=24时,程序对内壁边界的识别效果相对较差,尤其是在阶跃点附近更为明显;随着外壁面温度测点数目的增加,阶跃点处的识别效果逐渐变好,当M=72时,反演曲线与精确曲线高度吻合。结合表 1可进一步得出,外壁面测温点数越多,识别效果就越好。M=36时的平均相对误差为0.058%,M=72时的平均相对误差为0.011%,均可较好地识别出内壁边界形状。
|
图 4 锲形几何边界不同测温点数时的反演值与精确值 Fig.4 Inversion and exact values for a wedge-shaped geometric boundary with different numbers of measurement points |
设定内壁边界形状随正弦函数变化,即Case 3。
| $ R(\theta)=0.285+0.01 \sin \theta $ | (21) |
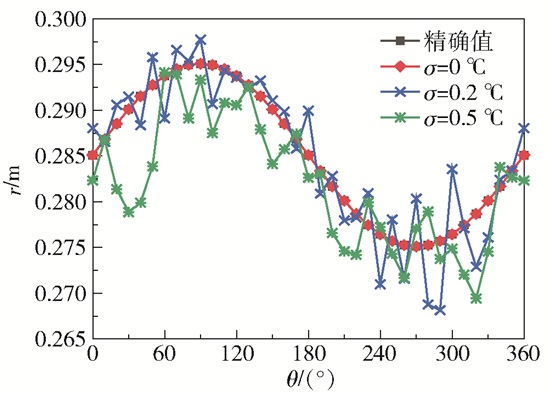
内壁面边界形状按式(21)以正弦规律变化,引入标准偏差,分析不同偏差对反演结果的影响。如图 5所示,可以看出当σ=0 ℃时,反问题得到的反演曲线与正问题得出的精确曲线几乎重合;当σ=0.2 ℃和σ=0.5 ℃时,两条反演曲线均在精确值附近上下小范围波动,且在σ=0.5 ℃时变化得相对更为明显。根据表 1不难进一步得出,随着标准偏差的增大,反演误差也随之增大,但3种标准偏差下的平均相对误差均不超过1.5%,说明采用此方法反演边界形状对测量误差的变化不敏感,具有一定的抗噪性。图 6是当边界形状为正弦函数时的迭代收敛历程图,由图可看出,迭代步长先大后小,且只需要迭代3次即可满足所设定的收敛条件。对比图 6(c)与图 6(d)可知,运用L-M算法可在低迭代步数下准确地识别出缺陷。
|
图 5 正弦几何边界不同测量误差时的反演值与精确值 Fig.5 Inversion and exact values of a sine geometric boundary with different measurement errors |
|
图 6 正弦函数边界缺陷反演时的收敛历程 Fig.6 Convergence history of sine function boundary defect inversion |
同样地,对于管道增厚缺陷,在外边界上也均匀设置36个测点,含有污垢的内壁面亦由36个均匀分布的离散节点拟合得到,可通过反演管道内径进而得出污垢的厚度。设定的内壁面污垢几何形状包括均匀增厚缺陷、沿周向变化的三角形函数以及椭圆函数,分别探讨这3种不同工况下的导热反问题。
3.2.1 均匀增厚设定内壁面有均匀厚度的污垢,即Case 4。
| $ R(\theta)=0.265 $ | (22) |
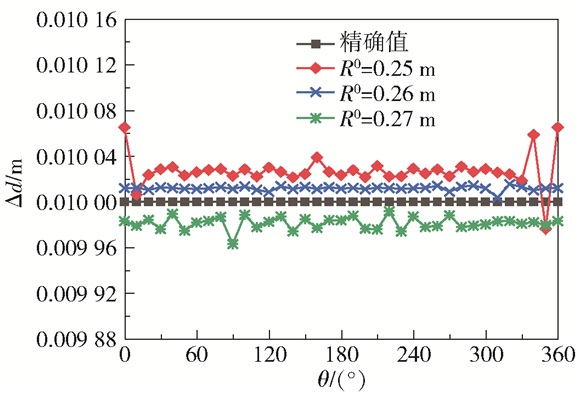
如式(22)所示,假设周向含有均匀污垢的圆管内径为0.265 m,即污垢的厚度为0.01 m,分别设置不同的初值R0,所得污垢厚度Δd反演结果如图 7所示。由图 7可以看出,不同初值下的反演值与精确值相差甚小,且反演曲线呈小范围波动。由表 2可得,3种初始值下反演的平均相对误差均不足0.1%,说明初值对均匀污垢反演结果的影响较小,程序对于内壁面均匀污垢有较好的识别能力。
|
图 7 不同初值下均匀污垢厚度的反演值与精确值 Fig.7 Inversion and exact values of uniform fouling with different initial values |
| 下载CSV 表 2 Case4~Case6平均相对误差值 Table 2 Mean relative error values of Case4 to Case6 |
设定内壁几何边界形状按三角形函数变化,即Case 5。
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \ R(\theta)= \\ \begin{cases}0.005 \theta+0.25, & \theta \in[0, {\rm{ \mathsf{ π} }})\\ -0.005(\theta-{\rm{ \mathsf{ π} }})+(0.005 {\rm{ \mathsf{ π} }}+0.25), & \theta \in[{\rm{ \mathsf{ π} }}, 2 {\rm{ \mathsf{ π} }}]\end{cases} \end{array} $ | (23) |
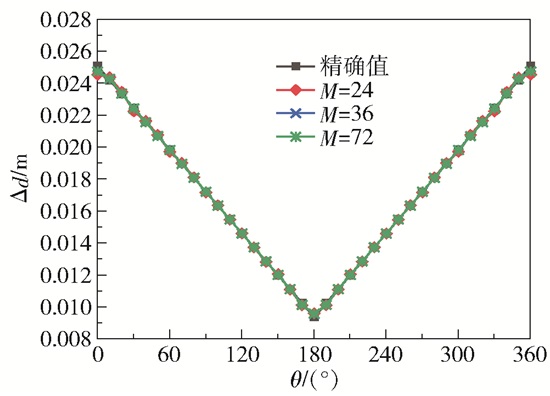
如图 8所示,含有污垢的管道内壁面半径(即内壁污垢形状)随周向呈三角形规律变化。根据式(23)对反演结果进行验证,同时探讨改变外壁面测温点个数对反演结果的影响。由表 2可知,增加外壁面测温点个数可以更加准确地识别出内壁面的污垢形状,但提高的程度有限,当测温点的个数达到一定值时,增加节点个数对识别精度的提高影响并不大。另外,由表 2结果也可看出,当测温点个数较少时识别精度仍然较高,M=24时的平均相对误差为0.033%,表明仍能较准确地识别出内壁面的污垢形状。
|
图 8 不同测温点数下三角形污垢厚度的反演值与精确值 Fig.8 Inversion and exact values of triangle fouling with different numbers of temperature measurement points |
设定内壁面几何边界形状以椭圆函数变化,即Case 6。
| $ R(\theta)=\sqrt{(0.27 \cos \theta)^{2}+(0.26 \sin \theta)^{2}} $ | (24) |
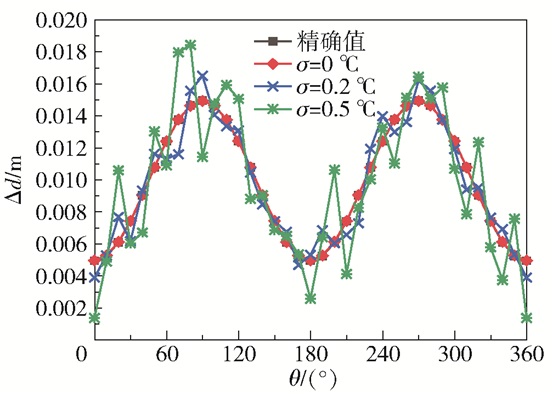
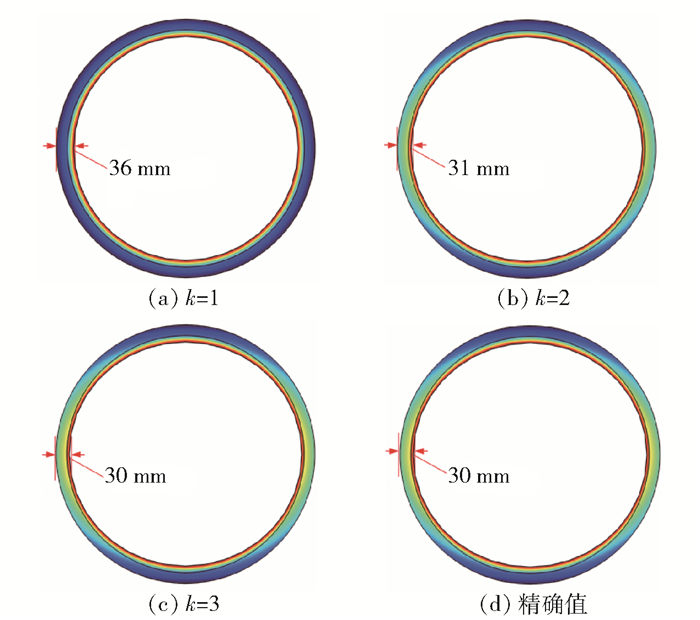
式(24)为内壁边界形状随椭圆函数变化的情况,即内壁污垢形状亦呈椭圆函数变化。图 9为不同标准偏差下污垢尺寸的反演值与精确值。由图可看出,无偏差下反演值与精确值二者的曲线走向基本同步;当存在标准偏差时,反演值围绕精确值附近上下波动,且随着标准偏差的增大,波动的幅度和频率也愈为明显。根据表 2可知,在标准偏差增大到0.5 ℃时,波动值仍可保持在1%以内,说明反演模型在识别内壁污垢时稳定性较好。图 10为当污垢以椭圆函数变化时的管道迭代收敛历程图。由图可以看出,对椭圆污垢的反演与对正弦减薄缺陷的反演一样,仅是经历3次迭代就达到了最终收敛,迭代步数较少。
|
图 9 不同测量误差下椭圆污垢厚度的反演值与精确值 Fig.9 Inversion and exact values of elliptical fouling for different measurement errors |
|
图 10 椭圆函数边界缺陷反演时的收敛历程 Fig.10 Convergence history of elliptic function boundary defect inversion |
(1) 通过设定多种工况进行数值模拟,验证了二维稳态导热反问题数学模型的有效性与精确性。研究结果显示,该反演模型能够实现对内壁面两类缺陷的识别,且具有较高的识别精度。
(2) 对圆管内壁腐蚀减薄及污垢增厚两类缺陷进行了反演结果稳定性的探究,计算结果表明,初值选取对反演结果无明显影响,反演精度随着外壁面测温点数目的增加而提高,但精度提高有限。
(3) 引入随机测量误差,探讨了反演结果对测量误差的敏感性。数值算例结果显示,本文算法具有一定的抗噪性,当存在σ=0.5 ℃的标准偏差时,仍能得到较为精确的结果。
目前,本文只研究了二维圆管内壁面缺陷的稳态识别,缺少基于具体实验的验证工作。下一步需要结合实际工况来优化二维圆管稳态导热反演模型,并进一步开发二维圆管瞬态导热反演模型。
| [1] |
ZHANG F L, YUAN Z H. The detection and evaluation for the internal defection in industrial pipeline based on the virtual heat source temperature field[J]. Journal of Thermal Analysis and Calorimetry, 2019, 137(3): 949-964. DOI:10.1007/s10973-018-07988-7 |
| [2] |
FAN C L, SUN F R, YANG L. A new computational scheme on quantitative inner pipe boundary identification based on the estimation of effective thermal conductivity[J]. Journal of Physics D: Applied Physics, 2008, 41(20): 205501. DOI:10.1088/0022-3727/41/20/205501 |
| [3] |
张林, 杨立, 范春利. 充分发展湍流管道内壁边界的红外定量识别[J]. 国防科技大学学报, 2019, 41(5): 185-192. ZHANG L, YANG L, FAN C L. Infrared quantitative identification for inner boundary of fully developed turbulent pipeline[J]. Journal of National University of Defense Technology, 2019, 41(5): 185-192. (in Chinese) |
| [4] |
范春利. 几何形状导热反问题方法与应用[M]. 北京: 科学出版社, 2015. FAN C L. Geometric inverse heat conduction problems: methods and applications[M]. Beijing: Science Press, 2015. (in Chinese) |
| [5] |
熊平, 陆祺, 卢涛, 等. 基于顺序函数法的圆管内部流体温度反演[J]. 原子能科学技术, 2020, 54(9): 1595-1603. XIONG P, LU Q, LU T, et al. Estimating fluid temperature of pipe based on sequential function specification method[J]. Atomic Energy Science and Technology, 2020, 54(9): 1595-1603. (in Chinese) |
| [6] |
韩雯雯, 卢涛. 基于共轭梯度法的圆管内部流体温度识别[J]. 工程热物理学报, 2015, 36(2): 371-375. HAN W W, LU T. Estimating fluid temperature of pipe by using conjugate gradient method[J]. Journal of Engineering Thermophysics, 2015, 36(2): 371-375. (in Chinese) |
| [7] |
HUANG C H, CHEN C W. A boundary-element-based inverse problem of estimating boundary conditions in an irregular domain with statistical analysis[J]. Numerical Heat Transfer, 1998, 33(2): 251-267. DOI:10.1080/10407799808915032 |
| [8] |
薛齐文, 杨海天, 胡国俊. 共轭梯度法求解瞬态传热组合边界条件多宗量反问题[J]. 应用基础与工程科学学报, 2004, 12(2): 113-120. XUE Q W, YANG H T, HU G J. Solving inverse heat conduction problems with multi-variables of boundary conditions in transient-state via conjugate gradient method[J]. Journal of Basic Science and Engineering, 2004, 12(2): 113-120. (in Chinese) DOI:10.3969/j.issn.1005-0930.2004.02.001 |
| [9] |
钱炜祺, 蔡金狮. 顺序函数法求解二维非稳态热传导逆问题[J]. 空气动力学学报, 2002, 20(3): 274-281. QIAN W Q, CAI J S. Solving two-dimensional transient inverse heat conduction problem with sequential function method[J]. Acta Aerodynamica Sinica, 2002, 20(3): 274-281. (in Chinese) DOI:10.3969/j.issn.0258-1825.2002.03.004 |
| [10] |
KIM S K, JUNG B S, KIM H J, et al. Inverse estimation of thermophysical properties for anisotropic composite[J]. Experimental Thermal and Fluid Science, 2003, 27(6): 697-704. DOI:10.1016/S0894-1777(02)00309-6 |
| [11] |
LEE H L, CHANG W J, CHEN W L, et al. An inverse problem of estimating the heat source in tapered optical fibers for scanning near-field optical microscopy[J]. Ultramicroscopy, 2007, 107(8): 656-662. DOI:10.1016/j.ultramic.2007.01.001 |
| [12] |
FAZELI H, MIRZAEI M. Shape identification problems on detecting of defects in a solid body using inverse heat conduction approach[J]. Journal of Mechanical Science and Technology, 2012, 26(11): 3681-3690. DOI:10.1007/s12206-012-0842-4 |
| [13] |
FAZELI H, MIRZAEI M, FOROOGHI P. Estimation of location and size of defects in a solid body via inverse heat conduction problem[C]//Proceedings of the 14th International Heat Transfer Conference. Washington DC, 2010: 387-396.
|
| [14] |
SIAVASHI M, KOWSARY F, ABBASI-SHAVAZI E. Detection of flaws in a two-dimensional body through measurement of surface temperatures and use of conjugate gradient method[J]. Computational Mechanics, 2010, 46(4): 597-607. DOI:10.1007/s00466-010-0501-5 |
| [15] |
KOWSARY F, SIAVASHI M. Prediction of internal flaw parameters in a two-dimensional body using steady-state surface temperature data and IHCP methods[C]//Second UKSIM European Symposium on Computer Modeling and Simulation. Liverpool, 2008: 341-346.
|
| [16] |
CHEN W L, YANG Y C, LEE H L, et al. Inverse estimation for unknown fouling geometry on inner wall of forced-convection pipe[J]. Applied Mathematics and Mechanics(English Edition), 2011, 32(1): 55-68. DOI:10.1007/s10483-011-1393-9 |
| [17] |
CHEN W L, YANG Y C. Inverse estimation for the unknown frost geometry on the external wall of a forced-convection pipe[J]. Energy Conversion and Management, 2009, 50(6): 1457-1464. DOI:10.1016/j.enconman.2009.02.017 |
| [18] |
CHEN W L, YANG Y C, LEE H L, et al. Estimation for inner surface geometry of a two-layer-wall furnace with inner wall made of functionally graded materials[J]. International Communications in Heat and Mass Transfer, 2018, 97: 143-150. DOI:10.1016/j.icheatmasstransfer.2018.07.009 |
| [19] |
WANG S H, LIN S C, YANG Y C. Geometry estimation for the inner surface in a furnace wall made of functionally graded materials[J]. International Communications in Heat and Mass Transfer, 2015, 67: 1-7. DOI:10.1016/j.icheatmasstransfer.2015.06.012 |
| [20] |
苟小龙, 张建涛, 王广军. 基于导热反问题的管道内部缺陷诊断[J]. 重庆大学学报, 2010, 33(2): 42-46. GOU X L, ZHANG J T, WANG G J. Defects detection in the inner surface of pipes based on inverse heat conduction problem[J]. Journal of Chongqing University, 2010, 33(2): 42-46. (in Chinese) |
| [21] |
范春利, 孙丰瑞, 杨立. 基于红外测温的圆管内壁不规则边界的识别算法研究[J]. 热科学与技术, 2006, 5(2): 112-117. FAN C L, SUN F R, YANG L. Algorithm study on identification of pipeline's irregular inner boundary for infrared thermography[J]. Journal of Thermal Science and Technology, 2006, 5(2): 112-117. (in Chinese) DOI:10.3969/j.issn.1671-8097.2006.02.004 |
| [22] |
张林, 范春利, 孙丰瑞, 等. 基于APDL的管道内壁边界识别算法[J]. 红外与激光工程, 2015, 44(5): 1477-1484. ZHANG L, FAN C L, SUN F R, et al. Identification algorithm of pipelines' inner boundary based on APDL[J]. Infrared and Laser Engineering, 2015, 44(5): 1477-1484. (in Chinese) DOI:10.3969/j.issn.1007-2276.2015.05.015 |
| [23] |
CHENG C H, CHANG M H. Shape identification by inverse heat transfer method[J]. Journal of Heat Transfer, 2003, 125(2): 224-231. DOI:10.1115/1.1560152 |
| [24] |
HUANG C H, TSAI C C. A transient inverse two-dimensional geometry problem in estimating time-dependent irregular boundary configurations[J]. International Journal of Heat and Mass Transfer, 1998, 41(12): 1707-1718. DOI:10.1016/S0017-9310(97)00266-4 |
| [25] |
张林, 杨立, 寇蔚, 等. 基于一维加权法的交界面边界形状识别[J]. 红外技术, 2018, 40(6): 590-597. ZHANG L, YANG L, KOU W, et al. Inverse identification of interface geometry in a multiple region domain based on one-dimensional weighting method[J]. Infrared Technology, 2018, 40(6): 590-597. (in Chinese) |
| [26] |
MOHASSEB S, MORADI M, SOKHANSEFAT T, et al. A novel approach to solve inverse heat conduction problems: coupling scaled boundary finite element method to a hybrid optimization algorithm[J]. Engineering Analysis with Boundary Elements, 2017, 84: 206-212. DOI:10.1016/j.enganabound.2017.08.018 |
| [27] |
LIU F B. A hybrid method for the inverse heat transfer of estimating fluid thermal conductivity and heat capacity[J]. International Journal of Thermal Sciences, 2011, 50(5): 718-724. DOI:10.1016/j.ijthermalsci.2010.11.020 |
| [28] |
GARCÍA E, MÉRESSE D, POMBO I, et al. Identification of heat partition in grinding related to process parameters, using the inverse heat flux conduction model[J]. Applied Thermal Engineering, 2014, 66(1-2): 122-130. DOI:10.1016/j.applthermaleng.2014.01.048 |
| [29] |
XIE T, HE Y L, TONG Z X, et al. An inverse analysis to estimate the endothermic reaction parameters and physical properties of aerogel insulating material[J]. Applied Thermal Engineering, 2015, 87: 214-224. DOI:10.1016/j.applthermaleng.2015.05.008 |
| [30] |
ZHANG B W, MEI J, ZHANG C Y, et al. A general method for predicting the bank thickness of a smelting furnace with phase change[J]. Applied Thermal Engineering, 2019, 162: 114219. DOI:10.1016/j.applthermaleng.2019.114219 |








