2. 陆军航空兵学院 航空机械工程系, 北京 101123;
3. 93146部队, 北京 100000
2. Department of Aviation Machinery Engineering of Army Aviation Institute, Beijing 101123;
3. 93146 Troops, Beijing 100000, China
随着现代工业的快速发展,旋转机械设备越来越大型化、复杂化和智能化[1],如何保证旋转设备的高可靠性安全运行,提高其工作效率,已成为当前亟需解决的关键问题之一。滚动轴承作为旋转机械设备的重要部件,在复杂的工作条件下易发生疲劳损伤[2-3],进而影响设备的运行效率与安全。因此,对滚动轴承进行有效、可靠、准确的剩余使用寿命预测具有重要的实际意义。基于预测的剩余寿命开展及时的维护工作,可提高设备的整体运转效率,避免了在传统的维护工作中存在的设备得不到及时维护、设备发生故障的风险增加以及健康状态下维护次数过多而造成的资源浪费等问题[4]。
鉴于轴承的振动信号中包含大量的运行状态信息[5],当前多以设备的振动监测数据为基础进行剩余寿命的预测研究[6]。通常,采集的振动信号中包含数据异常点和噪声,而这些噪声会给预测结果带来误差,因此需要对原始振动信号进行去噪处理。Beale等[7]提出了自适应小波包阈值降噪算法用于消除风力涡轮机叶片的振动噪声。许志华等[8]研究了基于变分模态分解的风机齿轮箱振动信号降噪方法。王大兴[9]针对轴承振动信号提出了经验模态分解与小波包多阈值相结合的降噪方法,有效剔除了信号中的异常数据点。
在实现振动信号的降噪处理后,就需要提取表征轴承退化状态的特征,目前主要使用信号处理的方式提取常见的时域特征、频域特征和时频域特征等[10]。在提取的众多特征中,存在着部分冗余特征和对轴承退化状态不敏感的特征,因此需要对其进行约简,以获得有效的敏感特征作为预测模型的输入,从而提高模型的预测精度。常用的特征约简方法包括相关系数法、互信息法(mutual information, MI)、流形学习[11]和主成分分析(principal component analysis, PCA)[12]等。然而,相关系数法和互信息法只是对提取的多维特征进行筛选[13],并没有考虑特征之间的冗余性,若特征之间存在信息重叠,则容易产生预测模型的“过拟合”现象,进而影响模型的预测精度[14],而PCA可以消除特征之间的冗余信息[12]。近年来,智能算法的持续改进与发展为剩余寿命的预测研究提供了新思路,如双向长短时记忆神经网络[15]、改进隐马尔可夫模型[16]、基于Bayesian optimization and hyperband (BOHB)的深度置信网络[17]以及深度卷积神经网络[18]等都取得了较好的预测效果。但这些算法的结构较为复杂且超参数众多,而支持向量回归(support vector regression, SVR)算法的泛化能力和非线性映射能力强且结构简单[19],能有效解决小样本问题[20]。
基于以上分析,本文提出了一种基于MI-PCA结合SVR的滚动轴承剩余寿命预测方法。通过小波包降噪算法实现原始振动信号的去噪处理,并提取时域、频域和时频域特征;然后计算特征与剩余寿命之间的互信息值进行特征筛选,进而结合PCA算法获取敏感特征用于SVR的输入;最后建立SVR预测模型,实现轴承剩余寿命的精准预测。滚动轴承的全寿命试验数据验证表明,与基于MI和基于PCA的SVR模型相比,所提模型具有更高的预测精度,有利于开展及时的设备维护工作,提高设备的运转效率。
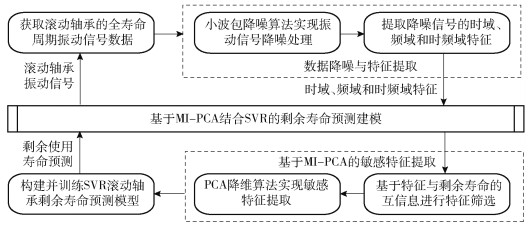
1 剩余寿命预测建模 1.1 建模流程为了实现滚动轴承剩余使用寿命的精准预测,本文以轴承的振动信号数据为基础,提出了基于MI-PCA结合SVR的剩余寿命预测建模方法。流程包括3个部分:(1)利用小波包降噪算法实现原始振动信号的预处理,并提取表征轴承退化状态的时域、频域和时频域特征;(2)基于特征与剩余寿命的互信息值进行特征筛选,再通过PCA算法获取敏感特征用于SVR模型的输入;(3)建立并训练SVR回归预测模型,实现轴承的剩余寿命预测。具体的建模流程如图 1所示。
|
图 1 剩余寿命预测建模流程 Fig.1 The process of remaining useful life prediction modeling |
由于旋转机械设备结构的复杂性以及工作条件的多样性,导致采集的滚动轴承振动信号中包含大量的噪声[21],染噪后的信号数据会影响轴承剩余寿命预测的精度。因此,本文首先采用小波包降噪算法对原始振动信号进行去噪处理。小波包降噪的关键在于信号的分解与重构,相比于传统的小波变换,小波包分析不仅对每层中的低频部分进行分解,而且对高频部分也进行分解[22],能够有效提高信号高频段的分辨率,从而使得信号的表达更为精确。为了进一步挖掘振动信号中的隐含状态信息,使用信号处理的方法从不同角度提取表征轴承退化状态的特征。一般可以从时域、频域和时频域中提取相关特征,以充分利用振动信号数据实现剩余寿命的精准预测。
在提取频域特征时,首先利用快速傅里叶变换将去噪后的时域振动信号x(t)(t=1, 2, …, n)转换为频域振动信号y(k)(k=1, 2, …, m),然后提取相关的频域特征。
在提取时频域特征时,首先通过经验模态分解将时域振动信号从高频至低频分解为若干个本征模态函数(intrinsic mode function, IMF),即IMF分量c(t)(t=1, 2, …, n)。为了保证分量信号的有效性,选取前3阶IMF分量的有效值作为时频域特征。本文提取的时域、频域和时频域特征如表 1所示。
| 下载CSV 表 1 提取的时域、频域和时频域特征 Table 1 The time-domain, frequency-domain and time-frequency-domain features |
互信息是两个随机变量之间相互依赖的度量, 用来衡量两个变量的相互关联程度,表示两个变量之间含有相同信息的部分[23]。假设两个随机变量X和Y,其各自的边缘概率密度函数和联合概率密度函数分别为p(x),p(y)和p(x, y),则它们的互信息值I如式(1)所示。
| $ I(\mathit{\boldsymbol{X}};\mathit{\boldsymbol{Y}}) = \sum\limits_{{x_i} \in X, {y_j} \in Y} p \left( {{x_i}, {y_j}} \right)\lg \frac{{p\left( {{x_i}, {y_j}} \right)}}{{p\left( {{x_i}} \right)p\left( {{y_j}} \right)}} $ | (1) |
若X和Y的互信息值为0,表示两个变量为无关变量或相互独立变量,即二者没有相互包含的信息;反之,互信息值越大,表示两个变量之间相互关联的程度越高,包含的相同信息量也就越多。本文通过计算特征与剩余寿命之间的互信息值进行特征筛选,保留与剩余寿命关联度较高的特征。
1.3.2 主成分分析主成分分析法是一种常用的数据降维方法,其基本原理是将具有一定相关性的原始变量经线性变化转换为一组互不相关的变量,且第一变量集中了原始变量所包含的主要信息[24]。基于PCA降维的转换公式如式(2)所示。
| $ {\mathit{\boldsymbol{Z}}_{m \times 1}} = {\mathit{\boldsymbol{L}}_{m \times s}}{\mathit{\boldsymbol{X}}_{s \times 1}} = \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_1} = {\mathit{\boldsymbol{l}}_{11}}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{l}}_{12}}{\mathit{\boldsymbol{x}}_2} + \cdots + {\mathit{\boldsymbol{l}}_{1s}}{\mathit{\boldsymbol{x}}_s}}\\ {{\mathit{\boldsymbol{z}}_2} = {\mathit{\boldsymbol{l}}_{21}}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{l}}_{22}}{\mathit{\boldsymbol{x}}_2} + \cdots + {\mathit{\boldsymbol{l}}_2}{\mathit{\boldsymbol{x}}_s}}\\ \vdots \\ {{\mathit{\boldsymbol{z}}_m} = {\mathit{\boldsymbol{l}}_{m1}}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{l}}_{m2}}{\mathit{\boldsymbol{x}}_2} + \cdots + {\mathit{\boldsymbol{l}}_{ms}}{\mathit{\boldsymbol{x}}_s}} \end{array}} \right\} $ | (2) |
式中,X和Z分别为原始变量和转换后的变量,L为荷载矩阵,即转换矩阵,s为原始变量维数,m为转换后的变量维数,且m≤s。本文首先基于互信息法筛选主要特征,然后利用PCA减少主要特征之间的冗余和重叠信息,从提取的多维特征中获取关键敏感特征,作为预测模型的输入。
1.4 支持向量回归预测模型支持向量机(support vector machine, SVM)是一种用于解决小样本、非线性及高维模式识别下统计估计和预测问题的机器学习方法[25]。支持向量回归是SVM函数在回归拟合领域的应用。SVR的基本思想是在高维特征空间上寻找一个最优超平面,能够使训练集样本距离该超平面最近,并将该超平面作为回归模型对未知数据进行预测。假设训练样本为(x1, y1), (x2, y2), …, (xn, yn),xi∈Rn为模型输入,yi∈R为模型期望输出,n为训练样本个数,则回归函数可表示为
| $ f(\mathit{\boldsymbol{x}}) = \sum\limits_{i = 1}^n {\left( {{\mathit{\alpha }_i} - \mathit{\alpha }_i^*} \right)} K\left( {{\mathit{\boldsymbol{x}}_i}, \mathit{\boldsymbol{x}}} \right) + \mathit{\boldsymbol{b}} $ | (3) |
式中,b为偏置向量;αi和αi*为拉格朗日算子;K(xi, x)为核函数。核函数可以将低维空间的线性不可分问题转化为高维特征空间的线性可分问题。考虑到滚动轴承的退化趋势呈非线性,本文采用参数较少且非线性映射能力较强的高斯核函数解决SVR的回归预测问题。高斯核函数的表达式为
| $ K\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right) = \exp \left( { - \frac{{{{\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right\|}^2}}}{{{\mathit{\sigma }^2}}}} \right) $ | (4) |
式中,σ为高斯核函数的指数,影响着SVR模型的预测精度。
1.5 模型评估指标本文采用平均相对泛化误差EARG(average relative generalization error, ARGE)、均方根误差ERMS(root mean square error, RMSE)和相对误差ER(relative error, RE)来评估模型的回归预测能力,计算公式分别如下。
| $ {E_{{\rm{ARG}}}} = \frac{1}{n}\sum\limits_{k = 1}^n {\frac{{\left| {{P_{{\rm{out}}, k}} - {E_{{\rm{out}}, k}}} \right|}}{{{E_{{\rm{out}}, k}}}}} $ | (5) |
| $ {E_{{\rm{RMS}}}} = \sqrt {\frac{1}{n}\sum\limits_{k = 1}^n {{{\left( {{P_{{\rm{out}}, k}} - {E_{{\rm{out}}, k}}} \right)}^2}} } $ | (6) |
| $ {E_{{\rm{R}}, k}} = \frac{{\left| {{P_{{\rm{out}}, k}} - {E_{{\rm{out}}, k}}} \right|}}{{{E_{{\rm{out}}, k}}}} \times 100\% $ | (7) |
式中,Pout, k为模型的预测输出,Eout, k为模型的期望输出,n为模型输入样本个数,k表示第k个样本。
2 试验验证 2.1 试验数据以IEEE PHM12轴承加速性能退化试验的全寿命数据[26]为例验证所提方法的有效性。试验数据来自如图 2所示的PRONOSTIA试验台。通过加速度传感器采集轴承在水平和垂直两个方向上的振动信号,每间隔10 s采集一次数据,设置采样频率为25.6 kHz,每次采样0.1 s,因此每次可采集2 560个振动加速度。该数据集共包含3种工况下17个滚动轴承的全寿命周期试验数据,工况划分如表 2所示。由于轴承水平方向振动信号包含更多的状态信息[26],因此本文以工况1下轴承1水平方向的振动信号为研究对象,构建基于MI-PCA结合SVR的滚动轴承剩余寿命预测模型。

|
图 2 PRONOSTIA试验台 Fig.2 The PRONOSTIA test rig |
| 下载CSV 表 2 工况划分设置 Table 2 The working condition division settings |
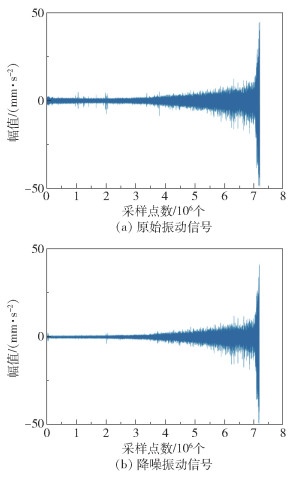
首先,采用小波包降噪算法处理轴承1的原始振动信号,其原始振动信号及降噪后的振动信号如图 3所示。从图中可以看出降噪后的数据更加平滑,剔除了异常数据点,并保留了原始振动信号中的有效信息。
|
图 3 原始信号和小波包降噪信号的对比 Fig.3 Comparison of raw signals and wavelet packet denoising signals |
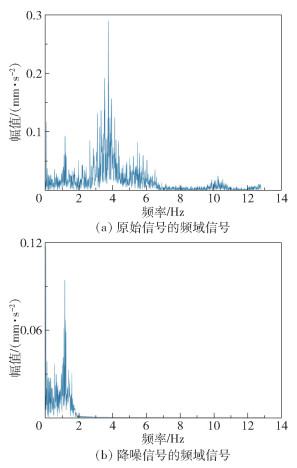
为了更好地突出显示小波包降噪的效果,选取某一次采集的振动信号进行分析,同时将时域振动信号转换为频域信号,以便更直观地分析降噪效果。图 4为小波包降噪前后的频域信号对比,可以看出小波包降噪方法可以在一定程度上滤除噪声,而且能够保留原始信号的有效信息,即降噪后的频域信号含有峰值,可表征轴承的磨损状况[27],从而可提取出对轴承退化敏感的特征。
|
图 4 原始信号和小波包降噪信号的频域信号对比 Fig.4 Frequency-domain signals comparison of raw signals and wavelet packet denoising signals |
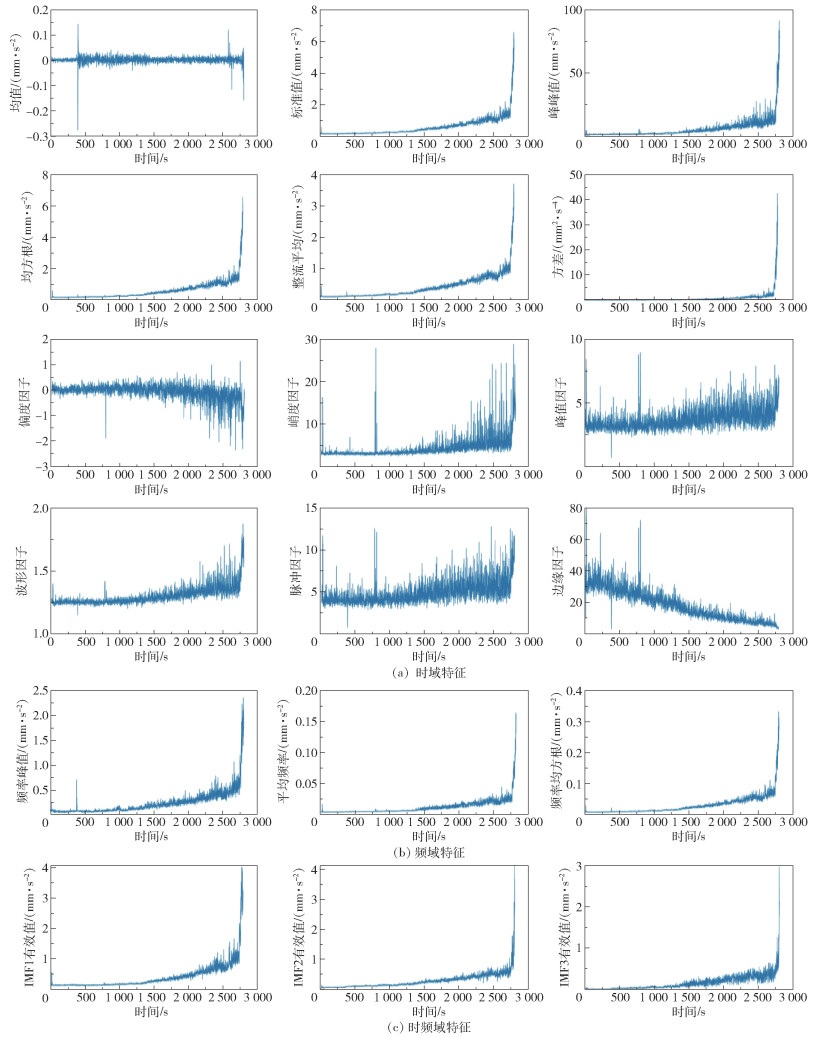
图 5为提取的18个时域、频域和时频域特征。从图 5可以看出,部分特征的退化趋势不明显,无法表征轴承的退化状态,因此首先采用互信息法筛选对轴承退化状态较为敏感的特征。表 3为提取的特征与真实剩余寿命的互信息计算结果,将互信息的平均值设置为阈值,保留互信息值大于阈值的特征。
|
图 5 降噪信号的时域、频域和时频域特征 Fig.5 Time-domain, frequency-domain and time-frequency-domain features of denoising signals |
| 下载CSV 表 3 特征与真实剩余寿命的互信息值 Table 3 Mutual information values of features and true remaining useful life |
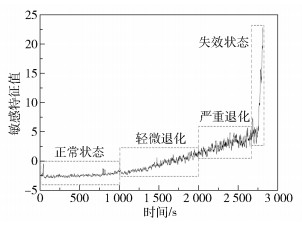
本文案例计算的阈值为7.28,剔除7个对轴承退化状态不敏感的特征,然后基于保留的11个特征进行PCA降维,选取累积贡献率大于90%的第一主元变量作为敏感特征[28],结果如图 6所示。从图 6可以看出,敏感特征可以很好地表征轴承的退化状态,即正常状态、轻微退化、严重退化和失效状态。
|
图 6 敏感特征 Fig.6 The sensitive feature |
将提取的敏感特征作为SVR模型的输入,将轴承的真实剩余寿命作为SVR模型的期望输出,对模型进行训练和测试。选取4种退化状态中的各50个样本进行测试,为了验证基于MI-PCA的SVR模型预测结果的准确性,分别建立基于MI和基于PCA的SVR回归预测模型对相同的样本进行测试。
表 4为3种预测模型的评估指标结果。从表 4可以看出,3种模型对前3种退化状态剩余寿命的预测误差较低,对失效状态的预测误差较大,然而MI-PCA-SVR模型的预测误差要远小于另外两种模型。总体来看,MI-SVR模型、PCA-SVR模型以及MI-PCA-SVR模型的平均预测准确率分别为90%、93%和97%,MI-PCA-SVR模型的预测准确率最高,预测误差最低,说明采用MI-PCA方法对输入样本进行降维处理可提高模型的预测精度。
| 下载CSV 表 4 3种模型评估结果 Table 4 Evaluation results for three models |
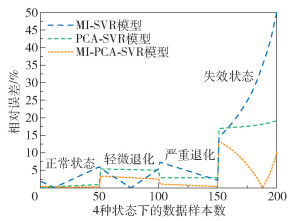
图 7为3种模型的相对误差曲线。从图 7可以看出,MI-PCA-SVR模型在严重退化和失效状态下的预测误差均小于MI-SVR模型和PCA-SVR模型。此外,MI-SVR模型的相对误差曲线波动较大,其相对误差最高可达50%,而MI-PCA-SVR模型的相对误差曲线较平稳,总体误差均在13%以内。结合表 4的RMSE计算结果和图 7的误差曲线,说明MI-PCA-SVR模型的稳定性要优于另外两种模型。基于以上分析,采用基于MI-PCA的SVR模型能够实现滚动轴承剩余寿命的精准预测。
|
图 7 3种模型的相对误差曲线 Fig.7 Relative error curves for the three models |
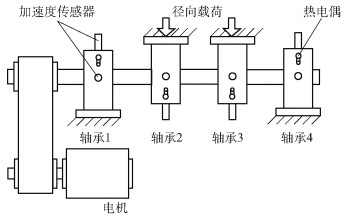
为进一步验证所提方法的有效性,采用美国辛辛那提大学智能维护系统中心(Intelligent Maintenance System, IMS)的滚动轴承全寿命周期试验数据进行案例分析与验证。试验数据来自图 8所示的试验台,通过加速度传感器采集轴承的振动信号,每间隔10 min采集一次数据,设置采样频率为20 kHz,采样点数为204 800。试验结束后共取得3个数据集。本文以数据集2中轴承1运行的全寿命周期加速疲劳振动数据作为研究对象,构建基于MI-PCA结合SVR的滚动轴承剩余寿命预测模型。
|
图 8 IMS试验台 Fig.8 The IMS test rig |
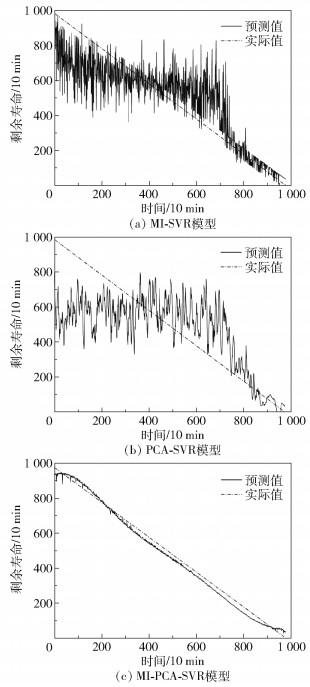
为体现本文所提方法的全局优势,分别使用MI-SVR模型、PCA-SVR模型和MI-PCA-SVR模型预测轴承1的全过程剩余使用寿命。3种方法的预测结果如图 9所示。从图 9可以看出,MI-SVR模型和PCA-SVR模型在轴承的正常运行及初始退化阶段预测值和实际值之间的误差较大,随着时间的推移,在轴承的退化后期,误差逐渐缩小,而MI-PCA-SVR模型的整体预测误差均较小,预测值在实际值上下波动。此外,为了衡量模型预测结果的稳定性,计算得到MI-SVR模型、PCA-SVR模型和MI-PCA-SVR模型的RMSE值分别为14.922 7、20.065 2和2.609 0,表明本文所提方法的剩余寿命预测结果更加稳定。通过分析3种模型的预测结果曲线以及RMSE评估指标值可以得出,本文提出的MI-PCA-SVR模型的预测精度更高,而且预测结果的稳定性最优。
|
图 9 3种模型的剩余寿命预测结果 Fig.9 Remaining useful life prediction results for the three models |
为了提高旋转机械设备的运转效率,实现设备的智能维护,本文提出了一种基于MI-PCA结合SVR模型的滚动轴承剩余寿命预测方法。首先利用小波包降噪算法消除原始振动信号中的噪声点对预测精度的影响,并基于降噪数据提取时域、频域和时频域特征。然后计算提取的特征与轴承真实剩余寿命的互信息值进行特征筛选,进而通过PCA降维算法剔除筛选特征之间的冗余信息,获取表征轴承退化状态的敏感特征。最后以敏感特征作为模型的输入数据实现SVR模型的训练和测试。试验结果表明,基于MI-PCA的敏感特征提取方法可以充分挖掘振动信号中的状态信息,有效区分轴承退化过程中的不同状态;且基于MI-PCA构建的SVR模型可实现正常状态、轻微退化、严重退化和失效状态这4种退化状态下剩余寿命的精准预测,为开展及时有效的设备维护工作提供了有力依据。
符号说明x(t)—时域振动信号,mm/s2
y(t)—频域振动信号,mm/s2
c(t)—IMF分量,mm/s2
X—均值,mm/s2
Xss—标准差,mm/s2
Xpp—峰峰值,mm/s2
Xrms—均方根,mm/s2
Xr—整流平均,mm/s2
Xs—方差,mm2/s4
CL—偏度因子
Kr—峭度因子
C—峰值因子
S—波形因子
I—脉冲因子
M—边缘因子
f1—平均频率,mm/s2
f2—频率均方根,mm/s2
f3—频率峰值,mm/s2
I1—IMF1有效值,mm/s2
I2—IMF2有效值,mm/s2
I3—IMF3有效值,mm/s2
| [1] |
SHAO K X, FU W L, TAN J W, et al. Coordinated approach fusing time-shift multiscale dispersion entropy and vibrational Harris hawks optimization-based SVM for fault diagnosis of rolling bearing[J]. Measurement, 2021, 173: 108580. DOI:10.1016/j.measurement.2020.108580 |
| [2] |
HU Z X, WANG Y, GE M F, et al. Data-driven fault diagnosis method based on compressed sensing and improved multi-scale network[J]. IEEE Transactions on Industrial Electronics, 2020, 67(4): 3216-3225. DOI:10.1109/TIE.2019.2912763 |
| [3] |
王琇峰, 文俊. 基于噪声信号和改进VMD的滚动轴承故障诊断[J]. 噪声与振动控制, 2021, 41(2): 118-124. WANG X F, WEN J. Fault diagnosis of rolling bearings based on noise signal and improved VMD[J]. Noise and Vibration Control, 2021, 41(2): 118-124. (in Chinese) DOI:10.3969/j.issn.1006-1355.2021.02.019 |
| [4] |
朱丽娟. 机械设备运行可靠性评估的发展与思考[J]. 山东工业技术, 2014(23): 45. ZHU L J. The development and thinking of mechanical equipment operation reliability evaluation[J]. Shandong Industrial Technology, 2014(23): 45. (in Chinese) |
| [5] |
LI Z H, TAO Y, ABU-SIADA A, et al. A new vibration testing platform for electronic current transformers[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68: 704-712. DOI:10.1109/TIM.2018.2854939 |
| [6] |
王银刚. 基于振动数据分析的轴承典型故障预测研究[D]. 天津: 中国民航大学, 2020. WANG Y G. Research on typical failure prediction of bearing based on vibration data analysis[D]. Tianjin: Civil Aviation University of China, 2020. (in Chinese) |
| [7] |
BEALE C, NIEZRECKI C, INALPOLAT M. An adaptive wavelet packet denoising algorithm for enhanced active acoustic damage detection from wind turbine blades[J]. Mechanical Systems and Signal Processing, 2020, 142: 106754. DOI:10.1016/j.ymssp.2020.106754 |
| [8] |
许志华, 潘庭龙. 基于变分模态分解的风机齿轮箱振动信号降噪方法研究[J]. 机电工程, 2021, 38(1): 129-132. XU Z H, PAN T L. Noise reduction method of fan gearbox vibration signal based on variational mode decomposition[J]. Journal of Mechanical & Electrical Engineering, 2021, 38(1): 129-132. (in Chinese) DOI:10.3969/j.issn.1001-4551.2021.01.021 |
| [9] |
王大兴. 滚动轴承振动信号降噪及故障识别研究[D]. 兰州: 兰州理工大学, 2020. WANG D X. Research on de-noising and fault identification of rolling bearing vibration signal[D]. Lanzhou: Lanzhou University of Technology, 2020. (in Chinese) |
| [10] |
WANG F T, LIU X F, DENG G, et al. Remaining life prediction method for rolling bearing based on the long short-term memory network[J]. Neural Processing Letters, 2019, 50(2): 2437-2454. |
| [11] |
SHI M K, ZHAO R Z, WU Y C, et al. Fault diagnosis of rotor based on local-global balanced orthogonal discriminant projection[J]. Measurement, 2021, 168: 108320. DOI:10.1016/j.measurement.2020.108320 |
| [12] |
戴邵武, 陈强强, 丁宇. 基于时域特征的滚动轴承寿命预测[J]. 计算机测量与控制, 2019, 27(10): 60-63. DAI S W, CHEN Q Q, DING Y. Prediction for rolling bearing remaining life based on time domain features[J]. Computer Measurement & Control, 2019, 27(10): 60-63. (in Chinese) |
| [13] |
孟建军, 胡文涛. 基于互信息和SVR的滚动轴承剩余寿命预测[J]. 机械设计与研究, 2020, 36(6): 92-95. MENG J J, HU W T. Prediction of the remaining useful life of rolling bearings based on mutual information and SVR[J]. Machine Design and Research, 2020, 36(6): 92-95. (in Chinese) |
| [14] |
丁公博, 农振学, 王超, 等. 基于MI-PCA与BP神经网络的石羊河流域中长期径流预报[J]. 中国农村水利水电, 2019(10): 66-69. DING G B, NONG Z X, WANG C, et al. Long-term runoff forecasting model based on MI-PCA and BP neural network in Shiyang River Basin[J]. China Rural Water and Hydropower, 2019(10): 66-69. (in Chinese) DOI:10.3969/j.issn.1007-2284.2019.10.013 |
| [15] |
ELSHEIKH A, YACOUT S, OUALI M S. Bidirectional handshaking LSTM for remaining useful life prediction[J]. Neurocomputing, 2019, 323: 148-156. DOI:10.1016/j.neucom.2018.09.076 |
| [16] |
CHEN Z, LI Y P, XIA T B, et al. Hidden Markov model with auto-correlated observations for remaining useful life prediction and optimal maintenance policy[J]. Reliability Engineering and System Safety, 2019, 184: 123-136. DOI:10.1016/j.ress.2017.09.002 |
| [17] |
HARIS M, HASAN M N, QIN S Y. Early and robust remaining useful life prediction of supercapacitors using BOHB optimized deep belief network[J]. Applied Energy, 2021, 286: 116541. DOI:10.1016/j.apenergy.2021.116541 |
| [18] |
马忠, 郭建胜, 顾涛勇, 等. 基于改进卷积神经网络的航空发动机剩余寿命预测[J]. 空军工程大学学报(自然科学版), 2020, 21(6): 19-25. MA Z, GUO J S, GU T Y, et al. A remaining useful life prediction for aero-engine based on improved convolution neural networks[J]. Journal of Air Force Engineering University (Natural Science Edition), 2020, 21(6): 19-25. (in Chinese) |
| [19] |
KAYA D. Optimization of SVM parameters with hybrid CS-PSO algorithms for Parkinson's disease in LabVIEW environment[J]. Parkinson's Disease, 2019, 2019: 2513053. |
| [20] |
SHI Y, GONG F R, WANG M Y, et al. A deep feature mining method of electronic nose sensor data for identifying beer olfactory information[J]. Journal of Food Engineering, 2019, 263: 437-445. DOI:10.1016/j.jfoodeng.2019.07.023 |
| [21] |
杨旭, 邱明, 陈立海, 等. 基于PSO-RWE的自适应小波阈值函数滚动轴承振动信号去噪方法[J]. 航空动力学报, 2020, 35(11): 2339-2347. YANG X, QIU M, CHEN L H, et al. Adaptive wavelet threshold function based on PSO-RWE for vibration signal denoising of rolling bearing[J]. Journal of Aerospace Power, 2020, 35(11): 2339-2347. (in Chinese) |
| [22] |
陈长征, 魏巍. 基于改进LMD与小波包降噪对故障弱信号的提取[J]. 机械设计与制造, 2020(1): 165-168, 172. CHEN C Z, WEI W. Extraction of weak fault signal based on improved LMD and wavelet packet de-nosing[J]. Machinery Design & Manufacture, 2020(1): 165-168, 172. (in Chinese) |
| [23] |
KRASKOV A, STÖGBAUER H, GRASSBERGER P. Estimating mutual information[J]. Physical Review E, 2004, 69: 066138. |
| [24] |
余忠永, 黄俊, 许二敏, 等. 基于PCA降维的多特征行人再识别[J]. 信息通信, 2019(4): 13-16. YU Z Y, HUANG J, XU E M, et al. Multi-feature pedestrian re-identification based on PCA dimension reduction[J]. Information & Communications, 2019(4): 13-16. (in Chinese) |
| [25] |
陈芳, 程献宝, 黄安民, 等. 基于人工蜂群算法优化SVM的NIR杉木弹性模量预测[J]. 林业科学, 2021, 57(1): 161-168. CHEN F, CHENG X B, HUANG A M, et al. Elastic modulus prediction of Cunninghamia lanceolata based on artificial bee colony algorithm SVM and NIR[J]. Scientia Silvae Sinicae, 2021, 57(1): 161-168. (in Chinese) |
| [26] |
SOUALHI A, MEDJAHER K, ZEROUNI N. Bearing health monitoring based on Hilbert-Huang transform, support vector machine, and regression[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(1): 52-62. |
| [27] |
纪俊卿, 张亚靓, 孟祥川, 等. 自适应小波阈值滚动轴承故障振动信号降噪方法[J]. 哈尔滨理工大学学报, 2021, 26(2): 124-130. JI J Q, ZHANG Y L, MENG X C, et al. Adaptive wavelet threshold rolling bearing fault vibration signal denoising method[J]. Journal of Harbin University of Science and Technology, 2021, 26(2): 124-130. (in Chinese) |
| [28] |
王佳瑜. 数据驱动的缓变微小故障早期诊断及剩余寿命预测[D]. 开封: 河南大学, 2017. WANG J Y. Data-driven early diagnosis and residual useful life prediction of slowly varying small fault[D]. Kaifeng: Henan University, 2017. (in Chinese) |








