2. 北京化工大学 材料科学与工程学院, 北京 100029
2. College of Materials Science and Engineering, Beijing University of Chemical Technology, Beijing 100029, China
随着现代工程技术的快速发展,粉体原料和制品的需求逐年增加,如何制备并分级得到窄粒度分布的超细粉体受到广泛关注。涡流空气分级机由于具有操作简单、粒径可调、高效节能等优点,被广泛用于化工、制药、建材加工、燃料电池等各个行业[1-2]。分级机结构是影响分级性能的关键因素,目前国内外学者主要从以下两个方面开展对分级机结构的研究:(1)对现有设备关键组件如转笼、导风叶片、喂料装置等进行结构改进和优化[3-5];(2)通过分级机淘洗区内部的辅助组件改善分级机内的流场分布。张胜林等[6]设计了一种新型下锥体结构用于优化分级机内部的流场分布,该新型下锥体采用环状全断面进风,可使气流轴向速度分布均匀,避免了分选盲区的情况出现,提高了分级机的再次分选能力和分级效率。刁雄等[7]对比分析了分级机内导流片的有无及叶片的数量和尺寸对流场的影响,研究发现安装导流片可以优化流场的分布,导流片的尺寸和数量对流场的压力、速度和颗粒的质量浓度分布均有较大影响。周岩等[8]对卧式分级机内部进行改进,在分级机内部增加三角形扰流组件,提高物料的二次分散效果。Sun等[9]对进风口处的三角形挡板进行了研究,发现挡板将主进风分为两部分,且两部分气流速度逐渐增加有利于原料的分散;此外,由于挡板的阻碍,气流进入分级室后形成无二次涡的偏心旋流,使得流场分布均匀。上述研究成果表明,空气分级机淘洗区辅助组件对其内部的流场分布及颗粒的分级效果具有显著影响。因此,本文以立式涡流分级机为研究对象,通过数值模拟的方法探究位于淘洗区的扰流锥对分级机内部的流场分布和颗粒分级的影响,并进行物料实验验证,为分级机内部辅助组件的优化提供理论指导。
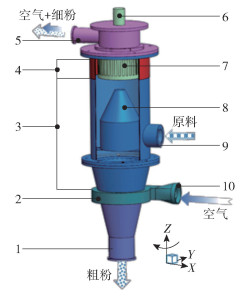
1 立式涡流空气分级机模型 1.1 工作原理及模型建立涡流空气分级机主要结构如图 1所示,其核心部件为转笼,利用转笼高速旋转时产生的离心力和气流曳力使粗细颗粒分离。分级机的主要工作原理如下:由于风机的抽吸作用在装置内部形成负压,空气通过进风口进入分级机,在进气蜗壳作用下形成旋转气流,气流在淘洗区筒体内沿着扰流锥旋流向上,上升到转笼和筒体内壁之间的环形区后,经过转笼叶片间通道(转笼由电机轴带动绕Z轴顺时针转动),再由细粉出口离开分级机。粉体通过喂料口由螺旋加料装置进入淘洗区筒体进行预分散。预分散可以使粗大的颗粒由于重力作用落入粗粉收集漏斗收集为粗粉,较小的颗粒随着旋流上升的气流上升至环形区,粗细颗粒主要在环形区进行分级。细颗粒在环形区会因受到的空气曳力大于惯性离心力而随着气流进入转笼,再随气体从细粉出口流出;粗颗粒在环形区会因为受到的空气曳力小于惯性离心力而向筒体的内壁面运动,最后与壁面碰撞后失去动能,在重力作用下下落,经过淘洗区筒体最后到达粗粉收集漏斗收集为粗粉。
|
1—粗粉收集漏斗;2—进气蜗壳;3—淘洗区筒体;4—环形区;5—细粉出口;6—电机轴;7—转笼;8—扰流锥;9—喂料口;10—进风口。 图 1 立式涡流空气分级机结构示意图 Fig.1 Schematic of the vertical turbo air classifier |
利用三维建模软件Solidworks对立式涡流空气分级机的主体结构进行建模,主要尺寸如下:进风口截面宽50 mm,高34 mm;转笼内外缘直径分别为126 mm和156 mm,高90 mm;在直径为141 mm的圆周上均布36个转笼叶片,叶片与所在位置圆切线呈120°倾角,转笼叶片的长、宽、高分别为15、5、90 mm。
淘洗区筒体由上部的圆柱和下部的圆台组成,圆柱部分的直径为200 mm,高300 mm,圆台上、下底面直径分别为200 mm和158 mm,高90 mm。淘洗区筒体内的扰流锥与筒体同轴,扰流锥底面圆心为模型原点,设其所在平面为Z=0。扰流锥由上、下两部分组成,上部分是上、下底面直径分别为30、140 mm,高105 mm的圆台,下部分是直径140 mm、高100 mm的圆柱。
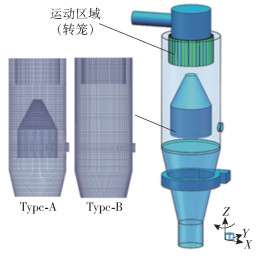
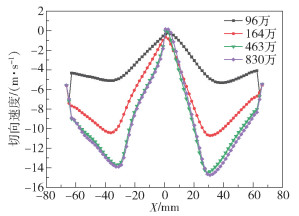
1.2 网格划分及模拟参数设置利用前处理软件ICEM-CFD对有/无扰流锥的分级机模型进行网格划分,有、无扰流锥结构分别用Type-A和Type-B表示,如图 2所示。因为分级机整体结构为类圆柱形,所以采用“O”型网格划分方法来产生规则的六面体网格。在数值模拟之前,分别以96万、164万、463万和830万的网格模型进行网格独立性验证。取不同Z平面上不同位置处的测线,比较其切向速度、径向速度和轴向速度的大小,例如选取Z=300 mm平面上Y=0、X=-65~65 mm的一条测线,得到不同网格数量模型在该测线的切向速度分布,如图 3所示。可以看出当网格数量为463万时切向速度值基本不再变化。为节省计算时间并保证计算准确性,最终确定Type-A网格数为463万。Type-B模型网格独立性验证同上,最终确定网格数为444万。采用ANSYS-Fluent软件对流场进行模拟,由于分级机内部是存在旋涡的湍流流场,因此选用重整化群(RNG)k-ε双方程模型,该模型针对旋涡在湍流流场中的运动作了特定优化,可提高模拟的准确性[10]。采用多重参考坐标系模型(multiple reference frame,MRF)作为运动区域计算模型,其中转笼为运动区域,其余部分为静止区域。采用SIMPLEC算法,该算法通过压力与速度的耦合来提高收敛性,设置残差精度为10-4。边界条件中设置进口风类型为“velocity-inlet”,出口类型为“outflow”。为便于表述,采用进风口风速(单位m/s)-转笼转速(单位r/min)来表示操作参数的组合, 如29-800工况即为进风口风速29 m/s,转速800 r/min。本文选用的转笼转速分别为800 r/min和1 600 r/min,旨在反映不同工况下流场的分布规律。
|
图 2 立式涡流空气分级机网格图 Fig.2 Meshes of the vertical turbo air classifier |
|
图 3 网格独立性验证 Fig.3 Independence verification of the CFD meshes |
压差是空气分级机重要的测量指标之一,常被用于验证模拟结果的准确性[11-12]。本文通过对比29-800和29-1 600两种不同工况下的单相气流实验压差和模拟压差数据,来验证数值模型的可靠性。模拟压差为进风口的面积加权平均静压与细粉出口的面积加权平均静压之差,实验压差为U型压差计(CJM-580型,衡水创纪仪器仪表有限公司)测量的进风口和细粉出口的压差,结果如表 1所示,实验测量压差和模拟结果相差在4%以内,说明模拟结果真实可靠。
| 下载CSV 表 1 实验压差和模拟压差的对比 Table 1 Comparison of the experimental and numerical values of the pressure differences |
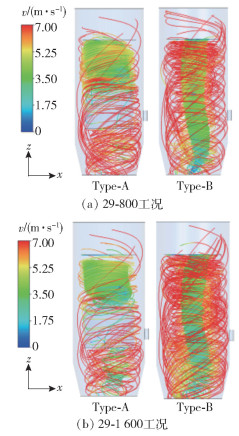
图 4为Type-A和Type-B两种模型在29-800和29-1 600两种工况下的流线分布图。可以看出Type-A模型的扰流锥明显阻碍了旋涡的形成。不过随着旋转气流沿着轴向继续上升至筒体中部,由于扰流锥直径减小,气流的过流面积增大,导致在淘洗区筒体顶部形成了新的偏心旋涡。Type-B模型由于没有扰流锥的阻碍作用,在筒体内部的旋涡从底部一直延伸到顶部。扰流锥的有无使得两种模型中旋涡的形成产生差异,从而影响速度v的分布。Type-A模型淘洗区筒体内气流的绝对速度整体较小,而Type-B模型该区域的气流绝对速度较大(图中红色区域)。气流速度对颗粒的分散性能有着重要影响,较高的风速可以提高细颗粒的分离效果[13]。淘洗区筒体内气流速度较小会导致颗粒不能充分预分散,使得细颗粒团聚为假大颗粒,“鱼钩效应”明显。
|
图 4 淘洗区筒体内两种模型的流线分布图 Fig.4 Gas path lines of Type-A and Type-B in the elutriation chamber |
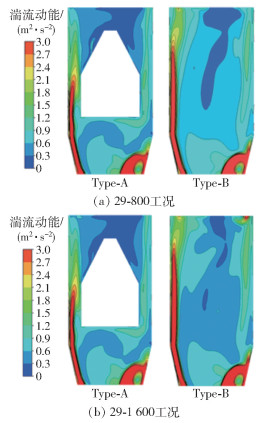
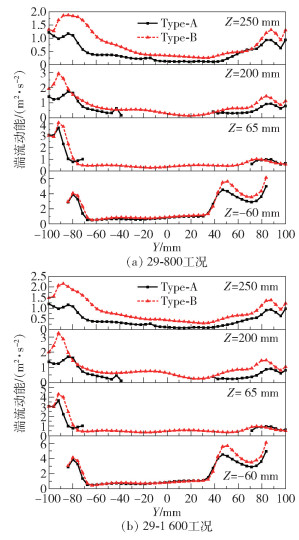
湍流动能k可以体现高频脉动的小尺寸湍涡数量,湍流动能越大,表明高频脉动的小尺寸湍涡数量越多。图 5为29-800和29-1 600两种工况下Type-A和Type-B模型在X=0截面的湍流动能分布云图。可以看出湍流动能在筒体的中间位置较小,两侧位置较大,这是因为气流在上升过程势必会撞击壁面导致气流产生高频脉动的小尺寸湍涡。其中在淘洗区筒体右下角位置出现极值情况,这是因为此位置正对进风口,气体经过进气蜗壳的加速作用沿轴向旋流上升,气流紊乱且流速较大,因此该位置的湍流动能大。为了进一步说明淘洗区筒体位置的湍流动能分布情况,分析不同平面的不同测线上的湍流动能分布,发现其分布规律基本一致。以X=0截面上的4条测线(Z=-60、65、200、250 mm)为代表,对比不同测线上的湍流动能分布情况,如图 6所示。可以看出在两种工况下,4条测线上Type-A模型中测点的湍流动能均小于Type-B模型中对应测点的湍流动能,说明Type-A模型中高频脉动的小尺寸湍涡数量较少。粉料团聚体的解吸和粉体的分散作用是高频脉动的小尺寸湍涡与物料相互作用导致的结果[14]。较少的淘洗区筒体内小尺寸湍涡数量尽管有利于气流平稳上升至环形区,但是会导致颗粒不能充分预分散,使得细颗粒团聚为假大颗粒,“鱼钩效应”明显。
|
图 5 湍流动能分布云图(X=0) Fig.5 The turbulence kinetic energy contours of Type-A and Type-B (X=0) |
|
图 6 淘洗区筒体测线湍流动能曲线(X=0,Z=-60、65、200、250 mm) Fig.6 The turbulence kinetic energy curves of Type-A and Type-B(X=0, Z=-60, 65, 200, 250 mm) |
选取转笼区域不同高度的Z平面,对模拟结果进行对比分析,发现Z平面高度对转笼和环形区径向速度分布的影响不大,因此以转笼中间平面(Z=345 mm)为例进行对比分析。
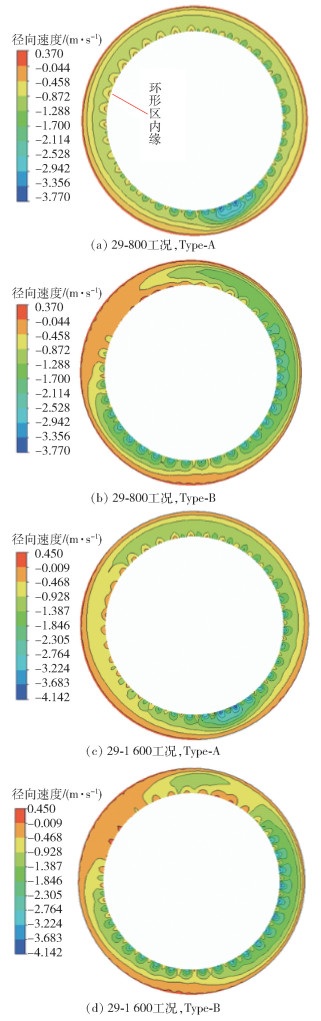
图 7为Type-A和Type-B在环形区的径向速度分布云图,图中径向速度为负代表速度方向指向圆心。可以看出在两种工况下,两种模型在环形区内缘的径向速度梯度变化较明显,这是因为转笼叶片的转动对附近气流产生扰动,使得气流流动不平稳,导致紧邻叶片的环形区内缘处径向速度产生明显的梯度变化。在29-800工况下,Type-A模型相对于Type-B模型径向速度分布较为均匀。Type-A模型在环形区的大部分区域径向速度在-0.87~-1.29 m/s范围内,但右下角位置处的径向速度有突变,这是由单口进风所致,该情况多发生于旋风分离器中[15-17]。Type-B模型的径向速度整体上呈现左侧数值较小、右侧数值较大的分布规律,在环形区的大部分区域径向速度在-0.87~-2.11 m/s范围内,其梯度变化大于Type-A模型且数值较大。在29-1 600工况下,Type-A模型环形区的径向速度分布均匀,大部分区域的径向速度在-0.47~ -1.39 m/s范围内;Type-B模型大部分区域的径向速度在-0.93~-1.85 m/s范围内,梯度变化大于Type-A模型且数值较大。
|
图 7 环形区径向速度云图(Z=345 mm) Fig.7 The radial velocity contours of Type-A and Type-B in the annular region (Z=345 mm) |
为了进一步验证两种模型在环形区径向速度分布的均匀性,在Z=345 mm平面上分别取R=80、85、90、95 mm这4条环线,在环线上各取100个测点,获得相对应的径向速度并计算标准差σ,其计算公式为
| $ \mathit{\sigma } = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{v_i} - \bar v} \right)}^2}} }}{{n - 1}}} $ | (1) |
式中,vi为测点的径向速度数值;n为测点个数。
通过标准差来定量分析环形区速度分布的均匀性。由于转笼转速对环形区径向速度分布的影响较小,且29-1 600工况的速度分布曲线与29-800工况呈现的规律相似,故以29-800工况的速度分布曲线为例。
图 8为29-800工况下4条环线上的径向速度分布曲线。图 8(a)为R=80 mm环线的径向速度分布,可以看出相邻的两个测点之间速度波动较大,这是因为R=80 mm环线为环形区内缘,此处受到叶片转动的影响径向速度变化较大,因此相邻的测点间的差值较大,曲线呈锯齿状,计算得到该环线上Type-A和Type-B模型的径向速度标准差σ分别为0.575和0.756,表明后者的波动更剧烈。R=85 mm和90 mm为环形区中部的环线,此时转笼叶片的转动对径向速度影响减小,相邻测点间的径向速度波动减小,从图 8(b)、(c)可以看出曲线的锯齿状程度减小,且趋于平缓。R=85 mm时Type-A和Type-B模型的径向速度标准差分别为0.376、0.517,R=90 mm时分别为0.232、0.485,说明Type-B模型的径向速度波动更剧烈。R=95 mm环线位置接近环形区壁面,叶片转动对径向速度的影响最小,相邻测点间的径向速度差值更小,曲线整体平缓过渡,且由于壁面的阻碍作用径向速度数值减小。Type-A和Type-B模型的径向速度标准差分别为0.129和0.372,表明Type-B模型的径向速度波动更剧烈。由此可以看出Type-A模型的标准差均小于Type-B模型,即在环形区Type-A模型的径向速度比Type-B的分布更均匀。此外,可以看到在Type-A模型的4条环线中,80号测点附近均出现径向速度的突变,这是因为80号测点位于环形区的右下角范围,该突变是由分级机单口进风结构所致,说明单口进风结构对Type-A模型的影响更为明显,这与图 7中Type-A模型环形区的径向速度云图分布特点一致。

|
图 8 环形区环线径向速度曲线(Z=345 mm) Fig.8 The radial velocity curves of Type-A and Type-B in the annular region (Z=345 mm) |
由上述分析可得,Type-A模型在环形区中径向速度分布均匀但数值较小,Type-B模型径向速度分布不均但数值较大,说明扰流锥的存在可以使气流平稳地沿轴线方向旋转上升,但也增加了能量的损耗,使得上升到环形区的气流速度降低。
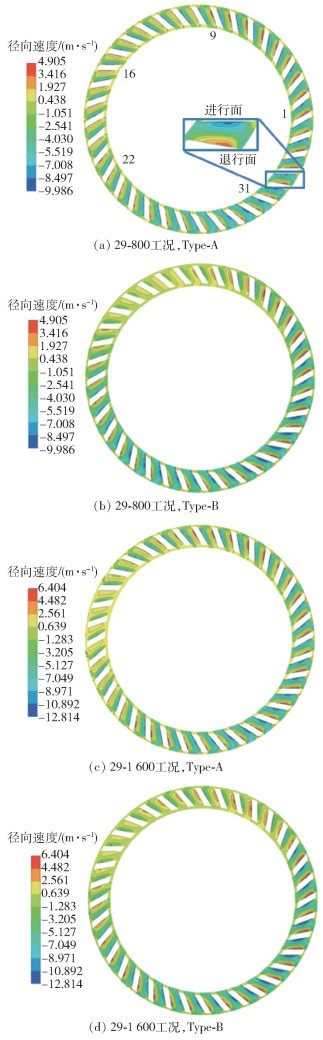
3.2 扰流锥对转笼叶片间通道径向速度的影响图 9为29-800和29-1 600工况下,Type-A和Type-B模型在转笼叶片间通道径向速度分布云图。为了方便描述叶片间通道位置,依次给各个叶片间通道做序号,标记为1~36,如图 9(a)所示。两种工况下,Type-A和Type-B模型径向速度分布云图均显示出叶片进行面径向速度为负值,叶片退行面径向速度为正值的现象,说明叶片间通道产生了反旋涡,反旋涡的形成会使得进入转笼叶片间通道的细粉颗粒在反旋涡的作用下返回到粗粉中,不利于颗粒分级[18]。从图 9(a)、(c)中可以看出Type-A模型各转笼叶片间通道径向速度分布基本相同;从图 9(b)、(d)中可以看出Type-B模型在9~16叶片间通道的径向速度梯度变化较小,而31~36叶片间通道的径向速度梯度变化较大,在各转笼叶片间通道径向速度分布不均匀。
|
图 9 转笼叶片间通道径向速度云图(Z=345 mm) Fig.9 The radial velocity contours of Type-A and Type-B in the channel of the rotor cage (Z=345 mm) |
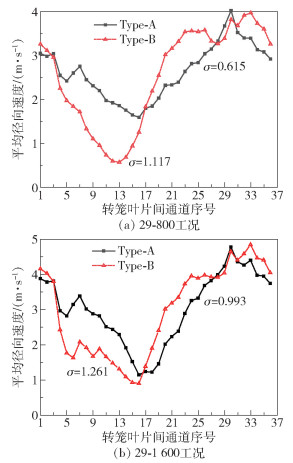
为了进一步验证两种模型在转笼叶片间通道径向速度分布的均匀性,在每个叶片间通道处设置50个均匀分布的测点,根据测点径向速度的标量值计算每个叶片间通道测点的平均径向速度,通过叶片间通道测点的平均径向速度分布曲线来分析圆周上各个叶片间通道径向速度分布情况,如图 10所示。可以看出,Type-A模型较Type-B模型速度曲线的波动幅度更小。计算曲线标准差,在29-800工况下,Type-A和Type-B模型的曲线标准差分别为0.615和1.117;在29-1 600工况下,Type-A和Type-B模型的曲线标准差分别为0.993和1.261。不同工况下Type-A模型平均径向速度的标准差均比Type-B模型的小,说明Type-A模型在圆周上各个叶片间通道的径向速度分布比Type-B模型的更均匀。叶片间通道速度场的均匀分布有利于细粉产品在不同位置进入时均能顺利进入转笼,同时减小了粗细颗粒相互混杂的概率,从而提高分级效果。
|
图 10 转笼叶片间通道平均径向速度分布曲线 Fig.10 The average radial velocity curves of Type-A and Type-B in the channel of the rotor cage |
为了对比Type-A模型和Type-B模型中颗粒的运动情况,进一步揭示扰流锥对颗粒分级的作用,在连续相模拟的基础上加入离散相,模拟颗粒分级的效果。
ANSYS-Fluent软件为求解多相流问题提供了多种方法,其中在空气分级机领域最常用的是离散相模型(discrete phase model,DPM)。许多研究人员将离散相模型与实验结果进行比较,结果证明该模型能够准确地预测空气分级机内颗粒的分级效率[19-20]。
多相流离散相模型的选择主要取决于模型中的颗粒质量加载率vp和体积加载率kp,vp和kp计算公式如下[21-22]。
| $ {v_{\rm{p}}} = \frac{{{\mathit{\alpha }_{\rm{p}}}{\mathit{\rho }_{\rm{p}}}}}{{{\mathit{\alpha }_{\rm{f}}}{\mathit{\rho }_{\rm{f}}}}} $ | (2) |
| $ {k_{\rm{p}}} = \frac{{{\mathit{\alpha }_{\rm{p}}}}}{{{\mathit{\alpha }_{\rm{f}}}}} = {v_{\rm{p}}}\frac{{{\mathit{\rho }_{\rm{f}}}}}{{{\mathit{\rho }_{\rm{p}}}}} $ | (3) |
式中,αp为单位时间内通过有效截面的颗粒体积;αf为单位时间内通过有效截面的气体体积;ρp为颗粒密度;ρf为气体密度。
立式涡流空气分级机介质为空气,密度为1.293 kg/m3,物料为碳酸钙,密度为2 700 kg/m3。本文采用进口风速为29 m/s,当喂料速度为12 kg/h时,计算得到质量加载率vp为0.052,体积加载率kp为0.002 5%。因体积加载率小于10%,可认为分级机内颗粒稀疏,颗粒对流场的影响很小,满足单相耦合的稳态DPM要求。
以29-800工况为例,颗粒设置为碳酸钙,颗粒入射面为喂料口所在平面,该平面直径为30 mm。设置细粉出口所在面的类型为“escape”,粗粉收集漏斗为“trap”,其余壁面设置为“reflect”,法向反弹系数kn和切向反弹系数kt设置为[13]
| $ {k_{\rm{n}}} = \left\{ {\begin{array}{*{20}{l}} {3.474 \times {{10}^{ - 4}}{{(\mathit{\beta } - 50)}^2} + 0.4,}&{\mathit{\beta } \le {50° }}\\ {0.4,}&{\mathit{\beta } > {50° }} \end{array}} \right. $ | (4) |
| $ {k_{\rm{t}}} = \left\{ {\begin{array}{*{20}{l}} {0.9 - 0.005\mathit{\beta },}&{\mathit{\beta } \le {50° }}\\ {0.4 + 0.005\mathit{\beta },}&{\mathit{\beta } > {50° }} \end{array}} \right. $ | (5) |
式中,β为撞击角度。
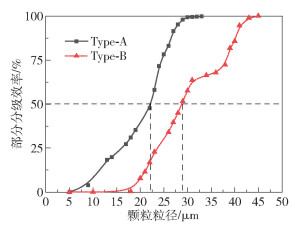
为了反映颗粒在复杂的湍流流场中的运动情况,使用随机游走模型(discrete random walk model,DRW)[23]增强湍流对颗粒流运动的随机性影响。为了保证获得完整的追踪颗粒的运动情况,设置最大计算步数为50 000,积分尺寸为0.005。连续相上加载粒径为5~50 μm的颗粒,模拟该工况下不同粒径碳酸钙的分级效率曲线。追踪各个粒径下颗粒的分级情况,每次设置800个同一粒径颗粒通过喂料口进入分级机,通过模拟计算得到不同粒径的逃逸、捕获情况,最后以逃逸颗粒占颗粒总数的分数为纵坐标(模拟所得部分分级效率),颗粒粒径为横坐标绘制部分分级效率曲线,结果如图 11所示。可以得到Type-A模型和Type-B模型的分级粒径d50分别为22.18 μm和28.78 μm。模拟所得Type-A模型和Type-B模型的分级精度K(d25/d75)分别为65.53%和60.19%。由离散相模拟结果可以得出,淘洗区筒体内置扰流锥可使分级粒径减小22.93%,分级精度提高8.87%。
|
图 11 离散相模拟部分分级效率曲线 Fig.11 The partial classification efficiency curves simulated by the discrete phase model |
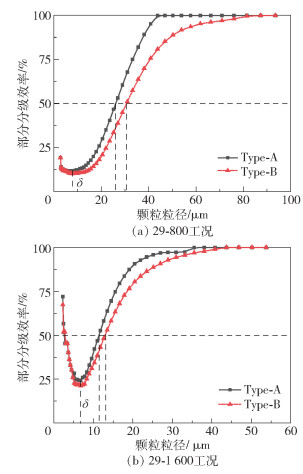
为验证所得数值模拟结果,以碳酸钙为原料,在29-800和29-1 600两种工况下对有、无扰流锥两种结构的分级机进行物料分级实验,碳酸钙原料粒度微分分布如表 2所示。通过激光粒度分析仪(LT3600型,珠海真理光学仪器有限公司)对原料及分级产物进行粒度测定,并计算粗粉部分的分级效率,得到的部分分级效率曲线如图 12所示。由部分分级效率曲线分别计算分级粒径d50和分级精度K,结果如表 3所示。
| 下载CSV 表 2 碳酸钙原料粒度微分分布 Table 2 Differential distribution of calcium carbonate particle size |
|
图 12 分级实验部分分级效率曲线 Fig.12 The experimental partial classification efficiency curves |
| 下载CSV 表 3 分级实验性能指标 Table 3 The experimental classification performance indexes |
在29-800、29-1 600两种工况下,Type-A模型的分级粒径较小且分级精度较高。29-800工况下,Type-A模型比Type-B模型的分级粒径减小了13.2%,分级精度提高了4.2%;29-1 600工况下,Type-A模型的分级粒径减小了12.18%,分级精度提高了4.9%。Type-A模型流场分布均匀,上升至环形区的细颗粒可以均匀地通过转笼叶片间通道,而Type-B模型流场速度较大,分级粒径也较大,径向速度分布的不均导致大颗粒在某些位置进入转笼,分级精度降低。
分级机内由细颗粒团聚产生的假大颗粒很容易被收集为粗粉,旁路值是部分分级效率曲线上的最小值,表示混入被收集为粗粉的细粉的质量分数,它是衡量分级效率的重要指标之一,旁路值越小,分级效率越高。如图 12所示,在29-800工况下Type-A模型的部分分级效率曲线中旁路值δ为11.49%,Type-B模型为10.07%;29-1 600工况下,Type-A模型旁路值为24.11%,Type-B模型旁路值为21.13%。在不同工况下,Type-A模型的旁路值均比Type-B模型的大,表明Type-A模型收集到的粗粉中合格的细粉量较多。假大颗粒在螺旋喂料机作用下进入筒体时,由于Type-A模型在淘洗区筒体内的气流相对均匀,湍流动能较小,因此对于假大颗粒的分散效果略差,导致旁路值较大,进入粗粉中的细粉量略多。
5 结论(1) 在淘洗区筒体内,扰流锥的存在会阻碍旋涡的形成,气流绝对速度整体较小;筒体内小尺寸高频脉动的湍涡数量变少,使得气流能够平稳上升至环形区,但会导致进入淘洗区筒体的原料不能充分预分散,“鱼钩效应”明显。
(2) 扰流锥可以有效提升环形区和转笼叶片间通道径向速度分布的均匀性,使得细粉产品在转笼不同位置进入时均能顺利进入转笼,减小粗细颗粒相互混杂的概率,提高分级精度;扰流锥的存在使得气流上升过程中能耗增大,气流径向速度减小。
(3) 颗粒的离散相模型模拟结果进一步表明扰流锥的存在可以减小分级粒径,提高分级精度。碳酸钙的分级实验结果与离散相模拟结果一致。此外,扰流锥会导致粉体不能在筒体内充分分散,粗粉产品中含有较多的细粉,旁路值较大。
| [1] |
KARINKANTA P, ILLIKAINEN M, NIINIMÄKI J. Pulverisation of dried and screened Norway spruce (Picea abies) sawdust in an air classifier mill[J]. Biomass and Bioenergy, 2012, 44: 96-106. DOI:10.1016/j.biombioe.2012.04.022 |
| [2] |
党栋, 王克俭. 加料速度对分级机内部流场的影响[J]. 化工学报, 2015, 66(S1): 159-164. DANG D, WANG K J. Effect of feeding rate on flow field inside classifier[J]. CIESC Journal, 2015, 66(S1): 159-164. (in Chinese) |
| [3] |
REN W J, LIU J X, YU Y. Design of a rotor cage with non-radial arc blades for turbo air classifiers[J]. Powder Technology, 2016, 292: 46-53. DOI:10.1016/j.powtec.2016.01.024 |
| [4] |
PRONOBIS M, MROCZEK K, TYMOSZUK M, et al. Optimisation of coal fineness in pulverised-fuel boilers[J]. Energy, 2017, 139: 655-666. DOI:10.1016/j.energy.2017.07.057 |
| [5] |
WU S B, LIU J X, YU Y. Design of a new double layer spreading plate for a turbo air classifier[J]. Powder Technology, 2017, 312: 277-286. DOI:10.1016/j.powtec.2017.02.044 |
| [6] |
张胜林, 谌永祥, 李双跃. 分级机三次风进风装置的流场研究[J]. 中国粉体技术, 2014, 20(3): 21-24. ZHANG S L, CHEN Y X, LI S Y. Research on flow field of the third wind inlet device of classifier[J]. China Powder Science and Technology, 2014, 20(3): 21-24. (in Chinese) |
| [7] |
刁雄, 李双跃, 李良超, 等. SCX分级机进料管流场数值分析与结构优化[J]. 化学工程, 2012, 40(4): 31-35. DIAO X, LI S Y, LI L C, et al. Flow field numerical analysis and structure optimization for feeding pipe of SCX superfine classifier[J]. Chemical Engineering, 2012, 40(4): 31-35. (in Chinese) DOI:10.3969/j.issn.1005-9954.2012.04.008 |
| [8] |
周岩, 孙国刚, 蒋绍洋, 等. 分级装置: CN 206240790U[P]. 2017-06-13. ZHOU Y, SUN G G, JIANG S Y, et al. Classification equipment: CN 206240790U[P]. 2017-06-13. (in Chinese) |
| [9] |
SUN Z P, LIANG L L, LIU C Y, et al. CFD simulation and performance optimization of a new horizontal turbo air classifier[J]. Advanced Powder Technology, 2021, 32(4): 977-986. DOI:10.1016/j.apt.2021.01.041 |
| [10] |
ADAMČK M, SVĚRÁK T, PECIAR P. Parameters effecting forced vortex formation in blade passageway of dynamic air classifier[J]. Acta Polytechnica, 2017, 57(5): 304-315. DOI:10.14311/AP.2017.57.0304 |
| [11] |
HAGEMEIER T, GLÖCKNER H, ROLOFF C, et al. Simulation of multi-stage particle classification in a zigzag apparatus[J]. Chemical Engineering & Technology, 2014, 37(5): 879-887. |
| [12] |
SUN Z P, SUN G G, LIU J X, et al. CFD simulation and optimization of the flow field in horizontal turbo air classifiers[J]. Advanced Powder Technology, 2017, 28(6): 1474-1485. DOI:10.1016/j.apt.2017.03.016 |
| [13] |
冯乐乐, 吴玉新, 王景玉, 等. 转轮式分级器切割粒径的预测模型[J]. 化工进展, 2018, 37(12): 4579-4585. FENG L L, WU Y X, WANG J Y, et al. Prediction model for cut size in turbo air classifiers[J]. Chemical Industry and Engineering Progress, 2018, 37(12): 4579-4585. (in Chinese) |
| [14] |
刘家祥, 何廷树, 夏靖波. 涡流空气分级机内湍流涡频谱对其性能的影响[J]. 北京化工大学学报, 2003, 30(5): 48-51. LIU J X, HE T S, XIA J B. The effect of frequency spectrum of the eddies of turbulent flow in a turbo classifier on its classification characteristics[J]. Journal of Beijing University of Chemical Technology, 2003, 30(5): 48-51. (in Chinese) DOI:10.3969/j.issn.1671-4628.2003.05.013 |
| [15] |
宋健斐, 魏耀东, 时铭显. 蜗壳式旋风分离器内气相流场非轴对称特性分析[J]. 化工学报, 2007, 58(5): 1091-1096. SONG J F, WEI Y D, SHI M X. Analysis of asymmetry of gas-phase flow field in volute cyclone[J]. Journal of Chemical Industry and Engineering(China), 2007, 58(5): 1091-1096. (in Chinese) DOI:10.3321/j.issn:0438-1157.2007.05.005 |
| [16] |
董振洲. 出入口结构及入口气速对旋风分离器内旋流非稳态特性的影响[D]. 太原: 太原理工大学, 2019. DONG Z Z. Effects of inlet and outlet structure and inlet gas velocity on unsteady characteristics of swirl flow in cyclone separator[D]. Taiyuan: Taiyuan University of Technology, 2019. (in Chinese) |
| [17] |
SAFIKHANI H, ZAMANI J, MUSA M. Numerical study of flow field in new design cyclone separators with one, two and three tangential inlets[J]. Advanced Powder Technology, 2018, 29(3): 611-622. DOI:10.1016/j.apt.2017.12.002 |
| [18] |
刘家祥, 徐德龙, 赵江平, 等. 涡流分级机内惯性反旋涡对颗粒分选的影响[J]. 西安建筑科技大学学报, 1998, 30(1): 63-66. LIU J X, XU D L, ZHAO J P, et al. The effects of inertia counter-rotating vortices in vortex classifier on particle classification[J]. Journal of Xi'an University of Architecture & Technology, 1998, 30(1): 63-66. (in Chinese) |
| [19] |
FENG L L, ZHANG H, HU L L, et al. Classification performance of model coal mill classifiers with swirling and non-swirling inlets[J]. Chinese Journal of Chemical Engineering, 2020, 28(3): 777-784. DOI:10.1016/j.cjche.2019.12.002 |
| [20] |
GUIZANI R, MHIRI H, BOURNOT P. Effects of the geometry of fine powder outlet on pressure drop and separation performances for dynamic separators[J]. Powder Technology, 2017, 314: 599-607. |
| [21] |
于勇. FLUENT入门与进阶教程[M]. 北京: 北京理工大学出版社, 2008: 146, 157-159. YU Y. Basic FLUENT introduction and advanced tutorial[M]. Beijing: Beijing Institute of Technology Press, 2008: 146, 157-159. (in Chinese) |
| [22] |
王金东, 吕志利, 刘树林, 等. 基于FLUENT的气动喷砂两相流场分析[J]. 科学技术与工程, 2009, 9(17): 5113-5115, 5119. WANG J D, LV Z L, LIU S L, et al. FLUENT based on the pneumatic blasting two-phase flow field analysis[J]. Science Technology and Engineering, 2009, 9(17): 5113-5115, 5119. (in Chinese) DOI:10.3969/j.issn.1671-1815.2009.17.050 |
| [23] |
SAFIKHANI H, AKHAVAN-BEHABADI M A, SHAMS M, et al. Numerical simulation of flow field in three types of standard cyclone separators[J]. Advanced Powder Technology, 2010, 21(4): 435-442. |








