2. 中国核动力研究设计院 核反应堆系统设计技术重点实验室, 成都 610213
2. Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu 610213, China
当饱和蒸汽与过冷水直接接触时,蒸汽会发生冷凝相变,这一过程即为蒸汽的直接接触冷凝。直接接触冷凝过程是一种较强烈的热质传递过程,在化工、能源和核电等领域中广泛存在[1-4]。在压水反应堆发生主管道破裂的失水事故(LOCA)时,应急堆芯冷却系统(ECCS)将过冷的安注水注入到冷管段中,安注水与蒸汽发生直接接触冷凝,导致管内出现以温度和压力振荡为特征的汽液两相振荡现象,并易在T型管主支管交汇区域(主管道上的安注接管咀处)产生循环热疲劳[5]。
Reyes等[6]分析了advanced plant experimental test facility-CE (APEX-CE)实验中冷管段处的回流现象, 采用弗劳德数来判断两相流体是否混合充分。任五岳等[7]开展了不同蒸汽量和不同安注水流量下T型管的冷凝实验,用主、支管动量比来判断主管内的温度分布情况,并建立适用于两相流热混合的无量纲动量比关系式来划分主管内的回流和水跃所造成的温度分布特性。
随着计算水平的进步,数值计算成为解决流动和传热问题的有效方法。Gulawani等[8]提出双阻力冷凝模型,并对超音速蒸汽直接接触冷凝进行了数值模拟。Shah等[9]采用欧拉-欧拉两相流模型并结合双阻力模型,研究了蒸汽射流泵内的直接接触冷凝现象。Li等[10]采用流体体积分数(VOF)模型和双阻力模型研究了静止大池内亚音速蒸汽射流的直接接触冷凝过程,数值计算得到的蒸汽羽流演化特征与Chan等[11]得到的实验结果可以较好地吻合。
本文使用FLUENT软件并编写用户自定义函数(UDF),对T型管内的安注过程进行数值模拟分析,得到安注过程蒸汽直接接触冷凝各物理量的时空演变规律,分析了蒸汽质量流量变化对主管道内压力与温度的影响。
1 数学模型 1.1 控制方程本文采用VOF模型追踪T型管中汽液接触界面的变化情况,利用大涡湍流(LES)模型捕捉瞬态流场及温度场的变化。VOF模型和LES模型在蒸汽直接接触冷凝数值计算领域内应用广泛, 控制方程可参阅相关文献[10, 12]。
1.2 冷凝模型蒸汽直接接触冷凝过程选用双阻力冷凝模型来构建两相间的热传递机制。在双阻力冷凝模型中做以下假设:蒸汽为过热或者饱和状态;安注水为过冷态;蒸汽与安注水相交界面处的温度为饱和温度;冷凝在饱和状态下进行[8, 13]。
单位体积内气泡的传热面积Awg为
| $ A_{\mathrm{wg}}=\frac{6 \alpha_{\mathrm{g}}}{d_{\mathrm{g}}} $ | (1) |
式中,dg为气泡的平均直径,αg为蒸汽体积分数。dg的计算式为[14]
| $ d_{\mathrm{g}}= \begin{cases}0.0015, & \theta<0 \mathrm{~K} \\ 0.0015-0.0001 \theta, & 0 \mathrm{~K} \leqslant \theta \leqslant 13.5 \mathrm{~K} \\ 0.00015, & \theta>13.5 \mathrm{~K}\end{cases} $ | (2) |
式中,θ为安注水的过冷度,θ=Ts-Tw,其中Tw为安注水温度,Ts为压力对应的饱和温度。
热量从蒸汽侧通过汽液界面传递到安注水侧,因此界面传热系数分为蒸汽侧传热系数hg和安注水侧传热系数hw。
安注水侧的传热系数计算公式为
| $h_{\mathrm{w}}=\frac{k_{\mathrm{w}} N u_{\mathrm{w}}}{d_{\mathrm{g}}} $ | (3) |
式中,kw为水的导热系数,Nuw为水的努赛尔数。
水的努赛尔数计算式为
| $ N u_{\mathrm{w}}= \begin{cases}2.0+0.6 {Re}^{0.5} {Pr}^{0.33}, & 0 <{Re} <776.06 \\ 2.0+0.27 {Re}^{0.62} {Pr}^{0.33}, & 0 <{Pr} <250 \\ & 776.06 \leqslant {Re} \\ & 0 <{Pr} <250\end{cases} $ | (4) |
| $ \begin{aligned} {Pr}=c_{p} \mu_{\mathrm{w}} / k_{\mathrm{w}} \end{aligned} $ | (5) |
| $ {Re}=\rho_{\mathrm{w}}\left|u_{\mathrm{g}}-u_{\mathrm{w}}\right| d_{\mathrm{g}} / \mu_{\mathrm{w}} $ | (6) |
式中,Re为相对雷诺数,Pr为普朗特数,ug为蒸汽流速,cp为水的定压比热,ρw为水的密度,uw为水的流速,μw为水的动力黏度。
在计算过程中认为蒸汽处于饱和状态,忽略蒸汽可能出现的过热度。
界面与安注水侧之间的对流传热热流密度为
| $ q_{\mathrm{w}}=h_{\mathrm{w}}\left(T_{\mathrm{s}}-T_{\mathrm{w}}\right) $ | (7) |
界面传递到安注水侧的总热量为
| $Q_{\mathrm{w}}=q_{\mathrm{w}}+m_{\mathrm{gw}} H_{\mathrm{ws}} $ | (8) |
式中,mgw为界面处的相变速率,Hws为饱和水焓值。
蒸汽侧传递到界面的总热量为
| $Q_{\mathrm{g}}=m_{\mathrm{gw}} H_{\mathrm{gs}} $ | (9) |
式中,Hgs为饱和蒸汽焓值。
根据界面处的总热量平衡关系得到
| $ Q_{\mathrm{w}}=Q_{\mathrm{g}} $ | (10) |
界面上的相变速率为
| $ m_{\mathrm{gw}}=\frac{q_{\mathrm{w}}}{H_{\mathrm{gs}}-H_{\mathrm{ws}}} $ | (11) |
式中,Hgs-Hws为蒸汽的冷凝潜热。
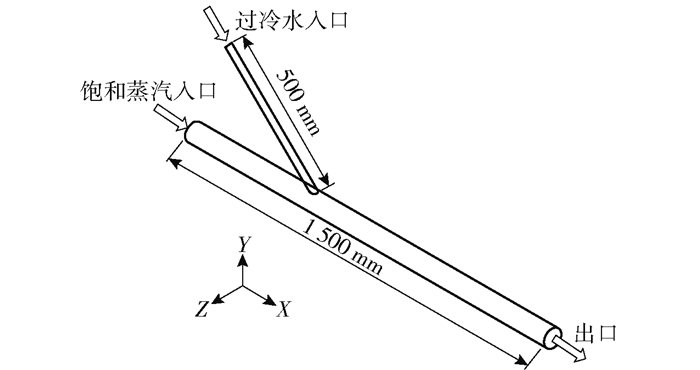
2 物理模型及参数设置本文以典型三环路压水堆核电厂为研究对象,在发生LOCA事故后,自动触发能动的安注系统并向冷管段注入过冷安注水。所研究的物理模型尺寸采用西安交通大学应急堆芯冷却系统实验尺寸[15]。如图 1所示,安注管长500 mm,内径为22 mm,与主管的角度为45°;主管长1 500 mm,内径为70 mm,主管中心与主管左侧入口之间的距离为500 mm。支管入口为安注水入口,主管左侧入口为饱和蒸汽入口。重力的方向设置为-Y。
|
图 1 物理模型 Fig.1 Physical model |
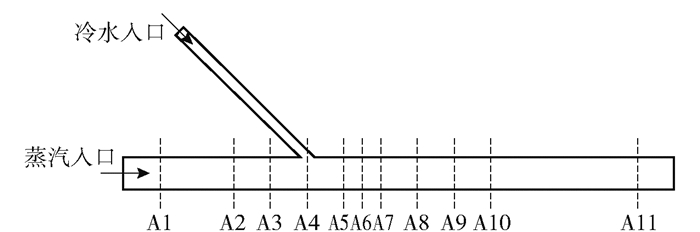
如图 2所示,计算过程中在主管左侧入口至出口之间布置了11个监测面,A1~A11各截面的位置分别为-400、-200、-100、0、100、150、200、300、400、500、900 mm。每个截面各布置上下2个监测点,与上下壁面之间的距离分别为5 mm。
|
图 2 监测点位置 Fig.2 Location of detection points |
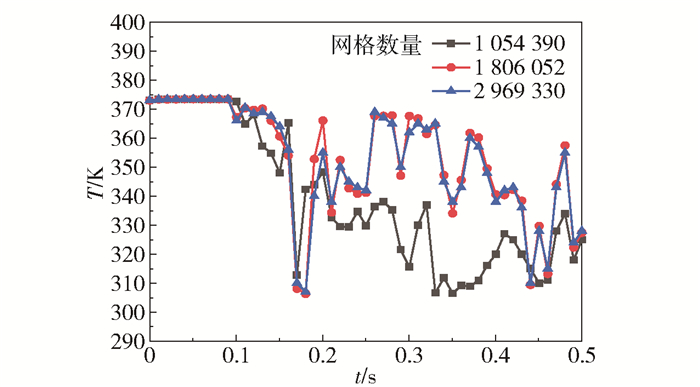
网格模型如图 3所示,为结构化六面体网格,对T型管近壁面区域进行了网格加密处理。用不同数量网格进行无关性验证,对比了同一监测点处温度的波动趋势,结果如图 4所示。为了减小计算成本并且保证结果准确,本文对T型管划分的网格数量为1 806 052,边界层网格层数设置为10,增长率设置为1.1,第一层网格高度取0.05 mm,y+值为5。

|
图 3 网格模型 Fig.3 Mesh model |
|
图 4 网格无关性验证 Fig.4 The mesh independence test |
在典型三环路压水堆发生LOCA后,注入冷管段的安注流量只与注入点背压大小相关,而主管道中的蒸汽流量受破口位置和破口尺寸大小的影响,参数变化范围较大,因此本文基于LOCA后的瞬态特性,选取典型的过冷安注水流量,分析不同蒸汽质量流量对管内安注过程的影响。安注水质量流量Mw为50 kg/h,安注水温度Tw为298.15 K,蒸汽温度Tg为373.15 K,支管角度为45°,压力为0.1 MPa,蒸汽流量Mg分别设置为30、40、50 kg/h和60 kg/h,对应工况1~4。饱和蒸汽和安注水入口采用质量流量入口,出口为压力出口,管壁为无滑移壁面绝热边界[16-17]。在计算初始时刻选用Patch的方法使支管和主管内分别充满安注水和饱和蒸汽。最大和最小时间步长分别为5×10-5 s和1×10-6 s。为保证数值模拟结果的准确性,将库朗数控制在2以内。
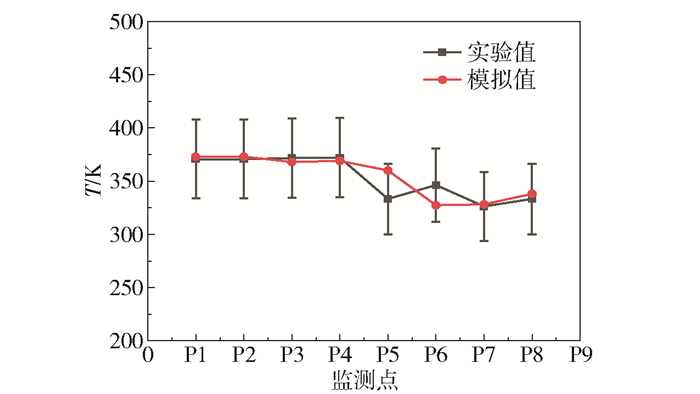
3 模拟结果分析 3.1 实验验证图 5为工况3数值模拟结果与西安交通大学ECCS实验结果[16]的比较。将实验得到的主管内截面P1~P8上底部监测点处的温度值与数值模拟得到的温度值进行对比,误差线数值为15%,表明数值模拟结果与实验数据具有较高的吻合度。监测点5、6处的误差较大,但在误差允许范围内,因此本文采用的数值模拟方法可以有效预测安注过程的直接接触冷凝现象。
|
图 5 温度分布比较 Fig.5 Comparison of temperature distribution |
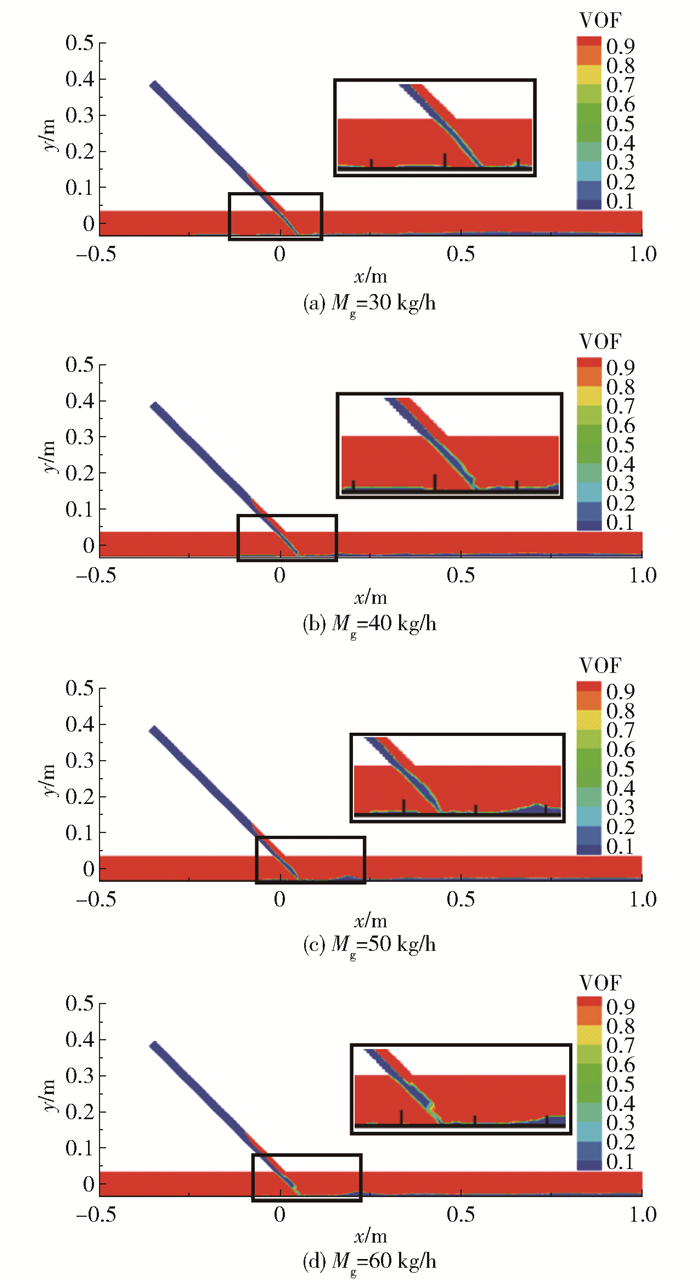
图 6为t=2.0 s时刻不同工况条件下的汽液两相体积分布云图。汽液两相之间存在明显的界面,界面下方为安注水,上方为蒸汽。由于蒸汽动量较小,不足以带动向上游回流的安注水向下游流动,因此低蒸汽流量条件下在主管上游区域可以看到明显的安注水回流现象。
|
图 6 体积分数云图 Fig.6 Volume fraction contours |
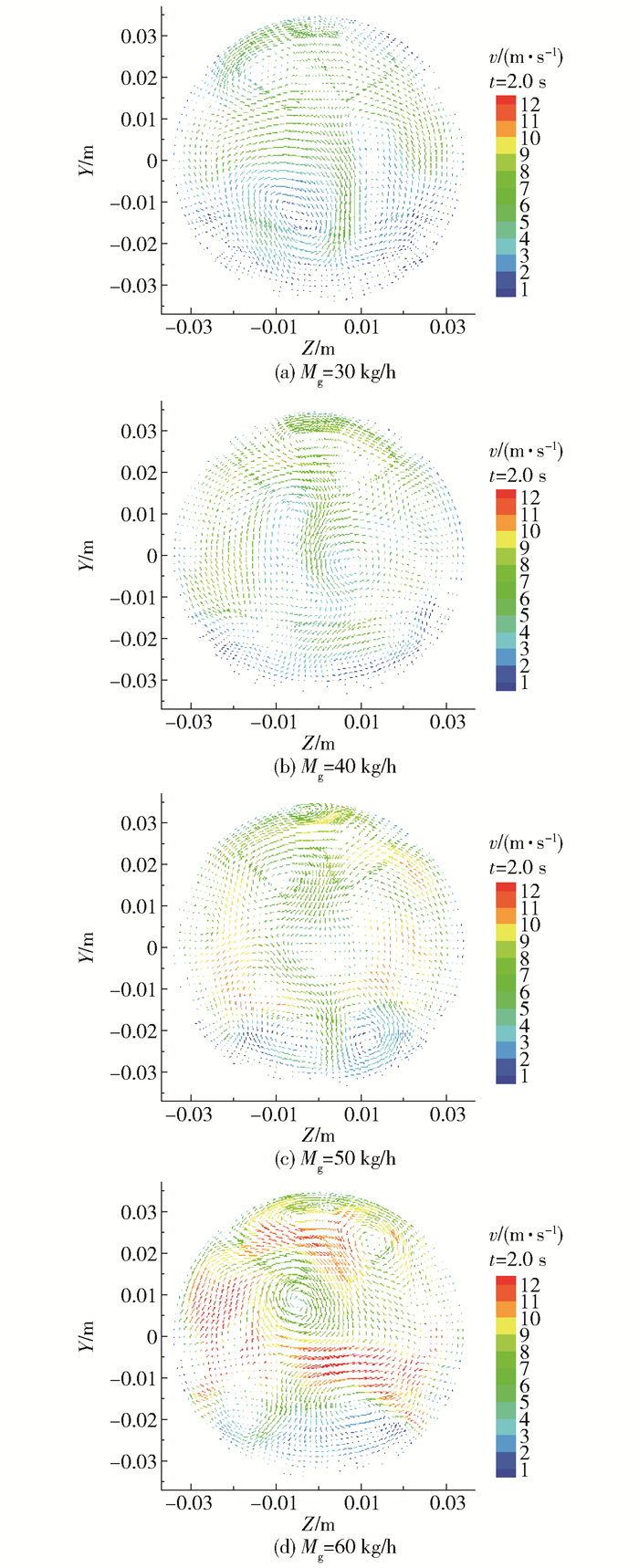
图 7为横截面X=0.1 m上的速度矢量图。由图可知,4种蒸汽流量下横截面中都出现了速度旋涡,速度扰动主要发生在汽液界面以上的区域。随着主管内的蒸汽流量增大,流体速度增大,横截面中速度旋涡的数量增加。
|
图 7 速度矢量图 Fig.7 Velocity vectors |
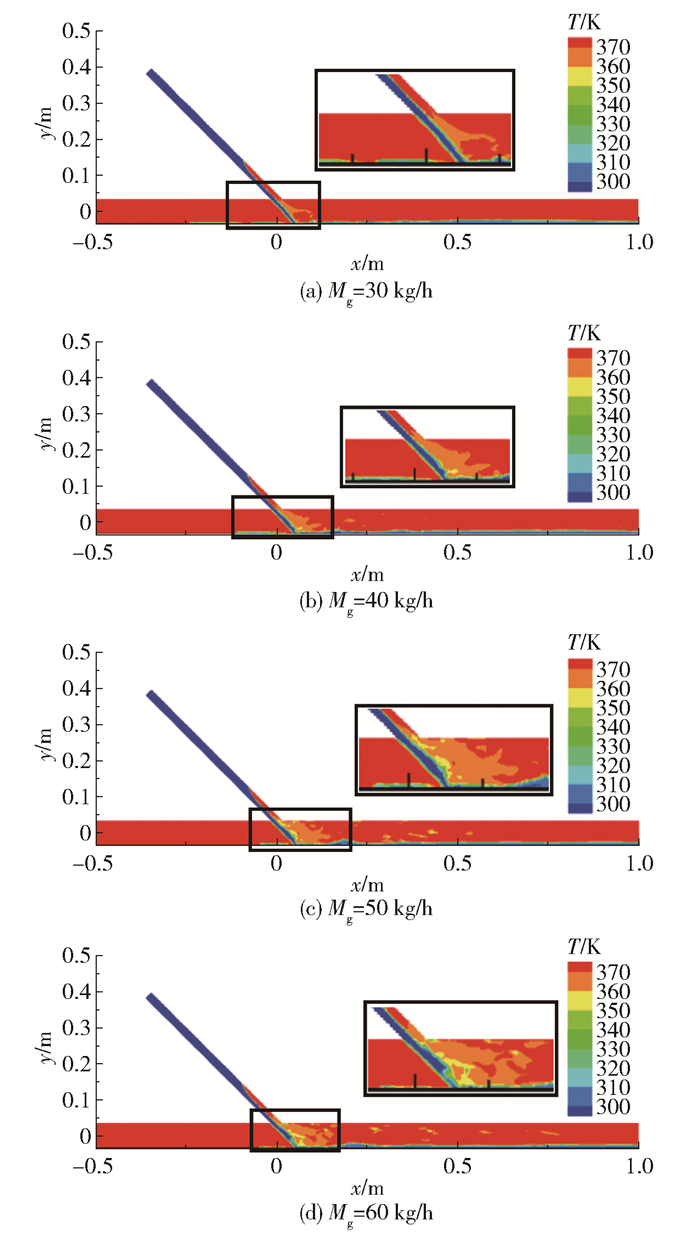
图 8为t=2.0 s时刻不同工况下的温度云图,可以看出温度分布与相分布具有一致性。安注水与饱和蒸汽在主管中心区域发生剧烈热混合,主管中心区域存在温度过渡区。在主管道蒸汽流量较小时,安注水冲入主管底部并向上下游流动,绝大部分热量和动量交换发生在主管中心区域。
|
图 8 温度云图 Fig.8 Temperature contours |
对监测点温度进行无量纲化处理,定义无量纲温度为
| $ T_{i}^{*}=\frac{T_{i}-T_{\mathrm{w}}}{T_{\mathrm{s}}-T_{\mathrm{w}}} $ | (12) |
无量纲时均温度为
| $ T_{\text {mean }}^{*}=\frac{1}{N} \sum\limits_{i=1}^{N} T_{i}^{*} $ | (13) |
式中,Ti为监测点处的温度,N为采样时间点总数。
无量纲时均温度分布如图 9所示。由于安注水在主管中经过热混合后主要分布在主管底部,因此底部测点的温度波动比顶部更加明显。从图 9(a)可以发现,A4截面顶部监测点处的温度变化较明显,且当蒸汽流量为50 kg/h和60 kg/h时,A5至A9截面范围内都出现了无量纲温度波动逐渐增加的现象,原因是蒸汽流量增加,热混合作用剧烈,导致温度过渡区域范围增大(图 6和图 8)。

|
图 9 无量纲时均温度分布 Fig.9 Distribution of dimensionless time-average temperature |
图 9(b)中,由于安注水回流现象(见图 6和图 8),在低蒸汽流量时,截面A2至截面A4的底部无量纲时均温度呈下降趋势。当蒸汽流量为60 kg/h时,主管段中两相流有更高的动量带动安注水向下游方向流动,回流区域范围减小,主管段内蒸汽流量的增加能够阻止安注水回流。
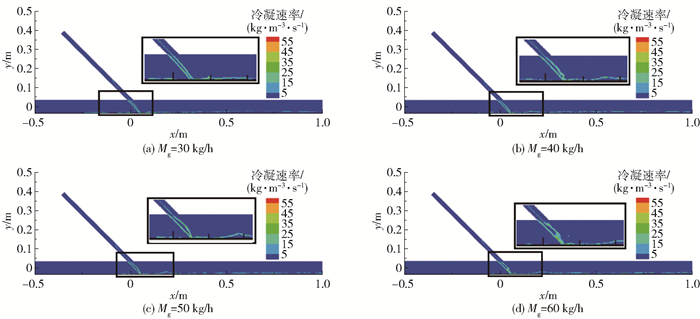
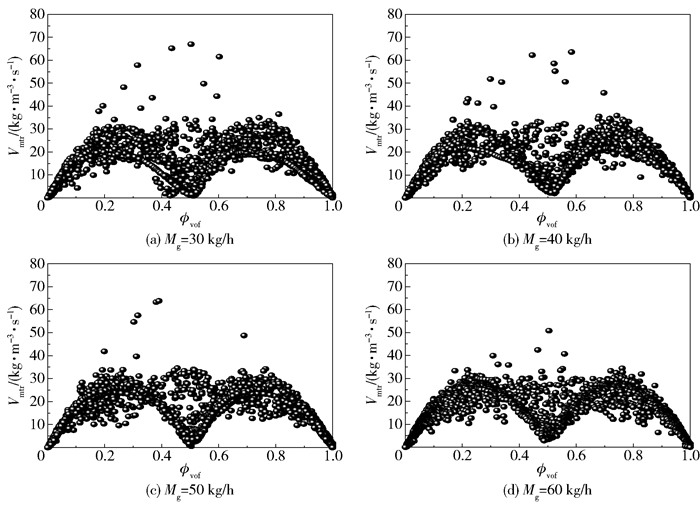
3.6 瞬时冷凝速率图 10为t=2.0 s时刻不同工况下的冷凝速率分布云图。结合图 6可以看出,冷凝发生在安注水与饱和蒸汽的相交界面处。图 11为冷凝速率随蒸汽体积分数的变化情况,图中纵坐标Vmtr为瞬态冷凝速率,横坐标Φvof为蒸汽体积分数。
|
图 10 冷凝速率云图 Fig.10 Condensation rate contours |
|
图 11 瞬态冷凝速率分布 Fig.11 Distribution of transient condensation rate |
横坐标为0或1时对应的冷凝速率接近0,表明当流体为纯安注水或纯蒸汽状态时冷凝现象不明显。蒸汽体积分数为0.3~0.7区域内的冷凝速率较大,由于管道内蒸汽和安注水会发生随机湍动并产生速度旋涡,且安注水侧存在不同厚度的热边界层,因此在不同位置处冷凝速率存在差异。
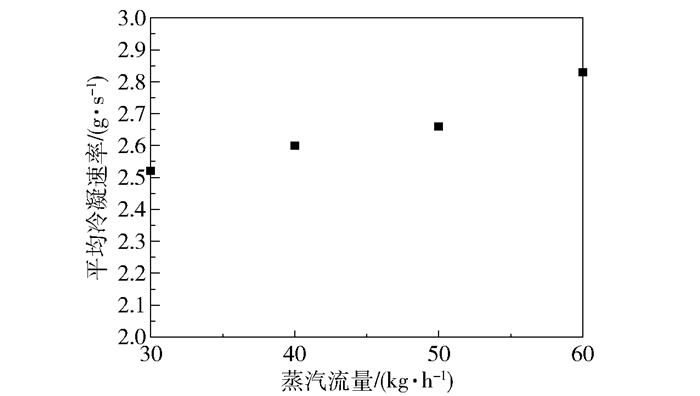
平均冷凝速率为T型管内某一时刻的冷凝速率。图 12给出了t=2.0 s时刻平均冷凝速率随蒸汽流量的变化,从图中可以看出,蒸汽流量越大,T型管内的平均冷凝速率越大。
|
图 12 平均冷凝速率 Fig.12 Average condensation rate |
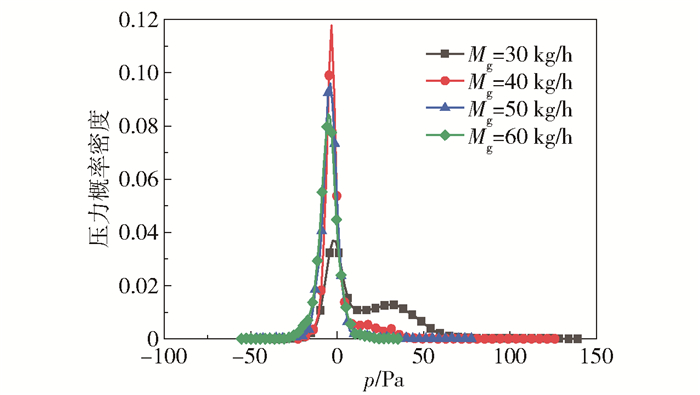
图 13为监测点(100 mm,-30 mm, 0)处的压力概率密度分布。在汽液界面附近由于存在直接接触冷凝现象,压力振荡明显。管道内压力谷值出现的原因为当安注水中的蒸汽泡破裂后,由于直接接触冷凝作用导致蒸汽泡附近区域的压力骤降至负压;压力峰值出现的原因为附近的安注水迅速冲向负压区域,液体加速后,液体相互撞击导致的局部水击现象会产生强烈的冲击力。蒸汽流量增大,由于流体动量增加导致的压力波动更剧烈,因此负压值更高。
|
图 13 压力概率分布 Fig.13 Probability distribution of pressure |
(1) 当蒸汽流量较小时,安注过程中在主管上游会发生安注水回流现象,主管内蒸汽流量的增加能够阻止安注水回流。
(2) 安注过程主管内压力振荡明显,蒸汽流量增加,负压值更高。
(3) 冷凝发生在安注水与饱和蒸汽的相交界面处,蒸汽体积分数为0.3~0.7区域内的冷凝速率较大。
| [1] |
HEINZE D, SCHULENBERG T, BEHNKE L. A physically based, one-dimensional three-fluid model for direct contact condensation of steam jets in flowing water[J]. International Journal of Heat and Mass Transfer, 2017, 106: 1041-1050. DOI:10.1016/j.ijheatmasstransfer.2016.10.076 |
| [2] |
KWIDZINSKI R. Experimental investigation of condensation wave structure in steam-water injector[J]. International Journal of Heat and Mass Transfer, 2015, 91: 594-601. DOI:10.1016/j.ijheatmasstransfer.2015.08.008 |
| [3] |
SHAH A, CHUGHTAI I R, INAYAT M H. Experimental and numerical investigation of the effect of mixing section length on direct-contact condensation in steam jet pump[J]. International Journal of Heat and Mass Transfer, 2014, 72: 430-439. DOI:10.1016/j.ijheatmasstransfer.2014.01.032 |
| [4] |
PATEL G, TANSKANEN V, KYRKI-RAJAMÄKI R. Numerical modelling of low-Reynolds number direct contact condensation in a suppression pool test facility[J]. Annals of Nuclear Energy, 2014, 71: 376-387. DOI:10.1016/j.anucene.2014.04.009 |
| [5] |
BROWNE M W, BANSAL P K. An overview of condensation heat transfer on horizontal tube bundles[J]. Applied Thermal Engineering, 1999, 19(6): 565-594. DOI:10.1016/S1359-4311(98)00055-6 |
| [6] |
REYES J N, GROOME J T, LAFI A Y, et al. PTS thermal hydraulic testing in the OSU APEX facility[J]. International Journal of Pressure Vessels and Piping, 2001, 78(2/3): 185-196. |
| [7] |
任五岳, 汪刘, 于国军, 等. T型管直接接触冷凝特性实验研究[J]. 原子能科学技术, 2017, 51(4): 641-646. REN W Y, WANG L, YU G J, et al. Direct contact condensation characteristics experiment research in T-junction[J]. Atomic Energy Science and Technology, 2017, 51(4): 641-646. (in Chinese) |
| [8] |
GULAWANI S S, DAHIKAR S K, MATHPATI C S, et al. Analysis of flow pattern and heat transfer in direct contact condensation[J]. Chemical Engineering Science, 2009, 64(8): 1719-1738. DOI:10.1016/j.ces.2008.12.020 |
| [9] |
SHAH A, CHUGHTAI I R, INAYAT M H. Numerical simulation of direct-contact condensation from a supersonic steam jet in subcooled water[J]. Chinese Journal of Chemical Engineering, 2010, 18(4): 577-587. DOI:10.1016/S1004-9541(10)60261-3 |
| [10] |
LI S Q, WANG P, LU T. Numerical simulation of direct contact condensation of subsonic steam injected in a water pool using VOF method and LES turbulence model[J]. Progress in Nuclear Energy, 2015, 78: 201-215. DOI:10.1016/j.pnucene.2014.10.002 |
| [11] |
CHAN C K, LEE C K B. A regime map for direct contact condensation[J]. International Journal of Multiphase Flow, 1982, 8(1): 11-20. DOI:10.1016/0301-9322(82)90003-9 |
| [12] |
郭志军, 卢涛, 朱维宇, 等. T型通道内冷热流体混合过程的热波动大涡模拟[J]. 热科学与技术, 2009, 8(2): 118-123. GUO Z J, LU T, ZHU W Y, et al. Large-eddy simulations of thermal fluctuation for mixing of hot and cold fluids in T-junction[J]. Journal of Thermal Science and Technology, 2009, 8(2): 118-123. (in Chinese) DOI:10.3969/j.issn.1671-8097.2009.02.005 |
| [13] |
李树谦. T型圆管内蒸汽直接接触凝结的实验研究与数值模拟[D]. 北京: 北京化工大学, 2016. LI S Q. Experimental study and numerical simulation of steam direct contact condensation in a circular tee junction[D]. Beijing: Beijing University of Chemical Technology, 2016. (in Chinese) |
| [14] |
ANGLART H, NYLUND O. CFD application to prediction of void distribution in two-phase bubbly flows in rod bundles[J]. Nuclear Engineering and Design, 1996, 163(1/2): 81-98. |
| [15] |
任五岳, 田文喜, 边嘉伟, 等. T型管热混合温度波动特性研究[J]. 原子能科学技术, 2017, 51(8): 1371-1378. REN W Y, TIAN W X, BIAN J W, et al. Experiment study on temperature fluctuation characteristics of two-phase thermal mixing in T-junction[J]. Atomic Energy Science and Technology, 2017, 51(8): 1371-1378. (in Chinese) |
| [16] |
FENG T T, WANG M J, SONG P, et al. Numerical research on thermal mixing characteristics in a 45-degree T-junction for two-phase stratified flow during the emergency core cooling safety injection[J]. Progress in Nuclear Energy, 2019, 114: 91-104. DOI:10.1016/j.pnucene.2019.03.009 |
| [17] |
李树谦, 卢涛, 邱庆刚. T型圆管内蒸汽直接接触凝结数值模拟[J]. 热科学与技术, 2016, 15(1): 33-39. LI S Q, LU T, QIU Q G. Simulation of direct contact condensation in a tee junction[J]. Journal of Thermal Science and Technology, 2016, 15(1): 33-39. (in Chinese) |








