导热正问题(direct heat conduction problem,DHCP)是根据边界条件、初始条件等去计算导热物体的整个温度场,而导热反问题(inverse heat conduction problem,IHCP)则是根据某一部分的温度场来识别物体的几何缺陷[1]、算子[2]、物体内部热源[3]、边界条件[4]等未知参数。在核级管道系统中,很有必要对一些具有特殊安全性的管道进行热疲劳分析。热疲劳分析需要得到内壁面的温度波动,而管道的结构完整性决定了直接测量存在一定困难,由于导热反问题可用于间接、无损、快速、准确地获得内壁面的温度波动,对于保证管道的安全运行具有重要意义[5]。
导热反问题的不适定性对此类问题的解决增加了一定的难度,国内外学者所采用的算法也各不相同。Xie等[6]采用控制容积积分法与Levenberg-Marquardt优化方法对绝热材料的热物性参数进行了瞬态识别;张林等[7]利用Levenberg-Marquardt算法识别了充分发展的湍流管道内壁的几何边界;Mohasseb等[8]应用遗传算法反演了方形板边界热流密度;钱炜祺等[9]采用顺序函数法与有限控制体积法对二维圆环域外边界热流密度反演问题进行了计算;Chen等[10]运用共轭梯度法估算了双层壁炉内壁面的几何形状;卢涛等[11]采用共轭梯度法反演了三维T型管内壁面的瞬态温度。作为一种梯度类算法,共轭梯度法具有抗不适定性的优点,因而被广泛地应用于导热反问题中[12]。熊平等[13]将高斯消元法与共轭梯度法结合,可较快地反演出一维圆管的内壁面温度;Han等[14]基于共轭梯度法对对流边界条件进行了反演,同时得出了二维与三维的计算时间,但反演所需时间较长;Xiong等[15]运用Gauss-Seidel点迭代法结合共轭梯度法精确地得出了内壁面的瞬态温度,但识别速度较低;后来他们进一步改进了优化方法[16],提出了一种结合顺序函数法和共轭梯度法优点的序列共轭梯度法来反演待定热流,有效地提升了反演速率,但反演精度有所降低。
目前大多数文献通过研究不同导热反问题的优化方法来提高反演速率,但很少有研究通过改进反演算法中的导热计算来提高其反演速率。本文通过改进正问题的求解方法,将求解一维非稳态导热问题的托马斯算法(tridiagonal matrix algorithm,TDMA)与线迭代相结合,提出TDMA线迭代法,将二维问题转化为多个一维问题,以提高二维导热反问题的计算速率;分别将TDMA线迭代法和常用的Gauss-Seidel点迭代法与适用性较强的共轭梯度法相结合,通过构造数值试验分析两种计算方法反演的精确性和抗噪性,并探讨两种导热计算方法对反问题反演速率的影响。
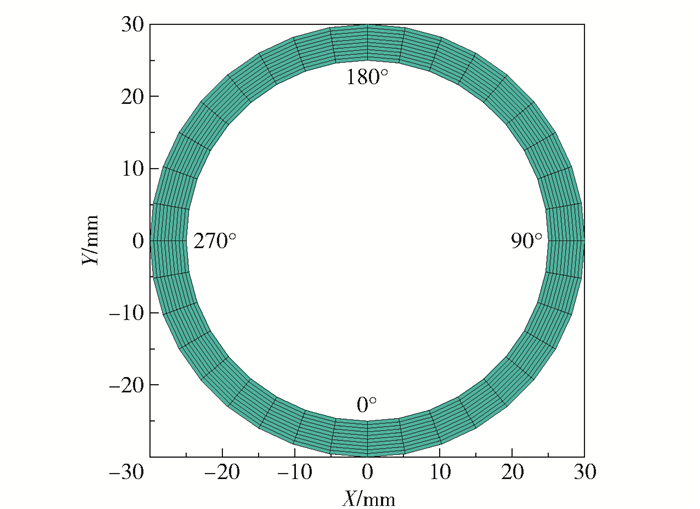
1 物理模型的建立二维圆管物理模型见图 1。管道外径R1=30 mm,壁厚d=5 mm。管道导热系数k=17.60 W/(m ·K),外壁面对流换热系数hf=100 W/(m2 ·K),环境温度Tf =20 ℃,密度ρ=7 850 kg/m3, 比热容c= 465 J/(kg ·K),时间步长Δt=1 s,总计算时间N=30 s。对二维圆管截面在空间上采用均分网格进行离散,其中周向均分为36份,径向均分为10份,网格量为360,网格节点数为396个。
|
图 1 二维圆管的物理模型和网格数 Fig.1 Physical model and grid number of a two-dimensional circular tube |
圆管的导热偏微分方程为
| $ \rho c \frac{\partial T}{\partial t}=\frac{1}{r} \frac{\partial}{\partial r}\left(k r \frac{\partial T}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial}{\partial \varphi}\left(k \frac{\partial T}{\partial \varphi}\right), S \in \varOmega $ | (1) |
假设导热系数和对流换热系数均为常数。给定内壁面为第一类边界条件,外壁面为第三类边界条件,则边界条件为
| $ T_{S}=T(t), S \in { wall\_in } $ | (2) |
| $ -k\left(\frac{\partial T}{\partial n}\right)_{S}=h_{\mathrm{f}}\left(T_{\mathrm{w}}-T_{\mathrm{f}}\right), S \in { wall\_out } $ | (3) |
初始条件为
| $ T=T_{0}, t=0 $ | (4) |
式中,T为圆管温度;t为时间;r为圆管极径位置;φ为圆管极角位置;Tw为圆管外壁面温度;S为圆管壁面;Ω为圆管内部。
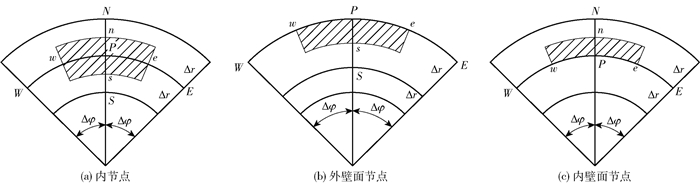
2.1.1 离散方法分别对式(1)~(4)在时间上和空间上离散,本文采用控制容积积分法进行数学模型离散,极坐标下的网格节点如图 2所示。在时间间隔[t, t+Δt]内,将式(1)对图 2(a)所示的控制容积作积分可得式(5);假定非稳态项中的T随x呈阶梯形分布,扩散项中T随t作隐式阶梯变化,则可得式(6);简化式(6),省略上标t+Δt来表示所求时刻的节点温度,用上标0替换上标t表示初始时刻的已知节点温度,最终得到内节点离散方程式(7)。同理,对圆管内外边界条件采用相同的方法进行数值离散,可推得内边界离散方程(8)和外边界离散方程(9)。在给定的定解条件下,即可对上述瞬态导热正问题进行数值求解。
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \int_{s}^{n} \int_{w}^{e} \int_{t}^{t+\Delta t} \rho c \frac{\partial T}{\partial t} r \mathrm{d} r \mathrm{d} \varphi \mathrm{d} t=\int_{s}^{n} \int_{w}^{e} \int_{t}^{t+\Delta t} \frac{1}{r} \frac{\partial}{\partial r}(k r \\ \left.\frac{\partial T}{\partial r}\right) r \mathrm{d} r \mathrm{d} \varphi \mathrm{d} t+\int_{s}^{n} \int_{w}^{e} \int_{t}^{t+\Delta t} \frac{1}{r^{2}} \frac{\partial}{\partial \varphi}\left(k \frac{\partial T}{\partial \varphi}\right) r \mathrm{d} r \mathrm{d} \varphi \mathrm{d} t \end{array} $ | (5) |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ (\rho c)_{P}\left(T_{P}^{t+\Delta t}-T_{P}^{t}\right) r_{P} \Delta r \Delta \varphi=\left(\frac{k_{n}\left(T_{N}^{t+\Delta t}-T_{P}^{t+\Delta t}\right)}{\Delta r}\right. \\ r_{n} \Delta \varphi-\frac{k_{s}\left(T_{P}^{t+\Delta t}-T_{S}^{t+\Delta t}\right)}{\Delta r} r_{s} \Delta \varphi+\frac{k_{e}\left(T_{E}^{t+\Delta t}-T_{P}^{t+\Delta t}\right)}{r_{e} \Delta \varphi} \Delta r- \\ \left.\frac{k_{w}\left(T_{P}^{t+\Delta t}-T_{W}^{t+\Delta t}\right)}{r_{w} \Delta \varphi} \Delta r\right) \cdot \Delta t \end{array} $ | (6) |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ (\rho c)_{P}\left(T_{P}-T_{P}^{0}\right) r_{P} \Delta r \Delta \varphi=\left(\frac{k_{n}\left(T_{N}-T_{P}\right)}{\Delta r} r_{n} \Delta \varphi-\right. \\ \left.\frac{k_{s}\left(T_{P}-T_{S}\right)}{\Delta r} r_{s} \Delta \varphi+\frac{k_{e}\left(T_{E}-T_{P}\right)}{r_{e} \Delta \varphi} \Delta r-\frac{k_{w}\left(T_{P}-T_{W}\right)}{r_{w} \Delta \varphi} \Delta r\right) \cdot \\ \Delta t \end{array} $ | (7) |
| $ T_{P}=T(t) $ | (8) |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ (\rho c)_{P}\left(T_{P}-T_{P}^{0}\right) r_{P} \frac{\Delta r}{2} \Delta \varphi=\left(\frac{k_{e}\left(T_{E}-T_{P}\right)}{r_{e} \Delta \varphi} \frac{\Delta r}{2}-\right. \\ \frac{k_{w}\left(T_{P}-T_{W}\right)}{r_{w} \Delta \varphi} \frac{\Delta r}{2}+\frac{k_{s}\left(T_{S}-T_{P}\right)}{\Delta r} r_{s} \Delta \varphi+h_{\mathrm{f}}\left(T_{\mathrm{f}}-T_{P}\right) \\ \left.r_{n} \Delta \varphi\right) \cdot \Delta t \end{array} $ | (9) |
|
图 2 极坐标下的网格节点 Fig.2 Grid node in polar coordinates |
式中,P、N、S、W、E分别表示所研究节点及其相邻的4个节点;n、e、w、s表示相应的界面;Δφ表示相邻两节点间的周向角度;Δr表示相邻两节点间的径向长度。
2.1.2 数值求解方法数值求解方法分为直接解法和迭代解法,本文分别采用Gauss-Seidel点迭代法和TDMA线迭代法进行求解。
离散方程可写成以下通用形式
| $ a_{P} T_{P}=a_{E} T_{E}+a_{W} T_{W}+a_{N} T_{N}+a_{S} T_{S}+b $ | (10) |
其中TP0的相关项已包括于b中。
1) Gauss-Seidel点迭代法
Gauss-Seidel点迭代法的单步迭代通过取邻点的最新值来代入计算。假设先沿着径向由内向外进行扫描,再沿着周向从0°位置开始顺时针方向进行扫描,Gauss-Seidel迭代式为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ a_{P} T_{P}^{(n)}=a_{E} T_{E}^{(n-1)}+a_{W} T_{W}^{(n)}+a_{N} T_{N}^{(n-1)}+a_{S} T_{S}^{(n)}+ \\ b, \varphi \in(0,2 {\rm{ \mathsf{ π} }}) \end{array} $ | (11) |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ a_{P} T_{P}^{(n)}=a_{E} T_{E}^{(n-1)}+a_{W} T_{W}^{(n-1)}+a_{N} T_{N}^{(n-1)}+a_{S} T_{S}^{(n)}+ \\ b, \varphi=0 \end{array} $ | (12) |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ a_{P} T_{P}^{(n)}=a_{E} T_{E}^{(n)}+a_{W} T_{W}^{(n)}+a_{N} T_{N}^{(n-1)}+a_{S} T_{S}^{(n)}+b, \\ \varphi=2 {\rm{ \mathsf{ π} }} \end{array} $ | (13) |
式中,n表示本次迭代,n-1表示上一次迭代。
2) TDMA线迭代法
TDMA线迭代法构造了一种采用直接法与迭代法相结合的多维问题代数方程求解方法,即沿径向将二维问题转化为一维隐式格式,在每个一维隐式格式的求解中均采用高斯消元法进行计算,将五对角矩阵问题转换为三对角矩阵问题并采用TDMA算法进行求解,最终通过沿周向从0°位置开始顺时针方向扫描进行线迭代求解。
根据式(10),假设某一极角下的径向节点均为待求量,而周向节点为已知量,设此时的常数项为b′,则离散表达式为
| $ a_{P} T_{P}=a_{N} T_{N}+a_{S} T_{S}+b^{\prime} $ | (14) |
式中,b′=aETE+aWTW+b。
将式(14)转换为如下一般方程组形式
| $ A_{i} T_{i}=B_{i} T_{i+1}+C_{i} T_{i-1}+D_{i} $ | (15) |
对于边界节点,代数方程为二元方程;而对于中间节点,代数方程均为三元方程,可经过逐步消元将中间节点三元方程转化为二元方程,具体形式如下
| $ T_{i-1}=P_{i-1} T_{i}+Q_{i-1} $ | (16) |
当从前向后消元进行到最后的边界方程时,该二元方程即化为一元方程,可直接求得该边界节点的温度值。联立式(15)与式(16)可得出Pi、Qi的递归通式,再结合式(16)从后向前即可依次求出不同径向位置处的节点温度Ti。
将上述求解过程程序化,并在给定定解条件下利用该通用计算程序对二维圆管温度场进行数值求解,即可获得管道各节点的时域温度变化。
2.2 导热反问题导热正问题是一个定解问题,而导热反问题是是一个最优化问题。因此, 本文采用共轭梯度法作为最优化问题的求解方法。
2.2.1 共轭梯度法为了获得精确的内壁面温度,构建该最优化问题的目标函数为
| $ J(T)=\sum\limits_{t=1}^{N} \sum\limits_{j=1}^{M}\left(T_{I, j, t, \mathrm{cal}}-T_{I, j, t, \mathrm{mea}}\right)^{2} $ | (17) |
式中,M为外壁面测点数;TI, j, t, cal为反问题求得的外壁面温度计算值;TI, j, t, mea为外壁面温度测量值。
求解敏度问题。设内壁面节点数为K,将导热正问题的控制方程式分别对T0, k, n求偏导,得到敏度系数求解方程组为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \rho c \frac{\partial}{\partial t}\left(\frac{\partial T_{i, j, t}}{\partial T_{0, k, n}}\right)=\frac{1}{r} \frac{\partial}{\partial r}\left(k r \frac{\partial}{\partial r}\left(\frac{\partial T_{i, j, t}}{\partial T_{0, k, n}}\right)\right)+\frac{1}{r^{2}} \\ \frac{\partial}{\partial \varphi}\left(k \frac{\partial}{\partial \varphi}\left(\frac{\partial T_{i, j, t}}{\partial T_{0, k, n}}\right)\right), S \in \varOmega \end{array} $ | (18) |
| $ \left(\frac{\partial T_{0, j, t}}{\partial T_{0, k, n}}\right)_{S}=\left\{\begin{array}{ll} 1, & \text { while } j=k \& \& t=n \\ 0, & \text { else } \end{array} S \in\right. { wall\_in } $ | (19) |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ -k\left(\frac{\partial}{\partial n}\left(\frac{\partial T_{I, j, t}}{\partial T_{0, k, n}}\right)\right)_{S}=h_{\mathrm{f}}\left(\frac{\partial T_{I, j, t}}{\partial T_{0, k, n}}\right)_{S}, \quad S \in\\ wall\_out \end{array} $ | (20) |
| $ \frac{\partial T_{i, j, 0}}{\partial T_{0, k, n}}=0, t=0 $ | (21) |
采用与导热正问题相同的求解方法(Gauss-Seidel点迭代法或TDMA线迭代法)进行求解,提取出外壁面测点温度对内壁面节点温度的敏度系数
求解伴随问题,即目标函数梯度
| $ \frac{\partial J}{\partial T_{k, n}}=2 \sum\limits_{t=1}^{N} \sum\limits_{j=1}^{M}\left(T_{I, j, t, \text { cal }}-T_{I, j, t, \text { mea }}\right) \frac{\partial T_{j, t}}{\partial T_{k, n}} $ | (22) |
内壁面温度迭代式为
| $ \left(T_{k, n}\right)^{b+1}=\left(T_{k, n}\right)^{b}-\beta^{b}\left(d_{k, n}\right)^{b} $ | (23) |
式中,b为迭代步数;(Tk, n)b+1为迭代计算得到的新的内壁面节点温度;βb为迭代步长;(dk, n)b表示迭代搜索方向。βb和(dk, n)b可由式(24)~(26)求得。
| $ \left(d_{k, n}\right)^{b}=\left(\frac{\partial J}{\partial T_{k, n}}\right)^{b}+\gamma^{b}\left(d_{k, n}\right)^{b-1} $ | (24) |
| $ \gamma^{b}=\frac{\sum\limits_{n=1}^{N} \sum\limits_{k=1}^{K}\left[\left(\frac{\partial J}{\partial T_{k, n}}\right)^{b}\right]^{2}}{\sum\limits_{n=1}^{N} \sum\limits_{k=1}^{K}\left[\left(\frac{\partial J}{\partial T_{k, n}}\right)^{b-1}\right]^{2}} $ | (25) |
式中,γb为共轭系数,且当b=0时,设定γ0=0。
迭代步长为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \beta^{b}= \\ \frac{\sum\limits_{t=1}^{N} \sum\limits_{j=1}^{M}\left(\left(T_{I, j, t, \text { cal }}\right)^{b}-T_{I, j, t, \text { mea }}\right) \sum\limits_{n=1}^{N} \sum\limits_{k=1}^{K}\left(\frac{\partial T_{j, t}}{\partial T_{k, n}}\right)^{b}\left(d_{k, n}\right)^{b}}{\sum\limits_{t=1}^{N} \sum\limits_{j=1}^{M}\left[\sum\limits_{n=1}^{N} \sum\limits_{k=1}^{K}\left(\frac{\partial T_{j, t}}{\partial T_{k, n}}\right)^{b}\left(d_{k, n}\right)^{b}\right]^{2}} \end{array} $ | (26) |
共轭梯度法的收敛目标为
| $ \left|J(T)^{b+1}-J(T)^{b}\right| \leqslant \mu $ | (27) |
式中,μ为一小正数。
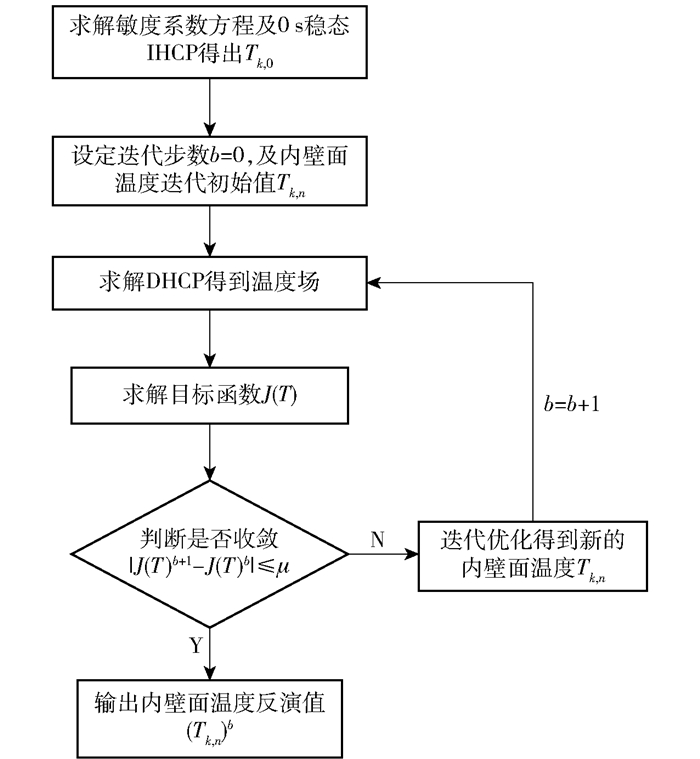
2.2.2 反演流程图利用共轭梯度法求解导热反问题的流程图如图 3所示。首先,计算敏度系数方程,求解0 s稳态导热反问题,得到初始条件;其次,设定迭代初始场及迭代步数b=0,满足定解条件后进行导热正问题的计算,得到外壁面温度值,并求出目标函数;最后根据是否达到收敛目标来决定返回重新计算或输出最终反演值。
|
图 3 反演流程图 Fig.3 Chart of the inversion progress |
通过第2节所构建的二维瞬态导热反问题数学模型进行C语言通用计算程序的编写,分别验证基于两种求解方法(Gauss-Seidel点迭代与TDMA线迭代)导热反问题的精确性。首先设定内壁面温度值,并利用导热正问题程序计算所得出的外壁面温度模拟真实测量值,为导热反问题分析提供输入数据,所设定的内壁面温度值作为校验数据。分别探讨3种不同工况下的导热反问题,这3种工况设定的内壁面节点温度包括随时间变化的阶跃式函数(Case 1)、三角形函数(Case 2)以及同时随时间和空间变化的正弦函数(Case 3)。
在实际测温过程中,测量温度必定会存在测量误差。为验证反演结果对引入测量误差的敏感性,本文在导热正问题计算得到的外壁面温度精确值的基础上引入随机误差,模拟实际的测量值。
| $ T_{I, j, t, \text { mea }}=T_{I, j, t, \text { exact }}+\sigma \omega $ | (28) |
式中,TI, j, t, mea为外壁面温度测量值;TI, j, t, exact为由正问题计算得到的外壁面温度精确值;σ为标准偏差;ω为[-2.576, 2.576]区间内服从标准正态分布的随机数,该区间能达到99%的测量可靠度。
为了验证内壁面温度反演值与精确值之间的偏离程度,定义平均相对误差
| $ \xi=\frac{1}{N} \sum\limits_{t=1}^{N}\left|\frac{T_{0, j, t, \text { exact }}-T_{0, j, t, \text { est }}}{T_{0, j, t, \text { exact }}}\right| \times 100 \% $ | (29) |
式中,T0, j, t, exact为内壁面温度精确值;T0, j, t, est为内壁面温度反演值;ξ越小,则说明反演值与精确值之间的偏离程度越小,反演值越接近于精确值。
3.1.1 随时间变化的阶跃式温度设定内壁面阶跃式温度变化为Case 1
| $ T(t)= \begin{cases}200, & t \in[0,10) \cup(20,30] \\ 100, & t \in[10,20]\end{cases} $ | (30) |
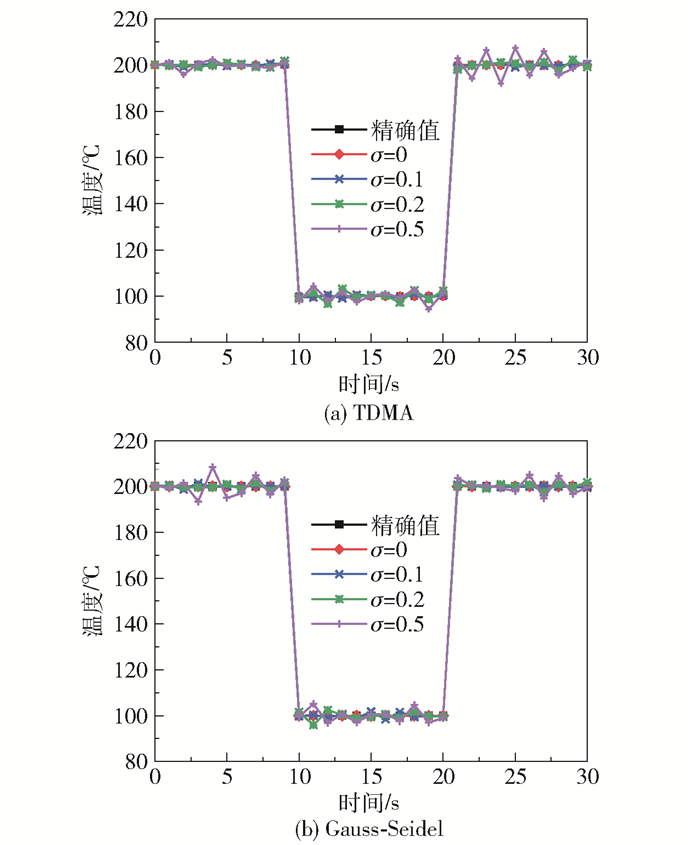
式(30)表示内壁面温度按照阶跃式规律变化。图 4表示当内壁面呈阶跃式温度变化时,在不同的标准偏差下,基于两种求解方法所得的反演温度值与精确温度值。由图 4可以看出,当标准偏差σ=0和0.1时,反问题反演温度曲线与正问题精确温度曲线几乎重合。当σ=0.2时,两种方法的反演温度均在精确温度附近上下小范围波动,且Gauss-Seidel点迭代反演温度的波动程度要略明显于TDMA线迭代。表 1为不同标准偏差下的平均相对误差。由表 1可以看出,当标准偏差σ=0.2时,Gauss-Seidel点迭代与TDMA线迭代反演平均相对误差分别为0.914 01%和0.750 64%,说明二者的反演精度较好且相差较小。当标准偏差达到σ=0.5时,Gauss-Seidel点迭代与TDMA线迭代反演的平均相对误差分别为1.793 02%和1.800 00%,说明测量偏差对两种方法的反演精度都有一定的影响。
|
图 4 阶跃式温度变化的反演值与精确值 Fig.4 Inversion value and exact value of the step temperature change |
| 下载CSV 表 1 Case 1和Case 2平均相对误差值 Table 1 Mean relative error values for Case 1 and Case 2 |
设定内壁面三角形温度变化为Case 2
| $ T(t)= \begin{cases}5 t+180, & t \in[0,15) \\ -5(t-15)+255, & t \in[15,30]\end{cases} $ | (31) |
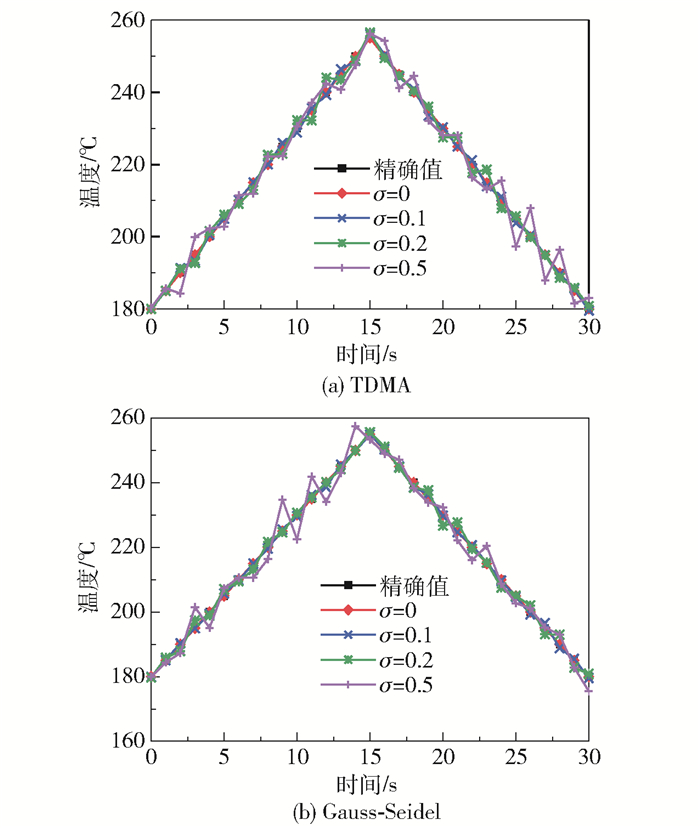
根据式(31)验证内壁面温度呈三角形规律变化情况下的反演结果。由图 5可以看出,随着标准偏差的增大,反演温度误差也随之增大,且在精确值附近上下波动。由图 5和表 1可得出,当标准偏差σ=0时,两种方法的反演平均相对误差在0.000 02%左右,说明在无测量误差下,两种方法的反演值非常接近精确值,正问题和反问题所获得的温度分布高度相似。当σ=0.2时,应用两种方法得到的反演温度波动不明显,平均相对误差较小。当标准偏差σ=0.5时,Gauss-Seidel点迭代法与TDMA线迭代法得到的反演温度的波动幅度相对较大,平均相对误差分别为1.512 72%和1.611 71%。由上述结果可以看出平均相对误差均随着标准偏差的增大而增大,且在同一标准偏差下,两种方法的反演误差较为接近。
|
图 5 三角形温度变化的反演值与精确值 Fig.5 Inversion value and exact value of the triangle temperature change |
设定内壁面正弦温度变化为Case 3
| $ T(t, \varphi)=200+20 \sin \left(\frac{{\rm{ \mathsf{ π} }}}{15} t\right)+15 \sin \varphi $ | (32) |
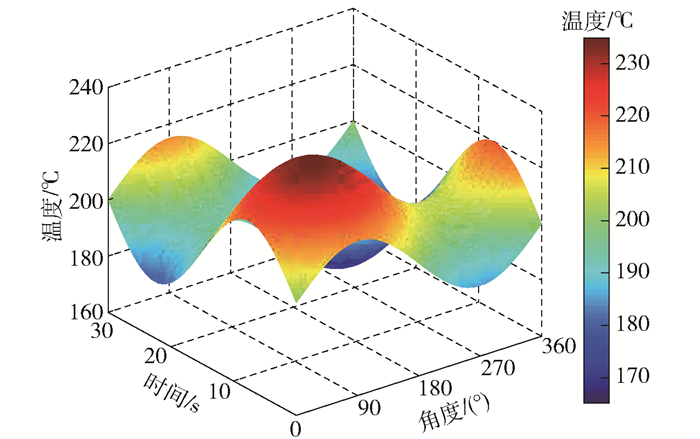
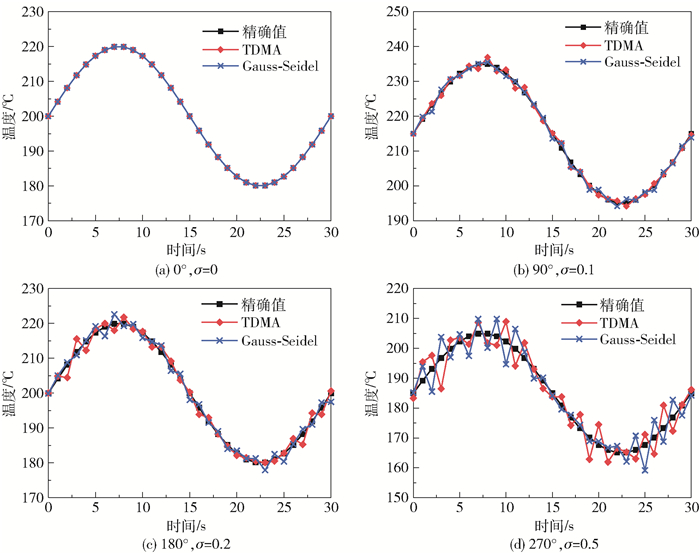
管道内壁面温度随时间和空间呈正弦规律变化,如图 6所示。根据式(32)对反演结果进行验证。图 7为两种计算方法在给定4个不同的标准偏差下,对应4个不同位置(图 1所示)处的内壁面时域温度变化。可以看出两种方法的反演结果虽然围绕精确值波动的方向不一致,但波动频率和幅度较为接近。表 2为在不同标准偏差下,沿周向均匀分布的4个角度处的平均相对误差值。通过对比可进一步发现,在同一标准偏差下两种方法各个角度处的平均相对误差相差较小,并且随着标准偏差的增大,两种求解方法在各个角度处的平均相对误差也相应增大。由表 1和表 2可得出,当标准偏差增大到σ=0.5时ξ波动值仍可以保持在2%左右,说明基于两种方法的反演精度对测量误差的变化不敏感,具有一定的抗噪性。
|
图 6 随时间和空间正弦变化的内壁面温度 Fig.6 Sinusoidal change in the inner wall temperature with time and space |
|
图 7 随时间和空间正弦温度变化的反演值与精确值 Fig.7 The inversion value and the exact value of sinusoidal temperature change with time and space |
| 下载CSV 表 2 Case 3平均相对误差值 Table 2 Mean relative error values for Case 3 |
表 3为3台不同PC计算机的性能参数,以同一算例为基础,采用C语言编译器VC++6.0,分别在上述3台PC计算机上进行计算。对基于两种求解方法的通用计算程序,采用计时函数clock()精准计时,并将程序运行时间进行对比,结果如表 4所示。可以看出,Gauss-Seidel点迭代法程序运行所用时间是TDMA线迭代法程序运行时间的3倍左右,表明基于TDMA线迭代法程序的运行速度要明显优于基于Gauss-Seidel点迭代法的程序,具有更高的计算效率。
| 下载CSV 表 3 各PC计算机性能参数 Table 3 Performance parameters of each PC computer |
| 下载CSV 表 4 程序运行时间对比 Table 4 Comparison of program running times |
(1) 在不考虑外壁测温误差条件下,通过数值模拟验证了基于控制容积积分法的导热正问题以及基于共轭梯度法的优化算法所构建的二维瞬态导热反问题数学模型的有效性与精确性。研究结果显示,Gauss-Seidel点迭代法与TDMA线迭代法反演的内壁面温度均具有较高的识别精度。
(2) 当存在外壁测温误差时,探讨了反演结果对测量误差的敏感性。计算结果表明,反演误差随着标准偏差的增大而增大,但Gauss-Seidel点迭代法与TDMA线迭代法仍能够较准确地识别出内壁面温度波动,即使标准偏差增大到σ=0.5时,所反演内壁面温度的平均相对误差仍可保持在2%左右,具有一定的抗噪性。
(3) 将基于两种求解方法的通用程序分别在不同PC计算机上运行,结果显示,相较于常用的Gauss-Seidel点迭代法,TDMA线迭代法在保持求解精度的基础上,求解速度有明显的提升,能够较快地反演得到内壁面温度波动,具有更高的计算效率。
从目前的研究可以看出,三维IHCP与二维IHCP的计算效率差异很大,三维IHCP所耗费的时间要远远高于二维IHCP。因此,今后的研究重点是进一步探讨如何通过改进正问题的求解方法来提高三维IHCP的计算效率。
| [1] |
ZHANG F L, YUAN Z H. The detection and evaluation for the internal defection in industrial pipeline based on the virtual heat source temperature field[J]. Journal of Thermal Analysis and Calorimetry, 2019, 137(3): 949-964. DOI:10.1007/s10973-018-07988-7 |
| [2] |
KIM S K, JUNG B S, KIM H J, et al. Inverse estimation of thermophysical properties for anisotropic composite[J]. Experimental Thermal and Fluid Science, 2003, 27(6): 697-704. DOI:10.1016/S0894-1777(02)00309-6 |
| [3] |
LEE H L, CHANG W J, CHEN W L, et al. An inverse problem of estimating the heat source in tapered optical fibers for scanning near-field optical microscopy[J]. Ultramicroscopy, 2007, 107(8): 656-662. DOI:10.1016/j.ultramic.2007.01.001 |
| [4] |
胡国俊. 传热中的多宗量反演研究[D]. 大连: 大连理工大学, 2002. HU G J. Research on multi-quantity inversion in heat transfer[D]. Dalian: Dalian University of Technology, 2002. (in Chinese) |
| [5] |
LEJEAIL Y, KASAHARA N. Thermal fatigue evaluation of cylinders and plates subjected to fluid temperature fluctuations[J]. International Journal of Fatigue, 2005, 27(7): 768-772. DOI:10.1016/j.ijfatigue.2005.01.007 |
| [6] |
XIE T, HE Y L, TONG Z X, et al. An inverse analysis to estimate the endothermic reaction parameters and physical properties of aerogel insulating material[J]. Applied Thermal Engineering, 2015, 87: 214-224. DOI:10.1016/j.applthermaleng.2015.05.008 |
| [7] |
张林, 杨立, 范春利. 充分发展湍流管道内壁边界的红外定量识别[J]. 国防科技大学学报, 2019, 41(5): 185-192. ZHANG L, YANG L, FAN C L. Infrared quantitative identification for inner boundary of fully developed turbulent pipeline[J]. Journal of National University of Defense Technology, 2019, 41(5): 185-192. (in Chinese) |
| [8] |
MOHASSEB S, MORADI M, SOKHANSEFAT T, et al. A novel approach to solve inverse heat conduction problems: coupling scaled boundary finite element method to a hybrid optimization algorithm[J]. Engineering Analysis with Boundary Elements, 2017, 84: 206-212. DOI:10.1016/j.enganabound.2017.08.018 |
| [9] |
钱炜祺, 蔡金狮. 顺序函数法求解二维非稳态热传导逆问题[J]. 空气动力学学报, 2002, 20(3): 274-281. QIAN W Q, CAI J S. Solving two-dimensional transient inverse heat conduction problem with sequential function method[J]. Acta Aerodynamica Sinica, 2002, 20(3): 274-281. (in Chinese) DOI:10.3969/j.issn.0258-1825.2002.03.004 |
| [10] |
CHEN W L, YANG Y C, LEE H L, et al. Estimation for inner surface geometry of a two-layer-wall furnace with inner wall made of functionally graded materials[J]. International Communications in Heat and Mass Transfer, 2018, 97: 143-150. DOI:10.1016/j.icheatmasstransfer.2018.07.009 |
| [11] |
卢涛, 李春永. 基于共轭梯度法对T型管内壁瞬态温度的识别[J]. 热科学与技术, 2011, 10(1): 45-50. LU T, LI C Y. Identifying of inner wall unsteady temperature at T-junction using conjugate gradient method[J]. Journal of Thermal Science and Technology, 2011, 10(1): 45-50. (in Chinese) DOI:10.3969/j.issn.1671-8097.2011.01.008 |
| [12] |
HUANG C H, CHEN C W. A boundary-element-based inverse problem of estimating boundary conditions in an irregular domain with statistical analysis[J]. Numerical Heat Transfer, 1998, 33(2): 251-267. DOI:10.1080/10407799808915032 |
| [13] |
熊平, 艾红雷, 卢涛, 等. 一维非稳态导热反问题反演管道内壁面温度波动[J]. 核动力工程, 2018, 39(2): 96-100. XIONG P, AI H L, LU T, et al. Inverse problem of one-dimensional unsteady heat conduction deducing temperature fluctuation of inner wall of pipe[J]. Nuclear Power Engineering, 2018, 39(2): 96-100. (in Chinese) |
| [14] |
HAN W W, CHEN H B, LU T. Estimation of the time-dependent convective boundary condition in a horizontal pipe with thermal stratification based on inverse heat conduction problem[J]. International Journal of Heat and Mass Transfer, 2019, 132: 723-730. DOI:10.1016/j.ijheatmasstransfer.2018.02.119 |
| [15] |
XIONG P, LU T, LIU B. Inversion of the inner wall temperature of the two-dimensional pipe based on conjugate gradient method[C]//Proceedings of the 16th International Heat Transfer Conference. Beijing, 2018.
|
| [16] |
XIONG P, DENG J, LU T, et al. A sequential conjugate gradient method to estimate heat flux for nonlinear inverse heat conduction problem[J]. Annals of Nuclear Energy, 2020, 149: 107798. DOI:10.1016/j.anucene.2020.107798 |








