引言

近年来，关于考虑恐惧效应对生态系统种群的影响的研究成为新的热点。恐惧效应是猎物持续心理压力的表现，已有研究表明，它可以减少猎物的觅食时间、转移其觅食区域，使猎物的生长率、繁殖率降低，从而间接影响猎物的种群数量^[1-4]。恐惧效应通常可用满足一定条件的函数f(k, y)表示，这里k为恐惧系数，y为捕食者种群密度。2016年，Wang等^[5]首次建立了二维带恐惧效应的捕食者-被捕食者模型，研究表明恐惧效应可影响周期轨的稳定性。随后，Panday等^[6]建立了第一个三维带恐惧效应的三物种食物链模型，从理论上分析了解的边界性、持久性及平衡点的存在性，并通过数值模拟发现，随着恐惧系数k_i(i=1, 2)的增大，三物种种群密度可由混沌变为稳定的周期性振荡直至达到定态平衡。

本文以文献[6]中带恐惧效应的三物种食物链模型为研究对象，运用中心流形定理和分支理论讨论了模型中的局部分支问题，从理论上严格证明了supercritical Hopf分支、subcritical Hopf分支、transcritical分支和saddle-node分支的存在性。研究结果表明分支是引起种群失稳、产生周期性振荡的根本原因，从而揭示了恐惧效应是维持种群稳定的重要因素，进一步丰富和完善了恐惧效应对三物种食物链模型中种群动态影响的研究。

1 理论分析 1.1 带恐惧效应的三物种食物链模型

考虑如下模型^[6]

$ \left\{\begin{array}{l} \frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{x}{1+k_{1} y}(1-x)-\frac{a_{1} x y}{1+b_{1} x} \\ \frac{\mathrm{d} y}{\mathrm{~d} t}=\frac{a_{1} x y}{1+b_{1} x} \frac{1}{1+k_{2} z}-\frac{a_{2} y z}{1+b_{2} y}-d_{1} y \\ \frac{\mathrm{d} z}{\mathrm{~d} t}=\frac{a_{2} y z}{1+b_{2} y}-d_{2} z \end{array}\right. $

(1)

式中，x、y、z分别表示被捕食者、中间捕食者和上层捕食者的种群密度；$ \frac{1}{1+k_{1} y}、\frac{1}{1+k_{2} z}$为恐惧效应函数，其中k₁表示被捕食者对中间捕食者的恐惧系数，k₂表示中间捕食者对上层捕食者的恐惧系数，取值为0.01；其余参数的含义与取值详见文献[6]。

1.2 平衡点的存在性与稳定性

本文选取k₁为分支参数，结合模型的实际意义，取k₁∈(0, 10)，x、y、z为非负数，则系统(1)满足实际意义的平衡点如下：

$ O_{1}(0, 0, 0), O_{2}(1, 0, 0) $

$ O_{3}\left(0.105\ 263, \frac{1}{k_{1}} \sqrt{\frac{1}{4}+0.235\ 457 k_{1}}-\frac{1}{2 k_{1}}, 0\right) $

$ \begin{array}{l} \ \ \ \ \ \ O_{4}\left(\frac{2+\beta}{6}, 0.125, \sqrt{\frac{6\ 250(2+\beta)}{3(4+\beta)}+2\ 256.25}-\right.\\ \left.52.5\right) \end{array} $

$ \begin{array}{l} \ \ \ \ \ \ O_{5}\left(\frac{2-\beta}{6}, 0.125, \sqrt{\frac{6\ 250(2-\beta)}{3(4-\beta)}+2\ 256.25}-\right.\\ \left.52.5\right) \end{array} $

其中$\beta=\sqrt{8.5-0.937\ 5 k_{1}} $。运用动力系统的定性和稳定性理论进行分析可得如下结论。

结论1

1) 当k₁∈(0, 1.623 42)∪(7.756 05, 9.066 666)时，系统存在5个平衡点，包含4个saddles和1个source；

2) 当k₁∈(1.623 42, 4.8)∪(4.8, 4.818 66)∪(5.863 32, 7.069 25)∪(7.069 25, 7.756 05)时，系统存在5个平衡点，包含3个saddles、1个source和1个sink；

3) 当k₁∈(4.818 66, 5.863 32)时，系统存在5个平衡点，包含2个saddles、1个source和2个sinks；

4) 当k₁∈(9.066 666, 10)时，系统存在3个平衡点，均为saddles；

5) 当k₁=1.623 42, 4.8, 4.818 66, 5.863 32, 7.069 25, 7.756 05, 9.066 666时，系统只存在1个非双曲平衡点，其余为双曲平衡点。

1.3 平衡点的局部分支 1.3.1 Hopf分支

由结论1中的5)可知，当k₁=1.623 42时，系统(1)有一个非双曲平衡点O₄(0.773 6, 0.125, 8.428 026)，其特征值为{-0.376 717, ±0.090 73i}。令x₁=x-0.773 6，y₁=y-0.125，z₁=z-8.428 026，ρ=k₁-1.623 42，代入系统(1)中，再将坐标变换后得到的系统的右端函数在(x₁, y₁, z₁)=(0, 0, 0)处泰勒展开

$ \dot{\boldsymbol{Y}}=\mathrm{D} f(\boldsymbol{X}) \boldsymbol{Y}+\boldsymbol{F}(\boldsymbol{Y}) $

(2)

式中，X=(0.773 6, 0.125, 8.428 026)，Y=(x₁, y₁, z₁)^T，F(Y)=(f₁, f₂, f₃)^T。将系统(2)变换成可使用中心流形定理的标准形式，构造可逆变换矩阵

$ \boldsymbol{T}=\left(\begin{array}{ccc} -0.985\ 362 & -0.392\ 471 & -0.069\ 607 \\ 0.097\ 611 & 0.152\ 13 & 0 \\ -0.139\ 762 & 0 & 0.904\ 422 \end{array}\right) $

令

$ \boldsymbol{Y}=\boldsymbol{T} \boldsymbol{U} $

(3)

式中，U=(x₂, y₂, z₂)^T。将式(3)代入式(2)中，可得

$ \dot{\boldsymbol{U}}=\boldsymbol{T}^{-1} \mathrm{D} f(\boldsymbol{X}) \boldsymbol{T} \boldsymbol{U}+\boldsymbol{T}^{-1} \boldsymbol{F}(\boldsymbol{T} \boldsymbol{U}) $

(4)

式中，$ \boldsymbol{T}^{-1} \mathrm{D} f(\boldsymbol{X}) \boldsymbol{T}=\left(\begin{array}{ll}\boldsymbol{A} & 0 \\ 0 & \boldsymbol{B}\end{array}\right)$, $ \boldsymbol{A}=-0.376\ 717$, $ \boldsymbol{B}= \left(\begin{array}{cc} 0 & -0.090\ 73 \\ 0.090\ 73 & 0 \end{array}\right)$, $ \boldsymbol{T}^{-1} \boldsymbol{F}(\boldsymbol{T} \boldsymbol{U})=\left(g_{1}, g_{2}, g_{3}\right)^{\mathrm{T}}$，其中

$ \begin{aligned} &\ \ \ \ \ \ g_{1}=0.020\ 327 \rho-0.002\ 112 \rho^{2}+0.073\ 096 \rho x_{2}+ \\ &0.041\ 317 \rho y_{2}+0.004\ 421 \rho z_{2}+\cdots \end{aligned} $

$ \begin{aligned} &\ \ \ \ \ \ g_{2}=-0.013\ 043 \rho+0.001\ 355 \rho^{2}-0.046\ 901 \rho x_{2}- \\ &0.02651 \rho y_{2}-0.002\ 836 \rho z_{2}+\cdots \end{aligned} $

$ \begin{aligned} &\ \ \ \ \ \ g_{3}=0.003\ 141 \rho-0.000\ 326 \rho^{2}+0.011\ 296 \rho x_{2}+ \\ &0.006\ 385 \rho y_{2}+0.000\ 683 \rho z_{2}+\cdots \end{aligned} $

把参数ρ看作新的动态变量

$ \dot{\rho}=0 $

(5)

新系统(4)、(5)的平衡点O(x₂, y₂, z₂, ρ)=(0, 0, 0, 0)存在一个三维局部中心流形，可以表示为

W_loc³(O)={(x₂, y₂, z₂, ρ)∈R⁴|x₂=h(y₂, z₂, ρ), h(0, 0, 0)=0, Dh(0, 0, 0)=0, |y₂|＜δ₁, |z₂|＜δ₂, |ρ|＜δ₃, δ_i(i=1, 2, 3)充分小}。

下面计算局部中心流形。局部中心流形满足

$ \begin{array}{l} \ \ \ \ \ \ \ \ \varPhi\left(h\left(y_{2}, z_{2}, \rho\right)\right)=\left(D_{y_{2}} h\left(y_{2}, z_{2}, \rho\right), D_{z_{2}} h\left(y_{2}, z_{2}, \right.\right. \\ \rho))\left(\boldsymbol{B}\left(\begin{array}{l} y_{2} \\ z_{2} \end{array}\right)+\left(\begin{array}{l} g_{2} \\ g_{3} \end{array}\right)\right)-\boldsymbol{A} h\left(y_{2}, z_{2}, \rho\right)-g_{1}=0 \end{array} $

(6)

将h(y₂, z₂, ρ)在(y₂, z₂, ρ)=(0, 0, 0)处泰勒展开

$ \begin{array}{l} \ \ \ \ \ \ \ \ h\left(y_{2}, z_{2}, \rho\right)=a y_{2}^{2}+b z_{2}^{2}+c \rho^{2}+d y_{2} z_{2}+e \rho y_{2}+ \\ f \rho z_{2}+O\left(|\bar{\rho}|^{3}\right) \end{array} $

(7)

其中$|\bar{\rho}|=\sqrt{y_{2}^{2}+z_{2}^{2}+\rho^{2}}$。将式(7)代入式(6)中，由同类项系数之和为0可得

$ \begin{aligned} &\ \ \ \ \ \ \ \ h\left(y_{2}, z_{2}, \rho\right)=0.461\ 178 y_{2}^{2}+0.128\ 936 z_{2}^{2}+ \\ &0.009\ 442 \rho^{2}+0.47\ 2164 y_{2} z_{2}+0.124\ 223 \rho y_{2}+ \\ &0.055\ 85 \rho z_{2}+O\left(\left|\bar{\rho}\right|^{3}\right) \end{aligned} $

(8)

将式(8)代入系统(4)、(5)中，可得系统(4)、(5)限制在平衡点O的局部中心流形上的系统(9)、(10)。

$ \left\{\begin{array}{l} \dot{y}_{2}=-0.090\ 73 z_{2}-0.013\ 043 \rho+0.001\ 355 \rho^{2}- \\ \ \ \ \ \ \ \ \ 0.004\ 922 z_{2}^{2}-0.215\ 799 y_{2}^{2}-0.026\ 51 y_{2} \rho- \\ \ \ \ \ \ \ \ \ 0.002\ 836 z_{2} \rho-0.187\ 23 y_{2} z_{2}-0.000\ 584 \rho^{3}- \\ \ \ \ \ \ \ \ \ 0.711\ 073 y_{2}^{3}-0.029\ 558 z_{2}^{3}-0.181\ 638 \rho y_{2}^{2}- \\ \ \ \ \ \ \ \ \ 0.122\ 233 \rho y_{2}-0.018\ 447 \rho z_{2}^{2}-0.014\ 124 \rho^{2} y_{2}- \\ \ \ \ \ \ \ \ \ 0.004\ 482 \rho^{2} z_{2}-0.731\ 845 y_{2}^{2} z_{2}- \\ \ \ \ \ \ \ \ \ 0.280\ 321 y_{2} z_{2}^{2}+\cdots=p\left(y_{2}, z_{2}, \rho\right) \\ \dot{z}_{2}=0.090\ 73 y_{2}+0.003\ 141 \rho+0.055\ 346 y_{2}^{2}- \\ \ \ \ \ \ \ \ \ 0.000\ 326 \rho^{2}+0.000\ 683 z_{2} \rho+0.006\ 385 y_{2} \rho+ \\ \ \ \ \ \ \ \ \ 0.008\ 122 y_{2} z_{2}+0.089\ 835 y_{2}^{3}+0.003\ 12 z_{2}^{3}+ \\ \ \ \ \ \ \ \ \ 0.019\ 54 \rho y_{2} z_{2}+0.030\ 257 \rho y_{2}^{2}+0.002\ 719 \rho z_{2}^{2}+ \\ \ \ \ \ \ \ \ \ 0.000\ 788 z_{2} \rho^{2}+0.002\ 376 y_{2} \rho^{2}+0.109\ 875 y_{2}^{2} z_{2}+ \\ \ \ \ \ \ \ \ \ 0.038\ 222 y_{2} z_{2}^{2}+0.000\ 141 \rho^{3}+\cdots=q\left(y_{2}, z_{2}, \rho\right) \end{array}\right. $

(9)

$ \dot{\rho}=0 $

(10)

系统(9)、(10)满足如下条件：p(0, 0, 0)=0，q(0, 0, 0)=0，$a=\frac{1}{16}\left[p_{y_{2} y_{2} y_{2}}+p_{y_{2} z_{2} z_{2}}+q_{y_{2} y_{2} z_{2}}+ q_{z_{2} z_{2} z_{2}}\right]\left.\right|_{(0, 0, 0)} $$ +\frac{1}{16 \times 0.090\ 73}\left[p_{y_{2} z_{2}}\left(p_{y_{2} y_{2}}+p_{z_{2} z_{2}}\right)- q_{y_{2} z_{2}}\left(q_{y_{2} y_{2}}+q_{z_{2} z_{2}}\right)-p_{y_{2} y_{2}} q_{y_{y} y_{2}}+p_{z_{2} z_{2}} q_{z_{2} z_{2}}\right]\left.\right|_{(0, 0, 0)}$$ = -0.018\ 515 \neq 0, d=\left.\frac{\mathrm{dRe}(\lambda(\rho))}{\mathrm{d} \rho}\right|_{\rho=0}=-0.012\ 914 \neq 0$。其中Re(λ(ρ))为系统(9)中平衡点O的特征值的实部。因此系统(9)、(10)的平衡点O发生了Hopf分支，并在平衡点的小邻域内产生一族周期轨。因为d＜0，a＜0，故当ρ＜0(|ρ|充分小)时，在平衡点的小邻域内产生一族稳定的周期轨。同理还可从理论上严格证明，当k₁取其他参数值时，平衡点O₄和O₅也会发生Hopf分支，故可得结论2。

结论2

1) 当k₁=1.623 42时，系统(1)的平衡点O₄发生supercritical Hopf分支。当k₁＜1.623 42时，平衡点O₄是不稳定的，并且在O₄的局部邻域内产生了一族稳定的周期轨。

2) 当k₁=4.818 66时，平衡点O₅发生supercritical Hopf分支。当k₁＜4.818 66时，平衡点O₅是不稳定的，并且在O₅的小邻域内产生了一族稳定的周期轨。

3) 当k₁=5.863 32时，平衡点O₅发生subcritical Hopf分支。当k₁＜5.863 32时，平衡点O₅是稳定的，并且在O₅的小邻域内产生了一族不稳定的周期轨。

4) 当k₁=7.756 05时，平衡点O₄发生subcritical Hopf分支。当k₁＜7.756 05时，平衡点O₄是稳定的，并且在O₄的小邻域内产生了一族不稳定的周期轨。

1.3.2 transcritical分支

由结论1中的5)，当k₁=4.8时，系统(1)有一个非双曲平衡点O₅(0, 0.125, -5)，其特征值为{0.029 282, -0.109 282, 0}，可得限制在(x₃, y₃, z₃, φ)=(0, 0, 0, 0)的二维局部中心流形上的系统(11)为

$ \left\{\begin{array}{l} \dot{z}_{3}=-0.048\ 828 \varphi z_{3}+0.018\ 998 z_{3}^{2}+\cdots=f\left(z_{3}, \varphi\right) \\ \dot{\varphi}=0 \end{array}\right. $

(11)

因系统(11)满足f(0, 0)=0，$ \frac{\partial f}{\partial z_{3}}(0, 0)=0, \frac{\partial f}{\partial \varphi}(0, 0)=0$, $ \frac{\partial^{2} f}{\partial z_{3}^{2}}(0, 0)=0.037\ 996, \frac{\partial^{2} f}{\partial z_{3} \partial \varphi}(0, 0)=-0.048\ 828$，故当k₁=4.8时，系统(1)在平衡点O₅(0, 0.125, -5)处发生了transcritical分支。通过类似的推导可得，当k₁=7.069 25时，系统(1)在平衡点(0.105 263, 0.125, 0)处也发生了transcritical分支。在平衡点(0.105 263, 0.125, 0)的局部邻域内，当k₁ > 7.069 25时，系统有两个平衡点，1个saddle O₃和1个source O₅，这两个平衡点在k₁=7.069 25处重合为1个平衡点(0.105 263, 0.125, 0)；当k₁ < 7.069 25时，系统(1)有两个平衡点，1个source O₃和1个saddle O₅。

1.3.3 saddle-node分支

由结论1中的5)，当k₁=9.066 666时，系统(1)有一个非双曲平衡点(0.333 375, 0.125, 4.928 057)，其特征值为{0.039 415±0.438 067i, 0}，可得限制在平衡点(x₄, y₄, z₄, μ)=(0, 0, 0, 0)的二维局部中心流形上的系统(12)。

$ \left\{\begin{aligned} &\dot{z}_{4}=-0.001\ 468 \mu-0.000\ 163 \mu z_{4}-0.000\ 307 z_{4}^{2}+\\ &\ \ \ \ \ \ \ \ \ 0.000\ 078 \mu^{2}+\cdots=g\left(z_{4}, \mu\right) \\ &\dot{\mu}=0 \end{aligned}\right. $

(12)

因系统(12)满足$g(0, 0)=0, \frac{\partial g}{\partial z_{4}}(0, 0)=0 $, $\frac{\partial g}{\partial \mu}(0, 0)=-0.001\ 486, \frac{\partial^{2} g}{\partial z_{4}^{2}}(0, 0)=-0.000\ 614 $，所以当k₁=9.066 666时，系统(1)在平衡点(0.333 375, 0.125, 4.928 057)处经历了saddle-node分支。在平衡点(0.333 375, 0.125, 4.928 057)的局部邻域内，当k₁>9.066 666时，系统(1)没有平衡点；当k₁=9.066 666时，系统(1)有1个平衡点；当k₁ < 9.066 666时, 系统(1)有两个平衡点，即1个saddle O₄和1个source O₅。

2 数值模拟

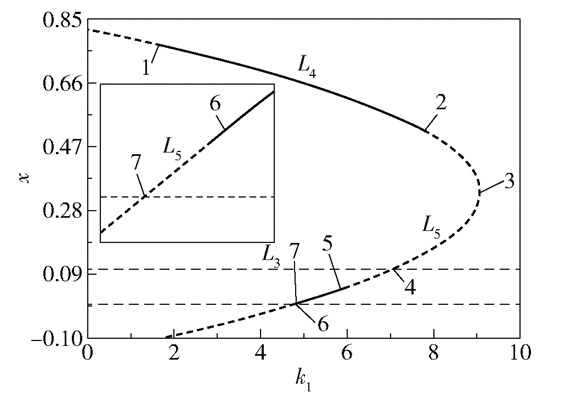
图 1是被捕食者的种群密度x关于k₁的分支图。L_i(i=3, 4, 5)表示发生分支的平衡点O_i(i=3, 4, 5)曲线。其中平衡点的分支类型和分支参数值总结于表 1，表中HB、SNB、TB分别表示Hopf分支、saddle-node分支和transcritical分支，以HB¹为例，上标表示发生分支的序号，k₁⁽ⁱ⁾(i=1, 2, …, 7)表示第i个分支的参数值。

平衡点O₄和O₅在k₁⁽³⁾处发生SNB³且重合。随着恐惧系数k₁的减小，当k₁⁽²⁾ < k₁ < k₁⁽³⁾时，平衡点O₄和O₅是不稳定的。不稳定的平衡点O₄在k₁⁽²⁾处发生HB²并获得稳定性，又在k₁⁽¹⁾处发生HB¹失去稳定性。在k₁ < k₁⁽¹⁾的小邻域内，三物种种群密度呈稳定的周期振荡。

当k₁⁽⁴⁾ < k₁ < k₁⁽²⁾时，平衡点O₃和O₅的不稳定性随着k₁的减小而降低，O₃和O₅在k₁⁽⁴⁾处重合并发生TB⁴。当k₁ < k₁⁽⁴⁾时，平衡点O₃不稳定，O₅不再具有实际意义。平衡点O₅在k₁⁽⁵⁾处发生HB⁵获得稳定性，又在k₁⁽⁶⁾处发生HB⁶失去稳定性。不稳定的O₅在k₁⁽⁷⁾处发生TB⁷。

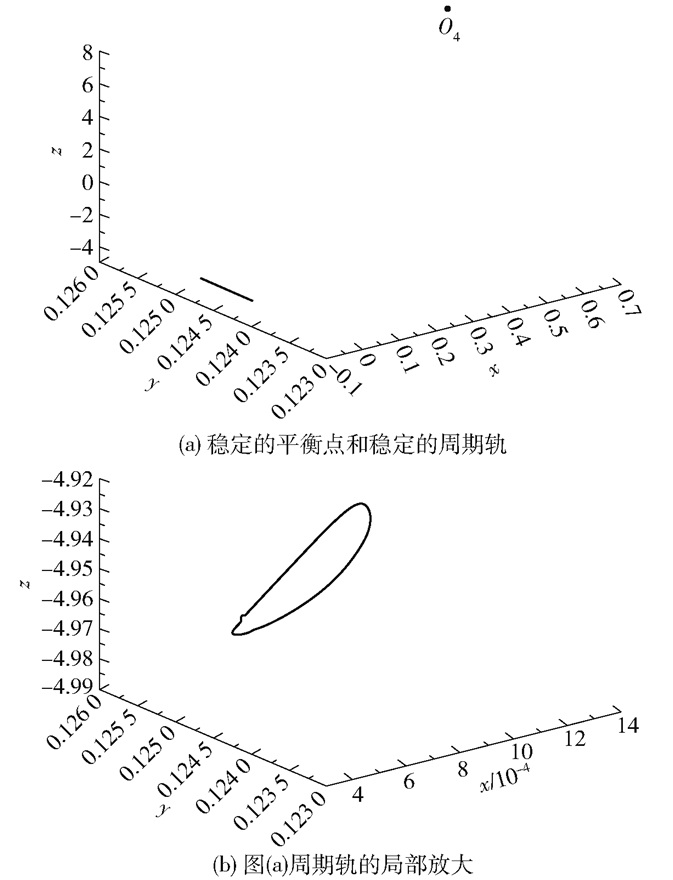
由结论2中的2)、4)可知，三物种的种群密度存在双稳定现象，当k₁=4.818 49时，取初始值为(0.000 724, 0.125 125, -4.953 48)，可模拟出系统有一个稳定的平衡点O₄和一个稳定的周期轨共存，如图 2所示。

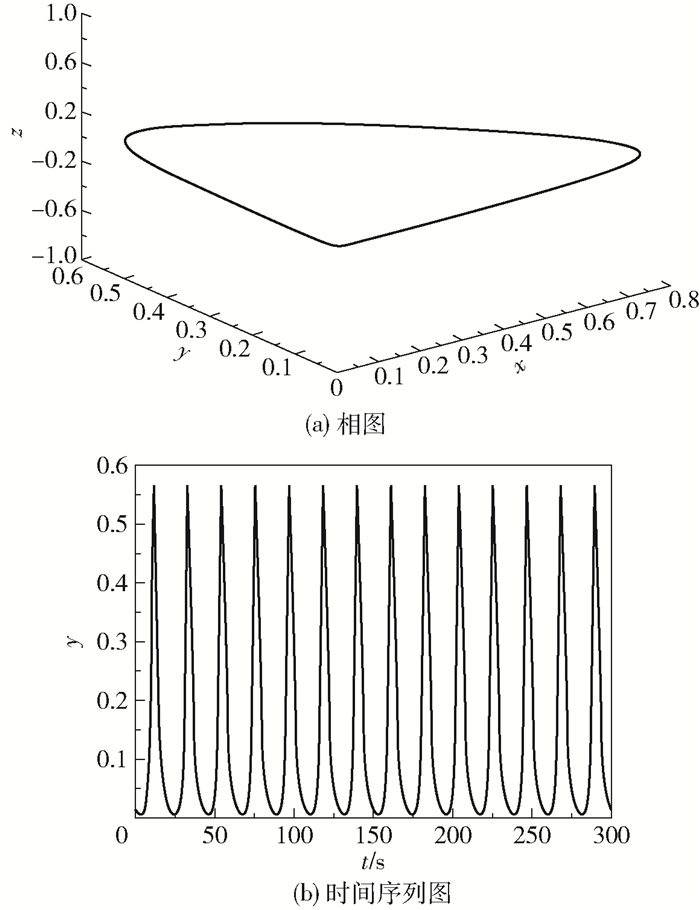
由图 3可以看出，当k₁=9.1时，中间捕食者的种群密度呈周期性振荡。

3 结论

本文研究了恐惧效应对三物种食物链模型种群动态的影响，分析了supercritical Hopf分支、subcritical Hopf分支、transcritical分支和saddle-node分支的存在性。研究结果表明当恐惧系数低于分支值1.623 42时，三物种的种群密度呈稳定的周期性振荡；当恐惧系数k₁保持在一定水平，即k₁∈(1.623 42, 4.818 44)∪(5.863 32, 7.756 05)时，三物种的种群密度呈单稳态；当k₁∈(4.818 44, 4.818 66)时，三物种的种群密度出现双稳定现象，系统有一个稳定的平衡点和一个稳定的周期轨共存；当k₁∈(4.818 66, 5.863 32)时，系统有两个稳定的平衡点共存；当k₁∈(7.756 05, 10)时，被捕食者的种群密度失稳，出现周期性振荡现象。因此恐惧效应是稳定三物种动态的重要因素。