近年来,卷积神经网络(CNN)成为图像处理、自然语言处理和语音识别等领域的研究热点[1-2]。CNN涉及大量的运算,但是传统的冯诺依曼结构不能充分发挥神经网络并行处理的优势,导致其难以在一些便携式硬件平台上应用。由于CNN的结构比较特殊,既包含大量的乘加法运算,也涉及大量的内存数据访问,因此如何设计出计算性能和功耗相平衡的架构是设计人员首要关注的问题。在现有的通用计算平台中,现场可编程门阵列(field programmable gate array, FPGA)是相对比较理想的硬件平台,它有丰富的寄存器资源、运算资源、存储资源、IO资源和高速接口,便于卷积运算单元和流水线结构的设计,也方便CNN网络中间数据的缓存以及与片外存储的交互。这些优势都很适合于CNN推理阶段的应用。因此,有许多研究人员提出了基于FPGA的深度学习算法的硬件快速运算方案[3]。
Chen等[4]设计的CNN专用芯片将中间缓存数据存储在内部,能获得较高的并行度,但其结构固定、灵活性较差,不具有通用性。Lu等[5-8]采用Winograd算法来实现卷积运算,能够有效减少数字信号处理单元(digital signal processor,DSP)资源的消耗,不过这种快速算法只适合于较小尺寸卷积核的CNN,不适用于通用的卷积网络。Zhang等[9]提出采用快速傅里叶变换(fast Fourier transform,FFT)的方法将卷积运算转换到频域,通过这种方式乘累加运算就变为了点乘运算,计算性能得到提高,但是只适用于较大尺寸的卷积核。Qiu等[10]提出了单指令多数据(single instruction multiple data,SIMD)的加速器模型,有效地解决了中间数据的存储问题,但是由于没有考虑传输时延,其实际性能与理论相差较大。Zhao等[11]提出一种二值化网络,以按位逻辑运算代替乘加运算,减少了数据存储所需的容量,有利于数字化电路的设计。Yonekawa等[12]在二值化网络的基础上作了改进,用异或非操作代替乘法操作,节省了硬件资源,并提高了计算性能,然而二值化网络存在一定程度的精度损失。
本文设计了一种卷积神经网络的并行计算架构,用来解决一些关键问题。首先,为解决卷积核通用性的问题,设计了一种并行流水卷积运算结构,可以根据需求修改乘法器和加法器资源,以适应不同尺寸的卷积核;此外,这种流水线设计减少了卷积运算中数据缓冲区的大小,从而提高了整体计算速度;其次,为了减少中间缓冲区,还设计了一种流水线存储结构,图像和权值数据可以从片外存储输入,这种设计减少了CNN加速IP和片外存储的交互时间,可以在最大程度上提升系统的吞吐率;最后,为了解决运算复杂的问题,采用浮点数定点化的设计方法,将图像和权值数据定点化为16 bit数,损失了少部分的精度,但大大降低了计算的复杂性,也能最大程度上地利用DSP资源。
1 卷积神经网络定点化处理通常在训练阶段CNN网络采用的是32位浮点精度的参数,一定程度上可以保证网络的收敛和准确度。但是在FPGA上浮点运算消耗的DSP资源远比定点运算多,加速器的实现也会更加复杂。卷积神经网络中含有大量冗余的数据,如果采用浮点数处理的方法则会占用大量的硬件存储资源,同时也会增加功耗,因此本文采用定点化计算,以一定准确度的下降为代价,不仅可以减少数据存储量,也降低了功耗。
Holt等[13]的研究发现,16 bit定点数既能维持一定的分类精度,也能有效地降低能耗。定点数可以由式(1)来表示
| $ x_{\text {fixed }}=\sum\limits_{i=0}^{b_{\rm{w}}-1} B_{i} 2^{-p} 2^{i} $ | (1) |
式中,bw为xfixed的位宽,p为定点数的阶码,Bi∈{0, 1}。定点数xfixed采用补码表示,最高位为符号位。
浮点数xfloat与定点数xfixed的相互转化如下
| $ x_{\rm {fixed }}=({\rm { int }})\left(x_{\rm {float }} 2^{b_{\rm{w}}}\right) $ | (2) |
| $ x_{\rm {float }}=({\rm { float }}) x_{\rm {fixed }} 2^{-b_{\rm{w}}} $ | (3) |
由于定点数位宽有限,可以将xfloat转换为xfixed,再转换为新浮点数yfloat,这样可以节省计算资源,但会出现精度的略微损失。
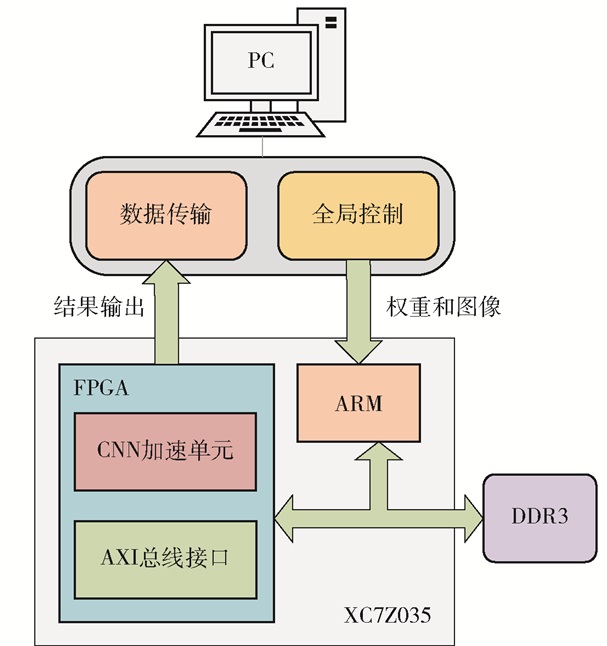
2 CNN加速器设计 2.1 CNN加速器的系统结构CNN加速器的整体系统架构如图 1所示,其主要由PC和FPGA两部分组成,其中PC端负责传输图像数据、权值参数和偏置参数以及控制加速器开始工作;FPGA端负责CNN运算的整个过程。两部分通过AXI总线进行数据传输。该设计结构能够实时处理图像,通过Advanced RISC Machines (ARM)端对FPGA端的控制可以处理较大尺寸的图像,降低对片内资源的消耗;将控制和运算分离,能够一定程度上优化整个软硬件系统的时序。
|
图 1 CNN加速器的架构 Fig.1 Architecture of the CNN accelerator |
CNN加速器的控制部分位于PC端。首先将图像、权值和偏置数据由32位浮点数转为16位定点数,然后初始化数据传输通道,等待初始化完成,即数据已准备好,然后控制FPGA部分开始进行运算。在整个运算过程中,PC端根据FPGA端的运算状态来传输权值和偏置数据,当FPGA端运算结束后,结果数据发送回PC端,整个过程中PC端与FPGA端的交互主要依托于AXI总线。
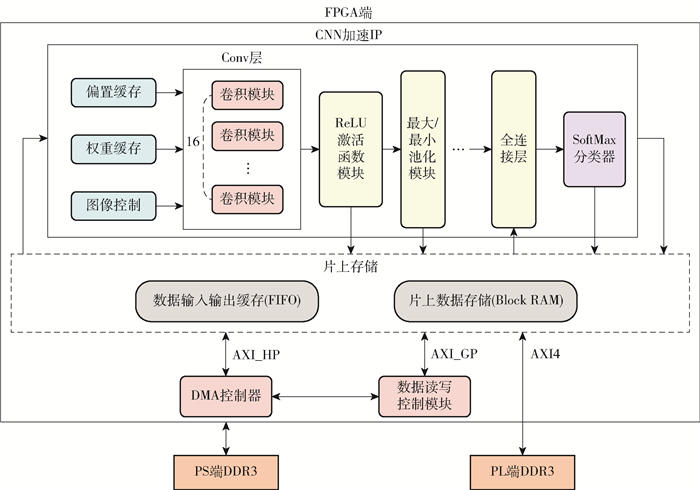
2.2 计算架构的设计CNN加速器的计算架构总体结构如图 2所示,其中卷积模块、最大/最小池化模块、ReLU激活函数模块、全连接层以及SoftMax模块负责图像的运算处理;图像控制、权值缓存模块、偏置缓存模块及片上存储负责数据的缓存和时序对齐;直接内存存取(direct memory access, DMA)模块主要从外部存储DDR3中将图像数据、权值数据和控制启动信号搬运到FPGA上的片上存储,其中权值数据会暂存至权值缓存模块中,图像数据经过图像控制模块后暂存下来;控制启动信号则通过数据读写控制模块发送给片上存储,供CNN加速器读取调用。在CNN运算单元结束后,结果从片上存储写回至PS端DDR3,整个过程中DMA均通过AXI4总线与外部DDR3通信。
|
图 2 加速器的计算架构 Fig.2 Computational architecture for the accelerator |
卷积运算是一系列的乘加运算,在硬件设计上需要考虑中间数据缓冲区的大小对整个系统计算性能的影响,而采用移位缓存的方法可以大大减少流水线结构下的延迟。为了适应不同尺寸的卷积核,需要设计通用的计算结构以便根据实际网络模型对卷积模块的运算资源进行修改,将图像控制和卷积运算结构进行分块设计,以提高泛用性。
卷积运算的计算公式为
| $ r_{j}=\sum\limits_{i=M_{j}} h_{i}^{n-1} w_{i j}^{n}+b_{j}^{n} $ | (4) |
| $ h_{j}^{n}=f\left(r_{j}^{n}\right) $ | (5) |
式中,hin-1为输入特征图,hjn为输出特征图,wijn为不同的卷积核,bjn为第n层的第j个输出特征图对应的偏置值,f(·)为卷积层的激活函数,一般取ReLU函数。
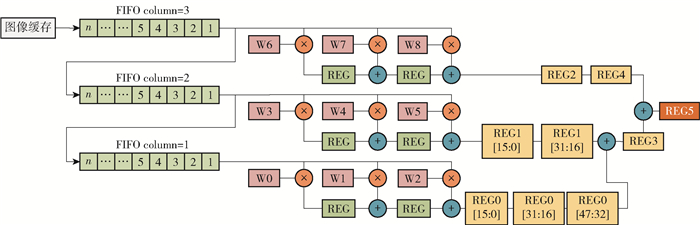
卷积运算结构由图像控制模块和卷积计算模块组成,如图 3所示。左边是图像控制模块,主要为了获得3行图像数据能匹配输入到卷积模块里,其主体由3个FIFO(first in first out)组成,经过一定时钟周期后可输出特征图的3行图像数据。右边是卷积计算模块,包含9个乘法器和8个加法器,这些均由内部的DSP实现。
|
图 3 卷积计算架构 Fig.3 Convolutional computing architecture |
常见的卷积计算结构采用加法树的结构,图像数据和权值数据同时输入,经过一系列的乘加计算得到最终结果。整个数据的缓冲区由图像缓冲区、权值缓冲区和卷积结果缓冲区组成,这些缓冲区在数据传输的时序问题上起着至关重要的作用。为了最大程度上减少数据缓冲的时间,将图像的数据输入和权值数据输入分开,优先配置权值,然后输入图像。由于图像数据是连续输入的,为了在每个周期都能输出一个正确的卷积结果,在3行乘累加结果后加入3个移位存储器。由于图像是按列输入的,移位存储器存储两行的卷积结果为下个周期的累加提供数据,这样的卷积流水线结构可以在每个周期都输出一个正确结果,大大减少了卷积结果缓冲区的大小,提升了运算速度。
2.4 池化模块的流水结构设计池化层的作用是剔除冗余的特征信息,防止网络的过拟合化,使CNN模型具有更高的容错能力。最大池化的操作是通过将特征图分解成多个2×2的像素矩阵,使得每个像素矩阵取最大值,然后将这些最大值按照特征图的原顺序排列,得到池化的结果,其计算公式如下。
| $ \boldsymbol{m}_{j}^{n}=g\left(\operatorname{down}_{\lambda, \tau}\left(\boldsymbol{h}_{j}^{n-1}\right)+\boldsymbol{\gamma}_{j}^{n}\right) $ | (6) |
式中,downλ, τ(hjn-1)表示池化函数,池化窗口一般取(2, 2);池化偏置项γjn一般取0矩阵;g(·)取函数g(x)=x。
池化层的输入数据是连续变化的,为了对尺寸大小为2的窗口进行下采样,需要先缓存两行的图像数据,在一定周期的比较后得到结果。为了提高系统的计算性能,将池化操作也设计成流水的结构。最大池化过程以2×2大小的采样窗口对特征图结果进行下采样,每次从下采样窗口中找到最大值然后输出结果。
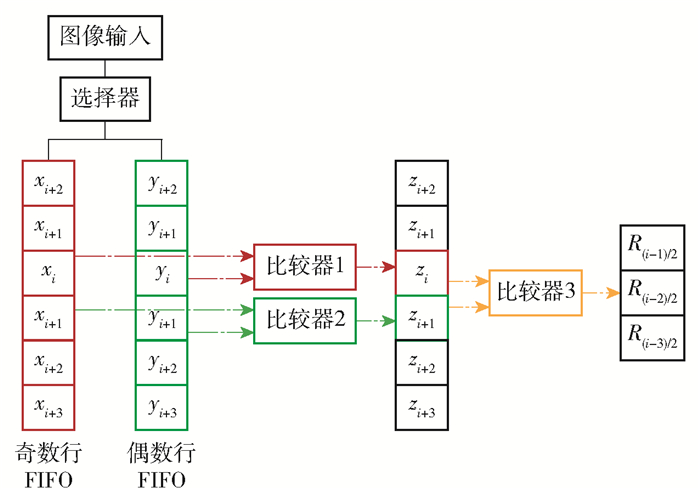
池化模块的设计结构如图 4所示,包含了1个数据选择器、2个计数器、2个FIFO模块和3个比较器。2个计数器分别负责计数输入奇数行和偶数行FIFO的数据数量,方便切换FIFO存储。比较器负责数据的比较,其主要的设计思路为通过分别比较特征图数据的奇数行和偶数行,得到两行中的较大值,然后比较这两个较大值得到最终结果。
|
图 4 最大池化模块 Fig.4 Maxpooling module |
如图 4所示,按照先奇后偶的顺序来缓存奇偶行的数据。当偶数行的FIFO非空时,两个FIFO同时输出数据到比较器。在第i个时钟周期先比较奇偶行数据xi和yi,取其中的较大值赋给zi;在第i+1个时钟周期再比较xi+1和yi+1,取其中的较大值赋给zi+1;之后再通过比较器比较zi和zi+1的值,取其中的较大值赋给最后的结果,这样就完成了下采样的过程。
2.5 存储结构的流水线设计CNN加速器的存储包括片上存储和片外存储。对于FPGA,片上存储主要由FIFO和Block RAM组成;片外存储主要是DDR。前者的容量小但速度快;后者容量大,但是传输速度慢,因此一般在数据量很小的情况下不使用片外存储。卷积计算的结果和中间结果的数据量较大,只能依靠片外存储DDR来缓存数据。除了权值buffer、偏置buffer和图像控制模块的FIFO,也有部分中间数据可以缓存在片上FIFO和Block RAM中。
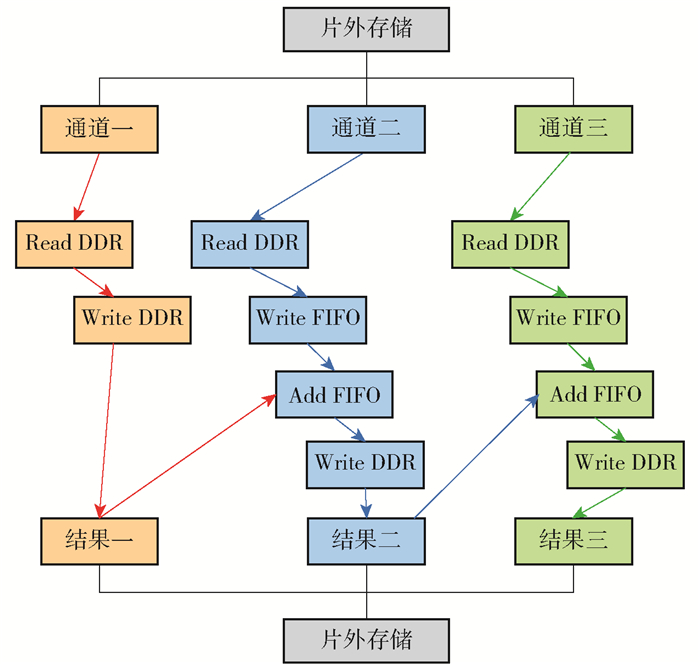
本文设计了基于流水线的存储结构,如图 5所示。主要是对卷积计算过程中不同通道的特征图进行累加,其中除了第一层卷积层的图像数据来自PS端的DDR外,后面的图像数据均来自于PL端的DDR,即不经过DMA的搬运过程。
|
图 5 流水线存储结构 Fig.5 Pipeline storage structure |
存储结构的流水线过程实现如下。
1) 从片外存储输出通道一的图像输入到图像控制器模块,这一部分是Read DDR的过程,同时将卷积运算和激活函数处理后的计算结果直接写入片外存储,即Write DDR过程。
2) 从片外存储输出通道二的数据到图像控制器模块,这是第一次Read DDR的过程,在图像控制器模块停止工作后,开始第二个Read DDR的过程,同时启动卷积运算。由于时序对齐问题,会将小部分卷积结果写入片上FIFO,然后进行通道一和通道二的结果累加,将累加结果写入片外DDR存储。
3) 重复步骤2),累加完所有通道的结果后,输入至池化模块进行处理,将最终结果写入片外DDR。
为了匹配片外DDR的数据带宽,也方便读写DDR,本文设计的卷积核并行度为16。在结束与片外DDR的交互后,最后结果写入片上Block RAM,以便于全连接层的读写调用。
2.6 SoftMax层的设计SoftMax函数的传统实现方法是使用查找表,即将输入的映射值提前存入ROM中,再将输入作为ROM的地址进行寻址,然后输出分类结果的概率值。但该方法有两个缺点:一是特征值映射时会采用四舍五入的操作,这样会降低分类精度;二是输入值位宽为16 bit,这样存入ROM的数据个数有65 536个,这些数据的存储会消耗大量片上资源。
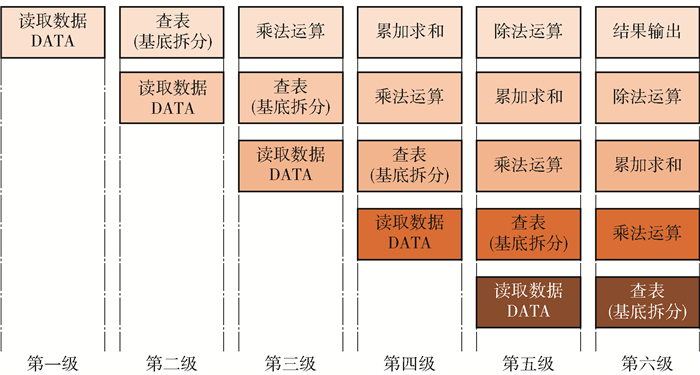
本文设计的SoftMax函数结构由5个ROM、5个乘法器、1个累加器、1个多路复用器和1个除法器组成。其中5个ROM分别存储4 bit数据映射的概率值;乘法器和累加器用来计算全连接层输出的映射值总和,再依次经过除法器的计算得到最后的结果。整个结构包括从读取数据到分类结果输出一共6个过程,采取六级流水线设计方法,如图 6所示。
|
图 6 六级流水线 Fig.6 Six levels of the pipeline |
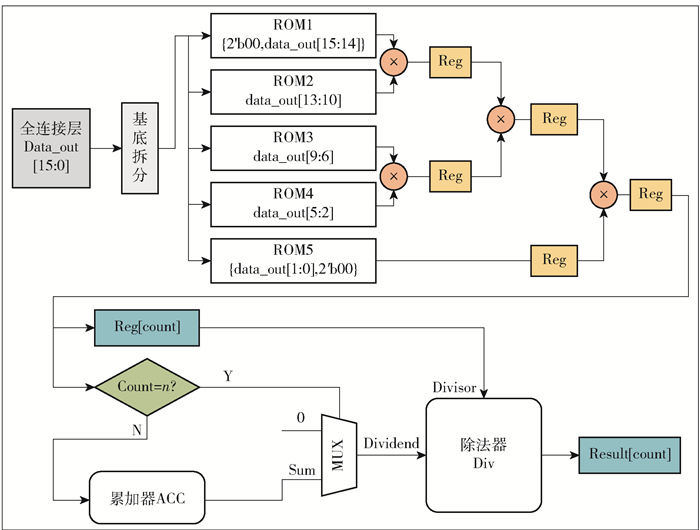
从SoftMax层输出的结果是最后归一化的分类结果,通过总线结构传输到ARM,最后的结果可以在PC端的可视化界面上输出。本文的设计结构如图 7所示,该软硬件系统能够实时地处理图像,随后输出可视化的结果,具有良好的交互性。
|
图 7 SoftMax函数结构图 Fig.7 Structure diagram of the SoftMax function |
本文实验使用Xilinx公司的电子自动化设计(electronic design automation,EDA)套件进行开发,主要分为软件和硬件两个部分。前者所用工具为Xilinx SDK 2017.4,后者为Vivado 2017.4。仿真工具采用Mentor公司的Modelisim。选用的开发板为米联客MZ7035FB,核心FPGA芯片为XC7Z035-FFG676-2I,主要基于Kintex-7架构,在PS和PL端各有1 GB大小的DDR3,除此之外,还支持外接子卡以实现功能的扩展。
实验采用的测试数据集是ImageNet数据集中1 000张224×224像素大小的图片,图像数据的定点化精度是16位,所用的网络为VGG16。在对比实验方面,CPU采用的是主频为3.5 GHz的i5-8350K处理器,GPU采用的是NVIDIA公司生产的GTX 2070,显卡带宽484 GB/s,显存为8 GB。
3.2 实验结果与分析 3.2.1 各模块资源占用情况本文设计的CNN加速器主要基于流水线架构,这样设计的优势是能够让整个系统在更高的时钟频率下工作,代价则是会耗费更多的寄存器资源。由于整个CNN运算过程均采用的是定点乘法和加法运算,而不是更复杂的浮点运算,因此能更好地管理整个系统的时序;除此之外,根据DDR3的带宽和DSP资源的限制,选择了卷积核并行度为16的特征图复用方法,经过综合布局布线后,消耗的总硬件资源如表 1所示,其中FF表示触发器,LUT表示查找表,BRAM表示片上块存储器。由表 1可知板卡资源的利用率较低,DSP资源的消耗主要来自卷积部分,存储结构中消耗的BRAM资源比较多,与输入数据集的特征图尺寸有关联。总的来说,在加速器结构所占板卡的资源中,DSP和BRAM所占的比例比较大,它们是决定加速器性能的重要指标,也是芯片架构选型的首要考虑条件;一般而言,FPGA芯片中DSP资源和RAM资源越多,越容易设计性能更强的CNN加速器。
| 下载CSV 表 1 各模块资源占用情况 Table 1 Resource occupancy of each module |
本文使用了1 000张来自ImageNet数据集的图片进行测试,软硬件的正确率比较差异不大,基于FPGA设计的加速器的识别分类正确率可达94.6%,与PC端实现的分类正确率(95.8%)仅相差1.2%。精度上的损失来源于量化的位宽大小,在一定程度上是可以接受的。
在不同FPGA平台的纵向对比上,计算性能是一个比较关键的指标,通常用单位GOP/s(每秒十亿次运算数)来描述,计算公式为[14]
| $ P=O p t / C l k_{-} n u m $ | (7) |
式中P代表计算性能,Clk_num是总的执行周期数,即完成运算所需要的时钟周期的个数,Opt是操作总数,其计算公式如下
| $ O p t=r o w \cdot {column} \cdot N \cdot M \cdot K \cdot K $ | (8) |
式中,row和column分别是输出特征图的行数和列数,N和M则是输入和输出特征图的数量,K是卷积核的尺寸大小。
表 2列出了不同FPGA平台对于CNN在计算性能和功耗方面的对比,可以发现相比文献[15]、[16]和文献[10],本文的设计在能效比(计算性能与功耗的比值,GOP/(s·W))方面有着明显的优势,但相比于Intel公司的集成度更高、架构更加先进的FPGA平台(文献[17]),还是有一些差距。然而本文工作较好地结合了低功耗和高计算性能的特点,具有一定的参考价值。
本文设计采用的是16 bit定点化,Holt等[13]指出浮点数定点化会伴随精度损失的情况出现,但这恰恰是为了降低系统计算的复杂度所必须承担的代价;而相比于8 bit定点化和更低精度的定点化,16 bit定点化的设计结构可以在CNN推理阶段获得更好的效果。
综上所述,本文设计的CNN加速器采用了流水线技术和并行技术,充分利用了FPGA的DSP和RAM资源,最大程度地发挥了FPGA设计的优势,相比架构更先进的加速平台(如Intel公司的Arria10),具有更好的功耗与成本优势。
| 下载CSV 表 2 加速器性能功耗对比 Table 2 Comparison of accelerator performance and power consumption |
本文提出了一种基于FPGA的卷积神经网络加速器,整体计算架构充分利用了流水线技术,在存储结构上也采用片上存储和片外存储的联合,可以支持较大图像的处理,在数据复用方面采用了特征图复用的方法,一次卷积运算的并行度为16,能够更大化地提升性能。利用ImageNet测试集来验证该加速器的性能,与Arria10相比具有较好的功耗与成本优势。采用16 bit定点化,一定程度上降低了系统的复杂度。
本文设计的CNN结构只针对同一尺寸大小的卷积核,并不适用于不同尺寸同时存在的卷积网络;同时除DSP和RAM资源外,开发板的触发器和LUT的资源利用率较低,因此未来的工作可以在这两个方面进行深入的研究,特别是提高CNN加速器的参数化,以适应越来越多变的卷积神经网络模型。
| [1] |
RAJARAMAN S, CANDEMIR S, KIM I, et al. Visualization and interpretation of convolutional neural network predictions in detecting pneumonia in pediatric chest radiographs[J]. Applied Sciences, 2018, 8(10): 1715. DOI:10.3390/app8101715 |
| [2] |
LI Y H, SONG B, KANG X, et al. Vehicle-type detection based on compressed sensing and deep learning in vehicular networks[J]. Sensors, 2018, 18(12): 4500. DOI:10.3390/s18124500 |
| [3] |
吴艳霞, 梁楷, 刘颖, 等. 深度学习FPGA加速器的进展与趋势[J]. 计算机学报, 2019, 42(11): 2461-2480. WU Y X, LIANG K, LIU Y, et al. The progress and trends of FPGA-based accelerator in deep learning[J]. Chinese Journal of Computers, 2019, 42(11): 2461-2480. (in Chinese) DOI:10.11897/SP.J.1016.2019.02461 |
| [4] |
CHEN Y J, LUO T, LIU S L, et al. Dadiannao: a machine-learning supercomputer[C]//201447th Annual IEEE/ACM International Symposium on Microarchitecture. Cambridge, UK: IEEE, 2014: 609-622.
|
| [5] |
YU J C, HU Y M, NING X F, et al. Instruction driven cross-layer CNN accelerator with Winograd transformation on FPGA[C]//2017 International Conference on Field Programmable Technology (ICFPT). Melbourne: IEEE, 2017: 227-230.
|
| [6] |
YU J C, GE G J, HU Y M, et al. Instruction driven cross-layer CNN accelerator for fast detection on FPGA[J]. ACM Transactions on Reconfigurable Technology and Systems, 2018, 11(3): 22. |
| [7] |
XIAO Q C, LIANG Y, LU L Q, et al. Exploring heterogeneous algorithms for accelerating deep convolutional neural networks on FPGAs[C]//201754th Design Automation Conference. Austin: IEEE, 2017: 1-6.
|
| [8] |
LU L Q, LIANG Y, XIAO Q C, et al. Evaluating fast algorithms for convolutional neural networks on FPGAs[C]//2017 IEEE 25th Annual International Symposium on Field-Programmable Custom Computing Machines. Napa: IEEE, 2017: 101-108.
|
| [9] |
ZHANG C, PRASANNA V. Frequency domain acceleration of convolutional neural networks on CPU-FPGA shared memory system[C]//Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. Monterey, 2017: 35-44.
|
| [10] |
QIU J T, WANG J, YAO S, et al. Going deeper with embedded FPGA platform for convolutional neural network[C]//Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. Monterey, 2016: 26-35.
|
| [11] |
ZHAO R, SONG W N, ZHANG W T, et al. Accelerating binarized convolutional neural networks with software-programmable FPGAs[C]//Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. Monterey, 2017: 15-24.
|
| [12] |
YONEKAWA H, NAKAHARA H. On-chip memory based binarized convolutional deep neural network applying batch normalization free technique on an FPGA[C]//2017 IEEE International Parallel and Distributed Processing Symposium Workshops. Orlando: IEEE, 2017: 98-105.
|
| [13] |
HOLT J L, BAKER T E. Back propagation simulations using limited precision calculations[C]//IJCNN-91-Seattle International Joint Conference on Neural Networks. Seattle: IEEE, 1991, 2: 121-126.
|
| [14] |
CHEN Y H, KRISHNA T, EMER J S, et al. Eyeriss: an energy-efficient reconfigurable accelerator for deep convolutional neural networks[J]. IEEE Journal of Solid-State Circuits, 2017, 52(1): 127-138. DOI:10.1109/JSSC.2016.2616357 |
| [15] |
LI H M, FAN X T, JIAO L, et al. A high performance FPGA-based accelerator for large-scale convolutional neural networks[C]//201626th International Conference on Field Programmable Logic and Applications. Lausanne: IEEE, 2016: 1-9.
|
| [16] |
GUO K Y, SUI L Z, QIU J T, et al. Angel-eye: a complete design flow for mapping CNN onto embedded FPGA[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2018, 37(1): 35-47. DOI:10.1109/TCAD.2017.2705069 |
| [17] |
ZHANG J L, LI J. Improving the performance of OpenCL-based FPGA accelerator for convolutional neural network[C]//Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. Monterey, 2017: 25-34.
|








