2. 中国北方发动机研究所(天津), 天津 300400;
3. 大庆石化公司炼油厂, 大庆 163700;
4. 西安现代控制技术研究所, 西安 710065
2. China North Engine Research Institute (Tianjin), Tianjin 300400;
3. Refinery of Daqing Petrochemical Company, Daqing 163700;
4. Xi'an Institute of Modern Control Technology, Xi'an 710065, China
发动机气门间隙的主要作用是为气门组件受热膨胀预留空间,防止出现因气门组件受热变形而导致的进排气效率降低甚至漏气现象,进而对机组性能造成负面影响。因此,合理设置气门间隙对发动机保持良好的动力性能具有重要意义[1]。目前,针对柴油机气门状态的监测大都是通过对缸盖振动信号的分析诊断实现[2-4],而缸盖振动信号属于典型的非平稳、非线性振动信号,信噪比低、处理难度大、故障信息难以捕捉,常用的频谱分析较难揭示该类信号的局部特征。
研究者们对非平稳、非线性信号的处理方法进行了多方面的研究,逐渐形成了相对完善的信号处理算法体系,如小波变换(WT)、局部均值分解(LMD)、希尔伯特-黄变换(HHT)、经验模态分解(EMD)等,广泛应用于设备故障诊断领域。结合上述数据处理方法,针对气门间隙异常故障,研究人员提出了多种故障诊断方法。牛家骅[5]应用集合经验模态分解(EEMD)相关系数法提取缸盖振动信号特征向量,结合支持向量机实现了包括气门间隙异常故障在内的多种故障识别;曹龙汉等[6]利用小波变换提取气门振动信号中的故障特征,建立了优化支持向量机的柴油机气门间隙故障诊断模型;王立勇等[7]通过Hilbert边际谱和边际能量谱进行故障特征提取,从而实现了气门间隙异常故障的诊断。然而HHT和EMD及其扩展方法存在端点效应、模态混叠等问题,小波变换方法需要选取基函数和分解层数,自适应性较差。
近年来,变分模态分解(VMD)方法成为研究热点[8],该方法可根据模态分解数量自适应调整各模态的最佳中心频率和有限带宽,克服了HHT和EMD等方法存在的模态混叠问题。目前,已有将VMD方法用于气门间隙异常故障诊断的研究。高清春等[9]将VMD-奇异值分解(SVD)方法和EMD-SVD方法分别应用于柴油机进排气门间隙故障的诊断,结果表明VMD-SVD方法的诊断效果更好;王双朋等[10]提出了结合VMD和排列熵的柴油机故障特征提取方法,解决了气门间隙异常故障诊断中存在的受噪声影响大、诊断准确率低的问题;蔡艳平等[11]提出一种基于阈值筛选的VMD分解和玛基诺-希尔时频分布(MHD)的时频分析方法,并结合支持向量机(SVM)实现了气门间隙故障的诊断识别;张海龙等[12]以不同类型的故障特征频率为基础,优化VMD分解中心频率的初始值,提高了计算效率和准确性;李华等[13]计算了VMD分解后各模态的峭度值,以最大峭度值对应的模态数量作为最优参数解;张树等[14]以散布熵为自适应函数,利用细菌觅食算法(BFA)对VMD参数进行参数组合寻优求解。但上述VMD及其改进方法仍存在不足,传统VMD方法的参数K和惩罚因子均是基于经验获取,当模态数量K值与惩罚因子设置不当时,会使分解效果不佳,甚至易引起模态混叠现象。而针对VMD方法的改进研究,如张海龙等[12]和李华等[13]虽然求得了模态数量K的最优解,但忽略了惩罚因子对分解效果的影响;张树等[14]虽然对模态数量和惩罚因子同时进行了优化,但BFA算法的初始参数仍需人为设定。
针对柴油机气门间隙异常故障诊断的研究现状及现有VMD数据处理方法的不足,本文结合柴油机缸盖振动信号噪声大、冲击多的特点,基于皮尔逊相关系数最小原则和功率谱熵最大原则分别对VMD方法中的模态数量和二次惩罚因子进行优化,并结合核密度估计(KDE)提出气门间隙异常故障识别方法,最后结合故障模拟实验台验证了本文方法的有效性。
1 改进的变分模态分解方法 1.1 基本原理VMD方法是一种完全非递归、自适应和准正交的信号分解方法,其本质是迭代地解决变分问题。根据预设的模态数量,VMD可以自适应地匹配每种模态的最佳中心频率和有限带宽,最终确定各个固有模态分量(IMF) uk(t)(k=1, 2, …, K)。原输入信号x(t)为各分量的和,分解步骤如下。
1) 每个模态的分解信号uk(t)由希尔伯特变换计算,从而得到单边谱
| $ \left[\delta(t)+\frac{\mathrm{j}}{{\rm{ \mathsf{ π} }} t}\right] u_{k}(t) $ | (1) |
式中,δ(t)为单位脉冲函数。
2) 通过指数项e-jωkt来调整各模态分量对应的中心频率
| $ \left[\left(\delta(t)+\frac{\mathrm{j}}{{\rm{ \mathsf{ π} }} t}\right) u_{k}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k} t} $ | (2) |
式中,ωk(k=1, 2, …, K)为各模态的中心频率。
3) 通过高斯平滑指数估计各分量的带宽,根据约束条件建立最优变分模态
| $ \begin{aligned} &\min \limits_{\left\{u_{k}\right\}, \left\{\omega_{k}\right\}}\left\{\sum\limits_{k=1}^{K}\left\|\partial_{t}\left[\left(\delta(t)+\frac{\mathrm{j}}{{\rm{ \mathsf{ π} }} t}\right) * u_{k}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k} t}\right\|_{2}^{2}\right\} \\ &\text { s. t. } \sum\limits_{k=1}^{K} u_{k}(t)=x(t) \end{aligned} $ | (3) |
式中,∂t为uk(t)对t的偏导,*为卷积运算符号。
4) 引入二次惩罚因子α和拉格朗日乘子λ(t)将原约束问题转换为非约束问题,其中,α可以保证信号的重构精度且不受高斯噪声的影响,λ(t)保证了约束条件的严格性。
| $ \begin{array}{l} \ \ \ \ \ \ L\left(\left\{u_{k}(t)\right\}, \left\{\omega_{k}\right\}, \lambda(t)\right)=\alpha \sum\limits_{k=1}^{K} \left\| \partial_{t}[(\delta(t)+\right. \\ \left.\left.\frac{\mathrm{j}}{{\rm{ \mathsf{ π} }} t}\right) * u_{k}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k} t}\left\|_{2}^{2}+\right\| x(t)-\sum\limits_{k=1}^{K} u_{k}(t) \left\|_{2}^{2}+\right. \\ \left\langle\lambda(t), x(t)-\sum\limits_{k=1}^{K} u_{k}(t)\right\rangle \end{array} $ | (4) |
5) 采用乘子交替方向算法(ADMM)交替迭代更新{uk(t)}、{ωk}和λ(t),找到增广拉格朗日表达式的鞍点。由此可以自适应地将信号分解为不同的模态信号。
1.2 优化策略在VMD方法中,模态数量K和二次惩罚因子α均是基于经验设定的,若要得到最佳的信号分解效果,需改变K值使相邻频段信号的差异最大化。因此,本文提出采用相邻频段分解信号的平均皮尔逊相关系数最小原则对K进行迭代确定,皮尔逊相关系数计算公式为
| $ \rho(X, Y)=\frac{\sum(X-\bar{X})(Y-\bar{Y})}{\sqrt{\sum(X-\bar{X})^{2} \sum(Y-\bar{Y})^{2}}} $ | (5) |
根据模态数量,本文所提出的相邻频段分解信号的平均皮尔逊相关系数计算如下。
| $ \bar{\rho}=\frac{1}{K-1} \sum\limits_{i=1}^{K-1} \rho\left(I_{i}, I_{i+1}\right) $ | (6) |
式中,I为信号分解后的各个IMF分量。
如果IMF分量中噪声占主要成分,则该分量信号的密集程度大,从而功率谱熵值较大[15]。为了得到合适的二次惩罚因子,本文通过计算高频噪声部分的功率谱熵,将最大功率谱熵对应的二次惩罚因子作为最优分解参数。
1.3 参数优化方法验证为了验证1.2节所提策略的有效性,构造了一个仿真信号来模拟柴油机缸盖振动信号。低频振动信号由两个正弦信号叠加而成,中高频冲击分量由两个不同的时域振荡衰减信号组成,具体结构如下。
| $ \begin{aligned} &y_{1}=\sin \left(2 {\rm{ \mathsf{ π} }} \omega_{1} t\right), 0 \leqslant t \leqslant 2 \\ &y_{2}=\sin \left(2 {\rm{ \mathsf{ π} }} \omega_{2} t\right), 0 \leqslant t \leqslant 2 \\ &y_{3}= \begin{cases}A_{1} \mathrm{e}^{-\frac{\zeta_{1}}{\sqrt{1-\zeta_1^2}} \omega_{3}\left(t-\tau_{1}\right)} \sin \left(2 {\rm{ \mathsf{ π} }} \omega_{3}\left(t-\tau_{1}\right)\right), & \tau_{1} \leqslant t \leqslant 2 \\ 0, & 0 \leqslant t<\tau_{1}\end{cases} \\ &y_{4}= \begin{cases}A_{2} \mathrm{e}^{-\frac{\zeta_{2}}{\sqrt{1-\zeta_{2}^2}} \omega_{4}\left(t-\tau_{2}\right)} \sin \left(2 {\rm{ \mathsf{ π} }} \omega_{4}\left(t-\tau_{2}\right)\right), &{\tau_{2} \leqslant t \leqslant 2} \\ {0, } &{0 \leqslant t<\tau_{2}}\end{cases} \\ &y=y_{1}+y_{2}+y_{3}+y_{4}+N \end{aligned} $ | (7) |
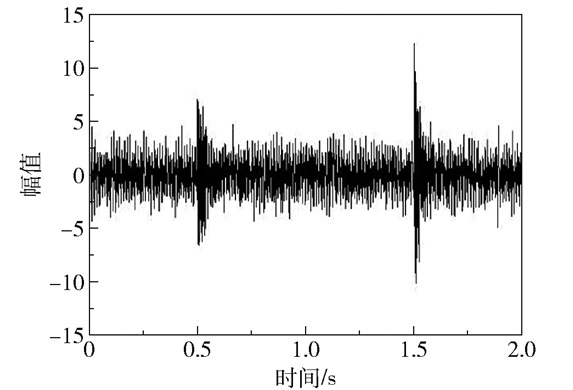
式中,各频率成分分别为ω1=80 Hz, ω2=160 Hz, ω3=400 Hz,ω4=600 Hz,幅值A1=8, A2=12,时间τ1=0.5 s,τ2=1.5 s,阻尼比ζ1=0.015, ζ2=0.01,N为噪声。采样频率为2 000 Hz。仿真信号如图 1所示。
|
图 1 仿真信号 Fig.1 Simulation signal |
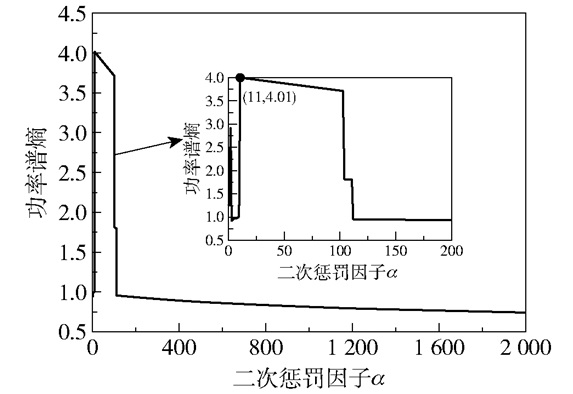
设初始模态数量K=5,二次惩罚因子α∈[1, 2 000],计算仿真信号高频分量的功率谱熵值,使用与最大功率谱熵值对应的α=11(图 2)作为最终的VMD分解参数。
|
图 2 二次惩罚因子与功率谱熵的关系曲线 Fig.2 The relationship between the quadratic penalty factor and the power spectrum entropy |
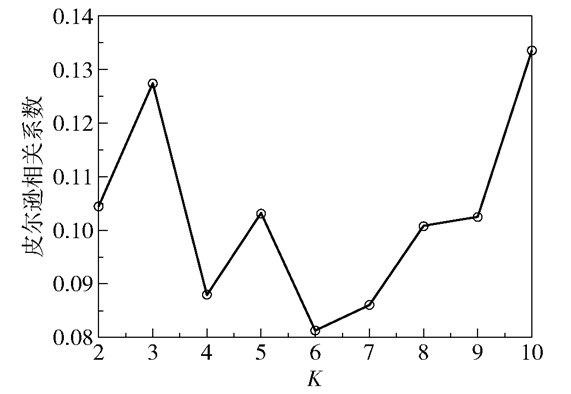
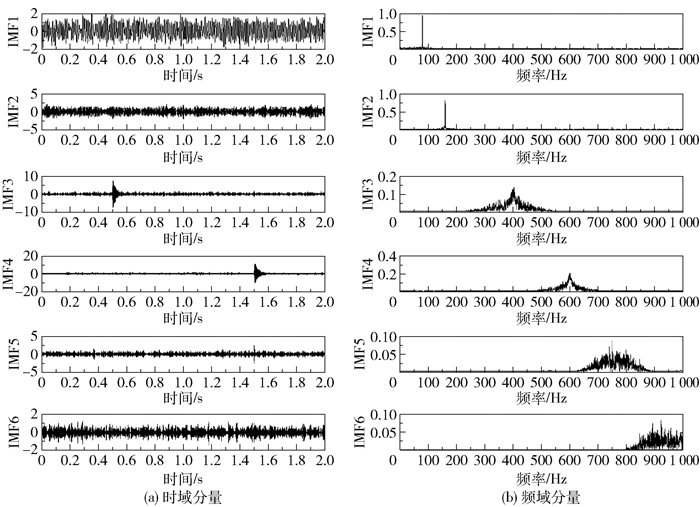
根据所选的α值,设置K值迭代区间K∈[2, 10]来求解最优K值。皮尔逊相关系数越小,则相邻频段信号的差异越大。如图 3所示,可以看出最佳的模态数量K=6。从图 4(a)、(b)可以看出,在本文提出的VMD参数优化方法下,各频段特征信号的分解效果均较好。
|
图 3 模态数量K与皮尔逊相关系数的关系曲线 Fig.3 The relationship between the number of modes and the Pearson correlation coefficient |
|
图 4 仿真信号VMD分解后的IMF分量 Fig.4 IMF components after VMD decomposition of the simulation signal |
为了验证所提方法的适用性,将得到的优化参数(α=11,K=6)与经验参数(α=2 000,K=6)[16-17]的VMD分解结果进行比较,采用余弦距离Dise(X, Y)来度量分解前后各信号分量的相似性,计算公式见式(8)。余弦距离越小,则相似度越高,分解效果越好。由表 1可知,采用优化参数的分解效果更好。
| $ {Dise}(X, Y)=1-\frac{\sum\limits_{i=1}^{n} X_{i} Y_{i}}{\sqrt{\sum\limits_{i=1}^{n} X_{i}^{2}} \sqrt{\sum\limits_{i=1}^{n} Y_{i}^{2}}} $ | (8) |
| 下载CSV 表 1 分解前后冲击信号分量的相似度 Table 1 Similarity of impact signal components before and after decomposition |
发动机气门间隙与气门启闭引起的冲击能量直接相关,当气门间隙过大时,在气门开启和关闭过程中产生的冲击振动能量会增加。因此,振动能量可以作为气门间隙故障的识别特征。
2.1 VMD参数选择实际缸盖振动信号由气门启闭冲击、发火冲击和噪声等多种冲击组成。对于实际的柴油机缸盖振动信号VMD分解参数的寻优设定问题,处理步骤如下。
1) 将采集到的柴油机缸盖信号按照周期长度(720°曲轴转角)截取。
2) 由于柴油机缸盖振动信号的冲击成分频段主要集中在中低频,噪声成分集中在中高频,因此先设置K=3,对二次惩罚因子进行VMD分解迭代,计算高频IMF分量的功率谱熵值,选取最大功率谱熵值所对应的二次惩罚因子。
3) 根据选取的二次惩罚因子,基于相邻频段分解信号的平均皮尔逊相关系数对模态数量K值进行迭代确定,选取平均皮尔逊相关系数最小的K值。
2.2 特征选择及排序故障诊断的准确性与所提取故障特征的有效性密切相关。核密度估计法是一种用于特征选择的有效方法,其原理为采用平滑的峰值函数来拟合观察到的数据点,进而模拟真实的概率分布曲线,计算公式为
| $ \hat{f}(x)=\frac{1}{n h} \sum\limits_{k=1}^{n} K\left(\frac{x-x_{k}}{h}\right) $ | (9) |
式中,参数h为带宽,K(x)为核函数,本文选择如下的高斯核函数
| $ K(x)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }}}} \exp \left(-\frac{x^{2}}{2}\right) $ | (10) |
用平均积分平方误差的大小来衡量h的优劣,其中E为求估计与实际分布函数误差的期望值。
| $ {MISE}(h)=E \int(\hat{f}(x)-f(x))^{2} \mathrm{~d} x $ | (11) |
由于正常与故障特征的重叠程度直接影响着故障识别精度,重叠程度越小,则特征的故障敏感性越强,因此采用核密度估计方法根据正常和故障模式下的特征数据计算重叠面积占比,并根据重叠面积占比进行升序排序,选取前70%的特征作为故障敏感特征。
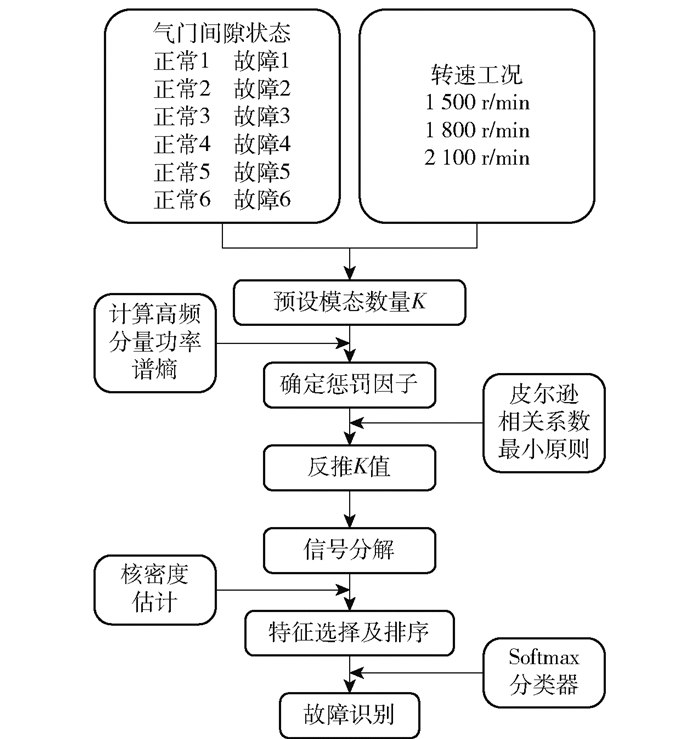
2.3 方法流程对柴油机缸盖振动信号进行整周期截取,再利用飞轮齿盘脉冲信号对缸盖振动信号进行角域编号。通过改进的VMD分解振动信号,对比分析正常和故障情况下的敏感频带,对分解后的模态分量进行筛选,提取气门开启和关闭下的角域信号,并针对其提取特征值形成特征集。基于正常与故障情况下特征数据概率密度分布的重合区域面积占比进行特征的排序与选择。最后使用Softmax单层神经网络对正常和故障数据进行分类。方法流程如图 5所示。
|
图 5 气门间隙故障识别方法流程图 Fig.5 Flow chart for the valve clearance fault identification method |
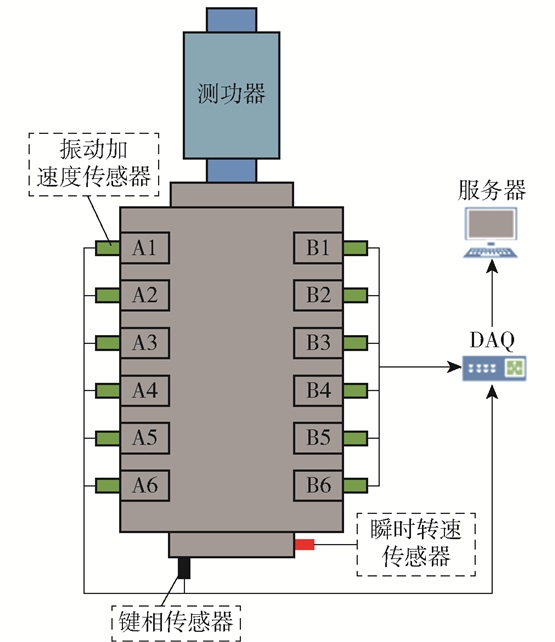
为了验证所提方法的有效性,在一台TBD234V12柴油机上进行验证实验。以柴油机缸盖上表面作为振动测点,通过键相传感器测量转速及确定各周期的起始位置,如图 6所示。
|
图 6 实验台布局 Fig.6 Layout of the test bench |
传感器信号由数据采集系统采集,其中数据采集卡具有16位模数转换器分辨率,每个通道的最大采样率为102.4 kHz,最多有32个模拟输入。信号由一台16 GB随机存取存储器存储,并由3.10 Hz Intel i7处理器进行处理。
气门故障仿真实验在1 500、1 800、2 100 r/min这3种工况下进行,负载保持在1 000 N·m不变。振动加速度传感器通过螺丝连接安装在气缸盖上,其采样频率为51 200 Hz,安装位置如图 7所示。

|
图 7 缸体振动传感器安装示意图 Fig.7 Diagram of the cylinder vibration sensor installation |
实验分为正常气门间隙实验和异常气门间隙下的实验两组。在异常气门间隙实验中共设置了6种气门间隙值,正常及异常气门间隙下的参数设置如表 2、3所示。
| 下载CSV 表 2 正常气门间隙参数设置 Table 2 Normal valve clearance parameter settings |
| 下载CSV 表 3 异常气门间隙参数设置 Table 3 Abnormal valve clearance parameter settings |
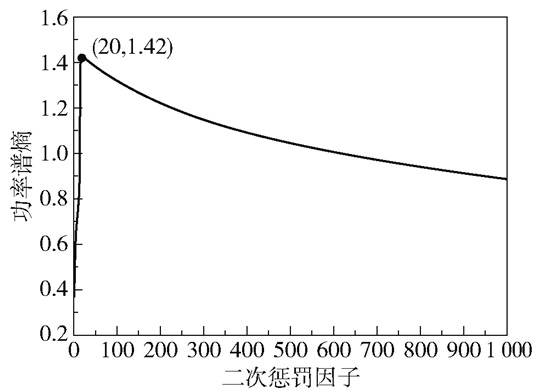
采用本文所提方法处理柴油机缸盖振动信号,信号长度为1个柴油机工作周期。如图 8所示,设置迭代区间为α∈[1, 1 000],得到最佳二次惩罚因子α=20。
|
图 8 二次惩罚因子与功率谱熵的关系曲线 Fig.8 The relationship between the quadratic penalty factor and the power spectrum entropy |
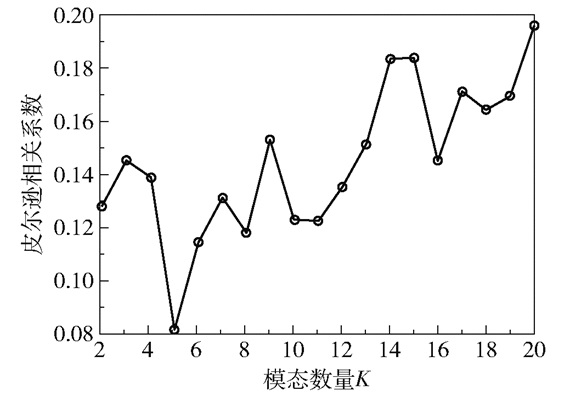
根据得到的二次惩罚因子(α=20)进行模态数量K的分解迭代。观察多组数据,将频谱大致分为10个以内的显著区域,因此设置迭代区间为K∈[2, 10],得到最佳模态数量K=5,如图 9所示。
|
图 9 模态数量K与皮尔逊相关系数的关系曲线 Fig.9 The relationship between the number of modes and the Pearson correlation coefficient |
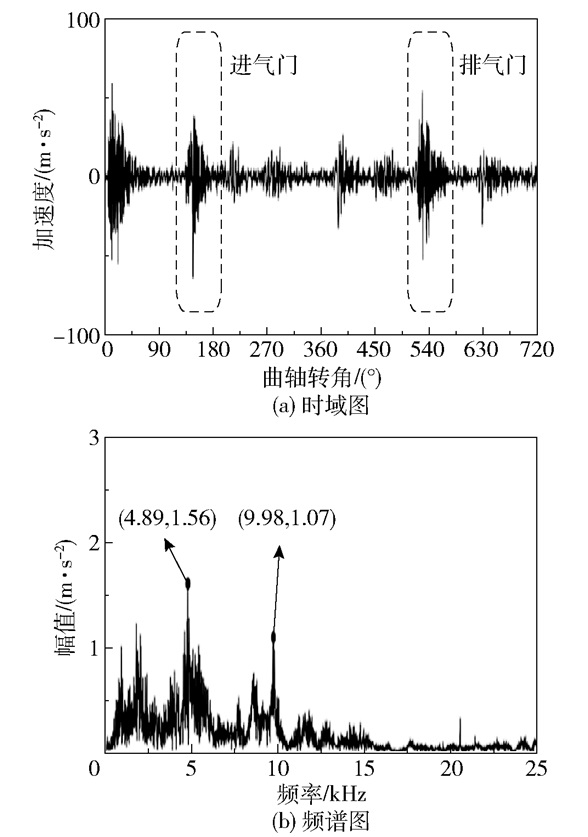
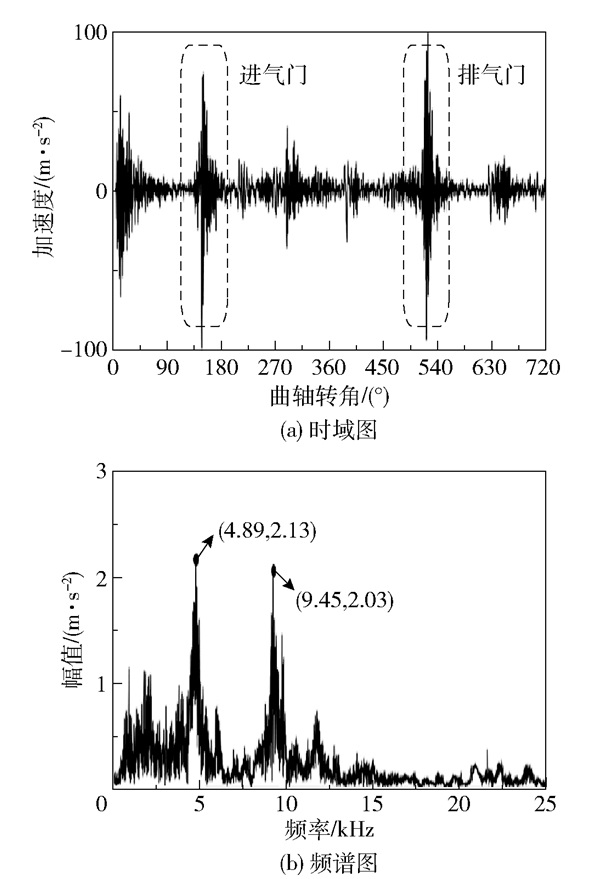
以B5缸的振动信号为例(排气门间隙增大0.3 mm),其发火角域在150°附近,排气门关闭和开启角度分别在540°和280°附近。如图 10、11所示,故障状态下排气门的开启冲击和关闭冲击都有一定程度的振动峰值增大现象,频域上对应以5 kHz和10 kHz为中心的频带振幅有明显的增大趋势,对应的频带幅值分别增大约36%和89%。
|
图 10 正常信号的时域图和频谱图 Fig.10 Time domain and frequency spectrum of the normal signal |
|
图 11 故障信号的时域图和频谱图 Fig.11 Time domain and freauency spectrum for the fault signal |
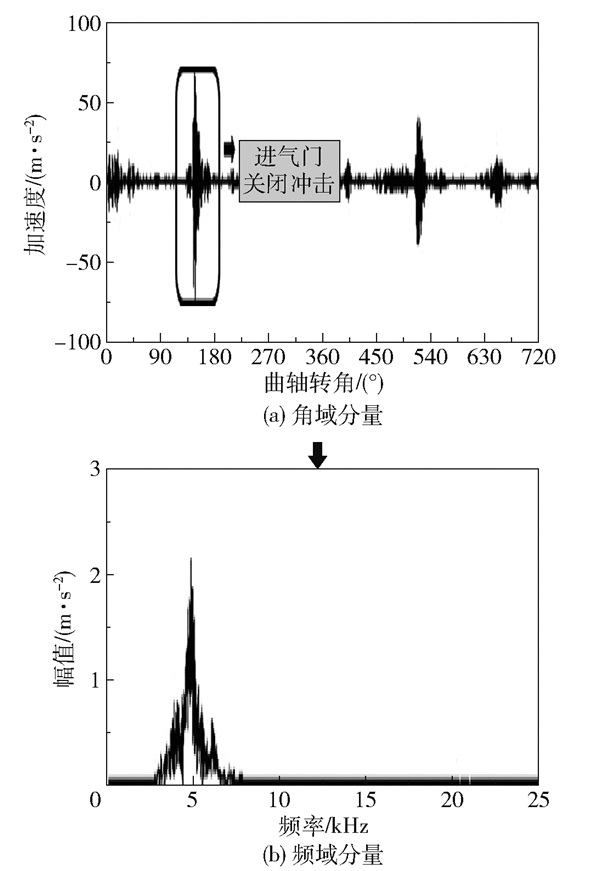
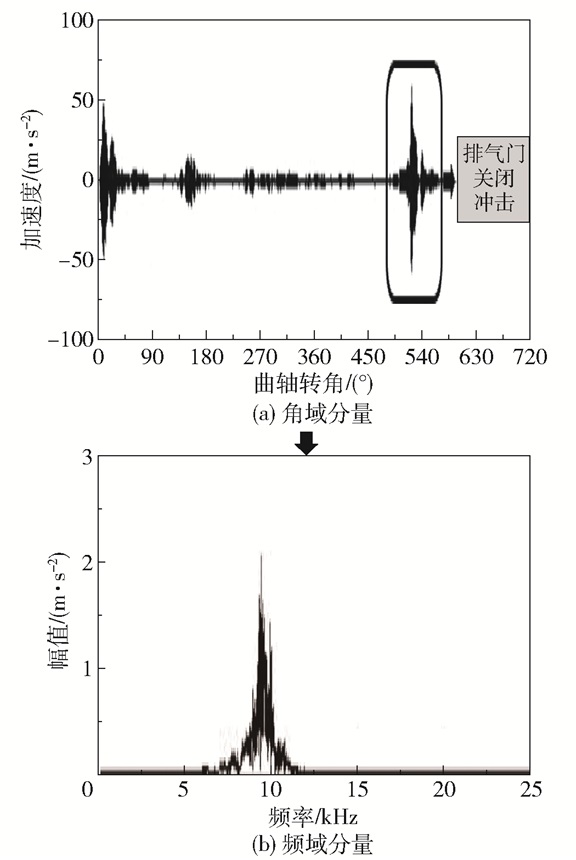
通过优化的VMD方法对故障信号进行自适应分解,得到各频段的分解信号及其频谱。如图 12、13所示,B5缸振动信号中5 kHz附近的频带信号对应进气门关闭冲击(IMF2),10 kHz附近的频带信号对应排气门关闭冲击(IMF3)。改进的VMD方法很好地将5 kHz(IMF2)左右和10 kHz(IMF3)左右的故障频段信号自适应地分解出来。
|
图 12 故障信号的IMF2分量 Fig.12 IMF2 component of the fault signal |
|
图 13 故障信号的IMF3分量 Fig.13 IMF3 component of the fault signal |
在柴油机振动监测信号中,大多有用的振动信息往往表现为冲击信号成分。根据表现特点,在出现故障时,振动信号中特定角域上会出现新的冲击成分。针对气门间隙异常故障信号的特点,自适应提取VMD分解后5 kHz频段和10 kHz频段信号的特征值,由于原始信号中包含最多的故障信息,因此提取原始信号的特征值为峰值(peak)、峰值因子(peak factor)、有效值(RMS)、方差(Var)、均方差(MSE)、峭度(Kurtosis)、重心频率(FC)和均方频率(MSF)。
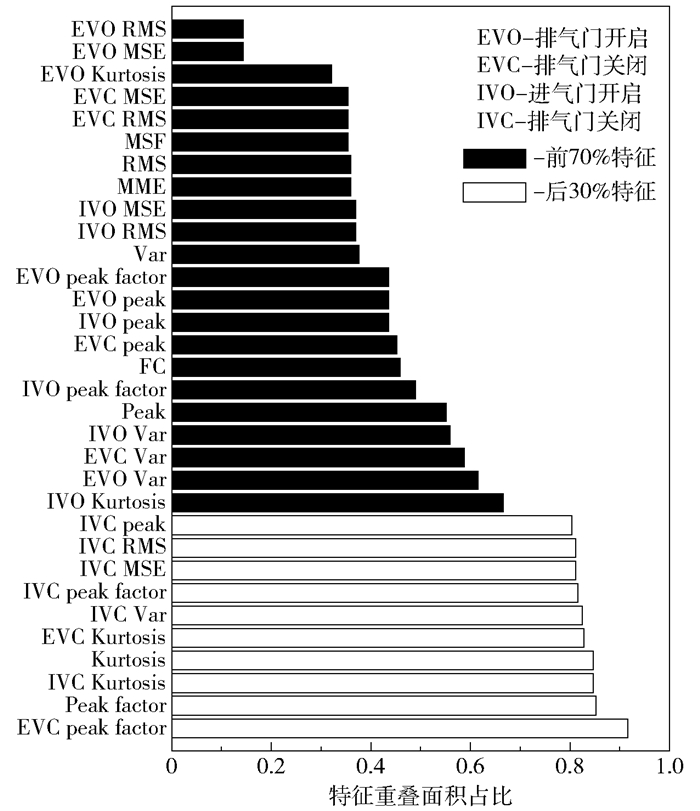
利用B5缸的正常和故障两组数据,研究各特征与故障间的关联程度。采用本文所提方法对正常与故障特征的概率分布重叠面积的占比大小进行升序排序,选取前70%特征作为故障识别特征集。正常与故障特征的概率分布重叠面积占比和排序如图 14所示。
|
图 14 特征排序 Fig.14 Feature ordering |
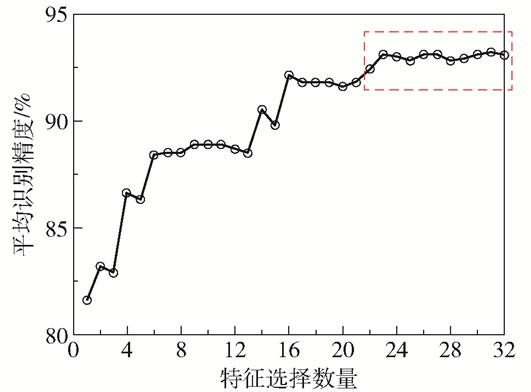
根据图 14中的特征排序,选择不同的特征数量,利用本文所提故障识别方法进行验证,当选取前22个特征后,识别精度趋于稳定,如图 15所示。
|
图 15 识别精度曲线 Fig.15 Identification accuracy curve |
本文实验共设置了3种不同的转速工况(1 500、1 800和2 100 r/min),对于每种工况下的正常或各故障情况,均有480个训练样本和480个测试样本。
对于实际的柴油机运行状态,应首先识别柴油机的正常或异常状态,再判断故障类型。将测试集中2 880组特征数据输入Softmax分类器进行分类处理,其中1 440组为正常特征数据,其余1 440组为异常特征数据。分类结果如表 4所示,可以看出与传统VMD方法相比,改进的VMD方法具有更高的识别率。
| 下载CSV 表 4 状态识别结果 Table 4 State recognition results |
在系统判定气门状态异常的前提下,有必要进一步确定气门故障类型。对于2 880组异常气门数据,6种故障状态数据各为480组,其中每种故障数据分为训练集(336组)和测试集(144组),进行训练和故障分类测试,识别结果如表 5所示。
| 下载CSV 表 5 故障类型识别结果 Table 5 Fault type identification results |
根据表 5的测试结果可知,基于改进的VMD方法对6种故障的平均识别率为86.9%,而基于传统VMD方法的平均识别率仅为78.5%。在故障1中,改进的VMD方法的识别率低于传统VMD方法,原因在于改进的VMD是将模态数量和二次惩罚因子基于整体数据进行全局适应性优化,这样虽牺牲了故障1的识别精度,但保证了所有故障类型的识别精度都处于较高水平。另外,气门间隙较大的情况(故障2和故障4)更容易被识别,且进气门和排气门间隙同时异常时(故障5和故障6)更容易被识别,其识别率达到90%以上。
4 结论针对典型的柴油机气门间隙异常故障,研究了基于改进变分模态分解和核密度估计的柴油机气门间隙异常故障识别方法。首先基于相邻频段分解信号的平均皮尔逊相关系数最小原则和噪声成分功率谱熵最大原则,提出了一种新的VMD参数优化策略;其次提出了一种基于核密度估计的故障敏感特征排序及选择方法,可减小数据量并提高计算效率。本文所提的气门间隙异常故障识别方法不仅可以识别不同转速工况下的气门间隙是否异常,还可以准确地识别出气门间隙异常的类型。
采用柴油机不同工况下气门间隙异常数据对所提方法进行验证,结果表明该故障识别方法能够有效地识别出气门间隙的特定故障类型,其平均识别率达到86%以上。下一步可将此气门间隙检测方法应用在不同的发动机上进行研究,并最终将其构建为实时监控系统。
| [1] |
张剑, 刘昌文, 毕凤荣, 等. 柴油机气门故障信号的双谱图形分形维数分析[J]. 内燃机学报, 2016, 34(3): 274-280. ZHANG J, LIU C W, BI F R, et al. Analysis of bispectrum image fractal dimension for valve train fault signals in diesel engine[J]. Transactions of CSICE, 2016, 34(3): 274-280. (in Chinese) |
| [2] |
畅志明. 基于EEMD分解和多信息熵的气门间隙故障信号研究[D]. 太原: 中北大学, 2018. CHANG Z M. Extraction of valve clearance fault signal from a high power density diesel engine[D]. Taiyuan: North University of China, 2018. (in Chinese) |
| [3] |
王祝平, 王为, 李小昱, 等. 基于EMD与神经网络的内燃机气门间隙故障诊断[J]. 农业机械学报, 2007, 38(12): 133-136, 147. WANG Z P, WANG W, LI X Y, et al. Fault diagnosis of engine valve based on EMD and artificial neural network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(12): 133-136, 147. (in Chinese) DOI:10.3969/j.issn.1000-1298.2007.12.033 |
| [4] |
李阳龙, 王立勇, 栾忠权, 等. 基于振动时频域特征的气门间隙故障诊断[J]. 石油机械, 2014, 12(9): 48-51. LI Y L, WANG L Y, LUAN Z Q, et al. Fault diagnosis of valve clearance based on time-domain characteristics of vibration[J]. China Petroleum Machinery, 2014, 12(9): 48-51. (in Chinese) DOI:10.3969/j.issn.1001-4578.2014.09.012 |
| [5] |
牛家骅. 基于EEMD和SVM联合诊断的发动机故障分析[D]. 呼和浩特: 内蒙古工业大学, 2015. NIU J H. Analysis of engine fault based on EEMD and SVM joint diagnosis[D]. Huhhot: Inner Mongolia University of Technology, 2015. (in Chinese) |
| [6] |
曹龙汉, 武明亮, 何俊强, 等. 基于DE SVM的柴油机气门故障诊断方法及应用[J]. 仪器仪表学报, 2011, 32(2): 323-328. CAO L H, WU M L, HE J Q, et al. Diesel engine valve fault diagnosis method based on DE SVM and its application[J]. Chinese Journal of Scientific Instrument, 2011, 32(2): 323-328. (in Chinese) |
| [7] |
王立勇, 贾然, 陈涛, 等. 基于Hilbert-Huang变换的往复发动机气门间隙故障诊断方法研究[J]. 制造业自动化, 2016, 38(5): 111-114, 123. WANG L Y, JIA R, CHEN T, et al. The research of the fault diagnosis about reciprocating engine valve clearance based on Hilbert-Huang transform[J]. Manufacturing Automation, 2016, 38(5): 111-114, 123. (in Chinese) DOI:10.3969/j.issn.1009-0134.2016.05.030 |
| [8] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [9] |
高清春, 胡甫才. 基于变分模态和奇异值分解的柴油机气门间隙故障诊断方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(4): 746-751. GAO Q C, HU F C. Research on the fault diagnosis method of diesel engine valve clearance based on variational mode and singular value decomposition[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2019, 43(4): 746-751. (in Chinese) DOI:10.3963/j.issn.2095-3844.2019.04.033 |
| [10] |
王双朋, 赵慧敏, 梅检民, 等. 基于VMD的发动机气门故障特征提取[J]. 军事交通学院学报, 2020, 22(11): 46-52. WANG S P, ZHAO H M, MEI J M, et al. Engine valve fault feature extraction based on VMD[J]. Journal of Military Transportation University, 2020, 22(11): 46-52. (in Chinese) |
| [11] |
蔡艳平, 范宇, 陈万, 等. 改进时频分析和特征融合在内燃机故障诊断中的应用[J]. 中国机械工程, 2020, 31(16): 1901-1911. CAI Y P, FAN Y, CHEN W, et al. Applications of improved time-frequency analysis and feature fusion in fault diagnosis of IC engines[J]. China Mechanical Engineering, 2020, 31(16): 1901-1911. (in Chinese) |
| [12] |
张海龙, 宋业栋, 李鑫, 等. 基于优化VMD与欧氏距离的柴油机故障识别[J]. 振动、测试与诊断, 2020, 40(5): 911-915, 1022-1023. ZHANG H L, SONG Y D, LI X, et al. Engine faults detection based on optimized VMD and Euclidean distance[J]. Journal of Vibration, Measurement & Diagnosis, 2020, 40(5): 911-915, 1022-1023. (in Chinese) |
| [13] |
李华, 伍星, 刘韬, 等. 变分模态分解和改进的自适应共振技术在轴承故障特征提取中的应用[J]. 振动工程学报, 2018, 31(4): 718-726. LI H, WU X, LIU T, et al. Application of variational mode decomposition and improved adaptive resonance technique in bearing fault feature extraction[J]. Journal of Vibration Engineering, 2018, 31(4): 718-726. (in Chinese) |
| [14] |
张树, 刘德平. BFA优化VMD参数的轴承故障诊断[J]. 组合机床与自动化加工技术, 2020(5): 45-47, 51. ZHANG S, LIU D P. Bearing fault diagnosis based on BFA optimized VMD parameters[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020(5): 45-47, 51. (in Chinese) |
| [15] |
江志农, 魏东海, 张进杰, 等. 基于VMD和SVD的柴油机气门间隙异常特征提取研究[J]. 振动与冲击, 2020, 39(16): 23-30. JIANG Z N, WEI D H, ZHANG J J, et al. A study on valve clearance anomaly feature extraction of diesel engines based on VMD and SVD[J]. Journal of Vibration and Shock, 2020, 39(16): 23-30. (in Chinese) |
| [16] |
马增强, 柳晓云, 张俊甲, 等. VMD和ICA联合降噪方法在轴承故障诊断中的应用[J]. 振动与冲击, 2017, 36(13): 201-207. MA Z Q, LIU X Y, ZHANG J J, et al. Application of VMD-ICA combined method in fault diagnosis of rolling bearings[J]. Journal of Vibration and Shock, 2017, 36(13): 201-207. (in Chinese) |
| [17] |
KUMAR A, GANDHI C P, ZHOU Y Q, et al. Variational mode decomposition based symmetric single valued neutrosophic cross entropy measure for the identification of bearing defects in a centrifugal pump[J]. Applied Acoustics, 2020, 165: 107294. |








