2. 北京化工大学 教育部高分子材料加工装备工程研究中心, 北京 100029
2. Polymer Processing Equipment Engineering Research Center, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
冷却单螺杆通常用在串联挤出发泡生产线中,主要用于冷却聚合物熔体,以优化熔体的强度和应变硬化性能,从而得到高质量的发泡产品。随着串联挤出生产线生产优质发泡材料的趋势不断扩大,人们对于冷却效果更好的冷却螺杆的需求也与日俱增。因此,如何提高螺杆的冷却效果已经成为聚合物发泡过程中十分重要的环节。
冷却单螺杆挤出机的螺杆几何形状对于生产线的经济运行和泡沫产品的质量至关重要,可以通过改变螺杆几何形状和熔体流动形式来提高螺杆的冷却效果。传统冷却单螺杆通常采用多头开槽螺杆,相对于传统螺杆,人们开发了不同类型的高性能冷却螺杆。例如,Rauwendaal[1]发明了一种高性能热传递(HHT)螺杆,该螺杆通过多头螺棱的相互交错改变熔体的流动形式,从而提高二阶挤出机的冷却能力。Fogarty[2]开发的Turbo螺杆在大导程多头螺杆的螺棱上开设矩形窗口,使各螺槽连通并形成循环通道,提高了螺杆的冷却能力。Barr[3]开发了能量传递提升的螺杆,该螺杆通过不同高度的螺棱来改变熔体流动形式,降低了熔体的温度梯度,使得熔体的温度分布更加均匀。但是,冷却单螺杆一直是由挤出机制造商根据与泡沫制造商签订的保密协议而开发的,关于冷却单螺杆的设计信息很少。
数值计算方法已经广泛应用在模拟聚合物加工的各种设备中,对于冷却单螺杆内聚合物熔体的传热研究也多集中在数值模拟方面。例如,Han[4]通过数值模拟方法分析了广泛用于热塑性泡沫挤出的冷却单螺杆挤出机的性能,结果表明,黏性剪切生热是导致熔体温度升高的主要原因之一。Wang等[5]通过伽辽金数值模拟的方法研究了多头螺纹螺杆构型对聚合物熔体均质化和冷却效果的影响,发现熔体在多头螺杆中的剪切应力较高,同时较长的停留时间促进了混合和冷却。范涛等[6]运用polyflow软件研究了螺棱断面形状对单螺杆挤出机熔融输送段熔体温度分布的影响,结果显示梯形断面的螺杆相对于矩形、锯齿形断面的螺杆更有利于热量传递。陈佳兴等[7]运用polyflow软件研究了橡胶在单螺杆挤出机内的三维非等温流动问题,结果表明,由于胶料自身的剪切变稀特性和温度依赖性,压力与温度上升的趋势会随着转速的升高而减缓。以上这些数值模拟方法需要建立模型、划分网格和迭代求解,整个过程较为复杂。本文基于聚合物熔体在冷却单螺杆内传热提出一种简便的数学模型,通过引入平均温度来表征螺槽深度方向的温度变化,利用平均剪切速率简化黏性生热的计算,将冷却单螺杆内聚合物熔体的三维流动与传热问题转化成二维平面问题,建立了冷却单螺杆内聚合物熔体传热模型;基于该模型分析了螺杆结构参数及工艺参数对聚合物熔体传热过程的影响;通过计算流体动力学(CFD)数值模拟的方法验证了传热模型的准确性。
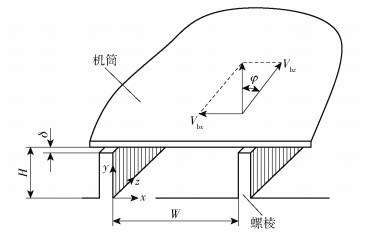
1 聚合物熔体传热模型 1.1 几何模型如图 1所示,将螺槽和机筒展开在两个平面上,沿螺槽方向为z方向,垂直于螺槽方向为y方向,建立相应的直角坐标系。螺槽深度为H,螺槽宽度为W,螺纹升角为φ,沿螺槽方向的速度分量为Vbz,垂直于螺槽的速度分量为Vbx。
|
图 1 螺槽和机筒展开后的几何结构 Fig.1 The geometry of the screw channel and barrel after unfolding |
基于聚合物熔体在冷却单螺杆内的流动,做出以下基本假设:
1) 熔体为不可压缩流体,流动定常;
2) 熔体不受重力作用,不考虑熔体的体积力与惯性力的作用;
3) 不考虑间隙漏流,忽略螺棱与机筒内表面的间隙的影响;
4) 压力只是x、z方向的函数;
5) 熔体在壁面不会产生滑移;
6) 在x和z方向上的热传导可忽略不计,取y方向上的平均温度表征该方向的温度变化;
7) 螺槽的曲率忽略不计。
基于以上基本假设,聚合物熔体在冷却单螺杆内满足如下能量方程。
| $ \rho c_{p} v_{z} \frac{\partial T}{\partial z}=k \frac{\partial^{2} T}{\partial y^{2}}+\dot{q} $ | (1) |
式中,ρ为聚合物熔体的密度,kg/m3;cp为聚合物熔体的比热容,J/(kg·K);vz为沿螺槽方向的速度分布,m/s;k为聚合物熔体的导热系数,W/(m·K);T为熔体温度,℃;
其中,
| $ \dot{q}={\eta} \dot{\gamma}^{2} $ |
式中,η为聚合物熔体的黏度,
| $ \dot{\gamma}=\frac{V_{\mathrm{b} z}}{H}=\frac{{\rm{ \mathit{ π} }} D N \cos \varphi}{60 H} $ |
式中,D为螺杆直径,m;N为螺杆转速,r/min。
以幂律流体作为聚合物熔体的本构方程,则冷却单螺杆内聚合物熔体黏性生热的计算公式如下所示。
| $ \dot{q}=K \dot{\gamma}^{n+1}=K\left(\frac{{\rm{ \mathit{ π} }} D N \cos \varphi}{60 H}\right)^{n+1} $ |
式中,K为聚合物熔体的稠度,
结合能量方程(1)给出各位置的边界条件如下。
在螺槽底部y=0位置的运动边界条件为
| $ \left\{\begin{array}{l} \left.v_{x}\right|_{y=0}=0 \\ \left.v_{z}\right|_{y=0}=0 \end{array}\right. $ |
在机筒表面y=H位置的运动边界条件为
| $ \left\{\begin{array}{l} \left.v_{x}\right|_{y=H}=V_{\mathrm{b} x}={\rm{ \mathit{ π} }} D N \sin \varphi \\ \left.v_{z}\right|_{y=H}=V_{\mathrm{b} z}={\rm{ \mathit{ π} }} D N \cos \varphi \end{array}\right. $ |
在螺槽底部y=0和在机筒表面y=H位置的热边界条件为
| $ \left\{\begin{array}{l} \left.k \frac{\partial T}{\partial y}\right|_{y=0}=\alpha_{\mathrm{s}}\left(T-T_{\mathrm{s}}\right) \\ \left.k \frac{\partial T}{\partial y}\right|_{y=H}=\alpha_{\mathrm{b}}\left(T_{\mathrm{b}}-T\right) \end{array}\right. $ | (2) |
式中,αs为螺杆表面的对流换热系数,W/(m2·K));αb为机筒表面的对流换热系数,W/(m2·K));Ts为螺杆表面温度,℃;Tb为机筒表面温度,℃。
入口边界条件为
| $ \left.T\right|_{z=0}=T_{0} $ | (3) |
式中,T0为聚合物熔体的入口温度,℃。
对能量方程(1)沿螺槽深度方向进行积分,得到冷却单螺杆内熔体温度变化。
| $ \rho c_{p} \int_{0}^{H} v_{z} \frac{\partial T}{\partial z} \mathrm{~d} y=k \int_{0}^{H} \frac{\partial^{2} T}{\partial y^{2}} \mathrm{~d} y+\int_{0}^{H} \dot{q} \mathrm{~d} y $ | (4) |
基于假设vz只是x、y的函数,与z无关,式(4)左侧可以表示为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \rho c_{p} \int_{0}^{H} v_{z} \frac{\partial T}{\partial z} \mathrm{~d} y=\rho c_{p} \int_{0}^{H} \frac{\partial\left(v_{z} T\right)}{\partial z} \mathrm{~d} y= \\ \rho c_{p} \frac{\partial}{\partial z} \int_{0}^{H} v_{z} T \mathrm{~d} y \end{array} $ | (5) |
熔体在螺槽中引用平均温度表征y方向的温度变化,即考虑整个螺槽深度上的平均温度
| $ \bar{T}=\frac{\int_{0}^{H} v_{z} T \mathrm{~d} y}{\int_{0}^{H} v_{z} \mathrm{~d} y} $ |
于是有
| $ \int_{0}^{H} v_{z} T \mathrm{~d} y=\bar{T} \int_{0}^{H} v_{z} \mathrm{~d} y $ | (6) |
将式(6)代入式(5),得到
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \rho c_{p} \int_{0}^{H} v_{z} \frac{\partial T}{\partial z} \mathrm{~d} y=\rho c_{p} \frac{\partial\left(\bar{T} \int_{0}^{H} v_{z} \mathrm{~d} y\right)}{\partial z}=\\ \rho c_{p} \frac{\partial \bar{T}}{\partial z} \int_{0}^{H} v_{z} \mathrm{~d} y \end{array} $ |
由润滑近似和冷却单螺杆内聚合物熔体质量守恒[8]可以得到
| $ \int_{0}^{H} v_{z} \mathrm{~d} y=\frac{G_{\mathrm{m}}}{\rho W} $ |
式中,Gm为聚合物熔体的产量,kg/h;W为螺槽宽度,mm。
于是有
| $ \rho c_{p} \int_{0}^{H} v_{z} \frac{\partial T}{\partial z} \mathrm{~d} y=c_{p} \cdot \frac{G_{\mathrm{m}}}{W} \cdot \frac{\partial \bar{T}}{\partial z} $ | (7) |
当引用平均温度表示熔体在螺槽中的温度变化时,结合热边界条件式(2),方程(4)右侧第一项可表示为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ k \int_{0}^{H} \frac{\partial^{2} T}{\partial y^{2}} \mathrm{~d} y=\left.k \frac{\partial T}{\partial y}\right|_{y=H}-\left.k \frac{\partial T}{\partial y}\right|_{y=0}=\alpha_{\mathrm{b}}\left(T_{\mathrm{b}}-\bar{T}\right)-\\ \alpha_{\mathrm{s}}\left(\bar{T}-T_{\mathrm{s}}\right) \end{array} $ | (8) |
方程(4)右侧第二项可以表示为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \int_{0}^{H} \dot{q} \mathrm{~d} y=\int_{0}^{H} K\left(\frac{{\rm{ \mathit{ π} }} D N \cos \varphi}{60 H}\right)^{n+1} \mathrm{~d} y= \\ K H\left(\frac{{\rm{ \mathit{ π} }} D N \cos \varphi}{60 H}\right)^{n+1} \end{array} $ | (9) |
将式(7)、(8)、(9)代入式(4),可得
| $ \begin{array}{l} \ \ \ \ \ \ \ \ c_{p} \frac{G_{\mathrm{m}}}{W} \frac{\partial \bar{T}}{\partial z}=\alpha_{\mathrm{b}}\left(T_{\mathrm{b}}-\bar{T}\right)-\alpha_{\mathrm{s}}\left(\bar{T}-T_{\mathrm{s}}\right)+ \\ K H\left(\frac{{\rm{ \mathit{ π} }} D N \cos \varphi}{60 H}\right)^{n+1} \end{array} $ | (10) |
对能量方程(10)进行截面积分,得到周向截面平均,即
| $ \begin{array}{l} \ \ \ \ \ \ \ \ c_{p} G_{\mathrm{m}} \frac{\partial \bar{T}}{\partial z}=\alpha_{\mathrm{b}} W\left(T_{\mathrm{b}}-\bar{T}\right)-\alpha_{\mathrm{s}} W\left(\bar{T}-T_{\mathrm{s}}\right)+ \\ K W H\left(\frac{{\rm{ \mathit{ π} }} D N \cos \varphi}{60 H}\right)^{n+1} \end{array} $ | (11) |
通常大直径螺杆能够进行螺杆内部冷却,小直径一般无法设置螺杆冷却,即
| $ c_{p} G_{\mathrm{m}} \frac{\partial \bar{T}}{\partial z}=\alpha_{\mathrm{b}} W\left(T_{\mathrm{b}}-\bar{T}\right)+K W H\left(\frac{{\rm{ \mathit{ π} }} D N \cos \varphi}{60 H}\right)^{n+1} $ | (12) |
Keum[9]给出了幂律流体在机筒表面的对流换热系数和修正系数C(n)。
幂律流体在机筒表面的对流换热系数计算如下所示。
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \frac{\alpha_{\mathrm{b}} D}{k}=0.807 \cdot\left(\frac{\rho c_{p} D^{2} N}{k}\right)^{\frac{1}{3}} \cdot\left(\frac{{\rm{ \mathit{ π} }} D^{2} \cos \varphi}{L H}\right)^{\frac{1}{3}} \cdot\left[1+ \right.\\ \left.C(n) \cdot \frac{H^{2}}{2 {\rm{ \mathit{ π} }} D N \cos \varphi} \cdot\left(\frac{H}{2 K} \cdot \frac{\partial P}{\partial z}\right)^{\frac{1}{n}}\right]^{\frac{1}{3}} \end{array} $ | (13) |
式中,L为螺杆长度,m;P为聚合物熔体受到的压力,Pa。
其中,修正系数C(n)为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ C(n)=\left[\left(\frac{H}{C_{1}}\right)^{\frac{n-1}{n}}+\frac{(n-1)\left(\frac{H}{C_{1}}\right)^{\frac{n-1}{n}} H}{n C_{1}}+\right. \\ \left.\frac{(n-1)(2 n-1)\left(\frac{H}{C_{1}}\right)^{\frac{n-1}{n}} H}{\left(n C_{1}\right)^{2}}+\cdots\right] \end{array} $ |
将式(13)和入口边界条件(3)代入方程(12)中,并对方程(12)进行求解,可得到冷却单螺杆内聚合物熔体沿着螺槽通道的平均温度分布,即聚合物熔体的传热理论分析模型为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \bar{T}=\left\{\frac{K W({\rm{ \mathit{ π} }} D N \cos \varphi)^{n+1}}{3600^{n+1} H^{n} c_{p} G_{\mathrm{m}}}-\exp \left\{0.807 \cdot \frac{W k}{D c_{p} G_{\mathrm{m}}} \cdot\right.\right. \\ \left(\frac{\rho c_{p} D^{2} N}{k}\right)^{\frac{1}{3}} \cdot\left(\frac{{\rm{ \mathit{ π} }} D^{2} \cos \varphi}{L H}\right)^{\frac{1}{3}} \cdot\left[1+C(n) \cdot \frac{H^{2}}{2 {\rm{ \mathit{ π} }} D N \cos \varphi} \cdot\right. \\ \left.\left.\left(\frac{H}{2 K} \cdot \frac{\partial P}{\partial z}\right)^{\frac{1}{n}}\right]^{\frac{1}{3}} \cdot z\right\}\left[\frac{K W({\rm{ \mathit{ π} }} D N \cos \varphi)^{n+1}}{3600^{n+1} H^{n} c_{p} G_{\mathrm{m}}}+0.807 \cdot\right. \\ \frac{W k}{D c_{p} G_{\mathrm{m}}} \cdot\left(\frac{\rho c_{p} D^{2} N}{k}\right)^{\frac{1}{3}} \cdot\left(\frac{{\rm{ \mathit{ π} }} D^{2} \cos \varphi}{L H}\right)^{\frac{1}{3}} \cdot[1+C(n) \cdot\\ \left.\left.\frac{H^{2}}{2 {\rm{ \mathit{ π} }} D N \cos \varphi} \cdot\left(\frac{H}{2 K} \cdot \frac{\partial P}{\partial z}\right)^{\frac{1}{n}}\right]^{\frac{1}{3}} \cdot\left(T_{0}-T_{\mathrm{b}}\right)\right]+0.807 \cdot \\ \frac{W k}{D c_{p} G_{\mathrm{m}}} \cdot\left(\frac{\rho c_{p} D^{2} N}{k}\right)^{\frac{1}{3}} \cdot\left(\frac{{\rm{ \mathit{ π} }} D^{2} \cos \varphi}{L H}\right)^{\frac{1}{3}} \cdot[1+C(n) \cdot \\ \left.\left.\frac{H^{2}}{2 {\rm{ \mathit{ π} }} D N \cos \varphi} \cdot\left(\frac{H}{2 K} \cdot \frac{\partial P}{\partial z}\right)^{\frac{1}{n}}\right]^{\frac{1}{3}}\right\} /\left\{0.807 \cdot \frac{W k}{D c_{p} G_{\mathrm{m}}} \cdot\right. \\ \left(\frac{\rho c_{p} D^{2} N}{k}\right)^{\frac{1}{3}} \cdot\left(\frac{{\rm{ \mathit{ π} }} D^{2} \cos \varphi}{L H}\right)^{\frac{1}{3}} \cdot\left[1+C(n) \cdot\right. \\ \left.\left.\frac{H^{2}}{2 {\rm{ \mathit{ π} }} D N \cos \varphi} \cdot\left(\frac{H}{2 K} \cdot \frac{\partial P}{\partial z}\right)^{\frac{1}{n}}\right]^{\frac{1}{3}}\right\} \end{array} $ |
聚合物熔体在冷却单螺杆中传热过程相当复杂,熔体温度变化也受到多种因素影响。影响熔体传热的因素主要可以归纳为被加工材料的物性参数、加工过程中的操作工艺参数和螺杆结构参数三大类[10],本文基于聚合物熔体传热理论分析模型,选取螺杆结构参数与操作工艺参数作为研究对象,探究它们对聚合物熔体冷却过程的影响。
选取直径45 mm的螺杆,螺棱宽度按照0.8% D的原则选取,螺棱法向宽度为3.5 mm,选择四头螺纹,采用聚苯乙烯熔体作为物料,机筒温度设置为100 ℃,熔体入口温度为200 ℃。研究螺槽深度、螺纹升角、螺杆转速和产量这4个参数对熔体降温过程的影响,具体参数值见表 1。
| 下载CSV 表 1 结构参数、工艺参数和物性参数 Table 1 Structural parameters, processing parameters and physical parameters |
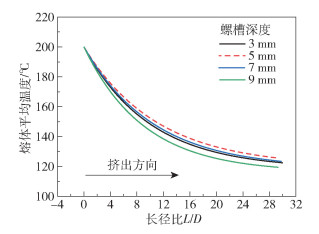
图 2为螺槽深度为3、5、7、9 mm的螺杆内聚合物熔体的平均温度沿挤出方向的降温曲线,图 3为螺杆长度为30D的螺杆内熔体的出口平均温度随螺槽深度的变化。
|
图 2 不同螺槽深度下熔体沿挤出方向的降温曲线 Fig.2 Variation in average temperature of the melt with channel depth |
|
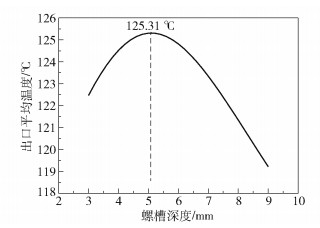
图 3 出口平均温度随螺槽深度的变化 Fig.3 Variation in average outlet temperature with channel depth |
从图 2可以看出,熔体平均温度沿着挤出方向逐渐降低。随着螺杆长度增加,熔体的降温速率逐渐减小,温度变化趋于平稳。从图 3可以看出,随着螺槽深度增大,熔体的出口平均温度先升高后降低。在螺槽深度为5.1 mm时熔体的出口平均温度达到最高,为125.31 ℃;当螺槽深度大于5.1 mm时,熔体的出口平均温度下降明显,在螺槽深度为9 mm时,出口平均温度降到最低,为119.22 ℃。由于聚合物的导热性差,且螺杆绝热,当螺槽深度加深后,熔体沿着螺槽深度方向的热量传递效率变低,熔体受到的剪切作用减弱,产生的黏性生热量减少。由熔体在螺槽内的平均停留时间
| $ \bar{t}=\frac{V}{Q} $ | (14) |
式中,V为螺槽容积,m3;Q为聚合物熔体的体积流量,m3/s。
螺槽深度方向的传热效率降低抑制了熔体冷却,而黏性生热量减少和停留时间增长促进了熔体冷却,随着螺槽深度增加,黏性生热和停留时间对熔体冷却的促进作用大于沿螺槽深度方向传热效率降低的抑制作用,因此,随着螺槽深度增加,出口平均温度出现先升高后降低的趋势。考虑到螺槽深度还会影响冷却单螺杆的输送能力,即螺槽深度越深,聚合物熔体的产量越大,在冷却单螺杆的设计过程中,应尽可能选择螺槽深度较深的螺杆来增强冷却单螺杆对熔体的冷却能力。
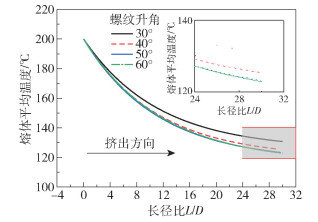
2.2 螺纹升角对熔体平均温度的影响图 4为螺纹升角为30°、40°、50°、60°的螺杆内聚合物熔体的平均温度沿挤出方向的降温曲线,图 5为螺杆长度为30D的螺杆内熔体的出口平均温度随螺纹升角的变化。
|
图 4 不同螺纹升角下熔体沿挤出方向的降温曲线 Fig.4 Variation in average temperature of the melt with the helix angle |
|
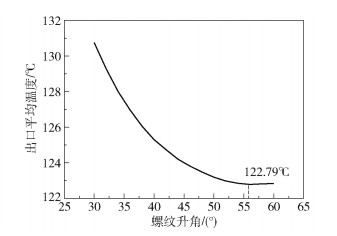
图 5 出口平均温度随螺纹升角的变化 Fig.5 Variation in average outlet temperature with the helix angle |
从图 4可以看出,熔体平均温度沿着挤出方向逐渐降低。随着螺杆长度增加,熔体的降温速率逐渐减小,温度变化趋于平稳;随着螺纹升角增加,螺纹升角对熔体降温曲线的影响越来越不明显。从图 5可以看出,随着螺纹升角增大,熔体的出口平均温度先降低后略微升高,且随着螺纹升角增大,螺纹升角对于熔体出口平均温度的影响越来越小。螺纹升角在30°~50°之间,出口平均温度下降曲线的斜率较大,说明此时螺纹升角对熔体降温的影响作用较大。当螺纹升角为56°时,出口平均温度最低,为122.79 ℃。当螺纹升角大于56°时,出口平均温度开始缓慢上升,螺纹升角为60°时,出口平均温度升至122.84 ℃。螺纹升角从56°增大到60°,出口平均温度仅上升了0.05 ℃,表明当螺纹升角大于56°时其对出口平均温度的影响很小。
熔体的出口平均温度随着螺纹升角增大出现先降低后略微升高的趋势是因为螺槽升角增大,熔体流动行程变短,熔体在螺槽内的停留时间变短。螺纹升角增大,熔体受到螺棱的剪切作用减小,熔体产生的黏性生热量减少。停留时间变短抑制了熔体冷却,黏性生热量减少促进了熔体冷却,两者共同作用使聚合物熔体的出口平均温度先降低后略微升高。
2.3 螺杆转速对熔体平均温度的影响图 6为螺杆转速为10、20、30、40 r/min的聚合物熔体的平均温度沿挤出方向的降温曲线,图 7为螺杆长度为30D的螺杆内熔体的出口平均温度随螺杆转速的变化。
|
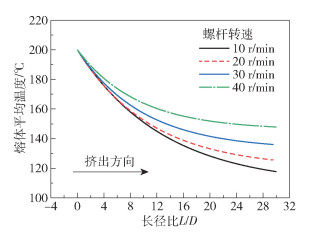
图 6 不同螺杆转速下熔体沿挤出方向的降温曲线 Fig.6 Variation in average temperature of the melt along the extrusion direction under different screw speeds |
|
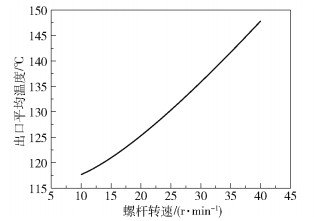
图 7 出口平均温度随螺杆转速的变化 Fig.7 Variation in average outlet temperature with the screw speed |
从图 6可以看出,熔体平均温度沿着挤出方向逐渐降低。随着螺杆长度增加,熔体的降温速率逐渐减小,温度变化趋于平稳;随着螺杆转速增大,聚合物熔体降温曲线的曲率越来越小,聚合物熔体的降温速率越来越小。从图 7可以看出,随着螺杆转速增大,熔体的出口平均温度升高,螺杆转速越大,聚合物熔体升温越明显。随着螺杆转速增大,聚合物熔体受到的剪切作用越明显,聚合物内部产生的黏性生热量越大。随着螺杆长度增大,聚合物内产生的热量无法及时被机筒带走,只能沿着挤出方向传递给挤出机下游,导致聚合物的降温速率随着转速增大而降低,因此,出口平均温度会随着转速增大而升高。
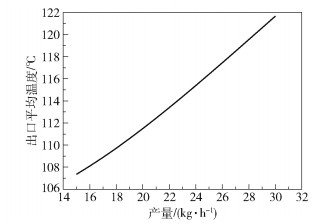
2.4 产量对熔体平均温度的影响图 8为产量为15、20、25、30 kg/h的聚合物熔体的平均温度沿着挤出方向的降温曲线,图 9为螺杆长度为30D的螺杆内熔体的出口平均温度随产量的变化。
|
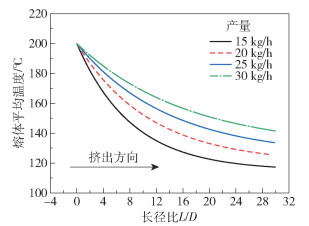
图 8 不同产量下熔体沿挤出方向的降温曲线 Fig.8 Variation in average temperature of the melt along the extrusion direction under different outputs |
|
图 9 出口平均温度随产量的变化 Fig.9 Variation in average outlet temperature with the output |
从图 8可以看出,熔体平均温度沿着挤出方向逐渐降低。随着螺杆长度增大,熔体的降温速率逐渐降低;产量越大,曲线曲率越小,熔体平均温度沿着挤出方向的降温速率越小。从图 9可以看出,随着产量增大,熔体的出口平均温度增大。随着产量增大,熔体在螺槽内的平均停留时间变短,熔体受到的剪切作用增大,产生的黏性生热量大,导致熔体的出口平均温度升高。增加螺杆长度有利于聚合物熔体冷却,增大产量不利于聚合物熔体冷却。因此,在设计冷却单螺杆过程中需要综合考虑各因素之间的相互作用。
3 模拟验证为了验证聚合物熔体传热理论分析模型的准确性,采用CFD模拟分析软件Fluent对该模型以及影响聚合物传热性能的结构参数与工艺参数进行验证。选择螺杆长度为2D(90 mm)的熔体模型作为研究对象,通过Fluent模拟计算出口截面的平均温度,并与聚合物熔体传热理论分析模型的计算结果进行对比。
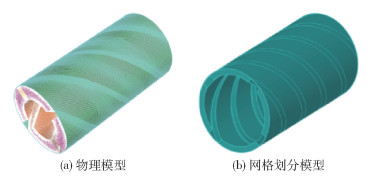
3.1 物理模型与网格划分以45 mm冷却单螺杆为研究对象,建立聚合物熔体流道的三维计算模型,根据不同结构参数分别对聚合物熔体模型进行三维建模和网格划分,对聚合物熔体流道采用正六面体结构化网格,这样有利于计算的收敛并减小计算量。图 10为螺槽深度5 mm、螺纹升角40°的物理模型与网格划分模型。
|
图 10 聚合物流体的物理模型和网格划分模型 Fig.10 Physical model and mesh generation model of polymer fluid |
聚合物熔体是一种非牛顿流体,其在螺杆内的流动特性较为复杂,为了简化螺杆内熔体的流动行为,做如下假设:
1) 流体为不可压缩流体,在螺杆中稳定流动,且充满流道;
2) 流体与螺杆和机筒壁面间无滑移,且忽略惯性力作用;
3) 熔体的密度、比热容、导热系数均为恒定值,不随温度改变;
4) 流体与机筒表面间传热良好,与螺杆表面间不存在热交换,即螺杆表面绝热。
基于上述假设,聚合物熔体流场的连续性方程为
| $ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0 $ |
运动方程为
| $ \frac{\partial p}{\partial x}=\frac{\partial \tau_{x x}}{\partial x}+\frac{\partial \tau_{y x}}{\partial y}+\frac{\partial \tau_{z x}}{\partial z} $ |
| $ \frac{\partial p}{\partial y}=\frac{\partial \tau_{x y}}{\partial x}+\frac{\partial \tau_{y y}}{\partial y}+\frac{\partial \tau_{z y}}{\partial z} $ |
| $ \frac{\partial p}{\partial z}=\frac{\partial \tau_{x z}}{\partial x}+\frac{\partial \tau_{y z}}{\partial y}+\frac{\partial \tau_{z z}}{\partial z} $ |
能量方程为
| $ \rho c_{p} \upsilon \nabla T=k \nabla^{2} T+\tau: \nabla \upsilon $ |
式中,τ为应力张量。
3.3 边界条件通过螺杆壁面的旋转代替螺杆旋转,设置不同转速。边界条件具体设置如下:
1) 动力学边界条件质量流量入口,压力出口,熔体与机筒间的壁面无滑移,螺杆壁面旋转。
2) 热力学边界条件聚合物熔体入口温度为200 ℃,熔体与机筒贴合壁面的温度为100 ℃。
3.4 本构方程与物性参数选择幂律流体作为本构方程,熔体稠度K为8 694 Pa·sn,非牛顿指数n为0.47。采用聚苯乙烯作为物料,具体物性参数为:密度978 kg/m3,比热容2 086 J/(kg·K),导热系数0.261 W/(m·K)。
3.5 网格无关性验证为了检验网格尺寸对数值模拟结果的影响,保证计算精度和结果准确性,避免网格大小及数量对计算结果产生较大影响,需要对计算模型进行网格无关性验证。使用螺槽深度为5 mm、螺纹升角为40°的螺杆,在聚合物产量为20 kg/h、转速为20 r/min的工艺条件下进行数值模拟,以出口平均温度作为评价指标来验证熔体模型网格大小和网格单元数对计算结果的影响。网格单元数和模拟结果如表 2所示。
| 下载CSV 表 2 熔体网格无关性验证 Table 2 Verification of melt grid independence |
由表 2可以看出,随着网格尺寸减小、网格单元数增加,出口平均温度升高。当网格尺寸从2 mm减小到1 mm时,网格单元数从45.38万增加到56.72万,出口平均温度的相对变化率小于0.5%,表明此时网格尺寸与网格单元数对计算结果的影响很小,可以满足网格无关性的要求,故本文采用1 mm的网格尺寸进行模拟计算。
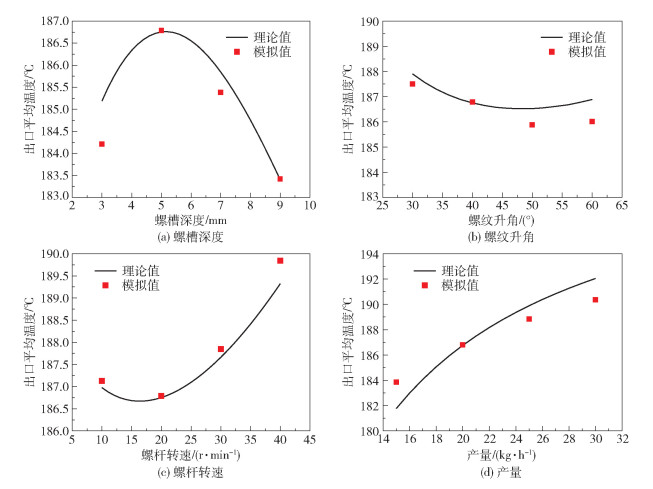
图 11为不同的结构参数与工艺参数条件下聚合物熔体的出口平均温度的计算值与模拟值对比图。从图中可以看出,随着螺槽深度的增大,出口平均温度出现先升高后降低的趋势;随着螺纹升角的增大,出口平均温度先降低后增大;当螺杆转速大于15 r/min时,随着螺杆转速的增大,出口平均温度增大;随着产量的增加,出口平均温度增大。模拟值与理论值基本吻合,最大相对误差为1.21%。但是随着螺杆直径增大,误差范围会增大,当螺杆直径大于90 mm时,螺杆绝热条件已经无法满足冷却要求,需要进行螺杆内部冷却。数值模拟过程说明聚合物熔体的传热分析模型是可靠的,可以预测聚合物熔体在冷却单螺杆内的降温过程。
|
图 11 出口平均温度随结构参数和工艺参数的变化 Fig.11 Variation in average outlet temperature with the structure parameters and process parameters |
本文建立了冷却单螺杆内聚合物熔体的传热理论分析模型,得到聚合物熔体在冷却单螺杆内传热平均温度的解析解。探究了结构参数与工艺参数对冷却单螺杆内聚合物熔体冷却过程的影响,结果表明,当螺槽深度为5~9 mm、螺纹升角为30°~50°时,通过增大螺槽深度和螺纹升角, 同时降低螺杆转速和减少产量,能够有效增强冷却单螺杆内聚合物熔体的冷却,此时该模型能够满足冷却单螺杆内聚合物熔体的降温需求。最终通过CFD数值模拟验证了聚合物熔体传热理论分析模型的准确性,模拟值与理论值基本吻合,最大相对误差为1.21%。以上结果表明,该模型能够预测冷却单螺杆内聚合物熔体的降温过程,可以为聚合物熔体降温过程提供一定的理论参考,用于指导冷却单螺杆的结构设计和工艺参数选择。
| [1] |
RAUWENDAAL C. New screw design for cooling extruders[J]. Plastics, Rubber and Composites, 2004, 33(9-10): 397-399. DOI:10.1179/174328904X24899 |
| [2] |
FOGARTY J. Thermoplastic foam extrusion screw with circulation channels: US 6609818 B1[P]. 2003-08-26.
|
| [3] |
BARR R A. Extruder screw with improved energy efficient melting: US 6599004 B2[P]. 2003-07-29.
|
| [4] |
HAN C D. Analysis of the performance of cooling extruders in thermoplastic foam extrusion[J]. Polymer Engineering and Science, 1988, 28(19): 1227-1239. DOI:10.1002/pen.760281904 |
| [5] |
WANG C, BUSSMANN M, PARK C B. Numerical investigation of the effect of screw geometry on the mixing of a viscous polymer melt[J]. Journal of Applied Polymer Science, 2010, 117(2): 775-784. DOI:10.1002/app.31039 |
| [6] |
范涛, 陈作炳, 汤帅, 等. 螺棱断面形状对单螺杆挤出机熔融输送段的影响[J]. 北京理工大学学报, 2017, 37(1): 24-29. FAN T, CHEN Z B, TANG S, et al. Effects of screw arris cross section shapes on the melt conveying section of single-screw extruder[J]. Transactions of Beijing Institute of Technology, 2017, 37(1): 24-29. (in Chinese) |
| [7] |
陈佳兴, 李子然. 单螺杆橡胶挤出机三维非等温流动数值模拟[J]. 材料科学与工艺, 2018, 26(1): 62-68. CHEN J X, LI Z R. Simulation of non-isothermal three-dimensional flow in the channel of a single-screw extruder for rubber material[J]. Materials Science and Technology, 2018, 26(1): 62-68. (in Chinese) |
| [8] |
戴干策. 聚合物加工中的传递现象[M]. 北京: 中国石化出版社, 1999. DAI G C. Transmission phenomenon in polymer processing[M]. Beijing: China Petrochemical Press, 1999. (in Chinese) |
| [9] |
KEUM J. Engineering analysis of devolatilization and reactive processing in intermeshing co-rotating twin screw extruders[D]. Akron: The University of Akron, 2004.
|
| [10] |
CAMPBELL G A. Analyzing troubleshooting single screw extrusion campbell[M]. Cincinnati: Hanser Publications, 2013.
|






