2. 北京化工大学 教育部高分子材料加工装备工程研究中心, 北京 100029
2. Polymer Processing Equipment Engineering Research Center, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
先进树脂基复合材料由于具有强度高、质量轻、耐腐蚀等优异性能而得到人们的青睐[1-2]。相对于热固复合材料,热塑性复合材料因其预浸料储存周期长、可连续高效率制备、冲击韧性高等优点,广泛应用于航天航空[3-4]、汽车工业等领域。近年来,在轻量化的大背景下,纤维增强热塑性复合材料更是受到人们的关注[5-6]。在纤维增强热塑性复合材料的制备过程中,浸渍模具是熔融浸渍过程中关键的设备,在浸渍过程中,树脂熔体在模具内部熔体压力的作用下渗透到纤维束中,从而实现浸渍过程[7-9]。聚酰胺又称尼龙,这类树脂的分子特征为含有重复酰胺键,酰胺键的存在使尼龙分子具有较强的极性且分子间易形成氢键,氢键的存在赋予了尼龙材料很好的力学性能[10-11]。但另一方面,酰胺基团具有较强的极性,是整个链的薄弱环节,易受热、氧、紫外线、水分等环境因素的影响而发生降解[12-14]。尼龙对高温较为敏感,故在浸渍过程中需要解决热降解的问题。尼龙在浸渍模具中的停留时间越长,越容易发生降解,从而影响制品的表面颜色及力学性能,因此需要控制树脂基体在浸渍模具中的停留时间。
定量预测停留时间以及设计对温度敏感型树脂的加工设备,需要对停留时间分布(RTD)函数有详细了解。在常规操作中,清理系统或转换材料所需要的时间,也取决于这个函数的特性。加工设备中RTD函数的计算和测量对于设计和操作具有重要意义,因此可以采用RTD函数对树脂在设备中的停留时间进行分析计算[15-18]。RTD函数[19] 分为内部函数g(t)dt和外部函数f(t)dt,其中,g(t)dt表示在t至t+dt这段停留时间内设备内部的流体体积分数,f(t)dt表示在这段停留时间内流出设备的流体体积分数。从这些定义中分别可以定义内部累积函数G(t)和外部累积函数F(t),对于连续式设备,外部累积函数F(t)的公式为:
目前对于停留时间的研究主要集中在螺杆挤出机和化工反应器方面[20-22],而针对连续纤维浸渍弯曲流道模具的停留时间的研究较少。本文基于外部RTD函数和自行设计的连续纤维弯曲流道模具,建立了便于直接使用的解析解形式的停留时间模型。采用Box-Behnken响应面法设计了5因素3水平的试验方案,通过引入所建立的停留时间模型分析了模具结构参数对树脂加工过程中停留时间的影响,并对模具结构参数进行了优化。
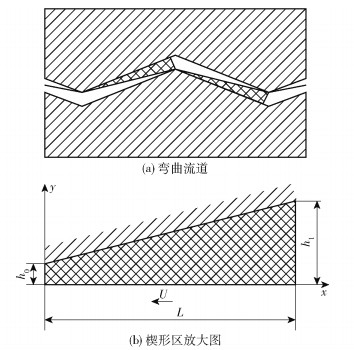
1 停留时间理论模型建立在牵引力作用下,纤维束在弯曲流道模具中移动时与流道壁面形成收敛的楔形区[23-24],楔形区是浸渍行为发生的主要区域(见图 1(a)),楔形区结构的放大图如图 1(b)所示。其中,h0为楔形区出口高度;h1为模具间隙;L为楔形区长度;U为牵引速度。
|
图 1 浸渍模具中的楔形区结构图 Fig.1 Structure diagram of the wedge-shaped zone in the impregnation mold |
楔形区内任意位置处的高度h为
| $ h=\frac{h_{1}-h_{0}}{L}(L-x)+h_{0} $ |
式中,x为楔形区中x方向上的坐标位置。
在弯曲流道的任意位置处,速度u都可以按照x方向的纳维-斯托克斯方程求得[25-26],由该方程可得到速度分布函数为
| $ u=U\left(1-\frac{y}{h}\right)+\frac{3 U}{h^{3}}\left(2 \frac{h_{1} h_{0}}{h_{1}^{2}-h_{0}^{2}}-h\right)\left(y^{2}-y h\right) $ | (1) |
式中,y为楔形区中y方向上的坐标位置。
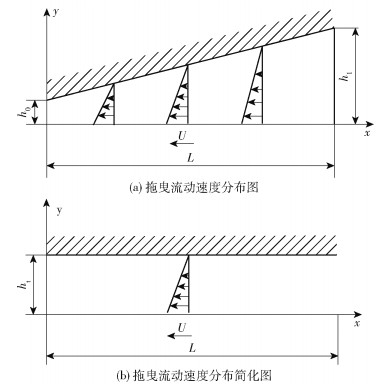
式(1)的第一项为拖曳流动速度分布函数,拖曳流动速度分布图如图 2(a)所示,树脂在纤维束中的拖曳流动可以简化为如图 2(b)所示的速度分布,简化之后在间距为ht的平行板之间全展、等温拖曳流动的速度分布为
| $ u=U\left(1-\frac{y}{h_{\mathrm{t}}}\right) $ |
|
图 2 楔形区拖曳流动润滑间隙的速度分布图及其简化图 Fig.2 Velocity distribution diagram of the drag flow lubrication gap in the wedge-shaped zone and its simplified diagram |
流体粒子的停留时间依赖粒子在流道中的位置,在位置y处的停留时间t为
| $ t=\frac{L}{u}=\frac{L}{U\left(1-\frac{y}{h_{\mathrm{t}}}\right)} $ |
通过计算可以得到关于时间的分布函数
| $ f(t) \mathrm{d} t=\frac{2 t_{0}^{2}}{t^{3}} \mathrm{~d} t $ |
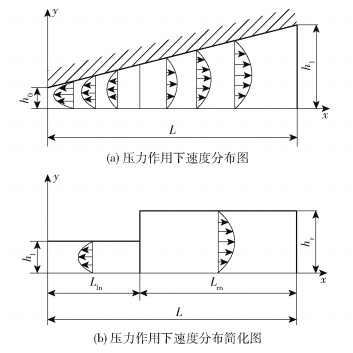
式(1)的第二项为压力作用下的速度分布函数(图 3(a)),简化后的速度分布如图 3(b)所示。定义速度系数Al为:
| $ u_{1}=A_{1}\left(y^{2}-y h_{1}\right) $ |
|
图 3 楔形区压力作用下润滑间隙的速度分布图及其简化图 Fig.3 Velocity distribution diagram of the lubrication gap and its simplified diagram under the action of wedge zone pressure |
式中,hl为简化后的左半段高度。
压力作用下左半段关于时间的分布函数为
| $ f(t) \mathrm{d} t=\frac{12 L_{\mathrm{ln}}^{2}}{A_{1}^{2} h_{1}^{3} t^{3}}\left(h_{1}^{2}-4 \frac{L_{\mathrm{ln}}}{A_{1} t}\right)^{\frac{1}{2}} \mathrm{~d} t $ |
式中,Lln为简化后的左半段长度。
压力作用下右半段关于时间的分布函数为
| $ f(t) \mathrm{d} t=\frac{12 L_{\mathrm{rn}}^{2}}{A_{\mathrm{r}}^{2} h_{\mathrm{r}}^{3} t^{3}}\left(h_{\mathrm{r}}^{2}-4 \frac{L_{\mathrm{rn}}}{A_{\mathrm{r}} t}\right)^{\frac{1}{2}} \mathrm{~d} t $ |
式中,Lrn为简化后的右半段长度,hr为简化后的右半段高度,Ar为右半段速度系数。
停留时间分布函数的理论模型外部累积函数F(t)为
| $ \begin{array}{l} \ \ \ \ F(t)=\int_{t_{0}}^{t} \frac{2 t_{0}^{2}}{t^{3}}+\frac{12 L_{\mathrm{ln}}^{2}}{A_{1}^{2} h_{1}^{3} t^{3}}\left(h_{1}^{2}-4 \frac{L_{\mathrm{ln}}}{A_{1} t}\right)^{\frac{1}{2}}-\frac{12 L_{\mathrm{rn}}^{2}}{A_{\mathrm{r}}^{2} h_{\mathrm{r}}^{3} t^{3}}\cdot \\ \left(h_{\mathrm{r}}^{2}-4 \frac{L_{\mathrm{rn}}}{A_{\mathrm{r}} t}\right)^{\frac{1}{2}} \mathrm{~d} t \end{array} $ |
聚酰胺(PA66),EPR27,平顶山神马工程塑料有限责任公司;玻璃纤维(T835),2400tex,纤维直径17 μm,泰山玻璃纤维有限公司;铜粉(示踪物质),6N级,300目(50 μm),中冶鑫盾合金公司。
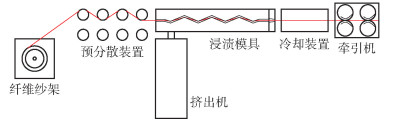
2.2 实验方法双螺杆挤出机由实验室自行设计组装,浸渍机头及浸渍模具、预分散架由实验室自行设计加工,熔融浸渍工艺流程如图 4所示。
|
图 4 熔融浸渍工艺流程 Fig.4 Process flow chart of the melt impregnation |
将聚酰胺在真空干燥箱(DZF-6050型,上海林频仪器股份有限公司)中于100 ℃烘干5 h,然后树脂在双螺杆挤出机中以熔融状态进入浸渍模具。将玻璃纤维放置在纱架上,纤维通过预分散装置进入浸渍模具。熔融浸渍后,预浸料由牵引机从浸渍模具口模牵出,通过循环水冷却装置冷却定型。
2.3 测试与分析 2.3.1 示踪物质的外部累积函数为了验证反映树脂在模具中停留时间的RTD函数,通过挤出物中示踪物质(铜粉)的浓度(示踪物质的颗粒数)除以加入示踪物质的总量来计算F(t),如式(2)所示。
| $ F(t)=\frac{\int_{0}^{t} C(t) \mathrm{d} t}{\int_{0}^{\infty} C(t) \mathrm{d} t} \times 100 \% $ | (2) |
式中,C(t)为时刻t时出口处示踪物质的浓度(示踪物质颗粒数)。
2.3.2 示踪物质颗粒数的计量首先确定取样间隔,然后取样,以第i个样条为例说明其测试过程:测定铜粉质量mi,除以单个铜粉质量m,计算出试样中的示踪物质颗粒数Ci,然后由式(3)进行迭加,绘制曲线。
| $ F(t)=\frac{\sum\limits_{i=0}^{n} C_{i}}{\sum\limits_{i=0}^{N} C_{i}} \times 100 \% $ | (3) |
式中,N为样条总数,n为第n个样条。
| $ \sum\limits_{i=0}^{N} C_{i}=\frac{M}{m} $ | (4) |
式中,M为铜粉总质量。因此,式(3)可以简化为
| $ F(t)=\frac{\sum\limits_{i=0}^{n} \frac{m_{i}}{m}}{\frac{M}{m}}=\frac{\sum\limits_{i=0}^{n} m_{i}}{M} \times 100 \% $ |
称取一定质量的铜粉,将其从双螺杆挤出机中加入,每个实验条件下测量3次,将含有铜粉的预浸料按照一定的时间间隔取样,使用游标卡尺分别测量其长度,然后放入已称重的坩埚内,在马弗炉(SX2-4-10型,武汉亚华电炉有限公司)中煅烧(550 ℃,4 h),取出后称重,减去纤维和坩埚的质量,即得出铜粉质量mi,其计算式如下。
| $ m_{i}=M_{1}-M_{2}-2.4 l $ |
式中,M1为纤维、坩埚和铜粉的总质量,g;M2为坩埚的质量,g;l为纤维束长度,m。
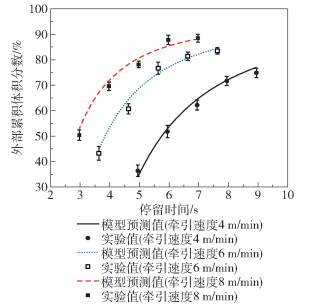
2.4 实验结果 2.4.1 牵引速度对停留时间分布函数的影响牵引速度是浸渍过程的重要工艺参数,图 5为在280 ℃、模具间隙1 mm下停留时间分布函数随牵引速度变化的曲线。从图中可以看出,外部累积体积分数相同时,随着牵引速度增加,停留时间变短。这是因为随着牵引速度增加,在其他工艺参数不变的条件下,树脂在浸渍模具中经历的时间更短。另外,还可以看出外部累积体积分数随着停留时间变化的实验值与模型预测值基本相符,说明本文建立的模型可以准确预测实验结果。
|
图 5 不同牵引速度下外部累积体积分数随停留时间的变化 Fig.5 External cumulative volume fraction as a function of residence time under different traction speeds |
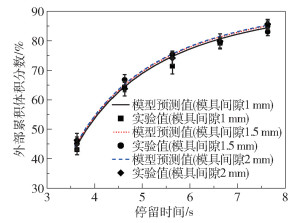
模具间隙对浸渍加工过程的影响比较重要,通过增加垫片的方式可以调整模具间隙。图 6为在280 ℃、牵引速度6 m/min下停留时间分布函数随模具间隙变化的曲线。从图中可以看出,随模具间隙增加,树脂的外部累积体积分数增加,但是增加的幅度很小。外部累积体积分数相同时,随着模具间隙的增加,停留时间稍有变短。另外,还可以看出外部累计体积分数随模具间隙变化的实验值与模型预测值基本相符,说明本文建立的模型可以准确预测实验结果。
|
图 6 不同模具间隙下外部累积体积分数随停留时间的变化 Fig.6 External cumulative volume fraction as a function of residence time under different mold gaps |
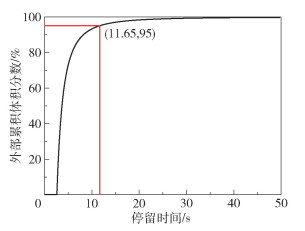
为了研究流道单元长度、流道圆角半径、流道单元个数、流道单元夹角、模具间隙这5个结构参数对弯曲流道模具停留时间的影响。采用Design Expert软件的Box-Behnken模块进行正交试验设计,设计了5因素3水平3响应的模拟试验方案,如表 1所示。试验响应为外部累积体积分数为95%时所对应的停留时间(t95)、浸渍程度和纤维断裂率。通过本文建立的停留时间理论模型可以容易地得到停留时间和外部累计体积分数的关系曲线,如图 7所示。可以看出,当外部累计体积分数为95%时,对应的停留时间为11.65 s。通过本文建立的停留时间模型可以计算出t95,而浸渍程度和纤维断裂率的计算参考袁满的模型[24]。
| 下载CSV 表 1 模拟试验方案 Table 1 Test program of the simulation |
|
图 7 停留时间分布函数 Fig.7 Residence time distribution function |
将各影响因素代入模型中,计算得到模拟试验结果,如表 2所示。
| 下载CSV 表 2 模拟试验结果 Table 2 Simulation test results |
对于影响不显著的交互项和二次项,可以将其忽略,只考虑影响显著的交互项和二次项,拟合得到如下传递函数模型。
| $ \begin{array}{l} \ \ \ \ \ \ \ \ t_{95}=11.95+13.09 A+1.67 B+10.30 C-1.46 D- \\ 1.35 E+2.66 A B+10.11 A C+5.92 A^{2}+3.32 C^{2} \end{array} $ |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ c=89.95+11.48 A-4.00 B+10.43 C-8.01 E- \\ 4.75 A^{2}-4.83 C^{2} \end{array} $ |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ p=0.80+1.82 A-3.20 B+1.53 C-2.37 E- \\ 1.50 A B-2.25 A E-1.26 B C+0.17 B D+2.26 B E- \\ 1.87 C E+2.46 B^{2}+1.75 E^{2} \end{array} $ |
式中,c为浸渍程度;p为纤维断裂率;A为流道单元长度;B为流道圆角半径;C为流道单元个数;D为流道单元夹角;E为模具间隙。
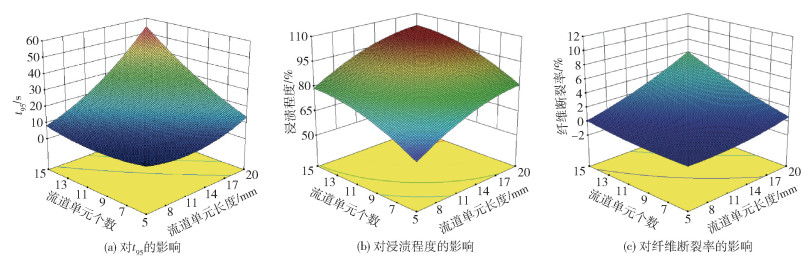
从传递函数中可以得到,模具参数对t95的影响程度由大到小分别为:流道单元长度>流道单元个数>流道圆角半径>流道单元夹角>模具间隙。模具参数对浸渍程度的影响程度由大到小分别为:流道单元长度>流道单元个数>模具间隙>流道圆角半径>流道单元夹角。模具参数对纤维断裂率的影响程度由大到小分别为:流道圆角半径>模具间隙>流道单元长度>流道单元个数>流道单元夹角。从传递函数的各影响程度的大小关系可知流道单元长度和流道单元个数对t95和浸渍程度的影响最为明显,图 8反映了流道单元长度和流道单元个数的交互影响。由图中可见,随着流道单元长度的增加,t95和浸渍程度增大,纤维断裂率增大。这是因为随着流道单元长度的增加,树脂在浸渍模具中经历的长度越长,停留时间也越长,树脂浸渍的时间也越长,因此浸渍程度越大,但是纤维束在模具中经历的时间越长,纤维受到的树脂熔体的剪切力也会越大,纤维断裂率也会增大。随着流道单元个数的增加,树脂经历高压区的次数增加,浸渍效果更好,但是模具总长度也会增加,树脂的停留时间也增加,熔融树脂对纤维的剪切力会增大,而且纤维所受的弯曲应力的次数也会增加,因此纤维断裂率就会增大。
|
颜色偏向红色代表影响程度大,偏向蓝色代表影响程度小,中间为过渡颜色。 图 8 流道单元长度和流道单元个数对浸渍过程的影响 Fig.8 The effects of the length of the runner unit and the number of runner units on the impregnation process |
对模拟试验结果进行分析并得到二次方传递函数模型之后,可以根据模拟试验的分析结果,采用Design Expert软件对影响t95、浸渍程度和纤维断裂率的各个参数进行优化,优化目标为使t95尽可能小,浸渍程度尽可能大,纤维断裂率尽可能小。
为了便于优化分析,需要将各个影响因素限定在一定的范围内,如表 3所示。根据所设置的限定条件,从Design Expert软件中可以得到优化后的各影响因素的推荐设定值,如表 4所示,在该工艺条件下,t95为13.92 s,浸渍程度可以达到97.5%,纤维断裂率为3.6%。
| 下载CSV 表 3 参数优化的限定条件 Table 3 Restricted conditions for parameter optimization |
| 下载CSV 表 4 优化后的影响因素推荐取值 Table 4 Recommended values of influencing factors after optimization |
(1) 基于停留时间分布函数和连续纤维加工模具,建立了便于直接使用的解析解形式的停留时间模型,通过实验验证了模型的可靠性,结果表明该模型可以准确预测树脂在浸渍模具中的停留时间。
(2) 采用Box-Behnken响应面法设计5因素3水平的试验方案,以流道单元长度、流道圆角半径、流道单元个数、流道单元夹角、模具间隙为影响因素,t95为响应,分析了各个参数对t95的影响程度,结果表明流道单元长度和流道单元个数的影响最大。
(3) 为了在树脂加工过程中实现更好的浸渍效果,通过优化得到模具结构的最优参数为:流道单元长度12.5 mm,流道圆角半径3 mm,流道单元个数10个,流道单元夹角160°,模具间隙1.4 mm。
| [1] |
陈祥宝. 聚合物基复合材料手册[M]. 北京: 化学工业出版社, 2004: 4-5. CHEN X B. Handbook of polymer-based composites[M]. Beijing: Chemical Industry Press, 2004: 4-5. (in Chinese) |
| [2] |
杜善义. 先进复合材料与航空航天[J]. 复合材料学报, 2007, 24(1): 1-12. DU S Y. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica, 2007, 24(1): 1-12. (in Chinese) DOI:10.3321/j.issn:1000-3851.2007.01.001 |
| [3] |
张婷. 高性能热塑性复合材料在大型客机结构件上的应用[J]. 航空制造技术, 2013(15): 32-35. ZHANG T. Applications of high performance thermoplastic composites for commercial airplane structural component[J]. Aeronautical Manufacturing Technology, 2013(15): 32-35. (in Chinese) DOI:10.3969/j.issn.1671-833X.2013.15.003 |
| [4] |
胡记强, 王兵, 张涵其, 等. 热塑性复合材料构件的制备及其在航空航天领域的应用[J]. 宇航总体技术, 2020, 4(4): 61-70. HU J Q, WANG B, ZHANG H Q, et al. Fabrication of thermoplastic composite components and their application in aerospace[J]. Astronautical Systems Engineering Technology, 2020, 4(4): 61-70. (in Chinese) |
| [5] |
魏莉霞, 马鸣图, 杨洁. 长纤维增强热塑性复合材料在汽车轻量化上的应用[J]. 新材料产业, 2013(9): 45-52. WEI L X, MA M T, YANG J. Application of long fiber reinforced thermoplastic composites in automobile lightweight[J]. Advanced Materials Industry, 2013(9): 45-52. (in Chinese) |
| [6] |
BAE S Y, YOON S M, KIM Y H. A study on the lightweight design of lift structure by composite materials[J]. Modern Physics Letters B, 2020, 34(7-9): 2040032. |
| [7] |
唐可, 信春玲, 张聪, 等. 连续纤维增强聚丙烯复合材料的熔融浸渍理论模型与表征[J]. 北京化工大学学报(自然科学版), 2015, 42(4): 44-49. TANG K, XIN C L, ZHANG C, et al. The impregnation model and characterization of continuous fiber reinforced polypropylene composites[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2015, 42(4): 44-49. (in Chinese) |
| [8] |
BATES P J, CHARRIER J M. Pulling tension monitoring during the melt impregnation of glass roving[J]. Polymer Composites, 2000, 21(1): 104-113. DOI:10.1002/pc.10169 |
| [9] |
张聪, 信春玲, 唐可, 等. 热塑性树脂连续浸渍过程的纤维断裂机制及实验[J]. 复合材料学报, 2015, 32(4): 983-988. ZHANG C, XIN C L, TANG K, et al. Fiber fracture mechanism in process of thermoplastic resin continuous impregnation and experiments[J]. Acta Materiae Compositae Sinica, 2015, 32(4): 983-988. (in Chinese) |
| [10] |
王红专, 高先明. 国内外聚酰胺现状与展望[J]. 化工生产与技术, 2008, 15(1): 38-40, 58. WANG H Z, GAO X M. Current status and prospects of polyamide at home and abroad[J]. Chemical Production and Technology, 2008, 15(1): 38-40, 58. (in Chinese) |
| [11] |
张爽爽. 长纤维增强尼龙6复合材料技术的研究与开发[D]. 北京: 北京化工大学, 2015. ZHANG S S. Research and development of long fiber reinforced polyamide 6 composites[D]. Beijing: Beijing University of Chemical Technology, 2015. (in Chinese) |
| [12] |
杨涛, 叶林, 舒颖. 丙烯酸酯类抗氧剂对聚酰胺的热氧稳定作用[J]. 高分子材料科学与工程, 2008, 24(3): 98-101. YANG T, YE L, SHU Y. The thermal stabilization effect of acrylate antioxidant on polyamide[J]. Polymer Materials Science & Engineering, 2008, 24(3): 98-101. (in Chinese) |
| [13] |
LEVCHIK S V, WEIL E D, LEWIN M. Thermal decomposition of aliphatic nylons[J]. Polymer International, 1999, 48(7): 532-557. DOI:10.1002/(SICI)1097-0126(199907)48:7<532::AID-PI214>3.0.CO;2-R |
| [14] |
STEPPAN D D, DOHERTY M F, MALONE M F. A simplified degradation model for nylon 6, 6 polymerization[J]. Journal of Applied Polymer Science, 1991, 42(4): 1009-1021. DOI:10.1002/app.1991.070420415 |
| [15] |
FOGLER H S. Elements of chemical reaction engineering[J]. Chemical Engineering Science, 1987, 42(10): 2493-2494. |
| [16] |
PINTO G, TADMOR Z. Mixing and residence time distribution in melt screw extruders[J]. Polymer Engineering and Science, 1970, 10(5): 279-288. DOI:10.1002/pen.760100505 |
| [17] |
CHEN L Q, PAN Z Q, HU G H. Residence time distribution in screw extruders[J]. AIChE Journal, 1993, 39(9): 1455-1464. DOI:10.1002/aic.690390905 |
| [18] |
POULESQUEN A, VERGNES B, CASSAGNAU P, et al. A study of residence time distribution in co-rotating twin-screw extruders. Part Ⅱ: experimental validation[J]. Polymer Engineering and Science, 2003, 43(12): 1849-1862. DOI:10.1002/pen.10157 |
| [19] |
塔德莫尔, 高戈斯. 聚合物成型加工原理[M]. 任冬云, 译. 北京: 化学工业出版社, 2009. TADMOR Z, GOGOS C G. Principles of polymer processing[M]. REN D Y, trans. Beijing: Chemical Industry Press, 2009. (in Chinese) |
| [20] |
WOLF D, WHITE D H. Experimental study of the residence time distribution in plasticating screw extruders[J]. AIChE Journal, 1976, 22(1): 122-131. |
| [21] |
JAGER T, SANTBULTE P, VAN ZUILICHEM D J. Residence time distribution in kneading extruders[J]. Journal of Food Engineering, 1995, 24(3): 285-294. |
| [22] |
SHAO Y L, AGARWAL R K, LI J G, et al. Computational fluid dynamics-discrete element model simulation of flow characteristics and solids' residence time distribution in a moving bed air reactor for chemical looping combustion[J]. Industrial and Engineering Chemistry Research, 2020, 59(40): 18180-18192. |
| [23] |
杨建军. 连续纤维增强热塑性复合材料浸渍模拟及优化研究[D]. 北京: 北京化工大学, 2016. YANG J J. Impregnation simulation and optimization study of continuous fiber reinforced thermoplastic composite materials[D]. Beijing: Beijing University of Chemical Technology, 2016. (in Chinese) |
| [24] |
袁满. 连续纤维增强热塑性复合材料浸渍过程优化研究[D]. 北京: 北京化工大学, 2019. YUAN M. Optimization of impregnation process of continuous fiber reinforced thermoplastic composites[D]. Beijing: Beijing University of Chemical Technology, 2019. (in Chinese) |
| [25] |
张兆顺, 崔桂香. 流体力学[M]. 2版. 北京: 清华大学出版社, 2006. ZHANG Z S, CUI G X. Fluid mechanics[M]. 2nd ed. Beijing: Tsinghua University Press, 2006. (in Chinese) |
| [26] |
朗格, 斯泰因希尔珀. 滑动轴承[M]. 王成焘, 曹永上, 译. 北京: 机械工业出版社, 1986: 103-111. LANG O R, STEINHILPER W. Sliding bearing[M]. WANG C T, CAO Y S, trans. Beijing: Machinery Industry Press, 1986: 103-111. (in Chinese) |








