保温层作为典型的多孔材质,其内部复杂的传热传质过程对于能源开发利用和工程隔热等领域至关重要[1-2],因此研究多孔材质的热质耦合传递具有重要的工程应用价值。陈威等[3]将多孔材质看作是均匀且连续的,采用能量和质量守恒方程,研究了传热传质过程中温度场和湿度场的变化情况;薛雨凝[4]建立了当量孔径计算模型,分析了均匀连续材质在不同相对湿度下冻结温度的变化情况。实际上,多孔材质是非均匀的且内部结构非常复杂,如果把多孔材质考虑为均匀连续模型,那么研究结果与真实情况会相差很大。张赛等[5]假定多孔材质为从常规尺度到微观尺度的光滑毛细管束模型,建立了多尺度并存的物理渗流模型,运用分形理论分析了微观结构参数对渗流系数和导热系数的影响;Xu等[6]和邱淑霞等[7]分析了多尺度光滑孔径的分布参数对渗流系数和扩散系数的影响。这些研究将多孔材质的孔隙通道表面考虑为光滑的理想状态,但在实际工程中,几乎不存在光滑的表面。王世芳等[8]运用热阻法得出非均匀半径毛细管道的渗流系数和导热系数;Wang等[9]分析了不同几何形状管道的渗流速度与微观结构参数之间的关系;Wu等[10]建立了多尺度的球状模型,将孔隙通道描述为不规则半径毛细管道,推导出不规则半径毛细管道内的渗流系数和导热系数;董道良等[11]建立了不同宽高比的粗糙元壁面模型,分析了粗糙元在稀疏和密集分布下对系统传热的影响;张春平[12]建立了粗糙表面管道模型,对粗糙微细通道内的流动和换热特性进行了研究,发现通道尺度越小,粗糙表面对流动和换热特性的影响越大。这些研究结果表明对于多孔材质而言,粗糙表面的影响是不可忽略的。张起生等[13]运用Gauss和蒙特卡洛分布规律对随机粗糙表面进行了数值模拟;张琳等[14]基于蒙特卡洛法和分形理论,进行了粗糙表面接触导热的计算;Yang等[15]建立了含有粗糙元的单根毛细管道模型,并且运用分形理论描述了粗糙元的分布情况,分析了单根粗糙毛细管道内部的渗流过程和对流换热过程;Ji等[16]根据三维分形函数建立了粗糙表面接触导热模型,并利用该模型对接触导热进行了研究。以上对于粗糙表面的研究,仅讨论了粗糙度这一个影响因素,未讨论粗糙元的分布情况对粗糙元的影响,不能准确地对粗糙表面进行描述。
为了准确体现保温层孔隙通道的粗糙表面对热质耦合传递过程的影响,本文基于孔隙通道分形分布规律,考虑了粗糙度和粗糙密集度两个影响因素,将孔隙通道描述为短周期正弦变化的毛细管道,得到粗糙毛细管道的渗流系数和对流换热系数模型,并且分析讨论了粗糙表面对渗流系数和对流换热系数的影响。
1 多孔材质的分形特征保温层内部的孔隙通道非常复杂,孔隙通道的大小和分布规律可由分形标度关系来表示[17]。
| $ N=\left(r_{\max } / r\right)^{D_{\mathrm{f}}} $ | (1) |
式中,r为单根毛细管道的平均半径,m;N为平均半径大于r的孔隙通道数目;rmax为孔隙通道的最大平均半径,m;Df为孔隙通道的面积分形维数。由于式(1)被认为是可连续的,所以进行微分可得平均半径r到r+dr区间的孔隙通道数目。
| $ -\mathrm{d} N=D_{\mathrm{f}} r_{\max }^{D_{\mathrm{f}}} r^{-\left(D_{\mathrm{f}}+1\right)} \mathrm{d} r $ | (2) |
式中,-dN>0,负号表示孔隙通道的半径大小与数目成反比。
孔隙通道的实际长度满足以下分形标度关系。
| $ L_{\mathrm{t}}(r)=r^{1-D_{\mathrm{t}}} L_{0}^{D_{\mathrm{t}}} $ | (3) |
式中,Lt (r)为孔隙通道的实际长度,m;L0为孔隙通道的特征长度,m;Dt为孔隙通道的迂曲分形维数。
孔隙率与孔隙通道半径的关系为
| $ \phi=\left(r_{\min } / r_{\max }\right)^{2-D_{\mathrm{f}}} $ | (4) |
式中,
如图 1所示,本文将凹凸不平的孔隙通道粗糙表面描述为呈短周期正弦变化的毛细管道,其表达式如下
| $ r(x)=r[1+\beta \sin (2 {\rm{ \mathsf{ π} }} x / b)] $ | (5) |

|
图 1 正弦变化的毛细管道模型 Fig.1 Capillary channel model with sinusoidal variation |
式中,r(x)为正弦变化的毛细管道实际半径,m,它随迂曲毛细管道的轴向实际长度Lt呈正弦周期变化;β为正弦变化的幅度,当β=0时,管道为理想状态下的光滑管道,当β=0.5时,管道不存在,这种情况无意义,故不在考虑范围之内;1/b定义为粗糙元的密集度,b值越小(取值小于1),正弦变化的周期2bπ也越小,即粗糙元越密集。
| $ \varepsilon=a / {\rm{ \mathsf{ π} }} b $ | (6) |
式中,ε定义为粗糙表面的粗糙度,用来描述毛细管道的粗糙程度;a=rβ,定义为粗糙元的高度;πb定义为粗糙元的底部宽度。同时,a可由式(6)表示为:a=πbε。
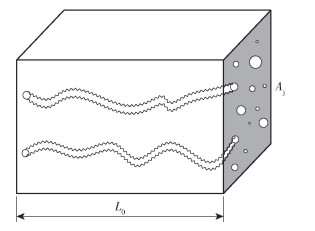
如图 2所示,将保温层内部所有孔隙通道都考虑为正弦变化的毛细管道,每根管道代表一个孔隙通道,且毛细管道的半径大小和分布符合分形标度关系,这样可以更加准确地表示粗糙孔隙通道的实际情况。
|
L0为孔隙通道的特征长度,Aj为单元的横截面积。 图 2 保温层粗糙孔隙通道模型 Fig.2 Rough pore channel model of the insulating layer |
根据Hagen-Poiseulle方程和流体连续性[17],单根粗糙毛细管道的流量与管道半径有以下关系。
| $ q\left(r_{\mathrm{b}}\right)=\frac{{\rm{ \mathsf{ π} }} r_{\mathrm{b}}^{4}}{8 \mu} \cdot \frac{\Delta P_{\mathrm{b}}}{L_{\mathrm{t}}(r)}=q\left(r_{\mathrm{t}}\right)=\frac{{\rm{ \mathsf{ π} }} r_{\mathrm{t}}^{4}}{8 \mu} \cdot \frac{\Delta P_{\mathrm{t}}}{L_{\mathrm{t}}(r)} $ | (7) |
式中,rb= r+a和rt= r-a分别为单根粗糙毛细管道的最大半径和最小半径;q(rb)和q(rt)分别为毛细管道的最大半径和最小半径处的流量,m3;μ为流体的黏性系数,Pa·s。
由于管道为正弦变化,管道内的压强差会发生变化,所以用管道的最大半径和最小半径两处的压强差之和来表示总压强差ΔP。
| $ \Delta P=\Delta P_{\mathrm{b}}+\Delta P_{\mathrm{t}} $ | (8) |
式中,ΔPb和ΔPt分别为毛细管道的最大半径和最小半径处的压强差,Pa。
最大半径处的压强差ΔPb可以由ΔP 表示为[10]
| $ \Delta P_{\mathrm{b}}=\frac{r_{\mathrm{t}}^{4}}{\left(r_{\mathrm{b}}^{4}+r_{\mathrm{t}}^{4}\right)} \Delta P $ | (9) |
联立式(7)和式(9),若以最大半径处的流量来表示单根粗糙毛细管道的流量,可得
| $ \begin{array}{l} \ \ \ \ q\left(r_{\mathrm{b}}\right)=\frac{{\rm{ \mathsf{ π} }} r^{4}(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}}{8 \mu} \cdot \frac{\Delta P}{L_{\mathrm{t}}(r)}\cdot \\ \frac{(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}}{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}+(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}} \end{array} $ | (10) |
联立式(2)和式(10),积分可得
| $ \begin{array}{l} \ \ \ \ Q_{1}=\int_{r_{\min }}^{r_{\max }} q\left(r_{\mathrm{b}}\right) \mathrm{d} N=\frac{{\rm{ \mathsf{ π} }}}{8 \mu} \cdot \frac{\Delta P}{L_{0}^{D_{\mathrm{t}}}}\cdot \\ \frac{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}}{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}+(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}} \cdot \frac{D_{\mathrm{f}} r_{\max }^{3+D_{\mathrm{t}}}}{3+D_{\mathrm{t}}-D_{\mathrm{f}}} \quad[1- \\ \left.\left(\frac{r_{\min }}{r_{\max }}\right)^{3+D_{\mathrm{t}}-D_{\mathrm{f}}}\right] \end{array} $ | (11) |
式中,Ql为粗糙毛细管道模型的总流量,m3。由于rmin/rmax→10-2,且迂曲分形维数一般取值为1<Dt<3,面积分形维数一般取值为0<Df<2,式(11)可以简化为
| $ \begin{array}{l} \ \ \ \ Q_{1}=\int_{r_{\min }}^{r_{\max }} q\left(r_{\mathrm{b}}\right) \mathrm{d} N=\frac{{\rm{ \mathsf{ π} }}}{8 \mu} \cdot \frac{\Delta P}{L_{0}^{D_{\mathrm{t}}}} \cdot\\ \frac{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}}{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}+(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}} \cdot \frac{D_{\mathrm{f}} r_{\max }^{3+D_{\mathrm{t}}}}{3+D_{\mathrm{t}}-D_{\mathrm{f}}} \end{array} $ | (12) |
设单根粗糙毛细管道的孔截面积为A0:
| $ A_{0}={\rm{ \mathsf{ π} }} r^{2}(x) $ | (13) |
对式(13)积分,可得总粗糙毛细管道的孔截面积Ak:
| $ A_{\mathrm{k}}=\int_{r_{\min }}^{r_{\max }} {\rm{ \mathsf{ π} }} r^{2}(x) \mathrm{d} N $ | (14) |
由于
| $ \begin{array}{l} \ \ \ \ A_{\mathrm{k}}=\int_{r_{\min }}^{r_{\max }} {\rm{ \mathsf{ π} }} r^{2}\left[1+\frac{({\rm{ \mathsf{ π} }} b \varepsilon)^{2}}{2}\right] D_{\mathrm{f}} r_{\max }^{D_{\mathrm{f}}} r^{-\left(D_{\mathrm{f}}+1\right)} \mathrm{d} r= \\ \frac{\left[1+\frac{({\rm{ \mathsf{ π} }} b \varepsilon)^{2}}{2}\right] {\rm{ \mathsf{ π} }} D_{\mathrm{f}} r_{\max }^{2}} { 2 - D _ { \mathrm { f } } } \left[1 - ( \frac { r _ { \min } } { r _ { \max } } ) ^ { 2 - D _ { \mathrm { f } } } \right] \end{array} $ | (15) |
根据式(15)和式(4),可得单元的横截面积Aj:
| $ \begin{array}{l} \ \ \ \ A_{j}=\frac{A_{\mathrm{k}}}{\phi}=\frac{\left[1+\frac{({\rm{ \mathsf{ π} }} b \varepsilon)^{2}}{2}\right] {\rm{ \mathsf{ π} }} D_{\mathrm{f}} r_{\max }^{2}}{2-D_{\mathrm{f}}} . \\ \frac{\left[1-\left(\frac{r_{\min }}{r_{\max }}\right)^{2-D_{\mathrm{f}}}\right]}{\left(\frac{r_{\min }}{r_{\max }}\right)^{2-D_{\mathrm{f}}}} \end{array} $ | (16) |
对于粗糙毛细管道内的渗流情况,根据达西定律,可以得到渗流系数的表达式为[18]
| $ \begin{array}{l} \ \ \ \ k_{\mathrm{c}}=\frac{Q_{1} \mu L_{0}}{A_{\mathrm{j}} \Delta P}=\frac{1}{8 L_{0}^{D_{\mathrm{t}}-1}} \cdot \frac{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}}{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}+(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}} \cdot \\ \frac{r_{\max }^{1+D_{\mathrm{t}}}}{3+D_{\mathrm{t}}-D_{\mathrm{f}}} \cdot \frac{2-D_{\mathrm{f}}}{\left[1+\frac{({\rm{ \mathsf{ π} }} b \varepsilon)^{2}}{2}\right]} \cdot \frac{\left(\frac{r_{\min }}{r_{\max }}\right)^{2-D_{\mathrm{f}}}}{\left[1-\left(\frac{r_{\min }}{r_{\max }}\right)^{2-D_{\mathrm{f}}}\right]} \end{array} $ | (17) |
式中,kc为粗糙毛细管道内的渗流系数,m2。为了更清楚地分析粗糙毛细管道内的渗流情况,将式(17)中的粗糙毛细管道内的渗流系数kc和光滑管道内的渗流系数k进行比较,二者的比值η为
| $ \begin{array}{l} \ \ \ \ \eta=\frac{k_{\mathrm{c}}}{k}=\frac{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}}{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}+(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}} \cdot \\ \frac{1}{\left[1+\frac{({\rm{ \mathsf{ π} }} b \varepsilon)^{2}}{2}\right]} \end{array} $ | (18) |
由式(18)可以看出,渗流系数的比值η与粗糙度ε和粗糙密集度1/b有关。
4 粗糙毛细管道对流换热系数 4.1 对流换热量联立式(16)和式(17),根据能量守恒定律,得到对流换热量的表达式为
| $ \begin{array}{l} \ \ \ \ Q_{\mathrm{r}}=\frac{k_{\mathrm{c}} \Delta P A_{\mathrm{j}} \rho c \Delta T_{1}}{\mu L_{0}}=\frac{{\rm{ \mathsf{ π} }} \rho c \Delta T_{1}}{8 \mu} \cdot \frac{\Delta P}{L_{0}^{D_{\mathrm{t}}}}\cdot \\ \frac{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}}{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}+(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}} \cdot \frac{D_{\mathrm{f}}}{3+D_{\mathrm{t}}-D_{\mathrm{f}}} r_{\max }^{3+D_{\mathrm{t}}} \end{array} $ | (19) |
式中,Qr为粗糙毛细管道在渗流过程中的对流换热量,kJ;ρ为流体密度,kg/m3;c为比热容,kJ/(kg·K);ΔT1为渗流过程中流体的温度差,℃。
4.2 对流换热面积多孔材质内部非常复杂,计算其内表面积十分困难。目前,实验测量法是已知比较常用的计算多孔材质内表面积的方法,但这种方法存在着不可避免的随机误差。本文根据构建的粗糙毛细管道模型,采用局部到整体的思路和比值的方法来计算多孔材质的内表面积。
因为管道存在正弦周期变化,且b的取值很小,所以一个正弦变化周期内的粗糙管道和光滑管道的表面积可表示为
| $ S_{\mathrm{c}}=4 {\rm{ \mathsf{ π} }} r \sqrt{\left(\frac{b {\rm{ \mathsf{ π} }}}{2}\right)^{2}+({\rm{ \mathsf{ π} }} b \varepsilon)^{2}} $ | (20) |
| $ S_{\mathrm{g}}=4 {\rm{ \mathsf{ π} }}^{2} r b $ | (21) |
式中,Sc和Sg分别为粗糙管道的表面积和光滑管道的表面积,m2。
将式(20)和式(21)进行比较,得到一个周期内Sc和Sg的比值α为
| $ \alpha=\frac{S_{\mathrm{c}}}{S_{\mathrm{g}}}=\frac{\sqrt{1+4 \varepsilon^{2}}}{2} $ | (22) |
由于局部比值与整体比值相等,可以得到整体粗糙毛细管道的内表面积为
| $ \begin{array}{l} \ \ \ \ A_{\mathrm{sc}}=\alpha A_{\mathrm{sg}}=\frac{\sqrt{1+4 \varepsilon^{2}} {\rm{ \mathsf{ π} }} L_{0}^{D_{\mathrm{t}}} D_{\mathrm{f}} r_{\max }^{2-D_{\mathrm{t}}}}{2-D_{\mathrm{f}}-D_{\mathrm{t}}}\cdot \\ {\left[1-\left(\frac{r_{\min }}{r_{\max }}\right)^{2-D_{\mathrm{f}}-D_{\mathrm{t}}}\right]} \end{array} $ | (23) |
式中,Asc和Asg分别为粗糙毛细管道的内表面积和光滑毛细管道的内表面积,m2。
4.3 对流换热系数对流换热过程中,对流换热系数可由牛顿冷却公式表示[19]。
| $ h=\frac{Q_{\mathrm{r}}}{A_{\mathrm{sc}} \Delta T_{2}}=\frac{k_{\mathrm{c}} \Delta P A_{\mathrm{j}} \rho c \Delta T_{1}}{\mu A_{\mathrm{sc}} \Delta T_{2}} $ | (24) |
式中,h为渗流过程中粗糙毛细管道内的对流换热系数,W/(m2·K);ΔT2为对流换热过程中流体与固体的温度差,℃。
将式(19)和式(23)代入式(24),可得
| $ \begin{array}{l} \ \ \ \ h=\frac{\rho c \Delta T_{1} \Delta P}{8 \mu \Delta T_{2} L_{0}^{2 D_{\mathrm{t}}}} \cdot \frac{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}}{(1+{\rm{ \mathsf{ π} }} b \varepsilon)^{4}+(1-{\rm{ \mathsf{ π} }} b \varepsilon)^{4}} \cdot \\ \frac{r_{\max }^{1+2 D_{\mathrm{t}}}}{3+D_{\mathrm{t}}-D_{\mathrm{f}}} \cdot \frac{2-D_{\mathrm{t}}-D_{\mathrm{f}}}{\sqrt{1-4 \varepsilon^{2}}} \cdot \frac{1}{1-\left(\frac{r_{\min }}{r_{\max }}\right)^{2-D_{\mathrm{t}}-D_{\mathrm{f}}}} \end{array} $ | (25) |
由式(24)和(25)可以看出,对流换热系数与渗流系数、粗糙度、粗糙密集度和分形维数密切相关。
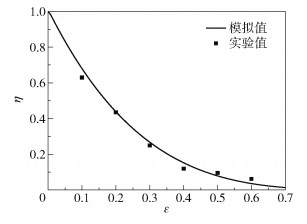
5 分析与讨论 5.1 渗流系数比值η与粗糙度ε的关系图 3为粗糙毛细管道渗流系数kc和光滑毛细管道渗流系数k的比值η与粗糙度ε之间的关系,其中,实验值来自文献[15],模拟值由式(18)通过matlab仿真得出。可以看出,随着粗糙度ε的增大,渗流系数的比值η呈下降趋势,并且下降趋势逐渐变缓,数值模拟曲线与实验数据相吻合。因为管道处于光滑的条件下,ε=0,此时kc=k,二者的比值η=1;随着ε的增大,管道变得粗糙,kc减小,比值η也逐渐减小。通过以上分析可知,对于毛细管道中的渗流过程,粗糙表面是不可忽略的。
|
图 3 粗糙毛细管道渗流系数和光滑毛细管道渗流系数的比值η与粗糙度ε的关系 Fig.3 Relationship between the ratio η of seepage coefficients of the rough capillary channel and the smooth capillary channel, and the roughness ε |
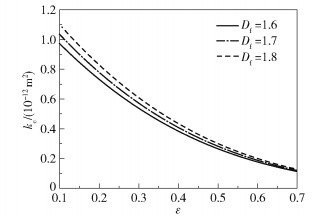
图 4为在不同的面积分形维数Df下粗糙毛细管道渗流系数kc与粗糙度ε的关系。实际工程中,多孔保温材质的孔隙率在0.4左右,此时面积分形维数Df取值1.7左右,迂曲分形维数Dt取值1.3左右。当Df分别为1.6、1.7、1.8时,kc随着ε的增大而减小,kc与ε呈负相关关系。这是因为粗糙度ε越大,孔隙通道半径r越小,所以kc越小。同时,图 4也表明,当ε相同时,Df越大,kc越大。这是因为Df越大,孔隙率越大,并且大孔隙通道的数量增加,流动性能提高,有利于渗流。
|
图 4 面积分形维数Df对粗糙毛细管道渗流系数kc的影响 Fig.4 Effect of the area fractal dimension Df on the seepage coefficient kc of the rough capillary channel |
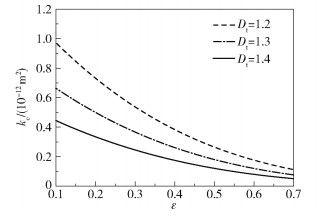
图 5为在不同的迂曲分形维数Dt下粗糙毛细管道渗流系数kc与粗糙度ε的关系。图 5表明,当ε相同时,Dt越大,kc越小。这是因为Dt越大,孔隙通道的迂曲程度越大,渗流过程中阻力越大,越不利于渗流。
|
图 5 迂曲分形维数Dt对粗糙毛细管道渗流系数kc的影响 Fig.5 Effect of the tortuous fractal dimension Dt on the seepage coefficient kc of the rough capillary channel |
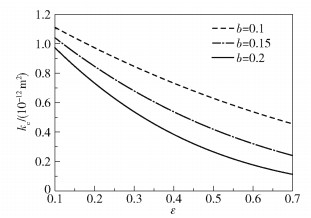
图 6为在不同的粗糙密集度1/b下粗糙毛细管道渗流系数kc与粗糙度ε的关系。当b分别为0.1、0.15、0.2时,kc随着ε的增大而减小,kc与ε呈负相关关系。同时,图 6也表明,当ε相同时,b值越小,1/b越大,kc越大。这是因为,1/b增大,粗糙元高度降低,所以kc增大。
|
图 6 粗糙密集度1/b对粗糙毛细管道渗流系数kc的影响 Fig.6 Effect of the roughness density 1/b on the seepage coefficient kc of the rough capillary channel |
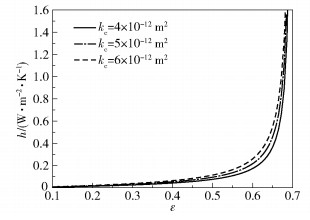
图 7为在不同的粗糙毛细管道渗流系数kc下对流换热系数h与粗糙度ε的关系。图 7表明,当ε相同时,h随着kc的增加而增大,这是因为kc增加,总流量Ql增加,对流换热量Qr增加,所以h增大。当kc分别为4×10-12、5×10-12、6×10-12 m2时,h随着ε的增加而增大,h与ε呈正相关关系。这是因为ε越大,粗糙毛细管道的内表面积Asc越大,Qr越大,所以h越大。同时,图 7也表明,当ε大于0.65时,h会快速增大。这是因为ε大于0.65时,孔隙通道的压强差ΔP会快速增大,所以Ql增加,Qr增加,h增大。
|
图 7 粗糙毛细管道渗流系数kc对对流换热系数h的影响 Fig.7 Effect of the seepage coefficient kc of the rough capillary channel on the convective heat transfer coefficient h |
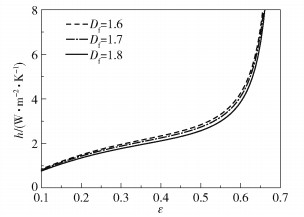
图 8为在不同的面积分形维数Df下对流换热系数h与粗糙度ε的关系。当Df分别为1.6、1.7、1.8时,h随着ε的增加而增大,h与ε呈正相关关系。这是因为,在渗流过程中,ε增大,kc会减小,但粗糙毛细管道的内表面积Asc会增大,并且在对流换热过程中影响大于kc,所以对流换热量Qr会增大。同时,由图 8还可以看出,当ε相同时,Df越大,h越小。这是因为Df越大,孔隙分布越均匀,Asc越小,所以Qr减少,h减小。
|
图 8 面积分形维数Df对对流换热系数h的影响 Fig.8 Effect of the area fractal dimension Df on the convective heat transfer coefficient h |
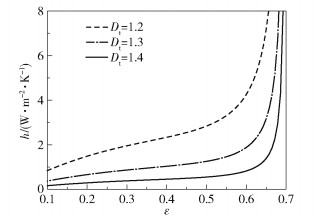
图 9为在不同的迂曲分形维数Dt下对流换热系数h与粗糙度ε的关系。图 9表明,当ε相同时,Dt越大,h越小。这是因为Dt越大,kc越小,渗流量越少,所以Qr减少,h减小。
|
图 9 迂曲分形维数Dt对对流换热系数h的影响 Fig.9 Effect of the tortuous fractal dimension Dt on the convective heat transfer coefficient h |
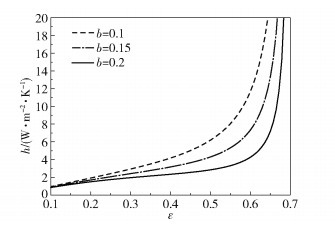
图 10为在不同的粗糙密集度1/b下对流换热系数h与粗糙度ε的关系。当b分别为0.1、0.15、0.2时,h随着ε的增加而增大,h与ε呈正相关关系。同时,图 10也表明,当ε相同时,b值越小,粗糙密集度1/b越大,h越大。这是因为,1/b增大,粗糙元数量增多并且粗糙元高度降低,kc增大,Qr也随之增大,所以h也随之增大。
|
图 10 粗糙密集度1/b对对流换热系数h的影响 Fig.10 Effect of the roughness density 1/b on the convective heat transfer coefficient h |
本文将多孔材质的粗糙毛细管道描述为正弦变化的毛细管道,建立了粗糙毛细管道渗流系数和对流换热系数的模型,分析了渗流系数和对流换热系数的各种影响因素,得到以下结论:
(1) 对于渗流过程,面积分形维数、粗糙密集度越大,渗流系数越大;迂曲分形维数、粗糙度越大,渗流系数越小。
(2) 对于对流换热过程,随着粗糙度、渗流系数、粗糙密集度的增加,对流换热系数会增大;随着面积分形维数、迂曲分形维数的增大,对流换热系数会减小。
| [1] |
JOHRA H, MARGHERITINI L, ANTONOV Y I, et al. Thermal, moisture and mechanical properties of Seacrete: a sustainable sea-grown building material[J]. Construction and Building Materials, 2021, 266: 121025. DOI:10.1016/j.conbuildmat.2020.121025 |
| [2] |
HOU S D, LIU F S, WANG S J, et al. Coupled heat and moisture transfer in hollow concrete block wall filled with compressed straw bricks[J]. Energy and Buildings, 2017, 135: 74-84. DOI:10.1016/j.enbuild.2016.11.026 |
| [3] |
陈威, 叶勇. 多孔介质粒径对建筑结构热质传递的影响[J]. 上海节能, 2016(2): 73-78. CHEN W, YE Y. Porous medium particle size's impact on building structure heat and mass transfer[J]. Shanghai Energy Conservation, 2016(2): 73-78. (in Chinese) |
| [4] |
薛雨凝. 建筑墙体材料内部水分冻结温度计算模型研究[D]. 徐州: 中国矿业大学, 2019. XUE Y N. Study on calculation model of freezing temperature of water in building wall material[D]. Xuzhou: China University of Mining and Technology, 2019. (in Chinese) |
| [5] |
张赛, 陈君若, 刘显茜. 气体有效扩散系数的分形模型[J]. 化学工程, 2013, 41(5): 39-43. ZHANG S, CHEN J R, LIU X X. Fractal model of gas effective diffusivity[J]. Chemical Engineering, 2013, 41(5): 39-43. (in Chinese) |
| [6] |
XU P, QIU S X, CAI J C, et al. A novel analytical solution for gas diffusion in multi-scale fuel cell porous media[J]. Journal of Power Sources, 2017, 362: 73-79. DOI:10.1016/j.jpowsour.2017.07.015 |
| [7] |
邱淑霞, 徐鹏, 杨茉. 多尺度多孔介质的有效气体渗流率研究[J]. 工程热物理学报, 2019, 40(6): 1375-1379. QIU S X, XU P, YANG M. The effective gas permeability of porous media with multi-scale pore structure[J]. Journal of Engineering Thermophysics, 2019, 40(6): 1375-1379. (in Chinese) |
| [8] |
王世芳, 吴涛. 多孔介质有效热导率的一种新模型[J]. 工程热物理学报, 2016, 37(12): 2626-2630. WANG S F, WU T. A new fractal model for the effective thermal conductivity of porous media[J]. Journal of Engineering Thermophysics, 2016, 37(12): 2626-2630. (in Chinese) |
| [9] |
WANG S F, WU T, QI H Y, et al. A permeability model for power-law fluids in fractal porous media composed of arbitrary cross-section capillaries[J]. Physica A: Statistical Mechanics and its Applications, 2015, 437: 12-20. DOI:10.1016/j.physa.2015.05.089 |
| [10] |
WU C Q, XU H J, ZHAO C Y. A new fractal model on fluid flow/heat/mass transport in complex porous structures[J]. International Journal of Heat and Mass Transfer, 2020, 162: 120292. DOI:10.1016/j.ijheatmasstransfer.2020.120292 |
| [11] |
董道良, 王伯福, 周全. 粗糙元的宽高比对Rayleigh-Benard对流系统传热的影响[C]//第三十届全国水动力学研讨会暨第十五届全国水动力学学术会议论文集(上册). 合肥, 2019: 52-59. DONG D L, WANG B F, ZHOU Q. Effect of the aspect ratio of the rough element on the heat transfer of the Rayleigh-Benard convection system[C]//Proceedings of the 30th National Conference on Hydrodynamics and the 15th National Conference on Hydrodynamics (Volume 1). Hefei, 2019: 52-59. (in Chinese) |
| [12] |
张春平. 粗糙度对微细通道内流动与换热特性影响的实验研究与理论分析[D]. 北京: 中国科学院工程热物理研究所, 2007. ZHANG C P. Experimental research and theoretical analysis on flow and heat transfer in microchannels with different surface roughness[D]. Beijing: Institute of Engineering Thermophysics, Chinese Academy of Sciences, 2007. (in Chinese) |
| [13] |
张起生, 王晓春, 谢鸣. 符合Gauss分布规律的随机粗糙表面数值模拟[J]. 燕山大学学报, 2008, 32(6): 503-506. ZHANG Q S, WANG X C, XIE M. Numerical simulation of random rough surfaces based on Gauss distribution[J]. Journal of Yanshan University, 2008, 32(6): 503-506. (in Chinese) DOI:10.3969/j.issn.1007-791X.2008.06.007 |
| [14] |
张琳, 冯妍卉, 王智学. 基于蒙特卡洛法和分形理论的接触导热计算[J]. 重庆理工大学学报(自然科学版), 2019, 33(7): 74-80. ZHANG L, FENG Y H, WANG Z X. Prediction of thermal contact conductance based on Monte Carlo simulation and fractal theory[J]. Journal of Chongqing University of Technology (Natural Science), 2019, 33(7): 74-80. (in Chinese) |
| [15] |
YANG S S, YU B M, ZOU M Q, et al. A fractal analysis of laminar flow resistance in roughened microchannels[J]. International Journal of Heat and Mass Transfer, 2014, 77: 208-217. |
| [16] |
JI C C, ZHU H, JIANG W. Fractal prediction model of thermal contact conductance of rough surfaces[J]. Chinese Journal of Mechanical Engineering, 2013, 26(1): 128-136. DOI:10.3901/CJME.2013.01.128 |
| [17] |
WEI M Q, DUAN Y G, FANG Q T, et al. Mechanism model for shale gas transport considering diffusion, adsorption/desorption and Darcy flow[J]. Journal of Central South University, 2013, 20(7): 1928-1937. |
| [18] |
徐鹏, 李翠红, 柳海成, 等. 多尺度多孔介质有效气体输运参数的分形特征[J]. 地球科学, 2017, 42(8): 1373-1378. XU P, LI C H, LIU H C, et al. Fractal features of the effective gas transport coefficient for multiscale porous media[J]. Earth Sciences, 2017, 42(8): 1373-1378. (in Chinese) |
| [19] |
何燕, 张晓光, 孟祥文. 传热学[M]. 北京: 化学工业出版社, 2015: 90-95. HE Y, ZHANG X G, MENG X W. Heat transfer[M]. Beijing: Chemical Industry Press, 2015: 90-95. (in Chinese) |








