由于非晶态合金是内部质点在三维空间不成周期性重复排列的固体,并且具有短程有序、长程无序的特点,所以其物理性质表现为“各向同性”。据此研究人员发现,非晶态合金在软磁材料[1]、电极材料[2]、机械工程材料[3]和催化剂[4-5]等领域具有较好的应用前景。而非晶态合金Co-Fe-P三元体系具有成本低、性能优异的特点,逐渐成为研究热点。
对于写磁头的磁芯材料而言,为了增加数据存储密度,必须开发具有高饱和磁化强度(最重要的因素)、低矫顽力和高电阻率的写头磁芯。CoFe合金在铁磁金属中具有最高的饱和磁化强度,但矫顽力和电阻率不太理想,而Co-Fe-P相较于CoFe有低矫顽力和高电阻率的特点[6]。在软磁材料的其他研究中,人们发现非晶态合金Co-Fe-P多孔中空的结构对施加的磁场很敏感[7],并且在常温下具有超顺磁性[8]。
相关研究表明非晶态合金Co-Fe-P在催化水解方面可与RuO2+Pt/C相媲美[9],同时在进一步的研究中,Huang等[10]认为非晶态合金Co-Fe-P优异的催化活性是因为钴原子与铁原子的协同作用、金属原子与磷原子的良好相互作用,以及其独特的高表面粗糙度的雪花状异质结构所产生的大电化学活性表面积。而Liu等[11]进一步研究发现Fe的掺入可以扰乱甚至破坏CoP的周期结构,引起活性中心的电子结构和电子密度的重新分布。在金属有机框架(MOF)-CoFeP催化剂研究中,Muthurasu等[12]认为,在碱性介质中,非晶态合金Co-Fe-P相互渗透的MOF网络的配体交换转化为丰富的多孔结构,对整个水裂解反应具有很强的协同效应。而在非晶态合金Co-Fe-P中空微球结构催化剂的研究中,Du等[13]认为其中空结构有助于增加暴露的活性物质以及增大与电解质的接触表面。
综上所述,非晶态合金Co-Fe-P在软磁材料和催化剂等领域的应用效果优于传统材料。而材料的结构稳定性对于其能否发挥作用有着至关重要的影响,所以需要对材料的微观结构进行研究。而现有的研究大都是宏观的实验研究,缺少微观理论研究,因此本文以材料非晶态转化过程中结构的稳定性、异构化的反应限度及趋势作为目标,对非晶态合金Co-Fe-P异构化反应的热力学与动力学进行研究,以期为下一步实际研究工作提供结构参考和理论依据。
1 模型与计算方法本文以Wang等[14]提出的Co0.63Fe0.21P0.16作为基础化学计量比,同时为了计算方便将其改为Co3FeP,并利用拓扑学原理[15]得出团簇Co3FeP的初始构型。
采用密度泛函理论[16]中可以对开壳层和过渡金属进行准确计算的B3LYP杂化(式(1))[17]和Lanl2dz赝势基组[18]对团簇所有的初始构型进行全参数优化和频率计算。
| $ B_{x c}^{\text {BLLYP }}=(1-a) E_{x}^{\mathrm{LSDA}}+a E_{x c}^{\lambda=0}+b \Delta E_{x}^{\mathrm{B} 88}+c \Delta E_{c}^{\mathrm{LYP}}+ \\ (1-c) \Delta E_{c}^{\mathrm{LSDA}} $ | (1) |
式中,BxcB3LYP表示B3LYP杂化泛函;ExLSDA表示局域自旋密度近似的交换项;Excλ=0表示λ=0时的精确交换量;ΔExB88表示Becke88交换泛函;ΔEcLYP表示LYP相关泛函;ΔEcLSDA表示局域自旋密度近似的相关项;参数a=0.20,b=0.72,c=0.81。在优化和计算中,对Co、Fe原子采用18-eECP的双ξ基组(3s,3p,3d/2s,2p,2d)[19]运算,对P原子采用Dunning/Huzinaga双ξ基组(9s,5p/3s,2p)[20]运算,并加上极化函数ξP.d=0.55[21]。优化收敛条件为最大作用力小于0.000 45,均方根作用力小于0.000 3,最大位移小于0.001 8,均方根位移小于0.001 2。
将经上述计算后得到的优化构型与过渡态理论相结合,计算并确定Co3FeP异构转化过程中过渡态的空间结构,再对已有的异构转化过程进行研究,优化收敛条件同上。所有计算均在计算机HP z440上采用Gaussian 09软件完成。反应机理为
| $ \text { 反应物 } \stackrel{\mathrm{RT} \text { 过程 }}{\longrightarrow}[\text { 过渡态 }]^{\#} \stackrel{\mathrm{TP} \text { 过程 }}{\longrightarrow} \text { 生成物 } $ |
其中,RT过程为反应物转化为过渡态的过程,TP过程为过渡态转化为生成物的过程。
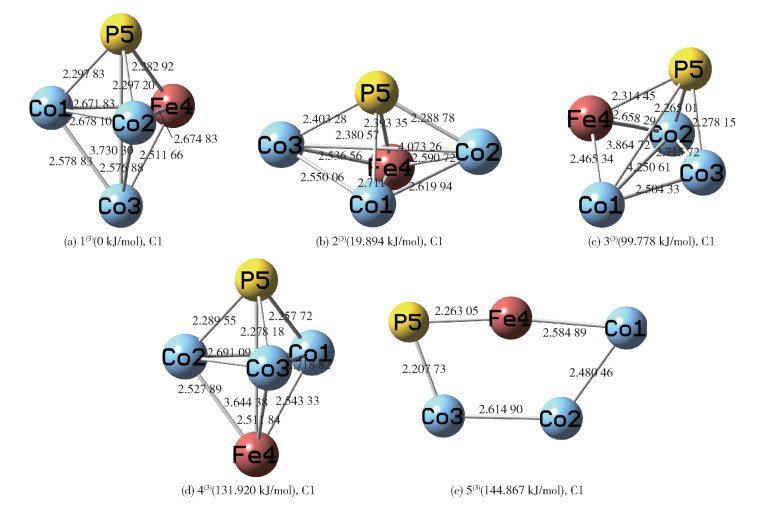
2 结果与讨论 2.1 团簇Co3FeP的优化构型及过渡态构型为了便于观察构型的空间结构,以能量最低的构型1(3)作为能量基准点(设其能量为0 kJ/mol),其他三重态优化构型和过渡态构型按照能量的相对大小依次列出,结果如图 1和图 2所示。由图 1可知,三重态构型的几何形态有三角双锥(构型1(3)、2(3)和4(3))、戴帽三角锥(构型3(3))和类平面五边形(构型5(3))。由图 2可知,对于过渡态构型而言,所有构型均为三角双锥。
|
上角标表示其自旋多重度,C1表示其对称性,下同;实线键上的数字(如2.297 83等)表示键长, |
|
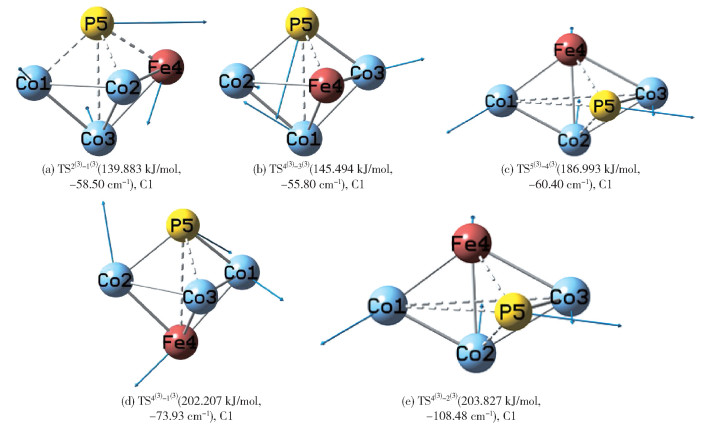
虚线表示生成键或断裂键,实线表示未改变键,箭头方向表示原子位移的方向,箭头长度表示原子位移的大小,括号内的负值(如-58.50 cm-1等)表示其虚频值。 图 2 团簇Co3FeP的过渡态(TS)构型图 Fig.2 Transition state (TS) configuration diagrams of the Co3FeP cluster |
在异构转化过程中,结合已有的计算数据对过渡态构型中的虚线进行分析可得,在所有的异构化反应中,发生Co1-P5键生成的反应有2(3)→1(3)(表示构型2(3)向1(3)的异构转化反应,反应命名规则下同)、4(3)→2(3)和5(3)→4(3),而发生Co1-P5键断裂的反应只有4(3)→3(3);对于Co2-P5键而言,发生键生成的反应有2(3)→1(3)、4(3)→2(3)和5(3)→4(3),并且这些异构转化反应均未发生键断裂;对于Fe4-P5键而言,发生键生成的反应有2(3)→1(3)、4(3)→1(3)和4(3)→3(3),发生键断裂的反应有5(3)→4(3)和4(3)→2(3);对于Co3-P5而言,发生键断裂的反应只有2(3)→1(3)和4(3)→1(3),而没有反应发生键生成。同时,从图 2中可以看出,所有的键断裂和键生成只发生在金属原子和非金属原子之间,说明金属原子与非金属原子所成的键对构型的稳定性有着至关重要的影响。
2.2 团簇Co3FeP异构转化的热力学分析 2.2.1 团簇Co3FeP的热力学参数在化学热力学中,物质的热力学能(U)、吉布斯自由能(G)、焓(H)、熵(S)是很多热力学研究的基本参数,因此为了深入研究团簇Co3FeP在热力学中异构化转化情况,将所有上述基本参数的数据列于表 1中。由化学热力学中对G、H、S的定义式可得:G=H-TS,U=H-pV,所以,H-U=pV,U-G=TS-pV,式中,T表示热力学温度,p表示压强,V表示体积。由表 1可得H-U和U-G均为正值,且H-U大于U-G,说明构型的熵值对其能量的影响比其体积值对能量的影响更大。
| 下载CSV 表 1 团簇Co3FeP优化构型的热力学参数 Table 1 Thermodynamic parameters of the optimized configurations of the Co3FeP cluster |
根据表 1中的数据,以不同构型作为研究对象,可以发现,所有构型的热力学能、吉布斯自由能和焓的大小顺序均满足:1(3) < 2(3) < 3(3) < 4(3) < 5(3);对于熵而言,虽然所有构型均为C1对称,但构型5(3)作为类平面结构更容易自发变形,所以构型5(3)的熵最大,这说明构型的空间结构对其熵有影响。
2.2.2 团簇Co3FeP异构化反应的限度和方向在进行异构化反应理论计算时,环境压强设置为101 325 Pa,温度设置为298.15 K,由范特霍夫方程(Van't Hoff equation)(式(2))和表 1中的数据,可计算出异构化反应的平衡常数K,进而可以对异构化反应的限度进行讨论,K的计算结果列于表 2中。
| $ \ln K=-\frac{\Delta H}{R T}+\frac{\Delta S}{R} $ | (2) |
| 下载CSV 表 2 团簇Co3FeP异构化反应的平衡常数K Table 2 Equilibrium constant K of the isomerization reaction of the Co3FeP cluster |
式中,ΔH表示反应的焓变,R为摩尔气体常数,T为热力学温度,ΔS为反应的熵变。
对于一个反应而言,平衡常数K的大小反映了化学反应进行的程度(即反应限度)。K值越大,说明该反应正向进行得越完全,平衡体系中生成物所占的比例越大;反之,反应越不完全,生成物所占的比例越小。对于一般反应而言,当K>105时,该反应正向进行的限度远大于逆向进行的限度;当10-5<K<105时,该反应正向进行的限度和逆向进行的限度相近;当K<10-5时,该反应正向进行的限度远小于逆向进行的限度。
根据表 2中的数据不难发现,在已有的异构化反应中,只有反应2(3)→1(3)和5(3)→4(3)的平衡常数小于105,而其他反应均大于105,说明反应2(3)→1(3)和5(3)→4(3)的反应程度不太彻底,反应物和生成物二者的转化率相差不大,而其他异构化反应的正反应限度远大于逆反应限度,反应程度较为彻底,反应正向进行的转化率接近100%。
除了对上述已存在的异构化反应的讨论外,通过范特霍夫方程和表 1中各优化构型的热力学参数,可以对任意一个异构化反应的限度进行预测,将部分异构化反应的预测结果列于表 3中。由表 3可得,所有异构化反应的K值均大于105,说明这些异构化反应进行得较为完全。
| 下载CSV 表 3 团簇Co3FeP异构化反应的平衡常数K的预测 Table 3 Prediction of the equilibrium constant K of the isomerization reaction of the Co3FeP cluster |
在一个反应中,吉布斯自由能变ΔG、焓变ΔH和熵变ΔS对于一个反应能否自发进行和进行方向有着至关重要的影响,ΔG<0在理论上可视为该反应能自发进行,ΔH<0表示反应为放热反应。因此通过对表 2和表 3中的数据分析可得,所有已存在和预测的异构化反应在理论上均能自发进行并且为放热反应。同时,由吉布斯-亥姆霍兹方程(Gibbs-Helmholtz equation)(ΔG=ΔH-TΔS)可得,在已存在的异构化反应中,由于反应4(3)→2(3)和5(3)→4(3)的熵变小于0,所以为了使反应的吉布斯自由能变小于0,需要较低的温度来抵消熵变小于0的影响,进而说明这两个异构转化反应在低温下易于自发进行。对于表 2中其他已存在的反应而言,由于ΔH<0,ΔS>0,说明在理论上这些已存在的反应在任何温度下均能自发进行。同理,通过对表 3中的预测反应分析可得,这些反应需要在较低的温度下才能自发进行。
2.3 团簇Co3FeP异构转化的动力学分析 2.3.1 团簇Co3FeP异构转化过程的活化能由于过渡态的能量对确定异构转化反应的活化能有重要作用,所以对过渡态构型使用二次收敛自洽场(SCF)流程的方法,近似求出其总能量。EaF表示异构化反应正向进行的活化能,EaB表示异构化反应逆向进行的活化能,结果如表 4所示。为了更直观地展现构型异构转化反应过程中能量的变化,依据表 4中的相关数据绘制出图 3。
| 下载CSV 表 4 团簇Co3FeP异构化反应的总能量及活化能 Table 4 Total energy and activation energy of the isomerization reaction of the Co3FeP cluster |

|
图 3 团簇Co3FeP异构化反应的势能面图 Fig.3 Potential energy surface diagram of the isomerization reaction of the Co3FeP cluster |
因为反应的活化能越大,反应越不容易进行,所以由表 4中的相关数据可发现,所有异构转化反应的EaF均小于EaB,说明在所有异构化反应中正向反应比逆向反应更容易进行,即能量高的构型更容易转化为能量低的构型。同时,由图 3可以发现,构型4(3)存在的异构转化反应最多,并且在4(3)→1(3)和4(3)→2(3)的异构转化中,构型4(3)生成过渡态的活化能相近(二者的差值仅为1.620 kJ/mol),说明构型4(3)生成过渡态构型
根据单分子反应完成97%时需要的反应时间t=-(ln0.03)/k
(其中
由图 3不难发现,理论上构型1(3)所拥有的能量最低且为所有异构化反应的最终产物。但在常温常压下,对于构型2(3)而言,由上述分析结论可得反应2(3)→1(3)很难发生,且构型2(3)转化为构型4(3)的活化能(183.932 kJ/mol)远大于88 kJ/mol,所以构型2(3)可以稳定存在。对于构型3(3)而言,由上述关于反应4(3)→3(3)的分析可得构型3(3)可以稳定存在。而对于构型4(3)而言,虽然在反应5(3)→4(3)中可以稳定存在,但在反应4(3)→1(3)、4(3)→2(3)和4(3)→3(3)中构型4(3)不能稳定存在,会迅速转化为对应的生成物,使构型4(3)迅速减少,导致反应5(3)→4(3)向正反应方向移动,进而促使构型5(3)转化为构型4(3)。同时,由于构型5(3)与构型4(3)的异构化反应中能量最高的过渡态构型
综上所述,在常温常压下,构型1(3)、2(3)和3(3)可以稳定存在,而构型4(3)和构型5(3)则会通过相关异构化反应转化为构型1(3)、2(3)和3(3)。
2.3.2 团簇Co3FeP异构化反应的反应速率及平衡常数过渡态理论认为生成物需要经历一个高能量的过渡状态(活化络合物),才能生成产物。同时,假设活化络合物可以生成产物,也可以返回为反应物,且返回到反应物的速率大于生成产物的速率,所以当反应物与活化络合物之间达到平衡时,反应的速率由活化络合物生成产物的速率来决定。
根据过渡态理论中实际速率常数
| 下载CSV 表 5 团簇Co3FeP异构化反应的反应速率常数和平衡常数 Table 5 Reaction rate constant and equilibrium constant of the isomerization reaction of the Co3FeP cluster |
对于同一反应而言,反应速率越大,反应进行得越快。观察表 5中的数据,可以发现所有异构化反应的正反应速率常数均大于逆反应速率常数,说明所有异构化反应均为正向进行的反应。并且除构型3(3)外,其他所有构型均可通过进行若干个异构化反应转变为构型1(3),即构型1(3)是大部分异构化反应的最终产物,说明构型1(3)最为稳定。根据2.2.2节中对反应限度的判断定义,结合表 5中的数据可以发现,反应2(3)→1(3)和5(3)→4(3)的K值依然小于105,而其他反应的K值仍大于105,这验证了上述结论:反应2(3)→1(3)和5(3)→4(3)不太彻底,其他异构化反应较为彻底。
将表 5中平衡常数K的数据和表 2中的数据相比对,可以发现不论是从化学热力学的角度,还是从化学动力学的角度对K值进行计算,二者所得出的值在数量级上基本一致,说明二者所得到的关于反应限度的结论是基本一致的。
2.3.3 团簇Co3FeP构型的结构复杂度由过渡态理论和阿伦尼乌斯公式(k=
| $ A=\left(k_{\mathrm{B}} T / h\right) \times\left(\mathrm{e}^{\Delta S / R}\right) $ |
式中,kB为玻耳兹曼常数,h为普朗克常数。由此可以发现指前因子A与反应活化过程的熵变有着密切联系。同时,因为活化络合物比反应物分子的熵值小,所以反应物结构越复杂,活化过程中的熵变、指前因子与反应速率常数也越小。因此以过渡态构型作为每个反应的结构复杂度的基准,以正、逆反应指前因子的大小作为每个反应中构型复杂度的比较值。将过渡态构型的熵值和指前因子A的相关计算结果列于表 6中。
| 下载CSV 表 6 过渡态构型的熵及异构化反应的指前因子 Table 6 Entropy of transition state configurations and pre-exponential factor of the isomerization reactions |
从表 6中指前因子的相关数据可以发现,在反应2(3)→1(3)中,正反应的指前因子大于逆反应的指前因子,表明构型1(3)的结构复杂度比构型2(3)高;同理,对反应4(3)→1(3)、4(3)→2(3)、4(3)→3(3)和5(3)→4(3)的正、逆反应指前因子进行分析可得,4(3)的结构复杂度比构型1(3)、3(3)和5(3)低,比构型2(3)高。综上所述,优化构型的结构复杂度的大小关系应满足:1(3)>4(3)>2(3),3(3)>4(3),5(3)>4(3)。同时,因为构型的熵值与结构复杂度的大小关系相同,所以结合表 1中各构型的熵值不难发现,其熵值大小也满足上述关系,并且根据表 1可将大小关系进一步简化为:5(3)>3(3)>1(3)>4(3)>2(3),这不仅说明构型5(3)的结构复杂度最高,也再次说明化学反应的动力学与热力学分析结论的一致性和可相互验证性。
3 结论本文利用密度泛函理论对团簇Co3FeP及异构化反应进行计算,从化学反应热力学和动力学的角度出发,以范特霍夫方程、吉布斯-亥姆霍兹方程、活化能、过渡态理论和阿伦尼乌斯公式作为切入点进行讨论,得出以下结论:
(1) 根据对过渡态构型中成断键的分析可得,构型的稳定性主要由金属原子与非金属原子所成的键决定,所以在实际开发中应注意金属原子与非金属原子之间的作用力。
(2) 虽然所有构型均为C1对称,但构型5(3)的熵值最大、结构复杂度最高,表明构型的空间结构对其熵值有影响。
(3) 所有异构化反应的正反应速率常数均大于逆反应速率常数,说明所有异构化反应正向进行的速率更大。
(4) 反应2(3)→1(3)在常温下较难发生;反应5(3)→4(3)在常温下的正、逆反应限度相近且二者均可发生;反应4(3)→1(3)和4(3)→2(3)的正反应在常温下进行得较为完全且更容易发生,逆反应几乎不进行且很难发生;反应4(3)→3(3)的正、逆反应在常温下均能进行,但正反应更容易发生且进行得更彻底。
(5) 构型1(3)、2(3)和3(3)较为稳定,是异构化反应的最终产物,因此在相关材料的开发中,应首先考虑这3种构型。
| [1] |
SHARKO S A, SEROKUROVA A I, ZUBAR T I, et al. Multilayer spin-valve CoFeP/Cu nanowires with giant magnetoresistance[J]. Journal of Alloys and Compounds, 2020, 846: 156474. DOI:10.1016/j.jallcom.2020.156474 |
| [2] |
XIAO J H, ZHOU H, WANG S, et al. A collaborative strategy for boosting lithium storage performance of iron phosphide by fabricating hollow structure and doping cobalt species[J]. Chemistry Select, 2020, 5(36): 11378-11382. |
| [3] |
SHEN Y, ZHENG X C, ZHENG G P. Mechanical properties and crystallization behaviors of microstructured Co-Fe-P amorphous alloys[J]. Metallurgical and Materials Transactions A, 2011, 42(1): 211-218. DOI:10.1007/s11661-010-0437-6 |
| [4] |
PENG Z, QIU X Y, CAI G Y, et al. Simultaneous tuning of the cation content and pore structure of cobalt-iron bimetal phosphide to enhance the electrochemical oxygen evolution[J]. Journal of Alloys and Compounds, 2020, 842: 155784. DOI:10.1016/j.jallcom.2020.155784 |
| [5] |
YAO R, WU Y, WANG M H, et al. Amorphous CoFeP/NC hybrids as highly efficient electrocatalysts for water oxidation[J]. International Journal of Hydrogen Energy, 2019, 44(57): 30196-30207. DOI:10.1016/j.ijhydene.2019.09.214 |
| [6] |
TASLIMI H, SOHI M H, MEHRIZI S, et al. Studies of the effects of addition of P and Cr on microstructure and electrical resistivity of nanocrystalline CoFe thin films[J]. Journal of Materials Science: Materials in Electronics, 2015, 26(5): 2962-2968. DOI:10.1007/s10854-015-2783-z |
| [7] |
ZHENG G P, LU X, HAN Z. Synthesis and electro-magneto-mechanical properties of graphene aerogels functionalized with Co-Fe-P amorphous alloys[J]. Micromachines, 2016, 7(7): 117. DOI:10.3390/mi7070117 |
| [8] |
LI D, ARACHCHIGE M P, KULIKOWSKI B, et al. Control of composition and size in discrete CoxFe2-xP nanoparticles: consequences for magnetic properties[J]. Chemistry of Materials, 2016, 28(11): 3920-3927. DOI:10.1021/acs.chemmater.6b01185 |
| [9] |
ZHAO C H, WEI F, LV H L, et al. Fe (Ⅲ) ions-assisted aniline polymerization strategy to nitrogen-doped carbon-supported bimetallic CoFeP nanospheres as efficient bifunctional electrocatalysts toward overall water splitting[J]. Materials, 2021, 14(6): 1473. DOI:10.3390/ma14061473 |
| [10] |
HUANG X K, GONG L, XU H, et al. Hierarchical iron-doped CoP heterostructures self-assembled on copper foam as a bifunctional electrocatalyst for efficient overall water splitting[J]. Journal of Colloid and Interface Science, 2020, 569: 140-149. DOI:10.1016/j.jcis.2020.02.073 |
| [11] |
LIU S L, MU X Q, JI P X, et al. Constructing a rod-like CoFeP@Ru heterostructure with additive active sites for water splitting[J]. ChemCatChem, 2020, 12(20): 5149-5155. DOI:10.1002/cctc.202000911 |
| [12] |
MUTHURASU A, OJHA G P, LEE M, et al. Integration of cobalt metal-organic frameworks into an interpenetrated Prussian blue analogue to derive dual metal-organic framework-assisted cobalt iron derivatives for enhancing electrochemical total water splitting[J]. The Journal of Physical Chemistry C, 2020, 124(27): 14465-14476. DOI:10.1021/acs.jpcc.0c03086 |
| [13] |
DU Y M, QU H Q, LIU Y R, et al. Bimetallic CoFeP hollow microspheres as highly efficient bifunctional electrocatalysts for overall water splitting in alkaline media[J]. Applied Surface Science, 2019, 465: 816-823. DOI:10.1016/j.apsusc.2018.09.231 |
| [14] |
WANG T Y, WANG C, JIN Y, et al. Amorphous Co-Fe-P nanospheres for efficient water oxidation[J]. Journal of Materials Chemistry A, 2017, 5(48): 25378-25384. DOI:10.1039/C7TA08720A |
| [15] |
徐诗浩, 方志刚, 韩建铭, 等. 团簇V3B2成键及磁学性质研究[J]. 广西师范大学学报(自然科学版), 2017, 35(3): 89-96. XU S H, FANG Z G, HAN J M, et al. Bonding and magnetic properties of cluster V3B2[J]. Journal of Guangxi Normal University (Natural Science), 2017, 35(3): 89-96. (in Chinese) |
| [16] |
王美玲, 方志刚, 秦渝, 等. 团簇NiMo3P极化率与催化性质的研究[J]. 北京化工大学学报(自然科学版), 2020, 47(5): 38-45. WANG M L, FANG Z G, QIN Y, et al. Polarizability and catalytic properties of NiMo3P clusters[J]. Journal of Beijing University of Chemical Technology (Natural Science), 2020, 47(5): 38-45. (in Chinese) |
| [17] |
秦渝, 方志刚, 张伟, 等. 团簇Co3NiB催化析氢活性研究[J]. 江西师范大学学报(自然科学版), 2020, 44(1): 56-62. QIN Y, FANG Z G, ZHANG W, et al. The study on the catalytic properties of cluster Co3NiB in the hydrogen evolution reaction[J]. Journal of Jiangxi Normal University (Natural Science), 2020, 44(1): 56-62. (in Chinese) |
| [18] |
李雯博, 方志刚, 赵振宁, 等. 团簇Co5B2反应活性的DFT研究[J]. 广西师范大学学报(自然科学版), 2017, 35(4): 76-83. LI W B, FANG Z G, ZHAO Z N, et al. DFT study on the reactive activity of cluster Co5B2[J]. Journal of Guangxi Normal University (Natural Science), 2017, 35(4): 76-83. (in Chinese) |
| [19] |
HAY P J, WADT W R. Ab initio effective core potentials for molecular calculations-potentials for the transition metal atoms Sc to Hg[J]. The Journal of Chemical Physics, 1985, 82(1): 270-283. DOI:10.1063/1.448799 |
| [20] |
李历红, 方志刚, 赵振宁, 等. 团簇Ni3CoP电子性质与磁性研究[J]. 江西师范大学学报(自然科学版), 2019, 43(2): 160-166. LI L H, FANG Z G, ZHAO Z N, et al. The study on the electronic and magnetic properties of cluster Ni3CoP[J]. Journal of Jiangxi Normal University (Natural Science), 2019, 43(2): 160-166. (in Chinese) |
| [21] |
FANG Z G, HU H Z, GUO J X. Quantum chemical study on geometry and property of cluster Ni4P[J]. Chinese Journal of Structural Chemistry, 2006, 25(1): 7-16. |
| [22] |
秦渝, 方志刚, 赵璐璐, 等. 团簇Co3NiB2异构化反应的动力学与热力学研究[J]. 江西师范大学学报(自然科学版), 2021, 45(1): 67-74. QIN Y, FANG Z G, ZHAO L L, et al. The study on the dynamics and thermodynamics of isomeric transformation of cluster Co3NiB2[J]. Journal of Jiangxi Normal University (Natural Science), 2021, 45(1): 67-74. (in Chinese) |








