2. 福建省船舶与海洋工程重点实验室, 厦门 361021;
3. 厦门大学 航空航天学院, 厦门 361102
2. Fujian Provincial Key Laboratory of Marine and Offshore Engineering, Xiamen 361021;
3. School of Aerospace Engineering, Xiamen University, Xiamen 361102, China
固体氧化物燃料电池(solid oxide fuel cell, SOFC)的工作温度在600~1 000 ℃之间,是一种很有前途的可持续能源转换装置,具有广泛的应用前景。该装置的优点是效率高、燃料灵活、污染物排放低,并且可以与热电联产利用SOFC产生的余热实现能量的充分利用。然而较高的工作温度也给该技术带来严峻的挑战,如材料的选择、热管理、可靠性和耐久性等等。与温度及其分布相关的热管理因可以对电池完整性、电池电压、电流密度分布和功率输出等方面产生直接影响,是决定电池性能和堆栈行为的关键因素[1-3]。
SOFC是一种大时滞、强耦合和非线性的动态装置,分析其动态特性行为需要精确的动力学模型。目前学界已在SOFC的非线性动力学建模方面取得许多进展[4-6]。这些模型适合用于电堆结构的设计和优化,但对于控制器的设计来说却过于复杂。因此为提高SOFC的寿命和性能,采取现代控制策略作为SOFC的电控器算法势在必行。燃料利用率、堆栈终端电压和堆栈内温度是SOFC系统控制的3个最重要变量,其中燃料利用率和堆栈终端电压对负载的阶跃变化的响应速度较快,且具有较强的非线性,因此采用模型预测控制(model predictive control,MPC)对其进行控制;而堆栈内温度对负载阶跃变化的响应速度缓慢,传统的比例积分微分(proportion integration differentiation,PID)控制即可以满足控制需求。MPC是近年来备受关注的一种先进控制方法[7-9]。文献[10]针对燃料流量和燃料利用率,在现有技术的约束条件下提出一种约束计算有效的非线性模型预测控制算法。文献[11]针对SOFC系统实际操作中存在的问题,提出一种带区域跟踪的SOFC系统模糊模型预测控制方法,将模糊模型与预测控制相结合以达到控制要求。文献[12]提出了高温管式SOFC的动态准二维模型,并结合喷射器和预转化器模型,使用受限的多输入多输出(multi-input multi-output,MIMO)模型预测控制算法进行闭环仿真,仿真结果证明该算法可实现有效的负荷跟踪、可操作性的约束控制和抑制干扰。文献[13]基于带约束的收缩视界模型预测控制方法和基于虚拟参考反馈整定的数据驱动方法来识别控制器参数,结果表明两种控制方法均能在无超调或无超调的约束范围内提供鲁棒的功率跟踪性能。
为了满足直流负载电压的稳定性及SOFC的耐用性和安全性的要求,本文在保证燃料利用率处于设定值的前提下提出一种基于支持向量机(support vector machine,SVM)的非线性模型预测控制算法,用于控制堆栈电压。鉴于预测模型的预测精度和准确度直接影响预测控制的效果,因此采用人工蜂群算法(artificial bee colony algorithm,ABC)优化支持向量机,并利用Lipschitz quotients准则来确定ABC-SVM预测模型的输入阶数以达到提高预测模型精度和减小计算量的目的。仿真实验也验证了本文所提方法的有效性和优越性。
1 SOFC物理模型在本文的研究体系中,希望可以相对容易地对模型预测控制器进行设计,因此对其进行一些简化和假设。根据本文设计要求对SOFC系统作出如下假设:
1) 堆内充入的燃料和空气均为理想气体;
2) 由于气体分布的偏差很小,因此假设电池间的气体分布均匀;
3) 电池间没有热传递,每个电池都有相同的温度和电流密度;
4) 电堆和周围环境之间没有热交换;
5) 沿电极传输气体的通道有一个固定的体积和较小的尺寸,因此在电堆中有一个恒定的压力。
1.1 电堆电压在以氢气为燃料的燃料电池中,氢气在阳极表面释放电子,电子通过外部负载进入电池阴极与氧结合产生氧离子,氧离子通过电解质到达阳极与氢离子结合产生水。该过程如下。
| $ \text { 阳极 }\ \ \ \ \mathrm{H}_{2}+\mathrm{O}^{2-} \rightarrow \mathrm{H}_{2} \mathrm{O}+2 \mathrm{e}^{-} $ | (1) |
| $ \text { 阴极 } \quad \frac{1}{2} \mathrm{O}_{2}+2 \mathrm{e}^{-} \rightarrow \mathrm{O}^{2-} $ | (2) |
由于电极间存在电位差E从而发生氧化还原反应,电路中的离子流由Nernst方程表示
| $ E=E^{0}+\frac{R T}{2 F} \ln \frac{p_{\mathrm{H}_{2}} p_{\mathrm{O}_{2}}^{1 / 2}}{p_{\mathrm{H}_{2} \mathrm{O}}} $ | (3) |
式中,E0为标准电动势;R和F分别为通用气体常数和法拉第常数;T为堆栈内平均温度;pH2、pO2和pH2O分别为氢气、氧气和水蒸气的分压。
SOFC堆栈通常由多个单电池堆叠,则对于N0个串联堆叠的燃料电池,其堆栈终端电压(考虑电阻、活化、浓度损失)为
| $ V_{\mathrm{s}}=V_{0}-\eta_{\mathrm{Ohm}}-\eta_{\mathrm{con}}-\eta_{\mathrm{act}} $ | (4) |
式中,Vs为堆栈的终端电压;V0为堆栈的开路电压;ηOhm、ηact和ηcon分别为电阻损失电压、活化损失电压和浓度损失电压。
开路电压、电阻损失电压、活化损失电压和浓度损失电压的计算公式分别为
| $ V_{0}=N_{0} E^{0}+\frac{N R T}{2 F} \ln \frac{p_{\mathrm{H}_{2}} p_{\mathrm{O}_{2}}^{1 / 2}}{p_{\mathrm{H}_{2} \mathrm{O}}} $ | (5) |
| $ \eta_{\mathrm{Ohm}}=r(T) I $ | (6) |
| $ \eta_{\mathrm{act}}=a+b \lg I $ | (7) |
| $ \eta_{\mathrm{con}}=\frac{R T}{2 F} \ln \left(1-\frac{I}{I_{\mathrm{L}}}\right) $ | (8) |
式中,I为堆栈电流;电池电阻r(T)为关于电池温度T的函数;IL为堆栈的极限电流;a和b分别为Tafel常数和斜率[14]。
各气体分压根据Padullés等[15]提出的方法计算。
| $ p_{\mathrm{H}_{2}}(s)=\frac{1 / K_{\mathrm{H}_{2}}}{1+\tau_{\mathrm{H}_{2}} s}\left(q_{\mathrm{H}_{2}}^{\mathrm{in}}-2 K_{\mathrm{r}} I\right) $ | (9) |
| $ p_{0_{2}}(s)=\frac{1 / K_{\mathrm{O}_{2}}}{1+\tau_{\mathrm{O}_{2}} s}\left(q_{\mathrm{O}_{2}}^{\mathrm{in}}-K_{\mathrm{r}} I\right) $ | (10) |
| $ p_{\mathrm{H}_{2} \mathrm{O}}(s)=\frac{1 / K_{\mathrm{H}_{2} \mathrm{O}}}{1+\tau_{\mathrm{H}_{2} \mathrm{O}} s} 2 K_{\mathrm{r}} I $ | (11) |
式中,$K_{\mathrm{r}}=\frac{N_{0}}{4 F}$;qH2in、qO2in分别为入口氢气和氧气的摩尔流率;KH2、KO2和KH2O分别为氢气、氧气和水蒸气的阀摩尔常数;定义$\tau_{\mathrm{H}_{2}}=\frac{V_{\mathrm{an}}}{K_{\mathrm{H}_{2}} R T}$是与氢气流速相关的时间常数,仅为电池温度T的函数,其中Van为阳极室的体积,类似的得到τO2和τH2O。
1.2 燃料处理器富含氢元素的燃料(如天然气等)从燃料存储器经过燃料阀进入燃料处理器中,燃料处理器将富含氢元素的燃料转换为富含氢气的燃料和副产品。假设副产品与式(1)中的水蒸气完全反应。本文的燃料处理器模型采用一种简单的一阶传递函数,取燃料转换时间常数τf=5 s[1],则氢气入口流速的计算如式(12)所示。
| $ q_{\mathrm{H}_{2}}^{\mathrm{in}}=\frac{q_{\mathrm{f}}}{1+\tau_{\mathrm{f}} s} $ | (12) |
其中,根据式(1)、(2)可知氢气和氧气消耗的物质的量比为2 ∶1,但为保证氢气完全反应和调节温度需要过量的氧气,因此本文取氢气和氧气的流速比为1.145 ∶1[1]。
1.3 燃料利用率燃料利用率是SOFC重要的操作变量之一,燃料利用率的大小对电池堆栈有很大的影响。当燃料利用率较高时(高于0.9),意味着堆栈内的燃料浓度较低,对电堆会遭成不可逆的损害,从而大大削减电堆的使用寿命和性能;而当燃料利用率低于0.7时,则会造成燃料的浪费和终端电压的异常升高,当尾气处理不当时又会造成环境污染,严重时甚至可能发生爆炸,威胁到工作人员的生命安全[2]。
燃料利用率uc的定义为
| $ u_{\mathrm{c}}=\frac{q_{\mathrm{H}_{2}}^{\mathrm{in}}-q_{\mathrm{H}_{2}}^{\text {out }}}{q_{\mathrm{H}_{2}}^{\mathrm{in}}}=\frac{q_{\mathrm{H}_{2}}^{\mathrm{r}}}{q_{\mathrm{H}_{2}}^{\mathrm{in}}}=\frac{N I}{2 F q_{\mathrm{H}_{2}}^{\mathrm{in}}} $ | (13) |
式中,qH2out、qH2r分别为氢气出口和反应摩尔流速。假设在稳态下燃料利用率是恒定的,由式(13)可知电堆的电流与燃料输入量成正比,因此稳态下电堆的电流和燃料输入量关系为
| $ q_{\mathrm{H}_{2}}^{\mathrm{in}}=\frac{N I}{2 F u_{\mathrm{c}}} $ |
文献[1]表明堆栈稳态下燃料利用率应在0.7~ 0.9之间,本文取堆栈电流I=250 A,则稳态时燃料利用率uc=0.83。
2 SOFC控制策略 2.1 燃料利用率控制燃料利用率是SOFC的重要参数。考虑电堆的动态变化,当电流发生微小变化时保持燃料利用率恒定,则恒燃料利用率下的进口燃料流速的微小变化可以通过求解式(13)的全微分方程来表示。
| $ \Delta u_{\mathrm{c}}=\frac{N \Delta I}{2 F q_{\mathrm{H}_{2}}^{\mathrm{in}, 0}}-\frac{N I^{0} \Delta q_{\mathrm{H}_{2}}^{\mathrm{in}}}{2 F\left(q_{\mathrm{H}_{2}}^{\mathrm{in}, 0}\right)^{2}} $ | (14) |
式中,I0和qH2in, 0分别为标称堆栈电流和标称氢气流速。燃料利用率保持恒定,即Δuc=0,将其带入式(14)可得
| $ \Delta q_{\mathrm{H}_{2}}^{\mathrm{in}}=\frac{q_{\mathrm{H}_{2}}^{\mathrm{in}, 0}}{I^{0}} \Delta I $ |
燃料利用率控制策略如图 1所示。
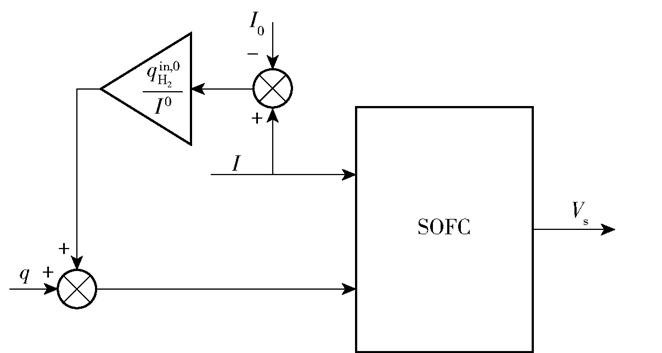
|
图 1 恒燃料利用率控制策略 Fig.1 Constant fuel utilization control strategy |
对于给定的训练样本D={(x1, y1), (x2, y2), …, (xm, ym)}, 构造非线性回归函数
| $ f\left(\boldsymbol{x}_{k}\right)=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{k}+b $ |
式中,xk=(x1, x2, …, xn)为k时刻的样本输入;b为偏置;w为法向量。支持向量机回归问题可转化为[16]
| $ \begin{aligned} &\min \limits_{\boldsymbol{w}, b, \xi, \xi^{*}} \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum\limits_{i=1}^{m}\left(\xi_{i}+\xi_{i}^{*}\right) \\ &\text { s.t. }\left\{\begin{array}{l} y_{i}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}-b \leqslant \varepsilon+\xi_{i} \\ \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b-y_{i} \leqslant \varepsilon+\xi_{i}^{*} \\ \xi_{i}, \xi_{i}^{*} \geqslant 0 \quad i=1,2, \cdots, m \end{array}\right. \end{aligned} $ | (15) |
式中,C为正则化常数;ξ,ξi*为松弛变量。引入拉格朗日乘子构建拉格朗日函数并借助其对偶问题来求解式(15),即
| $ \begin{aligned} &\max \limits_{\alpha, \alpha^{*}} \sum\limits_{i=1}^{m}\left[y_{i}\left(\alpha_{i}^{*}-\alpha_{i}\right)-\varepsilon\left(\alpha_{i}^{*}+\alpha_{i}\right)\right]- \\ \frac{1}{2} & \sum\limits_{i=1}^{m} \sum\limits_{j=1}^{m}\left(\alpha_{i}^{*}-\alpha_{i}\right)\left(\alpha_{j}^{*}-\alpha_{j}\right) \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}_{j} \\ &\text { s.t. }\left\{\begin{array}{l} \sum\limits_{i=1}^{m}\left(\alpha_{i}^{*}-\alpha_{i}\right)=0 \\ 0 \leqslant \alpha_{i}^{*}, \alpha_{i} \leqslant C \end{array}\right. \end{aligned} $ |
式中,αi*、αi为拉格朗日乘子。求解该问题得到最优的拉格朗日乘子,即可得到SVM的解为
| $ f\left(\boldsymbol{x}_{k}\right)=\sum\limits_{i=1}^{m}\left(\alpha_{i}^{*}-\alpha_{i}\right) \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}_{k}+b $ |
设ϕ (x)为x 映射后的特征向量,则其在特征空间对应的模型为
| $ f\left(\boldsymbol{x}_{k}\right)=\sum\limits_{i=1}^{m}\left(\alpha_{i}-\alpha_{i}^{*}\right) \boldsymbol{\phi}\left(\boldsymbol{x}_{k}\right)^{\mathrm{T}} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b $ |
根据Mercer条件, 核函数κ(xk, xi)= ϕ(xk)T · ϕ(xi),则SVM预测模型输出为
| $ f\left(\boldsymbol{x}_{k}\right)=\sum\limits_{i=1}^{m}\left(\alpha_{i}-\alpha_{i}^{*}\right) \boldsymbol{\kappa}\left(\boldsymbol{x}_{k}, \boldsymbol{x}_{i}\right)+b $ |
本文取核函数为高斯核函数(径向基函数)
| $ \boldsymbol{\kappa}\left(\boldsymbol{x}_{k}, \boldsymbol{x}_{i}\right)=\exp \left(-\frac{\left\|\boldsymbol{x}_{k}-\boldsymbol{x}_{i}\right\|^{2}}{2 \sigma^{2}}\right) $ |
式中,σ为高斯核函数的带宽。
2.2.2 SOFC预测控制MPC是一种基于预测模型、滚动优化和误差校正的反馈控制策略。恒燃料利用率控制下SOFC电堆的ABC-SVM预测模型采用非线性自回归滑动平均模型(NARX)[17],表达式为
| $ \left\{\begin{array}{l} U(k+d)=f(U(k+d-1), \cdots, U(k+d-n), \\ \ \ \ \ \ \ q(k), \cdots, q(k-m), I(k), \cdots, I(k-m)) \\ \text { s.t. } q_{\min } \leqslant q(k) \leqslant q_{\max }, I_{\min } \leqslant I(k) \leqslant I_{\max }, \\ \ \ \ \ \ \ k=1,2, \cdots, N \end{array}\right. $ | (16) |
式中,q(k)和I(k)分别为燃料流速和电堆电流在k时刻的输入,U(k+d)为k时刻输入对应的输出,n和m分别为输入、输出的阶次,d为输出延迟。本文采用ABC-SVM对非线性f(·)进行估计,通过估计参数C和σ即可得到恒燃料利用率下电堆的非线性辨识模型为
| $ \begin{array}{l} \ \ \ \ \ \ \hat{U}(k+d)=\sum\limits_{i=1}^{N}\left(\alpha_{i}-\alpha_{i}^{*}\right) \exp \\ \left(-\frac{\left\|\boldsymbol{x}_{k}-\boldsymbol{x}_{i}\right\|^{2}}{2 \sigma^{2}}\right)+b \end{array} $ | (17) |
式中,$\widehat U$(k+d)为ABC-SVM模型预测的输出。人工蜂群算法是一种基于蜂群采蜜行为的仿生物智能全局优化算法[18],通过人工蜂群优化算法来估计SVM参数(C和σ),则优化问题可转化为
| $ \begin{aligned} &\ \ \ \ \ \ \min \limits_{C, \sigma} \frac{1}{N} \sum\limits_{k=1}^{N}[(\hat{U}(k)-U(k))]^{2} \\ &\text { s.t. } 0<C, \sigma \leqslant 1\ 000 \end{aligned} $ | (18) |
式中,N为训练数据的个数。本文选择的预测模型结构如式(16)所示,模型的结构完全由m和n决定。在近几十年的发展中,出现了许多选择非线性模型阶数的方法,本文采用He等[19]提出的Lipschitz quotients准则,根据输入输出数据决定非线性系统的结构。将式(16)结构改写为紧凑型
| $ U=f\left(x_{1}, x_{2}, \cdots, x_{k}\right) $ |
式中,k为输入变量数目,k=n+2m+2。设x =[x1, x2, …, xk]T,根据输入输出对(x(i), U(i))定义Lipschitz quotients为
| $ q_{i, j}^{(k)}=\frac{|U(i)-U(j)|}{|\boldsymbol{x}(i)-\boldsymbol{x}(j)|}, i \neq j $ | (19) |
式中,|x(i)- x (j)|为输入数据中两个不同点间的距离;|U(i)-U(j)|为输出数据中两个不同点间的距离。式(19)可以扩展为
| $ q_{i, j}^{(k)}=\frac{|U(i)-U(j)|}{\sqrt{\left(x_{1}(i)-x_{1}(j)\right)^{2}+\cdots+\left(x_{m}(i)-x_{m}(j)\right)^{2}}} $ |
根据文献[19]可知,qi, j(k)可用来判断是否缺少一个或者多个必要的输入变量,或包含一个或多个冗余的输入变量。例如,当缺少一个必要变量时,qi, j(k-1)要比qi, j(k)大甚至无法计算,相反当输入变量冗余时,qi, j(k+1)会比qi, j(k)或大或小但不明显。式(20)用来标识输入变量的最佳数目。
| $ q^{(k)}=\left(\prod\limits_{i=1}^{p} \sqrt{k} q^{(k)}(i)\right)^{\frac{1}{p}} $ | (20) |
式中,p∈[0.01N, 0.02N],q(k)(i)为第i个qi, j(k)的最大值。则式(20)的停止标准可定义为
| $ \frac{\left|q^{(k+1)}-q^{(k)}\right|}{\max \left(1,\left|q^{(k)}\right|\right)}<\varepsilon $ | (21) |
其中,ε=0.1即可满足所有的情况。
SOFC是一种大时滞、多输入且多输出的非线性系统。根据Lipschitz quotients准则,可以得到非线性自回归滑动平均模型最佳输入变量的阶数m和n。动力学模型的输入变量(q(k), I(k))、对应的输出电压U(k+d)以及ABC-SVM预测模型的输入变量则是根据动力学模型过去的输入输出和当前的输入组成,x (k)=[U(k+d-1), …, U(k+d-n), q(k), …, q(k-m), I(k), …, I(k-m)],可由ABC-SVM模型得到输出估计量$\widehat U$ (k+d)。在预测控制中,为了实现对未来输出的多步预测,本文根据式(16)、(17)建立p个串行的ABC-SVM模型,它们的原理相同,区别只是输入量在时间上的相继移位,从而达到p步预测的目的[7]。对于i步输入变量中过去时刻的电压值由i-1步的ABC-SVM预测模型的输出电压表示,因此p步预测输出通过第p个ABC-SVM模型获得,定义为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hat U(k + d + p) = f(\hat U(k + d + p - 1), \cdots ,U(k + d + \\ p - n),q(k + p), \cdots ,q(k + p - m),I(k + p), \cdots ,\\ I(k - m + p)) \end{array} $ |
堆栈实际输出电压和ABC-SVM预测输出电压的误差为
| $ e(k+d)=U(k+d)-\hat{U}(k+d) $ | (22) |
通过由式(22)得到的误差来修正ABC-SVM预测模型的输出电压$\widehat U$(k+d+p),获得修正后的预测输出电压为
| $ \begin{array}{l} \ \ \ \ U_{p}(k+d+j)=\hat{U}(k+d+j)+e(k+d), j=1,2, \\ \cdots, p \end{array} $ |
本文设计的模型预测控制算法框图如图 2所示,其中TDL为延时阵列。MPC控制器实际上是在一定范围内基于预定的输入值对系统未来动态行为进行预测,进而求解在该预定输入值下系统输出的最小化成本函数的非线性优化问题,因此成本函数的选择关系到控制的效果。本文的成本函数包括预测输出电压和期望轨迹的二次函数,同时包括防止燃料流速变化过大的二次函数。成本函数定义为
| $ \begin{aligned} &\quad F=\sum\limits_{i=1}^{n_{0}}\left[\left(y_{r}(k+d+i)-U_{p}(k+d+i)\right)\right]^{2}+ \\ &\sum\limits_{j=1}^{m_{0}}[(q(k+j)-q(k))]^{2} \\ &\quad \text { s.t. } q \in[0.6,1.2] \end{aligned} $ |
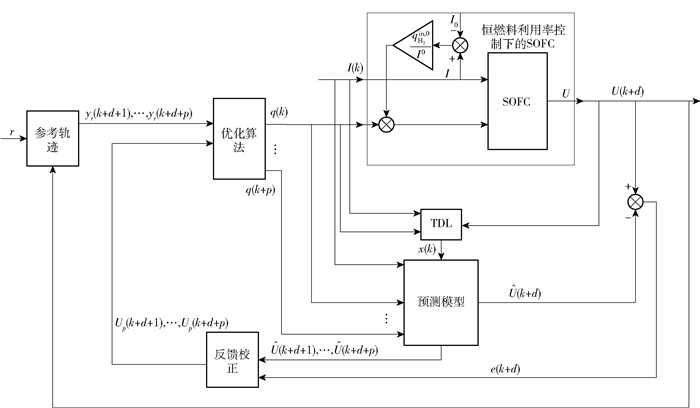
|
图 2 基于ABC-SVM模型的SOFC预测控制 Fig.2 SOFC predictive control based on the ABC-SVM model |
式中,yr为参考轨迹,q(k+j)为预测输入,n0为预测步长,m0为控制步长。
参考轨迹是通过将系统设置值r和SOFC动力学模型输出U进行比较得来,其定义为
| $ \begin{aligned} &\ \ \ \ y_{r}(k+d+i)=c^{i} U(k+d)+\left(1-c^{i}\right) r \quad(i=1, \\ &2, \cdots, p ; 0 \leqslant c \leqslant 1) \end{aligned} $ |
本文采用单步预测控制方法,因此为了获得最优的控制器输出q(k+1),采用黄金分割算法,该算法结构简单,可靠性强,是在实际中比较常用的一种在线优化算法。具体计算流程如下。
1) 设初始搜索区间为[a1, a2]=[qmin , qmax],定义搜索停止条件ξ,初始化k=1。初始搜索点为
| $ \begin{aligned} &a_{3}=a_{1}+0.382\left(a_{2}-a_{1}\right) \\ &a_{4}=a_{1}+0.618\left(a_{2}-a_{1}\right) \end{aligned} $ |
计算成本函数f3=F(a3)和f4=F(a4),并比较f3、f4。
2)若f3 < f4,则舍弃a2点,设新的搜索区间为[a1, a4]并作如下替换
| $ a_{2} \leftarrow a_{4}, a_{4} \leftarrow a_{3}, f_{4} \leftarrow f_{3} $ |
同时取新点a3=a1+0.382(a2-a1),并计算成本函数f3=F(a3)。
3) 若f3>f4,则舍弃a1点,设新的搜索区间为[a3, a2]并作如下替换
| $ a_{1} \leftarrow a_{3}, a_{3} \leftarrow a_{4}, f_{3} \leftarrow f_{4} $ |
同时取新点a4=a1+0.618(a2-a1),并计算成本函数f4=F(a4)。
4) 每次缩短区间后均进行一次判断,若满足
| $ \left|\frac{a_{1}-a_{2}}{a_{\min }-a_{\max }}\right| \leqslant \xi $ |
则停止迭代,返回最优点$q(k+1)=\frac{a_{1}+a_{2}}{2}$,k=k+1;否则返回步骤2)继续迭代。
本文设计的模型预测控制器为基于ABC-SVM的预测模型,预测模型算法流程如下。
1) 根据式(3)~(12)在Matlab/Simulink环境中建立SOFC动力学模型。
2) 采集数据。设q∈[0.6 1.2] mol/s,I∈[200 300]A,输入变量为均匀随机信号,收集输入、输出数据。
3) 数据归一化。归一化公式有很多种,为提高建模的精度和速度,本文选择归一化公式为$\frac{x_{i}-x_{i, \min }}{x_{i, \max }-x_{i, \min }}$。
4) 选择部分采集的数据计算出Lipschitz quotients,并确定SVM辨识模型的输入、输出阶数n和m。
5) 将采集的数据分为训练集和测试集,通过ABC算法优化SVM参数,并建立ABC-SVM预测模型。
3 仿真分析基于文献[6]和文献[13]给出的非线性SOFC动力学模型进行仿真,仿真平台为个人计算机,双核2.60 GHz内存,所有算法均采用Matlab/Simulink编程语言实现。
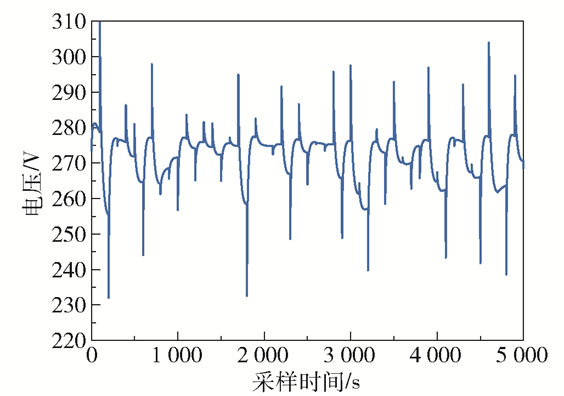
在数据采集阶段, 设q∈[0.6 1.2] mol/s,I∈[200 300] A,输入变量均由均匀随机序列产生,共采集t=5 000 s的数据,将前3 000 s数据作为训练集,后2 000 s数据作为测试集,燃料流速、电堆电流和电堆电压的采集数据分别如图 3~5所示。
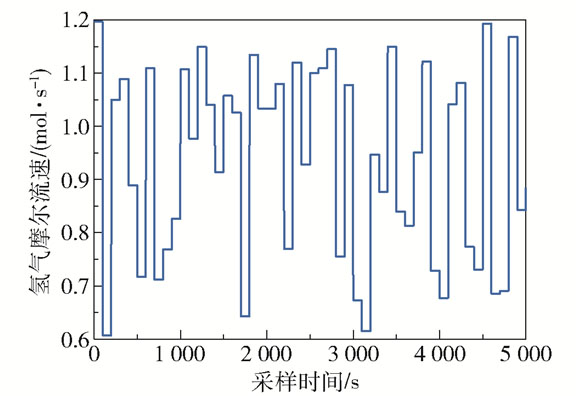
|
图 3 燃料流速 Fig.3 Fuel flow rate |
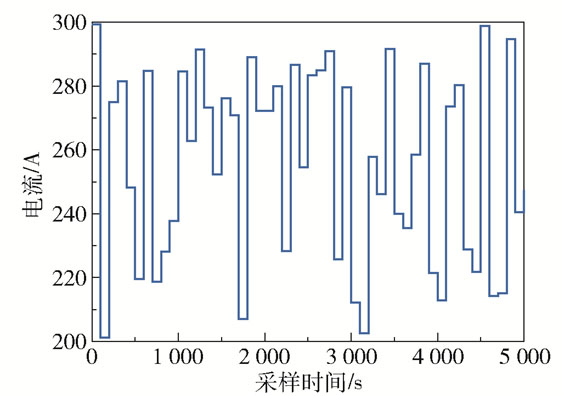
|
图 4 电堆电流 Fig.4 State current |
|
图 5 电堆电压 Fig.5 State voltage |
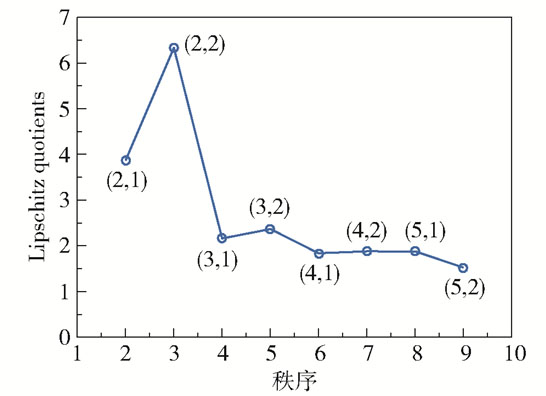
根据采集的输入、输出数据计算出Lipschitz quotients,并以此确定ABC-SVM辨识模型的结构。图 6显示了不同阶数的Lipschitz quotients,经计算在点(4,2)处满足停止条件(式(21)),因此确定非线性自回归滑动平均模型的最佳阶数为m=4和n=2。
|
图 6 Lipschitz quotients曲线 Fig.6 Lipschitz quotients curve |
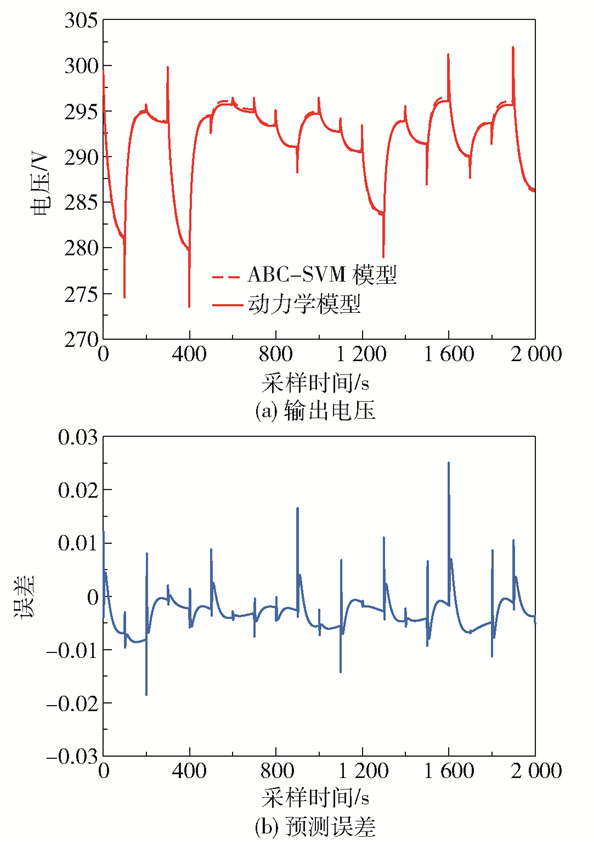
通过人工蜂群算法优化SVM参数进而得到堆栈的辨识模型,根据训练集训练ABC-SVM模型, 得到SVM的最优参数为C=485.207 9, σ=0.010 0。利用测试集测试所得到的ABC-SVM模型,测试结果如图 7所示。
|
图 7 动力学模型和ABC-SVM模型的输出结果 Fig.7 Output results of the kinetic model and the ABC-SVM model |
由图 7可知,ABC-SVM模型可以准确地预测堆栈的输出值。为显示所建模型的优越性,在相同的数据、初始条件和约束条件下将本文模型与支持向量机、遗传算法(genetic algorithm,GA)优化支持向量机(GA-SVM)、粒子群算法(particle swarm optimization, PSO)优化支持向量机(PSO-SVM)、误差反向传播(error back propagation, BP)神经网络和径向基函数(radical basis function, RBF)神经网络这5种算法进行了对比。将由式(18)计算的均方误差(MSE)作为算法的性能指标,仿真结果如表 1所示。
| 下载CSV 表 1 预测模型对比 Table 1 Comparison of prediction model |
由表 1可知,ABC-SVM模型在训练集和测试集上的均方误差相较于SVM、GA-SVM、PSO-SVM、BP和RBF均要更小,表明本文所建的ABC-SVM模型有着更高的精度和准确度,较符合预测控制对模型精度的设计需求。
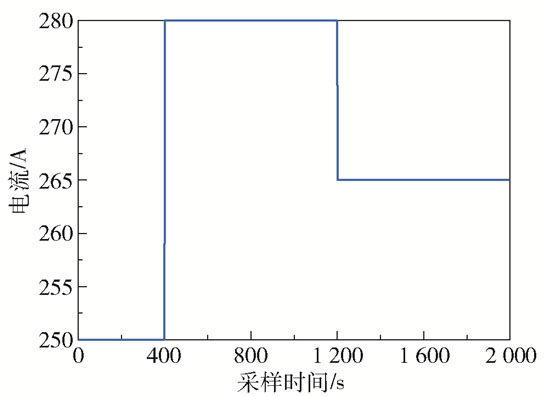
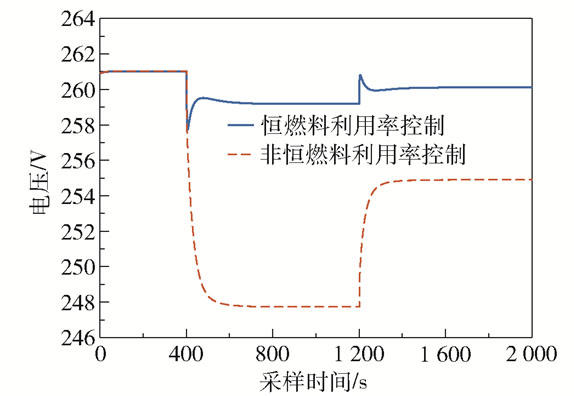
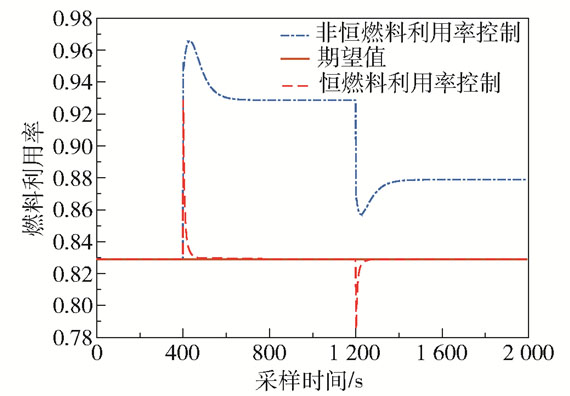
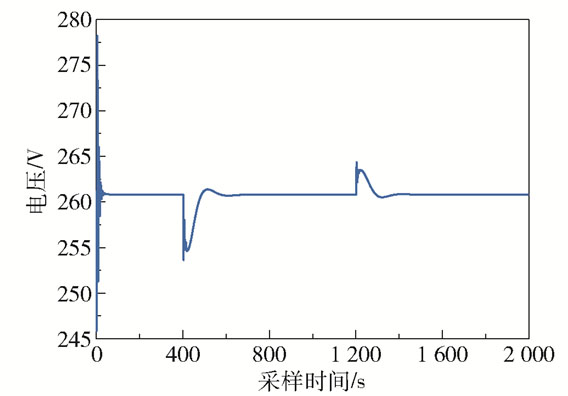
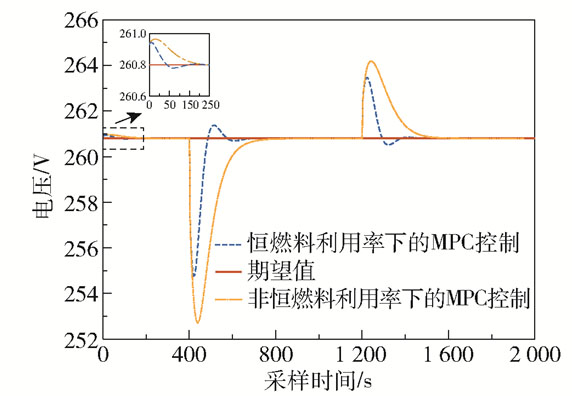
假设堆栈在稳态工作下的电流为250 A,堆栈的期望终端电压为261 V。假设负载电流轨迹如下:在t=400 s时,电流发生阶跃变化(由250 A阶跃至280 A);在t=1 200 s时,电流发生阶跃变化(由280 A阶跃至265 A),电流轨迹如图 8所示。当电流发生阶跃变化时,相对应的堆栈电压也发生变化,如图 9所示。从图 9可以看出在恒燃料利用率控制下电堆电压对电流的阶跃变化有更好的抵抗效果(电压变化量小以及达到稳态的时间短)。如图 10所示,在恒燃料利用率控制下,当干扰电流突变时可以控制燃料利用率稳定在设定值;相同条件下,当没有恒燃料利用率控制器的控制作用时燃料利用率有较长一段时间超过0.9,这将会损害堆栈的使用寿命和性能,在实验中是不允许发生的。图 11给出了k+1步预测模型的预测输出情况。为了进一步达到控制电堆电压的目的,在恒燃料利用率控制器作用下保持燃料利用率恒定,设计了一种基于支持向量机预测模型的预测控制器来控制堆栈电压,如图 12所示。由图 12的放大图可知当电堆启动和干扰电流突变时,恒燃料利用率控制下的堆栈预测控制电压超调较小且调节时间更短。在保证燃料利用率恒定的情况下,本文提出的预测控制算法既可以保证燃料利用率处于恒定值,也确保了堆栈电压能够跟踪电压设定值,且具有一定的自适应能力和鲁棒性。
|
图 8 负载电流阶跃 Fig.8 Load current step |
|
图 9 无MPC控制下的堆栈电压 Fig.9 Stack voltage without MPC control |
|
图 10 燃料利用率 Fig.10 Fuel utilization |
|
图 11 k+1步预测模型输出 Fig.11 k+1 step prediction model output |
|
图 12 MPC控制下的堆栈电压 Fig.12 Stack voltage under MPC control |
(1) 在考虑电堆浓度损耗的前提下提出ABC-SVM模型来识别输出电压和燃料流速之间的非线性动态行为,仿真实验结果表明了与传统的优化算法相比,所提ABC-SVM模型在模拟SOFC非线性动态特性方面有较好的精度和准确度。
(2) 燃料利用率是重要的控制变量之一,本文通过设计一种简单的控制回路,实现了对燃料利用率的恒定控制,并在此基础上提出一种基于ABC-SVM模型的非线性模型预测控制器,通过对氢气流速的控制实现了将堆栈电压稳定在设定值。仿真实验结果表明本文提出的控制策略既可以保持恒定的燃料利用率,又可以满足堆栈输出电压的控制要求。
| [1] |
TANG Y G, BU C N, LIU M M, et al. Application of ELM-Hammerstein model to the identification of solid oxide fuel cells[J]. Neural Computing and Applications, 2018, 29(2): 401-411. DOI:10.1007/s00521-016-2453-y |
| [2] |
AGUIAR P, ADJIMAN C S, BRANDON N P. Anode-supported intermediate-temperature direct internal reforming solid oxide fuel cell Ⅱ. Model-based dynamic performance and control[J]. Journal of Power Sources, 2005, 147(1): 136-147. |
| [3] |
FRENKEL W, RAUH A, KERSTEN J, et al. Experiments-based comparison of different power controllers for a solid oxide fuel cell against model imperfections and delay phenomena[J]. Algorithms, 2020, 13: 76. DOI:10.3390/a13040076 |
| [4] |
YU R, GUAN W B, ZHOU X D. Probing temperature inside planar SOFC short stack, modules, and stack series[J]. JOM, 2017, 69(2): 247-253. DOI:10.1007/s11837-016-2155-z |
| [5] |
CHENG H, JING S W, XU Y W, et al. Control-oriented modeling analysis and optimization of planar solid oxide fuel cell system[J]. International Journal of Hydrogen Energy, 2016, 41(47): 22285-22304. DOI:10.1016/j.ijhydene.2016.08.213 |
| [6] |
WU X L, XU Y W, ZHAO D Q, et al. Fault detection and assessment for solid oxide fuel cell system gas supply unit based on novel principal component analysis[J]. Journal of Power Sources, 2019, 436: 226864. DOI:10.1016/j.jpowsour.2019.226864 |
| [7] |
席裕庚. 预测控制[M]. 2版. 北京: 国防工业出版社, 2013: 149-152. XI Y G. Predictive control[M]. 2nd ed. Beijing: National Defense Industry Press, 2013: 149-152. (in Chinese) |
| [8] |
ZHENG Q G, XU Z G, ZHANG H B, et al. A turboshaft engine NMPC scheme for helicopter autorotation recovery maneuver[J]. Aerospace Science and Technology, 2018, 76: 421-432. DOI:10.1016/j.ast.2018.01.034 |
| [9] |
MORIYASU R, NOJIRI S, MATSUNAGA A, et al. Diesel engine air path control based on neural approximation of nonlinear MPC[J]. Control Engineering Practice, 2019, 91: 104114. DOI:10.1016/j.conengprac.2019.104114 |
| [10] |
ŁAWRYŃCZUK M. Constrained computationally efficient nonlinear predictive control of solid oxide fuel cell: tuning, feasibility and performance[J]. ISA Transactions, 2020, 99: 270-289. |
| [11] |
WU L, WU X, PAN L, et al. Fuzzy model predictive control of solid oxide fuel cell with zone tracking[J]. IFAC PapersOnLine, 2019, 52(4): 210-215. DOI:10.1016/j.ifacol.2019.08.180 |
| [12] |
SPIVEY B J, EDGAR T F. Dynamic modeling, simulation, and MIMO predictive control of a tubular solid oxide fuel cell[J]. Journal of Process Control, 2012, 22(8): 1502-1520. DOI:10.1016/j.jprocont.2012.01.015 |
| [13] |
CHEN S, KUMAR A, WONG W C, et al. Hydrogen value chain and fuel cells within hybrid renewable energy systems: advanced operation and control strategies[J]. Applied Energy, 2019, 233/234: 321-337. DOI:10.1016/j.apenergy.2018.10.003 |
| [14] |
SEDGHISIGARCHI K, FELIACHI A. Dynamic and transient analysis of power distribution systems with fuel cells—part Ⅰ: fuel-cell dynamic model[J]. IEEE Transactions on Energy Conversion, 2004, 19(2): 423-428. DOI:10.1109/TEC.2004.827039 |
| [15] |
PADULLÉS J, AULT G W, MCDONALD J R. An integrated SOFC plant dynamic model for power systems simulation[J]. Journal of Power Sources, 2000, 86(1/2): 495-500. |
| [16] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 121-139. ZHOU Z H. Machine learning[M]. Beijing: Tsinghua University Press, 2016: 121-139. (in Chinese) |
| [17] |
WU X J, ZHU X J, CAO G Y, et al. Predictive control of SOFC based on a GA-RBF neural network model[J]. Journal of Power Sources, 2008, 179(1): 232-239. DOI:10.1016/j.jpowsour.2007.12.036 |
| [18] |
靳方圆, 周海峰, 熊超. 基于ABC-SVM固体氧化物燃料电池电堆建模与仿真[J]. 集美大学学报(自然科学版), 2020, 25(4): 293-298. JIN F Y, ZHOU H F, XIONG C. Modeling and simulation of soild oxide fuel cell stack based on ABC-SVM[J]. Journal of Jimei University(Natural Science), 2020, 25(4): 293-298. (in Chinese) |
| [19] |
HE X D, ASADA H. A new method for identifying orders of input-output models for nonlinear dynamic systems[C]//1993 American Control Conference. San Francisco, 1993: 2520-2523.
|








