在发动机机械结构中存在着一些搭接结构组成的接合面,在高速旋转的情况下,这些接合面在法向存在接触、分离和碰撞等行为,在切向存在接触、滑移和干摩擦等行为。这些行为会引起系统结构在不同工作情况下发生动力学特性的改变,系统的振动响应也会随之发生变化[1-2],从而影响发动机的正常运转。因此对搭接、榫接摩擦结构转子的振动特性进行研究是很有必要的。
国内有许多学者对叶片间干摩擦结构的振动特性进行了研究。谢方涛等[3]研究了发动机中带冠叶片干摩擦搭接结构的动力学响应,用宏观滑动模型模拟提出了干摩擦扭转区域的数值计算方法,并通过有限元方法对结果进行了验证;龙伦等[4]研究了涡轮叶片带冠搭接结构的振动特性;袁巍等[5]研究了预扭叶片榫接结构的模态并开展了动应力试验,对叶片榫接结构的安装起到指导作用;郝淑英等[6]研究了连接结构松动的动力学特性,通过有限元方法探究连接刚度对双盘搭接系统固有频率和模态的影响;王本利等[7]研究了基于Iwan模型下的干摩擦转子的振动特性,得到了系统在轻微滑移下的振动的幅频曲线;李琳等[8]利用高阶谐波平衡法研究了叶片干摩擦搭接阻尼器对高阶激励的减振效果;李全通等[9]研究了榫接接触的叶片轮盘耦合的振动特性,分析了典型的叶盘搭接和榫接结构的接触刚度,并给出接触刚度的计算方法;陈香等[10]研究了叶片干摩擦阻尼结构的减振特性,通过试验分析了阻尼块与叶冠搭接结构在不同的搭接缝隙、搭接接触面积、接触面摩擦系数及材料下涡轮叶片的动力特性及减振效果。综上所述,目前国内的研究工作主要针对叶片间干摩擦结构的振动特性,用来指导叶片间干摩擦搭接结构的参数优化设计,但是对轮盘搭接摩擦结构的研究开展较少。而轮盘搭接结构目前在发动机如AL31-F航空发动机中存在实际应用,因此研究轮盘搭接结构的减振特性很有实际意义。
本文对某型燃气轮机压气机第三、第四级转子轮盘模型进行简化,研究了轮盘搭接结构的减振特性;搭建了轮盘搭接转子试验台、非搭接结构转子试验台和螺栓连接转子试验台,通过试验对比来分析搭接结构对转子系统振动的抑制效果。
1 搭接结构接触摩擦模型考虑到轮盘搭接结构接触面的干摩擦特性,采用带有迟滞特性的宏观滑移模型来模拟搭接结构的接触面摩擦。迟滞宏观滑移摩擦模型由理想库仑摩擦单元和1个线性弹簧串联起来组成[11]。
迟滞宏观滑移摩擦模型假设在搭接接触面间的摩擦滑移并不是突然发生的。当搭接接触面间的滑动载荷小于临界摩擦力时,接触点会存在一定的变形;随着振幅的增大, 滑动载荷大于临界摩擦力, 接触面间会产生相对滑移, 搭接转子振动时, 若两个搭接接触面的正压力为零, 即相邻两转盘间存在间隙, 则搭接结构间无摩擦, 两转盘接触面为自由滑动状态, 此时系统是线性的;若切向载荷始终小于接触面的摩擦力, 相邻转盘的搭接接触面之间会保持黏滞状态, 此时搭接阻尼结构只表现出刚度特性, 系统仍为线性系统;若临界摩擦力小于最大切向力, 则接触面既包括黏滞状态又包括滑动状态, 摩擦力与位移之间表现为一种非线性关系。此时的搭接接触面具有刚度特性和阻尼特性,通过改变搭接接触面的接触参数,即可以改变阻尼特性和减振效果。
采用迟滞宏观滑移模型对搭接接触摩擦面进行简化后, 研究搭接结构接触的阻尼转子系统的响应是一个复杂的非线性问题。关于摩擦接触动力学方程的求解方法主要有时域中的解析法和数值积分法,以及频域中的谐波平衡法(HBM)[12]和时-频交替法。
由于搭接结构接触摩擦中的非线性摩擦力较难求解,通常采用已经成功应用于阻尼结构优化设计中的谐波平衡法将非线性摩擦力转换为线性摩擦力,来对问题进行简化。本文采用一阶谐波平衡法,假设搭接摩擦结构的振动主要为基频振动, 只保留傅立叶级数中摩擦力展开项的一次项。用一阶谐波平衡法将搭接结构接触面的非线性摩擦力转化为等效刚度和等效阻尼对系统的影响。迟滞宏观滑移摩擦模型摩擦力的等效刚度及等效阻尼的计算式如式(1)、(2)所示[11]。
| $ k_{\mathrm{eq}}= \begin{cases}\frac{\mu N}{\pi B_{\mathrm{cr}}}\left(\frac{\theta^{*}-\sin 2 \theta^{*}}{2}\right), & B \geqslant B_{\mathrm{cr}} \\ k_{\mathrm{d}}=\frac{\mu N}{\pi B_{\mathrm{cr}}}, & B <B_{\mathrm{cr}}\end{cases} $ | (1) |
| $ C_{\mathrm{eq}}= \begin{cases}\frac{4 \mu N}{\pi \omega B_{\mathrm{cr}}^{2}}\left(B-B_{\mathrm{er}}\right), & B \geqslant B_{\mathrm{cr}} \\ 0, & B <B_{\mathrm{cr}}\end{cases} $ | (2) |
式中,keq为等效刚度;Ceq为等效阻尼;μ为动摩擦系数;ω为激振力频率;N为接触面正压力;B为接触面相对滑移幅值; Bcr=μN/kd为临界摩擦位移,kd为接触面剪切刚度;滞回模型参数θ*=arccos(1-Bcr/B)。
从式(1)、(2)可知,搭接结构接触面存在正压力,为系统提供了等效刚度,相当于提高了keq。当搭接接触面出现相对滑移时,即搭接结构转子工作时,搭接结构接触系统相对于非搭接结构转子存在一个等效阻尼项Ceq,对振动起削弱作用,通过摩擦耗散振动能量,从而达到减振效果。
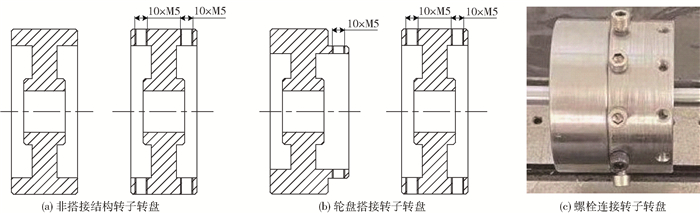
2 搭接结构减振试验 2.1 试验装置为了验证轮盘搭接摩擦结构对转子振动的抑制效果,设计了两盘无搭接、两盘搭接、螺栓连接(将两盘通过M5的螺栓连接)这3种试验转子(示意图见图 1),针对3种转子开展对比试验分析。
|
图 1 3种转子转盘示意图 Fig.1 Illustrations of the three types of rotor turntable |
轮盘搭接结构转子试验台、螺栓连接结构转子试验台及非搭接结构转子试验台分别如图 2(a)~(c)所示。试验转子轴由驱动电机通过柔性联轴器连接,转轴的直径为10 mm,转轴与转盘通过胀紧套连接在一起,两个轴承座间跨距为420 mm。试验过程中以电机主轴为水平基准,加速度传感器放置在右支撑上,测量转子在工作转速1 500 r/min下的径向加速度。

|
图 2 3种结构转子试验台 Fig.2 Test benches for the three types of rotors |
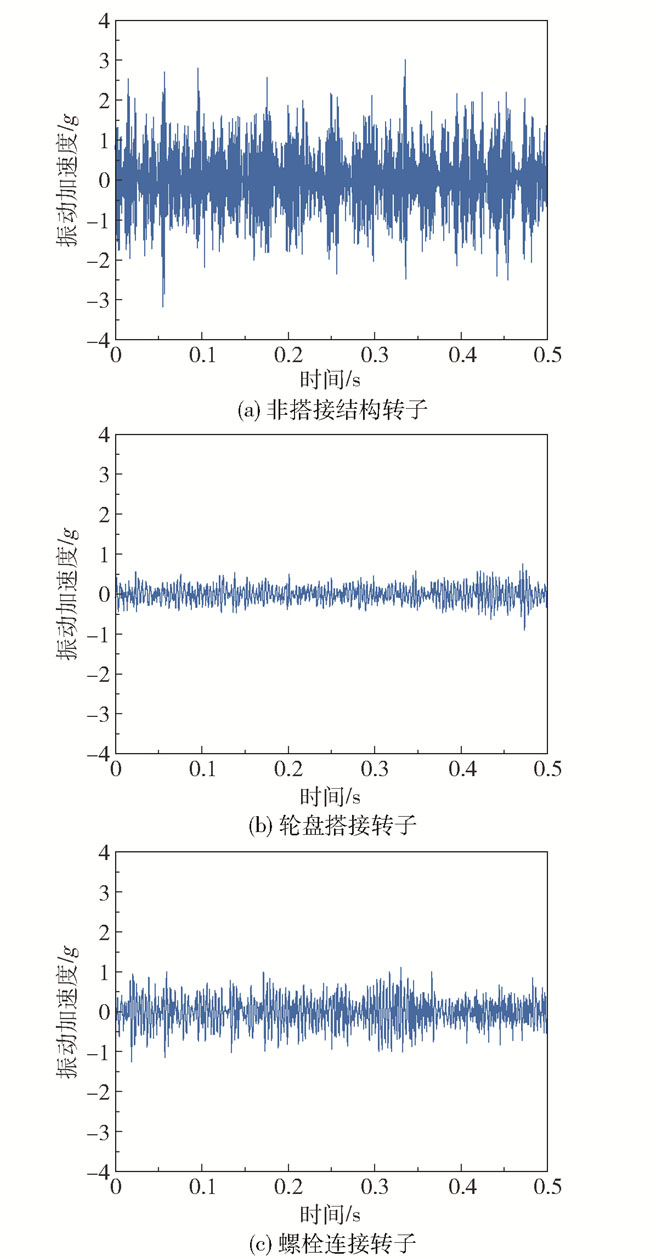
图 3是3种转子在1 500 r/min下的时域波形图,可以看出非搭接结构转子的振动加速度最大值达到3.176 g,轮盘搭接结构转子的振动加速度最大值减小到0.899 4 g,相对于非搭接结构转子降幅达到71.68%;螺栓连接结构转子的振动加速度最大值减小到1.256 g,相对于非搭接结构转子降幅为60.45%。
|
图 3 3种结构转子的时域波形图 Fig.3 Time-domain waveforms of the three types of rotors |
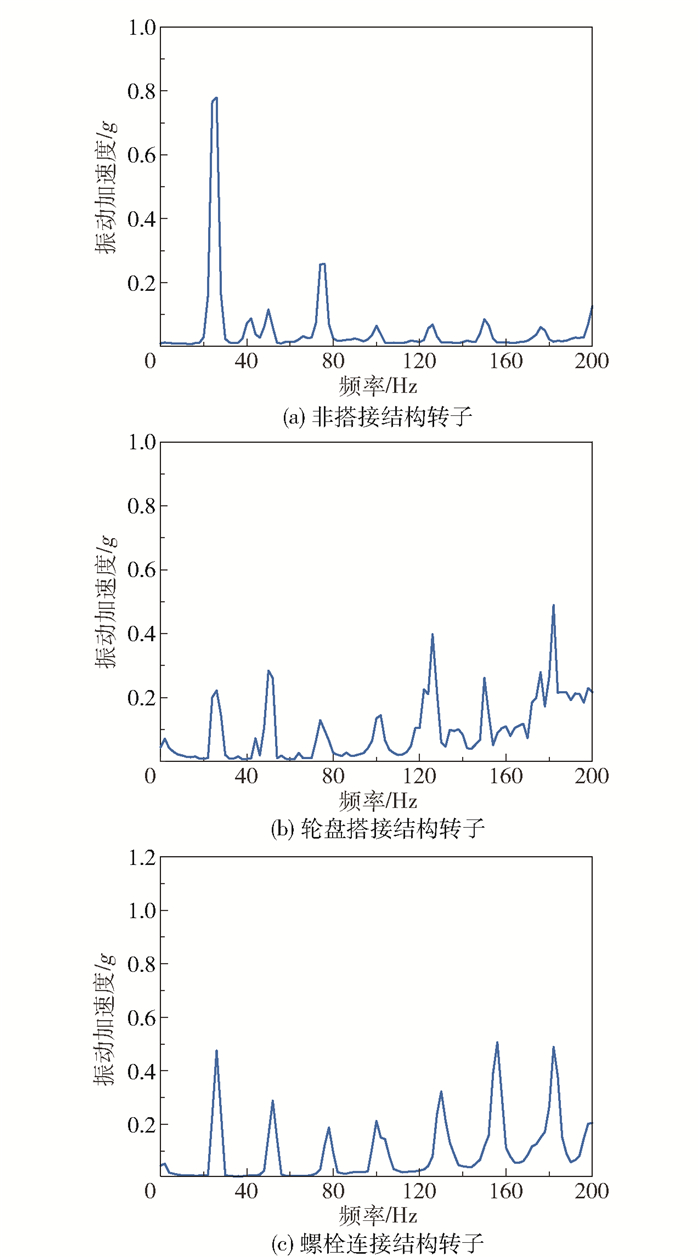
图 4(a)、(b)、(c)分别为非搭接转子、轮盘搭接转子、螺栓连接转子的频谱图。可以看出,在工频(25 Hz)上,采用轮盘搭接结构的振动加速度最小,非搭接结构转子的振动加速度最大,螺栓连接转子位于二者之间。且搭接结构转子和螺栓连接转子存在着较大的倍频分量,是明显的摩擦特征。在工频上,非搭接转子振动加速度为0.077 88 g,轮盘搭接结构转子振动加速度为0.022 15 g,与非搭接转子相比降幅为71.56%,螺栓连接转子振动加速度为0.047 59 g,与非搭接转子相比降幅为38.89%。螺栓连接结构增加了转子系统的刚度,可以降低转子振动;且搭接结构中存在摩擦耗散能量,对振动的削弱效果优于螺栓连接结构。
|
图 4 3种结构转子的频谱图 Fig.4 Spectrograms of the three types of rotors |
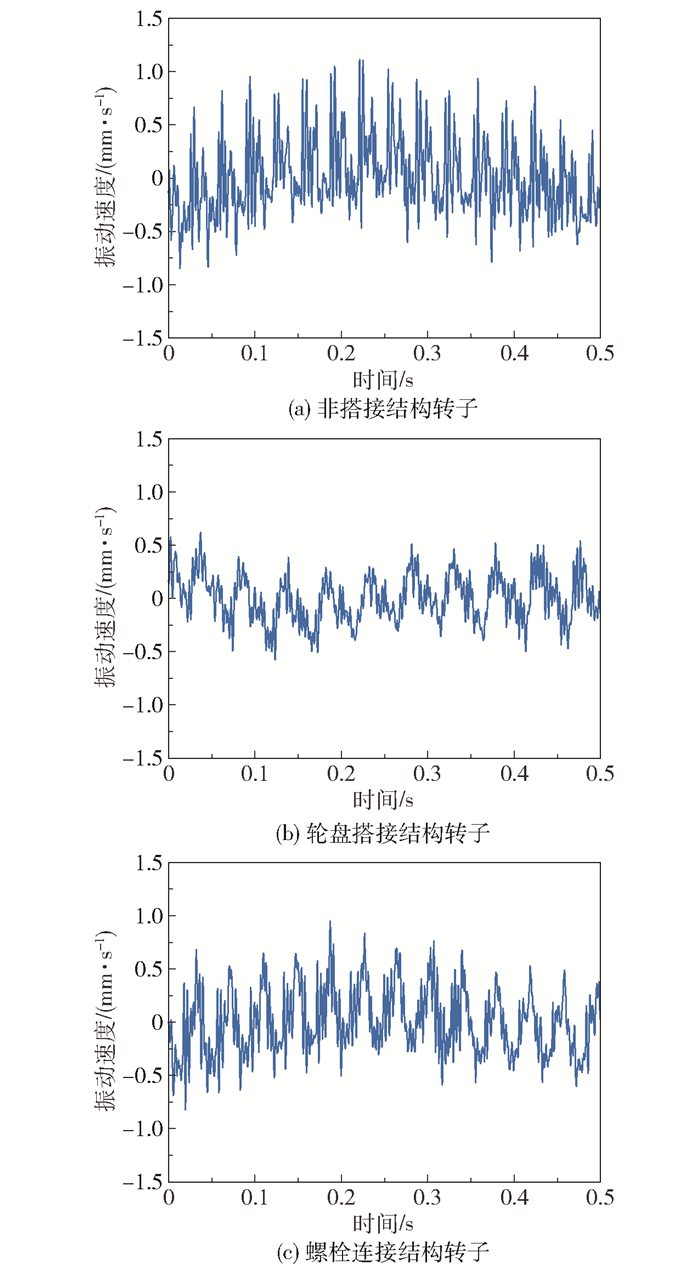
对3种结构搭接转子的径向加速度时域信号进行去直流趋势处理,然后积分,得到振动速度响应曲线如图 5所示。
|
图 5 3种结构转子的振动速度曲线 Fig.5 Vibration velocity curves of the three types of rotors |
由图 5可知,非搭接转子振动速度最大值为1.113 mm/s,轮盘搭接转子振动速度最大值为0.619 8 mm/s,相比非搭接转子下降44.31%,螺栓连接转子振动速度最大值为0.947 9 mm/s,相比非搭接结构转子下降14.83%。由上述结果可知,采用搭接结构可以有效降低转子的振动速度,振动速度最大值下降可达44.31%,采用螺栓连接结构同样可以降低转子的振动速度。这是因为螺栓连接结构增加了转子系统的刚度,可以降低转子振动;且搭接结构中存在摩擦耗散能量,因此对振动的削弱效果优于螺栓连接结构。因此搭接结构对振动速度有明显的降低效果。
产生上述试验结果的原因主要是,在轮盘搭接结构转子旋转时,搭接接触面出现相对滑移,搭接结构接触系统存在一个等效阻尼Ceq项, 且增大了系统的等效刚度,存在摩擦消耗能量,振动剧烈程度会下降。螺栓连接转子增大了接触面正压力,通过式(1)、(2)可知,相当于增加了转子系统的等效刚度,同样可以降低振动剧烈程度,但由于不存在阻尼项,螺栓连接结构转子对振动的削弱程度小于搭接结构转子。
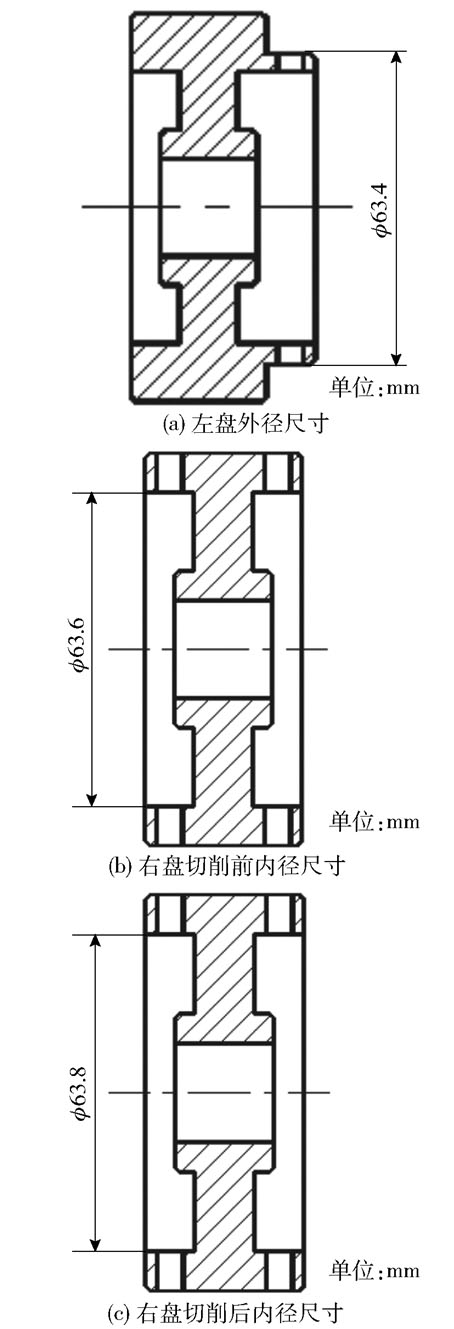
3 搭接间隙对减振效果的影响 3.1 试验装置为了探究两搭接盘的搭接间隙对减振效果的影响,搭建转子试验台如图 6所示。首先测量搭接轮盘转子在1 500 r/min工作转速下的振动位移响应;然后保持搭接轮盘左盘外径不变,将搭接轮盘右盘内径(半径)切削0.1 mm,切削前后的轮盘尺寸如图 7所示。最后测量转子在1 500 r/min下的振动位移响应。

|
图 6 改变间隙后的轮盘搭接结构转子试验台 Fig.6 View of the roulette lap structure rotor test bench after the gap change |
|
图 7 搭接轮盘切削前后尺寸图 Fig.7 Diameter of the overlapped rotor before and after cutting |
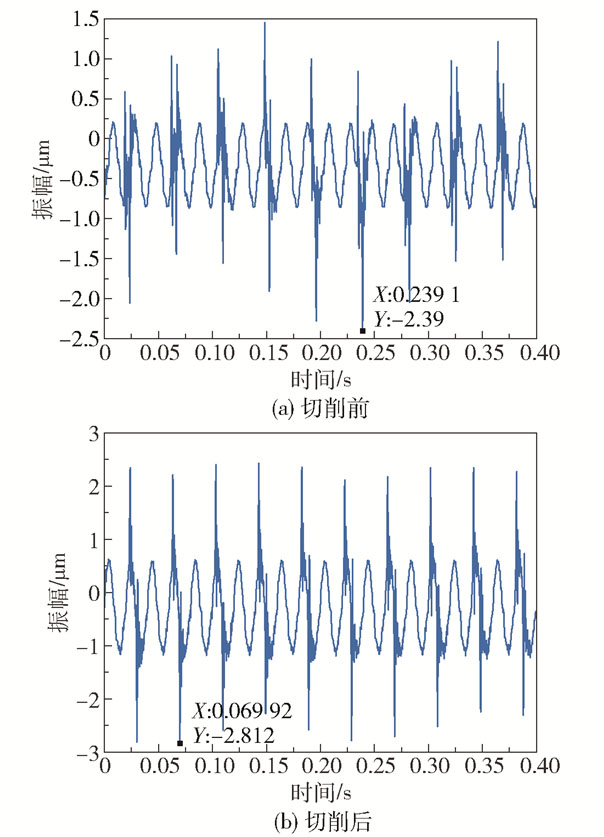
图 8(a)、(b)分别为切削前后轮盘搭接结构转子在1 500 r/min下的振动位移,两图中都出现了明显的振幅突增现象,说明在转动过程中存在摩擦。可以看出切削前最大振动位移达到2.39 μm,切削后最大振动位移为2.812 μm,相对于切削前增大了17.66%。振动位移变大的原因一是增大搭接转子间隙会减少两搭接面间的接触,摩擦接触时间减少,摩擦耗能降低,导致振动位移增大;二是搭接间隙增大,转子系统刚度减小,从而使得转动过程中的振动位移增大。
|
图 8 切削前后搭接转子的振动位移 Fig.8 Vibration amplitude of the overlapping rotor before and after cutting |
(1) 轮盘搭接结构转子在旋转时存在摩擦,从而消耗能量,振动加速度最大值与振动速度最大值下降,其振动加速度最大值相对于非搭接结构转子下降可达71.68%,振动速度最大值下降44.31%。螺栓搭接结构同样对转子系统有减振效果,相对于非搭接结构,其振动加速度最大值下降可达60.45%,振动速度最大值下降14.83%。
(2) 螺栓连接结构和搭接结构都增加了系统的等效刚度,均可降低转子的振动加速度。由于搭接结构转子在接触时还存在阻尼项,螺栓连接结构转子在旋转时的摩擦耗能小于搭接结构转子,使得搭接结构转子的减振效果优于螺栓连接结构转子。
(3) 增大搭接结构转子间隙会减少搭接转子的摩擦耗能,降低系统刚度,使得转动过程中的振动位移增大。
| [1] |
周传月, 邹经湘, 闻雪友, 等. 燃气轮机叶片-轮盘耦合振动特性计算[J]. 航空学报, 2000, 21(6): 545-547. ZHOU C Y, ZOU J X, WEN X Y, et al. Calculation of the blade-disc coupled vibration characteristics of a gas turbine[J]. Acta Aeronautica et Astronautica Sinica, 2000, 21(6): 545-547. (in Chinese) DOI:10.3321/j.issn:1000-6893.2000.06.017 |
| [2] |
李琳, 刘久周, 李超. 航空发动机中的干摩擦阻尼器及其设计技术研究进展[J]. 航空动力学报, 2016, 31(10): 2305-2317. LI L, LIU J Z, LI C. Review of the dry friction dampers in aero-engine and their design technologies[J]. Journal of Aerospace Power, 2016, 31(10): 2305-2317. (in Chinese) |
| [3] |
谢方涛, 崔璨, 马辉, 等. 一种求解干摩擦带冠叶片动力学响应的方法[J]. 振动工程学报, 2018, 31(1): 110-117. XIE F T, CUI C, MA H, et al. An approach to calculate the dynamic response of shrouded blade with dry friction[J]. Journal of Vibration Engineering, 2018, 31(1): 110-117. (in Chinese) |
| [4] |
龙伦, 冯娅娟, 吕彪. 某型带冠涡轮叶片振动特性及动应力测试数据分析[J]. 风机技术, 2018, 60(S1): 35-38. LONG L, FENG Y J, LV B. Analysis of vibration characteristics and dynamic stress test data of shrouded turbine blade[J]. Chinese Journal of Turbomachinery, 2018, 60(S1): 35-38. (in Chinese) |
| [5] |
袁巍, 陈国智, 张红晓, 等. 带冠预扭涡轮叶片模态分析及动应力测试验证[J]. 航空动力学报, 2020, 35(10): 2186-2194. YUAN W, CHEN G Z, ZHANG H X, et al. Modal analysis and dynamic stress tests verification of shrouded pretwist turbine blade[J]. Journal of Aerospace Power, 2020, 35(10): 2186-2194. (in Chinese) |
| [6] |
郝淑英, 陈予恕, 张琪昌. 连接结构松动对系统非线性动力学特性的影响[J]. 天津大学学报, 2001, 34(4): 452-454. HAO S Y, CHEN Y S, ZHANG Q C. Effects of connect loosing and sliding on dynamic characteristics[J]. Journal of Tianjin University, 2001, 34(4): 452-454. (in Chinese) DOI:10.3969/j.issn.0493-2137.2001.04.009 |
| [7] |
王本利, 张相盟, 卫洪涛. 基于谐波平衡法的含Iwan模型干摩擦振子非线性振动[J]. 航空动力学报, 2013, 28(1): 1-9. WANG B L, ZHANG X M, WEI H T. Harmonic balance method for nonlinear vibration of dry friction oscillator with Iwan model[J]. Journal of Aerospace Power, 2013, 28(1): 1-9. (in Chinese) |
| [8] |
李琳, 刘久周, 李超. 干摩擦阻尼器对宽频多阶次激励减振效果分析[J]. 航空动力学报, 2016, 31(9): 2171-2180. LI L, LIU J Z, LI C. Analysis on damping effect of dry friction damper under wideband multi-harmonic excitation[J]. Journal of Aerospace Power, 2016, 31(9): 2171-2180. (in Chinese) |
| [9] |
李全通, 通旭东, 冯璐璐, 等. 考虑榫接接触刚度的叶轮耦合振动特性计算方法研究[J]. 应用力学学报, 2014, 31(4): 525-529. LI Q T, TONG X D, FENG L L, et al. Investigation of the blade-disc coupled vibration analysis by considering the rabbet contact stiffness[J]. Chinese Journal of Applied Mechanics, 2014, 31(4): 525-529. (in Chinese) |
| [10] |
陈香, 朱靖, 李光辉, 等. 涡轮带冠叶片干摩擦阻尼减振试验[J]. 航空动力学报, 2012, 27(4): 817-823. CHEN X, ZHU J, LI G H, et al. Experiment on dry friction damping of shrouded turbine blades[J]. Journal of Aerospace Power, 2012, 27(4): 817-823. (in Chinese) |
| [11] |
黄文俊, 李录平. 透平叶片干摩擦阻尼减振研究综述[J]. 热力透平, 2006, 35(2): 95-100. HUANG W J, LI L P. A review of research on friction vibration damper of turbine blade[J]. Thermal Turbin, 2006, 35(2): 95-100. (in Chinese) DOI:10.3969/j.issn.1672-5549.2006.02.007 |
| [12] |
王威涛, 南国防. 基于哈密尔顿原理和谐波平衡法研究带冠叶片的振动特性[J]. 动力工程学报, 2020, 40(2): 117-122. WANG W T, NAN G F. Study on vibration characteristics of shrouded blades based on Hamilton principle and harmonic balance method[J]. Journal of Chinese Society of Power Engineering, 2020, 40(2): 117-122. (in Chinese) |








