T型管是核电管路系统中最常见的一种管道结构形式。T型管道的热疲劳是由冷热流体交汇引起的,由于冷热流体存在温差,管道在温度波动的作用下产生热应力,最终导致出现热疲劳现象,对核电的安全运行造成严重威胁。
Lee等[1]运用大涡模拟(LES)对T型管道内的冷热流体掺混进行数值模拟,并得出冷热流体湍流混合所引起的强化对流换热是管道热疲劳失效的主要原因。Zhang等[2]基于计算流体动力学-有限元分析方法(CFD-FEM) 和雨流计数法对T型管内的冷热流体混合进行了数值分析,构建了T型管冷热流体湍流混合的高周热疲劳计算方法。Hu等[3]利用LES模型对T型管内冷热流体的掺混过程进行了数值模拟,并根据主管与支管的动量比MR将混合流型分为壁面射流、偏转射流和冲击射流。Wegner等[4]通过改变T型支管角度提高了湍流的混合效果,并发现倾角的变化影响了涡结构和二次流,从而产生了不同的湍流混合效果。张越[5]对压器波动管进行大涡模拟,使用瞬态界面单向流固耦合方法对管道进行应力分析,并对管道进行了热疲劳评估,计算了管道的疲劳寿命。Kamaya[6-7]针对直管、弯管、T型管中的流动与传热现象进行简化,实现了管道的热-流-固耦合分析。
综上所述,目前对T型管道内冷热流体掺混过程中的流动与传热以及热疲劳评估已取得了很大的研究进展,但关于支管上游带有弯管的T型管结构尚无文献报道。本文改变了T型管的支管结构,研究支管上游不同曲率的弯管结构对管道的温度波动及热疲劳的影响。利用Fluent软件对T型管内冷热流体的湍流混合过程进行CFD数值模拟,对模拟结果进行分析,得出湍流混合过程的流动与传热特性;利用CFD-Post软件提取温度场和压力场的数据,并通过ANSYS Workbench平台将其动态加载到固体域模型,开展CFD-FEM瞬态流固耦合计算,得到固体热应力的分布及波动信息,并对危险位置进行了热疲劳分析。
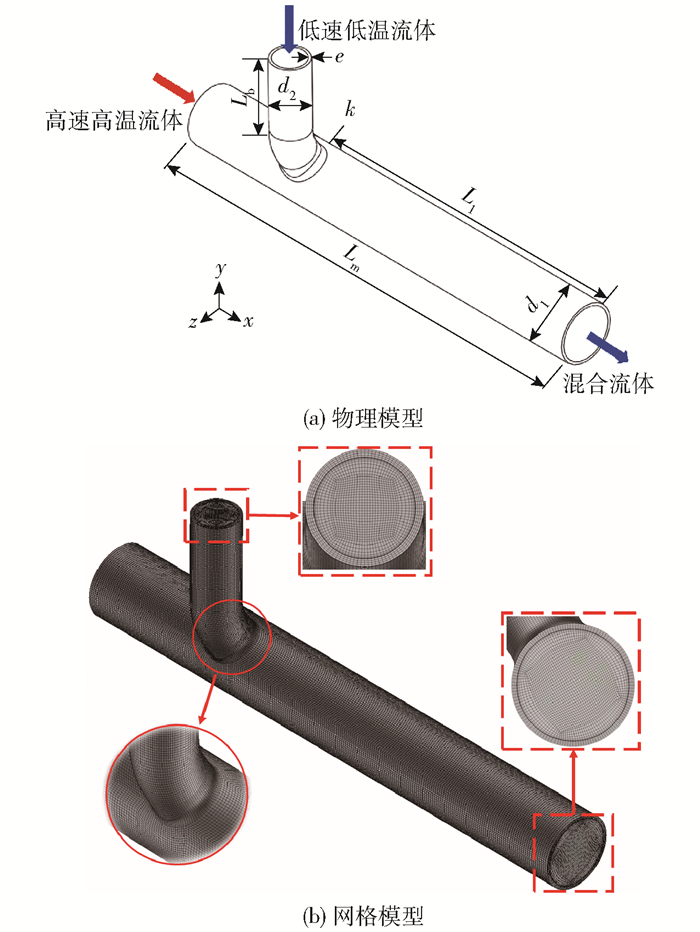
1 计算模型本文所用的物理模型如图 1(a)所示,主管内为高速高温的流体,支管内为低速低温的流体。在支管位置增加了不同曲率(曲率k=0.006,0.01,0.02)的弯管,对3种曲率支管弯管的T型管进行数值模拟及分析,研究不同曲率弯管对T型管冷热流体混合热疲劳的影响。T型管整体的结构参数如表 1所示,其中Lm为主管总长,L1为主管下游长,Lb为支管长,d1为管外径,d2为管内径, e为壁厚。对整个物理模型的固体域和流体域同时进行结构化网格划分,并对主支管相贯区及边界层位置进行加密处理。T型管结构化网格模型如图 1(b)所示,网格数量为1 358 638,第一层网格高度为0.05 mm,边界层数为10,边界层网格增长率为1.1。
|
图 1 T型管计算模型 Fig.1 Model of the simulation of T-junction |
| 下载CSV 表 1 T型管结构参数 Table 1 Structural parameters of T-junction |
T型管内冷热流体的掺混是一个复杂、多变的过程,为了更好地捕捉管内湍流混和瞬时波动及流动传热的特征细节,本文采用大涡模拟方法对T型管内冷热流体的掺混过程进行数值模拟[8-9],模拟过程考虑重力和浮升力的影响[10]。在大涡模拟动量方程的浮升力项中,对水的各项参数进行变物性设置。利用NIST软件对水的密度随温度的变化进行二阶多项式拟合,如式(1)所示。
| $ \rho = - 0.002\;3{T^2} + 0.988\;7T + 909.5 $ | (1) |
式中,ρ为水的密度,kg/m3, T为流体温度,K。
2 数值模拟 2.1 流场模拟流体计算的边界条件如表 2所示。计算过程中对水的密度、导热系数、动力黏度等进行变物性设置,并设置操作压力为7 MPa,将主管入口边界条件进行初始化。首先选用 k-ε模型将T型管内冷热流体混合过程计算至稳态收敛,将稳态收敛的计算结果作为LES瞬态计算的初始场。为了更好地捕捉冷热流体掺混瞬时热波动的特征细节,使用couple耦合求解器与二阶迎风式进行求解。瞬态计算的时间步长为0.005 s,温度监测点的监测频率为200 Hz,计算总时长为20 s。
| 下载CSV 表 2 流场计算边界条件 Table 2 Boundary conditions in the CFD simulation |
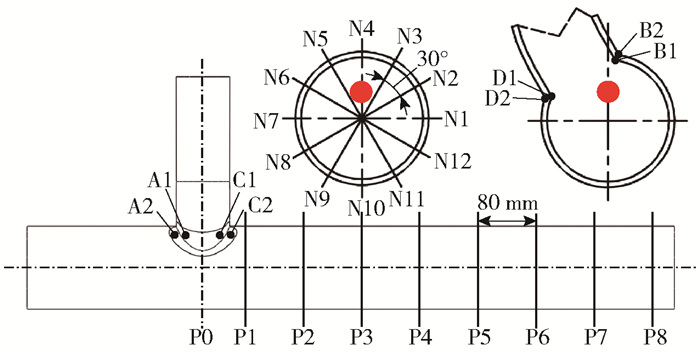
如图 2所示,为定量分析流场的温度波动情况,沿主管轴向每80 mm设置一个监测面(P1~P8),P0截面位于主支管相贯区,P1截面距离支管轴线50 mm;每个监测面间隔30°设置一个监测方向(N1~N12), 每个监测方向上设置2个监测点,即内壁面(I)和近壁面(F)1 mm处的流体监测点,如P2-N4-F-T(V)为P2截面N4方向近壁面流体温度(速度)监测点。
|
图 2 监测点的设置 Fig.2 The arrangement of monitoring points |
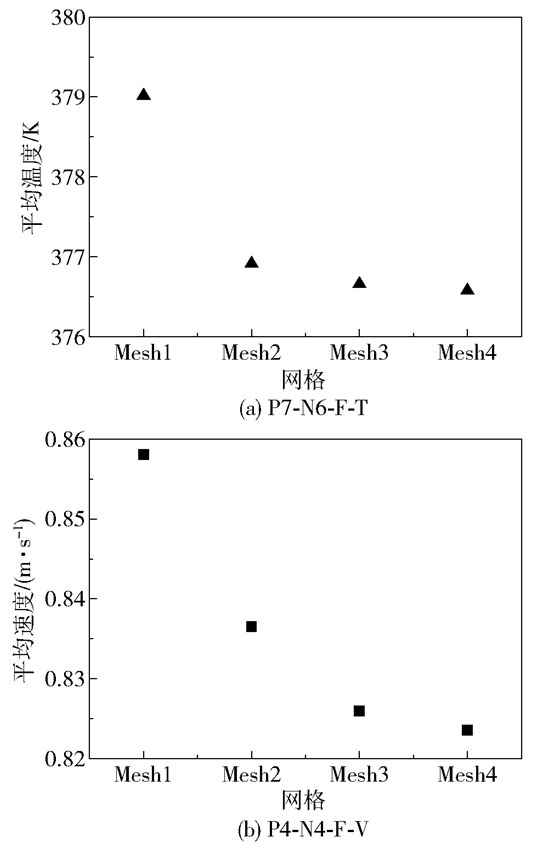
为了排除网格大小带来的计算误差,对网格模型进行无关性验证,其结构化网格划分方案如表 3所示。对4种网格进行数值计算,得到管内P7截面N6方向流体的平均温度和P4截面N4方向流体的平均速度随网格量增加所产生的变化如图 3所示。从图 3可以看出,Mesh1、Mesh2的计算结果与Mesh3、Mesh4相差较大,Mesh3与Mesh4两者的计算结果相差较小,考虑到计算的精度和效率,采用Mesh3作为后续数值计算的网格划分方案。
| 下载CSV 表 3 网格无关性验证划分方案 Table 3 Meshing scheme of the tee pipe for the grid independence test |
|
图 3 网格无关性验证 Fig.3 The grid independence test |
流固耦合计算需要设置管道固体材料的属性,本文T型管道所选择材料为316L不锈钢,在实际运行中管道的形变很小,可以忽略其对流场的影响,因此采用一种单向瞬态流固耦合的计算方法。将流场瞬态计算所得到的内壁面的压力场和固体域的温度场通过批处理的方法按照时间序列进行排列,并将其动态加载到固体计算域作为固体计算的边界条件和载荷。流固耦合计算的时间步长为0.01 s,计算时长为5 s(15~20 s)。固体监测点的设置如图 2所示,在流体监测点的基础上增加了主支管相贯区内壁面位置的8个监测点(A1、A2、B1、B2、C1、C2、D1、D2)。在流固耦合计算过程中,提取监测点的应力波动信号,用于后续的应力分析和热疲劳分析。固体计算的边界条件如表 4所示。
| 下载CSV 表 4 流固耦合计算边界条件 Table 4 Boundary conditions of the CFD-FEM simulation |
为了定量分析管内流体温度随时间的变化情况,定义温度的统计量[2, 5],即无量纲温度、无量纲时均温度Tmean*和无量纲均方根温度Trms*,其中无量纲温度是为了避免单位的影响,无量纲时均温度可以反映温度的分布情况,而无量纲均方根温度可以表征温度的波动程度。
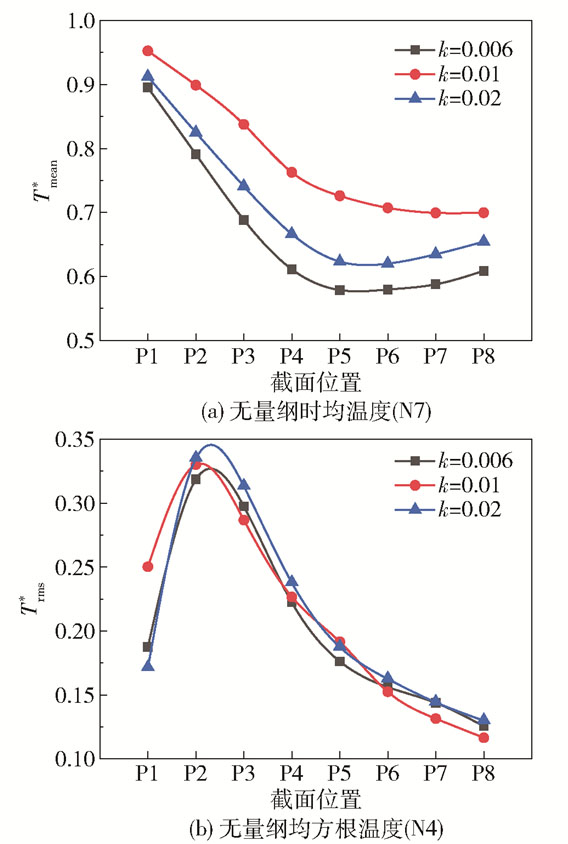
对3个不同曲率的模型的轴向温度进行无量纲处理后,发现其分布和波动具有一致性,冷、热流体在主支管相贯区位置汇合,在支管弯管的影响下,热交换区域发生偏转,热交换区域主要位于主管下游N4~N8方向,其中温度变化最为明显的是N7方向。温度波动是由冷热流体掺混引起的,温度波动主要发生在主管下游N3~N8方向,其中温度波动最剧烈的是N4方向。3种不同曲率支管弯管T型管沿N7方向的无量纲时均温度和沿N4方向的无量纲均方根温度的轴向分布如图 4所示。
|
图 4 无量纲温度轴向分布 Fig.4 Axial distributions of Tmean* and Trms* |
由图 4(a)可以看出,沿主管N7方向3种结构的温度均先降低后升高。在靠近相贯区的位置由于支管低温流体的流入,主管温度降低,而在远离相贯区的位置由于冷热流体充分混合,主管温度上升,其中在k=0.006的支管弯管结构中流体的偏转更为明显,这是由于该弯管曲率小,低温流体在主管发生了很大的周向偏转,冷热流体充分混合。图 4(b)对比了3种结构温度波动最剧烈位置(N4方向)的无量纲均方根温度沿主管轴向的变化情况,可以看出沿主管轴向3种结构的温度波动均呈先增大后减小的趋势。低温流体在相贯区与高温流体汇合,冷流体冲入主管,由于主管流速大,热交换区从主管轴心位置向内壁面偏转,在P2截面处热交换区偏转到内壁面位置。因此从P1到P2截面近壁面温度波动逐渐增大。随着冷热流体的充分混合,管内流体温度逐渐趋于稳定,温度波动的剧烈程度也逐渐降低, 温度波动最剧烈的区域在P2N4处。当支管弯管的曲率较大时,低温流体在主管内的周向偏转小,热交换区集中,导致温度波动较大。因此随着曲率的增大,温度波动的剧烈程度增大。
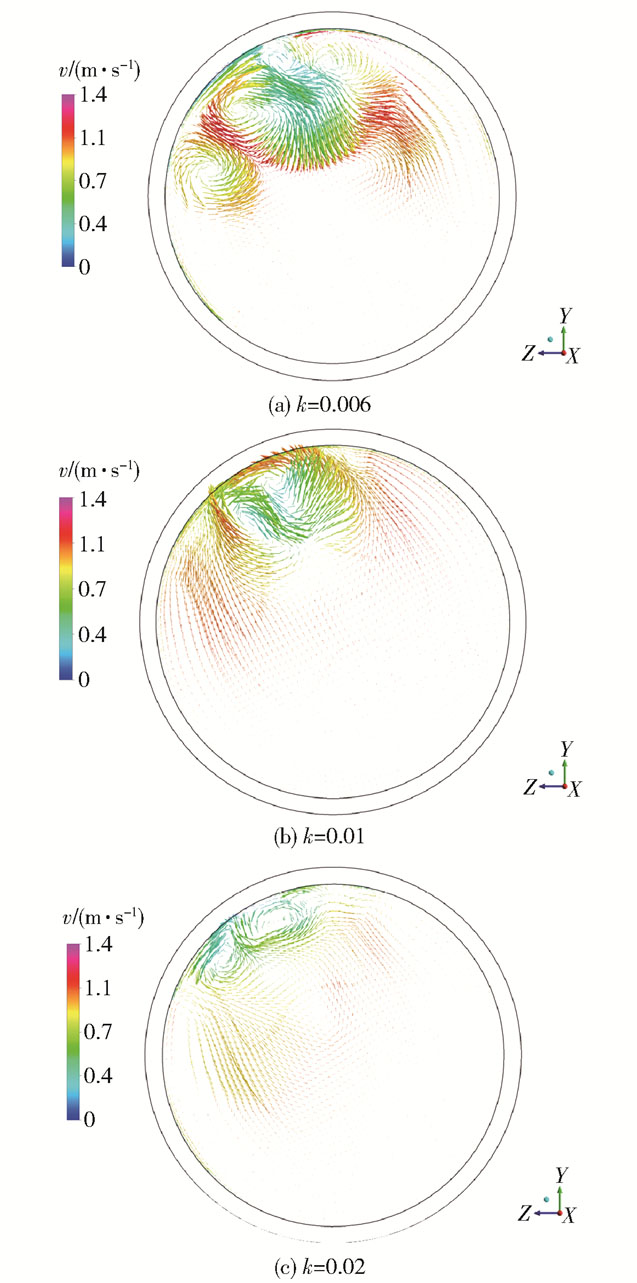
3.1.2 速度场对不同曲率支管弯管T型管道内冷热流体的混合过程进行研究。支管弯管能够影响主管内掺混流体的周向速度。20 s时3种结构在P2截面的速度矢量图如图 5所示,可以看出,周向速度主要位于支管入口区域(N4和N6),低温流体流经曲率小的弯管会产生较大的周向速度,因此随着曲率的增大周向速度减小。
|
图 5 P2截面周向速度矢量图(20 s) Fig.5 Vector of circumferential velocity of P2 at 20 s |
为了分析和研究主管内流体速度分布和波动的特征规律,本文引入时均速度Vmean和均方根速度Vrms,时均速度用来表征速度的分布规律,均方根速度用来表征速度的波动程度。
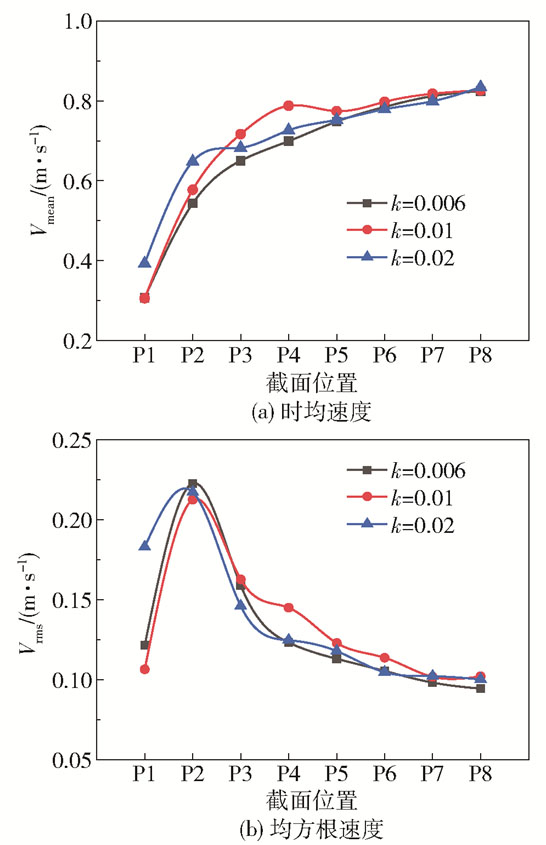
图 6为主管下游N5方向的速度的轴向分布情况。N5为支管入口位置,在此方向的速度变化及波动最为明显。由图 6(a)可以看出,3种结构的速度分布基本一致,均沿主管轴向逐渐增大。由于支管的低速流体在靠近支管入口位置占主导地位,因此近壁面流速相对较小;在远离支管入口位置,近壁面流体逐渐恢复为高速流体。图 6(b)为3种结构在N5方向沿主管轴向的均方根速度变化情况,可以看出3种结构的速度大小波动趋势一致,均随着主管轴向先增大后减小,这与温度波动具有一致性。支管低温流体与主管高温流体在相贯区混合,由于高温流体速度较大,热交换区由主管轴心位置向内壁面偏移,在P2截面处热交换区偏移至内壁面,速度波动最为剧烈,随着冷热流体的充分混合,速度波动逐渐趋于平稳。
|
图 6 速度的轴向分布(N5) Fig.6 Axial distributions of Vmean and Vrms(N5) |
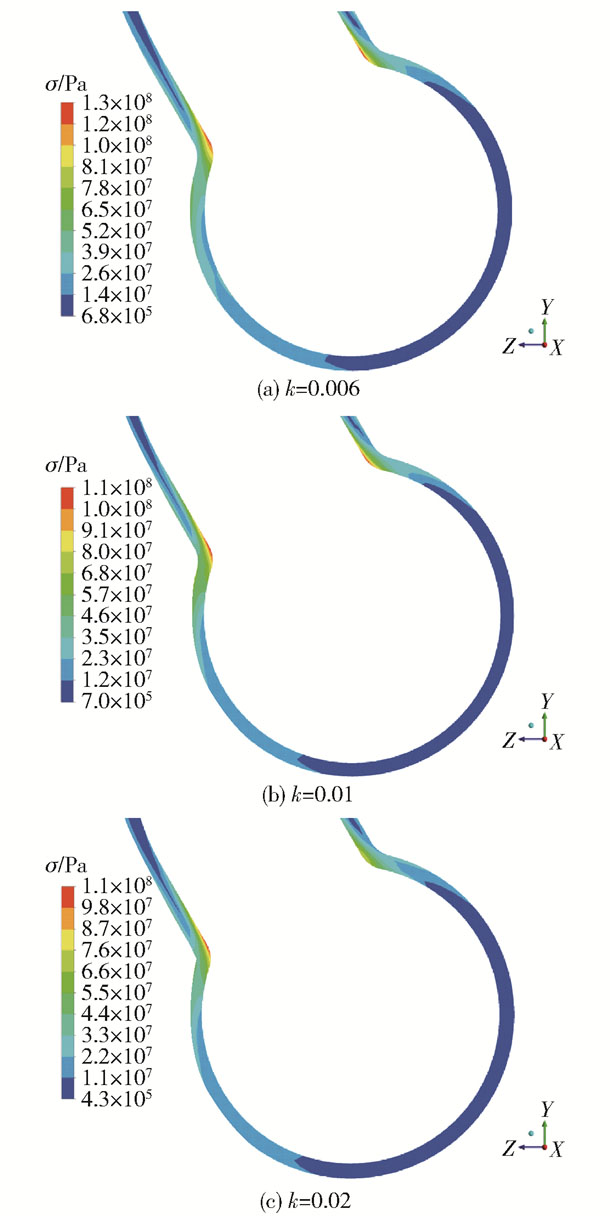
对3种结构经流固耦合计算得到的应力结果进行分析。图 7为20 s时3种结构在P0截面的等效应力σ分布图。可以看出,热应力集中区主要位于相贯区内壁面。热应力是由温度波动引起的,冷热流体在主支管相贯区交汇,产生较大的热应力;随着曲率的增大,热应力集中现象逐渐减弱, 这与温度及速度波动剧烈程度的变化趋势是一致的。
|
图 7 P0截面的等效应力分布(20 s) Fig.7 The equivalent stress distribution of P0 at 20 s |
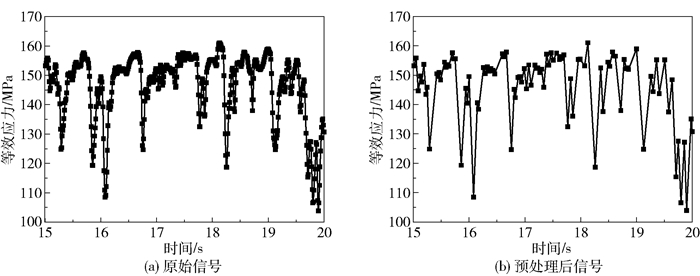
如图 8所示,提取流固耦合计算结果中监测点D1(曲率k=0.006)的应力波动信号,并对其进行预处理(只保留拐点信息)。
|
图 8 D1监测点的应力波动信号 Fig.8 Stress fluctuation information at the point D1 |
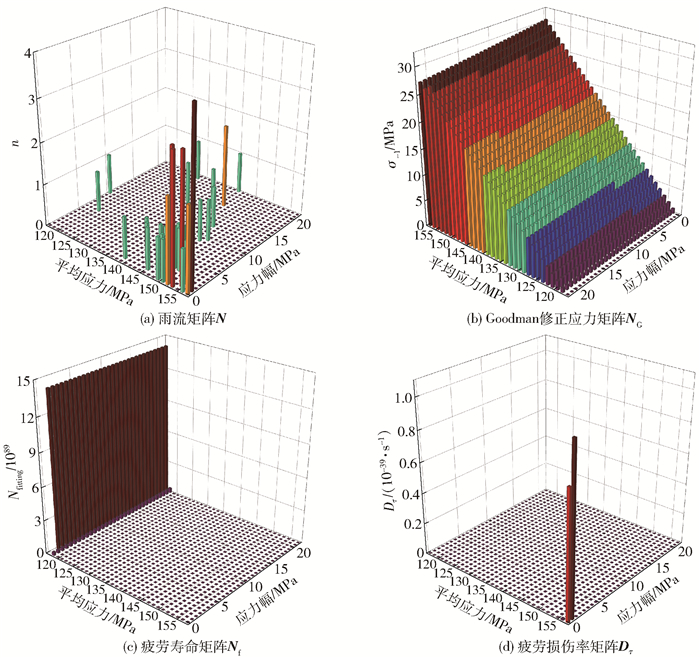
图 9为监测点D1的热疲劳损伤率评估结果。利用雨流计数法对预处理后的热应力波动信号进行统计学分析,处理后得到如图 9(a)所示的雨流矩阵N及实际循环次数n,利用Goodman曲线进行应力修正,将等效热应力转化为等效对称循环应力σ-1,并得到如图 9(b)所示的修正应力矩阵NG。数值模拟的工况较为理想化,而在实际工况中存在很多复杂的因素(环境、焊缝等),因此本文利用安全系数K修正对称循环应力,并放大载荷使结果更加保守,K取值为2。Goodman曲线为
| $ \sigma_{\mathrm{a}}=\sigma_{-1}^{*}\left(1-\frac{\sigma_{\mathrm{m}}}{\sigma_{\mathrm{b}}}\right) $ | (2) |
|
图 9 D1监测点的热疲劳损伤率评估 Fig.9 Estimation of the thermal fatigue damage rate at the point D1 |
式中,σ-1*为修正后的等效对称循环应力,σb为材料的强度极限,取σb=520 MPa,σa为应力幅,σm为平均应力。
利用应力-寿命曲线(S-N曲线)进行热疲劳评估。根据奥氏体不锈钢的疲劳寿命S-N曲线插值获得相关等效应力下的许用循环次数,当等效对称循环应力大于100 MPa时,满足S-N曲线的变化规律;当等效对称循环应力小于100 MPa时,许用循环次数无限增长,即不发生疲劳,但实际工况很难达到理论工况的标准,因此假定此种情况也满足S-N曲线的变化规律。对等效对称循环应力小于100 MPa时的疲劳寿命S-N曲线进行拟合,拟合公式为[5]
| $ \lg N_{\text {fitting }}=-8.467 \times 10^{-7} \times \sigma_{-1}^{*}+90.15 $ | (3) |
式中,Nfitting为Goodman修正应力对应的循环次数。
经疲劳寿命曲线处理后,可以获得如图 9(c)所示的不同平均应力σm和应力幅σa下的疲劳寿命矩阵Nf和许用循环次数Nfitting。将实际循环次数与许用循环次数相除,可获得疲劳损伤矩阵D。根据线性疲劳累计损伤准则,将D中元素求和,可得到疲劳累计损伤D。为了使得计算有更好的参考意义,并消除单位对评估造成的影响,以更加客观地分析管道的疲劳损伤,本文引入疲劳损伤率矩阵Dτ,所得结果如图 9(d)所示,疲劳累计损伤率Dτ和无量纲疲劳累计损伤率Dτ*的定义如下[5]。
| $ \begin{aligned} &D_{\tau, i, j}=\frac{D_{i, j}}{\tau} \end{aligned} $ | (4) |
| $ \begin{aligned} &D_{\tau}=\frac{D}{\tau} \end{aligned} $ | (5) |
| $ \begin{aligned} &D_{\tau}^{*}=\lg \left(\frac{D_{\tau}}{10^{-91}}\right) \end{aligned} $ | (6) |
式中,Dτ, i, j为疲劳损伤率矩阵Dτ中的各元素,τ为热应力波动信号时长,τ=5 s。
对提取出的所有监测点的热应力波动信号进行热疲劳损伤率评估,发现无量纲累计疲劳损伤率随支管弯管曲率的增大呈减小的趋势,k=0.02结构弯管的无量纲累计疲劳损伤最小,并得出危险位置为k=0.006结构的B1和D1监测点处,其无量纲疲劳累计损伤率分别为52.98和52.27。
4 结论(1) 利用大涡模拟对曲率k为0.006、0.01、0.02这3种结构的T型管冷热流体的湍流混合过程进行了数值预测,结果表明3种结构的温度分布和波动的趋势相似,曲率大的支管弯管结构产生了剧烈的温度波动。
(2) 低温流体流经弯管进入主管后,在主管内产生周向速度,且随着支管弯管曲率的增大,周向速度逐渐减小。
(3) 利用热-流-固耦合计算方法,获得了热应力的分布及波动情况,发现热应力集中主要位于主支管相贯区,热应力集中现象随支管弯管曲率的增大而减弱。
(4) 通过对热应力波动信号的统计学分析及处理完成了对管道的热疲劳评估,发现无量纲累计疲劳损伤率随支管弯管曲率的增大而减小,并确定了易疲劳点出现在k=0.006结构弯管的B1位置处,其无量纲疲劳累计损伤率为52.98。
| [1] |
LEE J I, HU L W, SAHA P, et al. Numerical analysis of thermal striping induced high cycle thermal fatigue in a mixing tee[J]. Nuclear Engineering and Design, 2009, 239: 833-839. DOI:10.1016/j.nucengdes.2008.06.014 |
| [2] |
ZHANG Y, LU T. Study of the quantitative assessment method for high-cycle thermal fatigue of a T-pipe under turbulent fluid mixing based on the coupled CFD-FEM method and the rainflow counting method[J]. Nuclear Engineering and Design, 2016, 309: 175-196. DOI:10.1016/j.nucengdes.2016.09.021 |
| [3] |
HU L W, KAZIMI M S. LES benchmark study of high cycle temperature fluctuations caused by thermal striping in a mixing tee[J]. International Journal of Heat and Fluid Flow, 2006, 27(1): 54-64. DOI:10.1016/j.ijheatfluidflow.2005.08.001 |
| [4] |
WEGNER B, HUAI Y, SADIKI A. Comparative study of turbulent mixing in jet in cross-flow configurations using LES[J]. International Journal of Heat and Fluid Flow, 2004, 25(5): 767-775. DOI:10.1016/j.ijheatfluidflow.2004.05.015 |
| [5] |
张越. 压水堆波动管流动与传热及热-力耦合结构应力、变形与疲劳研究[D]. 北京: 北京化工大学, 2017. ZHANG Y. The coupled thermo-hydro-mechanical analysis and thermal fatigue assessment for the pressurizer surge line[D]. Beijing: Beijing University of Chemical Technology, 2017. (in Chinese) |
| [6] |
KAMAYA M. Assessment of thermal fatigue damage caused by local fluid temperature fluctuation (part Ⅱ: crack growth under thermal stress)[J]. Nuclear Engineering and Design, 2014, 268: 139-150. DOI:10.1016/j.nucengdes.2013.12.042 |
| [7] |
KAMAYA M. Assessment of thermal fatigue damage caused by local fluid temperature fluctuation (part Ⅰ: characteristics of constraint and stress caused by thermal striation and stratification)[J]. Nuclear Engineering and Design, 2014, 268: 121-138. |
| [8] |
MING T Z, ZHAO J Y. Large-eddy simulation of thermal fatigue in a mixing tee[J]. International Journal of Heat and Fluid Flow, 2012, 37: 93-108. |
| [9] |
TIMPERI A. Conjugate heat transfer LES of thermal mixing in a T-junction[J]. Nuclear Engineering and Design, 2014, 273: 483-496. |
| [10] |
卢涛, 朱兴国. 浮升力对T型管道内冷热流体混合过程热波动的影响[J]. 热科学与技术, 2011, 10(4): 305-311. LU T, ZHU X G. Influence of buoyancy on thermal fluctuation of fluid mixing in T-junction[J]. Journal of Thermal Science and Technology, 2011, 10(4): 305-311. (in Chinese) |








