2. 北京化工大学 发动机健康监控及网络化教育部重点实验室, 北京 100029
2. Key Lab of Engine Health Monitoring-Control and Networking of Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
柴油发动机具有热效率高、经济性能好、扭矩大等优点[1],在交通运输业和国防领域应用广泛,因此对其进行故障监测,以保证其经济可靠地运行具有十分重要的意义。在实际使用过程中,由于柴油机的配气机构磨损,经常会出现气门间隙异常故障,导致产生柴油机进气不足、燃烧不充分、动力不足等问题[2]。
目前通常使用缸盖振动信号来对柴油机气门间隙状况进行监测。由于柴油机机械部件众多、背景噪声强烈、工况复杂多变,因此其缸盖振动信号是一种典型的非平稳信号,人为选取对噪声和工况不敏感的故障特征十分困难。
针对非平稳信号的分析问题,刘昱等[3]提出通过局部均值方法分解振动信号,但该方法会出现端点效应等问题,从而影响诊断精度;张超等[4]提出一种基于经验模态分解的分析方法,然而由于误差累积会出现模态混叠问题,使得识别准确度下降;张恒琪等[5]通过Wigner-Ville变换对非平稳信号进行分析,发现时频面存在很严重的交叉项干扰问题。而复Morlet变换是一种线性变换,不存在端点效应、模态混叠、交叉项干扰严重等问题,且该方法能够提供一个随频率改变的时频窗[6],是一种自适应时频分析方法。此外复Morlet小波与冲击信号也较为相似,适合分析带冲击的非平稳信号。
针对故障特征的提取问题,万晓静等[7]提出将振动信号经经验模态分解所得到的各分量的能量熵作为特征集合, 然后输入到诊断模型中;薛嫣等[8]提出一种基于熵特征和堆叠稀疏自编码的滚动轴承故障诊断方法。但上述特征提取方法费时费力且均需要一定的专家经验,无法适应大数据和智能化的需求。而基于AlexNet的神经网络技术在特征自动提取和图像识别精度上具有很大优势,且对噪声和工况不敏感[9]。
综上,本文首先通过复Morlet小波将柴油机气门间隙正常和异常的缸盖振动信号转换为时频图。其次将时频图划分为训练集和测试集,再将训练集和测试集输入到AlexNet神经网络进行模型训练与测试。然后通过Batch Normalization和Dropout技术改进网络结构,并优化神经网络超参数以提高模型的准确度和计算效率。最后将本文算法与传统的诊断算法进行对比,验证了本文所提方法的优越性。
1 复Morlet时频变换方法短时傅里叶变换的时频窗口保持不变,仅适合用于分析频率基本保持恒定的平稳信号,而连续小波变换则针对短时傅里叶变换分辨率固定的缺点进行了完善,是一种自适应的时频分析方法。
小波变换的难点在于小波基的选取,本文选择复Morlet小波基。首先它既提供幅值信息,还提供相位信息,且相位信息对突变的柴油机振动信号更敏感;其次复Morlet小波变换波形与柴油机振动信号均为带冲击的有阻尼自由衰减振动信号,二者有相似性,进而更有利于信号特征的提取[10]。
本文对柴油机缸盖振动信号h(t)进行连续小波变换,变换公式如下。
| $ W_{\phi}(\alpha, \tau)=|\alpha|^{-\frac{1}{2}} \int_{-\infty}^{+\infty} h(t) \phi^{*}\left(\frac{t-\tau}{\alpha}\right) \mathrm{d} t $ | (1) |
式中,α为小波基的伸缩状态,τ为时间平移因子,
| $ \phi(t)=\frac{1}{\sqrt{\pi f_{\mathrm{b}}}} \mathrm{e}^{\frac{-t^{2}}{f_{\mathrm{b}}}} \mathrm{e}^{2 \pi \mathrm{i} f_{\mathrm{c}} t} $ | (2) |
式中,fc为小波中心频率,fb为带宽参数。通过调整复Morlet小波基的中心频率和带宽参数,便可以获得适于分析柴油机缸盖振动信号的复Morlet小波基。
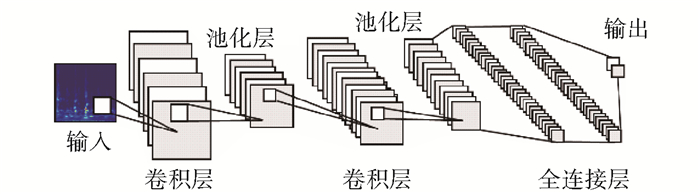
2 AlexNet神经网络AlexNet是一种经典的卷积神经网络(CNN),它可以挖掘二维图像的颜色、边缘、纹理、几何形状等特征,其一般结构示意图如图 1所示。
|
图 1 卷积神经网络结构 Fig.1 Convolutional neural network structure |
为减少图片冗余信息,本文对变换得到的时频图进行压缩,然后输入到卷积神经网络中。由于CNN使用梯度下降法来求解目标函数的最小值,为加快收敛速度,将分布于0~255像素值的时频图归一化至0~1之间。将归一化后的时频图Y与经过初始化的卷积核W进行卷积,计算公式如下。
| $ \boldsymbol{S}(i, j)=(\boldsymbol{Y} \times \boldsymbol{W})(i, j)=\sum\limits_{m} \sum\limits_{n} \boldsymbol{Y}(i+m, j+ \\ n) \boldsymbol{W}(m, n) $ | (3) |
式中,i, j, m, n表示矩阵各元素的位置,S为卷积结果。
卷积核通过与图像局部连接来提取图像特征,与全连接方式相比可以大幅降低图片冗余信息的影响。综合考虑求解速度和表现性能,本文选取3×3及5×5大小的卷积核来进行实验,文中卷积核、池化核、步长及图像尺寸的单位均为像素。
完成卷积运算后进行偏置处理,之后把计算结果输入至激活函数。ReLu激活函数无需求幂,运算简便,且在输出大于0的区域梯度为1,可以保证反向传播阶段神经网络参数的继续优化,故本文选用ReLu作为激活函数,其表达式为
| $ g(z)=\max \left(0, \ln \left(1+\mathrm{e}^{z}\right)\right) $ | (4) |
式中,z为激活函数的输入值,g为激活函数。
在激活步骤之后设置批标准化层将激活值规范化在线性区间,从而加快模型的收敛速度[11]。
随后进行池化步骤,由于最大池化技术对特征图的纹理信息提取效果更好,更适合挖掘时频图像的冲击特征,故选用最大池化技术。特征图在经过池化层后维度将降低,从而达到特征降维的目的。
池化之后设置Dropout层,将前向传播阶段部分特征检测器的激活结果以一定的概率忽略掉。在神经网络中引入该层会让模型不过分依赖某些局部特征,泛化能力更强,可以有效防止过拟合情况的出现[12]。
经过3个轮次的卷积、批标准化、池化、Dropout步骤后,将提取到的特征输入到全连接层进行特征组合从而完成分类。将输出结果与实际的标签值进行比对,利用反向传播算法逐层传递误差同时自适应优化网络权重及偏置值,通过不断的正向与反向传播,最终完成模型训练。
3 气门间隙异常故障诊断实验 3.1 实验装置和数据采集本文所用实验装置为TBD234V12型柴油机,其主要参数如表 1所示。通过在该柴油机缸盖上安装加速度传感器来获得缸盖振动信号,在飞轮上安装键相传感器来获得其键相信号,在非驱动端齿轮盘上安装瞬时转速传感器来获得其瞬时转速信号。数采系统采样频率为51 200 Hz,柴油机故障诊断实验台如图 2所示,柴油机故障诊断系统示意图如图 3所示。以7~12号缸为气门间隙故障模拟缸,在柴油机停机状态下,利用厚度尺设置间隙值,再通过转动螺钉进行气门间隙固定,共设置6组气门间隙正常和6组气门间隙异常的故障模拟实验,如表 2所示。为测试本文所提出的故障诊断方法在变工况条件下的诊断效果,故障模拟实验分别在12种工况下进行,如表 3所示。每种工况采集40~50组缸盖振动信号,然后将每组信号转换为一幅时频图。先对7号缸进气门间隙严重故障情况进行诊断,7号缸各关键相位如表 4所示。
| 下载CSV 表 1 TBD234V12型柴油机主要参数 Table 1 Main parameters of the TBD234V12 diesel engine |

|
图 2 柴油机故障诊断实验台 Fig.2 Diesel engine fault diagnosis test bench |
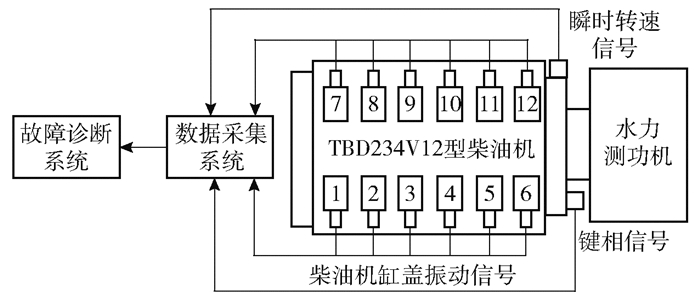
|
图 3 柴油机故障诊断系统示意图 Fig.3 Diagram of the diesel engine fault diagnosis system |
| 下载CSV 表 2 柴油机气门间隙情况 Table 2 Diesel engine valve clearance |
| 下载CSV 表 3 柴油机的不同工况 Table 3 Different working conditions of the diesel engine |
| 下载CSV 表 4 7号缸关键相位 Table 4 Key phases of cylinder 7 |
柴油机正常工作时,曲轴旋转一周键相传感器便进行一次采样,而曲轴旋转两周柴油机才进行一次点火。在截取两周期信号时,由于一般根据键相脉冲信号截取,会导致相位不一致的情况发生,因此需要对截取出来的周期信号进行相位调整,使得各关键相位一致,便于后续的图像识别。
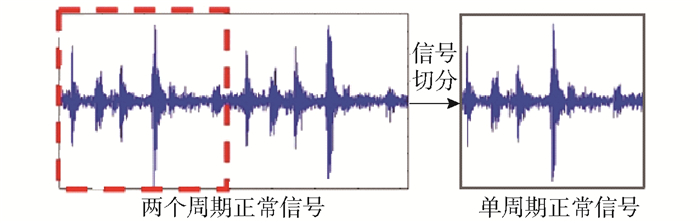
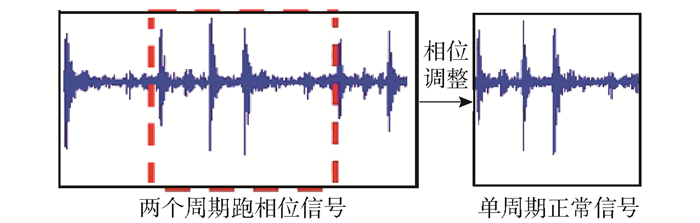
通过对点火相位处和点火相位后延360°处的冲击能量值进行比较,来判断是否发生跑相位。若没有跑相位情况出现,则点火角度对应的冲击能量值更大,将信号对中进行剪切取其中一份,如图 4所示;反之,则截取信号中间的一个完整周期,如图 5所示。
|
图 4 相位切分图 Fig.4 Phase slice diagram |
|
图 5 相位调整图 Fig.5 Phase adjustment diagram |
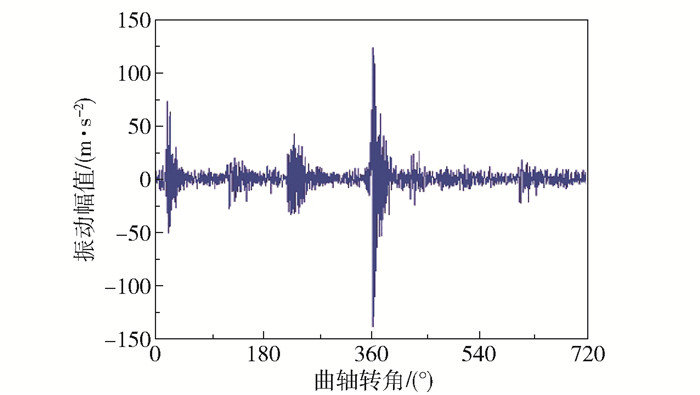
柴油机工作周期时长会随转速而发生变化,但其各关键相位却保持不变,因此在角域上分析信号更加方便。将柴油机振动时序信号转换到角域进行分析,经过相位调整和角域转换后的柴油机缸盖振动信号如图 6所示。
|
图 6 振动信号角域图 Fig.6 Vibration signal angular domain diagram |
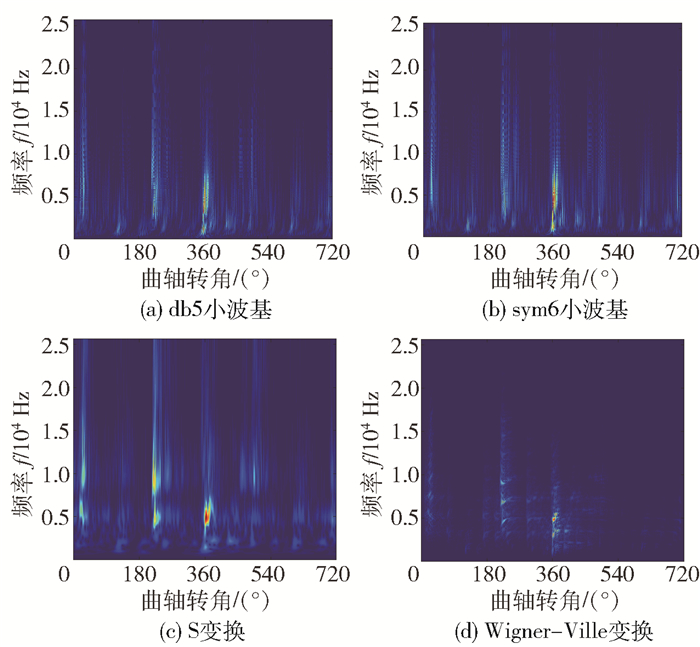
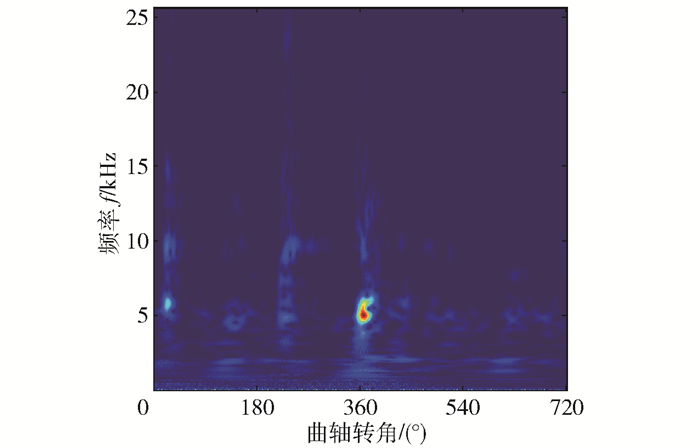
选取适合于分析冲击信号的db5小波基、sym6小波基、cmor3-3小波基、S变换和Wigner-Ville变换来获取时频图。从图 7、图 8可以看出:db5和sym6小波基对于部分高能量值的信号点无法分辨,且其整体频率分辨率较低;S变换在信号的高频区域频率分辨率较低,即高频分辨率不够准确;Wigner-Ville变换时频聚焦性良好,但交叉项干扰过多,此外能量值也较低,不利于后续的图像识别;而cmor3-3小波基时频分辨率较高,时频聚焦性好,图像清晰,更能揭示信号冲击能量值高的区域。
|
图 7 4种变换的时频图 Fig.7 Time-frequency diagrams of four transform methods |
|
图 8 cmor3-3小波基时频图 Fig.8 Time-frequency diagram of the cmor3-3 wavelet base |
综合比较以上结果,最后选择采用复Morlet小波即cmor3-3小波基将振动信号转换为时频图。
3.3 卷积神经网络的训练与测试通过复Morlet小波将7号缸在不同转速和扭矩下的振动数据进行变换,得到多种工况下正常气门间隙下的531幅时频图和进气门间隙异常增大故障下的537幅时频图。用500幅正常工况和500幅异常故障的时频图作为训练集,余下的31幅正常和37幅异常的时频图作为测试集。在初始AlexNet网络基础上,通过设置4层Batch Normalization和4层Dropout来改进AlexNet神经网络结构,以增强其诊断能力,改进后的神经网络结构如表 5所示。
| 下载CSV 表 5 基于AlexNet的网络结构 Table 5 Network structure based on AlexNet |
在优化的网络结构的基础上,通过控制变量法研究时频图像素值、卷积层卷积核大小、最小学习率、批处理数量(Batch Size)、Epoch数量对模型准确率的影响,结果如表 6所示。
| 下载CSV 表 6 调参情况 Table 6 Parameter tuning |
通过调参,找到了相对较优的参数可以使模型的准确率较高,且计算时间相对较短。较优参数如表 7所示,此时模型在多工况测试集下的准确率为98.91%。
| 下载CSV 表 7 AlexNet神经网络较优参数 Table 7 Optimal parameters of the AlexNet neural network |
第3节的振动信号是在多工况下采集的,模型的训练也是通过多工况数据完成的,多工况测试集的验证结果表明所提模型的准确率高,说明该方法可以很好地适应柴油机变负载和变转速的工况。但上文仅针对单一故障进行了研究,为充分验证本文方法的有效性和适应性,接下来对其他5种柴油机气门间隙异常故障模式进行训练和测试。不同故障模式下复Morlet变换+改进AlexNet方法的平均准确率和综合准确率如表 8所示。
| 下载CSV 表 8 复Morlet变换+改进AlexNet方法的准确率 Table 8 Accuracy of the complex Morlet and improved AlexNet method |
为了验证本文所提出的基于复Morlet变换+改进AlexNet神经网络进行柴油机气门间隙异常故障诊断方法的有效性,与两种传统的故障诊断方法进行对比实验:第一种为基于支持向量机(SVM)的柴油机气门间隙异常故障诊断方法,该方法通过手工提取气门启闭冲击组成特征向量来实现对柴油机气门间隙异常故障的诊断;第二种为基于主成分分析和支持向量机(PCA+SVM)的气门间隙异常诊断方法,该方法首先通过PCA技术对特征进行降维,然后再利用SVM对气门间隙故障情况分类。对比结果如表 9所示,可以看出本文所提方法的识别准确率更高。
| 下载CSV 表 9 不同方法综合准确率对比 Table 9 Comparison of the comprehensive accuracy of different methods |
本文提出了一种基于复Morlet变换+改进AlexNet神经网络的柴油机气门间隙异常故障诊断方法。首先根据柴油机缸盖振动信号非平稳的特点选择适于分析该信号的复Morlet时频变换方法;然后通过调整Batch Normalization层和Dropout层来优化网络结构,通过调整卷积核大小等超参数来提高模型的准确率,所构建的气门间隙故障诊断模型在测试集上的准确率达到了98.91%。最后对6种进排气门间隙故障进行识别,综合准确率达到了98.77%,明显高于传统的SVM算法。
| [1] |
罗兵富, 贺川, 付磊. 柴油发动机常见故障的维修与保养[J]. 装备维修技术, 2020(1): 154, 132. LUO B F, HE C, FU L. Repair and maintenance of common failures of diesel engines[J]. Equipment Maintenance Technology, 2020(1): 154, 132. (in Chinese) |
| [2] |
JAFARIAN K, MOBIN M, JAFARI-MARANDI R, et al. Misfire and valve clearance faults detection in the combustion engines based on a multi-sensor vibration signal monitoring[J]. Measurement, 2018, 128: 527-536. DOI:10.1016/j.measurement.2018.04.062 |
| [3] |
刘昱, 张俊红, 毕凤荣, 等. 基于LMD边际谱的柴油机气门故障诊断[J]. 内燃机工程, 2014, 35(6): 96-100. LIU Y, ZHANG J H, BI F R, et al. Diesel engine valve fault diagnosis based on LMD marginal spectrum[J]. Chinese Internal Combustion Engine Engineering, 2014, 35(6): 96-100. (in Chinese) |
| [4] |
张超, 陈建军, 郭迅. 基于EMD能量熵和支持向量机的齿轮故障诊断方法[J]. 振动与冲击, 2010, 29(10): 216-220. ZHANG C, CHEN J J, GUO X. Gear fault diagnosis method based on EMD energy entropy and support vector machine[J]. Journal of Vibration and Shock, 2010, 29(10): 216-220. (in Chinese) DOI:10.3969/j.issn.1000-3835.2010.10.045 |
| [5] |
张恒琪, 王超, 崔毅. 常规时频分析方法对比分析研究[J]. 信息通信, 2020(8): 55-56. ZHANG H Q, WANG C, CUI Y. Comparative analysis of conventional time-frequency analysis methods[J]. Information and Communications, 2020(8): 55-56. (in Chinese) DOI:10.3969/j.issn.1673-1131.2020.08.020 |
| [6] |
YUAN L H, LIAN D S, KANG X, et al. Rolling bearing fault diagnosis based on convolutional neural network and support vector machine[J]. IEEE Access, 2020, 8: 137395-137406. DOI:10.1109/ACCESS.2020.3012053 |
| [7] |
万晓静, 孙文磊, 陈坤. 基于CEEMD能量熵特征提取和VNWOA-LSSVM的风力机轴承故障诊断方法研究[J]. 机电工程, 2020, 37(10): 1186-1191. WAN X J, SUN W L, CHEN K. Fault diagnosis for wind turbine bearings based on CEEMD energy entropy and VNWOA-LSSVM[J]. Journal of Mechanical and Electrical Engineering, 2020, 37(10): 1186-1191. (in Chinese) DOI:10.3969/j.issn.1001-4551.2020.10.010 |
| [8] |
薛嫣, 朱静, 邓艾东. 基于熵特征和堆叠稀疏自编码器的滚动轴承故障诊断方法[J]. 工业控制计算机, 2020, 33(10): 44-46. XUE Y, ZHU J, DENG A D. A rolling bearing fault diagnosis method based on entropy feature and stack sparse autocoder[J]. Industrial Control Computer, 2020, 33(10): 44-46. (in Chinese) DOI:10.3969/j.issn.1001-182X.2020.10.016 |
| [9] |
李恒, 张氢, 秦仙蓉, 等. 基于短时傅里叶变换和卷积神经网络的轴承故障诊断方法[J]. 振动与冲击, 2018, 37(19): 124-131. LI H, ZHANG Q, QIN X R, et al. Fault diagnosis method for rolling bearings based on short-time Fourier transform and convolution neural network[J]. Journal of Vibration and Shock, 2018, 37(19): 124-131. (in Chinese) |
| [10] |
梁仲明, 滕宪斌, 杨期江, 等. 基于CEEMD-参数优化Morlet小波变换的柴油机振动信号冲击特征提取方法[J]. 船舶工程, 2020, 42(5): 90-96. LIANG Z M, TENG X B, YANG Q J, et al. Diesel engine vibration signal impact feature extraction method based on CEEMD-parameter optimized Morlet wavelet transform[J]. Ship Engineering, 2020, 42(5): 90-96. (in Chinese) |
| [11] |
GARBIN C, ZHU X Q, MARQUES O. Dropout vs. batch normalization: an empirical study of their impact to deep learning[J]. Multimedia Tools and Applications, 2020, 79: 12777-12815. DOI:10.1007/s11042-019-08453-9 |
| [12] |
ALMODFER R, XIONG S W, MUDHSH M, et al. Enhancing AlexNet for Arabic handwritten words recognition using incremental dropout[C]//2017 IEEE 29th International Conference on Tools with Artificial Intelligence (ICTAI). Boston, 2017: 663-669.
|








