2. 中广核研究院有限公司, 深圳 518005;
3. 北京化工大学 高端机械装备健康监控及自愈化北京市重点实验室, 北京 100029
2. China Nuclear Power Technology Research Institute Limited, Shenzhen 518005;
3. Beijing Key Laboratory for Health Monitoring and Self-recovery of High-end Mechanical Equipment, Beijing University of Chemical Technology, Beijing 100029, China
核电站反应堆内零部件在一回路冷却水冲击下可能发生松动或跌落,给反应堆运行带来较大安全隐患[1]。松脱件监测系统(loose parts monitoring system,LPMS)是保证核反应堆安全、稳定运行的系统之一,其中松脱件定位是LPMS中重要的一环,准确的定位能有效减少松脱件因碰撞对其他部件造成的后续损害,且有利于检修时尽快找到松脱件,保证检修人员的安全[2]。
目前国内外学者主要从建模分析和试验两方面对松脱件定位方法进行探究。文献[3]通过建立实际容器有限元模型并结合人工神经网络,实现了对松脱件的定位;文献[4]基于容器表面最短距离算法及有限元模型,对容器表面进行三维定位分析。然而上述两种方法主要依赖于容器的有限元模型,无法在实际应用中进行实时的定位分析。到达时差定位法是目前应用最为广泛的定位方法,文献[5]提出一种基于Wigner-Ville分布的时频分析方法来提取信号到达时差,但该方法计算量较大;文献[6]将希尔伯特变换应用于到达时差定位中,计算速度高,但冲击信号中存在其他振动波成分干扰,导致定位误差较大;文献[7]在文献[6]方法的基础上,结合连续小波变换使用网格定位法进行定位,然而网格定位法需一定的数据样本建立定位查询表,不适用于大型设备。
经验模态分解(empirical mode decomposition,EMD)是一种自适应的信号时频处理方法,能较好地适用于非平稳信号的处理[8-9]。EMD根据信号的局部时变特征进行自适应的时频分解[9],能有效应对冲击信号中振动波成分干扰的问题。通过对三角形定位算法误差进行分析发现,由3个传感器所组成的三角形内存在最小定位误差点,从而落点越靠近最小定位误差点,定位精度越高[10]。但是传统的三传感器布局无法改变落点与最小误差点之间的距离关系,采用多传感器布局从中选择最优的传感器组合能有效保证落点靠近最小定位误差点,提高定位精度。
综上所述,本文提出一种基于EMD与坐标寻优的松脱件定位方法,针对振动波成分干扰问题,通过对信号进行EMD处理,排除冲击信号中其他振动波成分的干扰,确定到达时间;针对三角形定位误差问题,采用多传感器布局,制定传感器选取策略,根据信号到达时间选取最优传感器组合用于定位分析,进一步提高定位精度;最后计算波速并建立定位方程组,求解坐标位置,并通过平板试验对所提方法进行验证。
1 EMD原理及三角形定位误差分析 1.1 经验模态分解原理EMD不需要事先选择基函数,能根据信号x(t)的局部时变特征自适应地对x(t)进行时频分解,将信号表示为一系列本征模函数(intrinsic mode function,IMF)分量与余项之和[11],如式(1)所示。
| $ x(t)=\sum\limits_{i=1}^{n} R_{i}+c_{n}(t) $ | (1) |
式中,Ri为各阶IMF分量,i代表阶数,cn(t)为残余项,n为Ri个数。各阶IMF分量分别代表一种振动模态,且从高到低包含了原信号中不同的频率成分。
1.2 三角形定位法误差分析三角形定位法基本原理为求3个已知半径(Ri,i=1,2,3)及圆心坐标的圆的交点所在。由于系统误差的存在,3个圆不再交于一点,而是构成了一个以定位点为中心的误差区域。令系统误差为r,误差区域为PAi,i=1,2,3,误差区域内切圆区域为PB,则有
| $ P_{A i}=\left\{\begin{array}{l} \left(x-x_{i}\right)^{2}+\left(y-y_{i}\right)^{2} \leqslant\left(R_{i}+r\right)^{2} \\ \left(x-x_{i}\right)^{2}+\left(y-y_{i}\right)^{2} \geqslant\left(R_{i}-r\right)^{2} \end{array}\right. $ | (2) |
| $P_{B}=\left\langle(x, y) \mid x^{2}+y^{2}=r^{2}, r>0\right\rangle $ | (3) |
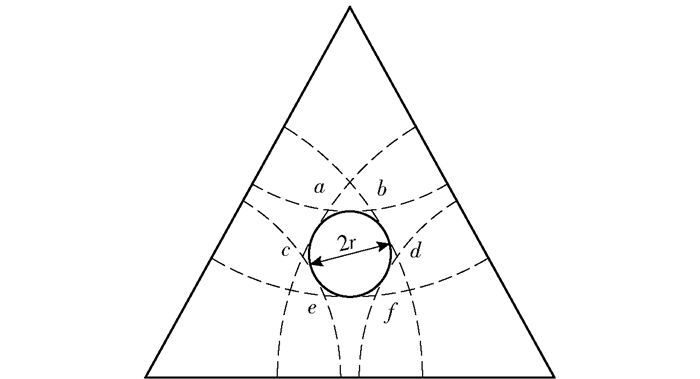
当r>0时,三圆相交形成一个由多条曲边组成的区域PA,如图 1所示,其面积代表定位误差的大小。其中,a、b、c、d、e、f分别为误差区域各顶点。
|
图 1 误差区域 Fig.1 Error zone |
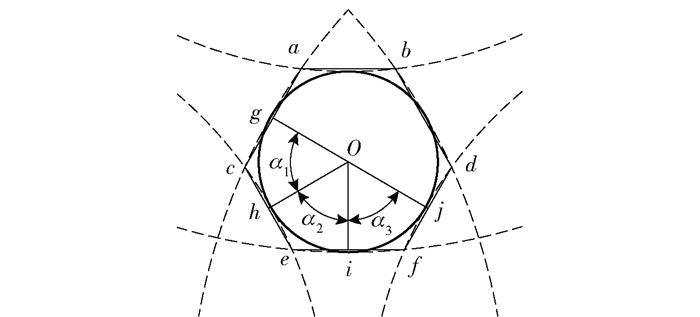
为便于计算区域PA的面积,连接误差区域顶点作PA的外接六边形PC,如图 2所示,O为误差区域内切圆圆心,g、h、i、j分别为边ac、ce、ef、fd的中点。
|
图 2 误差区域近似六边形 Fig.2 Approximate hexagon of the error zone |
当r较小时,可认为六边形区域PC面积与PA面积基本相同。令SC为六边形区域PC的面积,则SC可由式(4)表示。
| $ \begin{gathered} S_{C}=2 r^{2}\left(\tan \frac{\alpha_{1}}{2}+\tan \frac{\alpha_{2}}{2}+\tan \frac{\alpha_{3}}{2}\right) \geqslant 6 r^{2} \\ \sqrt{\tan \frac{\alpha_{1}}{2} \tan \frac{\alpha_{2}}{2} \tan \frac{\alpha_{3}}{2}} \end{gathered} $ | (4) |
式中,α1、α2、α3分别为Og与Oh、Oh与Oi、Oi与Oj之间的夹角。
当
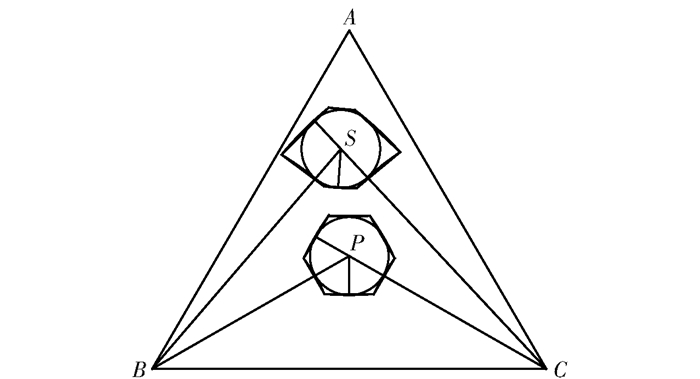
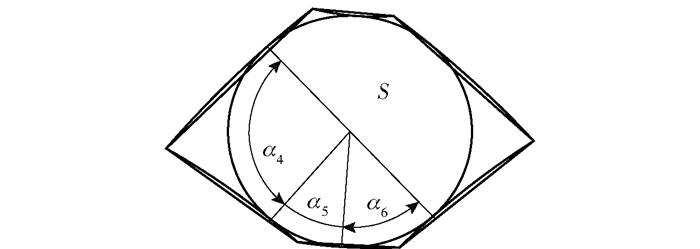
当落点S偏离最小误差点P时,误差区域形状改变,各测点与落点之间的角度随之变化。令落点改变后的区域为P′C,如图 3及图 4所示。令变化后的角度为α4、α5、α6,落点改变后六边形区域面积S′C可由式(5)表示。
| $ S_{C}^{\prime}=2 r^{2}\left(\tan \frac{\alpha_{4}}{2}+\tan \frac{\alpha_{5}}{2}+\tan \frac{\alpha_{6}}{2}\right) $ | (5) |
|
图 3 落点改变后的误差区域 Fig.3 Error area after the drop point is changed |
|
图 4 误差区域角度变化 Fig.4 The angle change of the error area |
结合式(5)及图 3可知,随着落点逐渐远离点P,各角度的变化和误差区域的面积增加,定位误差随之增大。
2 松脱件定位方法传感器所接收到的信号由多种振动波成分混叠而成,会对到达时间提取及波速计算造成干扰。EMD方法能将信号分解成多个代表不同频率成分的IMF分量,用以分离不同的振动波成分,有效排除其他振动波成分的干扰,提高定位精度。
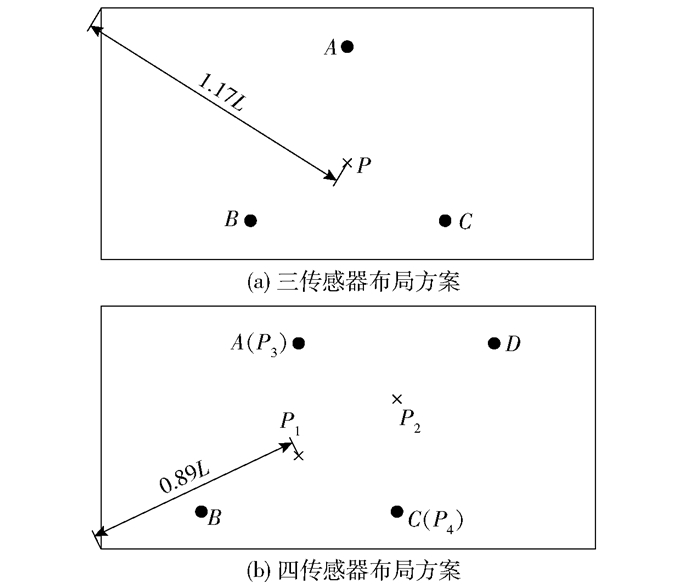
根据1.2节结论,在三角形定位法中存在最小误差点P,离P点越远则定位误差越大,而最大定位误差直接影响到定位方法的准确性。如图 5所示,令平板长度为2L,宽为L,在平板试验中,随着传感器数量增加,最小定位误差点P增加(如点P1、P2、P3及P4),则最大定位误差点与点P的距离更近,如三传感器布局中最大误差点与点P的距离为1.17L,四传感器布局中最大误差点与点P1的距离为0.89L。因此选用多传感器布局,合理选用传感器组合能进一步提高定位精度。
|
图 5 传感器布局方案对比 Fig.5 Comparison of sensor layout schemes |
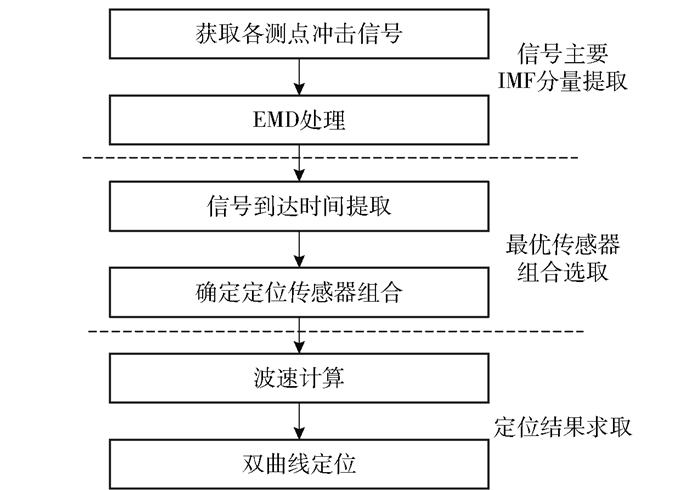
通过上述分析,提出基于EMD与坐标寻优的松脱件定位方法,该方法可分为冲击信号主要IMF分量提取、最优传感器组合选取、定位结果求取这3部分,方法流程如图 6所示,具体步骤如下。
|
图 6 松脱件定位方法流程图 Fig.6 Flow chart of the loose parts positioning method |
1) 冲击信号主要IMF分量提取。获取各传感器的冲击信号,对其进行EMD处理,并确定冲击信号主要IMF分量。信号主要IMF分量选取需遵循以下原则:①IMF分量幅值接近原信号;②IMF分量频谱能量集中频段与原信号保持一致。
2) 最优传感器组合选取。过程如下:①对信号主要IMF分量进行希尔伯特变换,包络线极值点对应的时间点即为碰撞产生能量以波速cg传播距离x的时刻[12],从而得到信号到达各个传感器的时间;②已知定位误差随着落点与点P间距离的减小而减小,因P点到达三角形各顶点的距离和最小,随着落点靠近P点,落点与三角形各顶点的距离和随之减小,假设信号到达各传感器的波速相同,则为保证落点靠近P点,传感器选取策略可描述为当存在3个以上传感器时,选择到达时间和最小的3个传感器进行定位分析。
3) 定位结果求取。过程如下:①将各参数带入式(6)计算波速;②确定定位用传感器组合后,带入式(7)所示定位方程,求解定位坐标。
| $ c_{g}=2 \omega_{\mathrm{m}}^{0.5}\left(\frac{E h^{2}}{12 \rho\left(1-\gamma^{2}\right)}\right)^{0.25} $ | (6) |
| $\left\{\begin{array}{l} \sqrt{\left(x-x_{A}\right)^{2}+\left(y-y_{A}\right)^{2}}- \\ \sqrt{\left(x-x_{B}\right)^{2}+\left(y-y_{B}\right)^{2}}=c_{g} \Delta t_{A B} \\ \sqrt{\left(x-x_{B}\right)^{2}+\left(y-y_{B}\right)^{2}-} \\ \sqrt{\left(x-x_{C}\right)^{2}+\left(y-y_{C}\right)^{2}}=c_{g} \Delta t_{B C} \end{array}\right. $ | (7) |
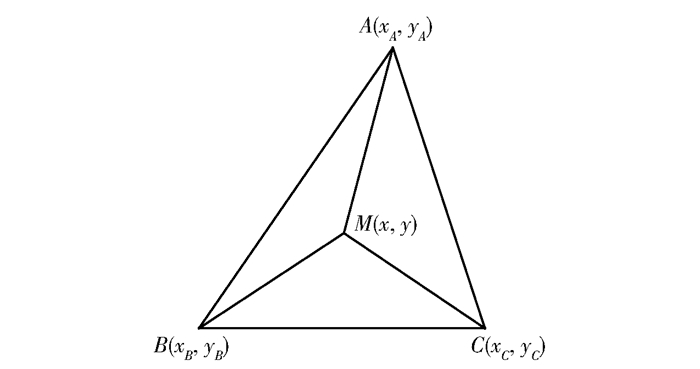
式中,ωm为信号主频率,Hz;E为钢板的弹性模量,MPa;h为钢板的厚度,m;ρ为介质密度,kg/m3;γ为钢板的泊松比;x、y为待求落点坐标,xA、yA、xB、yB、xC、yC为各传感器坐标,m;cg为波速,m/s;ΔtAB、ΔtBC为信号到达传感器A、B及传感器B、C的时间差,s。三角形定位法示意图如图 7所示。
|
图 7 三角形定位法示意图 Fig.7 Schematic illustration of the triangle location method |
本文设计了平板试验对所提松脱件定位方法进行验证,并与文献[4]及文献[7]中定位方法的准确性进行了对比。
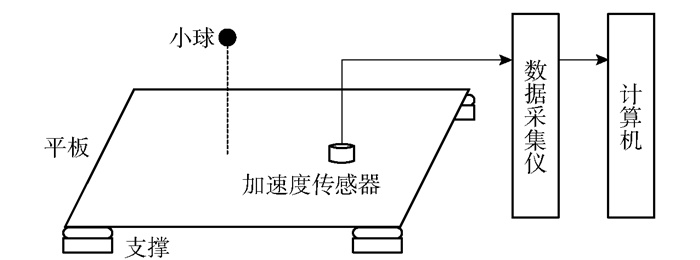
3.1 试验台及试验设计平板试验台如图 8所示,由平板、支撑、钢制小球、数据采集仪、加速度传感器及计算机等设备组成,平板实物如图 9所示。平板尺寸为1 200 mm×1 800 mm×10 mm,材料为Q345钢,采用海绵加垫木双重支撑,以隔绝支撑物对平板振动的影响。所使用的加速度传感器量程为500 g,频率响应范围为0.3~10 000 Hz。
|
图 8 平板试验台 Fig.8 Plate test bench |

|
图 9 试验平板 Fig.9 Test plate |
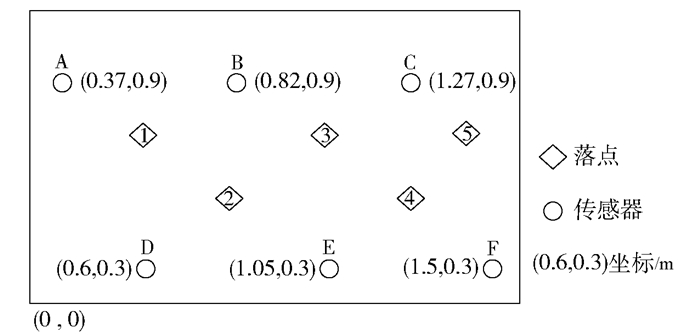
进行试验时,使用不同质量的小球从固定高度跌落,分别到达不同落点,传感器采集到加速度信号后将信号传输至数据采集仪内进行A/D转换,最后传输至计算机内进行存储及后续处理。在平板试验中,使用质量为110 g的小球距离平板上表面0.74 m高度处,于5个不同落点分别跌落,为避免偶然误差,相同条件下小球重复跌落20次。传感器及落点布置如图 10所示。数据采集器采样频率为25.6 kHz,采样点数为16 384。
|
图 10 传感器布局方案 Fig.10 Test sensor layout |
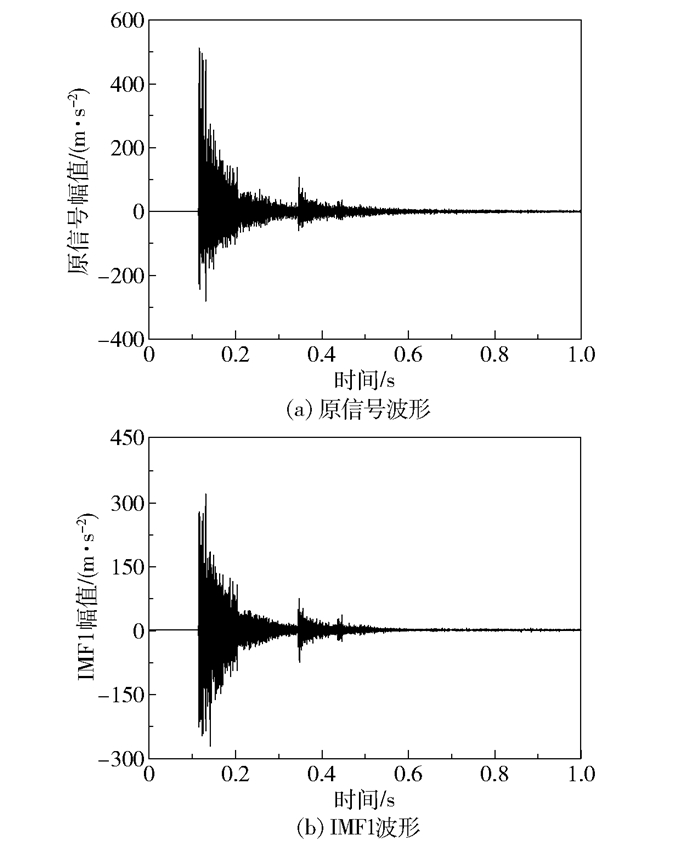
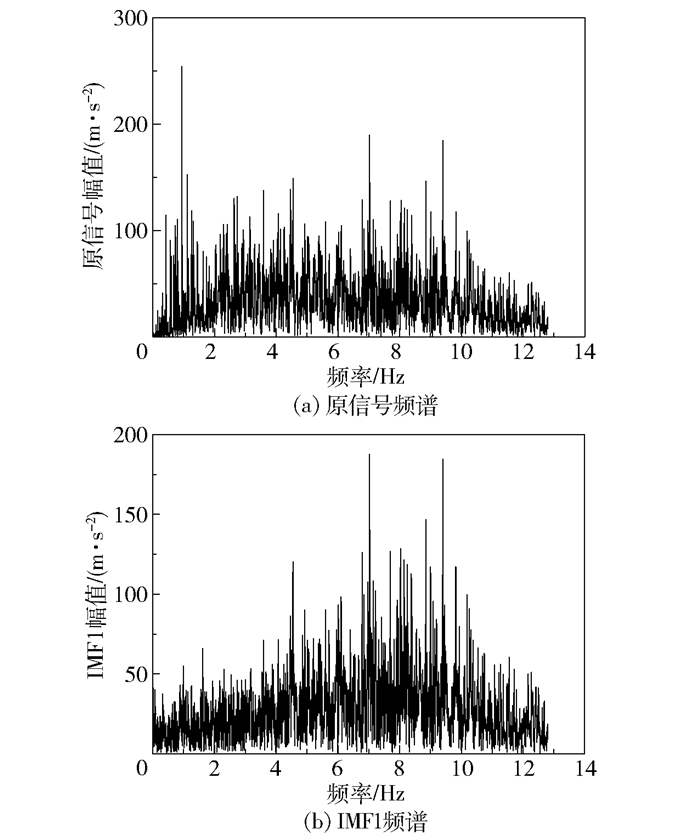
以落点1某次冲击信号为例,原信号与IMF1波形及频谱对比分别如图 11、12所示。可以看出,IMF1波形峰值接近原信号,且主要能量集中在4~10 Hz范围内,与原信号频谱一致,因此得出IMF1为信号的主要IMF分量。
|
图 11 落点1信号波形对比 Fig.11 Signal waveform comparison |
|
图 12 落点1信号频谱对比 Fig.12 Signal spectrum comparison |
对IMF1分量进行包络后,针对落点1提取出的信号到达各传感器的时间如表 1所示。根据传感器选取策略,取传感器A、B、D进行定位分析。
| 下载CSV 表 1 信号到达时间 Table 1 Signal arrival time |
同理对于其他落点信号,分析各测点信号的到达时间,得到各落点冲击信号最优的传感器组合如表 2所示。
| 下载CSV 表 2 最优传感器组合 Table 2 Optimal sensor combinations |
根据波速计算公式(式(6))得到波速,代入定位方程组(式(7)),得到定位坐标。采用相同的步骤取各落点某一次的冲击信号进行分析,得出各落点的定位结果如表 3所示。可以看出,各落点定位偏差均在0.2 m以下,最小定位偏差为0.02 m,最大定位偏差为0.19 m。且不同传感器组合的定位结果存在差异,对于各落点,相比于其他传感器组合,由表 2所得最优传感器组合的定位偏差最小,偏差均在0.2 m以下。
| 下载CSV 表 3 平板试验定位分析结果 Table 3 Location analysis results of the flat test |
固定取传感器组合ABD信号,得出不同落点在各方法下的定位偏差如表 4所示。相比于本文所提方法,文献[4]及文献[7]方法的定位偏差较大,其中,落点1的平均定位偏差最小,分别为0.13 m和0.20 m,文献[4]方法针对其他落点的定位偏差均超过0.20 m,文献[7]方法针对其他落点的定位偏差均超过0.40 m。
| 下载CSV 表 4 不同方法定位偏差对比 Table 4 Comparison of location errors for different methods |
通过上述分析可知,本文方法通过增加传感器个数得到多个定位结果,基于传感器选取策略有效保证了落点更接近某3个传感器所组成的三角形内的最小误差点P,因而可从多个定位结果中选取出定位偏差最小的结果,实现了定位方法的优化。
本文方法与文献[4]方法及文献[7]方法均采用相同的传感器组合进行定位分析,本文方法通过对冲击信号进行EMD处理提取出信号的主要IMF分量,有效排除了其他成分的干扰,使得对于信号到达各传感器时间的提取更为准确,从而减小了定位偏差,定位效果优于文献[4]方法及文献[7]方法(表 4)。
4 结论(1) 基于EMD与坐标寻优的松脱件定位方法通过EMD排除了其他振动波成分的干扰,增加了传感器个数并进行最优传感器组合的选取,使定位结果得到进一步优化,定位准确性提高。
(2) 本文所提方法解决了复杂信号中冲击信号主要IMF分量提取困难的问题,对于实际容器中松脱件的预警及质量估计具有一定的借鉴作用。
实际反应堆结构复杂,由波速所导致的误差可能会进一步扩大,今后的工作将更加关注于提高波速计算的准确性,并结合降噪方法使实际情况中松脱件的定位更为准确。
| [1] |
崔威杰, 郝祖龙, 郑金光. 基于小波包和BP网络的松脱件质量估计[J]. 实验室研究与探索, 2018, 37(2): 108-111. CUI W J, HAO Z L, ZHENG J G. Mass estimation of loose parts based on wavelet packet and BP neural networks[J]. Research and Exploration in Laboratory, 2018, 37(2): 108-111. (in Chinese) DOI:10.3969/j.issn.1006-7167.2018.02.027 |
| [2] |
CAO Y L, HE Y F, ZHENG H W, et al. An alarm method for a loose parts monitoring system[J]. Shock and Vibration, 2012, 19(4): 753-761. DOI:10.1155/2012/891085 |
| [3] |
MOON S, HAN S, KANG T, et al. Model-based localization and mass-estimation methodology of metallic loose parts[J]. Nuclear Engineering and Technology, 2020, 52(4): 846-855. DOI:10.1016/j.net.2019.10.005 |
| [4] |
LISKA J, KVNKEL S. Localization of loose part impacts on the general 3D surface of the nuclear power plant coolant circuit components[J]. Progress in Nuclear Energy, 2017, 99: 140-146. DOI:10.1016/j.pnucene.2017.05.004 |
| [5] |
KIM Y B, KIM S J, CHUNG H D, et al. A study on technique to estimate impact location of loose part using Wigner-Ville distribution[J]. Progress in Nuclear Energy, 2003, 43: 261-266. DOI:10.1016/S0149-1970(03)00033-7 |
| [6] |
杨将新, 郑华文, 曹衍龙, 等. 基于希尔伯特变换的核电站松脱件定位方法[J]. 机械工程学报, 2009, 45(12): 232-236. YANG J X, ZHENG H W, CAO Y L, et al. Estimation method for impact location of loose parts based on Hilbert transform[J]. Journal of Mechanical Engineering, 2009, 45(12): 232-236. (in Chinese) |
| [7] |
季田田, 方力先, 曾复, 等. 基于连续小波变换的Hilbert包络线松动部件定位方法[J]. 原子能科学技术, 2014, 48(6): 1087-1095. JI T T, FANG L X, ZENG F, et al. Hilbert envelope loose part location method based on continuous wavelet transform[J]. Atomic Energy Science and Technology, 2014, 48(6): 1087-1095. (in Chinese) |
| [8] |
刘东瀛, 邓艾东, 刘振元, 等. 基于EMD与相关系数原理的故障声发射信号降噪研究[J]. 振动与冲击, 2017, 36(19): 71-77. LIU D Y, DENG A D, LIU Z Y, et al. De-noising method for fault acoustic emission signals based on the EMD and correlation coefficient[J]. Journal of Vibration and Shock, 2017, 36(19): 71-77. (in Chinese) |
| [9] |
苏秀红, 李皓. 基于经验模态分解和小波阈值的冲击信号去噪[J]. 计算机测量与控制, 2017, 25(1): 204-208, 220. SU X H, LI H. Denoising of shock signal based on EMD and wavelet threshold[J]. Computer Measurement and Control, 2017, 25(1): 204-208, 220. (in Chinese) |
| [10] |
朱剑, 赵海, 徐久强, 等. 三角形定位算法的误差分析[J]. 东北大学学报(自然科学版), 2009, 30(5): 648-651. ZHU J, ZHAO H, XU J Q, et al. Error analysis of triangle location algorithm[J]. Journal of Northeastern University(Natural Science), 2009, 30(5): 648-651. (in Chinese) |
| [11] |
马宏伟, 张大伟, 曹现刚, 等. 基于EMD的振动信号去噪方法研究[J]. 振动与冲击, 2016, 35(22): 38-40. MA H W, ZHANG D W, CAO X G, et al. Vibration signal de-noising method based on empirical mode decomposition[J]. Journal of Vibration and Shock, 2016, 35(22): 38-40. (in Chinese) |
| [12] |
PARK G Y, CHEON S W, LEE C K, et al. An estimation method for impact location of loose parts[J]. Progress in Nuclear Energy, 2006, 48: 360-370. DOI:10.1016/j.pnucene.2005.09.012 |








