静态混合器是一种依靠管道内周期排列的螺旋元件对流体不断的分割、变形、移位及混合的在线、高效混合设备,与搅拌混合器相比,具有结构简单、空间占有率小、停留时间短、耗能低及维修成本低等优点[1-2],因此广泛应用于精细化工、水处理、制药工业、生物化工等工业过程[3]。
掌握静态混合器内流场的湍流特性规律对现有静态混合器的结构优化及新型静态混合元件的开发具有重要意义[4-6]。Tajima等[7]采用Kenics型静态混合器(KSM)对水和液态CO2生成CO2水合物的混合过程进行实验研究,结果表明湍流状态下随着KSM元件数量增加,液滴尺寸逐渐变小。Jaworski等[8]采用大涡模拟(LES)和非定常雷诺平均NS方程(RANS)两种方法,对KSM内两相流的湍动能和耗散率等参数估计进行了有效性分析。Regner等[9]利用计算流体动力学(CFD)软件分析了层流状态下不同长径比的Lightnin静态混合器(LSM)内的流场结构,研究发现带有曲率的混合元件交错处会产生径向二次流旋涡。本课题组前期采用大涡模拟分析KSM内二次流径向涡的形成诱因及演化过程,从多纵向涡的角度探讨了扭旋叶片对流体力学性能及传热性能的影响机理[10];并对LSM中高黏度流体的层流流动和混合特性进行数值模拟,发现LSM内高黏度流体的混合性能优于KSM[11];随后分析了LSM内湍流的传热特性和旋涡演化过程,结果表明半径尺度的强制涡受到LSM混合元件的影响逐渐耗散且被诱导形成两对迪恩涡,强化了LSM的传热性能[6]。
本征正交分解(POD)方法被许多学者用于对湍流流场的测量结果进行分析,Rempfer等[12]将POD应用于平板边界层内的相干结构和动力学行为的研究中,结果表明高阶的流动相干结构对转捩的产生有着十分重要的作用;余颖等[13]利用POD方法提取内置蜗杆传热管流场中的拟序结构,发现多对大尺度纵向涡结构的产生会提高强化传热效率;张建伟等[14]对双组分层对置撞击流的湍流速度场进行POD分解,发现低阶模态能够准确还原流场中的涡结构。
到目前为止,关于LSM的研究主要集中在湍流传热、层流混合等方面,而针对LSM的瞬态湍流特性及分布混合特性的研究尚未见文献报道。因此,本文利用POD方法提取流场的湍流结构,以期明晰LSM内流体的流动特性。采用平均涡量、拉伸率等参数表征LSM内流体的混合特性,为丰富LSM混合机理提供理论依据,并扩大其在工业上的应用范围。
1 数值模型 1.1 控制方程大涡模拟是流体力学中一种重要的数值模拟方法,其基本思想是直接计算大尺度涡,对于小涡则通过亚格子模型进行模拟。区别于直接数值模拟(DNS)和RANS方法,LES在对大涡解析的同时还对小涡进行模化,通过空间滤波操作过滤掉小涡,滤波后大涡控制方程为[15]
| $ \begin{aligned} \frac{\partial\left(\boldsymbol{u}_{i}\right)}{\partial t}+\frac{\partial}{\partial x_{j}}\left(\boldsymbol{u}_{i} \boldsymbol{u}_{j}\right)=-\frac{1}{\rho} \frac{\partial p}{\partial x_{i}}+\nu \nabla^{2} \boldsymbol{u}_{i}-\frac{\partial \boldsymbol{\tau}_{i j}}{\partial x_{j}} \end{aligned} $ | (1) |
| $ \frac{\partial \boldsymbol{u}_{i}}{\partial x_{i}}=0 $ | (2) |
式中,x为笛卡尔坐标系;ui和uj为流体速度;ρ、p和ν分别为流体的密度、压力和运动黏度。
亚格子应力τij定义为
| $\boldsymbol{\tau}_{i j}=-2 \mu_{t} \boldsymbol{S}_{i j}+\frac{1}{3} \delta_{i j} \boldsymbol{\tau}_{k k} $ | (3) |
其中,
| $ \boldsymbol{S}_{i j}=\frac{1}{2}\left(\frac{\partial \boldsymbol{u}_{i}}{\partial x_{j}}+\frac{\partial \boldsymbol{u}_{j}}{\partial x_{i}}\right) $ | (4) |
式中,Sij为应变速率张量,τkk为亚格子应力的各向同性部分。Smagorinsky-Lilly模型定义的亚格子湍流涡黏系数为[16]
| $ \mu_{t}=\rho L_{\mathrm{s}}^{2} \sqrt{2 \boldsymbol{S}_{i j} \boldsymbol{S}_{i j}} $ | (5) |
式中,Ls为亚网格尺度的混合长度。
1.2 本征正交分解本征正交分解方法由Lumley[17]首次提出,经Sirovich[18]改进后发展为“快照POD”,逐渐被广大学者用于复杂流场的降阶及特征提取。假设在混合器横截面内有m个离散采样点,每次采样同时获取每个采样点的三维速度值u(xm)。因此,获取N张快照脉动速度场数据,以矩阵U的形式表示为[19]
| $ \boldsymbol{U}=\left[\begin{array}{lllll} \boldsymbol{u}^{1} & \boldsymbol{u}^{2} & \boldsymbol{u}^{3} & \cdots & \boldsymbol{u}^{N} \end{array}\right]=\left[\begin{array}{cccc} u_{1}^{1} & u_{1}^{2} & \cdots & u_{1}^{N} \\ u_{2}^{1} & u_{2}^{2} & \cdots & u_{2}^{N} \\ \vdots & \vdots & \vdots & \vdots \\ u_{m}^{1} & u_{m}^{2} & \cdots & u_{m}^{N} \end{array}\right] $ | (6) |
式中,上标N表示快照数目,下标m代表三维速度的矢量位置。自相关矩阵为
| $ \boldsymbol{C}=\boldsymbol{U}^{\mathrm{T}} \boldsymbol{U} $ | (7) |
速度相关矩阵的特征向量和特征值为
| $ \boldsymbol{C A}=\lambda \boldsymbol{A} $ | (8) |
用式(8)计算得到的特征值及对应的特征向量去构建POD模态
| $ \phi^{i}=\frac{\sum\limits_{n=1}^{N} \boldsymbol{A}_{n}^{i} \boldsymbol{u}^{n}}{\left\|\sum\limits_{n=1}^{N} \boldsymbol{A}_{n}^{i} \boldsymbol{u}^{n}\right\|} $ | (9) |
式中,i=1, …, N,Ani为特征值λn对应的特征向量。
POD系数
| $ \boldsymbol{a}^{n}=\boldsymbol{\psi}^{\mathrm{T}} \boldsymbol{u}^{n} $ | (10) |
线性重构任意时刻的速度场
| $\boldsymbol{u}^{n}=\boldsymbol{u}(x)+\sum\limits_{i=1}^{N} a_{i}^{n} \phi^{i} $ | (11) |
假设圆管直径D=40 mm,总长度为560 mm,对含有元件长径比Ar分别为1.0、1.5、2.0和3.0的LSM流场进行比较分析。LSM内混合元件由两个半椭圆形板和两个三角形板组成,相邻两元件首尾相连且相互交错90°布置安装,几何模型如图 1所示。对于长径比Ar=1.5的LSM,两个交叉半椭圆板分别与轴截面成34°和146°,其他模型的具体几何参数见表 1。

|
图 1 不同长径比的LSM几何模型 Fig.1 Geometric models of LSM with different aspect ratios |
| 下载CSV 表 1 几何参数 Table 1 Geometrical parameters |
本文采用ANSYS FLUENT V16.1软件中的LES湍流模型,对图 1中4种不同长径比的LSM进行非稳态数值模拟。以水(密度ρ=998.2 kg/m3,黏度μ=0.001 003 Pa·s)作为工质。采用课题组前期对LSM湍流流动传热预测中的网格无关性验证结果[6],利用多面体网格对计算域进行离散化处理,采用10层边界层和1.2的网格增长率对壁面进行细化,总网格数量为1 597 947。
采用三维压力基求解器,并使用SIMPLEC算法对压力和速度耦合;梯度项求解采用Least Squares Cell Based离散法;压力离散采用标准形式,动量离散采用Bounded Central Differencing;采用用户自定义函数(user define function,UDF)设置速度入口边界[6],对应的雷诺数分别为1 990、3 981、5 971和7 962。出口边界条件设置为outflow。连续性方程收敛残差小于10-4,其余变量的收敛残差为10-6。
1.5 模型有效性大涡模拟在降低空间和时间分辨率的前提下可以对具有较高雷诺数和较复杂的湍流流动进行模拟,计算精度高。课题组前期采用LES方法对KSM内的流场进行研究,数值计算的速度分布和实验一致性较好[10]。LSM和KSM混合器都属于螺旋流静态混合器[9],具有相似的工作原理。因此,本文选用大涡模拟对Lightnin型静态混合器进行研究。
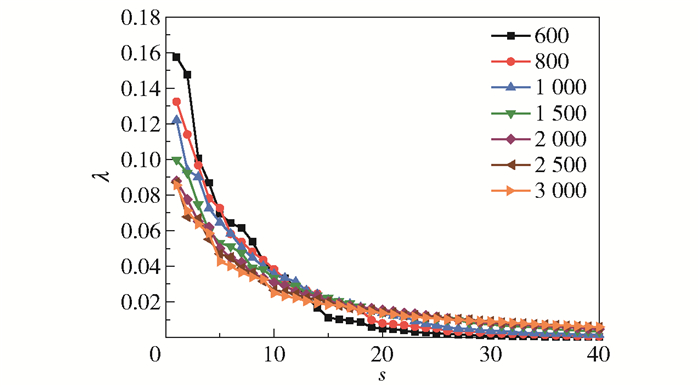
2 POD分析与结果讨论 2.1 采样数量选择为探究采样数量对POD分析精确度的影响,分析了不同采样数量下的模态能量分布,如图 2所示。从图中可以看出,随着模态阶数s的增加,POD模态的特征值λ迅速衰减,当模态阶数超过10之后,高阶模态所携带的能量较低。其中,前四阶模态携带的能量最多;在采样数量超过2 000时,前四阶的模态能量占整体的29%以上,且随着样本数量的增加低阶模态所包含的能量不再发生变化。因此,综合考虑计算精度及成本,选取采样数量为2 000。
|
图 2 Re=3 981、Ar=1.5条件下,z/l=2处不同样本数量的模态能量分布 Fig.2 Modal energy distributions for different numbers of samples at z/l=2, Re=3 981 and Ar=1.5 |
对LSM数值模拟所得的样本进行计算,评估不同模态下的二范数εL2(L2-norm)[20],具体公式如下。
| $ \varepsilon_{L 2}=\left\|\delta_{i, 1}-\delta_{i, 2}\right\|_{2} $ | (12) |
式中,δi, 1、δi, 2分别为两次不同采样频率样本中POD分解之后的第i阶模态。
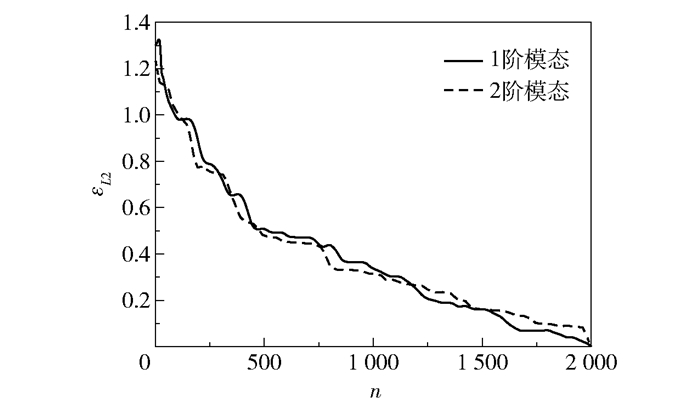
样本数量与模态收敛性之间的关系如图 3所示。由图可知,模态之间的差异随着样本数量的增加逐渐减小。当样本数量n小于500时,差异值变化明显,在样本数量很小的情况下,L2-norm可达到1.3左右。当n>1 000时,L2-norm小于0.3,并且逐渐趋于0,表明经POD得到的模态差异性稳定,即POD模态是收敛的。
|
图 3 不同样本数量下不同模态的二范数 Fig.3 L2-norm of the modes for different numbers of samples |
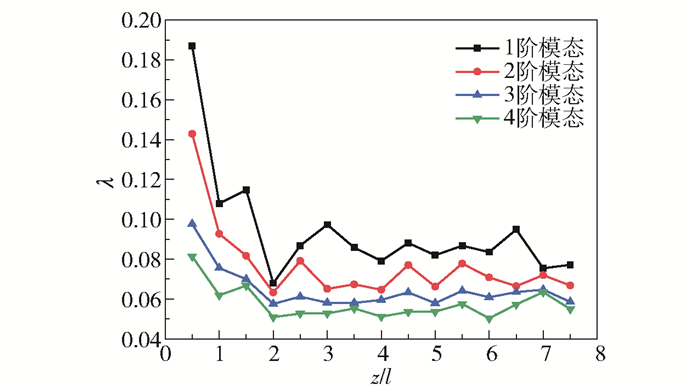
图 4为不同轴截面LSM内湍流流体前四阶模态的能量分布。从图 4可以看出,不同阶的模态能量在z/l=0~2范围内呈减小趋势,表明流场复杂度不断增加。在流场复杂度稳定后,1阶模态能量所占的湍动能分数在8%~10%,2阶模态能量所占湍动能分数在6%~8%,3阶模态能量所占湍动能分数在5%~7%,4阶模态能量所占湍动能分数在5%~6%。前四阶模态能量占总湍动能的24%~31%,包含了主要的大尺度旋涡结构信息。
|
图 4 Re=3 981和Ar=1.5条件下不同轴向位置的模态能量分布 Fig.4 Modal energy distributions for different axial positions at Re=3 981 and Ar=1.5 |
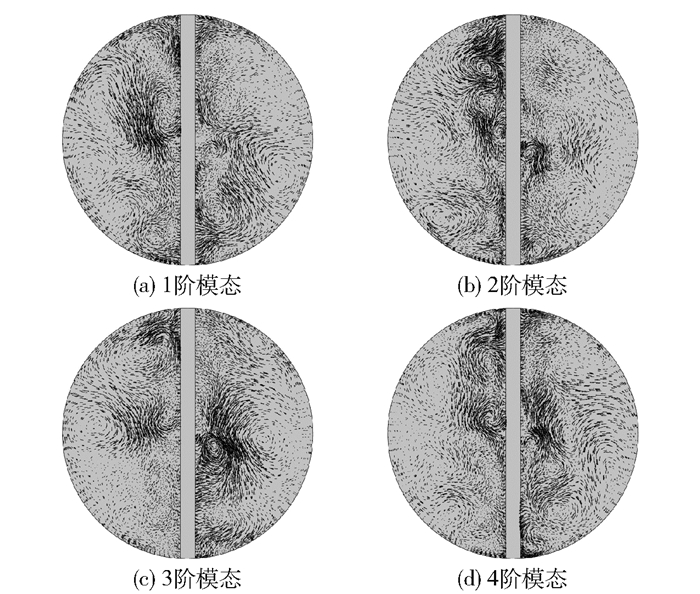
图 5为前四阶POD模态的径向速度矢量图。由于1阶模态包含着最多的流场信息,从图 5(a)可以清晰地看出在元件壁面存在两对大尺度旋涡结构且对称分布,周围无小尺度旋涡结构。随着模态能量的降低,在第2、3阶模态中小尺度旋涡数量逐渐增加,所提取的流场信息逐渐减少,这主要是由流场的复杂程度增加所致。在第4阶模态中旋涡结构开始散乱,小尺度的旋涡结构尺寸逐渐增大。
|
图 5 前四阶POD模态的径向速度矢量图 Fig.5 Radial velocity vectors of the first four POD modes |
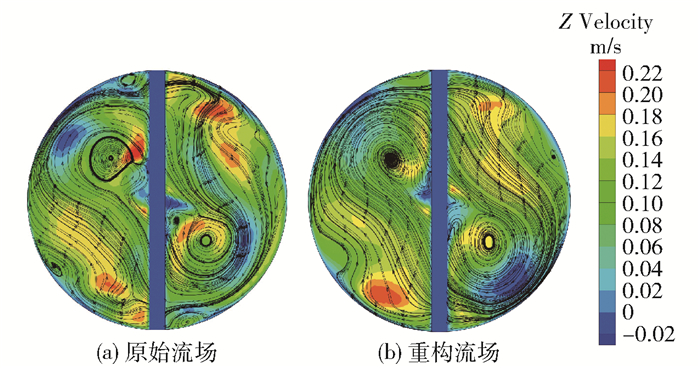
对LSM内的原始瞬态流场(图 6(a))进行40阶本征正交分解,利用前四阶模态重构流场流线图,如图 6(b)所示。对比发现,原始流场在管壁边缘处存在小尺度涡对,干扰流场大尺度相干结构的提取与分析。POD方法在时均速度场的基础上对任意时刻的原始流场进行线性重构,能够过滤小尺度的旋涡结构,同时保留半圆形流道内原始流场的特征,使核心流区域的径向二次流大尺度相干结构的空间分布更加明晰。
|
图 6 Re=3 981时原始和重构流场流线图对比 Fig.6 Comparison of original and reconstructed flow field streamlines at Re=3 981 |
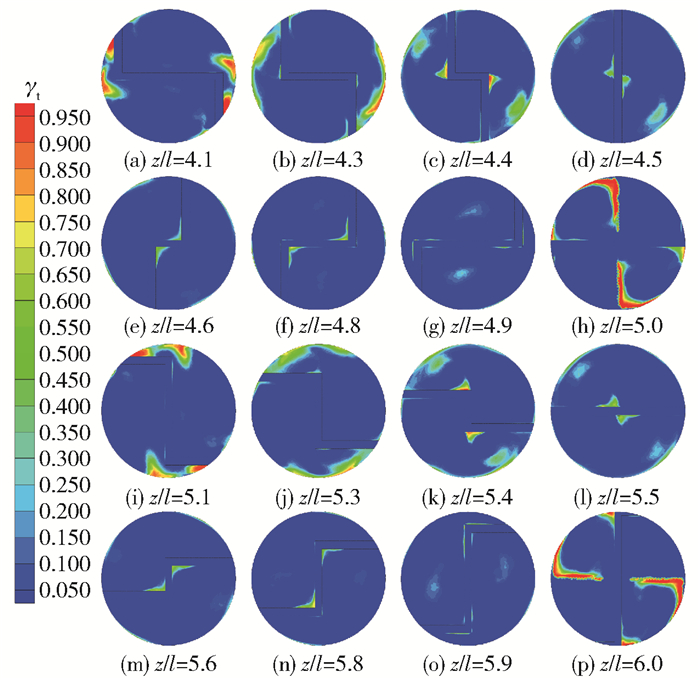
二次流能够强化静态混合器的混合性能。为了更好地了解LSM内的二次流分布,通过计算整个采样过程流场中选定位置处流速方向与主流方向相反的时间与总采样时间的比值得到回流系数γt。图 7为在z/l=4.1~6.0处LSM内的回流系数云图。由图中的高亮区域可以看出,回流主要发生在管壁与元件连接处附近以及元件中心截面处。
|
图 7 Ar=1.5,Re=3 981时不同轴截面的回流系数云图 Fig.7 Cross sectional contours of the reverse flow coefficient under the conditions Re=3 981 and Ar=1.5 |
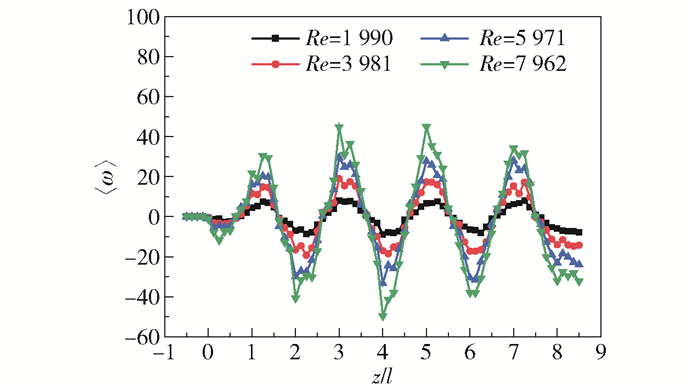
图 8描述了不同雷诺数下平均涡量〈ω〉随轴向位置的变化。从图中可知,受到元件旋向影响,不同轴截面内平均涡量分布具有正弦状的周期性变化规律。在混合器入口段无元件分布,没有旋涡产生,〈ω〉为0;在z/l=4.0~5.0范围内,〈ω〉逐渐增大,表明在一个混合元件周期内旋涡从正向涡逐渐向反向涡转变,峰值出现在左旋和右旋元件连接处;在z/l=5.0~6.0范围内,〈ω〉逐渐减小,表明旋涡从反向涡逐渐向正向涡转变。随着雷诺数的增加,涡量峰值出现不同程度的变化,当Re=1 990时,正向涡值的峰值平均值为6.37,而Re=3 981、5 971和7 962对应的正向涡值峰值平均值分别为15.83、25.33和36.39,涡量分别增大了148.5%、297.6%和322.7%,表明增大Re可提高LSM内流体的湍流程度。
|
图 8 不同雷诺数下LSM内不同轴向截面的平均涡量(Ar=1.5) Fig.8 Mean vorticity of different coaxial sections for different Reynolds numbers(Ar=1.5) |
前期的研究成果表明,静态混合器内的流动具有混沌混合特性[21]。采用拉伸率Λn这一指标对不同长径比和不同雷诺数下的LSM分布混合性能进行定量分析,拉伸率数值越大,代表强化分布混合能力越强。根据Ottino混合理论[22],每个粒子所经历的拉伸量可以通过小矢量的变形求出。
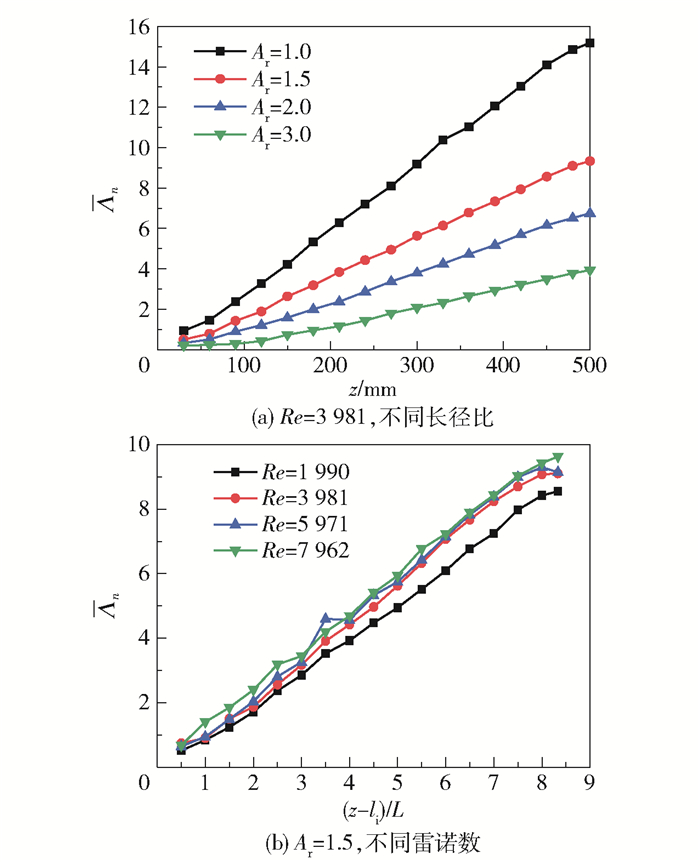
图 9为不同长径比和雷诺数下LSM内粒子拉伸率的几何平均值。由图 9可以发现,LSM内粒子的拉伸率均随轴向长度的增加而线性增长;在同一轴向位置,Ar=1.0对应的拉伸率最大,Ar=3.0对应的拉伸率最小,说明长径比越小,拉伸效果越明显。这是由于相同轴向距离内小长径比的混合叶片扭曲程度更大,径向二次流更明显,并且在相同长度的管路内,可以布置的小长径比的元件个数多于大长径比的元件个数,因此,流体微元在经过布置有小长径比元件的管路中时被拉伸的概率更大。从图 9(b)可以看出,随着雷诺数的增加,LSM的最大拉伸率和横截面的平均拉伸率均增大,Re=3 981、5 971和7 962下的拉伸率与Re=1 990时的相比,分别提高了11.5%、15.1%和18.9%。
|
图 9 不同长径比和雷诺数下的平均拉伸率变化 Fig.9 The average stretching rate for different aspect ratios and Reynolds numbers |
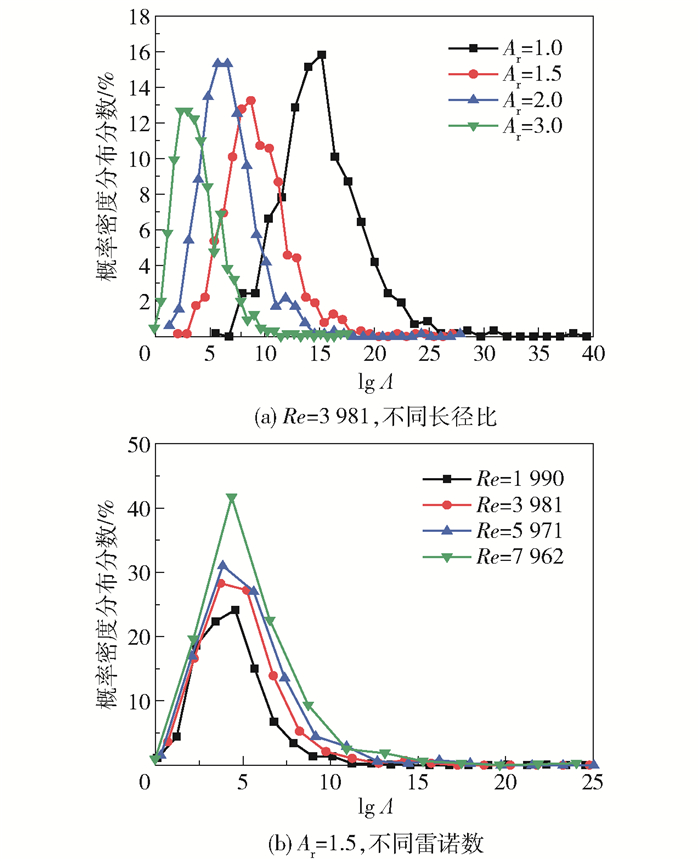
通过对LSM内的拉伸率数值进行统计学分析,可以定量评价流体的微观混合程度[21, 23]。图 10为LSM在不同长径比和不同雷诺数下出口截面的拉伸率概率密度分布。从图中可以看出,对流体有切割分流作用的LSM,其拉伸率概率密度分布曲线形状类似高斯分布曲线,说明拉伸率数值分布较为集中;径向二次流随着长径比的变小而增强,致使概率密度曲线向着高拉伸率方向移动,这是由于流体经过较大的拉伸变形,产生较高的拉伸率。Ar=1.0时曲线在尾部的震荡相较于其他长径比的要明显,这说明其内部的高拉伸率的粒子数量较多。随着长径比的增加,各曲线峰值逐渐向左移动,说明小长径比的混合元件对流体的混合能力较强。随着雷诺数的增加,拉伸率分布范围没有改变,但各个截面处平均拉伸率的概率密度增大,总体上提高了混合器的混合能力。
|
图 10 不同长径比和雷诺数下的拉伸率概率密度分布 Fig.10 The probability distributions of stretching rate for different aspect ratios and Reynolds numbers |
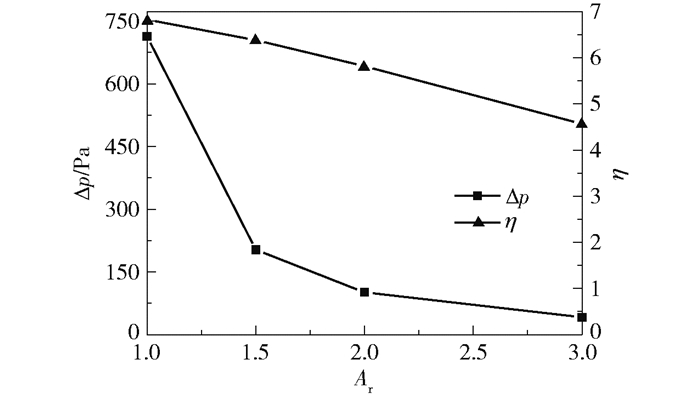
采用压降Δp和混合性能强化系数η来分析不同长径比的LSM的流动混合强化行为[11]。不同长径比LSM内的压降及混合性能强化系数的变化如图 11所示。可以看出压降Δp和混合性能强化系数η均随长径比的增大逐渐减小。在Re=3 981条件下,Ar=1.0的LSM内的压降Δp=712.9 Pa,混合性能强化系数η=6.8。随着长径比增加,Ar=1.5、2.0、3.0的LSM的压降分别是Ar=1.0时的28.5%、14.2%和0.06%,而混合性能强化系数分别是Ar=1.0时的93.5%、85.2%和66.9%。综上所述,在Ar=1.5时LSM的压降明显减小,同时具有较好的混合性能。
|
图 11 Re=3 981条件下不同长径比LSM的压降及混合性能强化系数 Fig.11 Pressure drop and mixing enhancement factor for LSM with different aspect ratios at Re=3 981 |
(1) 采用POD方法对LSM内的瞬态湍流流场进行分析,前四阶模态能量占总湍动能的24%~31%,蕴含主要的大尺度旋涡结构信息,可消除小尺度旋涡结构对流场的干扰。
(2) 对于同一长径比的LSM,涡量随着元件的轴向位置变化呈正弦状周期性变化,随着雷诺数的增加,不同轴向截面的平均涡量均增大。
(3) 对拉伸率的分析结果表明,LSM内部的拉伸变形随着雷诺数的增加而增加;流体微元在经过布置有小长径比元件的管路时被拉伸的概率更大。
(4) Ar=1.0时LSM的混合强化性能最好,然而与Ar =1.5、2.0、3.0时相比压降较高。综合压降和混合性能强化系数,Ar=1.5的LSM具有较好的混合性能,同时压降降低显著。
| [1] |
GHANEM A, LEMENAND T, DELLA VALLE D, et al. Static mixers: mechanisms, applications, and characterization methods-a review[J]. Chemical Engineering Research and Design, 2014, 92(2): 205-228. |
| [2] |
MENG H B, HAO Y N, YU Y F, et al. Experimental study of gas-liquid two-phase bubbly flow characteristics in a static mixer with three twisted leaves[J]. Korean Journal of Chemical Engineering, 2020, 37(11): 1859-1866. DOI:10.1007/s11814-020-0609-z |
| [3] |
禹言芳, 王丰, 孟辉波, 等. 旋流静态混合器内瞬态流动特性研究进展[J]. 化工进展, 2013, 32(2): 255-262, 282. YU Y F, WANG F, MENG H B, et al. Research progress of the characteristics of instantaneous flow in static mixer with twisted-leaves[J]. Chemical Industry and Engineering Progress, 2013, 32(2): 255-262, 282. (in Chinese) |
| [4] |
MENG H B, ZHU G X, YU Y F, et al. The effect of symmetrical perforated holes on the turbulent heat transfer in the static mixer with modified kenics segments[J]. International Journal of Heat and Mass Transfer, 2016, 99: 647-659. DOI:10.1016/j.ijheatmasstransfer.2016.03.110 |
| [5] |
MENG H B, JIANG X H, YU Y F, et al. Laminar flow and chaotic advection mixing performance in a static mixer with perforated helical segments[J]. Korean Journal of Chemical Engineering, 2017, 34(5): 1328-1336. DOI:10.1007/s11814-017-0035-z |
| [6] |
MENG H B, HAN M Q, YU Y F, et al. Numerical evaluations on the characteristics of turbulent flow and heat transfer in the Lightnin static mixer[J]. International Journal of Heat and Mass Transfer, 2020, 156: 119788. DOI:10.1016/j.ijheatmasstransfer.2020.119788 |
| [7] |
TAJIMA H, YAMASAKI A, KIYONO F. Continuous formation of CO2 hydrate via a Kenics-type static mixer[J]. Energy & Fuels, 2004, 18(5): 1451-1456. |
| [8] |
JAWORSKI Z, MURASIEWICZ H. LES and URANS modelling of turbulent liquid-liquid flow in a static mixer: turbulent kinetic energy and turbulence dissipation rate[J]. Chemical Papers, 2010, 64(2): 182-192. DOI:10.2478/s11696-009-0106-7 |
| [9] |
REGNER M, ÖSTERGREN K, TRÄGÅRDH C. Effects of geometry and flow rate on secondary flow and the mixing process in static mixers—a numerical study[J]. Chemical Engineering Science, 2006, 61(18): 6133-6141. DOI:10.1016/j.ces.2006.05.044 |
| [10] |
李权树, 魏思远, 龚斌, 等. Kenics型静态混合器充分发展段纵向涡演变分析[J]. 过程工程学报, 2016, 16(4): 549-555. LI Q S, WEI S Y, GONG B, et al. Analysis on evolution of longitudinal vortexes in fully developed zone of a Kenics static mixer[J]. The Chinese Journal of Process Engineering, 2016, 16(4): 549-555. (in Chinese) |
| [11] |
MENG H B, SONG M Y, YU Y F, et al. Enhancement of laminar flow and mixing performance in a Lightnin static mixer[J]. International Journal of Chemical Reactor Engineering, 2017, 15(3): 20160112. |
| [12] |
REMPFER D, FASEL H F. Evolution of three-dimensional coherent structures in a flat-plate boundary layer[J]. Journal of Fluid Mechanics, 1994, 260: 351-375. DOI:10.1017/S0022112094003551 |
| [13] |
余颖, 刘鹏, 郑年本, 等. 一种强化传热管内拟序结构的大涡模拟[J]. 工程热物理学报, 2019, 40(10): 2402-2406. YU Y, LIU P, ZHENG N B, et al. Large eddy simulation of coherent structures in a heat transfer enhancement tube[J]. Journal of Engineering Thermophysics, 2019, 40(10): 2402-2406. (in Chinese) |
| [14] |
张建伟, 马繁荣, 张志刚, 等. 双组水平喷嘴撞击流反应器流场POD分析[J]. 化工学报, 2018, 69(7): 2916-2925. ZHANG J W, MA F R, ZHANG Z G, et al. POD analysis of flow field in horizontal two-group nozzle impinging stream reactor[J]. CIESC Journal, 2018, 69(7): 2916-2925. (in Chinese) |
| [15] |
YANG Z Y. Large eddy simulation: past, present and the future[J]. Chinese Journal of Aeronautics, 2015, 28(1): 11-24. |
| [16] |
车健, 江锦波, 李纪云, 等. 节流孔出气模式对静压干气密封稳态性能影响[J]. 化工学报, 2020, 71(4): 1734-1743. CHE J, JIANG J B, LI J Y, et al. Effect of orifice exhaust mode on steady performance of hydrostatic dry gas seal[J]. CIESC Journal, 2020, 71(4): 1734-1743. (in Chinese) |
| [17] |
LUMLEY J L. The structure of inhomogeneous turbulent flows[C]//Atmospheric Turbulence and Radio Wave Propagation. Moscow: Nauka, 1967: 166-178.
|
| [18] |
SIROVICH L. Turbulence and the dynamics of coherent structures part Ⅰ: coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571. DOI:10.1090/qam/910462 |
| [19] |
MEYER K E, PEDERSEN J M, ÖZCAN O. A turbulent jet in crossflow analysed with proper orthogonal decomposition[J]. Journal of Fluid Mechanics, 2007, 583: 199-227. |
| [20] |
MULD T W, EFRAIMSSON G, HENNINGSON D S. Mode decomposition on surface-mounted cube[J]. Flow Turbulence Combust, 2012, 88: 279-310. DOI:10.1007/s10494-011-9355-y |
| [21] |
HOBBS D M, MUZZIO F J. The Kenics static mixer: a three-dimensional chaotic flow[J]. Chemical Engineering Journal, 1997, 67(3): 153-166. |
| [22] |
OTTINO J M. The kinematics of mixing: stretching, chaos, and transport[M]. Cambridge, USA: Cambridge University Press, 1989: 64-77.
|
| [23] |
AHMED I, POUDYAL H, CHANDY A J. Fill factor effects in highly-viscous non-isothermal rubber mixing simulations[J]. International Polymer Processing, 2019, 34(2): 182-194. |








