woodpile结构是平面外光学器件和集成光路中非常重要的平台,目前已经存在大量的相关报道[1-7],如波导耦合器[1]、超高Q值三维光子晶体纳米谐振器[3]等。同时,近年来2D-3D异质结结构因其二维结构设计的灵活性和简单性以及可以沿堆叠方向上制备密度集成电路而引起了广泛的关注[8-14],例如,Chutinan等[8-9]实现了位于不同平面层的波导的集成;Kawashima等[12]制造了一个L形的集成波导;Lin等[14]研究了包括两个波分复用器的平面外集成电路。
定向耦合器不仅是光学器件中的基本元器件,还是集成光路中的重要器件,可以用作功率分配器[15]、开关[16-19]、波分复用[19-20]等。有关二维结构中该器件的研究已有很多的理论和实验报道[15-25],例如,Gao等[15]提出了一种新型的定向耦合器功率分配器;Zablocki等[16]设计了一种可在2.9 V低压条件下工作的紧凑的光子晶体定向耦合器,该绝缘子在绝缘硅平台上具有150 kHz的电光频率,开关时间为620 ns;Qu等[23]设计了一种具有高消光比(-35.07 dB)、短耦合长度(24a)、输入/输出通道去耦合的新型2×2定向耦合器结构;Bao等[25]研究了宽频带、低损耗的太赫兹光子晶体光纤定向耦合器,发现在1 THz的中心频率、0.25 THz的带宽和9.2 dB的总设备损耗下其具有最佳性能。定向耦合器中的耦合长度是实现紧凑型集成电路的重要参数,超短耦合长度能够有效减小集成电路的体积。研究者们针对耦合长度的调节开展了很多工作[26-30],Moghaddam等[28]提出用正方晶格气孔结构代替三角晶格结构,在二维光子晶体(PC)中实现了小于3a的超短耦合长度;Feng等[30]在woodpile结构中通过控制输入波导和耦合波导之间中心区域的折射率实现了小于1.7a的超短耦合长度。
综上,目前对二维光子晶体结构或woodpile结构中定向耦合器耦合长度的研究已经较为完备,却很少有关于2D-3D异质结结构中定向耦合器耦合长度调节的报道。因此,本文采用时域有限差分法(FDTD)对2D-3D异质结结构中的定向耦合器进行了详细的分析、仿真和设计,同时考虑了非平面和平面的优化设计,获得了小于2a的超短耦合长度。
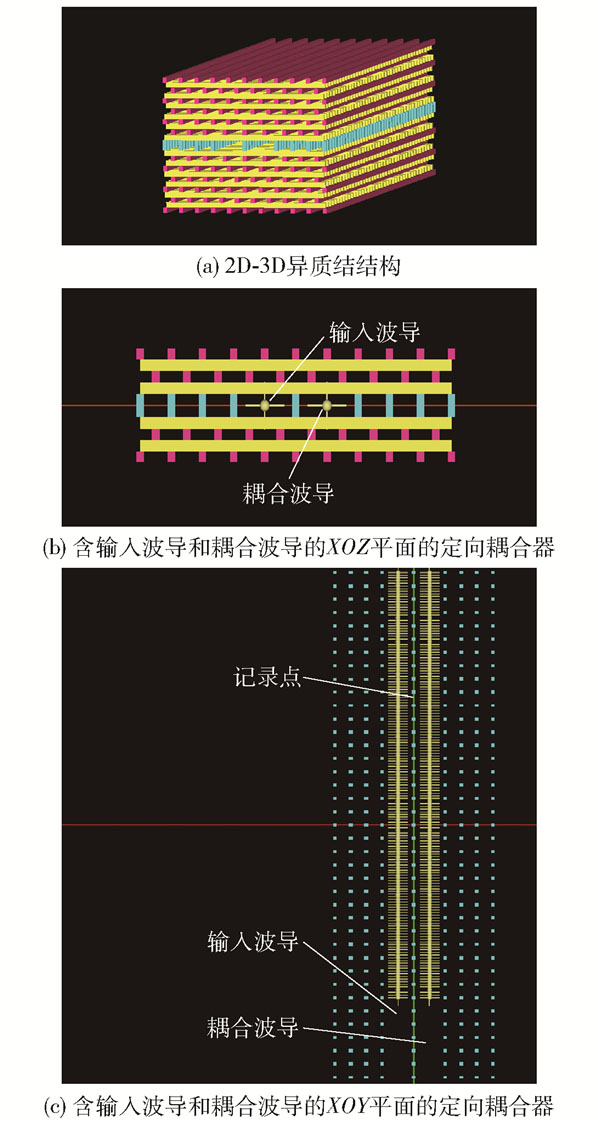
1 2D-3D异质结结构中的定向耦合器本文设计了样品大小为400 μm×100 μm× 78 μm、工作于太赫兹下的2D-3D异质结结构,如图 1(a)所示。由图 1可知,该结构包括1个二维光子晶体(蓝色介质柱)和2个对称放置的woodpile结构,在中间的二维光子晶体层引入平面定向耦合器,具体结构如图(b)和(c)所示。该定向耦合器包含1个输入波导和1个耦合波导,两波导之间的距离为2a,两波导之间又有一排介质柱。woodpile结构的介质柱参数为0.25a×0.3a,其中a代表同一层中相邻介质柱之间的距离。对于正方晶格的二维光子晶体,方形柱的参数为0.25a×0.25a×0.6a。在模拟过程中,a的大小为10 μm, 背景材料和介质柱的介电常数分别为1.0(空气)和11.9(硅)。通过FDTD方法进行模拟计算,得到2D光子晶体和woodpile结构的重叠带隙为0.360[c/a]~0.453[c/a](10.86 THz~13.6 THz),其中,c为真空中的光速。
|
图 1 异质结结构示意图以及XOZ平面和XOY平面中的定向耦合器 Fig.1 Schematic views of a 2D-3D hetero-structure and the direction coupler in the XOZ and XOY plane |
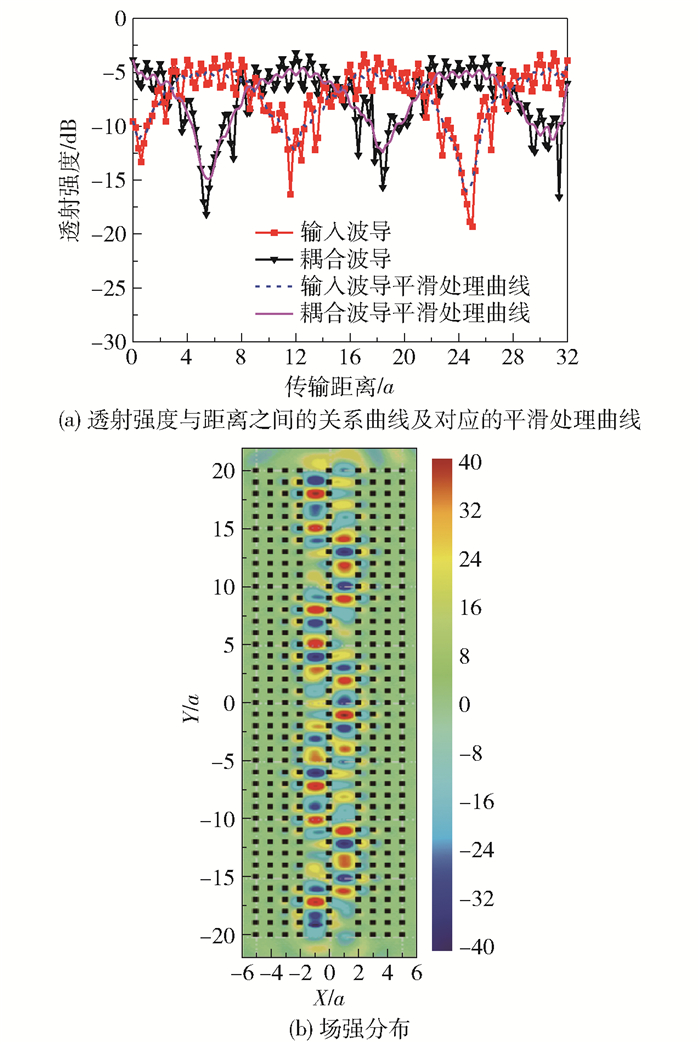
本文对2D-3D异质结结构中定向耦合器耦合长度的调制进行了详细的模拟计算。通常,耦合长度是通过分析色散关系来确定的。在本文的仿真中,耦合长度通过对透射光谱结合场分布分析来精确确定。如图 1(c)所示,在输入波导和耦合波导中分别设置了多个记录点,相邻记录点之间的间隔为0.2a。光源位于输入波导距离样品表面1.0a处,且传输方向为沿Y轴正方向。为了避免光源的影响,第一个记录点与光源之间的距离为6a。首先,模拟计算所有参数不变情况下的传输特性及此时的耦合长度。通过FDTD方法给出所有记录点的透射谱,再通过对透射谱进行分析得到输入波导和耦合波导中频率为0.403[c/a]时的透射强度随传输距离的变化关系,结果如图 2(a)所示。可以发现,该变化曲线按照类正弦曲线规律变化,传输信号在两个波导之间交替传输,而耦合长度为相邻的波峰与波谷之间的距离,因此,当频率为0.403 [c/a]时,耦合长度约为5a~6a。为了得到精确的耦合长度,对该频率的场分布进行模拟,结果如图 2(b)所示。可见,这一频率的传输信号在输入波导和耦合波导之间交替传输。通过分析传输强度与距离的关系曲线,可以得到传输强度随距离变化的周期为5.5a,即耦合长度。
|
图 2 频率为0.403[c/a]时透射强度和距离之间的关系曲线以及对应的场强分布 Fig.2 The relationship between transmission intensity and distance and the field strength distribution when the frequency is 0.403 [c/a] |
通过第1节的模拟,得到参数未作调整时定向耦合器的耦合长度为5.5a。对于密集型集成光路,较短的耦合长度有利于减小集成器件的尺寸。关于减小定向耦合器的耦合长度已存在一些报道[26-30],例如利用正方晶格代替三角晶格[28],或者减小耦合区域中的介质柱宽度[30]等。基于上述报道,为了获得较短的耦合长度,我们将二维光子晶体设计为正方晶格,并减小耦合区域中介质柱的宽度。在本文设计的2D-3D异质结结构中,定向耦合器上下两侧各有一个woodpile结构,该结构可以消除定向耦合器沿垂直方向的能量损失,同时可以通过调节woodpile结构参数改变其耦合长度。
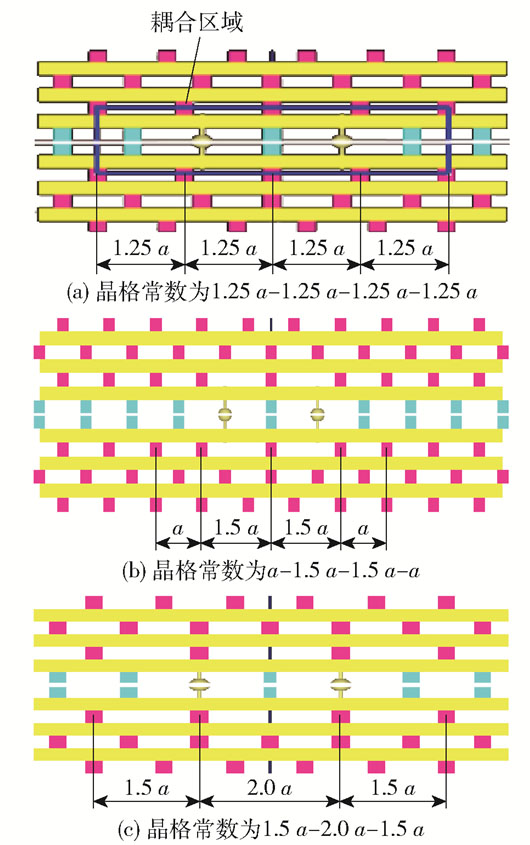
耦合长度的调节可以通过改变耦合区域的平均折射率来实现,降低耦合区域的平均折射率可以获得较短的耦合长度[27-30]。因此,首先考虑对woodpile结构进行晶格常数的调节。该结构的耦合区域为5a×40a×2.4a(图 3(a)中蓝色区域),考虑增加位于±0.75a堆叠层的晶格常数,以降低耦合区域的平均折射率,晶格常数可以从1a连续增加到2a。在本文的设计中考虑了3种情况,如图 3所示,晶格常数分别为1.25 a-1.25 a-1.25 a-1.25a(情况1)、a-1.5 a-1.5 a-a(情况2)和1.5 a-2.0 a-1.5a(情况3)。比较这3种情况,可以发现前两种设计的平均折射率几乎相等,但中心耦合区域仍然存在差异,第三种结构的平均折射率最小。它们之间的关系为n1≈n2>n3,其中n1,n2和n3分别对应3种情况的平均折射率。
|
图 3 非平面调节示意图 Fig.3 Schematic views of the off-plane adjustment |
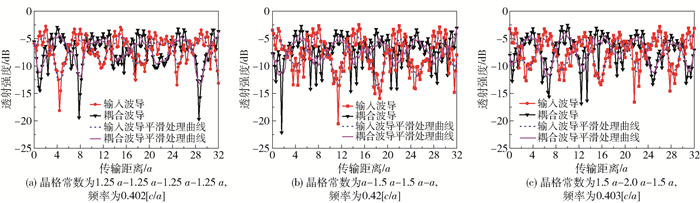
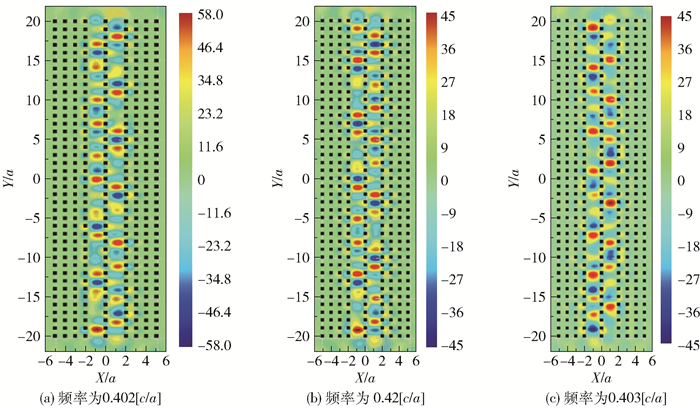
随后,通过FDTD方法对3种设计的透射光谱进行模拟和分析,根据仿真结果得出特定频率下透射强度与距离之间的关系曲线,结果如图 4(a)~(c)所示,对应频率分别为0.402 [c/a],0.42 [c/a]和0.403 [c/a]。与图 2(a)相比,可以发现所有的耦合长度都有了明显的减小。这一模拟结果充分证明,耦合长度的减小可以通过降低耦合区域中的平均折射率来实现。可以看出,图 4(a)、(b)和(c)对应的耦合长度分别约为3.5a~4.5a,3.0a~4.0a和2.0a~3.0a。为了确定耦合长度,模拟计算了特定频率下的场分布,结果分别如图 5(a)~(c)所示。通过分析,确定耦合长度分别为4.0a,3.5a和3.0a。
|
图 4 透射强度与传输距离之间的关系曲线 Fig.4 The relationship between the transmission intensity and the distance |
|
图 5 不同频率下的场分布图 Fig.5 Field distributions at different frequencies |
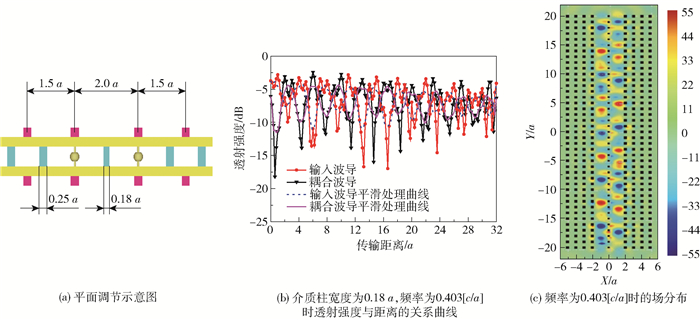
通过第2节的模拟,证明了利用非平面调节方法可以获得较短的耦合长度。为了进一步缩短耦合长度,还可以同时考虑其他优化方法。本课题组前期的研究工作表明,减小介质柱的宽度可以缩短耦合长度[30]。由图 1(c)可知,在输入波导和耦合波导之间有一排介质柱,因此考虑减小该排介质柱的宽度来进一步降低耦合区域的平均折射率。该介质柱的宽度可以从0.25a连续地调整到0,平面调节示意图如图 6(a)所示。通过FDTD方法详细模拟了当介质柱宽度为0.18a时所有记录点的透射光谱,频率为0.403 [c/a]时透射强度与距离之间的关系如图 6(b)所示。比较图 4(c)和图 6(b),可以发现耦合长度进一步缩短,约为1.5a~2a。为了准确地确定耦合长度,模拟了该频率下的场分布,结果如图 6(c)所示。分析得出该耦合长度为1.8a,小于2a,属于超短耦合长度。
|
图 6 平面调节的示意图,频率为0.403[c/a],介质柱宽为0.18a时透射强度与距离的关系曲线以及场分布图 Fig.6 Schematic illustration of plane adjustment, the relationship between transmission intensity and distance and the field strength distribution when the frequency is 0.403[c/a] and the width of the medium column is 0.18a |
上述模拟结果表明,在2D-3D异质结结构中,通过非平面和平面两种调节方法的结合,可以使得定向耦合器的耦合长度进一步缩短,获得小于2a的超短耦合长度。与二维结构中的平面调节方法相比,本文方法进一步缩短了定向耦合器的耦合长度。这一模拟结果在密度集成器件设计方面具有一定的应用意义,可以有效地减小集成器件的尺寸。
4 结论通过时域有限差分法模拟计算了2D-3D异质结结构中定向耦合器的超短耦合长度。基于降低耦合区域的平均折射率可以减小耦合长度这一方法手段,利用2D-3D异质结结构的堆叠特性,在同时考虑了非平面和平面优化设计后,可以获得小于2a的超短耦合长度。这一研究结果为耦合器器件设计和密集型集成光路尺寸的降低提供了理论支撑。
| [1] |
LIU R J, LI Z Y, ZHOU F, et al. Waveguide coupler in three-dimensional photonic crystal[J]. Optics Express, 2008, 16(8): 5681-5688. DOI:10.1364/OE.16.005681 |
| [2] |
BISWAS R, CHRISTENSEN C, MUEHLMEIER J, et al. Waveguide circuits in three-dimensional photonic crystals[J]. Photonics and Nanostructures-Fundamentals and Applications, 2008, 6(2): 134-141. |
| [3] |
TANG L L, YOSHIE T. Ultra-high-Q three-dimensional photonic crystal nano-resonators[J]. Optics Express, 2007, 15(25): 17254-17263. DOI:10.1364/OE.15.017254 |
| [4] |
TANG L L, YOSHIE T. Light localization in woodpile photonic crystal built via two-directional etching method[J]. IEEE Journal of Quantum Electronics, 2011, 47(7): 1028-1035. DOI:10.1109/JQE.2011.2152367 |
| [5] |
KAWASHIMA S, LEE L H, OKANO M, et al. Design of donor-type line-defect waveguides in three-dimensional photonic crystals[J]. Optics Express, 2005, 13(24): 9774-9781. DOI:10.1364/OPEX.13.009774 |
| [6] |
LIU R J, LI Z Y, FENG Z F, et al. Channel-drop filters in three-dimensional woodpile photonic crystals[J]. Journal of Applied Physics, 2008, 103(9): 094514. DOI:10.1063/1.2909982 |
| [7] |
FENG Z F, ZHANG D D, RAJA M Y A. Channel drop filters in woodpile-heterostructures[J]. Journal of Applied Physics, 2014, 115(8): 083102. DOI:10.1063/1.4866075 |
| [8] |
CHUTINAN A, JOHN S. Light localization for broadband integrated optics in three dimensions[J]. Physical Review B, 2005, 72(16): 161316. DOI:10.1103/PhysRevB.72.161316 |
| [9] |
CHUTINAN A, JOHN S. 3+1 dimensional integrated optics with localized light in a photonic band gap[J]. Optics Express, 2006, 14(3): 1266-1279. DOI:10.1364/OE.14.001266 |
| [10] |
TANG L L, YOSHIE T. High-Q hybrid 3D-2D slab-3D photonic crystal microcavity[J]. Optics Letters, 2010, 35(18): 3144-3146. DOI:10.1364/OL.35.003144 |
| [11] |
ZHANG D D, FENG Z F. Optimization for waveguide bends in 2D+3D hetero-structure[J]. Optik, 2013, 124(23): 6298-6301. DOI:10.1016/j.ijleo.2013.05.065 |
| [12] |
KAWASHIMA S, ISHIZAKI K, NODA S. Light propagation in three-dimensional photonic crystals[J]. Optics Express, 2009, 18(1): 386-392. |
| [13] |
LIN J, FENG Z F. Investigation for connecting waveguide in off-planar integrated circuits[J]. Applied Optics, 2017, 56(25): 7041-7045. DOI:10.1364/AO.56.007041 |
| [14] |
LIN J, FENG Z F, FENG S. Optical device terahertz integration in a two-dimensional-three-dimensional heterostructure[J]. Applied Optics, 2018, 5(2): 185-188. |
| [15] |
GAO Y F, ZHOU J, ZHOU M, et al. Design of novel power splitters by directional coupling between photonic crystal waveguides[J]. Optoelectronics Letters, 2010, 6(6): 417-420. DOI:10.1007/s11801-010-0017-4 |
| [16] |
ZABLOCKI M J, SHARKAWY A, EBIL O, et al. Electro-optically switched compact coupled photonic crystal waveguide directional coupler[J]. Applied Physics Letters, 2010, 96(8): 081110. DOI:10.1063/1.3330927 |
| [17] |
CUESTA-SOTO F, MARTÍNEZ A, GARCÍA J, et al. All-optical switching structure based on a photonic crystal directional coupler[J]. Optics Express, 2004, 12(1): 161-167. DOI:10.1364/OPEX.12.000161 |
| [18] |
YAMAMOTO N, OGAWA T, KOMORI K. Photonic crystal directional coupler switch with small switching length and wide bandwidth[J]. Optics Express, 2006, 14(3): 1223-1229. DOI:10.1364/OE.14.001223 |
| [19] |
HAXHA S, BELHADJ W, ABDELMALEK F, et al. Analysis of wavelength demultiplexer based on photonic crystals[J]. IEE Proceedings-Optoelectronics, 2005, 152(4): 193-198. DOI:10.1049/ip-opt:20050003 |
| [20] |
ZHENG G G, WANG Z S, ZHAO D L, et al. Wavelength-division-multiplexing system with photonic crystal self-collimation and co-directional coupling effect[J]. Optik, 2014, 125(11): 2638-2641. DOI:10.1016/j.ijleo.2013.11.034 |
| [21] |
HUANG C H, WU J N, LEE P Y, et al. The properties and design concepts of photonic directional couplers made of photonic crystal slabs[J]. Journal of Physics D: Applied Physics, 2010, 43(46): 465103. DOI:10.1088/0022-3727/43/46/465103 |
| [22] |
QUAN Y J, HAN P D, LU X D, et al. Optical interleaver based on directional coupler in a 2D photonic crystal slab with triangular lattice of air holes[J]. Optics Communications, 2007, 270(2): 203-206. DOI:10.1016/j.optcom.2006.09.005 |
| [23] |
QU Y, REN H L, JIANG C. A novel design of 2-D photonic crystal directional coupler with high extinction ratio and short coupling length[J]. IEEE Journal of Quantum Electronics, 2007, 43(11): 974-981. DOI:10.1109/JQE.2007.904458 |
| [24] |
ZIMMERMANN J, KAMP M, FORCHEL A, et al. Photonic crystal waveguide directional couplers as wavelength selective optical filters[J]. Optics Communications, 2004, 230(4-6): 387-392. DOI:10.1016/j.optcom.2003.11.026 |
| [25] |
BAO H L, NIELSEN K, RASMUSSEN H K, et al. Design and optimization of mechanically down-doped terahertz fiber directional couplers[J]. Optics Express, 2014, 22(8): 9486-9497. DOI:10.1364/OE.22.009486 |
| [26] |
KOSHIBA M. Wavelength division multiplexing and demultiplexing with photonic crystal waveguide couplers[J]. Journal of Lightwave Technology, 2001, 19(12): 1970-1975. DOI:10.1109/50.971693 |
| [27] |
STRASSER P, FLÜCKIGER R, WÜEST R, et al. InP-based compact photonic crystal directional coupler with large operation range[J]. Optics Express, 2007, 15(13): 8472-8478. DOI:10.1364/OE.15.008472 |
| [28] |
MOGHADDAM M K, ATTARI A R, MIRSALEHI M M. Improved photonic crystal directional coupler with short length[J]. Photonics and Nanostructures-Fundamentals and Applications, 2010, 8(1): 47-53. |
| [29] |
MARTINEZ A, CUESTA F, MARTI J. Ultra-short 2D photonic crystal directional couplers[J]. IEEE Photonics Technology Letters, 2003, 15(5): 694-696. DOI:10.1109/LPT.2003.810258 |
| [30] |
FENG Z F, FU T T, YAN B, et al. Investigation for ultra-shorten coupling length in woodpile structure[J]. Photonics and Nanostructures-Fundamentals and Applications, 2017, 23(11): 7-11. |








